Predicting the Average Composition of an AlFeNiTiVZr-Cr Alloy with Machine Learning and X-ray Spectroscopy

Abstract

A multi-principal element alloy (MPEA) is a type of metallic alloy that is composed of multiple metallic elements, with each element making up a significant portion of the alloy. In this study, the initial atomic percentage of elements in an (AlFeNiTiVZr)1-xCrx MPEA alloy as a function of the position on the surface was investigated using machine learning algorithms. Given the absence of a linear relationship between the atomic percentage of elements and their location on the surface, it is not possible to discern any clear association from the dataset. To overcome this non-linear relationship, the prediction of the atomic percentage of elements was accomplished using both decision tree (DT) and random forest (RF) regression models. The models were compared, and the results were found to be consistent with the experimental findings (a coefficient of determination R² of 0.98 is obtained with the DT algorithm and 0.99 with the RF one). This research demonstrates the potential of machine learning algorithms in the analysis of wavelength-dispersive X-ray spectroscopy (WDS) datasets.

1. Introduction

A multi-principal element alloy (MPEA) is a metallic alloy that is known to contain significant proportions of several metallic elements (at least two) [1,2,3]. Among the various elements, there is no linear relationship that leads to variations in the atomic percentage as a function of the surface position. To overcome this nonlinearity, machine learning can be used to overcome the challenge of predicting the atomic percentage of elements. The term “machine learning” (ML) refers to a group of techniques that enable computers to “learn” the correlation between numerical data representations and output values [4]. ML algorithms have the ability to achieve greater accuracy in predictions compared to conventional methods, and can analyze large datasets quickly, which saves time and resources. Additionally, they can recognize patterns and trends in data that may not be immediately apparent through conventional analyses. ML models can also adapt to changes in data over time, making them especially valuable for applications that require real-time analysis [5]. Numerous applications have made use of machine learning techniques such as the support vector machine (SVM), maximal entropy, and artificial neural network (ANN) [6]. Liu et al. established machine learning models to predict the Vickers hardness (Hv) of amorphous alloys [7]. Pan et al. developed an integrated composition–process–property design system for Cu-Cr-Ni-Co-Si-Zr alloys using machine learning and were able to recognize the relationship between Cu-Ni-Co-Si and Cu-Cr-Zr alloys [8]. Gao et al. used a machine learning model to predict the elastic properties and Poisson’s ratio of non-equiatomic high-entropy alloys (HEA) [9]. Islam et al. developed a neural network (NN) in a machine learning framework to detect the underlying data pattern using an experimental dataset and categorize the associated phase selection in MPEAs, providing insights on developing MPEAs [10]. Wu et al. used eight phase-related variables as input and analyzed six machine learning (ML) classification methods to identify MPEAs with outstanding strength–ductility [11]. Roy et al. presented an ML approach to down-select corrosion-resistant alloys focusing on MPEAs [12]. Manzoor et al. described a method that uses ML to predict the point defect energies in MPEAs using a database of the binary alloys that make up those alloys [13]. Sai et al. used four different machine learning (ML) techniques to estimate the room temperature fatigue lifetimes of single-phase Co_aCr_bFe_cMn_dNi_e and multi-phase Al_fCo_gCr_hFe_iMn_jNi_k systems [14]. These algorithms were RF, SVM, gradient boosting (GBOOST), and extreme gradient boosting (XGBOOST). Non-parametric models such as RF and DT have the ability to fit complex data distributions without requiring any assumptions about the underlying data. Additionally, they are capable of providing accurate predictions even when the data are noisy or contain outliers. RF and DT models are versatile enough to be used for both regression and classification problems, which makes them useful for a wide range of applications [15].

In this work, machine learning algorithms are used to study the influence of position on elements’ atomic percentage at the surface of an MPEA sample synthetized using physical vapor deposition (PVD). The process of depositing thin films through PVD methods has been widely adopted in various industries [16,17,18,19]. The atomic percentages of the constituent elements of an (AlFeNiTiVZr)1-xCrx alloy are predicted using decision tree (DT) and random forest (RF) machine learning methods for the first time.

2. Materials and Methods

This work was carried out on the basis of an experimental dataset consisting of acquisition points across a single axis of wavelength-dispersive X-ray spectroscopy (WDS) obtained from the work of Ruiz-Yi et al. [1,2]. WDS is better than energy-dispersive X-ray spectroscopy (EDS) when it comes to high-energy resolution, its detection limits, and its ability to detect elements with low atomic weights [20]. The samples were obtained by co-deposing an AlFeNiTiVZr metal alloy and a Cr target using magnetron sputtering. Magnetron sputtering has emerged as the preferred method for applying various coatings that are important in the industrial sector [21]. Further details regarding magnetron sputtering and sample preparation are presented elsewhere [2]. In this work, the use of both decision tree (DT) and random forest (RF) models is discussed. DT is a simple and interpretable machine learning algorithm that is commonly used for regression and classification tasks [22]. It is part of the supervised algorithms and can be used to predict a value from a set of parameters by modeling the relationships between the input data and target output. The interpretability of decision tree models makes them advantageous compared to other pattern recognition methods. This allows for easier identification of crucial characteristics and relationships between classes, informing future experiments and data analysis [23]. RF, which is a collection of DTs, typically produces better results than DT [24]. In recent years, the RF classifier has become increasingly popular due to its exceptional classification accuracy and efficient processing speed. The RF classifier provides dependable classifications by combining predictions from a group of decision trees. Additionally, the RF classifier can effectively pick and rank variables that have the highest ability to differentiate between target classes [24]. Keras [25], a popular deep learning library in Python, is used together with the Scikit-learn package [26] to implement the algorithms in home-made programs. Scikit-learn is a Python library that offers a unified interface for implementing machine learning algorithms. It also includes additional functions that are crucial to the machine learning process, such as data preparation methods, data sampling techniques, evaluation metrics, and tuning/optimization search tools for improving an algorithm’s performance [27]. Keras is a high-level neural network application programming interface (API) that is open source and written in Python. It was created by François Chollet. Keras can operate with various machine learning libraries, including TensorFlow (created by Google), CNTK (created by Microsoft), and Theano (created by the University of Montreal) [28]. A forest of 50 trees is used for the RF model, with 80% of the values being used for training and 20% of the values for testing. To improve the training results, the data are rescaled to a range of [0–1]. The algorithms and equations used in this study are described elsewhere [26], and the maximum depth of a tree, minimum number of samples in a leaf node, and minimum number of samples required at a leaf node are set to “None”, 1, and 1, respectively.

3. Results and Discussions

The average composition of the considered elements and the associated position on the (AlFeNiTiVZr)1-xCrx sample were obtained from Rui-Yi et al. [1]. The ranges of attributes of the dataset are presented in

Table 1. Ranges of attributes from Ruiz-Yi et al. [1].

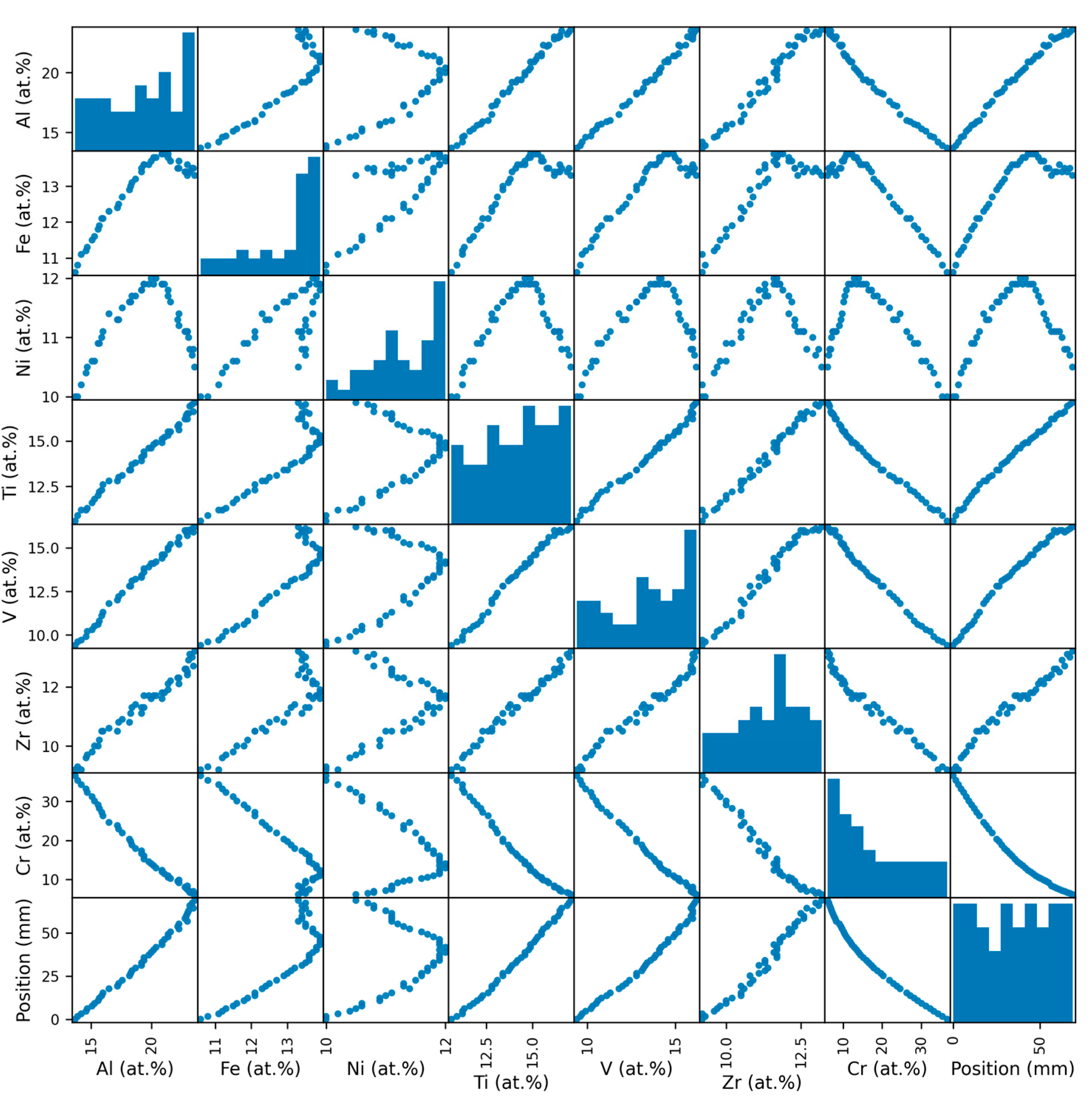
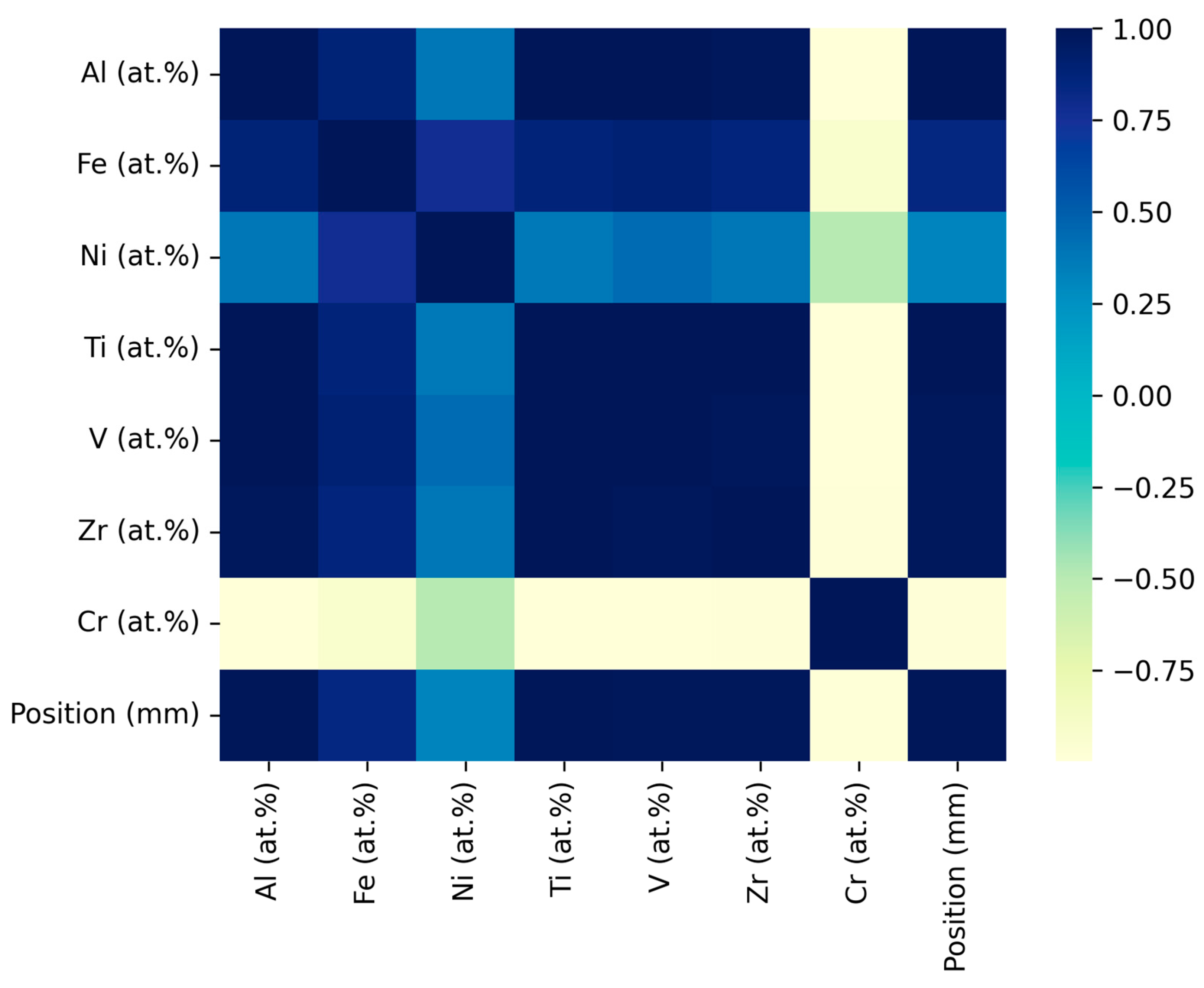
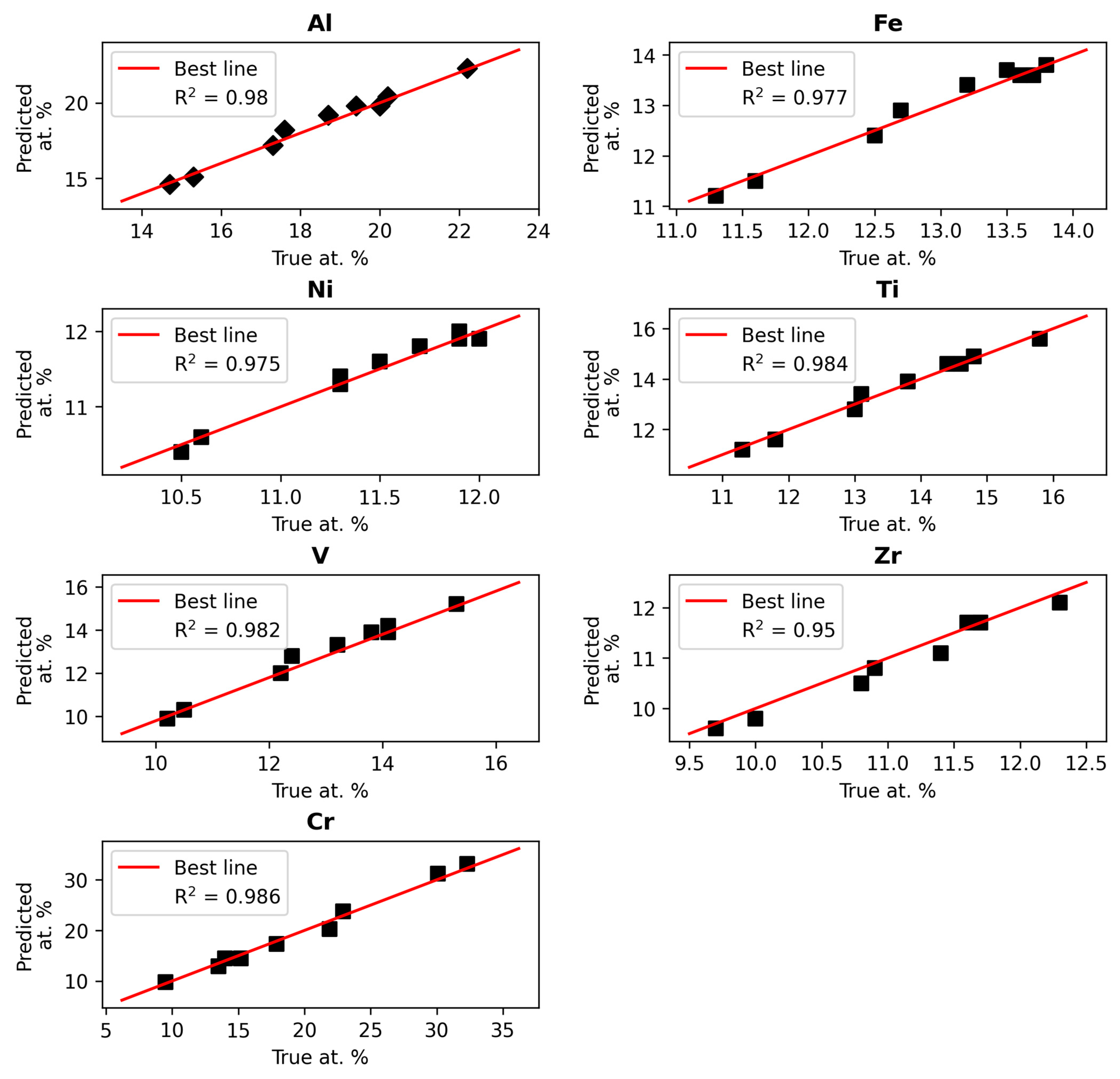
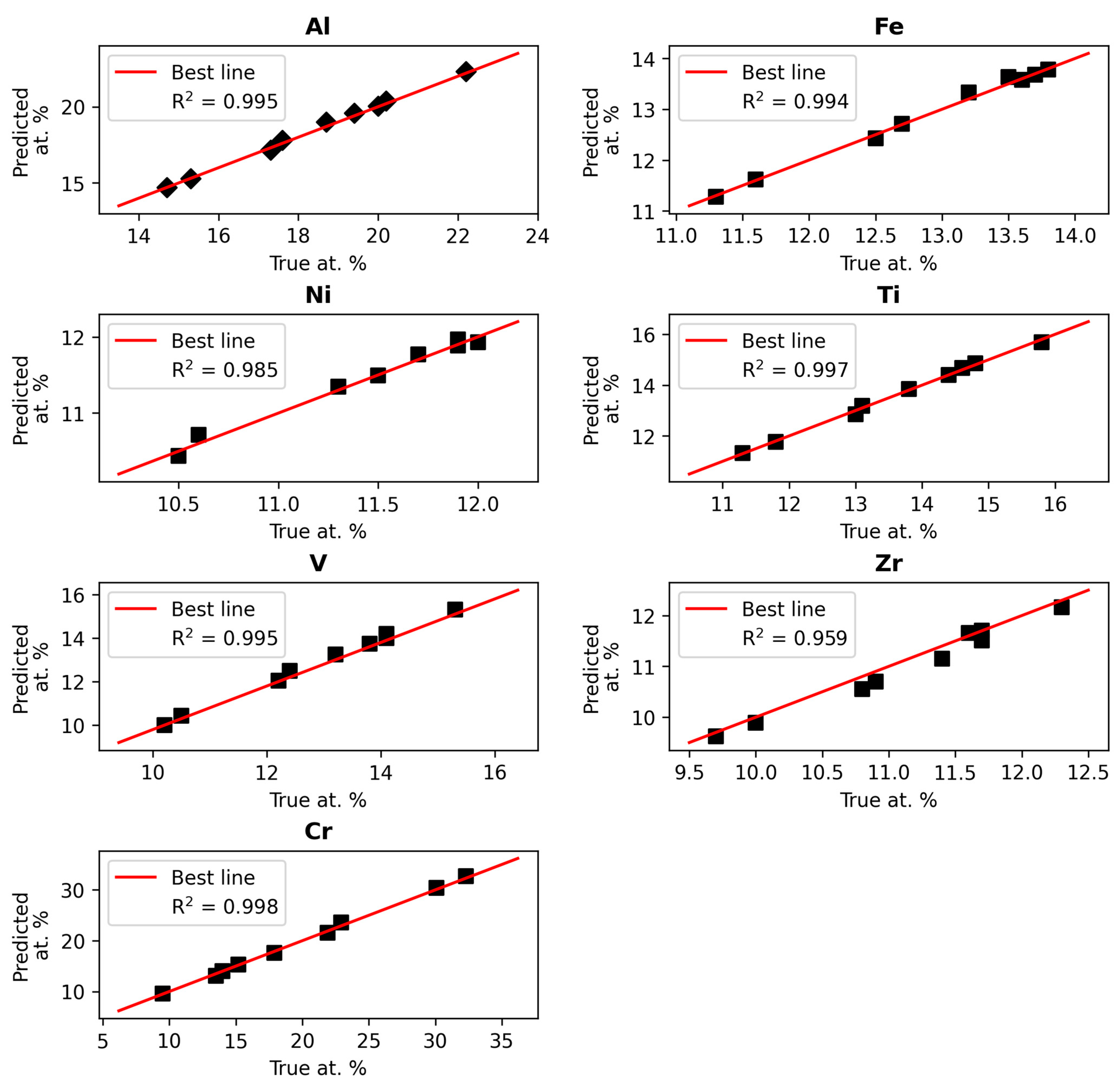
Attribute	Range
Al (at. %)	13.7–23.6
Fe (at. %)	10.6–13.9
Ni (at. %)	10–17
Ti (at. %)	10.6–17.1
V (at. %)	9.4–16.2
Zr (at. %)	9.2–13.2
Cr (at. %)	6.1–36.6
Position (mm)	0–68.7

.

Figure 1 shows a scatter matrix plot of the dataset. A scatterplot matrix is a useful tool for identifying linear correlations between multiple variables. It can be used to determine if any of the variables have similar relationships to the data. The process of creating a scatterplot matrix involves loading the data with multiple variables and visually examining the correlations between them. In this work, there is no strong relationship between all the variables (average atomic composition of Al, Fe, Ni, Ti, V, Zr, and Cr) and their position on the sample. The composition of Al, Ti, V, and Zr increases along the sample, while Cr decreases. Fe and Ni show different patterns; the amount of Fe increases and stabilizes, while the amount of Ni increases and decreases. Such differences might be related to the conditions of the deposition process, the cleanliness of the substrate, and the degree of adhesion between the substrate and the deposited material or diffusion effects [29].

Thus, it is challenging to predict the average amount of elements based on the position along the sample with variables that are not linearly dependent.

For the DT and RF models, the average composition of the elements of an (AlFeNiTiVZr)1-xCrx alloy is used as input values, while the corresponding position on the sample serves as the output. Distribution histograms of the attributes are presented in Figure 2. No Gaussian distributions of both the variables and the output are highlighted.

Figure 3 shows a correlation matrix map of the Pearson correlation coefficients [30], which determines the linear link between variables to evaluate the correlation between the features [11]. A correlation matrix is a type of matrix in numerical linear algebra that has the property of being symmetrical and positive semidefinite with diagonal entries equal to 1. This type of matrix is used in areas such as the preconditioning of linear systems and the evaluation of errors in methods for solving symmetric eigenvalue problems [31].

The related Pearson correlation coefficient with two variables X and Y is defined as follows:

$$\rho \left(X, Y\right)=\frac{cov\left(X, Y\right)}{{\sigma }_X{\sigma }_Y}$$

(1)

where the standard deviations of X and Y are represented by ${\sigma }_X$ and ${\sigma }_Y$, and $cov\left(X, Y\right)$ is the value of covariance [32]. A positive correlation is shown by numbers that are near to 1, while a negative correlation is indicated by values that are close to −1. There is no link between intermediates with values of 0. As seen in Figure 3, there is a positive correlation between most of the elements and the position, but this is not the case for the Cr. This result is expected, as the Cr is the only element whose amount only decreases with the sample position, as highlighted by Figure 1.

The two models were compared using a statistical measure. R-squared or coefficient of determination (R²) was used to assess the efficacy of the machine learning models [33]. Chicco et al. suggest that R-squared is the most informative measurement in many cases compared to other statistics such as symmetric mean absolute percentage error (SMAPE), mean absolute error (MAE) and its percentage variant (MAPE), mean square error (MSE), and the root mean square error (RMSE). It is recommended to use R-squared as the standard measure for evaluating regression analyses across various scientific fields [33].

Figure 4 and Figure 5 display the predicted values of atomic percentage of each element as a function of the true values for the two models (respectively DT and RF) concerning the test dataset. In both cases, the coefficients of determination are very high. The minimum R-squared value is 0.95 and 0.96 (respectively considering the DT and RF models) for the vanadium, and the maximum is 0.99 for the chromium. Both the DT and RF models can effectively predict the atomic percentage of elements, regardless of the position along the line, and could be considered to improve a sputter model.

Machine learning is a very pertinent method that should be considered to predict output value from several input variables that are not linearly dependent, and should be considered in multiple cases of alloy research, for example, in the case of harmonic alloys [34] or transformation-induced plasticity (TRIP) and twinning-induced plasticity (TWIP) alloys [35].

4. Conclusions

Two machine learning models were established from experimental values of the composition of elements of an (AlFeNiTiVZr)1-xCrx alloy, as measured using wavelength-dispersive X-ray spectroscopy. The decision tree and random forest models lead to relevant predicted values of the average composition of the elements, whatever the position along the line of measurements. A mean coefficient of determination of 0.98 is obtained with the decision tree algorithm, and 0.99 with the random forest one. This means that machine learning models are relevant and should be considered to improve a sputter model.