Charge Critical Phenomena in a Field Heterostructure with Two-Dimensional Crystal
Abstract
1. Introduction
2. Charge Properties. The Model
3. Results and Discussion
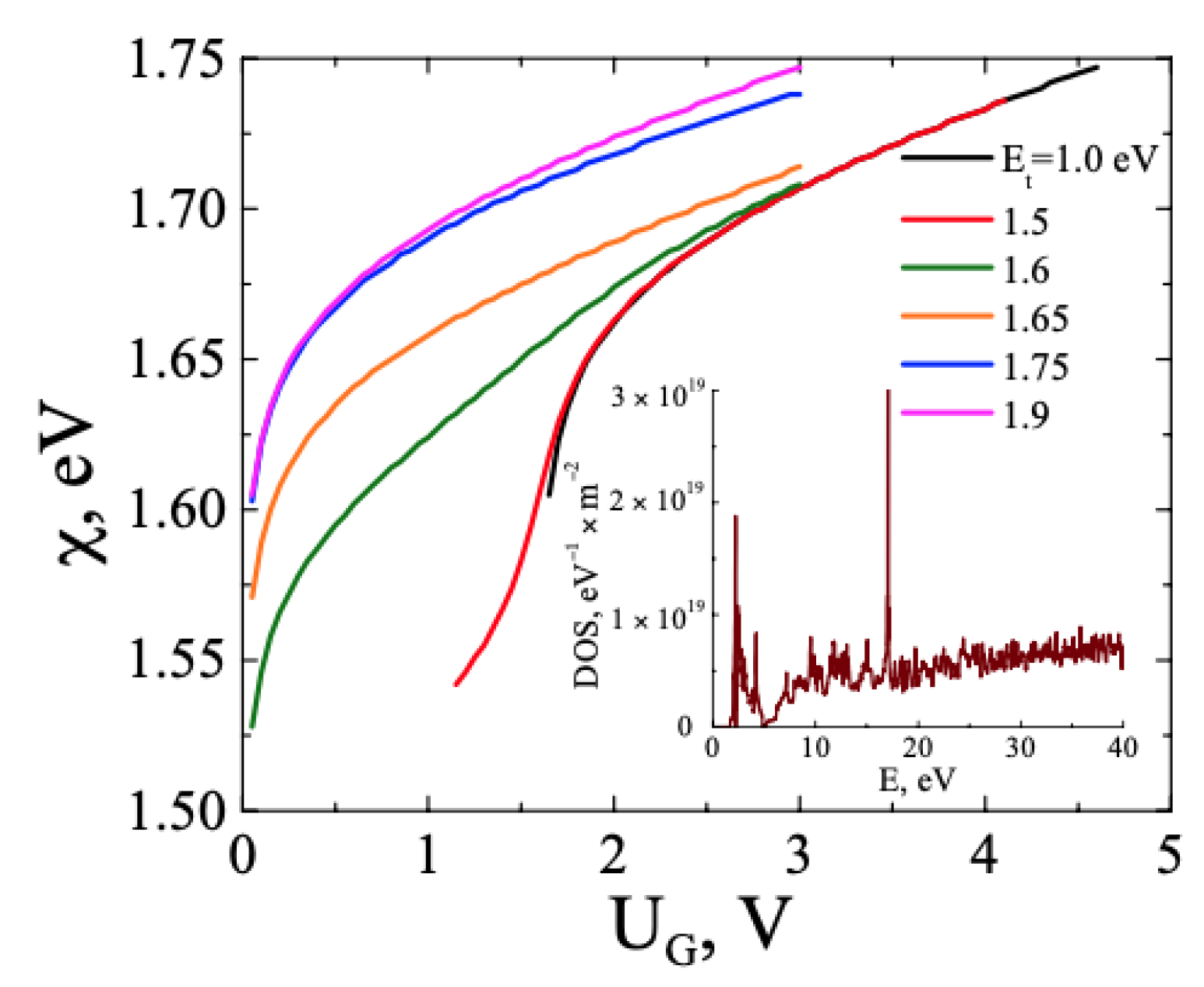
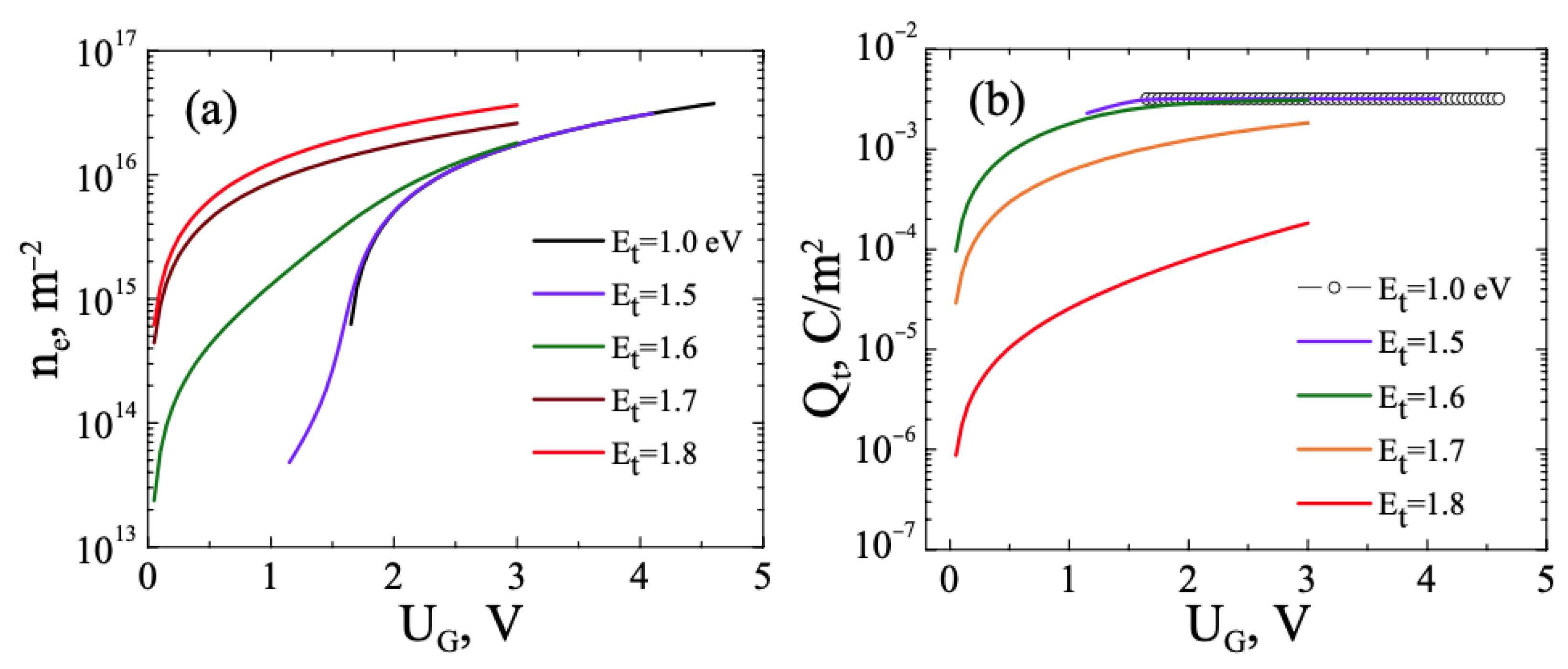
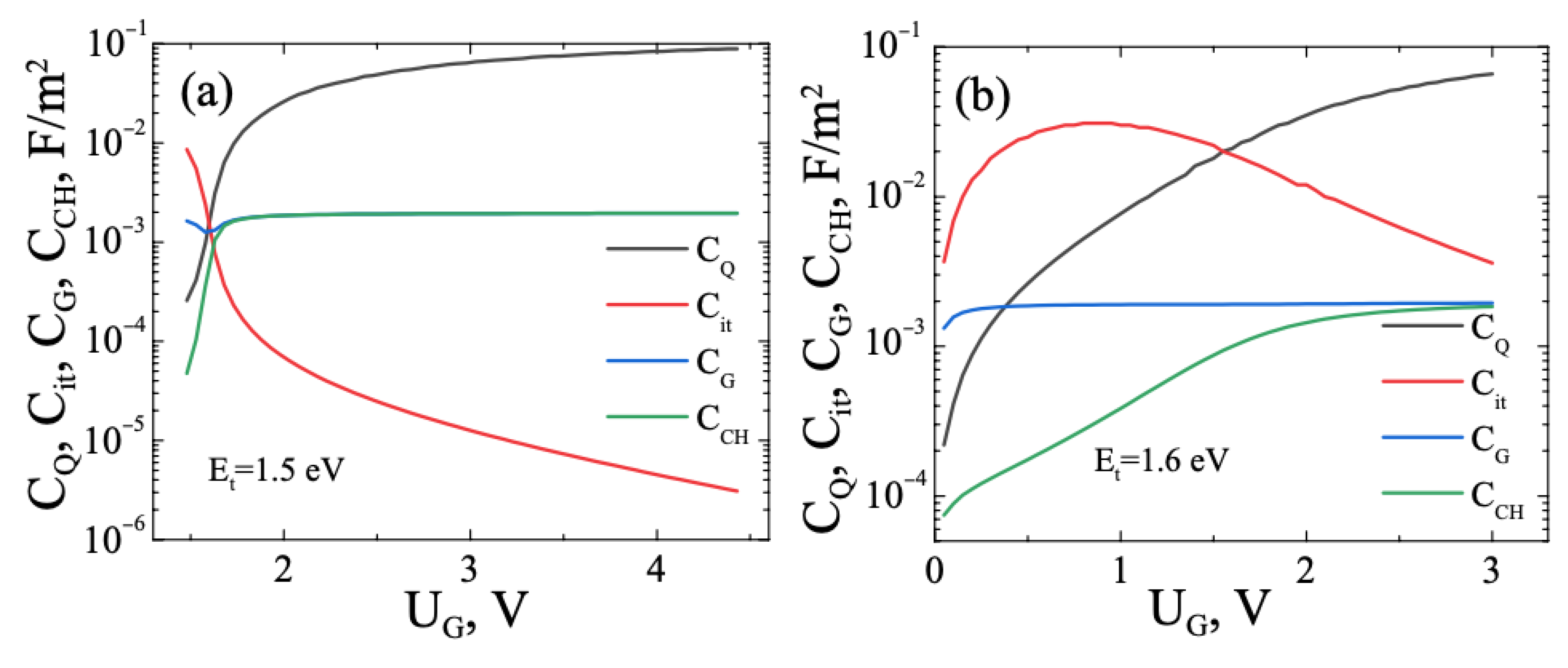
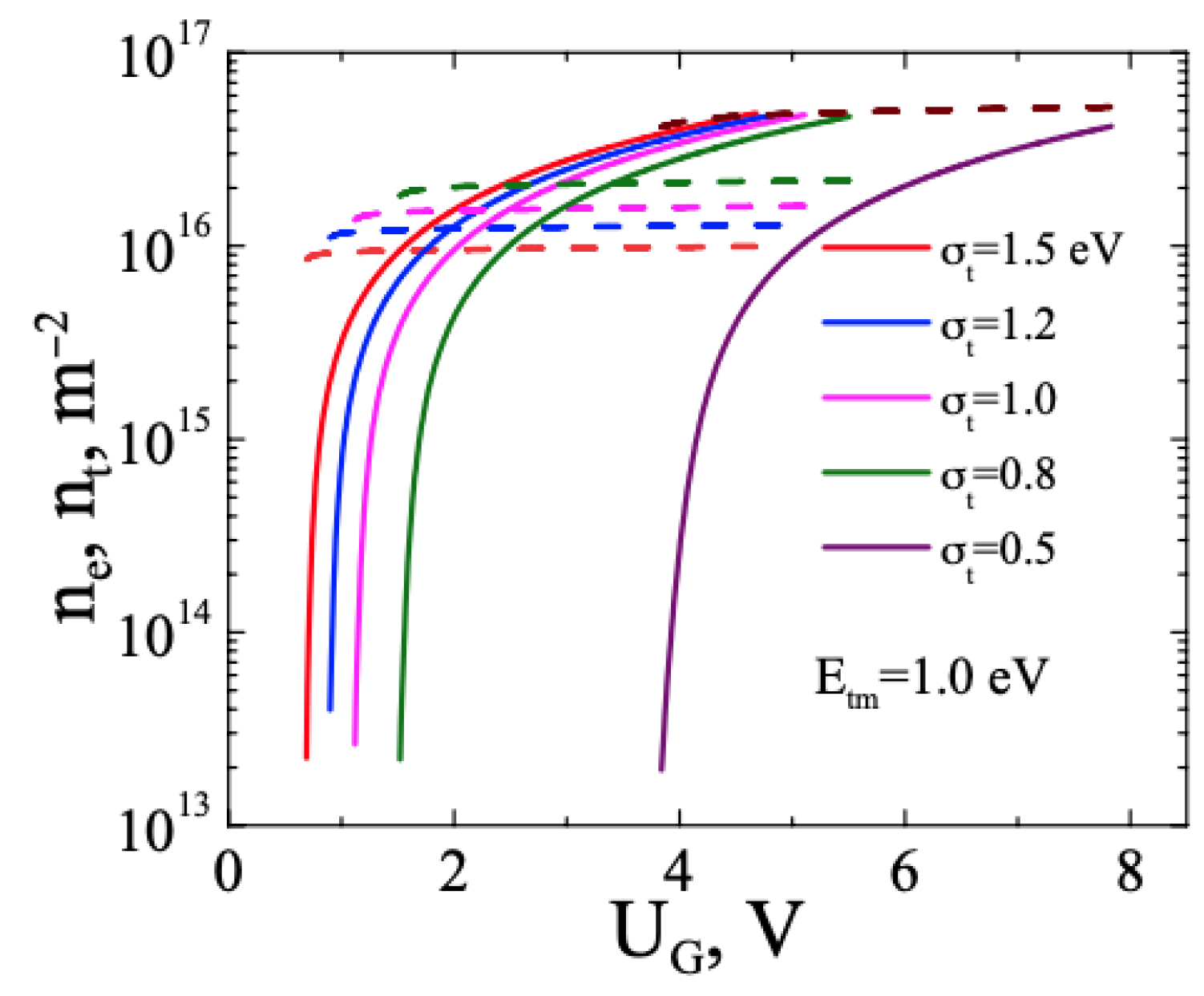
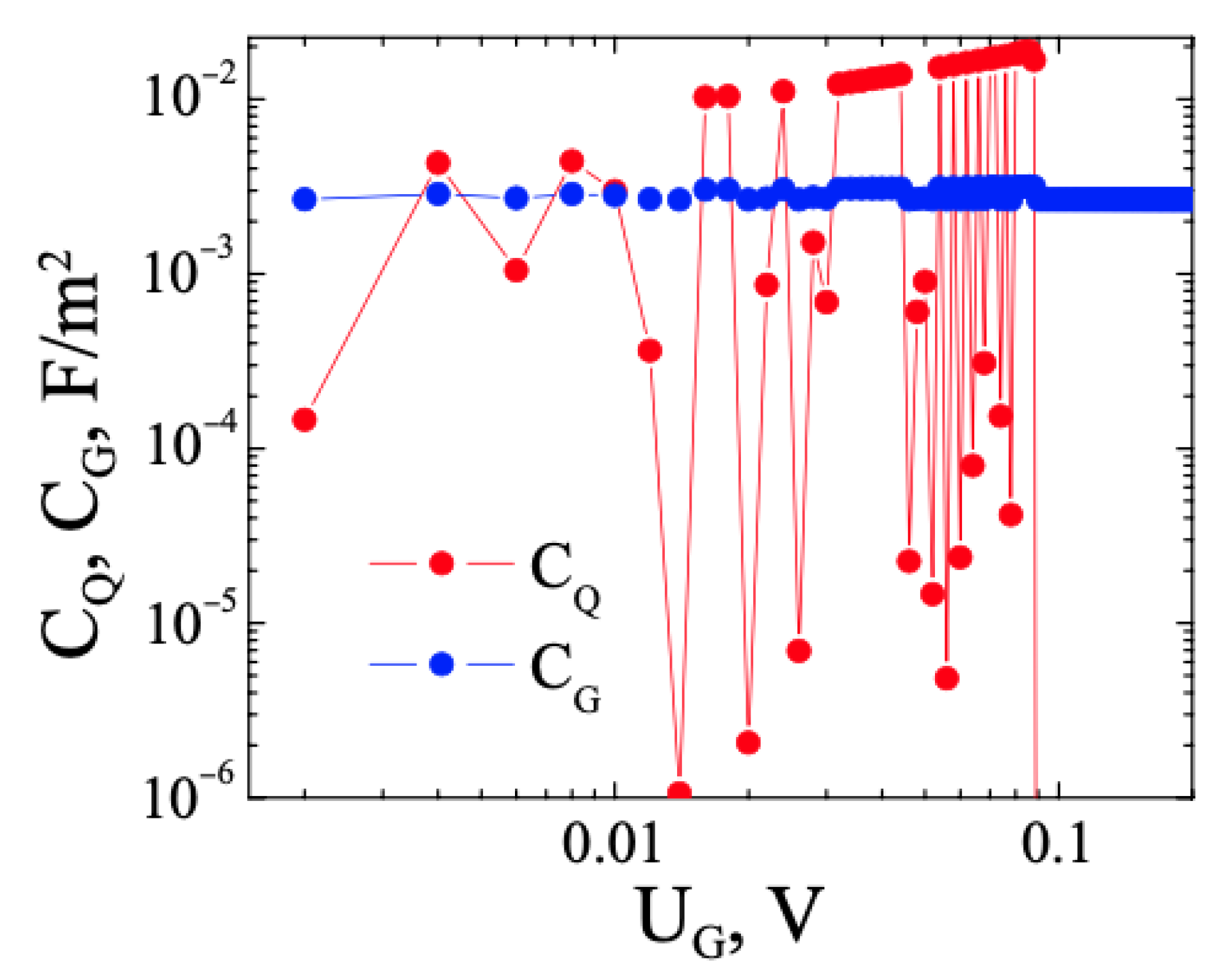
3.1. FHS MIS with TMD. Monoenergetic Traps
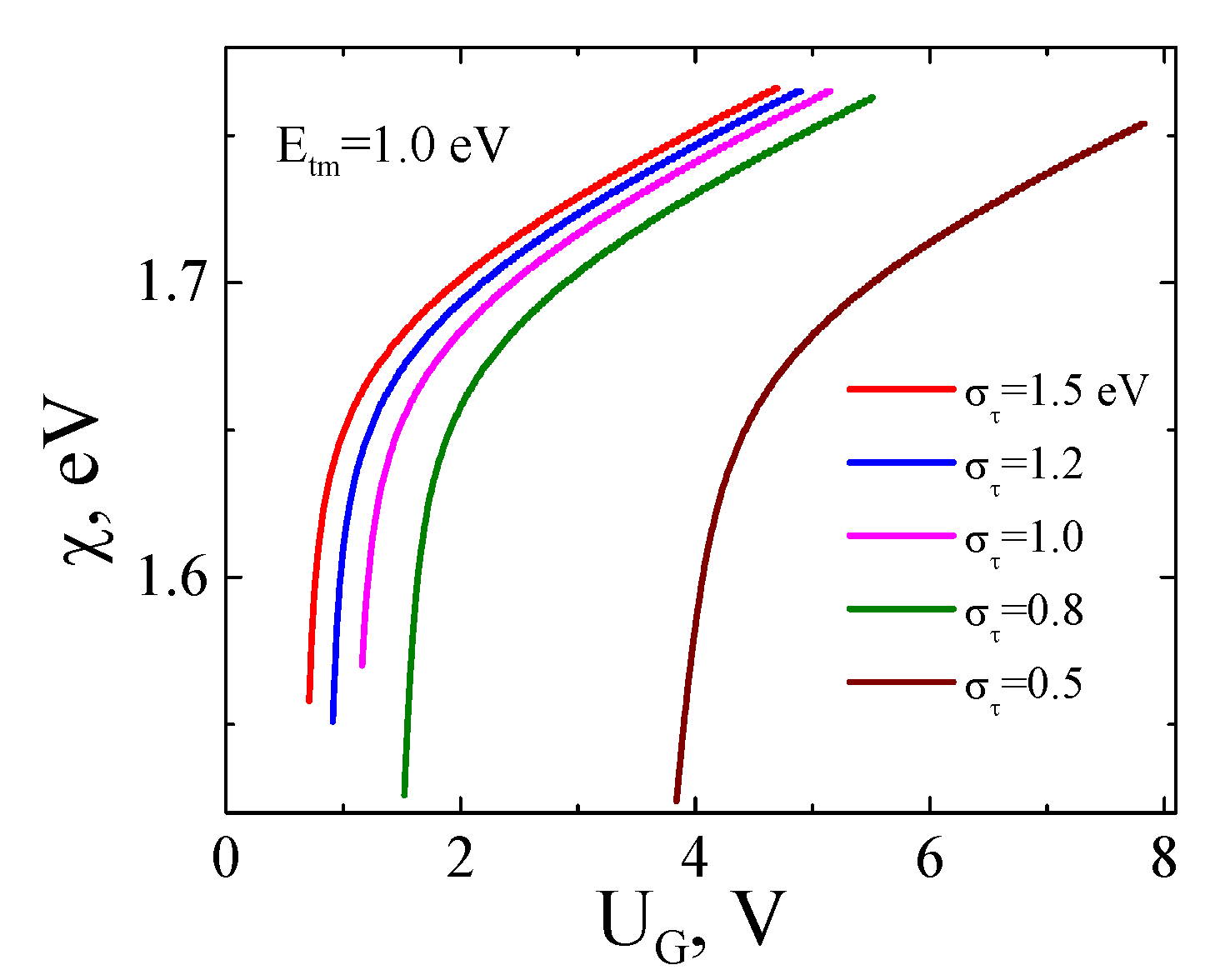
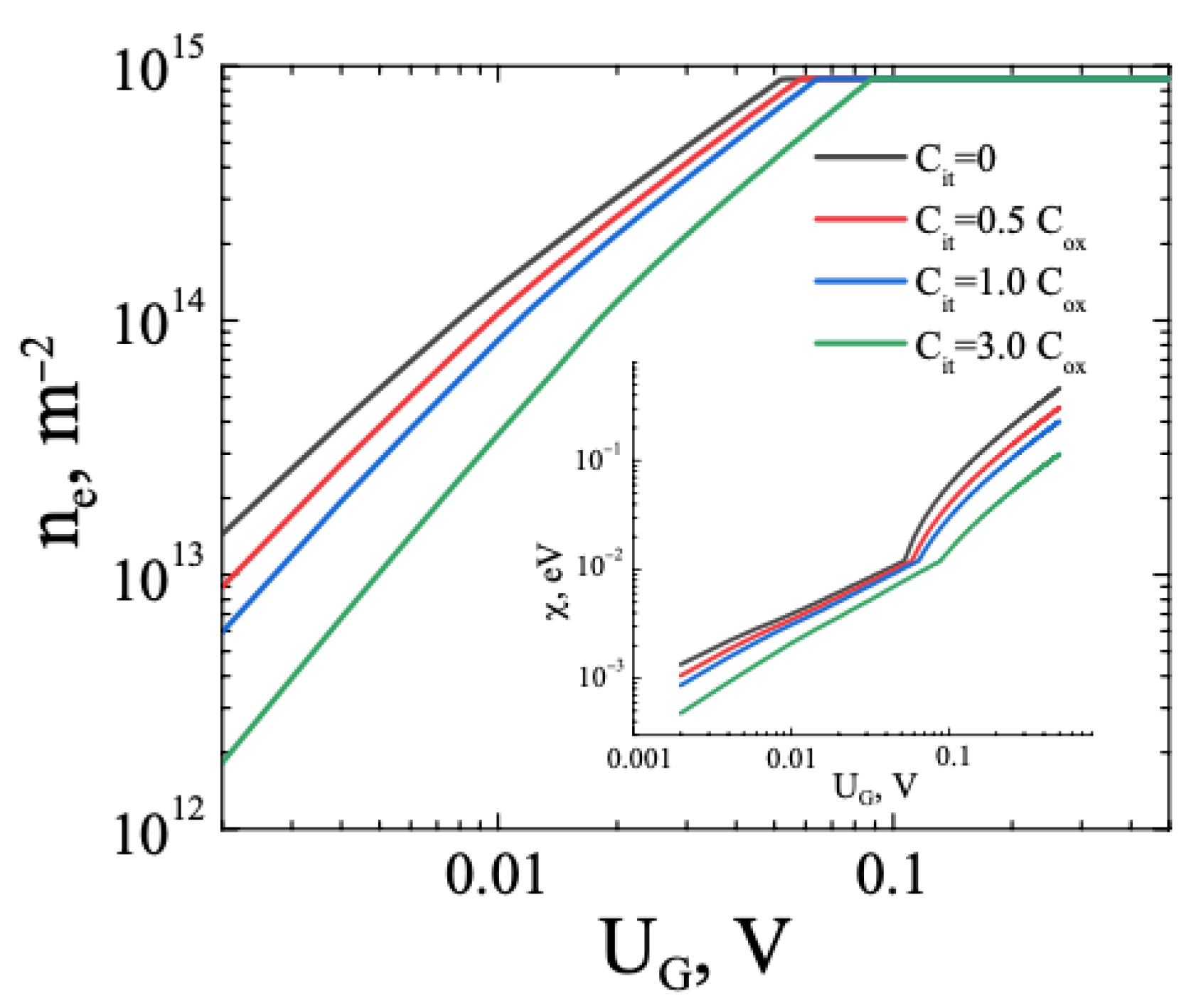
3.2. FHS MIS with TMD. Gauss Distribution for Trap Energies at the TMD–I Interface
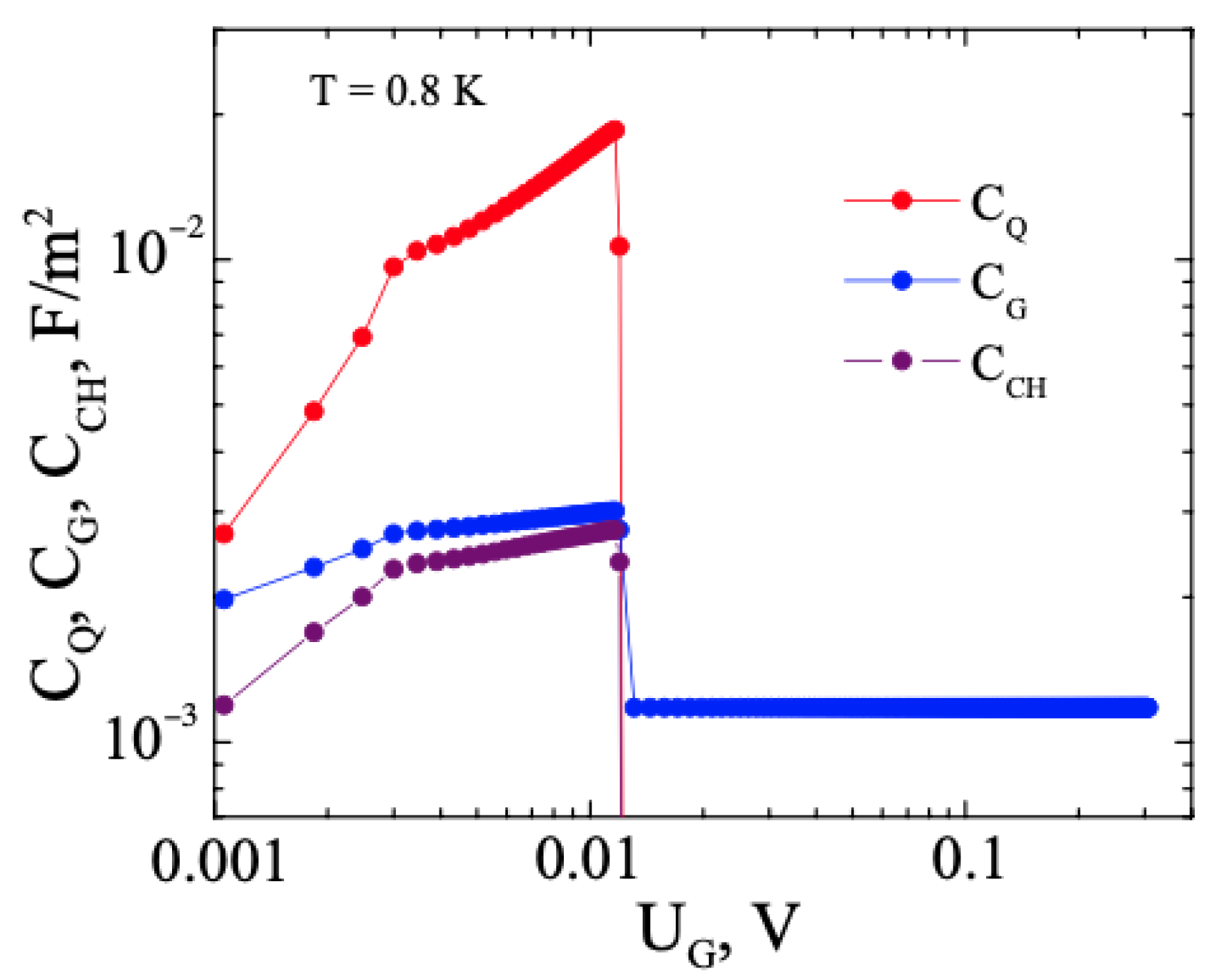
3.3. FHS MIS with WSM
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, X.; Liu, C.; Zhou, P. 2D semiconductors for specific electronic applications: From device to system. npj 2D Mater. Appl. 2022, 6, 51. [Google Scholar] [CrossRef]
- Nandan, K.; Agarwal, A.; Bhowmick, S.; Chauhan, Y.S. Two-dimensional semiconductors based field-effect transistors: Review of major milestones and challenges. Front. Electron. Sec. Nano Microelectron. 2023, 4, 127779. [Google Scholar] [CrossRef]
- Liu, C.; Chen, H.; Wang, S.; Liu, O.; Jiang, Y.-G.; Zvang, D.W.; Liu, M.; Zhou, P. Two-dimensional materials for next-generation computing technologies. Nat. Nanotechnol. 2020, 15, 545–557. [Google Scholar] [CrossRef] [PubMed]
- Wei, T.; Han, Z.; Zhong, X.; Xiao, Q.; Liu, T.; Xiang, D. Two dimensional semiconducting materials for ultimately scaled transistors. iScience 2022, 25, 105160. [Google Scholar] [CrossRef]
- Vergniory, M.G.; Elcoro, L.; Felser, C.; Regnault, N.; Bernevig, B.A.; Wang, Z. A complete catalogue of high-quality topological materials. Nature 2019, 566, 480–485. [Google Scholar] [CrossRef] [PubMed]
- Naher, M.I.; Naqib, S.H. An ab-initio study on structural, elastic, electronic, bonding, thermal, and optical properties of topological Weyl semimetal TaX (X = P, As). Sci. Rep. 2021, 11, 5592. [Google Scholar] [CrossRef] [PubMed]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Bernevig, A.; Weng, H.; Fang, Z.; Dai, X. Recent progress in the study of topological semimetals. J. Phys. Soc. Jpn. 2018, 87, 041001. [Google Scholar] [CrossRef]
- Lv, B.Q.; Qian, T.; Ding, H. Experimental perspective on three-dimensional topological semimetals. Rev. Mod. Phys. 2021, 93, 025002. [Google Scholar] [CrossRef]
- Krivosheeva, A.V.; Shaposhnikov, V.L.; Borisenko, V.E.; Lazzari, J.-L. Heterostructures of two-dimensional transition metal dichalcogenides: Formation, ab initio modelling and possible applications. Mater. Today Proc. 2022, 54 Pt 1, 73–79. [Google Scholar] [CrossRef]
- Yang, M.-X.; Luo, W.; Chen, W. Quantum transport in topological nodal-line semimetals. Adv. Phys. X 2022, 7, 2065216. [Google Scholar] [CrossRef]
- Burkov, A.A.; Hook, M.D.; Balents, L. Topological nodal semimetals. Phys. Rev. B 2011, 84, 235126. [Google Scholar] [CrossRef]
- Bi, R.; Yan, Z.; Lu, L.; Wang, Z. Nodal-knot semimetals. Phys. Rev. B 2017, 96, 201305. [Google Scholar] [CrossRef]
- Han, W.; Otani, Y.; Maekawa, S. Quantum materials for spin and charge conversion. npj Quant Mater. 2018, 3, 27. [Google Scholar] [CrossRef]
- Zhang, S.S.L.; Burkov, A.A.; Martin, I.; Heinonen, O.G. Spin-to-Charge Conversion in Magnetic Weyl Semimetals. Phys. Rev. Lett. 2019, 123, 187201. [Google Scholar] [CrossRef] [PubMed]
- Makovskaya, T.I.; Danilyuk, A.L.; Krivosheeva, A.V.; Shaposhnikov, V.L.; Borisenko, V.E. Charge properties of the MOS transistor structure with the channel made from a two–dimensional crystal. Russ. Microelectron. 2020, 49, 507–515. [Google Scholar] [CrossRef]
- Kaushik, N.; Mackenzie, D.M.A.; Thakar, K.; Goyal, N.; Mukherjee, B.; Boggild, P.; Petersen, D.H.; Lodha, S. Reversible hysteresis inversion in MoS2 field effect transistors. npj 2D Mater. Appl. 2017, 1, 34. [Google Scholar] [CrossRef]
- Late, D.J.; Liu, B.; Matte, H.S.S.R.; Dravid, V.P.; Rao, C.N. Hysteresis in single-layer MoS2 field effect transistors. ACS Nano, 2012; 6, 5635–5641. [Google Scholar] [CrossRef]
- Shu, J.P.; Wu, G.; Guo, Y.; Liu, B.; Wei, X.; Chen, Q. The intrinsic origin of hysteresis in MoS2 field effect transistors. Nanoscale 2016, 8, 3049–3056. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-C.; Dumcenco, D.O.; Huang, Y.-S.; Suenaga, K. Atomic mechanism of the semiconducting-to-metallic phase transition in single–layered MoS2. Nat. Nanotechnol. 2014, 9, 391–396. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Sebastian, A.; Pop, E.; McClellan, C.J.; Franklin, A.D.; Grasser, T.; Knobloch, T.; Illarionov, Y.; Penumatcha, A.V.; Appenzeller, J.Z.; et al. Transistors based on two–dimensional materials for future integrated circuits. Nat. Electron. 2021, 4, 786–799. [Google Scholar] [CrossRef]
- Jiménez, D. Drift-diffusion model for single layer transition metal dichalcogenide field-effect transistors. Appl. Phys. Lett. 2012, 101, 243501. [Google Scholar] [CrossRef]
- Cao, W.; Kang, J.; Liu, W.; Banerjee, K. A Compact Current-Voltage Model for 2D Semiconductor Based Field-Effect Transistors Considering Interface Traps, Mobility Degradation, and Inefficient Doping Effect. IEEE Trans. Electron Devices 2014, 61, 4282–4290. [Google Scholar] [CrossRef]
- Martino, E.; Crassee, I.; Eguchi, G.; Santos-Cottin, D.; Zhong, R.D.; Gu, G.D.; Berger, H.; Rukelj, Z.; Orlita, M.; Homes, C.C.; et al. Two-Dimensional Conical Dispersion in ZrTe5 Evidenced by Optical Spectroscopy. Phys. Rev. Lett. 2019, 122, 217402. [Google Scholar] [CrossRef] [PubMed]
- Rukelj, Z.; Homes, C.C.; Orlita, M.; Akrap, A. Distinguishing the gapped and Weyl semimetal scenario in ZrTe5: Insights from an effective two-band model. Phys. Rev. B 2020, 102, 125201. [Google Scholar] [CrossRef]
- McCormick, T.M.; Kimchi, I.; Trivedi, N. Minimal models for topological Weyl semimetals. Phys. Rev. B 2017, 95, 075133. [Google Scholar] [CrossRef]
- Zebrev, G.I. Graphene Field Effect Transistors: Diffusion-Drift Theory. In Physics and Applications of Graphene—Theory; Mikhailov, S., Ed.; IntechOpen, Rijeka, Croatia, 2011; Chapter 23, pp. 475–498. [CrossRef]
- Marin, E.G.; Bader, S.J.; Jena, D. A New Holistic Model of 2-D Semiconductor FETs. IEEE Trans. Electron Devices 2018, 65, 1239–1245. [Google Scholar] [CrossRef]
- Najam, F.; Tan, M.L.P.; Ismail, R.; Yu, Y.S. Two-dimensional (2D) transition metal dichalcogenide semiconductor field-effect transistors: The interface trap density extraction and compact model. Semicond. Sci. Technol. 2015, 30, 075010. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; 826p. [Google Scholar]
- Kao, K.-C.; Hwang, W. Electrical Transport in Solids with Particular Reference to Organic Semiconductors; Pergamon Press: Oxford, UK, 1981; 663p. [Google Scholar]
- Luryi, S. Quantum Capacitance Devices. Appl. Phys. Lett. 1988, 52, 501–503. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Anishchenko, V.S.; Neiman, A.B.; Moss, F.; Shimansky-Geier, L. Stochastic resonance: Noise-enhanced order. Physics-Uspekhi 1999, 42, 7–36. [Google Scholar] [CrossRef]
- Liang, T.; Lin, J.; Gibson, Q.; Kushwaha, S.; Liu, M.; Wang, W.; Xiong, H.; Sobota, J.A.; Hashimoto, M.; Kirchmann, P.S.; et al. Anomalous Hall effect in ZrTe5. Nat. Phys. 2018, 14, 451–455. [Google Scholar] [CrossRef]
- Zheng, H.; Hasan, M.Z. Quasiparticle interference on type-I and type-II Weyl semimetal surfaces: A review. Adv. Phys. X 2018, 3, 1466661. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, S.-C.; Ali, M.N.; Felser, C.; Yan, B. Prediction of Weyl semimetal in orthorhombic MoTe2. Phys. Rev. B 2015, 92, 161107. [Google Scholar] [CrossRef]
- Takiguchi, K.; Wakabayashi, Y.K.; Irie, H.; Krockenberger, Y.; Otsuka, T.; Sawada, H.; Nikolaev, S.A.; Das, H.; Tanaka, M.; Taniyasu, Y.; et al. Quantum transport evidence of Weyl fermions in an epitaxial ferromagnetic oxide. Nat. Commun. 2020, 11, 4969. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Liu, L.; Liu, Q.; Li, L.; Shu, X.; Li, C.; Xie, Q.; Jiang, P.; Zheng, X.; Guo, R.; et al. Electric Field Control of the Magnetic Weyl Fermion in an Epitaxial SrRuO3 (111) Thin Film. Adv. Mater. 2021, 33, 2101316. [Google Scholar] [CrossRef] [PubMed]
- Toyoda, S.; Yamada, R.; Kaneko, Y.; Tokura, Y.; Ogawa, N. Weyl fermions in SrRuO3 detected by Brillouin light scattering. Appl. Phys. Lett. 2022, 120, 242408. [Google Scholar] [CrossRef]
- Sur, S.; Nandkishore, R. Instabilities of Weyl loop semimetals. New J. Phys. 2016, 18, 115006. [Google Scholar] [CrossRef]
- Amitani, T.; Nishida, Y. Dynamical chiral magnetic current and instability in Weyl semimetals. Phys. Rev. B 2023, 107, 014302. [Google Scholar] [CrossRef]
- Yadav, N.; Deo, N. Magnetotransport in Weyl semimetal with and without disorder and the effect of tilted magnetic field. Phys. E Low-Dimens. Syst. Nanostruct. 2023, 148, 115601. [Google Scholar] [CrossRef]
- Sukhachov, P.O.; Gorbar, E.V.; Shovkovy, I.A. Entropy Wave Instability in Dirac and Weyl Semimetals. Phys. Rev. Lett. 2021, 127, 176602. [Google Scholar] [CrossRef] [PubMed]
- Xue, F.; Zhang, X.-X. Instability and topological robustness of Weyl semimetals against Coulomb interaction. Phys. Rev. B 2017, 96, 195160. [Google Scholar] [CrossRef]
- Boettcher, I. Interplay of Topology and Electron-Electron Interactions in Rarita-Schwinger-Weyl semimetals. Phys. Rev. Lett. 2020, 124, 127602. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Du, G.; Zhang, B.; Zeng, Z. Scaling behavior of hysteresis in multilayer MoS2 field effect transistors. Appl. Phys. Lett. 2014, 105, 093107. [Google Scholar]
- Park, Y.; Baac, H.W.; Heo, J.; Yoo, G. Thermally activated trap charges responsible for hysteresis in multilayer MoS2 field-effect transistors. Appl. Phys. Lett. 2016, 108, 083102. [Google Scholar] [CrossRef]
- Illarionov, Y.Y.; Rzepa, G.; Waltl, M.; Knobloch, T.; Grill, A.; Furchi, M.M.; Mueller, T.; Grasser, T. The role of charge trapping in MoS2/SiO2 and MoS2/hBN field-effect transistors. 2D Mater. 2016, 3, 035004. [Google Scholar] [CrossRef]
- Illarionov, Y.Y.; Knobloch, T.; Waltl, M.; Rzepa, G.; Pospischil, A.; Polyushkin, D.A.; Furchi, M.M.; Mueller, T.; Grasser, T. Energetic mapping of oxide traps in doublegated MoS2 field-effect transistors. 2D Mater. 2017, 4, 025108. [Google Scholar] [CrossRef]
- Knobloch, T.; Rzepa, G.; Illarionov, Y.Y.; Waltl, M.; Schanovsky, F.; Stampfer, B.; Furchi, M.; Mueller, T.; Grasser, T. A Physical Model for the Hysteresis in MoS2 Transistors. J. Electr. Dev. Soc. 2018, 6, 972–978. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danilyuk, A.L.; Podryabinkin, D.A.; Shaposhnikov, V.L.; Prischepa, S.L. Charge Critical Phenomena in a Field Heterostructure with Two-Dimensional Crystal. Solids 2024, 5, 193-207. https://doi.org/10.3390/solids5020013
Danilyuk AL, Podryabinkin DA, Shaposhnikov VL, Prischepa SL. Charge Critical Phenomena in a Field Heterostructure with Two-Dimensional Crystal. Solids. 2024; 5(2):193-207. https://doi.org/10.3390/solids5020013
Chicago/Turabian StyleDanilyuk, Alexander L., Denis A. Podryabinkin, Victor L. Shaposhnikov, and Serghej L. Prischepa. 2024. "Charge Critical Phenomena in a Field Heterostructure with Two-Dimensional Crystal" Solids 5, no. 2: 193-207. https://doi.org/10.3390/solids5020013
APA StyleDanilyuk, A. L., Podryabinkin, D. A., Shaposhnikov, V. L., & Prischepa, S. L. (2024). Charge Critical Phenomena in a Field Heterostructure with Two-Dimensional Crystal. Solids, 5(2), 193-207. https://doi.org/10.3390/solids5020013





