Compressing the Channels in the Crystal Structure of Copper Squarate Metal-Organic Framework
Abstract
1. Introduction
2. Methods
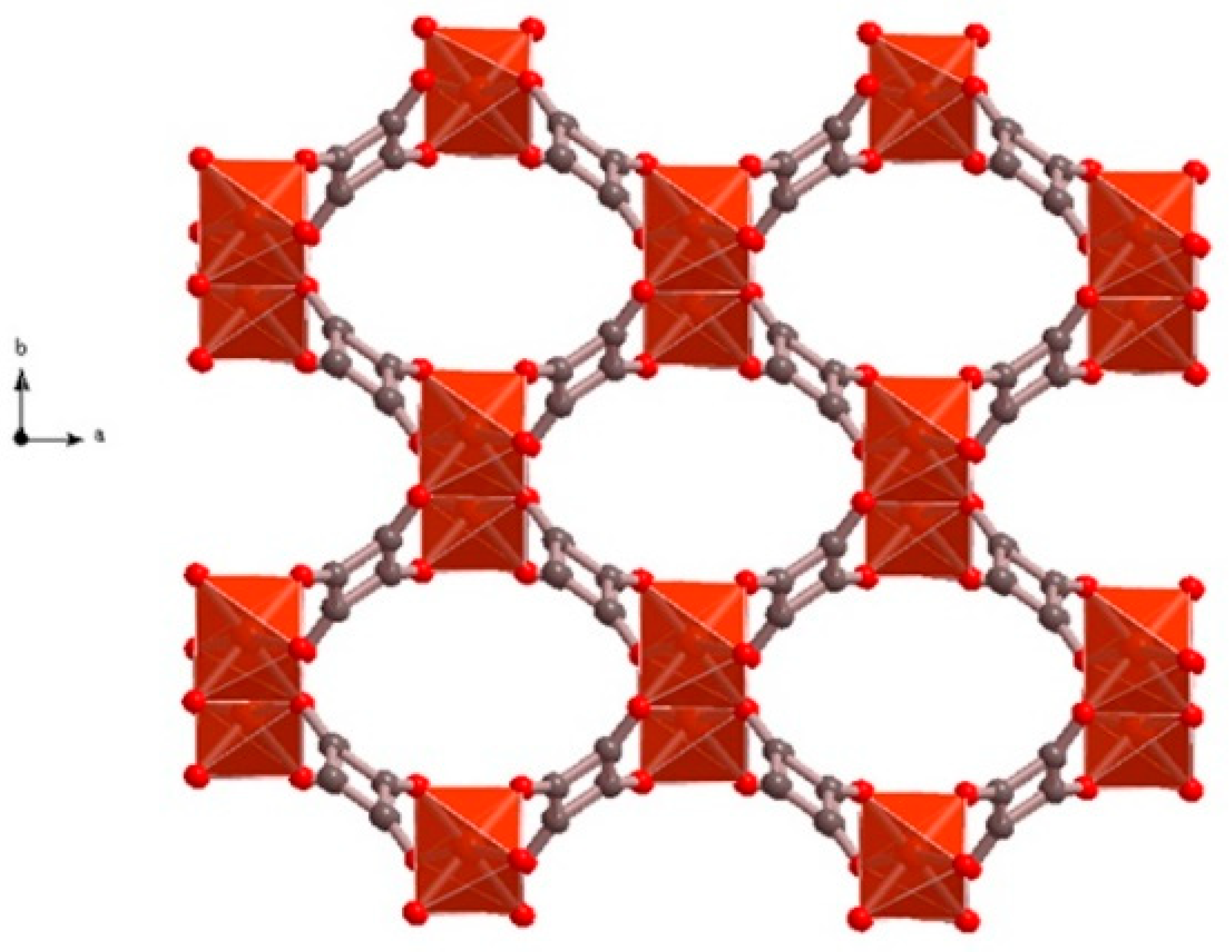
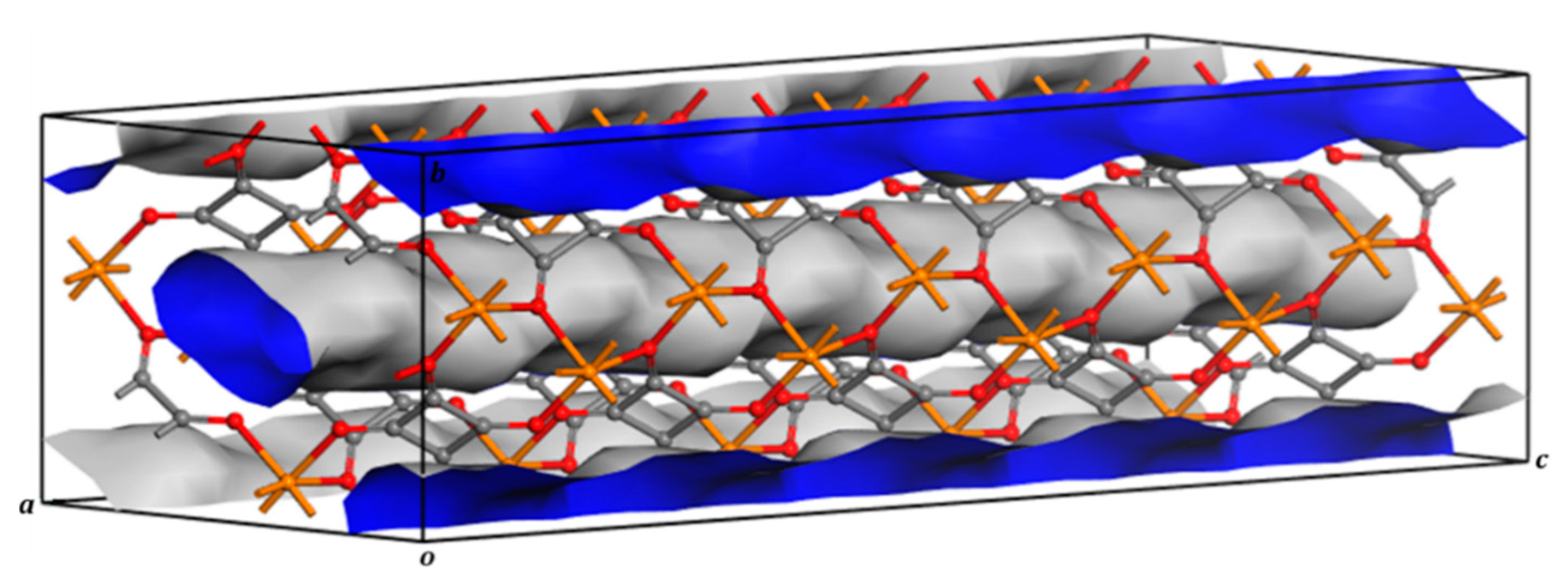
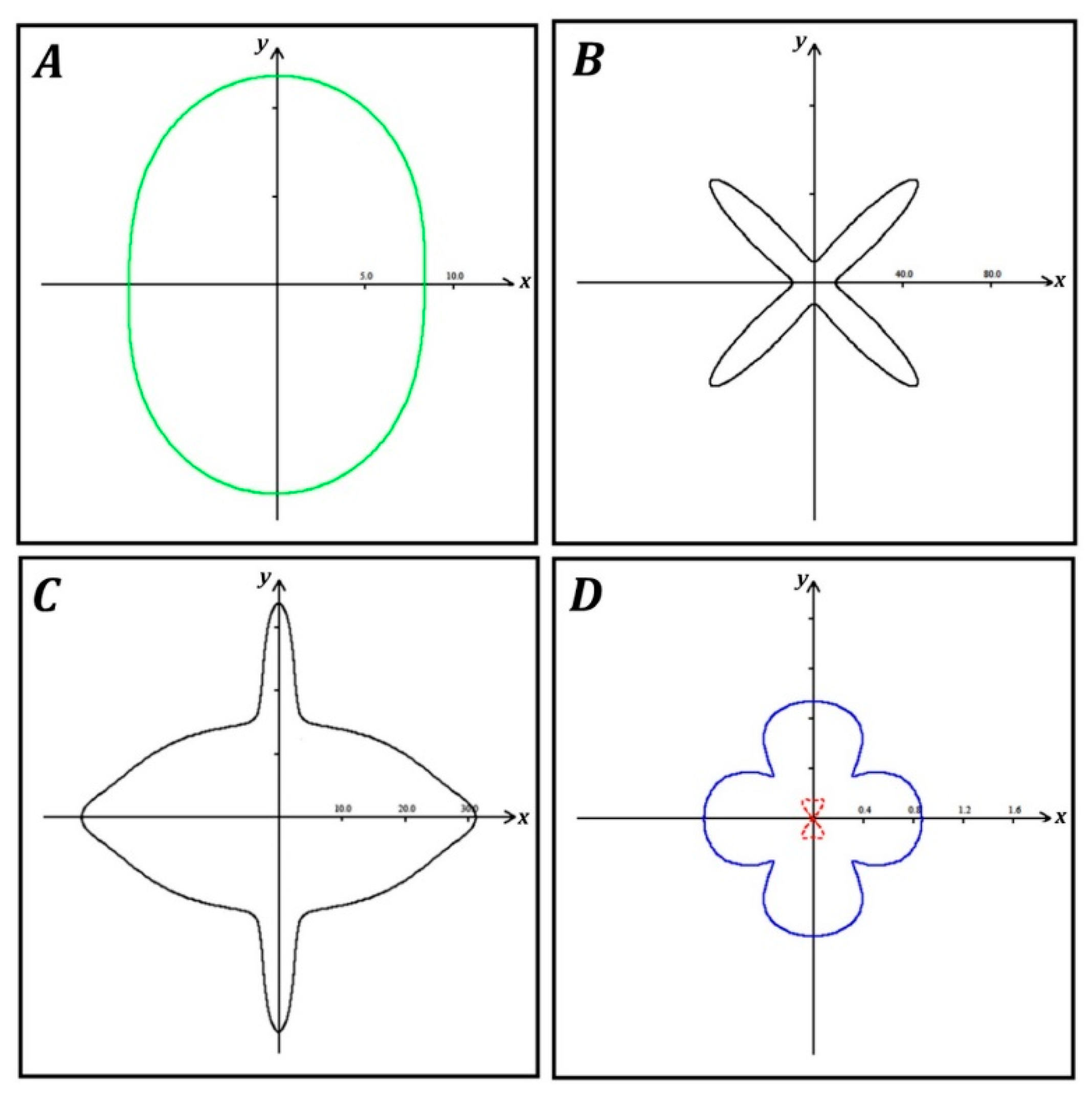
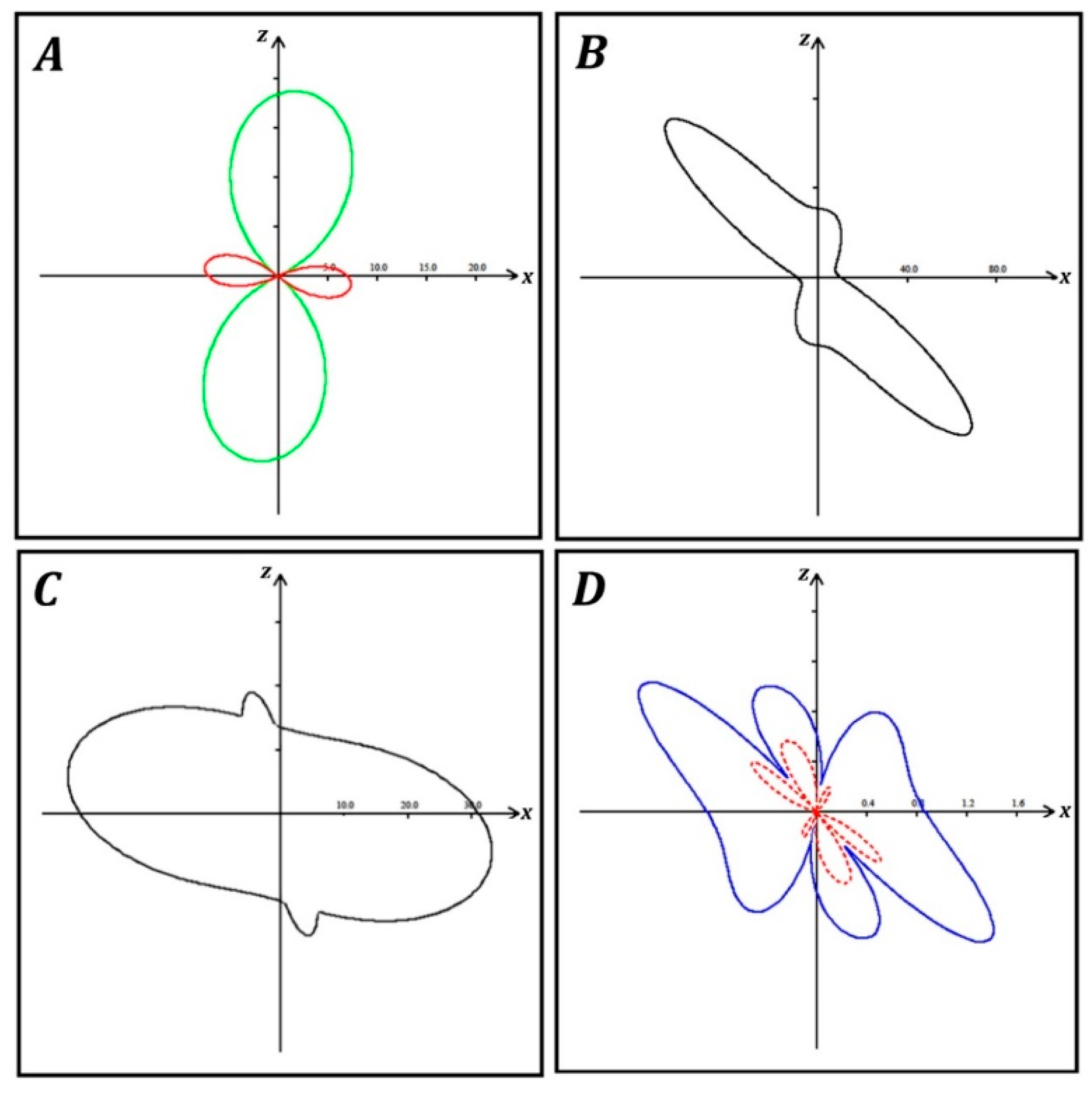
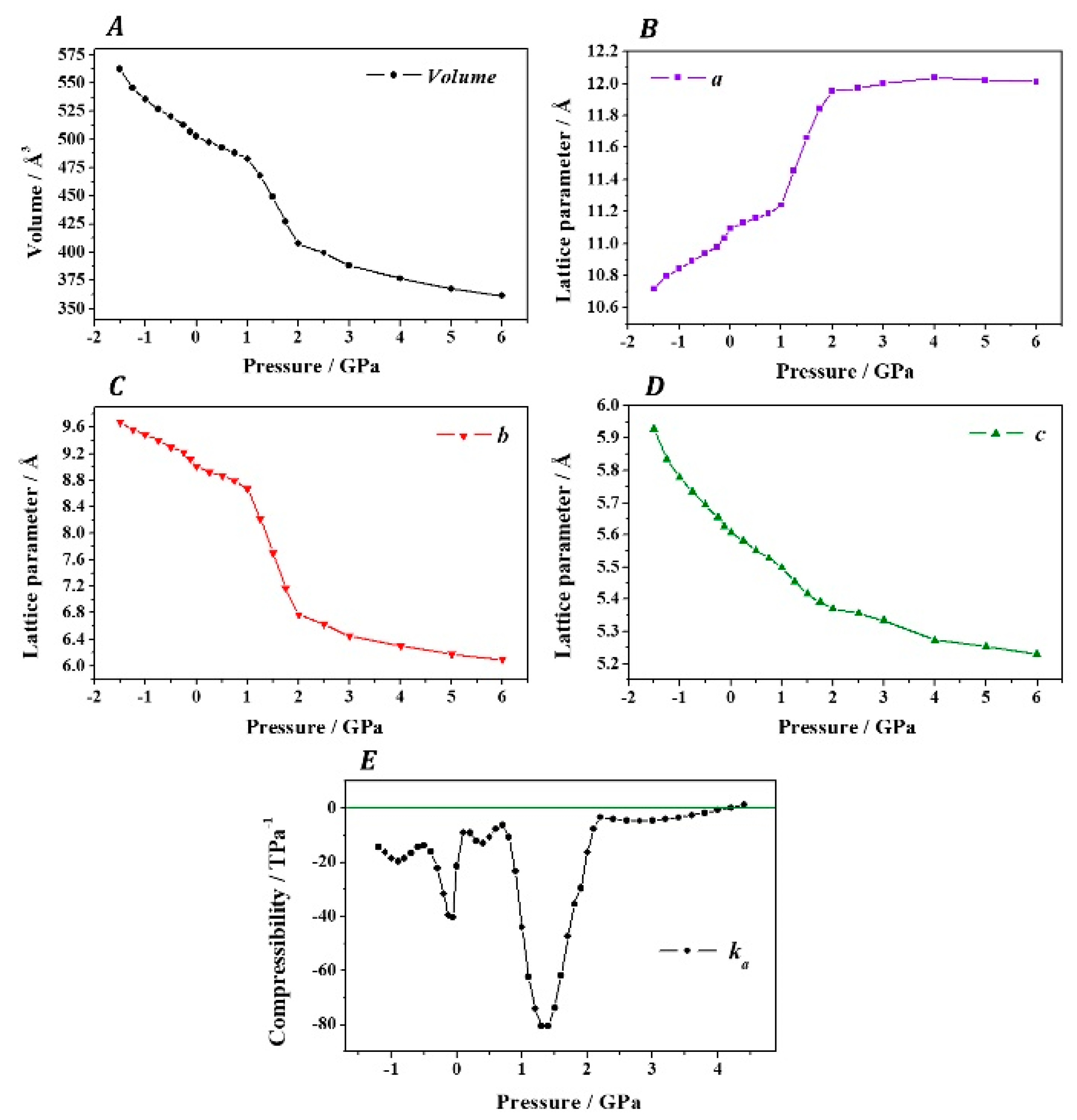
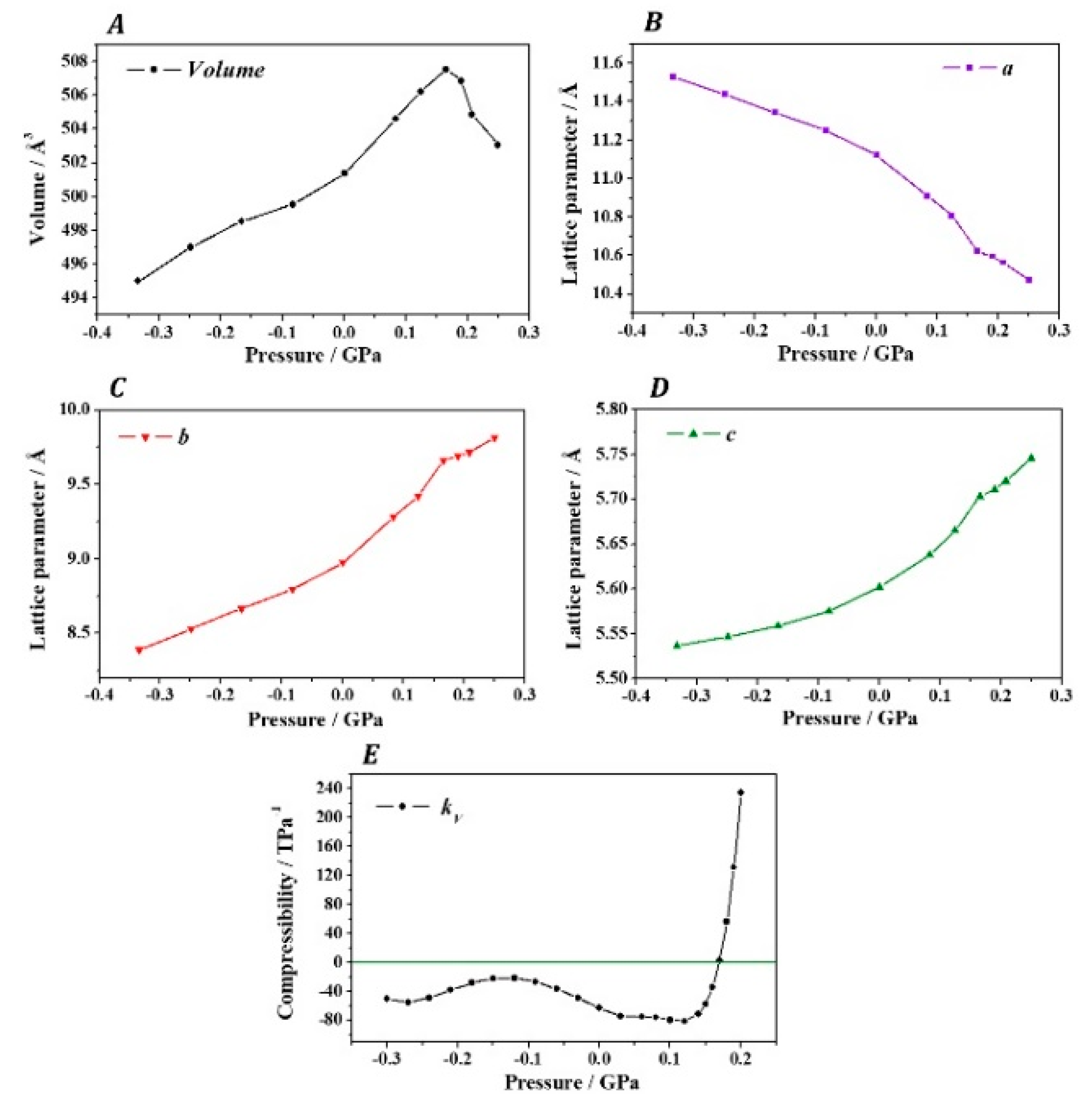
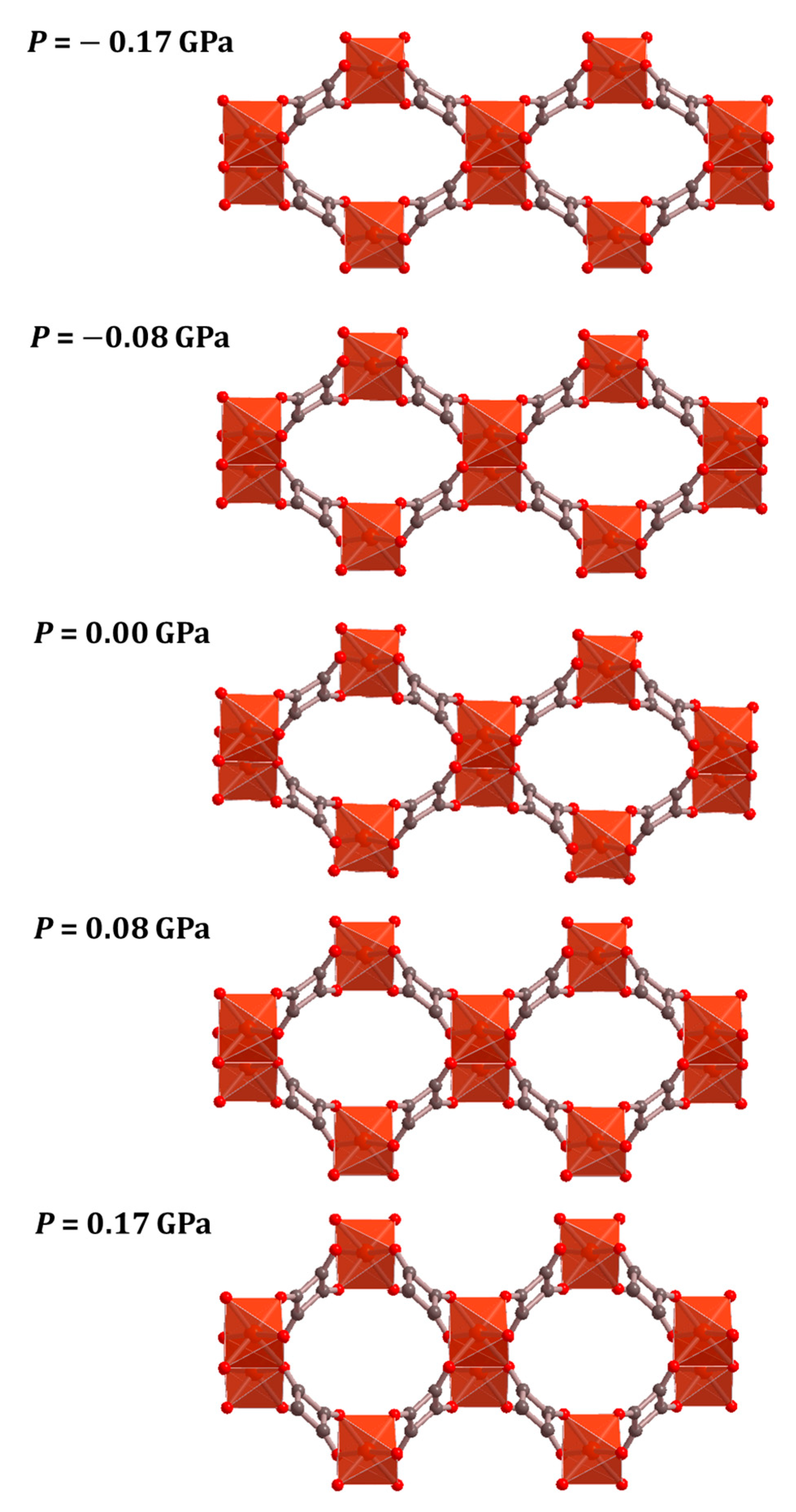
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baughman, R.H.; Stafström, S.; Cui, C.; Dantas, S.O. Materials with Negative Compressibilities in One or More Dimensions. Science 1998, 279, 1522–1524. [Google Scholar] [CrossRef] [PubMed]
- Cairns, A.B.; Goodwin, L. Negative Linear Compressibility. Phys. Chem. Chem. Phys. 2015, 17, 20449–20465. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R.S.; Wojciechowski, K.W. Negative Compressibility, Negative Poisson’s Ratio and Stability. Phys. Stat. Sol. 2008, 245, 545–551. [Google Scholar] [CrossRef]
- Colmenero, F. Anomalous mechanical behavior of the deltic, squaric and croconic cyclic oxocarbon acids. Mater. Res. Express 2019, 6, 045610. [Google Scholar] [CrossRef]
- Colmenero, F. Mechanical Properties of Anhydrous Oxalic Acid and Oxalic Acid Dihydrate. Phys. Chem. Chem. Phys. 2019, 21, 2673–2690. [Google Scholar] [CrossRef]
- Colmenero, F. Silver Oxalate: Mechanical Properties and Extreme Negative Mechanical Phenomena. Adv. Theor. Simul. 2019, 2, 1900040. [Google Scholar] [CrossRef]
- Colmenero, F.; Timón, V. Extreme negative mechanical phenomena in the zinc and cadmium anhydrous metal oxalates and lead oxalate dihydrate. J. Mater. Sci. 2020, 55, 218–236. [Google Scholar] [CrossRef]
- Colmenero, F. Organic acids under pressure: Elastic properties, negative mechanical phenomena and pressure induced phase transitions in the lactic, maleic, succinic and citric acids. Mater. Adv. 2020, 1, 1399–1426. [Google Scholar] [CrossRef]
- Lakes, R.S. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Lakes, R.S. Negative-Poisson’s-ratio materials: Auxetic solids. Annu. Rev. Mater. Res. 2017, 47, 63–81. [Google Scholar] [CrossRef]
- Nicolaou, Z.G.; Motter, A.E. Mechanical metamaterials with negative compressibility transitions. Nat. Mater. 2012, 11, 608–613. [Google Scholar] [CrossRef] [PubMed]
- Spinks, G.M.; Wallace, G.G.; Fifield, L.S.; Dalton, L.R.; Mazzoldi, A.; De Rossi, D.; Khayrullin, I.; Baughman, R.H. Pneumatic Carbon Nanotube Actuators. Adv. Mater. 2002, 14, 1728–1732. [Google Scholar] [CrossRef]
- Aliev, A.E.; Oh, J.; Kozlov, M.E.; Kuznetsov, A.A.; Fang, S.; Fonseca, A.F.; Ovalle, R.; Lima, M.D.; Haque, M.H.; Gartstein, Y.N.; et al. Giantstroke, superelastic carbon nanotube aerogel muscles. Science 2009, 323, 1575–1578. [Google Scholar] [CrossRef] [PubMed]
- Evans, K.E.; Alderson, A. Auxetic Materials: Functional Materials and Structures from Lateral Thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef]
- Uhoya, W.; Tsoi, G.; Vohra, Y.K.; McGuire, M.A.; Sefat, A.S.; Sales, B.C.; Mandrus, D.; Weir, S.T. Anomalous compressibility effects and superconductivity of EuFe2As2 under high pressures. J. Phys. Condens. Matter. 2010, 22, 292202. [Google Scholar] [CrossRef][Green Version]
- Jiang, X.; Molokeev, M.S.; Dong, L.; Dong, Z.; Wang, N.; Kang, L.; Li, X.; Li, Y.; Tian, C.; Peng, S.; et al. Anomalous mechanical materials squeezing three-dimensional volume compressibility into one dimension. Nat. Commun. 2020, 11, 5593. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Colmenero, F.; Jiang, X.; Li, X.; Li, Y.; Lin, Z. Negative area compressibility in silver oxalate. J. Mater. Sci. 2021, 56, 269–277. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Vella-Zarb, L.; Grima, J.N. Negative Linear Compressibility and Auxeticity in Boron Arsenate. Ann. Phys. 2020, 2020, 1900550. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2020, 19, 1563–1565. [Google Scholar] [CrossRef]
- Colmenero, F.; Sejkora, J.; Plášil, J. Crystal structure, infrared spectrum and elastic anomalies in tuperssuatsiaite. Sci Rep. 2020, 10, 7510. [Google Scholar] [CrossRef] [PubMed]
- Colmenero, F. Negative linear compressibility in nanoporous metal–organic frameworks rationalized by the empty channel structural mechanism. Phys. Chem. Chem. Phys. 2021, 23, 8508–8524. [Google Scholar] [CrossRef] [PubMed]
- Dinnebier, R.E.; Nuss, H.; Jansen, M. Anhydrous CuC4O4, a Channel Structure solved from X-ray Powder Diffraction Data. Z. Anorg. Allg. Chem. 2005, 63, 2328–2332. [Google Scholar]
- Payne, M.C.; Teter, M.P.; Ailan, D.C.; Arias, A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Bonales, L.J.; Colmenero, F.; Cobos, J.; Timón, V. Spectroscopic Raman Characterization of Rutherfordine: A Combined DFT and Experimental Study. Phys. Chem. Chem. Phys. 2016, 18, 16575–16584. [Google Scholar] [CrossRef]
- Colmenero, F.; Bonales, L.J.; Cobos, J.; Timón, V. Density Functional Theory Study of the Thermodynamic and Raman Vibrational Properties of γ-UO3 Polymorph. J. Phys. Chem. C 2017, 121, 14507–14516. [Google Scholar] [CrossRef]
- Colmenero, F.; Bonales, L.J.; Cobos, J.; Timón, V. Thermodynamic and mechanical properties of rutherfordine mineral based on density functional theory. J. Phys. Chem. C 2017, 121, 5994–6001. [Google Scholar] [CrossRef]
- Colmenero, F.; Timón, V. Study of the structural, vibrational and thermodynamic properties of natroxalate mineral using density functional theory. J. Solid State Chem. 2018, 263, 131–140. [Google Scholar] [CrossRef]
- Weck, P.F.; Gordon, M.E.; Greathouse, J.A.; Bryan, C.R.; Meserole, S.P.; Rodriguez, M.A.; Payne, M.C.; Kim, E. Infrared and Raman spectroscopy of α-ZrW2O8: A comprehensive density functional perturbation theory and experimental study. J. Raman. Spectrosc. 2018, 49, 1373–1384. [Google Scholar] [CrossRef]
- Malakkal, L.; Prasad, A.; Oladimeji, D.; Jossou, E.; Ranasinghe, J.; Szpunar, B.; Bichler, L.; Szpunar, J. Atomistic and experimental study on thermal conductivity of bulk and porous cerium dioxide. Sci. Rep. 2019, 9, 6326. [Google Scholar] [CrossRef]
- Colmenero, F.; Plášil, J.; Sejkora, J. The crystal structures and mechanical properties of the uranyl carbonate minerals roubaultite, fontanite, sharpite, widenmannite, grimselite and cejkaite. Inorg. Chem. Front. 2020, 7, 4197–4221. [Google Scholar] [CrossRef]
- Colmenero, F. Thermodynamic properties of the uranyl carbonate minerals roubaultite, fontanite, widenmannite, grimselite, čejkaite and bayleyite. Inorg. Chem. Front. 2020, 7, 4160–4179. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Cote, M.; Louie, S.G.; Cohen, M.L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-zone Integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Yu, R.; Zhu, J.; Ye, H.Q. Calculations of Single-Crystal Elastic Constants Made Simple. Comput. Phys. Commun. 2010, 181, 671–675. [Google Scholar] [CrossRef]
- Colmenero, F.; Cobos, J.; Timón, V. Periodic DFT Study of the Structure, Raman Spectrum and Mechanical Properties of Schoepite Mineral. Inorg. Chem. 2018, 57, 4470–4481. [Google Scholar]
- Colmenero, F.; Plášil, J.; Sejkora, J. The Layered Uranyl Silicate Mineral Uranophane-β: Crystal Structure, Mechanical Properties, Raman Spectrum and Comparison with the α-Polymorph. Dalton Trans. 2019, 48, 16722–16736. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Downs, R.T.; Bartelmehs, K.L.; Gibbs, G.V.; Boisen, M.B. Interactive Software for Calculating and Displaying X-Ray or Neutron Powder Diffractometer Patterns of Crystalline Materials. Am. Mineral. 1993, 78, 1104–1107. [Google Scholar]
- Wang, Y.; Stucky, G.D.; Williams, J.M. Is squaric acid square? A Combined X-Ray and Neutron Diffraction Study of 3,4-Dihydroxycyclobut-3-ene-1,2-dione. J. Chem. Soc. Perkin Trans. 1974, 2, 35–38. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.X. Necessary and Sufficient Elastic Stability Conditions in Various Crystal Systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A Computer Program for the Analysis and Representation of Anisotropic Elastic Properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]

| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| PBE | 11.1926 | 9.1271 | 5.7595 | 90.0 | 116.07 | 90.0 | 528.5049 | 2.207 |
| PBE + disp | 11.1578 | 9.1640 | 5.5982 | 90.0 | 117.78 | 90.0 | 506.4448 | 2.303 |
| B3LYP | 11.1829 | 9.2835 | 5.9160 | 90.0 | 114.88 | 90.0 | 557.1953 | 2.093 |
| PBEsol | 11.0961 | 9.0074 | 5.6076 | 90.0 | 116.26 | 90.0 | 502.6355 | 2.320 |
| Exp. [25] | 10.6869(4) | 8.9394(4) | 5.6747(1) | 90.0 | 117.60(2) | 90.0 | 480.4546 | 2.427 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colmenero, F.; Lobato, Á.; Timón, V. Compressing the Channels in the Crystal Structure of Copper Squarate Metal-Organic Framework. Solids 2022, 3, 374-384. https://doi.org/10.3390/solids3020026
Colmenero F, Lobato Á, Timón V. Compressing the Channels in the Crystal Structure of Copper Squarate Metal-Organic Framework. Solids. 2022; 3(2):374-384. https://doi.org/10.3390/solids3020026
Chicago/Turabian StyleColmenero, Francisco, Álvaro Lobato, and Vicente Timón. 2022. "Compressing the Channels in the Crystal Structure of Copper Squarate Metal-Organic Framework" Solids 3, no. 2: 374-384. https://doi.org/10.3390/solids3020026
APA StyleColmenero, F., Lobato, Á., & Timón, V. (2022). Compressing the Channels in the Crystal Structure of Copper Squarate Metal-Organic Framework. Solids, 3(2), 374-384. https://doi.org/10.3390/solids3020026







