Numerical Simulation of Particle-Laden Flow and Soot Layer Formation in Porous Filter
Abstract
:1. Introduction
2. Numerical Methods

3. Results and Discussion
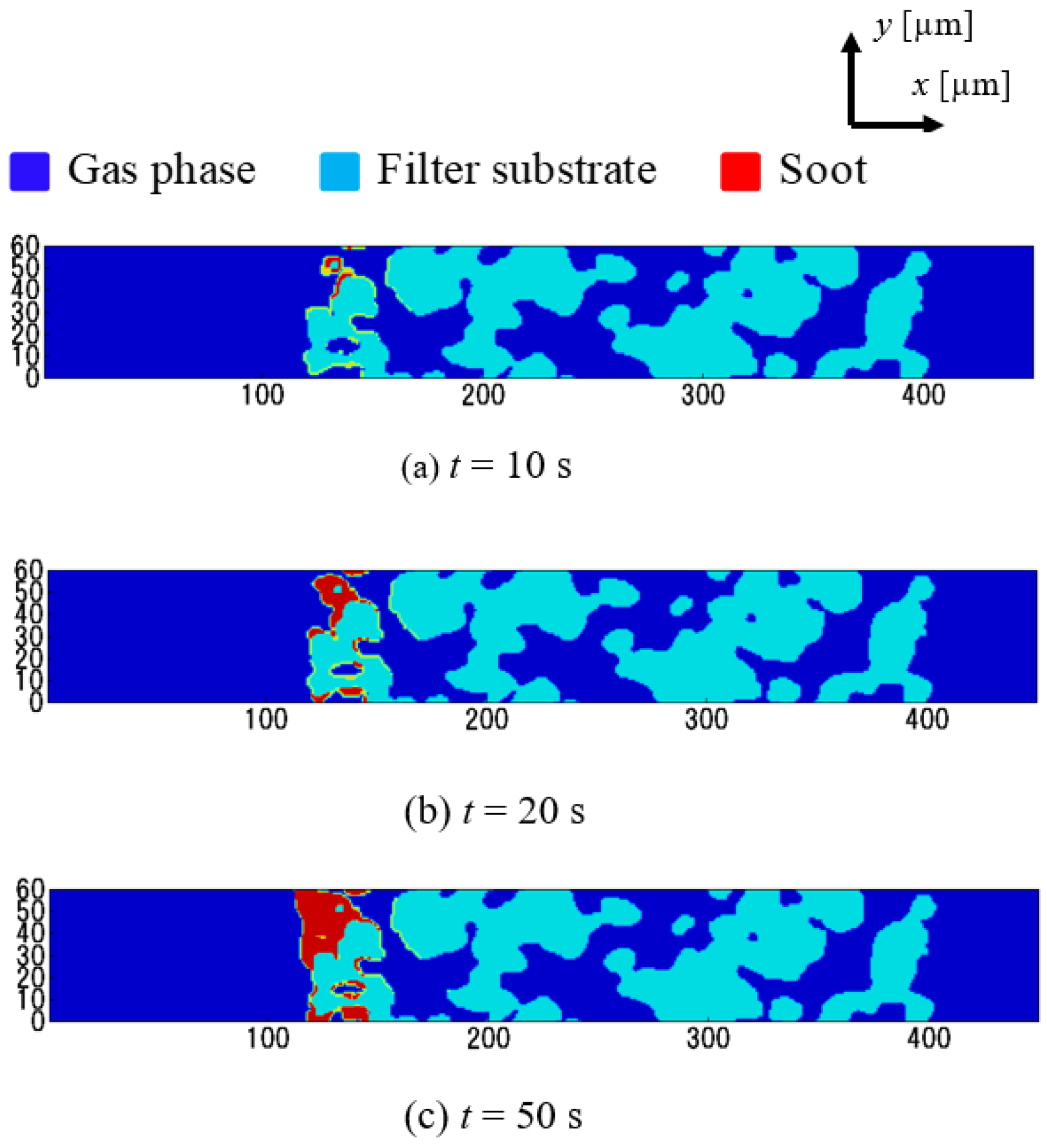
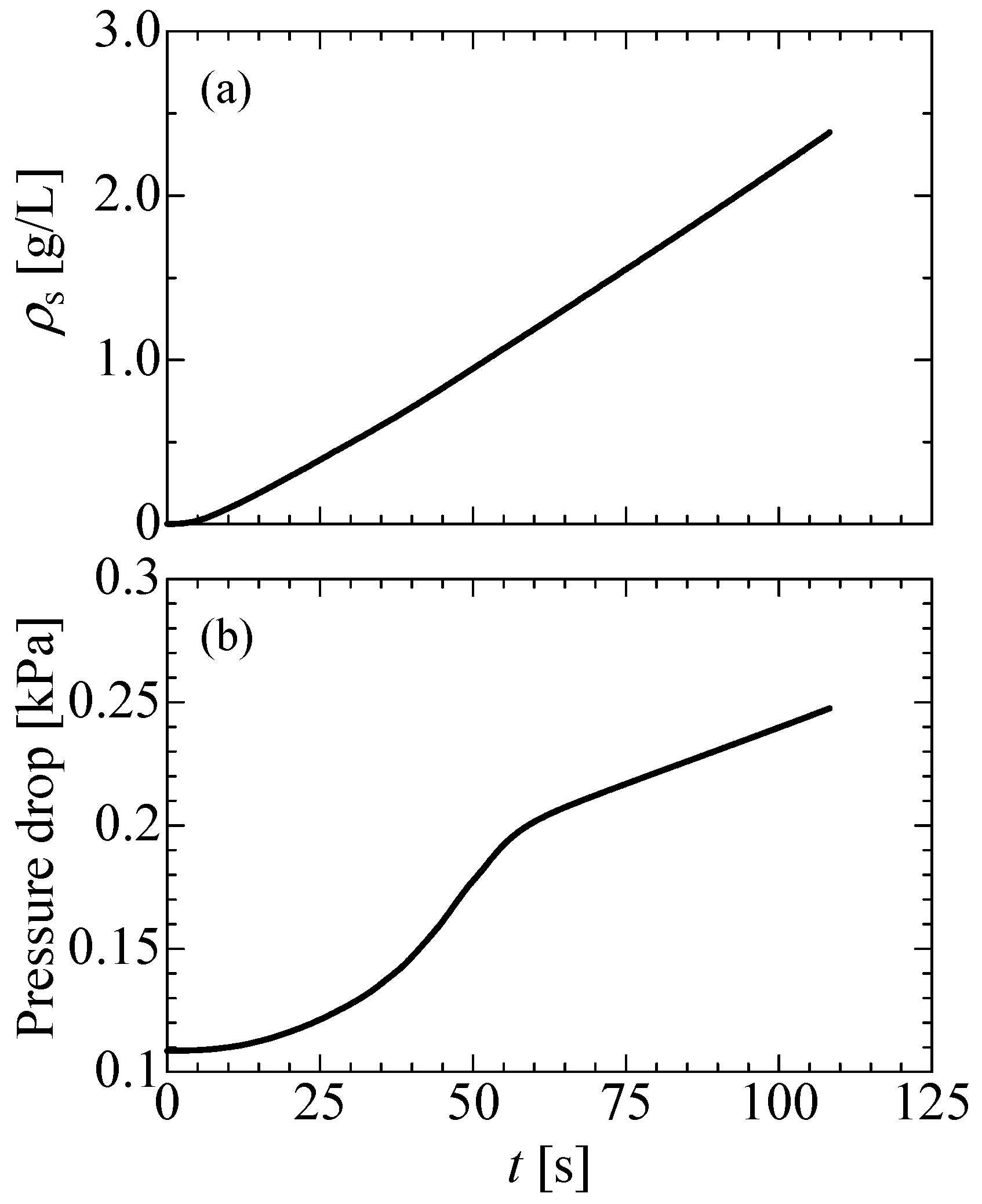
3.1. Soot Deposition Region and Pressure Drop
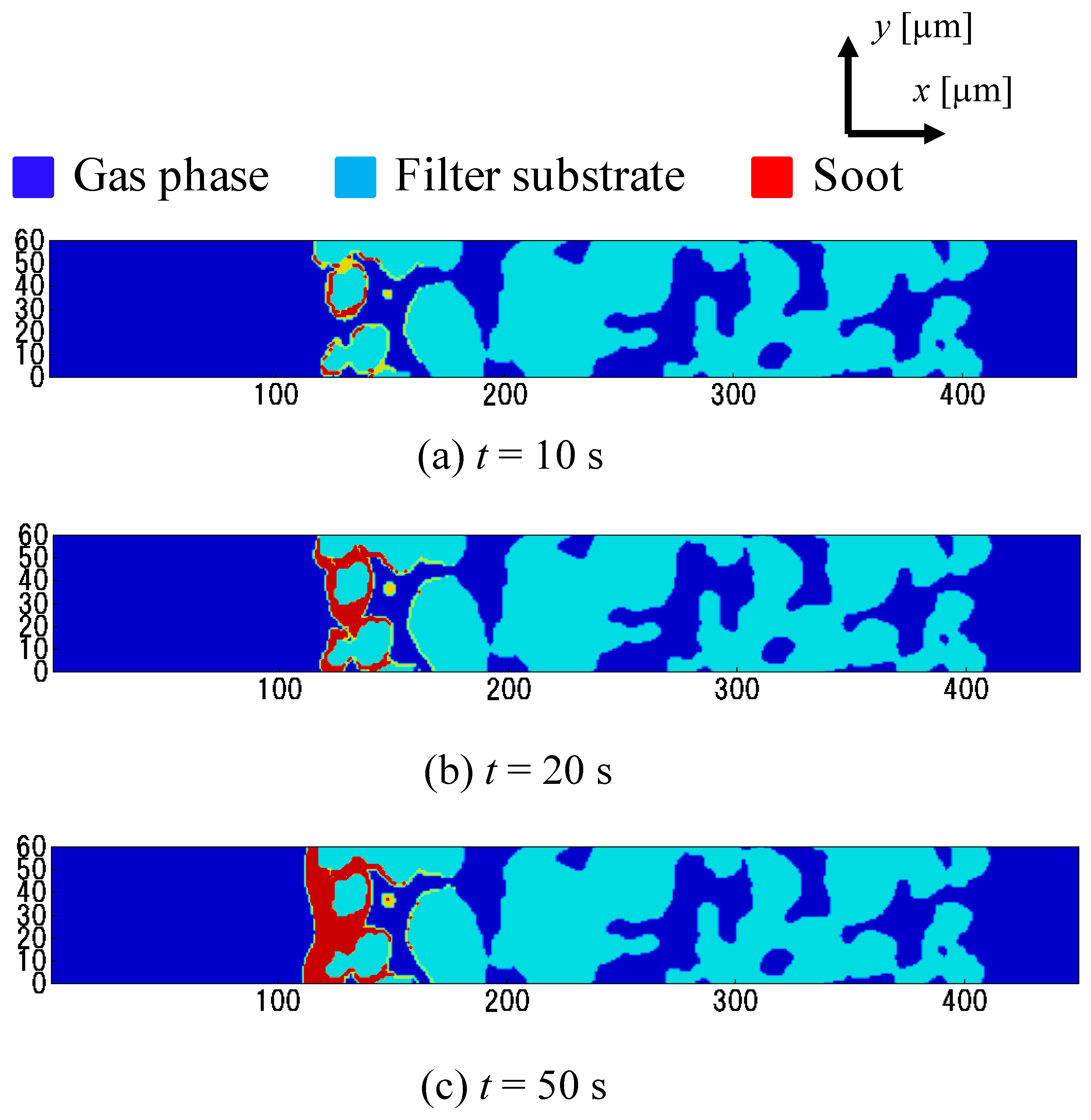
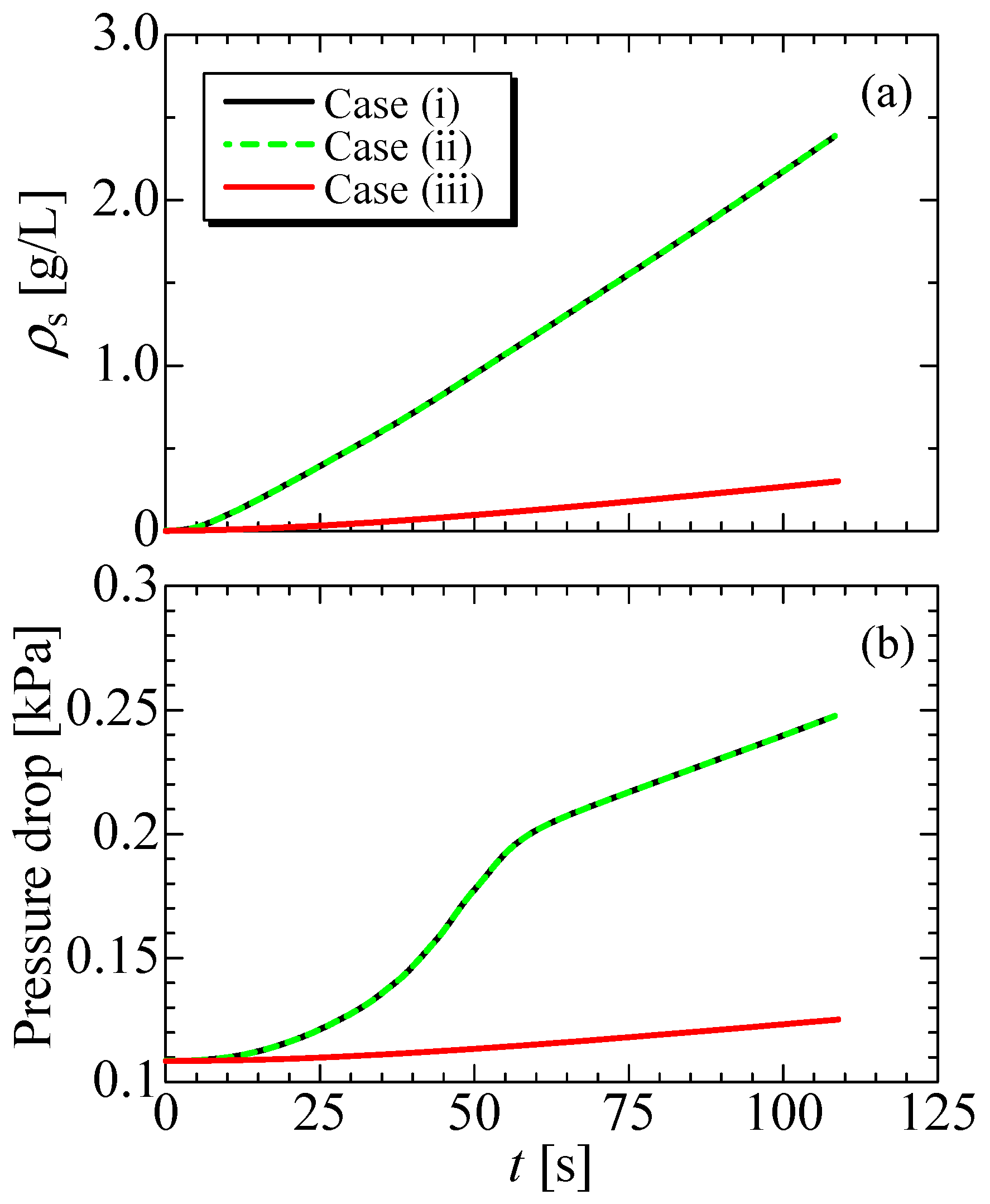
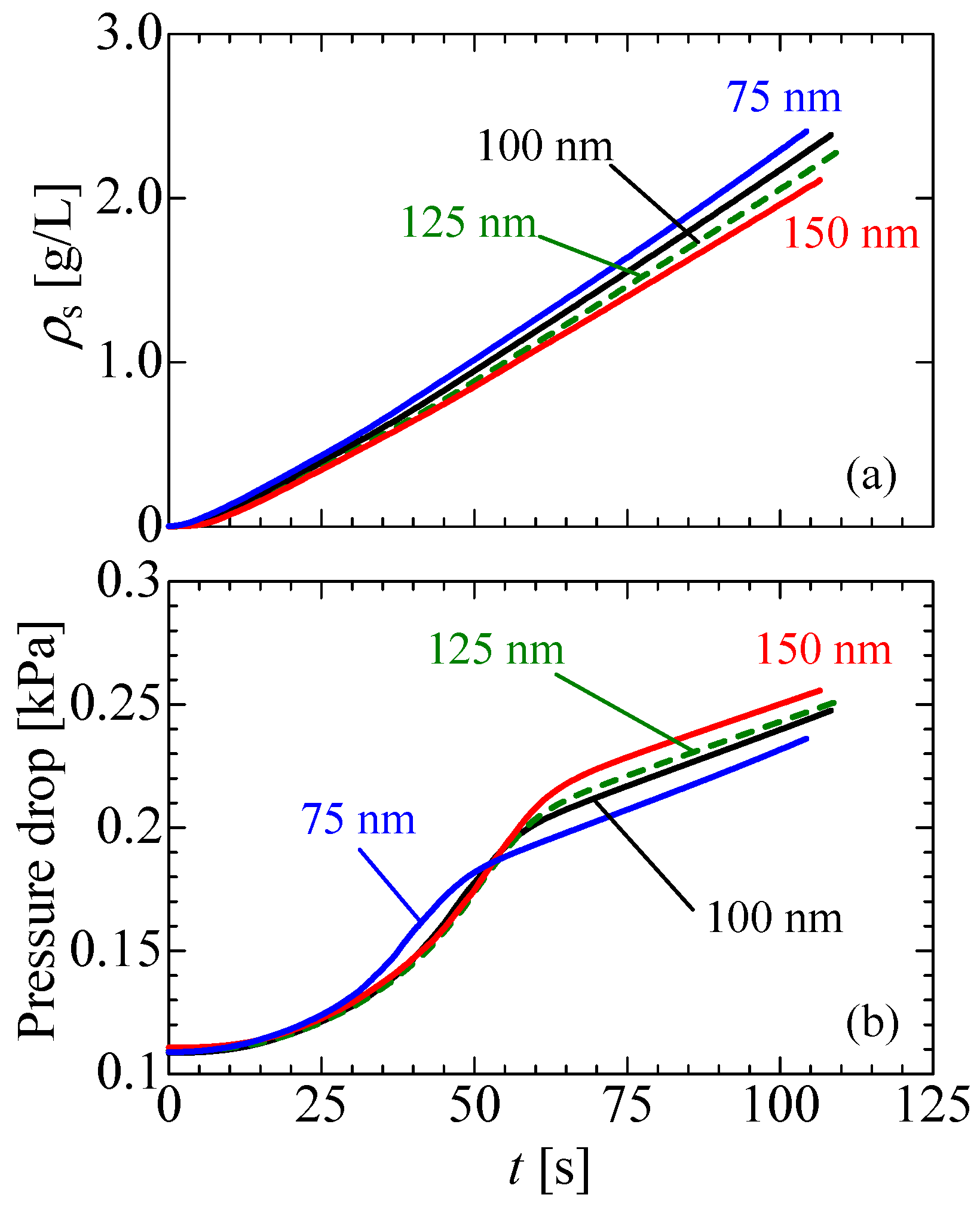
3.2. Effect of Soot Size on Pressure Drop
4. Conclusions
- (1)
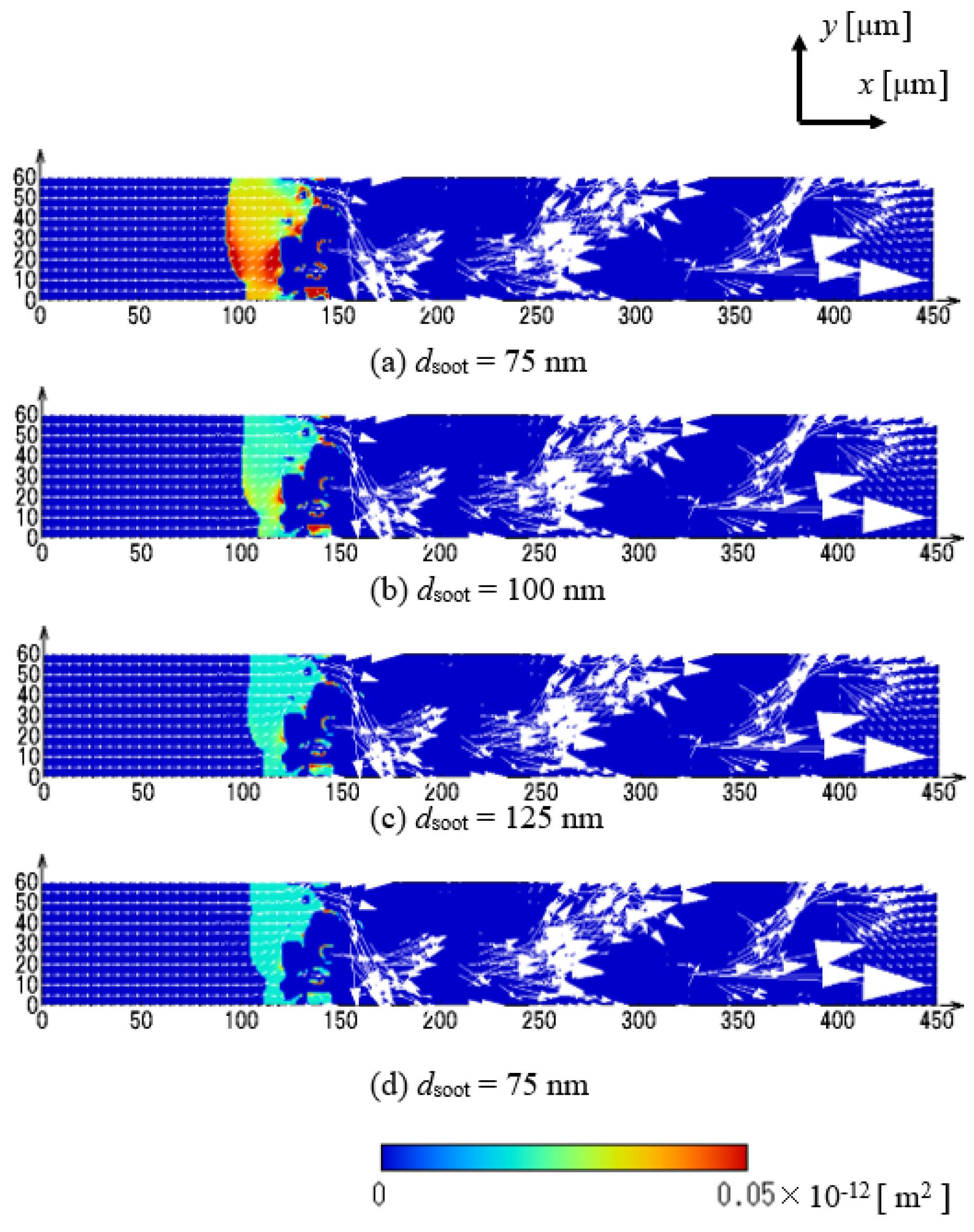
- The contributions of the Brownian diffusion and the interception effect were evaluated quantitatively. The soot deposition mainly occurs due to the Brownian diffusion. The soot deposition region is restricted to the area of the upstream of the filter wall surface.
- (2)
- Independent of the soot size, the shift from the depth filtration to the surface filtration is observed. By checking the soot deposition region, the pressure drop increases steeply during the depth filtration. Once all pores on the filter wall surface are covered with soot, the pressure rise is reduced, showing the linear increase during the surface filtration. As the soot size is smaller, the shift to the surface filtration appears earlier.
- (3)
- As the soot size is smaller, the soot layer forming on the filter wall surface becomes sparse. The resultant soot permeability of the smaller soot is larger. Then, due to the larger soot permeability, the pressure drop of the smaller soot is expectedly reduced. However, the smaller soot is trapped more efficiently by the Brownian diffusion. Then, only in the earlier stage of the filtration, the pressure drop of the smaller soot is larger. After that, the pressure drop is conversely smaller. Therefore, for discussing the pressure drop, it is important to consider where the soot deposition occurs as well as the deposited soot mass in the filter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Zervas, E.; Poulopoulos, S.; Philippopoulos, C. CO2 emissions change from the introduction of diesel passenger cars: Case of Greece. Energy 2006, 31, 2579–2589. [Google Scholar] [CrossRef]
- Knecht, W. Diesel engine development in view of reduced emission standards. Energy 2008, 33, 264–271. [Google Scholar] [CrossRef]
- Kong, H.; Yamamoto, K. Simulation on soot deposition in in-wall and on-wall catalyzed diesel particulate filters. Catal. Today 2019, 332, 89–93. [Google Scholar] [CrossRef]
- Kittelson, D.B. Engines and nanoparticles: A review. J. Aerosol Sci. 1998, 29, 575–588. [Google Scholar] [CrossRef]
- Kennedy, I.M. The health effects of combustion-generated aerosols. Proc. Combust. Inst. 2007, 31, 2757–2770. [Google Scholar] [CrossRef]
- Schejbal, M.; Štěpánek, J.; Marek, M.; Kočí, P.; Kubíček, M. Modelling of soot oxidation by NO2 in various types of diesel particulate filters. Fuel 2010, 89, 2365–2375. [Google Scholar] [CrossRef]
- Tzamkiozis, T.; Ntziachristos, L.; Samaras, Z. Diesel passenger car PM emissions: From Euro 1 to Euro 4 with particle filter. Atmos. Environ. 2010, 44, 909–916. [Google Scholar]
- Lapuerta, M.; Oliva, F.; Agudelo, J.R.; Boehman, A.L. Effect of fuel on the soot nanostructure and consequences on loading and regeneration of diesel particulate filters. Combust Flame 2012, 159, 844–853. [Google Scholar] [CrossRef]
- Johnson, T.V. Vehicular emissions in review. SAE Int. J. Engines 2016, 9, 1258–1275. [Google Scholar] [CrossRef]
- Yamamoto, K.; Tajima, Y. Mechanism for pressure drop variation caused by filtration of diesel particulates. Int. J. Engine Res. 2019, 22, 632–639. [Google Scholar] [CrossRef]
- Yamamoto, K.; Kato, H.; Suzuki, D. Pressure response during filtration and oxidation in diesel particulate filter. Emiss. Control Sci. Technol. 2019, 5, 24–30. [Google Scholar] [CrossRef]
- Chundru, V.R.; Parker, G.G.; Johnson, J.H. Development of a Kalman filter estimator for simulation and control of NOx and PM in a SCR catalyst on a DPF. Int. J. Engine Res. 2021, 22, 2407–2421. [Google Scholar]
- Gong, J.; Viswanathan, S.; Rothamer, S.A.; Foster, D.A.; Rutland, C.J. Dynamic heterogeneous multiscale filtration model: Probing micro and macroscopic filtration characteristics of gasoline particulate filters. Environ. Sci. Technol. 2017, 51, 11196–11204. [Google Scholar] [CrossRef] [PubMed]
- Czerwinski, J.; Comte, P.; Heeb, N.; Mayer, A.; Hensel, V. Nanoparticle Emissions of DI Gasoline Cars with/without GPF; SAE Technical Paper 2017-01-1004; SAE: Warrendale, PA, USA, 2017; pp. 1–8. [Google Scholar]
- Viswanathan, S.; Rothamer, D.A.; Foster, D.E.; Fansler, T.D.; Zelenyuk, A.; Stewart, M.; Bell, D.M. Evolution of deep-bed filtration of engine exhaust particulates with trapped mass. Int. J. Engine Res. 2017, 18, 543–559. [Google Scholar] [CrossRef]
- Jang, J.; Lee, J.; Choi, Y.; Park, S. Reduction of particle emissions from gasoline vehicles with direct fuel injection systems using a gasoline particulate filter. Sci. Total Environ. 2018, 644, 28–33. [Google Scholar] [CrossRef] [PubMed]
- Warner, J.R.; Dobson, D.; Cavataio, G. A study of active and passive regeneration using laboratory generated soot on a variety of SiC diesel particulate filter formulations. SAE Int. J. Fuels Lubr. 2010, 3, 149–164. [Google Scholar] [CrossRef]
- Chen, C.; Yao, A.; Yao, C.; Qu, G. Experimental study of the active and passive regeneration procedures of a diesel particulate filter in a diesel methanol dual fuel engine. Fuel 2020, 264, 116801. [Google Scholar] [CrossRef]
- R’Mili, B.; Boréave, A.; Meme, A.; Vernoux, P.; Leblanc, M.; Noël, L. Physico-chemical characterization of fine and ultrafine particles emitted during diesel particulate filter active regeneration of Euro5 diesel vehicles. Environ. Sci. Technol. 2018, 52, 3312–3319. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Li, Z.; Wang, Y.; Li, Z.; Li, M.; Jiao, P.; Cai, D. Simulation study of NO2-assisted regeneration performance of variable cell geometry catalyzed diesel particulate filter. Process. Saf. Environ. Prot. 2021, 154, 211–222. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Wong, V.W.; Shuai, S.; Qi, J.; Wang, G.; Liu, F.; Hua, L. Experimental study of lubricant-derived ash effects on diesel particulate filter performance. Int. J. Engine Res. 2021, 22, 921–934. [Google Scholar]
- Yamamoto, K.; Yamauchi, K.; Takada, N.; Misawa, M.; Furutani, H.; Shinozaki, O. Lattice Boltzmann simulation on continuously regenerating diesel filter. Philos. Trans. A 2011, 369, 2584–2591. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, K.; Yamauchi, K. Numerical simulation of continuously regenerating diesel particulate filter. Proc. Combust. Inst. 2013, 34, 3083–3090. [Google Scholar] [CrossRef]
- Yamamoto, K.; Matsui, K. Diesel exhaust after-treatment by silicon carbide fiber filter. Fibers 2014, 2, 128–141. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, K.; Sakai, T. Effect of pore structure on soot deposition in diesel particulate filter. Computation 2016, 3, 274–284. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, K.; Toda, T. Numerical simulation on flow dynamics and pressure variation in porous ceramic filter. Computation 2018, 64, 52. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, K.; Kondo, S.; Suzuki, K. Filtration and regeneration performances of SiC fiber potentially applied to gasoline particulates. Fuel 2019, 243, 28–33. [Google Scholar] [CrossRef]
- Qian, Y.H.; D’Humie’res, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Eur. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Chopard, B.; Masselot, A.; Dupuis, A. A lattice gas model for erosion and particles transport in a fluid. Comput. Phys. Commun. 2000, 129, 167–176. [Google Scholar] [CrossRef]
- Yamamoto, K.; Komiyama, R.; Sakai, T. Flow and pressure variations through porous filter during soot filtration and regeneration. ASME J. Therm. Sci. Eng. Appl. 2019, 11, 1–6. [Google Scholar] [CrossRef]
- Konstandopoulos, A.G.; Skaperdas, E. Microstructural properties of soot deposits in diesel particulate traps. SAE Tech. Pap. 2002, 2002, 11. [Google Scholar]
- Wirojsakunchai, E.; Schroeder, E.; Kolodziej, C.; Foster, D.E.; Schmidt, N.; Root, T.; Kawai, T.; Suga, T.; Nevius, T.; Kusaka, T. Detailed Diesel Exhaust Particulate Characterization and Real-Time DPF Filtration Efficiency Measurements during PM Filling Process; SAE Technical Paper 2007-01-0320; SAE: Warrendale, PA, USA, 2007; pp. 1–8. [Google Scholar]
- Stratakis, G.A.; Psarianos, D.L.; Stamatelos, A.M. Experimental investigation of the pressure drop in porous ceramic diesel particulate filters. Proc. Inst. Mech. Eng. 2002, 216, 773–784. [Google Scholar] [CrossRef]
- Kladopoulou, E.A.; Yang, S.L.; Johnson, J.H.; Parker, G.G.; Konstandopoulos, A.G. A study describing the performance of diesel particulate filters during loading and regeneration—A lumped parameter model for control applications. SAE Tech. Pap. 2003, 112, 647–668. [Google Scholar]
- Uenishi, T.; Tanaka, T.; Shigeno, G.; Fukuma, T.; Kusaka, J.; Daisho, Y. A Quasi Two Dimensional Model of Transport Phenomena in Diesel Particulate Filters—The Effects of Particle and Wall Pore Diameter on the Pressure Drop; SAE Technical Paper 2015-01-2010; SAE: Warrendale, PA, USA, 2015; pp. 1–10. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamamoto, K.; Yagasaki, S. Numerical Simulation of Particle-Laden Flow and Soot Layer Formation in Porous Filter. Solids 2022, 3, 282-294. https://doi.org/10.3390/solids3020020
Yamamoto K, Yagasaki S. Numerical Simulation of Particle-Laden Flow and Soot Layer Formation in Porous Filter. Solids. 2022; 3(2):282-294. https://doi.org/10.3390/solids3020020
Chicago/Turabian StyleYamamoto, Kazuhiro, and Shota Yagasaki. 2022. "Numerical Simulation of Particle-Laden Flow and Soot Layer Formation in Porous Filter" Solids 3, no. 2: 282-294. https://doi.org/10.3390/solids3020020
APA StyleYamamoto, K., & Yagasaki, S. (2022). Numerical Simulation of Particle-Laden Flow and Soot Layer Formation in Porous Filter. Solids, 3(2), 282-294. https://doi.org/10.3390/solids3020020




