Abstract
In 1991 the layered organic compound -(BEDT-TTF)Cu(CN) with a triangular lattice was synthesized for the first time. Although, originally, the focus was on the superconducting properties under pressure, this frustrated Mott insulator has been the most promising quantum-spin-liquid candidate for almost two decades, widely believed to host gapless spin excitations down to . The recent observation of a spin gap rules out a gapless spin liquid with itinerant spinons and puts severe constraints on the magnetic ground state. This review evaluates magnetic, thermal transport, and structural anomalies around K. The opening of a spin gap yields a rapid drop of spin susceptibility, NMR Knight shift, spin-lattice relaxation rate, and -SR spin fluctuation rate, but is often concealed by impurity spins. The concomitant structural transition at manifests in thermal expansion, THz phonons and Cu NQR relaxation. Based on the field dependence of , a critical field of 30–60 T is estimated for the underlying spin-singlet state. Overall, the physical properties are remarkably similar to those of spin-Peierls compounds. Thus, a strong case is made that the ‘6K anomaly’ in -(BEDT-TTF)Cu(CN) is the transition to a valence-bond-solid state and it is suggested that such a scenario is rather the rule than the exception in materials with strong magnetic frustration.
Keywords:
charge-transfer salts; (BEDT-TTF)2X; geometrical frustration; quantum spin liquid; valence bond solid; strongly correlated electron systems; Mott insulators; Hubbard model; bandwidth tuning; metal-insulator transitions PACS:
71.30.+h; 78.30.Jw; 75.25.Dk
1. Introduction
Half a century ago, Philip W. Anderson formulated the idea of resonating valence bonds [1]. Since then, the intensely studied field of frustrated magnetism has been propelled by a plethora of theoretical toy models, predicting various quantum-spin-liquid (QSL) states with itinerant or even topological spin excitations [2,3,4,5]. On the experimental side, triangular lattices have been realized in organic compounds [6,7] and YbMgGaO4 [8,9,10], whereas kagome symmetry is studied in Herbertsmithite (ZnCu(OH)Cl) and related systems [11,12], as well as optical lattices of Rydberg atoms [13]. The exactly solvable Kitaev model predicts topological Majorana fermions on the honeycomb lattice [14], which triggered intense work on iridates and -RuCl [15,16,17,18,19,20]. Despite a rapidly growing number of candidate materials, no direct evidence for a QSL with itinerant excitations [21,22], so-called ‘spinons’, has been reported without any doubt. Particularly for the prime QSL candidates the magnetic ground state remains controversially discussed, e.g., about the presence or absence of a spin gap in Herbertsmithite [23,24,25]. For almost two decades, -(BEDT-TTF)Cu(CN) was considered to host a QSL state [21,22,26]. However, the recent detection of a spin gap by electron-spin-resonance (ESR) measurements [27] prompts a reassessment of the magnetic ground state of the title compound.
Among the QSL candidates, the organic charge-transfer salt -(BEDT-TTF)Cu(CN) received most attention, not least for being a model system of Mott physics [6,7,28]. After the compound was first synthesized in the group of Jack Williams in 1991 [29], its unconventional superconductivity aroused wide attention [30,31,32,33]. In 2003, the focus shifted on the magnetic properties as Shimizu et al. reported the absence of antiferromagnetic (AFM) order [34]. Due to its crystal structure with layers of (BEDT-TTF) dimers arranged in an almost ideal triangular lattice ( [35]), which is shown in Figure 1, it was suggested that geometrical frustration suppresses magnetic order giving rise to a QSL state [2,34]. Additionally, EtMeSb[Pd(dmit)] [36,37,38], -(BEDT-TTF)Ag(CN) [39,40] and -H(Cat-EDT-TTF) [41,42] lack AFM order and have been established as QSL candidates. Transport studies under pressure [39,43,44] combined with optical spectroscopy [45,46] revealed that these frustrated organic materials share a universal phase diagram (Figure 2a) that is valid for Mott insulators [45], including oxides [47,48]. A variation of the electronic bandwidth W allows to tune the correlation strength , where U is the on-site Coulomb repulsion, driving the metal-insulator transition (MIT)–in excellent agreement with the predictions of dynamical mean-field theory (DMFT) on the half-filled Hubbard model [49,50]. The Mott MIT is first-order type up to the critical endpoint , involving a region of phase coexistence [44,51,52,53], followed by a quantum-critical regime at the quantum Widom line (QWL) at [43,54,55].
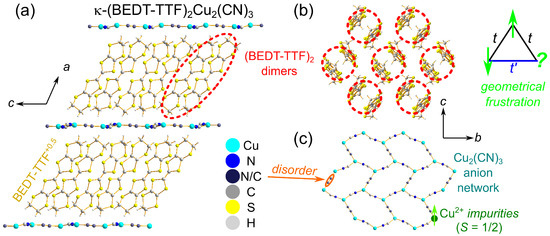
Figure 1.
Crystal structure of -(BEDT-TTF)Cu(CN) [29]. (a) Layers of organic BEDT-TTF donor molecules are separated by polymeric Cu(CN) anion sheets. (b) Within the planes, (BEDT-TTF) dimers carrying one electronic charge and spin form a nearly ideal triangular lattice ( [35]), yielding a Mott-insulating state [6,45] and pronounced effects of geometrical frustration [7,34]. (c) Sources of disorder in the anion network are the randomly oriented C/N atoms in the bridging CN-groups [56,57] and Cu impurities forming charged defects [27,30,58].
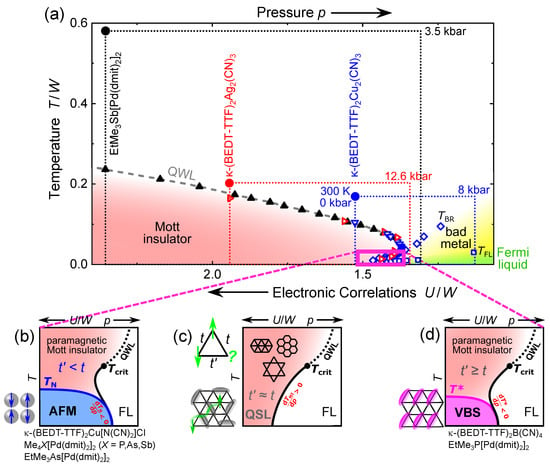
Figure 2.
(a) Unified phase diagram of genuine Mott insulators [44,45,46] based upon pressure-dependent measurements on EtMeSb[Pd(dmit)], -(BEDT-TTF)Ag(CN) and -(BEDT-TTF)Cu(CN) [39,43,44,46]. Dotted rectangles indicate experimentally covered T–p ranges starting from ambient conditions (, K marked by solid circles in respective color). Above the critical endpoint , the charge gap closes at the quantum-critical crossover (quantum Widom line QWL [43,54,55]) from a Mott insulator to incoherent semiconducting and bad metal states [45]. For the MIT is first-order type. At low T the spin degrees of freedom are decisive for the magnetic ground state and the transition to superconducting and Fermi-liquid (FL) phases [46,64]. (b) Near AFM interactions usually result in long-range order, seen in oxides (cuprates, VO [47,48]) and organic systems such as -(BEDT-TTF)Cu[N(CN)]Cl [65,66] or based on [Pd(dmit)] [7]. (c) Due to the lack of AFM order down to a few millikelvin [34,37,39,67], the frustrated triangular-lattice compounds () from (a) have been intensely discussed as QSL candidates [2,3,4,5,7]. (d) EtMeP[Pd(dmit)] [68,69,70,71] and -(BEDT-TTF)B(CN) [72,73] exhibit a VBS state below . Due to the Clausius–Clapeyron relation, the large spin entropy of the paramagnetic Mott state yields a positive slope of the insulator–metal boundary in the T–p phase diagram [6,7,45], whereas for AFM [51,66] or VBS [69,70].
Although Mott–Hubbard physics is by now firmly established in -(BEDT-TTF)Cu(CN) and related compounds [45], there has been a controversy about the origin of dielectric anomalies in the radiofrequency range (kHz–MHz) in several Mott organics, in particular whether they are related to quantum electric dipoles within the dimers [59,60,61,62]. However, these energy scales are 8–10 orders of magnitude smaller than eV [45], which rather suggests polarizations on length scales much bigger than a single dimer. Indeed, the relaxor response with in the Mott-insulating state [59] is compatible with the dynamics of domains [63], possibly linked to disorder of the bridging CN groups indicated in Figure 1c [56,57], whereas the strong enhancement nearby a MIT [61,62] has been recently assigned to first-order phase coexistence [44]. Although charge delocalization upon the transition from a Mott insulator to a bad metal, superconducting and Fermi-liquid phases (Figure 2a) is interesting on its own [31,46,64], this review focuses on the magnetic ground state towards .
At low temperatures, the spin degrees of freedom and the associated entropy become decisive for the very shape of the MIT, leading to different magnetic and non-magnetic configurations, as sketched in Figure 2b–d. The spin entropy of a paramagnetic Mott insulator exceeds that of the adjacent correlated metal, yielding a positive slope of the MIT in the T–p phase diagram—a similar manifestation of the Clausius–Clapeyron relation like the Pomeranchuk effect in superfluid He [74] and twisted bilayer graphene [75]. The ordered nature of AFM and valence-bond-solid (VBS) phases, on the other hand, implies a smaller entropy resulting in a negative slope for and , respectively. For a QSL with itinerant spinons, possibly realized in fully frustrated compounds with triangular, kagome, or honeycomb symmetry, is expected down to (Figure 2c).
The abovementioned organic candidate compounds were suggested to host a QSL state, based on a finite susceptibility [34,36,39] and non-zero Sommerfeld coefficient observed in specific heat measurements [26,38,39,76]. However, many other Mott-insulating systems with magnetic order or a spin gap are known to date. Weakly frustrated materials with , e.g., close to quadratic lattices like the cuprates [47], exhibit AFM order below . Typical examples, listed in Figure 2b, are (BEDT-TTF) compounds like -(BEDT-TTF)Cu[N(CN)]Cl [65,66] or (dmit)-based materials, such as EtMeAs[Pd(dmit)] or Me[Pd(dmit)] with P, As, Sb [7]. Different to Anderson’s RVB state with a dynamic, random configuration, valence bonds can form a VBS phase with a static crystalline pattern (Figure 2d), also known as ‘valence bond crystal’. In this case, the spins of neighboring sites form a singlet state, which is usually accompanied by a Peierls-like lattice distortion. Such nonmagnetic phases occur close to , e.g., in EtMeP[Pd(dmit)] [68,69,70,71], and, in particular, for quasi-1D () exchange interactions, like for -(BEDT-TTF)B(CN) with [72,73,77]. Other prominent examples are the spin-Peierls phases in linear-chain compounds [78,79,80].
The following sections summarize structural and magnetic properties reported over the last two decades, leading to the conclusion that -(BEDT-TTF)Cu(CN) does not exhibit a QSL state, but rather a nonmagnetic VBS phase. The main motivation for this work came from the results by Miksch et al. [27] who recently revealed a spin gap in multifrequency ESR studies. As will be seen, the formation of a spin-singlet state at K associated with the well known ‘6K anomaly’ [26,81] is apparent in a broad set of experimental results, including thermodynamic, structural, ultrasonic, optical, and magnetic probes. Since such anomalies occur not only in -(BEDT-TTF)Cu(CN), a similar scenario is suggested also for related QSL candidates.
2. Anatomy of the Magnetic Ground State of -(BEDT-TTF)Cu(CN)
The fingerprints of the magnetic and nonmagnetic phases mentioned in the introduction manifest in distinct ways in different observables. Ideally, a set of ‘standard’ measurements, including bulk magnetization and specific heat C, should suffice to unambiguously identify particular spin states. In materials subject to strong AFM exchange interactions, however, already a small number of paramagnetic impurities (e.g., a concentration − [82]) can conceal the response of the intrinsic spin system. More pronounced disorder can even smoothen out a phase transition until it cannot be recognized any more. Below, several physical properties of -(BEDT-TTF)Cu(CN) are listed that rule out (1) AFM and various QSL phases, and deliver the tell-tale signatures of a VBS transition: (2) spin gap, (3) anisotropic structural distortion. Section 2.4 provides an estimate of the critical field 30–60 T.
2.1. Absence of Magnetic Order
Early on, it was recognized that -(BEDT-TTF)Cu(CN) is a Mott insulator with dominant AFM interactions K [30,34], which results from the itinerant exchange mechanism when the electronic charge is localized [2]. As such, long-range order was expected like in the cuprates or VO [47,48]. However, it turned out that the magnetization does not exhibit an AFM transition (Figure 2b) that occurs in the sister compound -(BEDT-TTF)Cu[N(CN)]Cl [65]. Nuclear magnetic resonance (NMR) is an even more distinctive probe as it can detect (i) local moments through a line splitting in the NMR spectrum and (ii) a pronounced peak of the spin-lattice relaxation rate at the transition temperature resulting from strong AFM fluctuations [65]. Consistently, these features are also absent in the NMR properties of -(BEDT-TTF)Cu(CN) which nourished the idea of a QSL state [34,67], possibly with gapless spin excitations [21,22,26].
2.2. Evidence for a Spin Gap below K
Based on the original results by Shimizu et al. [34], there were two main arguments against a spin gap. (1) Although the magnetic susceptibility drops to zero upon paradigmatic VBS transitions [68,72,73,78,79,80], SQUID measurements on -(BEDT-TTF)Cu(CN) yield that remains finite down to 1.9 K [34,83]. (2) In addition, should also fall exponentially when a spin gap opens, but a power-law-like decrease for was seen in NMR data [34,67]. In the following, it will be shown that the low-temperature spin degrees of freedom probed by (Section 2.2.1) , (Section 2.2.2) , (Section 2.2.3) thermal transport, (Section 2.2.4) NMR Knight shift and -SR are in excellent agreement with a singlet ground state and paramagnetic impurities embedded in a spin-gapped matrix—as put forward in Ref. [82]. Note, signatures of disorder are rather the rule than the exception in frustrated materials [10,82,84,85,86,87,88]—inhomogeneity has been reported also for -(BEDT-TTF)Cu(CN) [27,30,58,67,89].
2.2.1. Spin Susceptibility
In materials the bulk susceptibility , e.g., obtained from SQUID measurements, contains components of the valence electrons (‘intrinsic’) and of impurity spins (‘extrinsic’). Of primary interest is the temperature dependence of , which is usually the dominant term in clean systems. However, a Curie-type contribution of paramagnetic defect spins, , can become relevant at low T if in a nonmagnetic state. Figure 3a presents the potential impact of impurities on . Upon the transition to a spin-gapped state, the intrinsic contribution is exponentially suppressed below ; Bulaevskii’s model of an alternating spin chain yields , which was used in Ref. [27]. When an impurity density of order 0.1% can easily exceed and become the dominant contribution [82]. In the anion layers of -(BEDT-TTF)Cu(CN) single crystals significant amounts of Cu were detected by ESR measurements [27,30,58], as indicated in Figure 1c. As these are charged defects, adjacent BEDT-TTF molecules are doped resulting in neutral dimers with . To that end, not only the spin of the Cu impurity itself contributes to , but also an unpaired dimer remains in the spin-gapped state as it cannot form a singlet with its neighboring site. Apart from Cu [27,30,58], different types of defects are expected, e.g., at domain walls [82,89].

Figure 3.
Magnetic susceptibility of -(BEDT-TTF)Cu(CN). (a) A weak temperature dependence at elevated temperatures is followed by a rapid drop of at due to the opening of a spin gap [27]. The reduction comes to a halt once becomes smaller than the contribution of impurity spins, which follows a Curie-like behavior until (C is the Curie constant). (b–e) The drop at is seen prominently in ESR experiments on single crystals [27,30] and, less pronounced, in SQUID measurements on polycrystals [34,83]. The upturn for , seen most clearly in (b), exhibits strong sample dependence due to a varying defect density. Miksch et al. [27] accomplished to identify and distinguish the intrinsic contribution from the impurity signal in the ESR spectra (d), establishing that the ground state of -(BEDT-TTF)Cu(CN) has a spin gap.
Figure 3b–e demonstrate the intrinsic and extrinsic contributions in obtained from ESR [27,30] and SQUID [34,83] measurements. As seen in panel (b), the ESR susceptibility from Komatsu et al. [30] indeed exhibits first a drop, due to the opening of a spin gap at K, followed by an upturn upon further cooling that corresponds to paramagnetic impurities. Crucially, the comprehensive results by Miksch et al. [27] enabled to separate from in the ESR spectra, directly evidencing that the intrinsic contribution vanishes while the defect signal increases with lower T (Figure 3d). Additionally, the bulk magnetization from Refs. [34,83] follows similar behavior (Figure 3c,e), albeit the drop around K is broadened and the upturn at lower T is less pronounced. This is likely the result of sample-to-sample variations with slightly different and impurity concentrations, as these SQUID data were acquired on polycrystalline samples. The greater sensitivity of ESR facilitates experiments on single crystals with the magnetic field aligned along well-defined axes. Note, also, the results of magnetic torque measurements [90] were successfully modelled by the field-dependent response of impurity spins [89].
2.2.2. NMR Spin-Lattice Relaxation Rate
is highly sensitive to phase transitions between paramagnetic, magnetic, and nonmagnetic states. For instance, strong AFM fluctuations yield a pronounced peak of the relaxation rate at , as observed for -(BEDT-TTF)Cu[N(CN)]Cl [65]. The opening of a spin gap, on the other hand, results in an exponential drop of the relaxation rate in an Arrhenius-type fashion , such as in the VBS systems EtMeP[Pd(dmit)] [70] and -(BEDT-TTF)B(CN) [73]. Although -(BEDT-TTF)Cu(CN) clearly does not exhibit a peak in at , ruling out AFM order [34,67], a clear-cut gap was observed neither. Instead of the expected exponential reduction, drops only a little (though noticeably) at and, below that, a broad maximum forms with a power-law-like tail down to 20 mK [34,67], as plotted in Figure 4b,c. When viewed in isolation, the behaviors (H [34]) and (C [67]) at K are indicative of spin excitations. However, with the knowledge of a spin gap opening at 6 K [27] and a dominant impurity response at lower temperatures assigned in Section 2.2.1, it is concluded that the power-law behavior at K does not reflect the intrinsic spin excitations of the valence electrons.
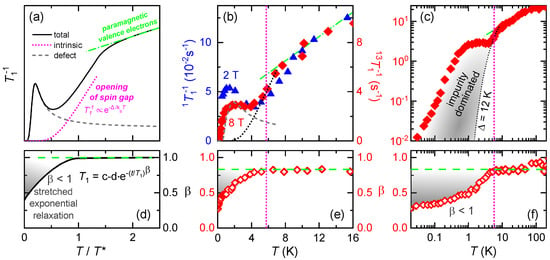
Figure 4.
Influence of paramagnetic impurities on NMR spin-lattice relaxation rate. (a) exhibits a rapid drop as a spin gap opens. In this nonmagnetic environment, paramagnetic impurities contribute a BPP-type relaxation (Equation (1)) forming a local maximum of at lower temperatures. (b) The H (blue; from Ref. [34]) and C (red; from Ref. [34]) relaxation rates of -(BEDT-TTF)Cu(CN) show similar behavior for . As the spin gap opens (dotted line indicates K) the drop of comes to a halt and a broad maximum appears. is smaller by a factor 80; note the different vertical scales. (c) The grey highlighted area indicates the impurity-dominated region in a double-logarithmic plot. (d–f) Inhomogeneous relaxation from the impurities brings about deviations from single-exponential behavior, with a stretching exponent for .
Having said that, the relaxation properties expected for paramagnetic impurities in a nonmagnetic system like -(BEDT-TTF)Cu(CN) are revisited based on Equation (1). Indeed, broad maxima illustrated in Figure 4a result from Bloembergen–Purcell–Pound (BPP) type relaxation [91]
with . Here, is the bandwidth of longitudinal field fluctuations and the Zeeman energy splitting of the , impurity spin levels. The polarization of the impurity spins in the applied magnetic field, probed at the NMR frequency , causes the activated behavior and a pronounced field dependence. The latter phenomenology is fully consistent with the larger peak value of in the H NMR data [34] as compared to the C measurements from Ref. [67], because the former were probed in smaller magnetic fields (2 T) than the latter (8 T). As shown in Figure 4b, the H and C results coincide for , where both reflect the relaxation from intrinsic spin excitations, but the response becomes field-dependent below as it is dominated by impurity spins when the spin gap opens. A random arrangement of the impurities yields a distribution of local fields that emerges from dipolar coupling over a distance r between impurity spin and nuclear site, resulting in a stretched-exponential recovery. This is exactly what is observed in experiment: As seen in Figure 4d–f, is constant in the intrinsic regime () and drops right below [67]. As noted in Ref. [27], the local fields deduced from C linewidth [67] and -SR data [92] are consistent with dipolar coupling to Cu impurities in the anion layers. Consistently, the broadening of NMR lines upon lowering temperature and increasing magnetic field [67] was reproduced by rare impurity spins in Ref. [89]. In addition to stretched-exponential recovery, a distribution of local fields can result in a regime with power-law-like temperature dependence of , similar to what is seen for K [34,67].
Based on the thorough assessment above and the discussion in Ref. [82], the relaxation below the local minimum at 4 K is assigned to paramagnetic impurities, whereas the behavior above that reflects the intrinsic response of valence electrons. In particular, the hump slightly above and the noticeable reduction in upon cooling below that correspond to the opening of a spin gap K, which agrees well with the drop in discussed in Figure 3. The characteristic behavior with a decrease in followed by a broad local maximum and a concomitant onset of stretched-exponential recovery sketched in Figure 4a,d is not unique to -(BEDT-TTF)Cu(CN), but has also been observed in the charge-ordered state of the weakly dimerized -(BEDT-TTF)Hg(SCN)Cl [82] and upon the VBS transitions of EtMeP[Pd(dmit)] [70] and -(BEDT-TTF)B(CN) [73]. Thus, the impurity response occurring in the nonmagnetic insulating states of all these organic compounds turns out to be a robust phenomenology of weakly disordered Mott-Hubbard systems with a spin gap.
2.2.3. Thermal Transport
The formation of spin singlets is evident, also, in observables that do not directly probe the magnetic properties. In particular, from thermal transport measurements a lack of itinerant spin excitations has been deduced as towards [93]. Since this result was in direct contradiction with specific heat results that suggested a scenario [26], the topic remained controversial and it took more than a decade until the spin gap was evidenced by a magnetic probe in the ESR measurements of Miksch et al. [27]. Another factor that baffled the community studying organic QSL candidates came from measurements of in EtMeSb[Pd(dmit)] that seemed to exhibit a non-zero offset towards [94], also accompanied by a finite Sommerfeld coefficient in the specific heat [38]. However, thorough reinvestigation by independent groups challenged this scenario by reporting [95,96], which suggests a spin gap also in the dmit-based QSL candidate, but the situation remains controversial [97] and there are comprehensive efforts to clarify these issues [98].
In insulating systems such as -(BEDT-TTF)Cu(CN) heat is carried by the spins of localized charges (electronic) and by phonons, yielding . The main conclusions in Ref. [93] were derived from the data at K, well below . Quantitatively, the gap size K estimated therein is much smaller than K that consistently describes and (Figure 3 and Figure 4). To assess this discrepancy, from Ref. [93] is compared to other spin-gapped systems in Figure 5. Strikingly, (b) thermal transport of -(BEDT-TTF)Cu(CN) resembles very much the behavior of (a) the spin-Peierls compounds CuGeO and NaVO: first reduces upon cooling through , but then rises forming a pronounced peak that has been attributed to phonons [99,100]. Here, the opening of the spin gap has distinct effects on and . Although the former vanishes upon the formation of singlets, the latter increases as phonon scattering off spin excitations is quenched. The thermal conductivity then forms a maximum and, below that, towards . Naturally, the scattering of phonons depends on the defect density; sample-to-sample variations have indeed been observed in Ref. [93] (Figure 5b).
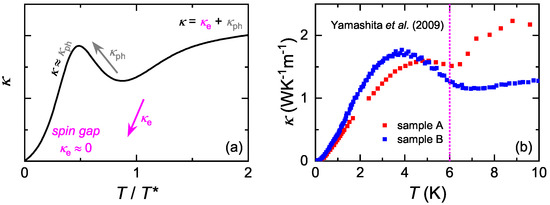
Figure 5.
(a) The thermal conductivity upon the transition to a VBS state is sketched based on the observations made in spin-Peierls compounds such as CuGeO and NaVO [99,100]. Electronic heat transport vanishes upon the opening of a spin gap at , yielding a drop of with cooling. At lower temperatures, the mean free path of phonons increases as the scattering off spin excitations is quenched in the singlet state. The associated enhancement of phononic thermal conductivity results in the formation of a maximum of for . (b) Strikingly similar behavior is seen for the thermal conductivity of -(BEDT-TTF)Cu(CN) reported by Yamashita et al. [93].
The similar phenomenology of [93] compared to the spin-Peierls systems [99,100] is fully consistent with a VBS scenario in the title compound. In that case, rapidly vanishes below and heat is carried primarily by phonons in the spin-gapped region of -(BEDT-TTF)Cu(CN), questioning the assumption in Ref. [93] that ’occupies a substantial portion in ’ for . If , then K estimated from Arrhenius fits in the range 0.1–0.2 K does not reflect the ’intrinsic’ spin degrees of freedom. Instead, it may rather be an ’extrinsic’ contribution to phonon scattering becoming dominant towards . Nevertheless, the lack of a non-zero at reported by Yamashita et al. [93] correctly indicates the absence of gapless spinons.
2.2.4. NMR Knight Shift and -SR
Figure 6 summarizes the anomalies of various physical properties around K: Panels (a–c) are assigned to changes of the crystal structure, while (d–g) indicate the opening of a spin gap in various magnetic properties. For instance, (d) the -SR data by Pratt et al. [92] yield a plateau with a rather T-independent spin-fluctuation rate at . Below , a distinct drop beyond the scatter of data points is observed upon cooling towards , indicating a loss of the intrinsic magnetization.
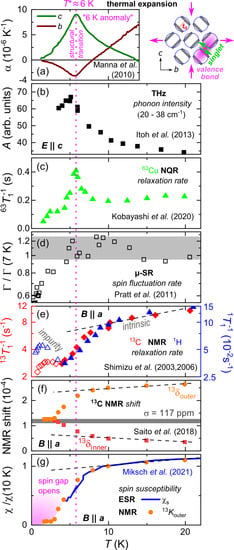
Figure 6.
Structural and magnetic anomalies around K. Data from Refs. [27,34,67,81,83,92,102,103]. Panels (a–c) are assigned to changes of the crystal structure, while (d–g) indicate the opening of a spin gap in various magnetic properties.
Apart from the magnetic susceptibility and spin-lattice relaxation rate, which are displayed in Figure 6g,e (see also Figure 3 and Figure 4), the NMR Knight shift K is commonly employed as a probe of the local magnetization. Due to weak hyperfine coupling of H nuclei, that are located in the ethylene end groups of the BEDT-TTF molecules as seen in Figure 1a, measurements on C sites sitting at the central C=C bonds with large charge density are required for this purpose. Similar to the difficulties in identifying the intrinsic contribution from and , elaborated in detail in Section 2.2.1 and Section 2.2.2 above, the inhomogeneous response below precluded a precise determination of K in initial NMR works [67]. In particular, the pronounced line broadening at low temperatures, that was assigned to impurity spins [89,101], imposes uncertainty to the NMR shift , where is the chemical shift.
Nevertheless, in a more recent NMR study Saito et al. [83] succeeded in acquiring for the inner and outer C sites, which is shown in Figure 6f. The grey bar indicates ppm, including an experimental uncertainty of 10 ppm. Although the Knight shift is negative for the former and positive for the latter, respectively, it is noted here that both reach a similar value indistinguishable from the chemical shift at K. This means that, within the experimental accuracy, the local susceptibility is zero as expected for a nonmagnetic VBS state. To that end, has been extracted from these data and plotted together with from the ESR studies by Miksch et al. [27] in Figure 6g. Remarkably, the susceptibility and Knight shift data show excellent agreement, which provides conclusive evidence for the gapped magnetic ground state of -(BEDT-TTF)Cu(CN).
2.3. Structural Distortion at the ‘6K Anomaly’
2.3.1. Thermodynamic Signatures
Following its observation as a hump-like feature in [26], the ‘6K anomaly’ of -(BEDT-TTF)Cu(CN) showed up in thermal expansion measurements as a pronounced lattice distortion [81], indicated in Figure 6a. The concomitant occurrence of structural modifications with the opening of a spin gap is, together with its similar anisotropy and size, reminiscent of the VBS transition in EtMeP[Pd(dmit)] [71] and the spin-Peierls transitions in linear-chain compounds like (TMTTF) and GeCuO [104,105]. Since the author is not aware of any QSL state coupled to such pronounced structural anomalies [2,3,4,5], it is concluded that the ground state of -(BEDT-TTF)Cu(CN) is a nonmagnetic VBS phase. The contraction along c and expansion along b upon cooling through indicate that the spin-singlet valence bonds are arranged across two dimers (forming BEDT-TTF tetramers) along directions, as indicated in the right part of Figure 6a.
Crucially, the specific heat hump at 6 K [26] agrees remarkably well with the thermodynamic signatures in thermal expansion, as pointed out by Manna et al. [81]. The associated entropy release of order 1 JKmol [26], which amounts to 17% of JKmol, is reasonably assigned to the singlet formation of paramagnetic spins upon the VBS transition. Note, due to the strong exchange coupling K [34] the spin polarization is significantly reduced at K compared to non-interacting spins with , hence the spin entropy at is smaller than . Although the thermodynamic fingerprints at corroborate the VBS scenario, fully in line with the opening of a spin gap seen by other probes (Section 2.2), the non-zero value of in the limit [26] remains elusive. The latter phenomenology was taken as evidence for a QSL state [26], but it was noted early on that the Sommerfeld coefficient was extracted over a confined dynamic range 0.3–1.5 K and entails only 2.5% of [106]. It is unlikely that such a small entropy reflects a bulk QSL phase and, instead, it was suggested that reflects domain wall fluctuations of a valence-bond glass [89]. Certainly, the rich insights from the specific heat measurements by Yamashita, Nakazawa, and coworkers [26,76] aroused large attention over the past decade and will remain subject of vivid discussions also in the upcoming years.
2.3.2. Vibrational Spectroscopy and NQR
Naturally, strong effects on the crystal lattice can be monitored also by vibrational probes. For example, the integrated phonon intensity (Figure 6b) probed by THz time-domain spectroscopy [102] exhibits a similar peak-like behavior as the thermal expansion coefficient . Although the spectral weight enhancement was initially assigned to the collective excitation of intra-dimer electric dipoles [102], frequency-domain THz measurements combined with thorough phonon calculations later identified these spectral features around 30 cm as lattice vibrations [57]. A close look at the resonance frequency of the charge-sensitive mid-infrared mode reveals a small increase in resonance frequency when cooling below 6 K [107], which is even smaller than the modest increase in linewidth by a few cm above observed in Raman measurements of the mode [108]. Although this is much smaller than charge disproportionation in charge-ordered compounds such as -(BEDT-TTF)Hg(SCN)Cl [109], it does not rule out minor differences of molecular ionicities on the order of 0.01e within BEDT-TTF tetramers carrying a spin singlet.
Another probe of structural changes is nuclear quadrupolar resonance (NQR) as it is sensitive to electric field gradients. In the case of -(BEDT-TTF)Cu(CN), Cu and Cu nuclei with are located within the anion layer, such that coupling to the spin degrees of freedom is small. The Cu relaxation rate in Figure 6c exhibits a sharp peak at [103], clearly distinct from the drop of seen in NMR [34,67], which is plotted in panel (e). In agreement with the thermal expansion results [81] this indicates a structural modification with possible symmetry breaking accompanying the opening of a spin gap at . Still, the involvement of a small charge disproportionation cannot be ruled out, as mentioned in the previous paragraph. Overall, the NQR results provide solid evidence that the ’6K anomaly’ is a second-order phase transition [103].
Despite these robust experimental signatures, it is noted that the relative length changes around amount to [81], which is more than one order of magnitude lower than the resolution of low-temperature X-ray studies [110]. In view of this small displacement, it is not surprising that the NQR spectra by Kobayashi et al. [103] did not reveal any significant modification. Therefore, a precise determination of the low-temperature lattice structure, required to reveal possible symmetry breaking, remains a desideratum for future experimental endeavours.
2.4. B–T Phase Diagram of the Spin-Gapped Ground State
Like all spin-singlet phases, also a VBS breaks down at sufficiently high magnetic fields. Upon preparation of this Review, the author realized that no estimate for the critical field of the nonmagnetic ground state of -(BEDT-TTF)Cu(CN) has been reported in literature so far. The field dependences of the spin properties— coincides at for 2 T (H) and 8 T (C; see Figure 4b and Figure 6e)—and the thermal expansion anomaly [81,111] are negligible for T. To that end, measurements with sizeable changes at larger magnetic fields are assessed. The ’6K anomaly’ in sound velocity [112] and microwave experiments [113] yields a weak but noticeable reduction by –0.5 K upon applying a magnetic field of 16 T. Figure 7a shows the field-dependent transition temperatures for different samples and microwave measurement frequencies from Ref. [113]. Although the value varies, which was assigned to small strains imposed to the single crystals mounted on a resonator [113], the field dependence is pretty similar and follows a BCS-type mean-field behavior . This phenomenology is similar to -(BEDT-TTF)B(CN) [73], as well as the spin-Peierls systems CuGeO and TMTTFPF close to [79,114,115,116,117], as illustrated by plotting their transitions on normalized field and temperature scales in Figure 7b.
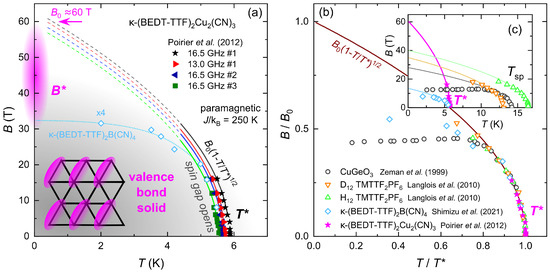
Figure 7.
(a) Field-temperature phase diagram of -(BEDT-TTF)Cu(CN) extracted from Ref. [113]. At small fields, the transition follows a BCS-type behavior with T. The sample (–) and frequency (13.0, 16.5 GHz) dependences of were assigned to different strain and microwave power conditions [113]. Light blue open diamonds indicate the transition in -(BEDT-TTF)B(CN) (from NMR measurements in Ref. [73]), for which the magnetic field values have been multiplied by a factor 4. It is suggested that the VBS state is suppressed by a critical field of 30–60 T. (b) Upon normalizing to and , the low-field data of the two -(BEDT-TTF) compounds [73,113] collapse with those of the spin-Peierls transitions in TMTTFPF and CuGeO [116,117]. Deviations from mean-field-like BCS behavior set in when has reduced below 80% of , which is indicated in (a) by the dashed extrapolated lines. (c) Despite its comparatively low transition temperature, -(BEDT-TTF)Cu(CN) yields the largest .
BCS-type behavior holds only close to and deviations occur for . In these systems, a plateau value smaller than the extrapolation is approached towards . Although the critical field is close to in CuGeO [116], it acquires a larger value for the organic compounds [73,117]. In -(BEDT-TTF)Cu(CN), a field strength T is associated with the BCS-type behavior. Comparison to the other VBS systems suggests that is in a range between 30 and 60 T. This is, to the author’s knowledge, the first estimate for the critical field of the VBS phase of -(BEDT-TTF)Cu(CN). It should be considered as a rough benchmark since the available data span a comparatively small dynamic range ( reduces by 10% in Ref. [113]).
A priori, such a huge seems excessively large as it is much bigger than that of -(BEDT-TTF)B(CN) —despite a similar [73]. This is indicated in Figure 7a, where its transition approximately matches that of the title compound upon multiplying the magnetic field values by a factor 4. Moreover, the critical field of -(BEDT-TTF)Cu(CN) is even higher than in the linear-chain spin-Peierls systems with transition temperatures more than twice as big [116,117], as seen by extrapolating from the BCS-type behavior in Figure 7c. One can only speculate about the physical reason for the extreme robustness towards external magnetic fields, whether it originates from a strongly disordered arrangement in form of a valence bond glass [89], from the two-dimensionality (as compared to the quasi 1D materials mentioned above) or from strong geometrical frustration that suppresses competing spin phases. To approach this issue, it is assessed whether the large value of is reasonable from a thermodynamic point of view. As discussed in Section 2.3.1, the entropy release at the ’6K anomaly’ (1 JKmol) amounts to 17% of JKmol [26]. In a rough estimate, 17% of the magnetic energy of paramagnetic spins coupled with K [34] corresponds to a field of 63 T, which is in the right ball park as T deduced from Figure 7a.
Note, an impurity response is seen also in the microwave signal below and becomes entirely suppressed for T [113], consistent with a complete polarization of impurities as put forward in Ref. [82] (see discussion in Section 2.2.2). Additionally, the pronounced frequency dependence of the impurity contribution is reasonable as the involved energy scale at GHz [113] corresponds to T. The large facilitates high-field studies of the magnetic properties, e.g., around 25 T where impurities are fully polarized (>99%) even at the transition, which is still at a temperature K easily reachable with standard He cryostats.
3. Conclusions and Outlook
Taken together, the anomalies around K in the magnetic, thermodynamic, thermal transport, and structural properties of -(BEDT-TTF)Cu(CN) summarized in Figure 3, Figure 4, Figure 5 and Figure 6 are consistent with a spin-gapped VBS state, similar to that reported in the layered organic Mott systems -(BEDT-TTF)B(CN) [72,73] and EtMeP[Pd(dmit)] [68,69,70,71]. Notably, already small amounts of disorder and defects are sufficient to conceal the intrinsic response of valence electrons in various magnetic probes [82], precluding a proper identification of the magnetic ground state in the past. This is elaborated in detail in Section 2.2.1 and Section 2.2.2, which highlight the fingerprints of impurity spins in the magnetic susceptibility and NMR spin-lattice relaxation rate , respectively. This review provides a straightforward strategy to identify possible nonmagnetic ground states of other QSL candidate systems based on their signatures in (i) magnetic (through field-dependent studies and magnetic resonance probes [27,34,67,82]), (ii) heat transport [93], and (iii) thermal expansion [81] experiments. A particular take-home message is that a circumstantial evaluation of these distinct physical properties is required to distinguish among various spin phases, such as AFM, VBS, or QSL.
Since its first synthesis 30 years ago [29], the quality of -(BEDT-TTF)Cu(CN) single crystals has been successively optimized enabling multifaceted experimental scrutiny. Other frustrated materials that came up more recently, such as -(BEDT-TTF)Hg(SCN)Br which was predicted to exhibit a quantum dipole liquid state [118], require more in-depth investigation. Difficulties with the crystal growth complicated a more circumstantial investigation of the QSL candidate -(BEDT-TTF)Ag(CN)–only two groups (Hiramatsu/Yoshida/Saito [39,40] and Hübner/Dressel [45]) have succeeded to synthesize it so far. Here, dilatometric experiments revealed an anisotropic structural anomaly around 11 K [119] reminiscent of Figure 6a. In view of the gapped excitations concluded from thermal transport experiments [95,96], thermal expansion studies on EtMeSb[Pd(dmit)] may provide useful information. Although dilatometric investigations on this compound were not reported so far, they can possibly reveal structural changes similar to the ‘6K anomaly’ in -(BEDT-TTF)Cu(CN) [81] and the VBS transition in EtMeP[Pd(dmit)] [71]; so far, no such anomaly has been identified in ultrasonic measurements along the out-of-plane direction of the dmit-based QSL candidate [120]. Additionally, the NMR properties of -(BEDT-TTF)Ag(CN) [39] and EtMeSb[Pd(dmit)] [36,37] show intriguing similarities with the behavior discussed in Figure 4, but thorough ESR investigations such as those of Miksch et al. [27] are pending.
Do Quantum Spin Liquids Exist in Solids?
In addition to various QSL phases predicted by theory [2,3,4,5], it remains unclear to what extent the required conditions can be satisfied in materials. Recently, there have been promising results towards topological QSL states in optical lattices of Rydberg atoms [13], but, strictly speaking, these systems lack a crucial component of crystalline solids: Magneto-elastic coupling among the valence electron spins and the lattice. The body of experimental data on -(BEDT-TTF)Cu(CN) discussed here suggests that the coupling of antiferromagnetically interacting spins to structural degrees of freedom becomes a crucial factor in essentially bulk materials upon approaching . Sooner or later, the system minimizes its energy by escaping from paramagnetic configurations of localized spins towards AFM or nonmagnetic states. In fact, NMR, NQR and thermal transport experiments lately provided evidence for spin-gapped singlets and the absence of fermionic spin excitations also in the paradigmatic kagome compound Herbertsmithite [23,25,121], which is subject to pronounced magneto-elastic coupling [122,123]–the pairing glue of VBS states.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The author declares that the data supporting the findings of this study are available within the paper. Further information can be provided by A.P.
Acknowledgments
The author thanks R. Valentí, S.E. Brown, M. Dressel and A. Kawamoto for fruitful discussions.
Conflicts of Interest
The author declares no conflict of interest.
References
- Anderson, P.W. Resonating valence bonds: A new kind of insulator? Mater. Res. Bull. 1973, 8, 153–160. [Google Scholar] [CrossRef]
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Savary, L.; Balents, L. Quantum spin liquids: A review. Rep. Prog. Phys. 2017, 80, 016502. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Kanoda, K.; Ng, T.K. Quantum spin liquid states. Rev. Mod. Phys. 2017, 89, 25003. [Google Scholar] [CrossRef]
- Broholm, C.; Cava, R.J.; Kivelson, S.A.; Nocera, D.G.; Norman, M.R.; Senthil, T. Quantum spin liquids. Science 2020, 367, eaay0668. [Google Scholar] [CrossRef] [Green Version]
- Powell, B.J.; McKenzie, R.H. Quantum frustration in organic Mott insulators: From spin liquids to unconventional superconductors. Rep. Prog. Phys. 2011, 74, 56501. [Google Scholar] [CrossRef]
- Kanoda, K.; Kato, R. Mott Physics in Organic Conductors with Triangular Lattices. Annu. Rev. Condens. Matter Phys. 2011, 2, 167–188. [Google Scholar] [CrossRef]
- Shen, Y.; Li, Y.D.; Wo, H.; Li, Y.; Shen, S.; Pan, B.; Wang, Q.; Walker, H.C.; Steffens, P.; Boehm, M.; et al. Evidence for a spinon Fermi surface in a triangular-lattice quantum-spin-liquid candidate. Nature 2016, 540, 559–562. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Zhang, J.; Li, Y.S.; Yu, Y.J.; Hong, X.C.; Zhang, Q.M.; Li, S.Y. Absence of Magnetic Thermal Conductivity in the Quantum Spin-Liquid Candidate YbMgGaO4. Phys. Rev. Lett. 2016, 117, 267202. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Adroja, D.; Bewley, R.I.; Voneshen, D.; Tsirlin, A.A.; Gegenwart, P.; Zhang, Q. Crystalline Electric-Field Randomness in the Triangular Lattice Spin-Liquid YbMgGaO4. Phys. Rev. Lett. 2017, 118, 107202. [Google Scholar] [CrossRef] [Green Version]
- Norman, M.R. Colloquium: Herbertsmithite and the search for the quantum spin liquid. Rev. Mod. Phys. 2016, 88, 041002. [Google Scholar] [CrossRef] [Green Version]
- Puphal, P.; Zoch, K.M.; Désor, J.; Bolte, M.; Krellner, C. Kagome quantum spin systems in the atacamite family. Phys. Rev. Mater. 2018, 2, 63402. [Google Scholar] [CrossRef] [Green Version]
- Semeghini, G.; Levine, H.; Keesling, A.; Ebadi, S.; Wang, T.; Bluvstein, D.; Verresen, R.; Pichler, P.; Kalinowski, K.; Samajdar, R.; et al. Probing topological spin liquids on a programmable quantum simulator. Science 2021, 374, 1242–1247. [Google Scholar] [CrossRef]
- Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006, 321, 2–111. [Google Scholar] [CrossRef] [Green Version]
- Singh, Y.; Gegenwart, P. Antiferromagnetic Mott insulating state in single crystals of the honeycomb lattice material Na2IrO3. Phys. Rev. B 2010, 82, 64412. [Google Scholar] [CrossRef]
- Plumb, K.W.; Clancy, J.P.; Sandilands, L.J.; Shankar, V.V.; Hu, Y.F.; Burch, K.S.; Kee, H.Y.; Kim, Y.J. α-RuCl3: A spin-orbit assisted Mott insulator on a honeycomb lattice. Phys. Rev. B 2014, 90, 41112. [Google Scholar] [CrossRef] [Green Version]
- Johnson, R.D.; Williams, S.C.; Haghighirad, A.A.; Singleton, J.; Zapf, V.; Manuel, P.; Mazin, I.I.; Li, Y.; Jeschke, H.O.; Valentí, R.; et al. Monoclinic crystal structure of α-RuCl3 and the zigzag antiferromagnetic ground state. Phys. Rev. B 2015, 92, 235119. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A.; Bridges, C.A.; Yan, J.Q.; Aczel, A.A.; Li, L.; Stone, M.B.; Granroth, G.E.; Lumsden, M.D.; Yiu, Y.; Knolle, J.; et al. Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet. Nat. Mater. 2016, 15, 733. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A.; Yan, J.; Knolle, J.; Bridges, C.A.; Stone, M.B.; Lumsden, M.D.; Mandrus, D.G.; Tennant, D.A.; Moessner, R.; Nagler, S.E. Neutron scattering in the proximate quantum spin liquid α-RuCl3. Science 2017, 356, 1055–1059. [Google Scholar] [CrossRef] [Green Version]
- Takagi, H.; Takayama, T.; Jackeli, G.; Khaliullin, G.; Nagler, S.E. Concept and realization of Kitaev quantum spin liquids. Nat. Rev. Phys. 2019, 1, 264–280. [Google Scholar] [CrossRef]
- Lee, S.S.; Lee, P.A. U(1) Gauge Theory of the Hubbard Model: Spin Liquid States and Possible Application to κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. Lett. 2005, 95, 36403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ng, T.K.; Lee, P.A. Power-Law Conductivity inside the Mott Gap: Application to κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. Lett. 2007, 99, 156402. [Google Scholar] [CrossRef] [Green Version]
- Fu, M.; Imai, T.; Han, T.H.; Lee, Y.S. Evidence for a gapped spin-liquid ground state in a kagome Heisenberg antiferromagnet. Science 2015, 350, 655–658. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khuntia, P.; Velazquez, M.; Barthélemy, Q.; Bert, F.; Kermarrec, E.; Legros, A.; Bernu, B.; Messio, L.; Zorko, A.; Mendels, P. Gapless ground state in the archetypal quantum kagome antiferromagnet ZnCu3(OH)6Cl2. Nat. Phys. 2020, 16, 469–474. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, W.; Singer, P.M.; Smaha, R.W.; He, W.; Wen, J.; Lee, Y.S.; Imai, T. Emergence of spin singlets with inhomogeneous gaps in the kagome lattice Heisenberg antiferromagnets Zn-barlowite and herbertsmithite. Nat. Phys. 2021, 17, 1109–1113. [Google Scholar] [CrossRef]
- Yamashita, S.; Nakazawa, Y.; Oguni, M.; Oshima, Y.; Nojiri, H.; Shimizu, Y.; Miyagawa, K.; Kanoda, K. Thermodynamic properties of a spin-1/2 spin-liquid state in a [kappa]-type organic salt. Nat. Phys. 2008, 4, 459–462. [Google Scholar] [CrossRef] [Green Version]
- Miksch, B.; Pustogow, A.; Javaheri Rahim, M.; Bardin, A.A.; Kanoda, K.; Schlueter, J.A.; Hübner, R.; Scheffler, M.; Dressel, M. Gapped magnetic ground state in quantum spin liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Science 2021, 372, 276–279. [Google Scholar] [CrossRef]
- Dressel, M.; Tomić, S. Molecular quantum materials: Electronic phases and charge dynamics in two-dimensional organic solids. Adv. Phys. 2020, 69, 1–120. [Google Scholar] [CrossRef]
- Geiser, U.; Wang, H.H.; Carlson, K.D.; Williams, J.M.; Charlier, H.A.; Heindl, J.E.; Yaconi, G.A.; Love, B.J.; Lathrop, M.W.; Schirber, J.E.; et al. Superconductivity at 2.8 K and 1.5 kbar in κ-(BEDT-TTF)2Cu2(CN)3: The first organic superconductor containing a polymeric copper cyanide anion. Inorg. Chem. 1991, 30, 2586–2588. [Google Scholar] [CrossRef]
- Komatsu, T.; Matsukawa, N.; Inoue, T.; Saito, G. Realization of Superconductivity at Ambient Pressure by Band-Filling Control in κ-(BEDT-TTF)2Cu2(CN)3. J. Phys. Soc. Jpn. 1996, 65, 1340–1354. [Google Scholar] [CrossRef]
- Kurosaki, Y.; Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Saito, G. Mott Transition from a Spin Liquid to a Fermi Liquid in the Spin-Frustrated Organic Conductor κ-(ET)2Cu2(CN)3. Phys. Rev. Lett. 2005, 95, 177001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shimizu, Y.; Kasahara, H.; Furuta, T.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Pressure-induced superconductivity and Mott transition in spin-liquid κ-(ET)2Cu2(CN)3 probed by 13C NMR. Phys. Rev. B 2010, 81, 224508. [Google Scholar] [CrossRef]
- Shimizu, Y.; Maesato, M.; Saito, G. Uniaxial Strain Effects on Mott and Superconducting Transitions in κ-(ET)2Cu2(CN)3. J. Phys. Soc. Jpn. 2011, 80, 74702. [Google Scholar] [CrossRef]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice. Phys. Rev. Lett. 2003, 91, 107001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kandpal, H.C.; Opahle, I.; Zhang, Y.Z.; Jeschke, H.O.; Valentí, R. Revision of Model Parameters for κ-Type Charge Transfer Salts: An Ab Initio Study. Phys. Rev. Lett. 2009, 103, 67004. [Google Scholar] [CrossRef] [Green Version]
- Itou, T.; Oyamada, A.; Maegawa, S.; Tamura, M.; Kato, R. Quantum spin liquid in the spin-1/2 triangular antiferromagnet EtMe3Sb[Pd(dmit)2]2. Phys. Rev. B 2008, 77, 104413. [Google Scholar] [CrossRef]
- Itou, T.; Oyamada, A.; Maegawa, S.; Kato, R. Instability of a quantum spin liquid in an organic triangular-lattice antiferromagnet. Nat. Phys. 2010, 6, 673–676. [Google Scholar] [CrossRef]
- Yamashita, S.; Yamamoto, T.; Nakazawa, Y.; Tamura, M.; Kato, R. Gapless spin liquid of an organic triangular compound evidenced by thermodynamic measurements. Nat. Commun. 2011, 2, 275. [Google Scholar] [CrossRef]
- Shimizu, Y.; Hiramatsu, T.; Maesato, M.; Otsuka, A.; Yamochi, H.; Ono, A.; Itoh, M.; Yoshida, M.; Takigawa, M.; Yoshida, Y.; et al. Pressure-Tuned Exchange Coupling of a Quantum Spin Liquid in the Molecular Triangular Lattice κ-(ET)2Ag2(CN)3. Phys. Rev. Lett. 2016, 117, 107203. [Google Scholar] [CrossRef] [Green Version]
- Hiramatsu, T.; Yoshida, Y.; Saito, G.; Otsuka, A.; Yamochi, H.; Maesato, M.; Shimizu, Y.; Ito, H.; Nakamura, Y.; Kishida, H.; et al. Design and Preparation of a Quantum Spin Liquid Candidate κ-(ET)2Ag2(CN)3 Having a Nearby Superconductivity. Bull. Chem. Soc. Jpn. 2017, 90, 1073–1082. [Google Scholar] [CrossRef]
- Isono, T.; Kamo, H.; Ueda, A.; Takahashi, K.; Kimata, M.; Tajima, H.; Tsuchiya, S.; Terashima, T.; Uji, S.; Mori, H. Gapless Quantum Spin Liquid in an Organic Spin-1/2 Triangular-Lattice κ-H3(Cat-EDT-TTF)2. Phys. Rev. Lett. 2014, 112, 177201. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, S.; Nakazawa, Y.; Ueda, A.; Mori, H. Thermodynamics of the quantum spin liquid state of the single-component dimer Mott system κ-H3(Cat-EDT-TTF)2. Phys. Rev. B 2017, 95, 184425. [Google Scholar] [CrossRef] [Green Version]
- Furukawa, T.; Miyagawa, K.; Taniguchi, H.; Kato, R.; Kanoda, K. Quantum criticality of Mott transition in organic materials. Nat. Phys. 2015, 11, 221–224. [Google Scholar] [CrossRef] [Green Version]
- Pustogow, A.; Rösslhuber, R.; Tan, Y.; Uykur, E.; Böhme, A.; Wenzel, M.; Saito, Y.; Löhle, A.; Hübner, R.; Schlueter, J.A.; et al. Low-temperature dielectric anomaly arising from electronic phase separation at the Mott insulator-metal transition. NPJ Quantum Mater. 2021, 6, 9. [Google Scholar] [CrossRef]
- Pustogow, A.; Bories, M.; Löhle, A.; Rösslhuber, R.; Zhukova, E.; Gorshunov, B.; Tomić, S.; Schlueter, J.A.; Hübner, R.; Hiramatsu, T.; et al. Quantum spin liquids unveil the genuine Mott state. Nat. Mater. 2018, 17, 773–777. [Google Scholar] [CrossRef]
- Pustogow, A.; Saito, Y.; Löhle, A.; Sanz Alonso, M.; Kawamoto, A.; Dobrosavljević, V.; Dressel, M.; Fratini, S. Rise and fall of Landau’s quasiparticles while approaching the Mott transition. Nat. Commun. 2021, 12, 1571. [Google Scholar] [CrossRef]
- Keimer, B.; Kivelson, S.A.; Norman, M.R.; Uchida, S.; Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 2015, 518, 179–186. [Google Scholar] [CrossRef]
- Hansmann, P.; Toschi, A.; Sangiovanni, G.; Saha-Dasgupta, T.; Lupi, S.; Marsi, M.; Held, K. Mott–Hubbard transition in V2O3 revisited. Phys. Status Solidi B 2013, 250, 1251–1264. [Google Scholar] [CrossRef] [Green Version]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef] [Green Version]
- Vollhardt, D. Dynamical mean-field theory for correlated electrons. Ann. Phys. (Berl.) 2012, 524, 1–19. [Google Scholar] [CrossRef]
- Limelette, P.; Georges, A.; Jérome, D.; Wzietek, P.; Metcalf, P.; Honig, J.M. Universality and Critical Behavior at the Mott Transition. Science 2003, 302, 89–92. [Google Scholar] [CrossRef] [Green Version]
- Limelette, P.; Wzietek, P.; Florens, S.; Georges, A.; Costi, T.A.; Pasquier, C.; Jérome, D.; Mézière, C.; Batail, P. Mott Transition and Transport Crossovers in the Organic Compound κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. Lett. 2003, 91, 16401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McLeod, A.S.; van Heumen, E.; Ramirez, J.G.; Wang, S.; Saerbeck, T.; Guenon, S.; Goldflam, M.; Anderegg, L.; Kelly, P.; Mueller, A.; et al. Nanotextured phase coexistence in the correlated insulator V2O3. Nat. Phys. 2016, 13, 80–86. [Google Scholar] [CrossRef] [Green Version]
- Terletska, H.; Vučičević, J.; Tanasković, D.; Dobrosavljević, V. Quantum Critical Transport near the Mott Transition. Phys. Rev. Lett. 2011, 107, 26401. [Google Scholar] [CrossRef] [PubMed]
- Vučičević, J.; Terletska, H.; Tanasković, D.; Dobrosavljević, V. Finite-temperature crossover and the quantum Widom line near the Mott transition. Phys. Rev. B 2013, 88, 75143. [Google Scholar] [CrossRef] [Green Version]
- Pinterić, M.; Čulo, M.; Milat, O.; Basletić, M.; Korin-Hamzić, B.; Tafra, E.; Hamzić, A.; Ivek, T.; Peterseim, T.; Miyagawa, K.; et al. Anisotropic charge dynamics in the quantum spin-liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2014, 90, 195139. [Google Scholar] [CrossRef] [Green Version]
- Dressel, M.; Lazić, P.; Pustogow, A.; Zhukova, E.; Gorshunov, B.; Schlueter, J.A.; Milat, O.; Gumhalter, B.; Tomić, S. Lattice vibrations of the charge-transfer salt κ-(BEDT-TTF)2Cu2(CN)3: Comprehensive explanation of the electrodynamic response in a spin-liquid compound. Phys. Rev. B 2016, 93, 081201. [Google Scholar] [CrossRef] [Green Version]
- Padmalekha, K.G.; Blankenhorn, M.; Ivek, T.; Bogani, L.; Schlueter, J.A.; Dressel, M. ESR studies on the spin-liquid candidate κ-(BEDT-TTF)2Cu2(CN)3: Anomalous response below T = 8 K. Phys. B Condens. Matter 2015, 460, 211–213. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Jawad, M.; Terasaki, I.; Sasaki, T.; Yoneyama, N.; Kobayashi, N.; Uesu, Y.; Hotta, C. Anomalous dielectric response in the dimer Mott insulator κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2010, 82, 125119. [Google Scholar] [CrossRef] [Green Version]
- Hotta, C. Quantum electric dipoles in spin-liquid dimer Mott insulator κ-ET2Cu2(CN)3. Phys. Rev. B 2010, 82, 241104. [Google Scholar] [CrossRef] [Green Version]
- Lunkenheimer, P.; Müller, J.; Krohns, S.; Schrettle, F.; Loidl, A.; Hartmann, B.; Rommel, R.; de Souza, M.; Hotta, C.; Schlueter, J.A.; et al. Multiferroicity in an organic charge-transfer salt that is suggestive of electric-dipole-driven magnetism. Nat. Mater. 2012, 11, 755. [Google Scholar] [CrossRef] [PubMed]
- Gati, E.; Winter, S.M.; Schlueter, J.A.; Schubert, H.; Müller, J.; Lang, M. Insights from experiment and ab initio calculations into the glasslike transition in the molecular conductor κ-(BEDT–TTF)2Hg(SCN)2Cl. Phys. Rev. B 2018, 97, 75115. [Google Scholar] [CrossRef] [Green Version]
- Fukuyama, H.; Kishine, J.I.; Ogata, M. Energy Landscape of Charge Excitations in the Boundary Region between Dimer–Mott and Charge Ordered States in Molecular Solids. J. Phys. Soc. Jpn. 2017, 86, 123706. [Google Scholar] [CrossRef]
- Furukawa, T.; Kobashi, K.; Kurosaki, Y.; Miyagawa, K.; Kanoda, K. Quasi-continuous transition from a Fermi liquid to a spin liquid in κ-(ET)2Cu2(CN)3. Nat. Commun. 2018, 9, 307. [Google Scholar] [CrossRef] [Green Version]
- Miyagawa, K.; Kawamoto, A.; Nakazawa, Y.; Kanoda, K. Antiferromagnetic Ordering and Spin Structure in the Organic Conductor, κ–(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. Lett. 1995, 75, 1174–1177. [Google Scholar] [CrossRef]
- Lefebvre, S.; Wzietek, P.; Brown, S.; Bourbonnais, C.; Jérome, D.; Mézière, C.; Fourmigué, M.; Batail, P. Mott transition, antiferromagnetism, and unconventional superconductivity in layered organic superconductors. Phys. Rev. Lett. 2000, 85, 5420–5423. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Emergence of inhomogeneous moments from spin liquid in the triangular-lattice Mott insulator κ-(ET)2Cu2(CN)3. Phys. Rev. B 2006, 73, 140407. [Google Scholar] [CrossRef] [Green Version]
- Tamura, M.; Nakao, A.; Kato, R. Frustration-Induced Valence-Bond Ordering in a New Quantum Triangular Antiferromagnet Based on [Pd(dmit)2]. J. Phys. Soc. Jpn. 2006, 75, 93701. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, Y.; Akimoto, H.; Tsujii, H.; Tajima, A.; Kato, R. Mott Transition in a Valence-Bond Solid Insulator with a Triangular Lattice. Phys. Rev. Lett. 2007, 99, 256403. [Google Scholar] [CrossRef] [Green Version]
- Itou, T.; Oyamada, A.; Maegawa, S.; Kubo, K.; Yamamoto, H.M.; Kato, R. Superconductivity on the border of a spin-gapped Mott insulator: NMR studies of the quasi-two-dimensional organic system EtMe3P[Pd(dmit)2]2. Phys. Rev. B 2009, 79, 174517. [Google Scholar] [CrossRef]
- Manna, R.S.; de Souza, M.; Kato, R.; Lang, M. Lattice effects in the quasi-two-dimensional valence-bond-solid Mott insulator EtMe3P[Pd(dmit)2]2. Phys. Rev. B 2014, 89, 45113. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, Y.; Ito, H.; Maesato, M.; Shimizu, Y.; Hayama, H.; Hiramatsu, T.; Nakamura, Y.; Kishida, H.; Koretsune, T.; Hotta, C.; et al. Spin-disordered quantum phases in a quasi-one-dimensional triangular lattice. Nat. Phys. 2015, 11, 679–683. [Google Scholar] [CrossRef]
- Shimizu, Y.; Maesato, M.; Yoshida, M.; Takigawa, M.; Itoh, M.; Otsuka, A.; Yamochi, H.; Yoshida, Y.; Kawaguchi, G.; Graf, D.; et al. Magnetic field driven transition between valence bond solid and antiferromagnetic order in a distorted triangular lattice. Phys. Rev. Res. 2021, 3, 23145. [Google Scholar] [CrossRef]
- Richardson, R.C. The Pomeranchuk effect. Rev. Mod. Phys. 1997, 69, 683–690. [Google Scholar] [CrossRef]
- Rozen, A.; Park, J.M.; Zondiner, U.; Cao, Y.; Rodan-Legrain, D.; Taniguchi, T.; Watanabe, K.; Oreg, Y.; Stern, A.; Berg, E.; et al. Entropic evidence for a Pomeranchuk effect in magic-angle graphene. Nature 2021, 592, 214–219. [Google Scholar] [CrossRef]
- Nakazawa, Y.; Yamashita, S. Thermodynamics of a Liquid-like Spin State in Molecule-based Magnets with Geometric Frustrations. Chem. Lett. 2013, 42, 1446–1454. [Google Scholar] [CrossRef]
- Mizukoshi, K.; Nakamura, Y.; Yoshida, Y.; Saito, G.; Kishida, H. Optical Evaluation of Electronic Anisotropy in a Triangular Lattice System κ-(BEDT-TTF)2B(CN)4. J. Phys. Soc. Jpn. 2018, 87, 104708. [Google Scholar] [CrossRef]
- Dumm, M.; Loidl, A.; Alavi, B.; Starkey, K.P.; Montgomery, L.K.; Dressel, M. Comprehensive ESR study of the antiferromagnetic ground states in the one-dimensional spin systems (TMTSF)2PF6,(TMTSF)2AsF6, and (TMTTF)2Br. Phys. Rev. B 2000, 62, 6512–6520. [Google Scholar] [CrossRef]
- Hase, M.; Terasaki, I.; Uchinokura, K. Observation of the spin-Peierls transition in linear Cu2+ (spin-1/2) chains in an inorganic compound CuGeO3. Phys. Rev. Lett. 1993, 70, 3651–3654. [Google Scholar] [CrossRef]
- Isobe, M.; Ueda, Y. Magnetic Susceptibility of Quasi-One-Dimensional Compound α’- NaV2O5 –Possible Spin-Peierls Compound with High Critical Temperature of 34 K–. J. Phys. Soc. Jpn. 1996, 65, 1178–1181. [Google Scholar] [CrossRef]
- Manna, R.S.; de Souza, M.; Brühl, A.; Schlueter, J.A.; Lang, M. Lattice Effects and Entropy Release at the Low-Temperature Phase Transition in the Spin-Liquid Candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. Lett. 2010, 104, 16403. [Google Scholar] [CrossRef] [PubMed]
- Pustogow, A.; Le, T.; Wang, H.H.; Luo, Y.; Gati, E.; Schubert, H.; Lang, M.; Brown, S.E. Impurity moments conceal low-energy relaxation of quantum spin liquids. Phys. Rev. B 2020, 101, 140401. [Google Scholar] [CrossRef] [Green Version]
- Saito, Y.; Minamidate, T.; Kawamoto, A.; Matsunaga, N.; Nomura, K. Site-specific 13C NMR study on the locally distorted triangular lattice of the organic conductor κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2018, 98, 205141. [Google Scholar] [CrossRef] [Green Version]
- Olariu, A.; Mendels, P.; Bert, F.; Duc, F.; Trombe, J.C.; de Vries, M.A.; Harrison, A. 17O NMR Study of the Intrinsic Magnetic Susceptibility and Spin Dynamics of the Quantum Kagome Antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. Lett. 2008, 100, 87202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freedman, D.E.; Han, T.H.; Prodi, A.; Müller, P.; Huang, Q.Z.; Chen, Y.S.; Webb, S.M.; Lee, Y.S.; McQueen, T.M.; Nocera, D.G. Site Specific X-ray Anomalous Dispersion of the Geometrically Frustrated Kagomé Magnet, Herbertsmithite, ZnCu3(OH)6Cl2. J. Am. Chem. Soc. 2010, 132, 16185–16190. [Google Scholar] [CrossRef]
- Zhu, Z.; Maksimov, P.A.; White, S.R.; Chernyshev, A.L. Disorder-Induced Mimicry of a Spin Liquid in YbMgGaO4. Phys. Rev. Lett. 2017, 119, 157201. [Google Scholar] [CrossRef] [Green Version]
- Kimchi, I.; Nahum, A.; Senthil, T. Valence Bonds in Random Quantum Magnets: Theory and Application to YbMgGaO4. Phys. Rev. X 2018, 8, 31028. [Google Scholar] [CrossRef] [Green Version]
- Itou, T.; Watanabe, E.; Maegawa, S.; Tajima, A.; Tajima, N.; Kubo, K.; Kato, R.; Kanoda, K. Slow dynamics of electrons at a metal-Mott insulator boundary in an organic system with disorder. Sci. Adv. 2017, 3, e1601594. [Google Scholar] [CrossRef] [Green Version]
- Riedl, K.; Valentí, R.; Winter, S.M. Critical spin liquid versus valence-bond glass in a triangular-lattice organic antiferromagnet. Nat. Commun. 2019, 10, 2561. [Google Scholar] [CrossRef] [Green Version]
- Isono, T.; Terashima, T.; Miyagawa, K.; Kanoda, K.; Uji, S. Quantum criticality in an organic spin-liquid insulator κ-(BEDT-TTF)2Cu2(CN)3. Nat. Commun. 2016, 7, 13494. [Google Scholar] [CrossRef] [Green Version]
- Abragam, A. Principles of Nuclear Magnetism; Oxford University Press: Hong Kong, China, 1983. [Google Scholar]
- Pratt, F.L.; Baker, P.J.; Blundell, S.J.; Lancaster, T.; Ohira-Kawamura, S.; Baines, C.; Shimizu, Y.; Kanoda, K.; Watanabe, I.; Saito, G. Magnetic and non-magnetic phases of a quantum spin liquid. Nature 2011, 471, 612. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, M.; Nakata, N.; Kasahara, Y.; Sasaki, T.; Yoneyama, N.; Kobayashi, N.; Fujimoto, S.; Shibauchi, T.; Matsuda, Y. Thermal-transport measurements in a quantum spin-liquid state of the frustrated triangular magnet nphys1134-m6gif1601313-(BEDT-TTF)2Cu2(CN)3. Nat. Phys. 2009, 5, 44–47. [Google Scholar] [CrossRef] [Green Version]
- Yamashita, M.; Nakata, N.; Senshu, Y.; Nagata, M.; Yamamoto, H.M.; Kato, R.; Shibauchi, T.; Matsuda, Y. Highly Mobile Gapless Excitations in a Two-Dimensional Candidate Quantum Spin Liquid. Science 2010, 328, 1246–1248. [Google Scholar] [CrossRef] [PubMed]
- Bourgeois-Hope, P.; Laliberté, F.; Lefrançois, E.; Grissonnanche, G.; de Cotret, S.R.; Gordon, R.; Kitou, S.; Sawa, H.; Cui, H.; Kato, R.; et al. Thermal Conductivity of the Quantum Spin Liquid Candidate EtMe3Sb[Pd(dmit)2]2: No Evidence of Mobile Gapless Excitations. Phys. Rev. X 2019, 9, 41051. [Google Scholar] [CrossRef] [Green Version]
- Ni, J.M.; Pan, B.L.; Song, B.Q.; Huang, Y.Y.; Zeng, J.Y.; Yu, Y.J.; Cheng, E.J.; Wang, L.S.; Dai, D.Z.; Kato, R.; et al. Absence of Magnetic Thermal Conductivity in the Quantum Spin Liquid Candidate EtMe3Sb[Pd(dmit)2]2. Phys. Rev. Lett. 2019, 123, 247204. [Google Scholar] [CrossRef] [Green Version]
- Yamashita, M.; Sato, Y.; Tominaga, T.; Kasahara, Y.; Kasahara, S.; Cui, H.; Kato, R.; Shibauchi, T.; Matsuda, Y. Presence and absence of itinerant gapless excitations in the quantum spin liquid candidate EtMe3Sb[Pd( dmit )2]2. Phys. Rev. B 2020, 101, 140407. [Google Scholar] [CrossRef] [Green Version]
- Kato, R.; Uebe, M.; Fujiyama, S.; Hengbo, C. A Discrepancy in thermal conductivity measurement data of quantum spin liquid β′-EtMe3Sb[Pd(dmit)2]2 (dmit = 1,3-dithiol-2-thione-4,5-dithiolate). Crystals 2022, 12, 102. [Google Scholar] [CrossRef]
- Ando, Y.; Takeya, J.; Sisson, D.L.; Doettinger, S.G.; Tanaka, I.; Feigelson, R.S.; Kapitulnik, A. Thermal conductivity of the spin-Peierls compound CuGeO3. Phys. Rev. B 1998, 58, R2913–R2916. [Google Scholar] [CrossRef] [Green Version]
- Vasil’ev, A.N.; Pryadun, V.V.; Khomskii, D.I.; Dhalenne, G.; Revcolevschi, A.; Isobe, M.; Ueda, Y. Anomalous Thermal Conductivity of NaV2O5 as Compared to Conventional Spin-Peierls System CuGeO3. Phys. Rev. Lett. 1998, 81, 1949–1952. [Google Scholar] [CrossRef] [Green Version]
- Gregor, K.; Motrunich, O.I. Nonmagnetic impurities in a S = 12 frustrated triangular antiferromagnet: Broadening of 13C NMR lines in κ-(ET)2Cu2(CN)3. Phys. Rev. B 2009, 79, 24421. [Google Scholar] [CrossRef] [Green Version]
- Itoh, K.; Itoh, H.; Naka, M.; Saito, S.; Hosako, I.; Yoneyama, N.; Ishihara, S.; Sasaki, T.; Iwai, S. Collective Excitation of an Electric Dipole on a Molecular Dimer in an Organic Dimer-Mott Insulator. Phys. Rev. Lett. 2013, 110, 106401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kobayashi, T.; Ding, Q.P.; Taniguchi, H.; Satoh, K.; Kawamoto, A.; Furukawa, Y. Charge disproportionation in the spin-liquid candidate κ-(ET)2Cu2(CN)3 at 6 K revealed by 63Cu NQR measurements. Phys. Rev. Res. 2020, 2, 42023. [Google Scholar] [CrossRef]
- de Souza, M.; Brühl, A.; Müller, J.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.P.; Lang, M. Thermodynamic studies at the charge-ordering and spin-Peierls transitions in (TMTTF)2X. Phys. B Condens. Matter 2009, 404, 494–498. [Google Scholar] [CrossRef]
- Winkelmann, H.; Gamper, E.; Büchner, B.; Braden, M.; Revcolevschi, A.; Dhalenne, G. Giant anomalies of the thermal expansion at the spin-Peierls transition in CuGeO3. Phys. Rev. B 1995, 51, 12884–12887. [Google Scholar] [CrossRef]
- Ramirez, A.P. A flood or a trickle? Nat. Phys. 2008, 4, 442–443. [Google Scholar] [CrossRef]
- Sedlmeier, K.; Elsässer, S.; Neubauer, D.; Beyer, R.; Wu, D.; Ivek, T.; Tomić, S.; Schlueter, J.A.; Dressel, M. Absence of charge order in the dimerized κ-phase BEDT-TTF salts. Phys. Rev. B 2012, 86, 245103. [Google Scholar] [CrossRef] [Green Version]
- Yakushi, K.; Yamamoto, K.; Yamamoto, T.; Saito, Y.; Kawamoto, A. Raman Spectroscopy Study of Charge Fluctuation in the Spin-Liquid Candidate κ-(BEDT-TTF)2Cu2(CN)3. J. Phys. Soc. Jpn. 2015, 84, 84711. [Google Scholar] [CrossRef]
- Drichko, N.; Beyer, R.; Rose, E.; Dressel, M.; Schlueter, J.A.; Turunova, S.A.; Zhilyaeva, E.I.; Lyubovskaya, R.N. Metallic state and charge-order metal-insulator transition in the quasi-two-dimensional conductor κ-(BEDT-TTF)2Hg(SCN)2Cl. Phys. Rev. B 2014, 89, 75133. [Google Scholar] [CrossRef]
- Jeschke, H.O.; de Souza, M.; Valentí, R.; Manna, R.S.; Lang, M.; Schlueter, J.A. Temperature dependence of structural and electronic properties of the spin-liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2012, 85, 35125. [Google Scholar] [CrossRef] [Green Version]
- Manna, R.S.; Hartmann, S.; Gati, E.; Schlueter, J.A.; De Souza, M.; Lang, M. Low-Temperature Lattice Effects in the Spin-Liquid Candidate κ-(BEDT-TTF)2Cu2(CN)3. Crystals 2018, 8, 87. [Google Scholar] [CrossRef] [Green Version]
- Poirier, M.; de Lafontaine, M.; Miyagawa, K.; Kanoda, K.; Shimizu, Y. Ultrasonic investigation of the transition at 6 K in the spin-liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2014, 89, 45138. [Google Scholar] [CrossRef]
- Poirier, M.; Parent, S.; Côté, A.; Miyagawa, K.; Kanoda, K.; Shimizu, Y. Magnetodielectric effects and spin-charge coupling in the spin-liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2012, 85, 134444. [Google Scholar] [CrossRef]
- Cross, M.C.; Fisher, D.S. A new theory of the spin-Peierls transition with special relevance to the experiments on TTFCuBDT. Phys. Rev. B 1979, 19, 402–419. [Google Scholar] [CrossRef] [Green Version]
- Cross, M.C. Effect of magnetic fields on a spin-Peierls transition. Phys. Rev. B 1979, 20, 4606–4611. [Google Scholar] [CrossRef] [Green Version]
- Zeman, J.; Martinez, G.; van Loosdrecht, P.H.M.; Dhalenne, G.; Revcolevschi, A. Scaling of the H- T Phase Diagram of CuGeO3. Phys. Rev. Lett. 1999, 83, 2648–2651. [Google Scholar] [CrossRef] [Green Version]
- Langlois, A.; Poirier, M.; Bourbonnais, C.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.P. Microwave dielectric study of spin-Peierls and charge-ordering transitions in (TMTTF)2PF6 salts. Phys. Rev. B 2010, 81, 125101. [Google Scholar] [CrossRef] [Green Version]
- Hassan, N.; Cunningham, S.; Mourigal, M.; Zhilyaeva, E.I.; Torunova, S.A.; Lyubovskaya, R.N.; Schlueter, J.A.; Drichko, N. Evidence for a quantum dipole liquid state in an organic quasi–two-dimensional material. Science 2018, 360, 1101–1104. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, S.; Gati, E.; Yoshida, Y.; Saito, G.; Lang, M. Thermal Expansion Studies on the Spin-Liquid-Candidate System κ-(BEDT-TTF)2Ag2(CN)3. Phys. Status Solidi B 2019, 256, 1800640. [Google Scholar] [CrossRef]
- Poirier, M.; Proulx, M.O.; Kato, R. Ultrasonic investigation of the organic spin-liquid compound EtMe3Sb[Pd(dmit)2]2. Phys. Rev. B 2014, 90, 45147. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Xu, Y.; Wang, L.; Zhao, C.C.; Tu, C.P.; Ni, J.M.; Wang, L.S.; Pan, B.L.; Fu, Y.; Hao, Z.; et al. Heat Transport in Herbertsmithite: Can a Quantum Spin Liquid Survive Disorder? Phys. Rev. Lett. 2021, 127, 267202. [Google Scholar] [CrossRef]
- Sushkov, A.B.; Jenkins, G.S.; Han, T.H.; Lee, Y.S.; Drew, D.H. Infrared phonons as a probe of spin-liquid states in herbertsmithite ZnCu3(OH)6Cl2. J. Phys. Condens. Matter 2017, 29, 95802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Pustogow, A.; Bories, M.; Puphal, P.; Krellner, C.; Dressel, M.; Valentí, R. Lattice dynamics in the spin-12 frustrated kagome compound herbertsmithite. Phys. Rev. B 2020, 101, 161115. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).