Mixed-Alkali Effect in Borate Glasses: Thermal, Elastic, and Vibrational Properties

Abstract

When oxide glasses are modified by dissimilar alkali ions, a maximum in the electric resistivity or the expansion coefficient appears, called the mixed-alkali effect (MAE). This paper reviews the MAE on the thermal, elastic, and vibrational properties of the mixed-cesium lithium borate glasses, x{(1−y)Cs₂O-yLi₂O}-(1−x)B₂O₃. For the single-alkali borate glasses, xM₂O(1−x)-B₂O₃ (M = Li, Na, K, Rb, and Cs), the glass transition temperature, T_g = 270 °C, of a borate glass monotonically increases as the alkali content x increases. However, for the mixed-cesium lithium borate glasses the T_g shows the minimum against the lithium fraction y. The dependences of the elastic properties on the lithium fraction y were discussed regarding the longitudinal modulus, Poisson’s ratio, and Cauchy-type relation. The internal vibrational bands related to the boron-oxide structural groups and the splitting of a boson peak were discussed based on Raman scattering spectroscopy. The MAE on various physical properties are discussed on the basis of the changes in the coordination number of the borons and the nonbridging oxygens caused by the dissimilar alkali ions.

1. Borate Glass and Alkali Modification

Crystals and crystalline materials have a three-dimensional periodic structure with translational and point symmetries, therefore, their physical properties are anisotropic. Glasses and amorphous materials have a random structure with no translational symmetry and no point symmetry, therefore their macroscopic physical properties are isotropic. A glass is formed through a liquid-glass transition by rapid cooling from a supercooled liquid state into a nonequilibrium glassy state. Various kinds of organic and inorganic glasses are known among polymers, drugs, minerals, metals, semiconductors, etc. Among the inorganic glasses, oxide network glasses such as SiO₂, B₂O₃, and P₂O₃, have attracted much attention for their widespread practical applications by the combination of hardness and transparency at room temperature. The network structure of oxide glasses is remarkably modified by alkali ions, and such a modification has been used to control the various physical properties of glasses such as the glass transition temperatures, elastic properties, etc.

Borate glass (B₂O₃) is one of the typical covalent network glasses. The network structure of the borate glass is formed by randomly connected planar BO₃ triangles and most of them form planar boroxol B₃O₆ rings [1]. Alkali metals remarkably modify the network structure of a borate glass, and the variation in the microscopic structure and related physical properties as a function of the alkali content has been extensively studied. The alkali ions in a borate glass induce the change of the boron coordination number of a boron atom from three to four and non-bridging oxygens are created as alkali content increases. Due to these changes of the covalent bonds in the network structure, various kinds of structural groups are formed such as pentaborate, dipentaborate, diborate, triborate, metabolite, etc., depending the alkali metals and their contents [2,3]. A rich variation of the structural units causes remarkable changes in the various physical properties. For example, the Poisson’s ratio of cesium borate glasses shows a minima and maxima with the increasing cesium content [4]. Such non-linear variations in the various physical quantities versus the alkali contents are called a “borate anomaly”.

The medium range order (MRO) is the arrangement of the structural units, which controls various physical properties such as the elastic constants and density. The MRO is estimated by the first sharp diffraction peak (FSDP) in the static structure factor, S(Q), measured by the neutron and X-ray diffraction experiments. The peak width ∆Q_fsdp of FSDP corresponds to a structural correlation length of L_fsdp = 2π/∆Q_fsdp, which defines the MRO. The peak value Q_fsdp corresponds to the real-space ordering with a periodicity of 2π/Q_fsdp [5]. Figure 1a shows the static structure factor S(Q) of the single-alkali borate glasses, 0.22M₂O-0.78B₂O₃ (M = Li, Na, K, Rb, and Cs) measured by neutron scattering [6]. The FSDP and the second peak are denoted by Q₁ and Q₂, respectively, in Figure 1a. The MRO correlation length L_fsdp = 2π/∆Q_fsdp was determined from the width of a peak at Q₁, i.e., ∆Q₁. The correlation between L_fsdp and the ionic radius R_ion [7] is shown in Figure 1b. For the larger alkali ions, L_fsdp is nearly proportional to R_ion. This relation indicates that a larger alkali ion occupies a void in the B-O network structure, while a smaller alkali ion M⁺ locates near a BO₄⁻ tetrahedron.

According to the study of the packing in alkali modified oxide glasses by Giri et al., ionic and covalent packings were discussed in terms of the relative volumes of the modified alkali cations compared to that of the networking forming oxygen [8]. For modifying alkali ions (K, Rb, and Cs) having an ionic radius larger than oxygen, the packing is dominated by the modifier alkali ions, and it is called ionic packing. Therefore, the linear relation between L_fsdp and the ionic radius R_ion nearly holds for the larger alkali ions. For the alkali ions (Li and Na) having an ionic radius smaller than oxygen, the packing is controlled by the oxygen covalent network, and it is called covalent packing. For the smaller alkali ions, the linear relation between L_fsdp and the ionic radius R_ion does not hold.

By modification of the oxide glasses by two dissimilar alkali ions, the maximum electric resistivity or the expansion coefficient were observed [9,10,11,12]. Such an anomalous variation is called the mixed-alkali effect (MAE) caused by the coexistence of two dissimilar alkali ions. For the various transport properties, such as the ionic conductivity and viscosity, a remarkable deviation from linearity was observed when one alkali cation substitutes for another at the totally fixed content of the alkali metals. In the MAE, interactions between dissimilar cations reduce their mobility, and remarkably affect the dynamic properties. Such interactions were thought to be associated with network-mediated “pairs” of dissimilar alkali ions, which are energetically favored relative to pairs of similar alkalis [13]. These non-linear behaviors are technologically important for developing low-loss electrical glasses. The non-transport physical properties, such as density, glass transition temperature, and elastic modulus, also reveal noticeable deviations from the linear variation of the alkali contents. However, the physical origins of the MAE on these non-transport properties are not yet clarified. This paper reviews the MAE of the borate glasses studied of the thermal analysis, neutron diffraction, ultrasonic method, Brillouin scattering, Raman scattering, and neutron inelastic scattering on the mixed-cesium lithium borate glasses, x{(1−y)Cs₂O-yLi₂O}-(1−x)B₂O₃. The glass transition temperature, heat capacity, elastic constants, internal Raman bands, and boson peaks show the deviation from the linear relation to lithium fraction. These various physical properties are discussed on the basis of the changes of coordination number of boron, creation of non-bridging oxygen, and dissimilar alkali ion pairs.

2. Glass Transition Temperatures

In various kinds of glasses, the liquid-glass transition temperature, T_g, has been extensively studied. However, the understanding of the nature of the T_g is still not enough. Kauzmann suggested the empirical relation, T_g ~ 2/3T_melt, where T_melt is the melting temperature [14]. Tanaka studied the correlation between the T_g and the average coordination number, z, per atom in covalent glasses. He found the empirical relation, ln T_g ≈ 1.6 K × z + 2.3 K, and it holds well for chalcogenide glasses [15]. Although there have been many studies to understand the nature of the glass transition, and to relate T_g to the glass network connectivity, there is still no universal relationship satisfied by almost all kinds of glass formers [16].

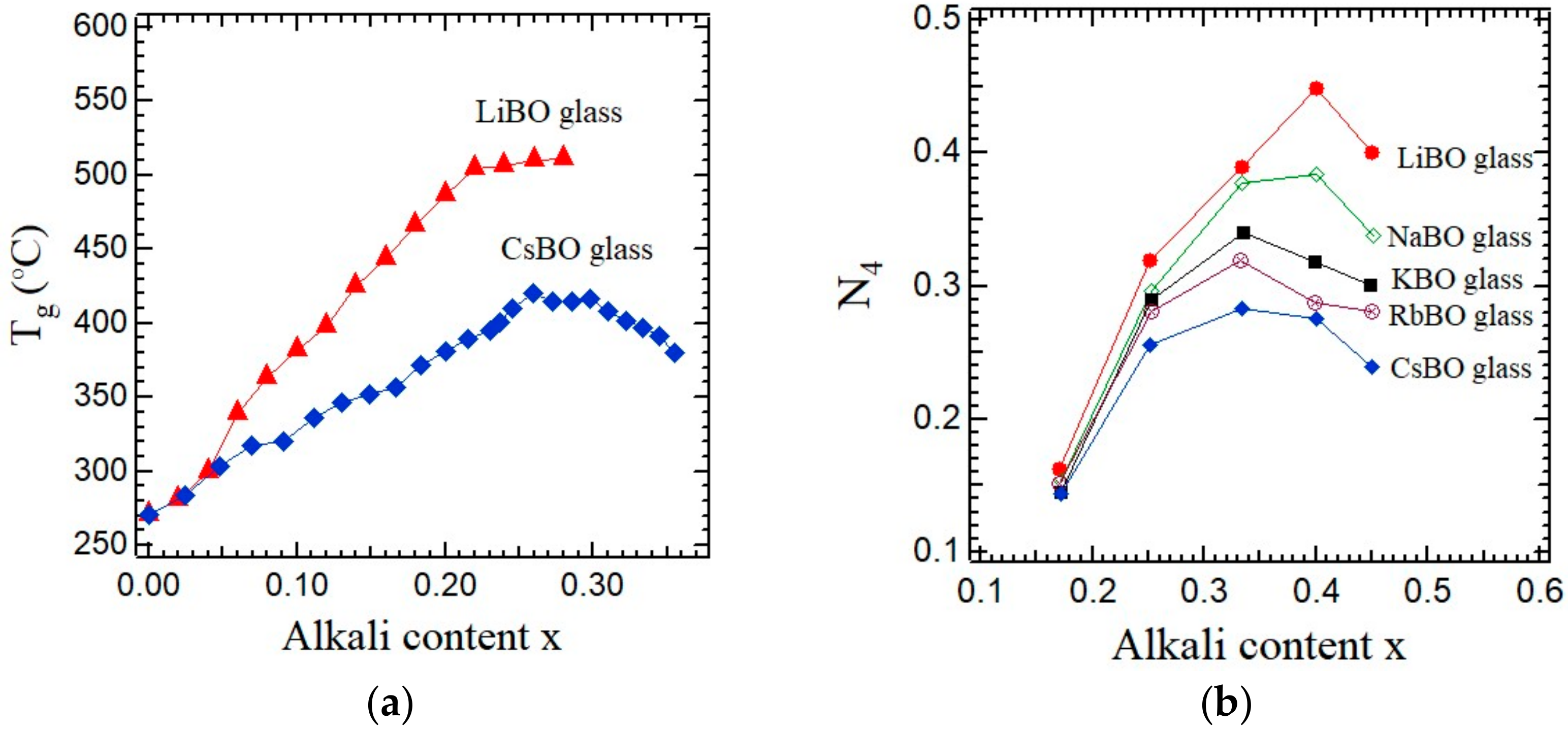
The T_g of single-lithium and cesium borate glasses show remarkable alkali content dependences as shown in Figure 2a [4]. In the single-lithium borate glasses, the T_g monotonically increases as the Li content x increases. In the single-cesium borate glasses, the T_g monotonically increases at first as the Cs content x increases. The maximum of the T_g appears at about x = 0.28, then decreases with a further increase in x. The difference in the alkali content dependences of the T_g between the lithium and cesium borate glasses is closely related to the difference in their network structures. Regarding the lithium borate glasses, Kerner discussed the relation between the T_g and the average coordination number of the glass former atoms [17]. However, the relation for other alkali borate glasses was not discussed.

Zhong and Bray studied the alkali dependence of the number fractions of boron with three and four coordination numbers in the single-alkali borate glasses, xM₂O-(1−x)B₂O₃ (M = Li, Na, K, Rb, and Cs), using NMR [18]. The coordination number of boron in the pure borate glass is three, while by the alkali modification, it changes to four and non-bridging oxygens are created. The number fractions of boron atoms with three and four coordination numbers are denoted by N₃ and N₄, respectively, where N₃ + N₄ = 1. In the single-alkali borate glasses, the correlation between the T_g and N₄ was reported as shown in Figure 2b [18]. The variations of the T_g and N₄ versus the alkali content x in Figure 2a,b are qualitatively in agreement. The variation of N₄ on the alkali content presumably arises from the competition between the two processes [4]. One process is the formation of BØ₄⁻ units with 4-coordinated boron, where Ø is a bridging oxygen and the positive alkali ion M⁺ is adjacent to the negative BØ₄⁻ unit to keep the local charge neutrality. As the alkali ion size decreases, this process is enhanced. In the lithium borate glass, this process is more active than that in the cesium borate glass. Another process is the formation of a negative nonbridging oxygen (NBO), O, on a BØ₂O⁻ unit. The positive alkali ion M⁺ is adjacent to the negative O⁻. As the alkali ion size increases, the negative Coulombic potential energy of the B-Ø–M⁺ configuration may decrease. In the cesium borate glass, this second process is more active than that in the lithium borate glass. Based on a comparison of plots of the lithium and cesium borate glasses between Figure 2a,b, the larger N₄ of the lithium borate glass is related to the higher T_g of the lithium borate glass. These results indicate that the first process of N₄ is more effective for the increase in the T_g.

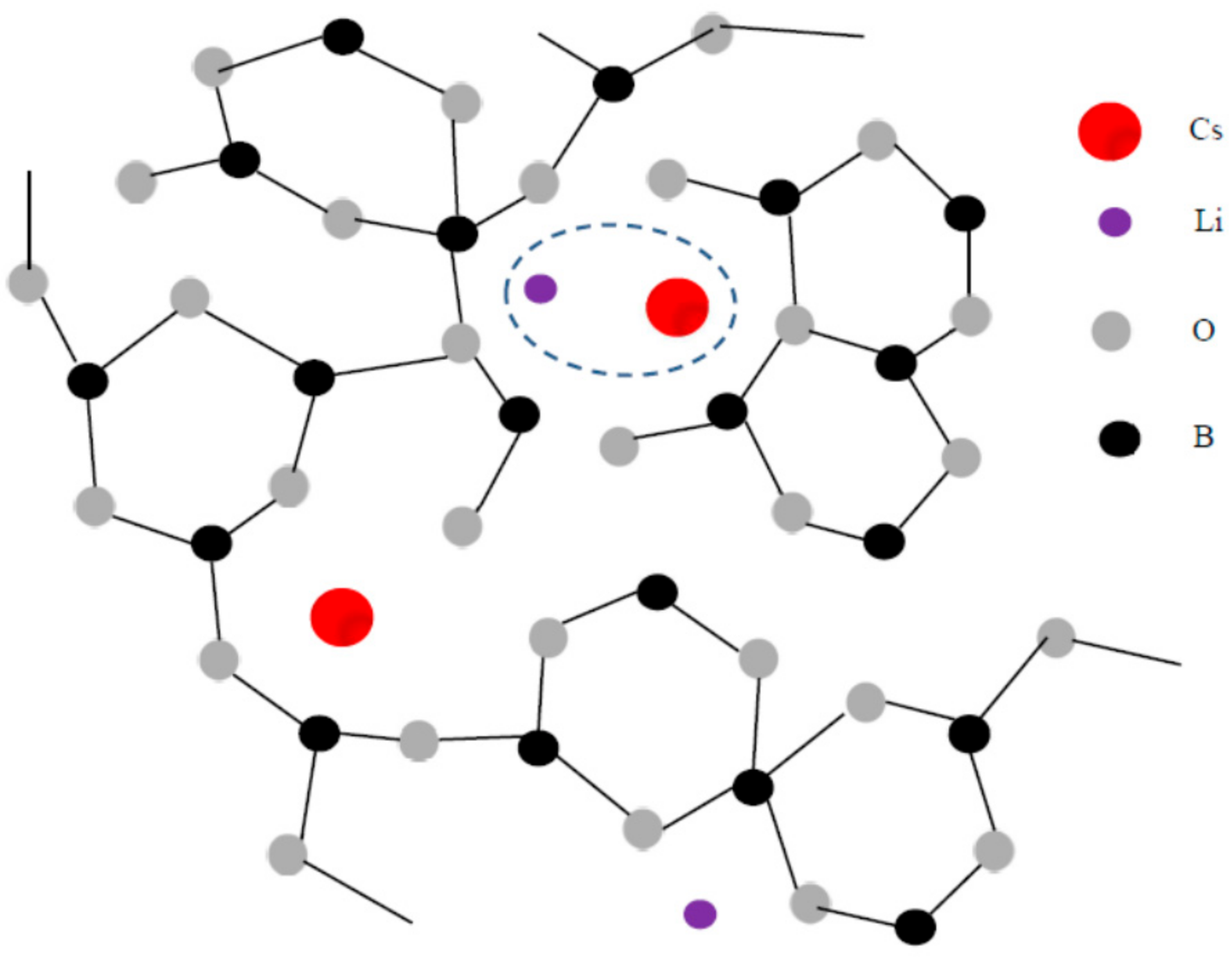
Next, we discuss the MAE on T_g. A schematic illustration of a mixed-lithium cesium borate glass is shown in Figure 3. As discussed in Section 1. “Borate glass and alkali modification” using the FSDP of a static structure factor S(Q), a smaller Li⁺ ion with the ionic radius of 0.60 A locates near the B atom, while a larger Cs⁺ ion with the ionic radius of 1.69 A locates in a larger void of the B-O network. Zhong and Bray also studied the MAE on the T_g by NMR [18]. They found that the measured N₄ for the mixed-alkali borate glasses is less than the N₄ (average) value expected from a simple superposition calculated by the following equation:

N₄ (average) = 0.5 N₄ (Li) + 0.5 N₄ (other alkali).

(1)

In some cases, N₄ (average) is even less than either of the N₄ values for the relevant single-alkali borate glasses. Ingram [19] made the following assumptions in an effort to explain the MAE: (1) in a mixed-alkali glass there is a preponderance of mixed-alkali pairs, e.g., (LiK)²⁺ as compared to the alkali pairs, e.g., (LiLi)²⁺; and (2) these mixed-alkali pairs are effectively immobilized.

Figure 4 shows the Li fraction y dependence of the T_g of the mixed-lithium cesium borate glasses, 0.28{(1−y)Cs₂O-yLi₂O}-0.72B₂O₃. The solid line shows the linear relation. A negative deviation from the linear dependence is clearly observed. The minimum glass transition temperature at about y = 0.2 was observed for the Li fraction y dependence of a fixed alkali content. By using the molecular dynamic simulations, Vegiri et al. reported that the abundance of the BØ₄⁻ units decreases from the single-lithium to cesium glasses and exhibits a negative deviation from linearity in the mixed-cesium lithium glasses [13]. The existence of a minimum at about y = 0.2 suggests a decrease in N₄ or an increase of the non-bridging oxygen around this fraction by the MAE. A similar minimum of the T_g for the constant alkali content was also reported in the mixed-cesium sodium borate glasses, 0.33{(1−y)Cs₂O-yNa₂O}-0.67B₂O₃, and a correlation was shown between T_g and N₄ determined by the infrared absorption [20]. A molecular dynamics investigation of mixed-alkali borate glasses reported that the abundance of BØ₄⁻ units was found to decrease from Li to Cs and to exhibit a negative deviation from linearity in the mixed-cesium lithium borate glasses [13]. The dissimilar (CsLi)²⁺ pair may locate in a larger void, and it suppresses the formation of the BØ₄⁻ units. The existence of a dissimilar pair can be the origin of the minimum T_g at about y = 0.2 in Figure 4.

3. Excess Heat Capacity at Low Temperatures

Glasses reveal the universal features of their thermal properties at low temperatures. The heat capacity shows an excess part and the thermal conductivity has a plateau at around 10 K [22,23]. These anomalous behaviors are closely related to the phonon dispersion in the terahertz frequency (THz) range. The excess heat capacity has been observed as the deviation from the Debye T³ law at low temperatures. The broad peak in a C_p/T³ vs. T plot is observed by this non-Debye excess heat capacity, where C_p is the heat capacity at a constant pressure. In the B₂O₃ glass, the peak of C_p/T³ was observed at the peak temperature, T_m = 5.8 K [24]. The origin of a peak is the low-energy excess part of the vibrational density of states (VDoS) over the Debye model defined by g(E)/E², where g(E) is VDoS. The peak of g(E)/E² has also been observed in the THz range of the inelastic scattering spectra, which is called the boson peak (BP) [23,25]. The temperature dependences of the heat capacity of the single-alkali borate glasses, 0.22M₂O-0.78B₂O₃ (M = Li, Na, K, Rb, Cs), were reported between 2 K and 150 K by the relaxation method [26]. With an increase in the ionic radius of the alkali ion, the T_m of C_p/T³ decreases. This fact is attributed to the enhancement of the contraction of the boron-oxygen network by the increase in the alkali charge density due to the decrease in the alkali ionic radius. It was found that the T_m is proportional to the shear modulus μ measured by an ultrasonic method.

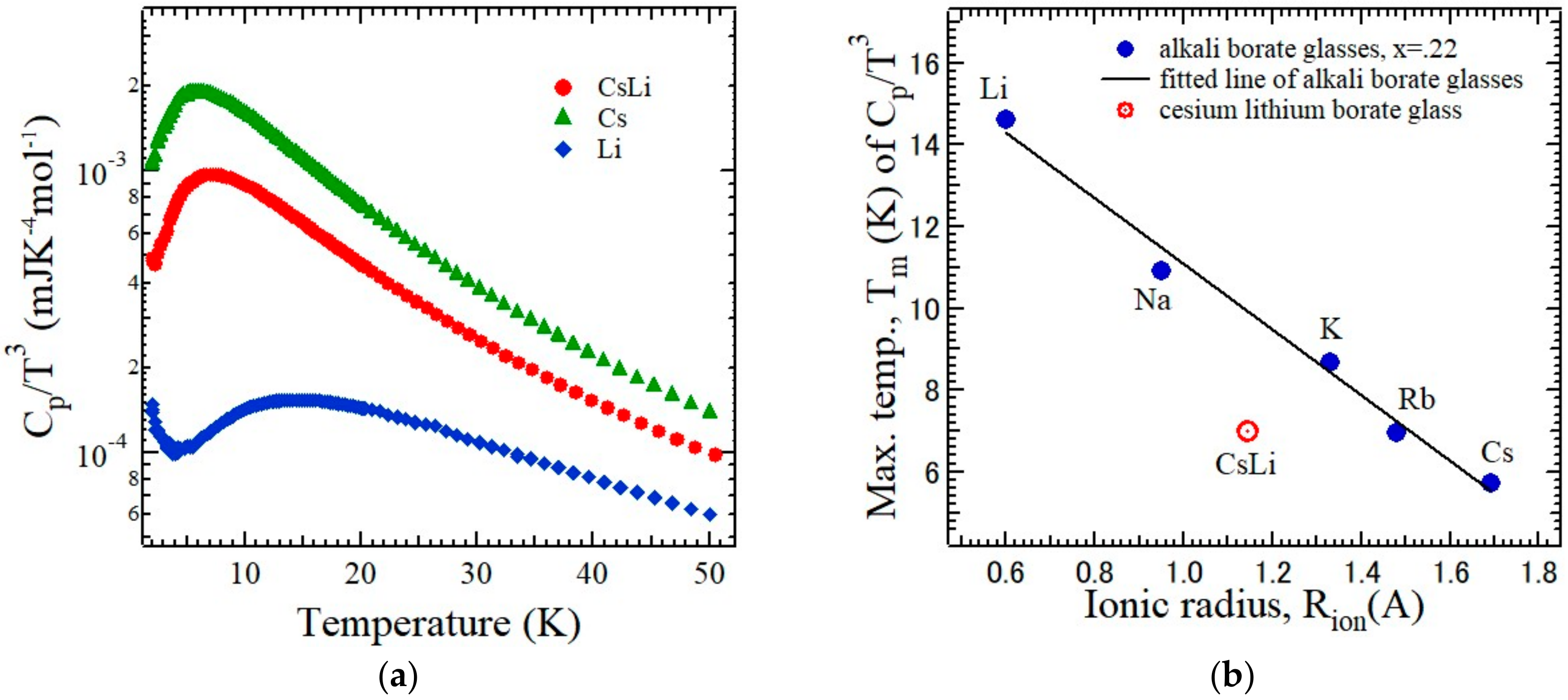
The temperature dependences of the heat capacity C_p of the mixed-alkali borate glasses, 0.11M₂O-0.11 M’₂O-0.78B₂O₃ (M, M’ = Li, K, and Cs), were measured using a relaxation calorimeter to investigate the MAE [27]. In order to discuss the excess heat capacity, the temperature dependence of C_p/T³ of a mixed-lithium cesium (LiCs) borate glass (M = Li, M’ = Cs) is plotted to investigate the deviation from the Debye T³ law at low temperatures as shown in Figure 5a, where the dependences of the single-cesium borate (M = M’ = Cs) and single-lithium borate (M = M’ = Li) glasses are also plotted for comparison [26]. The broad peaks of C_p/T³ were observed with the T_m in the range 5–15 K for all three glasses. To clarify the MAE, the T_m of the single-alkali and mixed-alkali borate glasses was plotted versus the ionic radius of alkali ion as shown in Figure 5b, where the ionic radius of the mixed-alkali glass is the arithmetical mean of the radius of the two alkali ions. The significant negative deviation of T_m of a mixed-cesium lithium borate glass from that of linearity of the single-alkali borate glasses between the alkali cation size and T_m was clearly observed. When two dissimilar alkali species are co-doped, a different modification of the boron-oxygen network appears. The number of the BØ₄⁻ units, N₄, in a mixed-alkali glass was lower than the value expected from that of a single-alkali borate glass. The result of molecular dynamic simulations predicted that the N₄ decreases from lithium to cesium in the mixed-cesium lithium glasses [20]. The negative deviation of T_m in the mixed-cesium lithium glass can be attributed to the decrease in the N₄ caused by the dissimilar alkali mixing. The existence of the (CsLi)²⁺ dissimilar pair may be the origin of the negative deviation in Figure 5b.

4. Elastic Properties

4.1. Longitudinal Modulus

The elastic properties are also sensitive for the network structure of the glasses. Since glasses are isotropic, the following elastic constants are defined, where V_L and V_T are the longitudinal and transverse sound velocities, respectively, and ρ is the density:

Poisson’s ratio: σ = (V_L² − 2V_T²)/2(V_L² − V_T²)

(2)

Longitudinal modulus: L = ρVL2

(3)

Shear modulus: μ = ρV_T²

(4)

In the single-alkali borate glasses, the longitudinal and transverse sound velocities were determined by ultrasonic pulse-echo methods at 10 MHz. The various elastic constants reveal the remarkable and non-linear dependences on the alkali contents. For example, the alkali content dependences of the longitudinal modulus, L, of alkali borate glasses are shown in Figure 6a [4].

For the single-alkali borate glasses, xM₂O-(1−x)B₂O₃ (M = Li, Na, K, Rb, and Cs) in the low alkali content range of 0 ≤ x ≤ 0.1, the plot of L versus the alkali content monotonically increases in the same way irrespective of the difference in the alkali ions [4]. This means that all kinds of alkali ions fill the voids of the initial B₂O₃ glass network in the same way. Above the content of x = 0.1, the elastic constants depend both on the species of the alkali ion, M⁺, and their content, x. These variations of L in the range x > 0.1 are related to the short-range three structural units, namely BØ₃, M⁺BØ₄⁻, and M⁺BOØ₂⁻. The L value increases when the structural unit M⁺BØ₄⁻ is formed, while L decreases when the other structural unit M⁺BOØ₂⁻ is formed. There is a correlation between the L value and the mole fraction of M⁺BØ₄⁻ or M⁺BOØ₂⁻, denoted by m₄ or by m₂, respectively.

In the single-lithium borate glass, L monotonically increases with the increase in x over the bulk glass formation range below x = 0.28, which is about 0.1 smaller than the other single-alkali borate glasses. This means that the formation of Li⁺BØ₄⁻ dominates over the formation of Li⁺BOØ₂⁻. Therefore, it holds that m₄ >> m₂ for the lithium borate glasses. In contrast, the L of the cesium borate glasses exhibits two peaks at about x = 0.10 and 0.30, and such variation in L is approximately divided into four characteristic x ranges:

(I)

the first range between x = 0 and 0.10 is defined as the range between the pure B₂O₃ and the first maximum at about x = 0.10. With the addition of M₂O (M = Li, Na, K, Rb, and Cs) to B₂O₃, BØ₃ is converted only into M⁺BØ₄⁻ and no M⁺BOØ₂⁻ is formed in this range.

(II)

the second range between x = 0.10 and 0.20 is defined as the range between the first maximum at about x = 0.10 and the minimum at about x = 0.20. L decreases as the alkali ions are changed from Li⁺ to Cs⁺. As a result, the mole fraction of M⁺BOØ₂⁻ increases, while the mole fraction of M⁺BØ₄⁻ decreases from the sodium to cesium borate glasses.

(III)

the third range between x = 0.20 and 0.30 is defined as the range between the minimum at about x = 0.20 and the second maximum at about x = 0.30. L decreases from the lithium to cesium borate glasses, while L in the third range is greater than that in the second range. The mole fraction of M⁺BØ₄⁻ increases, while the mole fraction of M⁺BOØ₂⁻ decreases from the sodium to cesium borate glasses. As a result, x₂ takes a maximum at about x = 0.20.

(IV)

the fourth range of x ≥ 0.30 is defined as the range above the second maximum at about x = 0.30. L gradually increases, then decreases in this range except for the lithium borate glass. As a result, no more M⁺BØ₄⁻ is formed in this range. The second maximum at about x = 0.30 is caused by the conversion of the residual BØ₃ into only M⁺BOØ₂⁻.

4.2. Poisson’s Ratio

Poisson’s ratio, σ, is defined as the ratio between the transverse contraction strain and longitudinal extension strain in a stretched bar. Previous studies of the relation of the Poisson’s ratio with the glass structure showed that it was greater than 0.25 when the ions themselves are deformed under stress in addition to the network distortion [28,29]. The alkali content dependences of Poisson’s ratio, σ, of the single-alkali borate glasses are shown in Figure 6b. All the values of the Poisson’s ratio are greater than 0.25 in the single-alkali borate glasses, and alkali ions themselves are deformed under stress. In all the single-alkali borate glasses, two minima appear, except for the lithium borate glass, due to the lower maximum of the Li content of 0.27. Since the Poisson’s ratio is related to the glass network connectivity, it is governed by the middle range super-structural borate groups. The behavior of the Poisson’s ratio is complicated, while it may be caused by the following two factors for this behavior:

(I)

One factor is the disproportionation reaction, M⁺BØ₄⁻ ⇒ M⁺BOØ₂⁻, between the borate structural units. The presence of M⁺BØ₄⁻, whose network connectivity is four, increases the connectivity with the surrounding (super) structural units, while the presence of M⁺BOØ₂⁻, whose network connectivity is two, decreases the connectivity with the surrounding (super) structural units.

(II)

The other factor is the presence of super-structural units, especially the pentaborate group, B₅O₆Ø₄⁻. The BØ₄⁻ unit that is included in a pentaborate group, whose network connectivity is also four, does not contribute to the connectivity with the surrounding (super) structural units, while the BØ₄⁻ unit itself in the pentaborate group contributes to L. Thus, the rigidity and the network connectivity are not the same concept. The presence of pentaborate groups was reported by a Raman spectroscopic study of the single-alkali borate glasses [30].

The elastic properties of the mixed-cesium lithium borate glasses, 0.28{(1−y)Cs₂O−yLi₂O}−0.72B₂O₃, were studied by Brillouin scattering. The right-angle scattering spectrum of a glass at y = 0.9 is shown in Figure 7a [22]. Peaks of the longitudinal acoustic (LA) and transverse acoustic (TA) modes were clearly observed. The Li fraction dependence of the LA and TA velocities for a constant alkali content were determined from the frequency shifts as shown in Figure 7b.

With the increase in the Li fraction y, the longitudinal modulus, L, determined from the LA velocity increases as shown in Figure 7c. From the lithium to cesium borate glasses, the mole fraction of M⁺BØ₄⁻ decreases, while the mole fraction of M⁺BOØ₂⁻ increases. The negative deviation was observed from a linear dependence of the L in Figure 7c. A similar negative deviation was also observed in the mixed-cesium lithium borate glasses, 0.25{(1−y)Cs₂O−yLi₂O}−0.75B₂O₃ [31]. These deviations show the enhancement of the change from the M⁺BØ₄⁻ to M⁺BOØ₂⁻ units caused by the appearance of dissimilar (CsLi)²⁺ pairs.

In the mixed-cesium lithium borate glasses, Poisson’s ratio was determined from the LA and TA velocities as shown in Figure 7d. The values of the Poisson’s ratio are greater than 0.25, and alkali ions themselves are deformed under stress in the mixed-alkali borate glasses. The Poisson’s ratio shows a monotonic decrease with the increasing lithium fraction. The scattering of the data points was caused by the weak intensity of the TA peaks in the Brillouin scattering spectra as shown in Figure 7a. No noticeable MAE was observed for Poisson’s ratio within the experimental uncertainty. It suggests that the influence of the MAE is slight for the glass network connectivity.

4.3. Cauchy-Type Relation

In isotropic systems, the number of independent elastic constants is only two, namely, the longitudinal (L or c₁₁) and shear (μ or c₄₄) moduli, where c₁₁ and c₄₄ are the elastic stiffness constants. Additional local symmetry conditions further reduce the number of independent elastic constants. The L/μ ratio is an indicator of the character of the force field; if atoms interact through a central potential, L/μ = 3, but if through a noncentral potential, L/μ > 3 [32]. However, most glasses are far from the central potential and the Cauchy relation, L = 3μ. The Cauchy-type relation, L = A + Bμ with B~3, was reported to hold for the high frequency limit values of the L and the μ for some types of glasses, where A is the material dependent constant [29,33].

The Cauchy-type relation holds well for the single-alkali borate and mixed-cesium lithium borate glasses as shown in Figure 8a,b, respectively [4,22]. The fitted values of the single-alkali borate glasses are A = 2.3 GPa and B = 3.1; the two values do not show a difference between the alkali ions. However, the fitted values of the mixed-cesium lithium borate glasses are A = 9.9 GPa and B = 2.8. For both glasses, the value of B is about 3, while the value of the mixed-cesium lithium borate glasses is slightly lower. The large value of A of the mixed-cesium lithium borate glasses may suggest that the MAE may induce a local anisotropy and enhance the deviation.

5. Vibrational Properties

Vibrational spectroscopy, such as Raman scattering and infrared (IR) spectroscopy, is a powerful tool to study the local atomic structure of condensed matters, especially glasses with random structures. When a center of symmetry exists, the exclusion principle holds, namely, the Raman active mode is IR inactive and the IR active mode is Raman inactive. However, glass has no center of symmetry due to its random structure. Generally, the modes higher than 200 cm⁻¹ are the internal mode of a molecule and the modes lower than 200 cm⁻¹ are the external modes reflecting the intermolecular interaction. In glasses the modes higher than 200 cm⁻¹ originate from groups of molecules and the structural units. While the modes lower than 200 cm⁻¹ originate from the vibrational modes of medium range order of the glass network structure, and the lowest frequency broad peak below 200 cm⁻¹ is called a boson peak. As discussed in Section 3, a boson peak is the low-energy excess part of the vibrational density of states (VDoS). Typical Raman scattering spectra of the alkali borate glasses between 10~1700 cm⁻¹ are shown in Figure 9 [22,34,35,36]. The remarkable variation of boson peaks below 200 cm⁻¹ was clearly observed. In addition the high frequency Raman bands above 200 cm⁻¹ also shows a noticeable variation, especially the middle frequency range between 700 and 850 cm⁻¹, where the modes of various structural units, such as the boroxol ring, pentaborate borate, metaborate groups, etc., were observed [37].

5.1. Internal Raman Bands

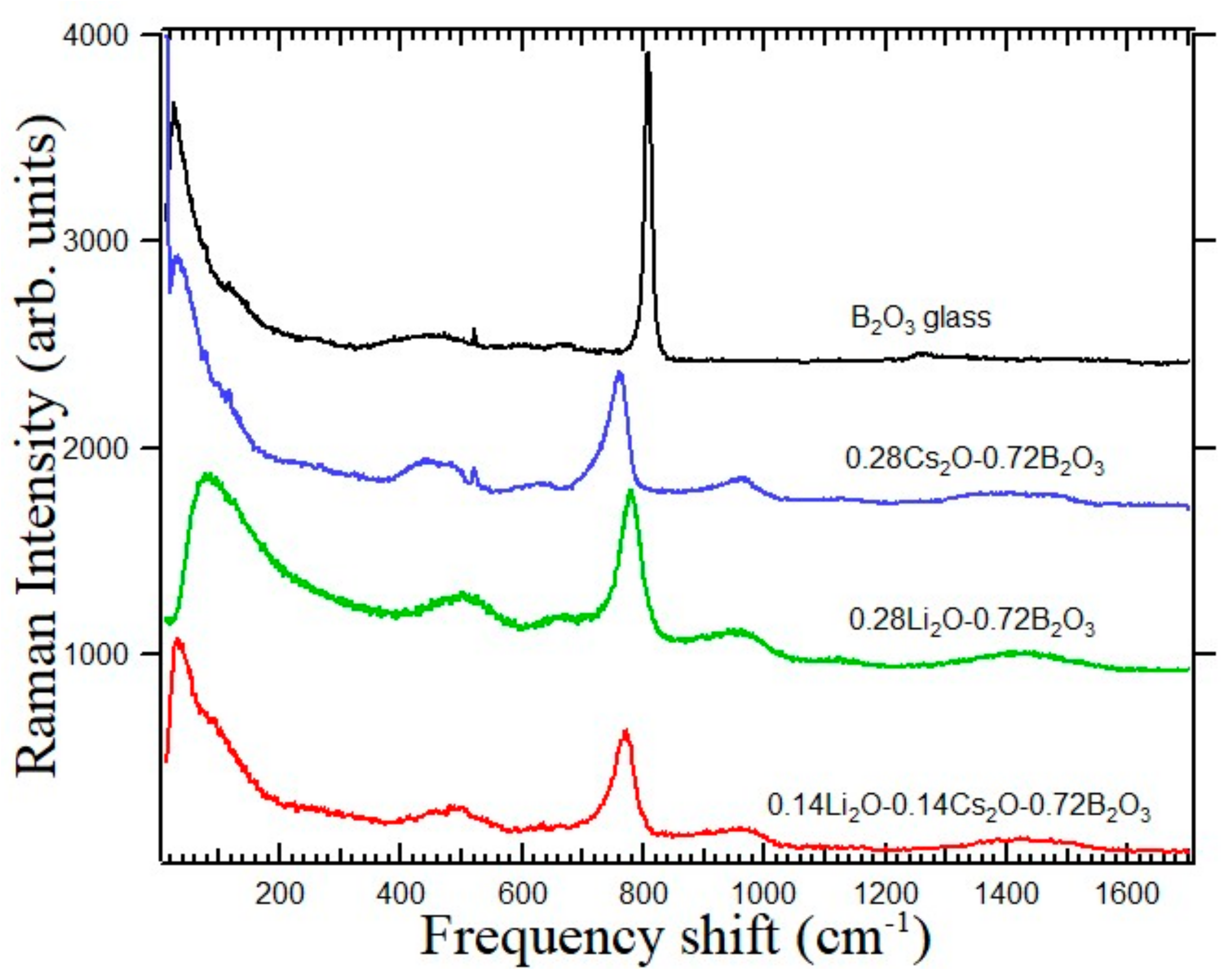
The intense and sharp peak at 808 cm⁻¹ of the B₂O₃ glass in Figure 9 is the localized symmetric breathing mode of the B₃O₃ planer boroxol ring with the coordination number of boron is three. When the B₂O₃ glass is modified by alkali ions, the coordination number of boron changes to four. As shown in Figure 9, for the 0.28Cs₂O-0.72B₂O₃ and 0.28Li₂O-0.72B₂O₃ glasses, the intense peak appears at 758 cm⁻¹ and 777 cm⁻¹, respectively [34]. The 0.14Cs₂O-0.14Li₂O-0.72B₂O₃ glass shows the intense peak at 770 cm⁻¹. The Raman scattering spectra of the 0.28{(1−y)Cs₂O-yLi₂O}-0.72B₂O₃ glasses with y = 0.2, 0.5, and 0.8 between 650 and 850 cm⁻¹ are shown in Figure 10a [22]. According to the analysis of the internal Raman bands, the average characteristic mode frequency of the pentaborate, dipentaborate, and chain type metaborate groups are 770, 755 and 730 cm⁻¹, respectively.

These band intensities were determined by a multi-peaks fitting. The intensities of these three characteristic modes as a function on the Li fraction are shown in Figure 10b. As the Li fraction y increases with a constant alkali content, the pentaborate groups increase, while the dipentaborate and chain type metaborate groups decrease. These dependences of the mode intensities are not linear with the Li fraction y, and such nonlinear changes of the structural units can be caused by the MAE.

5.2. Boson Peaks

In Figure 9, the boson peak spectrum of the B₂O₃ glass is well fitted by a log-normal function and its peak frequency is 26 cm⁻¹. According to the vibrational study by hyper-Raman scattering, the origin of the boson peak is attributed to the librational motions of two adjacent boroxole rings [38]. As shown Figure 9, the boson peak frequency of the 0.28Cs₂O-0.72B₂O₃ glass at 26 cm⁻¹ is nearly same as that of the B₂O₃ glass, while that of the 0.28Li₂O-0.72B₂O₃ glass at 72 cm⁻¹ is about three times of that of the B₂O₃ glass. The Cs ions with a large ionic size only slightly changes the boron-oxgen network structure by the low charge density. However, the Li ions with a small ionic size cause shrinking of the boron-oxygen network structure by the high charge density [26,39]. By application of high pressure, it was reported that the boson peak frequency significantly increases up to 68 cm⁻¹ at 4 GPa by shrinking of the boron-oxygen network structure [40].

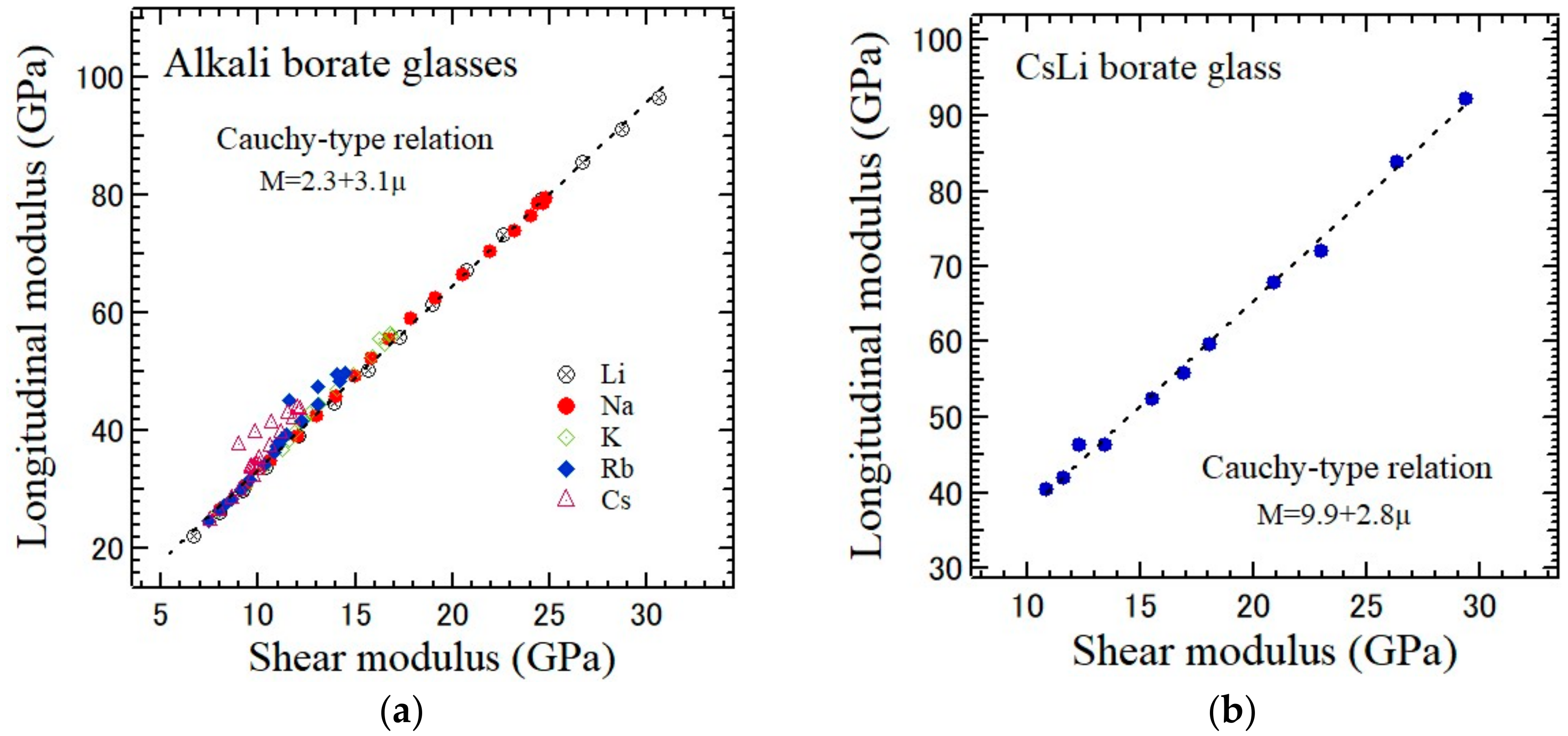
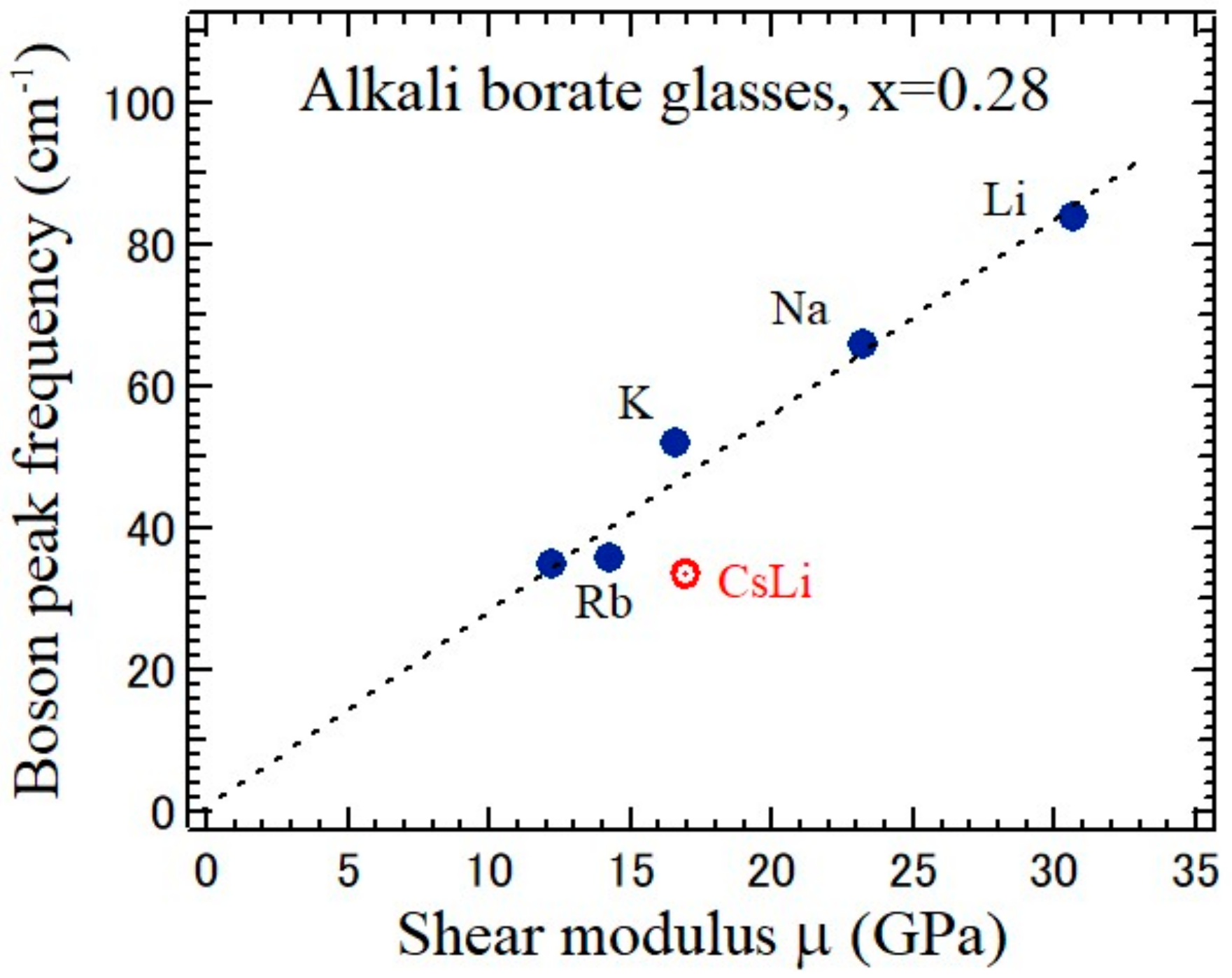
Figure 11 shows the relation between the boson peak frequency determined by Raman scattering versus the shear modulus determined by the ultrasonic method in the single-alkali borate glasses. The solid circles denote the values of the 0.28M₂O-0.72B₂O (M = Li, Na, K, Rb, and Cs) and the open circle denotes the value of the 0.14Cs₂O-0.14Li₂O-0.72B₂O₃ (CsLi) glasses [4,21]. The deviation of the plot of the mixed-cesium lithium borate glass (CsLi) from the linear relation of single-alkali borate glasses in Figure 11 may suggest the MAE.

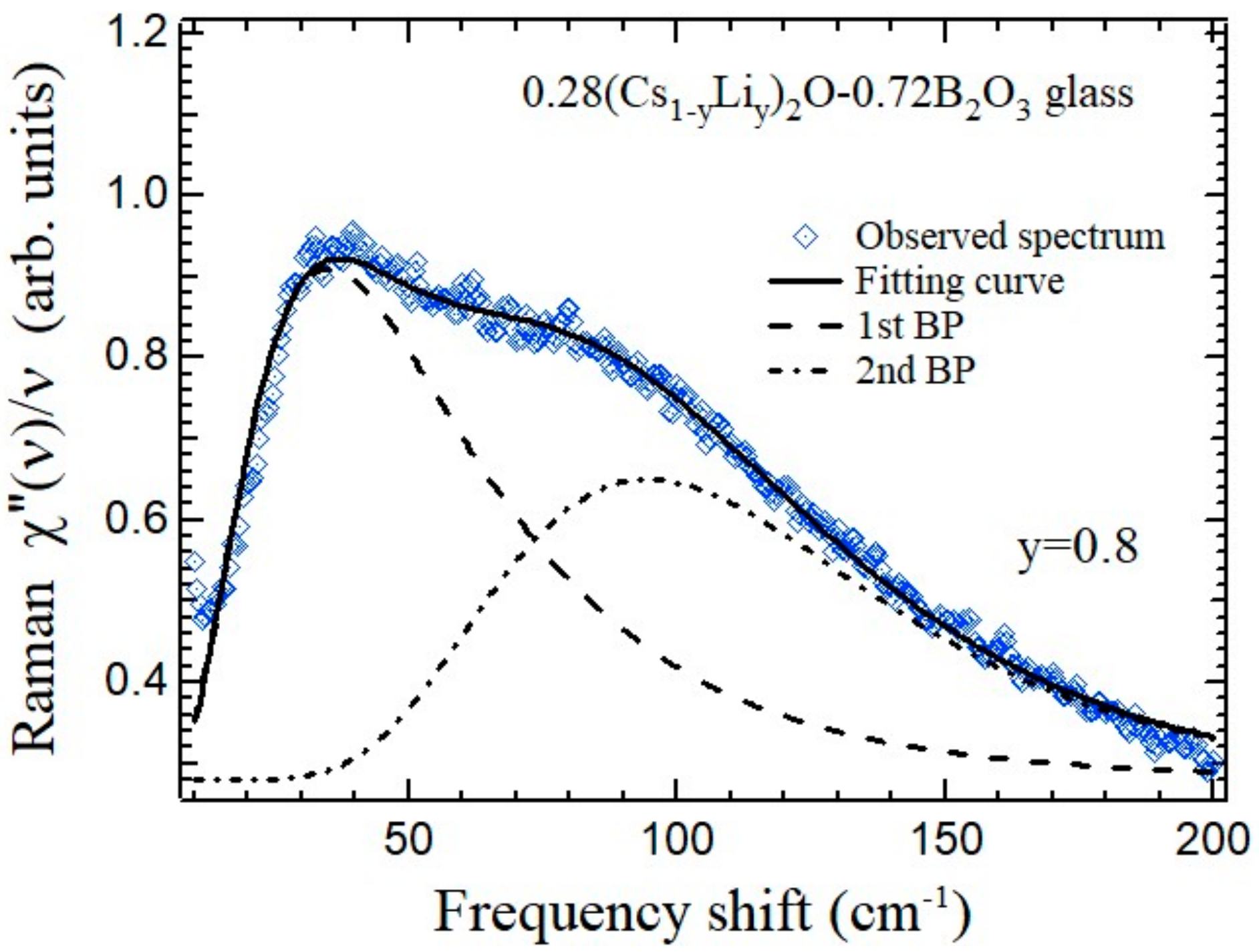
The boson peak spectra of the mixed-cesium lithium 0.28{(1−y)Cs₂O-yLi₂O}-0.72B₂O₃ glasses were studied by Raman scattering and splitting of the boson peak was observed [21]. The results of fitting of the boson peak spectrum of the 0.28{0.2Cs₂O-0.8Li₂O}-0.72B₂O₃ glass (y = 0.8) between 10 and 200 cm⁻¹ are shown in Figure 12 [21]. The boson peak of the single-alkali borate glasses is well fitted by a log-normal function. However, the boson peak of the mixed-alkali borate glasses has a distorted broad peak and such a single mode fitting is impossible. Therefore, the broad peak is fitted by two log-normal functions.

The fitted results indicate the splitting of a boson peak in the mixed-cesium lithium borate glasses. The origin of this splitting is probably related to two kinds of structural correlations related to the heterogeneous structure including the Cs-rich and Li-rich regions. The static structure factor, S_CsLi(Q), of the mixed-cesium lithium borate glasses cannot be reproduced by the average between S_Cs(Q) of the cesium borate and S_Li(Q) of the lithium borate glasses [41]. This fact means that there is no phase separation into the cesium borate and lithium borate glasses. The detailed analysis of the static structure factor, S_CsLi(Q), of the mixed-cesium lithium borate glasses and the boson peak spectra, S_CsLi(E), measured by neutron scattering will be published elsewhere.

6. Summary

The modification of oxide glasses by dissimilar alkali ions causes a maximum in the electric resistivity or the expansion coefficient, and that is called the mixed-alkali effect (MAE). MAE is very important not only in basic sciences but also in technology, while its mechanism is not yet clarified. In order to give new insights into MAE, this paper reviews the experimental studies on the glass transition temperature, heat capacity, elastic moduli, and optical vibrations in the mixed-cesium lithium borate glasses, x{(1−y)Cs₂O-yLi₂O}-(1−x)B₂O₃. For the single-alkali borate glasses, xM₂O(1−x)-B₂O₃ (M = Li, Na, K, Rb, and Cs), the glass transition temperature, T_g = 270 °C, of the pure borate glass monotonically increases as the alkali content x increases. However, for the mixed-cesium lithium borate glasses with a constant alkali content x, the T_g versus the lithium fraction y has a minimum. The excess heat capacity at low temperatures caused by the excess vibrational density of states, and it shows the nonlinear variation against the lithium fraction y. The lithium fraction dependences of elastic properties are analyzed about the longitudinal modulus, Poisson’s ratio, and Cauchy-type relation. In Raman scattering spectroscopy, the internal vibrational bands related to the boron-oxide structural groups shows a nonlinear variation versus the lithium fraction y. The boson peak of single-alkali borate glasses is a single peak, however, in the mixed-cesium lithium borate glasses the splitting of a boson peak occurs by MAE. These nonlinear behaviors on the thermal, elastic, and vibrational properties are discussed on the basis of the changes of glass network structure modified by dissimilar alkali ions. The possible origin of the MAE in the mixed borate glasses is the appearance of dissimilar alkali ion pairs with different ionic radii.