Transformation of Test Data for the Specification of a Viscoelastic Marlow Model
Abstract
1. Introduction
1.1. Hyperelasticity and Marlow Model
1.2. Combination of Hyperelasticity and Viscoelasticity
1.3. Instantaneous Response
1.4. Aim
2. Results
2.1. Stress Transformation and Compressibility
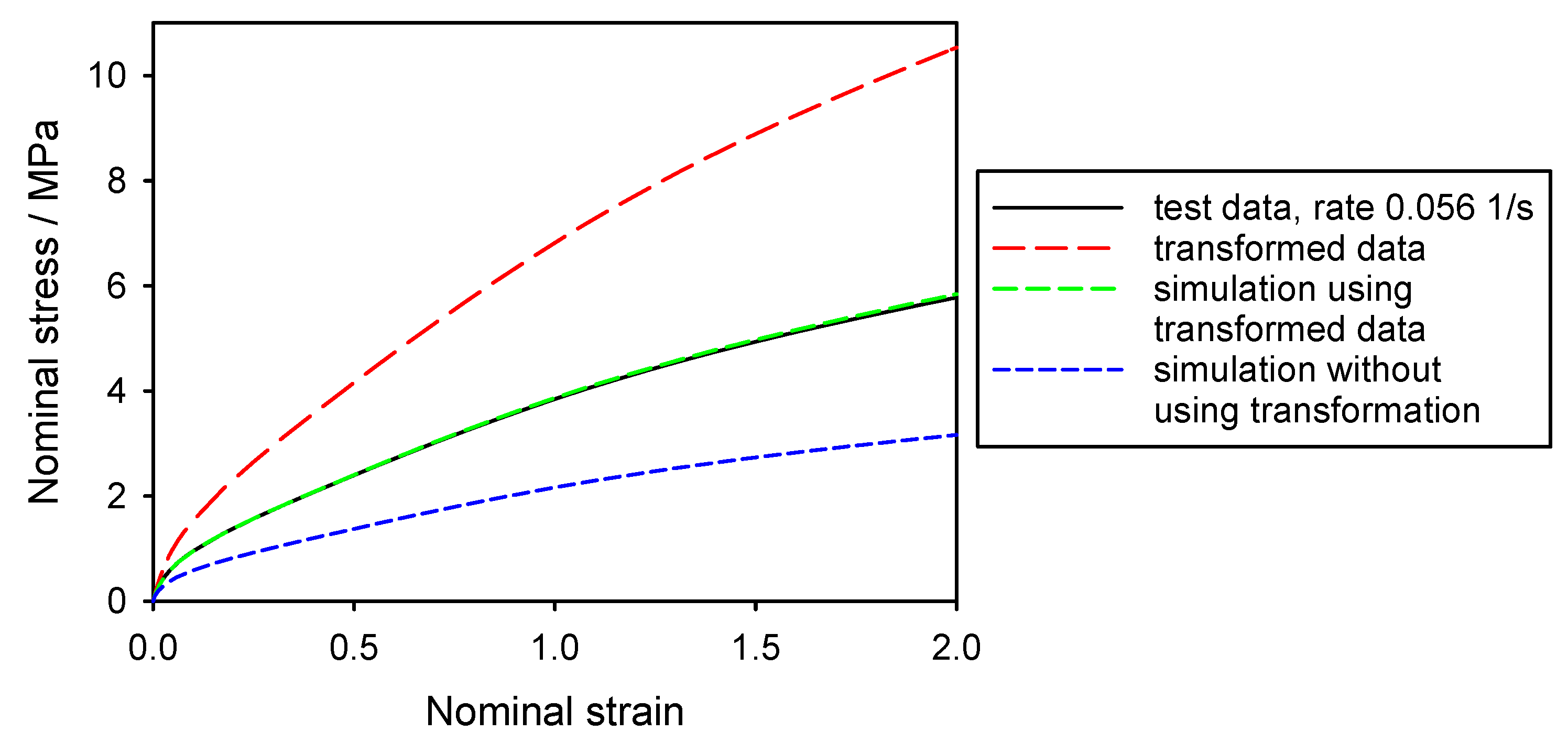
2.2. Viscoelasticity in Uniaxial Tension
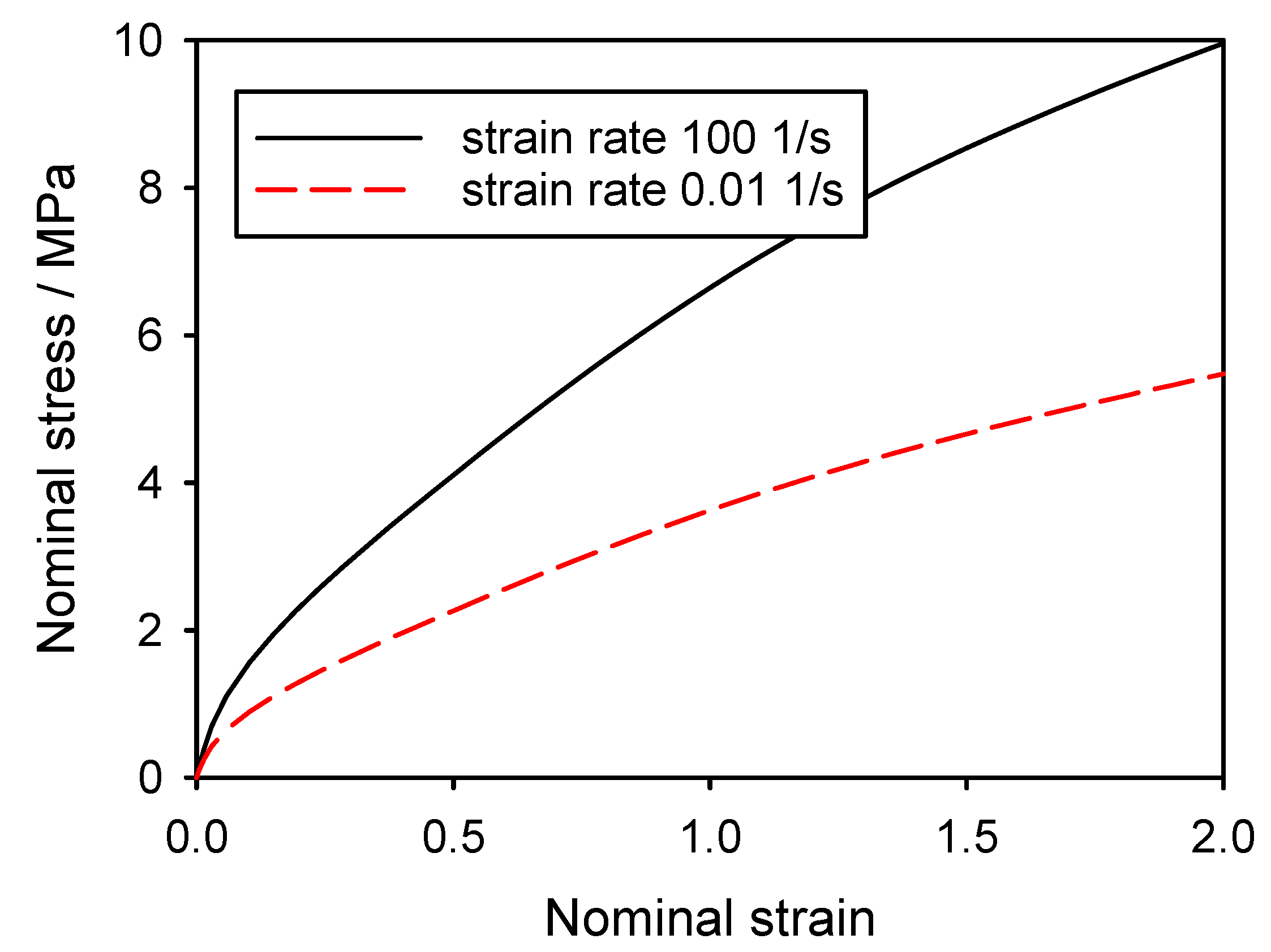
2.3. Consideration of Constant Strain Rate
2.4. Discretization of Stress Function
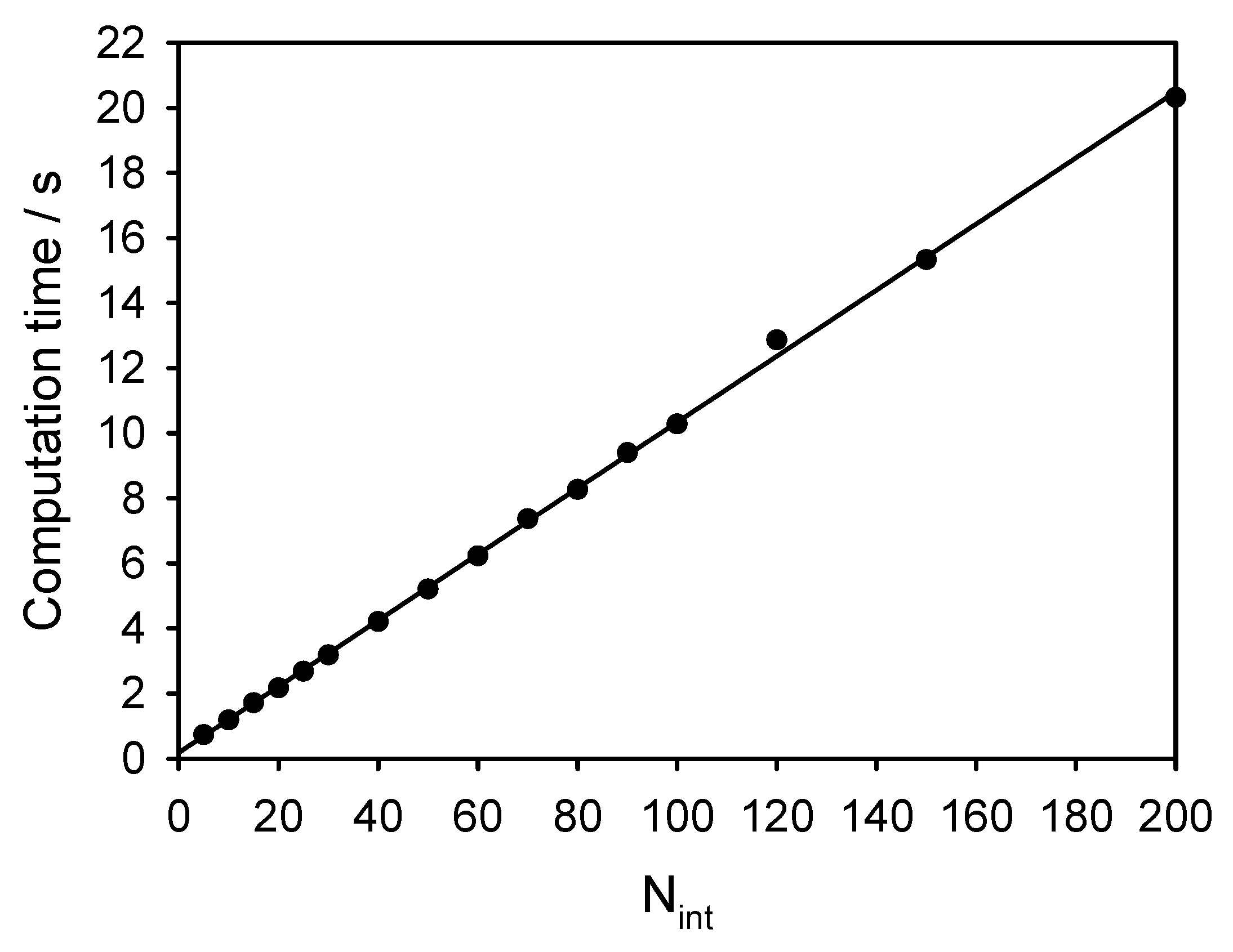
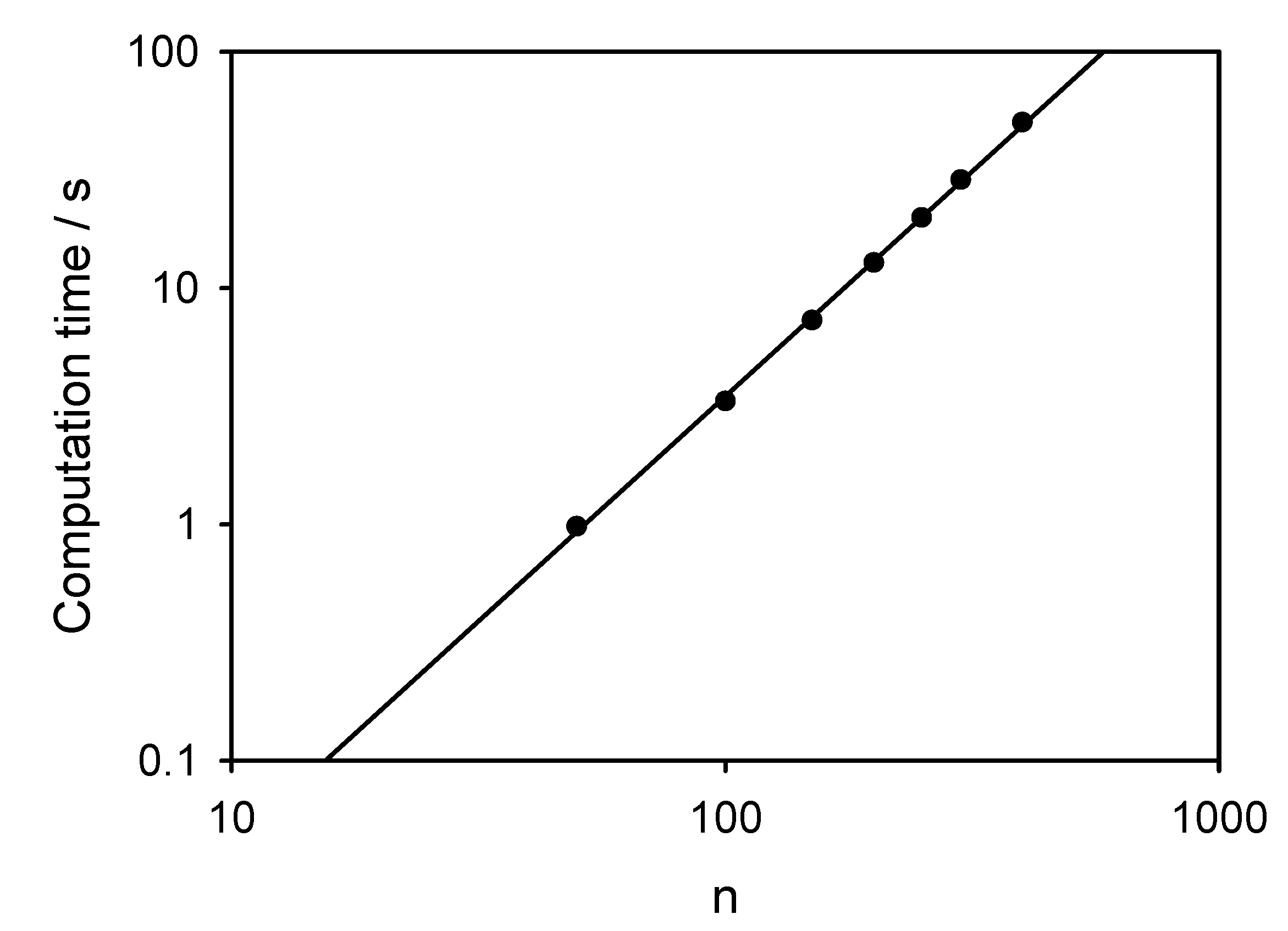
2.5. Implementation and Convergence
3. Discussion
- The model describes strain-rate dependence of the mechanical behavior.
- The model can be defined so that it fits exactly to the result of one experiment, e.g., a tensile test. In contrast, hyperelastic models based on a small set of parameters like polynomial models or Ogden’s model exhibit significant deviations from experimental data for some materials.
- The parameter identification is direct in the sense that it requires no optimization procedure. Consequently, the result does not depend on parameters of an optimization like the choice of an absolute or relative error measure, the optimization algorithm, or the initial values.
4. Materials and Methods
Funding
Acknowledgments
Conflicts of Interest
References
- Marckmann, G.; Verron, E. Comparison of Hyperelastic Models for Rubber-Like Materials. Rubber Chem. Technol. 2006, 79, 835–858. [Google Scholar] [CrossRef]
- Martins, P.A.L.S.; Natal Jorge, R.M.; Ferreira, A.J.M. A Comparative Study of Several Material Models for Prediction of Hyperelastic Properties: Application to Silicone-Rubber and Soft Tissues. Strain 2006, 42, 135–147. [Google Scholar] [CrossRef]
- Vahapoğlu, V.; Karadeniz, S. Constitutive Equations for Isotropic Rubber-Like Materials Using Phenomenological Approach: A Bibliography (1930–2003). Rubber Chem. Technol. 2006, 79, 489–499. [Google Scholar] [CrossRef]
- Steinmann, P.; Hossain, M.; Possart, G. Hyperelastic models for rubber-like materials: Consistent tangent operators and suitability for Treloar’s data. Arch. Appl. Mech. 2012, 82, 1183–1217. [Google Scholar] [CrossRef]
- Chagnon, G.; Rebouah, M.; Favier, D. Hyperelastic Energy Densities for Soft Biological Tissues: A Review. J. Elast. 2015, 120, 129–160. [Google Scholar] [CrossRef]
- Marlow, R.S. A general first-invariant hyperelastic constitutive model. In Constitutive Models for Rubber III; Busfield, J., Ed.; Balkema: Lisse, The Netherlands, 2003; pp. 157–160. [Google Scholar]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Yeoh, O.H.; Fleming, P.D. A new attempt to reconcile the statistical and phenomenological theories of rubber elasticity. J. Polym. Sci. Part Polym. Phys. 1997, 35, 1919–1931. [Google Scholar] [CrossRef]
- Esposito, M.; Sorrentino, L.; Krejčí, P.; Davino, D. Modelling of a visco-hyperelastic polymeric foam with a continuous to discrete relaxation spectrum approach. J. Mech. Phys. Solids 2020, 142, 104030. [Google Scholar] [CrossRef]
- Iqbal, M.; Li-Mayer, J.; Lewis, D.; Connors, S.; Charalambides, M. Mechanical characterization of the nitrocellulose-based visco-hyperelastic binder in polymer bonded explosives. Phys. Fluids 2020, 32, 023103. [Google Scholar] [CrossRef]
- Luo, Y.M.; Chevalier, L.; Monteiro, E.; Yan, S.; Menary, G. Simulation of the Injection Stretch Blow Molding Process: An Anisotropic Visco–Hyperelastic Model for Polyethylene Terephthalate Behavior. Polym. Eng. 2020, 60, 823–831. [Google Scholar] [CrossRef]
- Ramzanpour, M.; Hosseini-Farid, M.; Mclean, J.; Ziejewski, M.; Karami, G. Visco-hyperelastic characterization of human brain white matter micro-level constituents in different strain rates. Med. Biol. Eng. Comput. 2020, 58, 2107–2118. [Google Scholar] [CrossRef] [PubMed]
- Hesebeck, O.; Wulf, A. Hyperelastic constitutive modeling with exponential decay and application to a viscoelastic adhesive. Int. J. Solids Struct. 2018, 141, 60–72. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A. Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Zwanzig, R.; Mountain, R.D. High–Frequency Elastic Moduli of Simple Fluids. J. Chem. Phys. 1965, 43, 4464–4471. [Google Scholar] [CrossRef]
- Puosi, F.; Leporini, D. Communication: Correlation of the instantaneous and the intermediate-time elasticity with the structural relaxation in glassforming systems. J. Chem. Phys. 2012, 136, 041104. [Google Scholar] [CrossRef] [PubMed]
- Dyre, J.C.; Wang, W.H. The instantaneous shear modulus in the shoving model. J. Chem. Phys. 2012, 136, 224108. [Google Scholar] [CrossRef] [PubMed]
- Dassault Systèmes. Abaqus 2019. 2019. Available online: https://www.3ds.com/products-services/simulia/products/abaqus (accessed on 1 November 2020).
- Hesselbach, J.; Hesebeck, O.; Carrillo Beber, V. Geklebte Langzeitstabile Organoblech-Aluminium-Knotenverbindungen und deren Berechnung mit Einem Erweiterten Arruda-Boyce Werkstoffmodell; Report of IGF Project 19609 N; in preparation.
- Wolfram. Mathematica 11.1. 2017. Available online: https://www.wolfram.com/mathematica (accessed on 1 November 2020).
- Python 3.6.0. 2017. Available online: https://www.python.org (accessed on 1 November 2020).

| K | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| in s | in s | in s | in s | in s | in GPa | |||||
| 0.3539 | 0.08124 | 0.07458 | 1.692 | 0.05052 | 35.23 | 0.04117 | 733.5 | 0.04575 | 15275 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hesebeck, O. Transformation of Test Data for the Specification of a Viscoelastic Marlow Model. Solids 2020, 1, 2-15. https://doi.org/10.3390/solids1010002
Hesebeck O. Transformation of Test Data for the Specification of a Viscoelastic Marlow Model. Solids. 2020; 1(1):2-15. https://doi.org/10.3390/solids1010002
Chicago/Turabian StyleHesebeck, Olaf. 2020. "Transformation of Test Data for the Specification of a Viscoelastic Marlow Model" Solids 1, no. 1: 2-15. https://doi.org/10.3390/solids1010002
APA StyleHesebeck, O. (2020). Transformation of Test Data for the Specification of a Viscoelastic Marlow Model. Solids, 1(1), 2-15. https://doi.org/10.3390/solids1010002





