Abstract
Accurate prediction of the coal abrasive index (AI) is critical for optimizing coal processing efficiency and minimizing equipment wear in industrial applications. This study explores tree-based machine learning models; Random Forest (RF), Gradient Boosting Trees (GBT), and Extreme Gradient Boosting (XGBoost) to predict AI using selected coal properties. A database of 112 coal samples from the KwaZulu-Natal Coalfield in South Africa was used. Initial predictions using all eight input properties revealed suboptimal testing performance (R2: 0.63–0.72), attributed to outliers and noisy data. Feature importance analysis identified calorific value, quartz, ash, and Pyrite as dominant predictors, aligning with their physicochemical roles in abrasiveness. After data cleaning and feature selection, XGBoost achieved superior accuracy (R2 = 0.92), outperforming RF (R2 = 0.85) and GBT (R2 = 0.81). The results highlight XGBoost’s robustness in modeling non-linear relationships between coal properties and AI. This approach offers a cost-effective alternative to traditional laboratory methods, enabling industries to optimize coal selection, reduce maintenance costs, and enhance operational sustainability through data-driven decision-making. Additionally, quartz and Ash content were identified as the most influential parameters on AI using the Cosine Amplitude technique, while calorific value had the least impact among the selected features.
1. Introduction
Coal is a vital natural resource that has been utilized for centuries in various industrial applications, particularly in power generation, steel manufacturing, and cement production [1,2]. Its suitability for these applications depends on several factors, including its composition and physical properties [3,4]. Among the many parameters that influence the efficiency of coal processing, the abrasive index (AI) is one of the most significant [5]. This index provides essential insights into the coal’s behavior during milling, influencing both equipment wear and energy consumption during coal grinding [6]. The abrasive index (AI) is defined as the loss of mass (in milligrams) of standard steel blades used in grinding a coal sample under specified test conditions, as per the Wells et al. [7] and Spero [8] methods. Therefore, accurate prediction of AI is crucial for optimizing coal utilization in industrial processes. Coal with high abrasiveness increases maintenance costs due to accelerated wear and tear on machinery. Hence, predicting AI accurately can help industrial operators make better decisions regarding coal selection, minimize equipment downtime, and reduce operational costs [9,10].
AI is influenced by coal’s chemical and physical composition, with factors including moisture content (M), Ash content, volatile matter (VM), fixed carbon (FC), Pyrite, and quartz [9,11]. Quartz, being one of the hardest minerals present in coal, significantly contributes to AI by increasing wear on mills, crushers, and pulverizers [12]. Pyrite (FeS2), another highly abrasive mineral, enhances AI due to its hardness and tendency to accelerate material degradation in coal mills [7,13,14]. Ash content, which comprises various mineral impurities, particularly silica and iron oxides, further increases AI by introducing hard particles that intensify equipment wear [13]. While calorific value does not directly affect AI, it often correlates with coal quality and density, which may influence the presence of harder mineral inclusions and, consequently, abrasiveness [15,16]. Among these, the most common factors contributing to AI are quartz, calorific value, Pyrite, and Ash, as these have the most direct impact on coal abrasiveness [9]. Other properties such as M, VM, and FC also play a role in determining AI. Higher moisture levels can reduce coal abrasiveness by acting as a lubricant, decreasing friction between coal particles and grinding surfaces [17]. However, excessively high moisture can lead to clogging in pulverizers and inefficient milling. Lower VM content is often associated with denser coal structures, potentially increasing AI [9]. FC, which determines coal’s density and hardness, can contribute to AI by making coal more resistant to grinding and increasing wear on milling equipment [18].
Given the complexity and variability of these coal properties, there is a growing need for accurate methods to predict AI [19]. One of the traditional common methods to determine AI is using the laboratory testing which is time-consuming and costly. In addition, there are also several existing empirical formulas that can be used to determine the AI [8], however this method is limited to a certain type of data and most of these empirical formulas are also limited to certain behavior of the data such as linear and non-linear relationships. The ability to predict AI is crucial for industries that rely on coal as a fuel or raw material [20]. In power plants, low-abrasiveness coal ensures efficient milling, reducing energy consumption and improving combustion efficiency. Likewise, accurately predicting AI allows for better coal selection, optimizing the milling process and preventing unnecessary wear on machinery. By enabling better resource management, AI prediction also supports cost-effective blending strategies, ensuring that industries meet their desired specifications while minimizing waste and improving sustainability. Given the operational and economic implications of AI, various predictive methods are strongly recommended for further exploration, while traditional empirical models and laboratory analyses remain widely used.
In recent years, the use of machine learning (ML) algorithms for the prediction of various parameters can be seen in various industries such as construction [21], medical, and commercial [22]. ML has been used for the prediction of coal AI by using different coal properties. Some studies have used different ML methods for the prediction of coal AI [9,10] and show reasonably good prediction. However, another algorithm, which is tree-based ML, can be considered as another potential algorithm for the prediction of the AI. The tree-based ML models have the capability to handle large datasets and capture complex relationships between coal properties. Therefore, in this study, tree-based algorithms such as the Random Forest (RF), Gradient Boosting (GBT), and Extreme Gradient Boosting (XGBoost) are explored to assess the capability of the prediction of coal AI. RF enhances predictive stability by aggregating multiple decision trees, whereas GBT and XGBoost iteratively refine predictions by minimizing errors to improve accuracy. The key difference between GBT and XGBoost lies in their optimization strategies, where XGBoost incorporates advanced regularization techniques, parallel processing, and a more efficient handling of missing values, making it computationally faster and more robust than traditional GBT implementations.
These algorithms have shown promising results for different predictions. For example, RF has been used by Yan et al. [23] for the prediction of rock mass classification in tunnel construction and good results were obtained. GBT has also been used to predict the soil compression index (Cc), a key geotechnical parameter that quantifies soil deformation under load [24], and XGBoost was used by He et al. [25] to predict air-overpressure (AOp) resulting from blasting activities in granite quarries and was optimized using Bayesian optimization (BO) and random search (RS) to enhance predictive accuracy and minimize environmental impact. The studies carried out by previous authors have shown the potential of these algorithms; hence, these algorithms are further explored for the prediction of coal AI. By integrating ML with well-characterized coal datasets reported by Onifade et al. [9] based on the KwaZulu-Natal Coalfield, this study aims to enhance AI-driven predictive models for coal quality assessment, ultimately optimizing industrial coal utilization and reducing operational costs. The proposed framework leverages on selected coal properties such as CV (calorific value), Pyrite, Qtz (quartz), Ash, and AI (abrasive index) to refine coal selection, improve milling efficiency, and optimize combustion performance in coal-dependent industries.
In this study, our target is to propose several predictive models, i.e., RF, XGB, and GBT, and provide a comparative study of their prediction capabilities in estimating AI of coal using selected physicochemical properties of coal. Our methodological framework involves comprehensive data preprocessing, feature selection through importance analysis, and rigorous hyperparameter tuning to ensure robust model training. The contributions of this work include the following: establishing a predictive pipeline that integrates domain-driven feature refinement and outlier handling for enhanced accuracy, demonstrating a systematic comparison of tree-based models for AI prediction, and presenting a cost-effective and data-driven alternative model that supports optimized coal selection and operational sustainability.
2. Data Information
2.1. Description of the Study Area
The KwaZulu-Natal Coalfield is in the eastern part of South Africa, within the province of KwaZulu-Natal. It extends across multiple districts, including Utrecht, Newcastle, Vryheid, and Dundee, which have historically been major coal-producing areas. The coalfield lies between latitudes 27° S and 30° S and longitudes 29° E and 32° E, stretching inland from the coastal areas of Richards Bay and Durban. The KwaZulu-Natal is part of the Ecca Group within the Karoo Supergroup, a sedimentary sequence that was deposited during the late Carboniferous to early Jurassic periods (approximately 300–180 million years ago). The coal seams are primarily found in the Vryheid Formation of the Ecca Group, which consists of alternating layers of sandstone, mudstone, shale, and coal. The KwaZulu-Natal Coalfield contains bituminous coal, ranging from high-quality anthracite to lower-rank bituminous coal. The coal seams vary in thickness but are generally 1–3 m thick, with some localized thicker seams. The coal is generally high in Ash content and varies in sulfur content.
2.2. Sample Preparation and Testing
A total of 133 coal data samples were considered in this study before data processing and cleaning. In the same database, the information covers a wide spectrum of physical and chemical characteristics. These samples were prepared and analyzed following ASTM Standards to ensure the accuracy and reliability of the data. Each coal sample was crushed, blended, and subjected to a rotary splitter to generate sub-samples of consistent size fractions for testing according to ASTM [26]. The crushing process ensured that all coal fragments were reduced to a uniform particle size suitable for subsequent analysis. The blending step involved thoroughly mixing the crushed coal to achieve homogeneity and minimize variability within individual samples. A rotary splitter was then employed to divide the homogenized coal into smaller, representative sub-samples, ensuring that each fraction maintained the same compositional characteristics. The proximate analysis was conducted in accordance with the ASTM [27]. Approximately 1 g of coal sample was used for the analyses in determining the inherent moisture, Ash content, and VM present in the coal with FC calculated by difference. The ultimate and total sulfur (TS) analyses of the coal were performed according to ASTM [28] and ISO [29]. The calorific value as the measure of the heat content was determined in accordance with ASTM [30]. The AI was determined according to Wells et al. [7] and Spero [8]. This was accomplished by mechanically grinding 4 kg of coal in a steel pot, thoroughly leveled out over the blades and covered with a steel lid. Having introduced the coal into the steel pot, the stirrer rotated for 12,000 revolutions at 1500 rpm. The AI was determined after the test from the loss of mass in milligrams of the blades from its initial mass and mass after grinding.
2.3. Data Characteristics
The available data used in the initial data preprocessing comprised a total of 133 data samples where CV, Pyrite, M, VM, FC, TS, Qtz, and AI are the available parameters in the data. Onifade et al. [9] considered 89 data samples of the same database where CV, TS, M, VM, FC, Ash, Pyrite, and Hardgrove grindability index were used as inputs and AI was utilized as model output. In this study, a general flowchart of the steps involved in predicting AI is presented in Figure 1. After a series of preprocessing analyses on the data (see Figure 2 and Figure 3 for more information), we found that four of those parameters had more effects on the AI results, which are CV, Ash, Pyrite, and Qtz. These parameters were used in the analysis and modeling of this research as the lower number of input parameters will help increase interest from researchers or industry experts in the proposed model. Therefore, a total of 112 data samples were considered in this study, and their key distribution parameters such as mean, standard deviation, and range are presented in Table 1.
Figure 1.
A general flowchart of the study procedure.
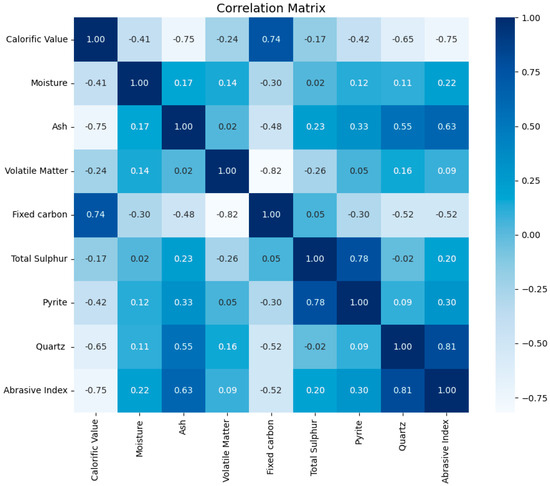
Figure 2.
Correlation matrix of the input.
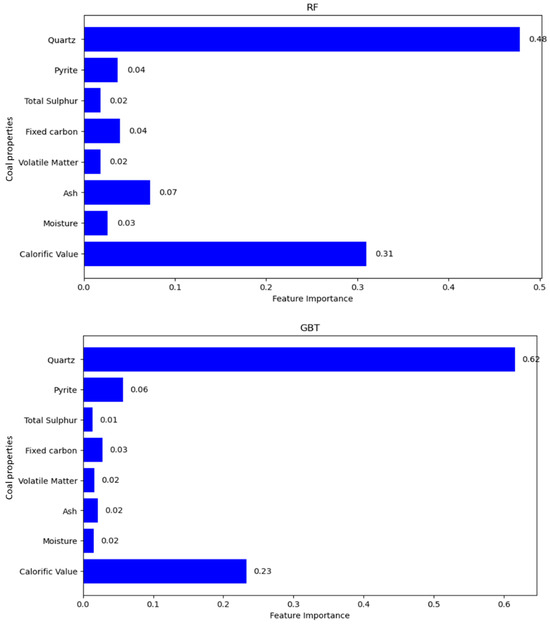
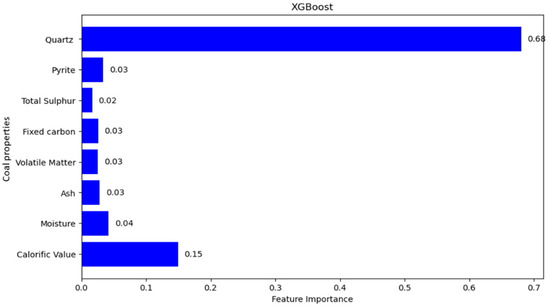
Figure 3.
Feature importance (RF, GBT, and XGBoost).

Table 1.
Descriptive statistics of the used data in the analysis (Adapted from [9]).
3. Methodology
The present study employs three prominent tree-based ML algorithms: RF, GBT, and XGBoost to develop predictive models for the AI. The selection of these algorithms was based on their documented efficacy in capturing complex and non-linear relationships characteristic of coal property datasets, as well as their capability to process multivariate datasets robustly [31,32,33]. RF builds an ensemble of decision trees, each trained on a bootstrapped subset of the data with random feature selection at each split. The final prediction is the average (regression) of individual tree outputs. The prediction for a given sample x is as follows:
where is the prediction from the decision tree, is the total number of trees, and is the predicted sample.
GBT builds trees sequentially, where each new tree attempts to correct the residual errors of the ensemble of previously built trees. The model prediction is updated iteratively as follows:
where is model after m iterations; is learning rate; and is decision tree trained on residuals.
XGBoost improves upon GBT by introducing regularization, parallel processing, missing value handling, and efficient pruning to prevent overfitting and improve computational performance.
where is the total objective function; n is number of training samples; is actual AI value of coal; is predicted AI value from the model; is the loss function; K is number of trees; is the regression tree; and ) is regularization function that penalizes complexity.
All models were developed using the Python programming language, utilizing widely adopted libraries such as scikit-learn and XGBoost. The development and analysis were carried out in the Jupyter Notebook environment.
A general flowchart of the steps involved in predicting AI is presented in Figure 1.
The experimental dataset consisted of eight key coal properties: CV, M, Ash, VM, FC, total sulfur (TS), pyrite, and Qtz. These input parameters were measured using standardized procedures outlined in Section 2.2, ensuring consistent and accurate laboratory results.
Prior to model training, the data underwent rigorous preprocessing. Initially, data consistency was verified, confirming completeness across all samples. Subsequently, outliers were identified through statistical approaches involving the interquartile range (IQR) and standard deviation criteria. Specifically, data points situated beyond ±3 standard deviations or 1.5 times the IQR from the quartiles were identified as potential outliers. Domain experts evaluated these flagged data points to determine their validity, retaining cases representing genuine geological variations and removing those identified as measurement anomalies or transcription errors. This expert-driven review ensured that removed data points did not unjustly limit the representativeness and diversity inherent within coal properties from the studied coalfield.
Following preprocessing, hyperparameter tuning was meticulously conducted to optimize model performance and avoid overfitting. For each ML algorithm, a systematic hyperparameter optimization approach combining grid search and random search methods was implemented. Cross-validation techniques, specifically five-fold cross-validation, were employed during this tuning phase to reliably estimate generalization performance. Optimal hyperparameters identified through this procedure included the number of trees, maximum tree depth, learning rate, subsample ratio, and regularization parameters specific to each algorithm. These hyperparameters were carefully adjusted based on initial performance feedback to ensure a balance between model complexity and generalization capability, guided by both computational efficiency and domain-specific understanding of coal property interactions.
After hyperparameter optimization, the dataset was partitioned into training and testing subsets using an 80/20 split. The optimized models were then trained on the larger training subset and independently evaluated on the testing subset, ensuring a reliable assessment of each model’s predictive capability and generalizability to unseen data. This validation strategy, complemented by cross-validation, provided robust insights into model stability and effectiveness across various data scenarios.
An initial modeling iteration employed all eight coal properties to predict the AI. Subsequently, a feature importance analysis was performed to identify the most influential predictors within each model. Features consistently exhibiting minimal predictive power across all three algorithms were critically reviewed against geological knowledge and literature insights. Following expert evaluation, parameters exhibiting limited contribution to predictive accuracy and lacking geochemical significance were excluded, resulting in a refined set of predictors comprising CV, Qtz, Ash, and Pyrite. This iterative refinement process ensured that the final models relied on scientifically and practically meaningful predictors, enhancing interpretability and reducing model complexity.
A second modeling iteration, using only the refined subset of influential parameters, was then conducted. Performance evaluation criteria included the coefficient of determination (R2) and correlation coefficient (R), ensuring objective quantification of predictive accuracy. Additionally, cross-validation was employed throughout both model-building stages to rigorously assess the stability and robustness of predictions, mitigating risks associated with potential overfitting. Regularization techniques, subsampling, and depth restrictions were employed as additional measures against overfitting, ensuring that developed models demonstrated both predictive reliability and practical utility.
Finally, results obtained from each modeling stage were interpreted in the context of coal processing implications, emphasizing their potential impact on equipment selection, operational efficiency, and maintenance cost reduction within coal-dependent industries. The comprehensive methodological approach outlined here, encompassing detailed preprocessing, rigorous hyperparameter tuning, systematic feature selection, and careful model evaluation, ensured robust, reproducible, and accurate predictive models capable of effectively predicting coal abrasiveness from physicochemical coal properties.
4. Results and Discussion
In the initial modeling phase, all eight coal properties were used to predict the AI through RF, GBT, and XGBoost. Model performance was assessed using two key statistical measures: the R2 and the (R). These metrics were calculated as follows:
where is measured AI, is computed AI, is mean measured AI, and n is the number of data points.
The initial evaluation results (Table 2) indicated a notable disparity between the training and testing datasets, with testing dataset R2 values ranging from 0.63 to 0.72, significantly lower than the corresponding training dataset performance. This discrepancy suggested potential overfitting and data-related issues such as noise or outliers. These results are graphically presented in Figure 2, clearly highlighting the differences between training and testing performance.

Table 2.
Coefficient of determination (R2) for training and testing.
To investigate and address the observed discrepancies, feature importance analyses were conducted using the RF, GBT, and XGBoost algorithms. Importance scores are unitless and represent the relative contribution of each feature to the model’s predictive performance (normalized to sum to 1). Results of this analysis, depicted in Figure 3, indicated that CV, Qtz, Ash, and Pyrite content were consistently ranked as the most influential variables. Qtz’s high impact on AI was attributed to its hardness and consequent abrasive action, while Ash and Pyrite contributed substantially due to their abrasive mineral impurities and intrinsic hardness, respectively. CV, while indirectly linked to abrasiveness, strongly correlated with coal hardness and density.
Based on these insights, a refined modeling iteration was conducted using only these identified critical parameters: CV, Qtz, Ash, and Pyrite. As shown in Figure 4, this refinement markedly improved predictive performance.
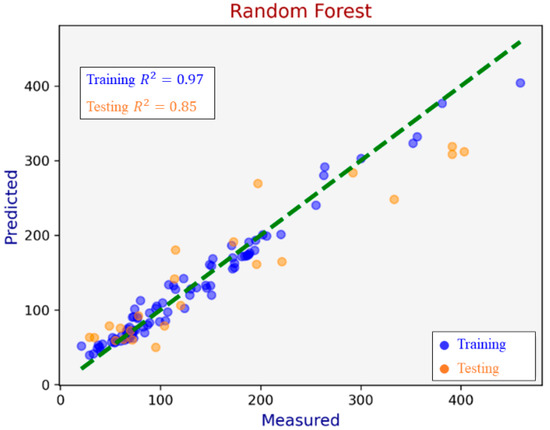
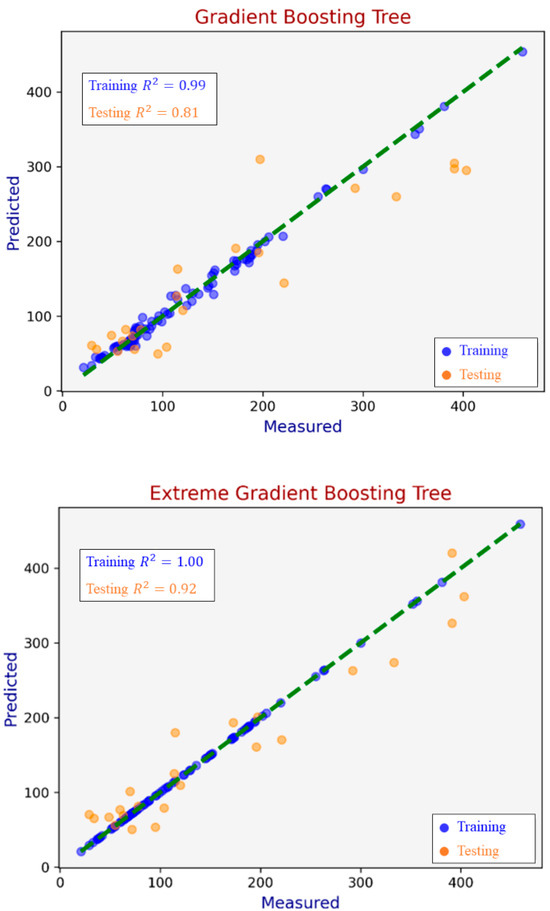
Figure 4.
Predictions of the tree-based ML models.
XGBoost emerged as the most accurate model, achieving a high testing dataset R2 of 0.92, while RF and GBT yielded R2 values of 0.85 and 0.81, respectively. This performance enhancement confirms XGBoost’s superior capability in modeling intricate non-linear interactions among influential coal properties.
It can be noticed that the R2 value of 1.00 on the training dataset from XGBoost suggests a potential risk of overfitting, particularly given the limited size of the dataset. However, the performance on the validation/test set remains consistent with high R2, which indicates the model has reasonable generalization ability. Future studies with larger datasets or alternative validation methods are recommended to further confirm the model’s performance.
The improved predictive accuracy demonstrates considerable advantages over traditional laboratory-based measurements of AI, providing significant operational efficiencies. By enabling rapid and precise AI estimations from readily obtainable coal property data, these predictive models can directly inform and improve coal selection, blending processes, and operational decision-making. This facilitates reduced equipment wear, minimizes downtime, and optimizes maintenance schedules, thus enhancing overall operational cost-effectiveness.
Furthermore, the identification of Qtz, Ash, and Pyrite as major abrasive contributors provides practical guidance for targeted coal beneficiation strategies aimed at reducing abrasive mineral content. This targeted beneficiation strategy can lead to substantial improvements in operational sustainability by reducing both resource consumption and environmental impacts. These findings provide a robust foundation for future research. It is recommended that subsequent studies further validate these predictive models across different coalfields, incorporate additional relevant coal properties, and explore the integration of real-time sensor data to enhance model accuracy and operational applicability.
4.1. Taylor Diagram Analysis
To have a better understanding of the behavior of the predictive models and their capacities in predicting AI during training and testing stages, a Taylor diagram was analyzed. This diagram is a compact way to demonstrate predictive model performance in a graphical aspect. In other word, this diagram examines the model capacity based on observed (measured) and predicted values when comparing multiple models or simulations simultaneously. This will give a better understanding of the outcome compared to traditional ways of calculating performance indices. The same diagram was first developed and used in climate science and then was applied in many engineering and science applications.
By using the measured and predicted AI values for the training and testing sets of all predictive models, the Taylor diagrams were generated as shown in Figure 5. According to the comparative performance of the predictive techniques, the XGB model demonstrates superior performance in the training phase among the XGB, GBT, and RF models in estimating AI. This is evident, as indicated by its closer alignment with the reference point. A similar trend is observed in the testing phase; however, the overall accuracy of all three predictive models is lower compared to the training phase. This may be due to the limited amount of data used in this study, potential overfitting, or challenges in generalizing to unseen data. The RF and GBT models were also found to be capable of predicting AI with moderate accuracy compared to XGB in both the training and testing phases. Overall, the ability of these tree-based models to predict AI is evident, and they can be used as substitutes for practical applications in real-world projects.
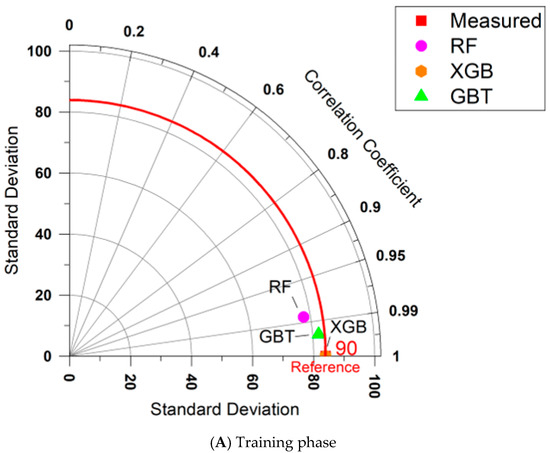
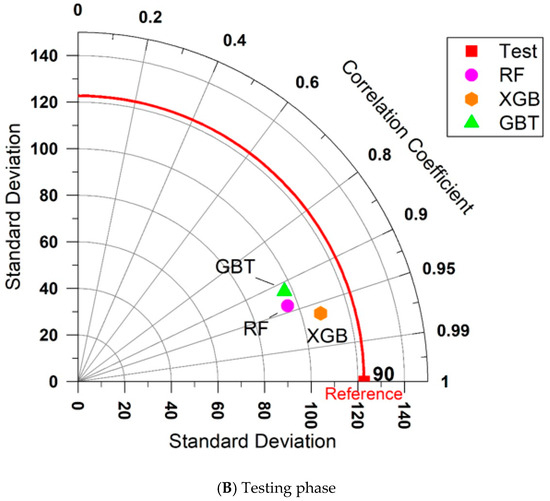
Figure 5.
Taylor diagrams for all proposed predictive models.
4.2. Model Comparison and Generalization
A fair way of evaluating is to compare the proposed model with similar models published previously. The authors of this study tried to propose a model with a higher level of generalization compared to the original study conducted by Onifade et al. [9]. In this way, this study used 112 data samples from the same site with a wider range of input parameters compared to the study conducted by Onifade et al. [9] with 89 data samples. The range of input parameters used in this study is wider, and this will help to apply this model to a wider range of inputs in future projects.
Another point that needs to be discussed is related to the number of input or effective parameters to propose a new model. The practical application of a new model is to allow other researchers or practitioners a real and easy way of applying the same model. Preparing a larger number of input parameters is more difficult compared to a lower number if someone wishes to use it in the future. Onifade et al. [9] used seven input parameters while this study considered only four parameters as inputs. This again will make our model easier to apply in practice and more attractive for researchers or industry professionals who prefer models with fewer required input parameters. It should be noted that the performance prediction of our model is not as good as Onifade et al. [9]; however, the proposed model provides a balance between simplicity and acceptable accuracy, making it a practical option for cases where data availability is limited or rapid estimation is needed.
4.3. Sensitivity Analysis
Sensitivity analysis is a good way to understand more about the effects of input variables on the output. This will help to identify the most and least effective parameters used in that specific database. Although there are several techniques for analyzing the effects of inputs on output of the system, the Cosine Amplitude technique is one of the simplest and easiest to implement. The Cosine Amplitude technique quantifies the linear association between each input variable and the output (AI) by computing the cosine of the angle between their respective vectors in multi-dimensional space. The value ranges between 0 and 1, where values closer to 1 indicate a stronger association. Since it is a dimensionless metric, no physical unit applies. It can quantify the degree of linear association between input and output parameters. In the area of data analysis, this technique recognizes the greatest influence of each input on the output by measuring the strength and direction of their relationships in a scale-independent manner. The range of cosine values is between 0 and 1, where 1 indicates the greatest influence and 0 indicates the least importance of that specific input parameter. Table 3 shows the effects of input parameters on the system output. The most effective parameter on AI is Qtz with a weight of 0.953, and the least effective parameter on AI is CV with a weight of 0.768.

Table 3.
The effects of input features on the system output.
5. Limitations and Future Studies
Despite the robustness and predictive success of the presented methodology, several limitations need to be acknowledged. Firstly, the coal samples used in this study were sourced exclusively from the KwaZulu-Natal coalfield, potentially constraining the generalizability of these predictive models to other geographic regions with differing geological characteristics. Therefore, the performance of the developed models may vary when applied to other coalfields with distinct geochemical and geological profiles. Secondly, although careful measures were employed during data preprocessing and outlier detection, the manual evaluation by domain experts introduced an element of subjectivity. This approach, while ensuring data integrity, may limit reproducibility across different research contexts, particularly where expert judgment criteria vary.
Another limitation pertains to hyperparameter tuning. While extensive grid and random search methods were implemented, advanced techniques such as Bayesian optimization could potentially further enhance model performance by efficiently exploring the hyperparameter space and potentially discovering more optimal configurations. Such advanced optimization strategies might uncover configurations capable of even greater predictive performance.
Additionally, the current study focused primarily on coal physicochemical properties without considering other potentially influential factors, such as hardness, microscopic coal textures, and particle size distribution, all of which might provide further predictive insights and model enhancement.
In light of these limitations, future research directions are suggested to enhance both the depth and breadth of this research field. It is recommended that subsequent studies validate these predictive models using coal samples from diverse geographic regions, thus assessing generalizability and broadening the practical applicability of the models. Moreover, future research could leverage automated outlier detection methods to enhance reproducibility and minimize subjective biases introduced by manual assessments.
Advanced hyperparameter tuning methods, such as Bayesian optimization and genetic algorithms, are encouraged for future exploration to further refine predictive capabilities. Incorporating additional mechanical and microscopic properties of coal into predictive models could offer enhanced insights into the complex relationships governing coal abrasiveness, potentially leading to improved predictive accuracy and practical applicability.
Lastly, the integration of real-time monitoring technologies and sensor-based data collection within coal processing plants could facilitate the development of dynamic, real-time predictive systems, thereby enabling proactive maintenance strategies, real-time coal blending optimization, and enhanced operational decision-making. Such advancements would significantly contribute to operational efficiency, sustainability, and economic viability in the coal processing industry.
6. Conclusions
This study successfully demonstrates the potential of tree-based ML algorithms in predicting the coal AI. Through a comprehensive analysis of RF, GBT, and XGBoost, we identified CV, Qtz, Ash, and Pyrite as the most influential factors in coal AI prediction. The results indicate that XGBoost provides the highest accuracy (R2 = 0.92), outperforming RF (R2 = 0.89) and GBT (R2 = 0.85). This highlights XGBoost’s capability in capturing complex, non-linear relationships between coal properties and abrasiveness, making it a valuable tool for predictive modeling in coal processing industries. The main findings are summarized as follows:
Testing dataset performance was lower than the training dataset at the first stage of the analysis, indicating noisy or outlier data that necessitated cleaning and filtering.
CV, Qtz, Ash, and Pyrite are the most influential properties for the prediction of coal AI in the original database; however, quartz was the most effective one among these four parameters.
Beyond the predictive accuracy, these ML-based approaches offer a cost-effective and efficient alternative to traditional laboratory methods, which are often time-consuming and resource-intensive. By leveraging data-driven models, industries can optimize coal selection, minimize equipment wear, reduce maintenance costs, and enhance operational sustainability. With further refinements and real-world validation, this approach has the potential to become an industry standard, streamlining decision-making and improving efficiency in coal-related operations.
Author Contributions
Conceptualization, All authors; methodology, M.A., C.Y.H. and D.J.A.; software, C.Y.H. and D.J.A.; validation, D.J.A., M.O. and M.K.; formal analysis, C.Y.H.; D.J.A., H.F. and M.K.; investigation, M.O. and M.K.; resources, H.F. and D.J.A.; data curation, M.O., M.K. and D.O.S.; writing All authors; writing-review and editing, All authors; visualization, M.A., C.Y.H., M.O. and D.J.A.; supervision, M.O., M.K. and D.J.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Finkelman, R.B.; Wolfe, A.; Hendryx, M.S. The future environmental and health impacts of coal. Energy Geosci. 2021, 2, 99–112. [Google Scholar] [CrossRef]
- Jiang, L.; Xue, D.; Wei, Z.; Chen, Z.; Mirzayev, M.; Chen, Y.; Chen, S. Coal decarbonization: A state-of-the-art review of enhanced hydrogen production in underground coal gasification. Energy Rev. 2022, 1, 100004. [Google Scholar] [CrossRef]
- Alam Munshi, T.; Jahan, L.N.; Howladar, M.F.; Hashan, M. Prediction of gross calorific value from coal analysis using decision tree-based bagging and boosting techniques. Heliyon 2024, 10, e23395. [Google Scholar] [CrossRef] [PubMed]
- Rehman, A.; Ma, H.; Ozturk, I.; Alvarado, R.; Oláh, J.; Liu, R.; Qiang, W. The enigma of environmental sustainability and carbonization: Assessing the connection between coal and oil rents, natural resources, and environmental quality. Gondwana Res. 2024, 128, 1–13. [Google Scholar] [CrossRef]
- Babu, K.A.; Lawrence, A.; Sivashanmugam, P. Grindability studies on blended coals of high-ash Indian coals with low-ash imported coals. Int. J. Coal Prep. Util. 2018, 38, 433–442. [Google Scholar] [CrossRef]
- Idris, A.; Man, Z.; Bustam, A.; Rabat, N.E.; Uddin, F.; Mannan, H.A. Grindability and abrasive behavior of coal blends: Analysis and prediction. Int. J. Coal Prep. Util. 2022, 42, 1143–1169. [Google Scholar] [CrossRef]
- Wells, J.; Wigley, F.; Foster, D.; Livingston, W.; Gibb, W.; Williamson, J. The nature of mineral matter in a coal and the effects on erosive and abrasive behaviour. Fuel Process. Technol. 2005, 86, 535–550. [Google Scholar] [CrossRef]
- Spero, C. Assessment and prediction of coal abrasiveness. Fuel 1990, 69, 1168–1176. [Google Scholar] [CrossRef]
- Onifade, M.; Lawal, A.I.; Bada, S.O.; Khandelwal, M. Predictive modelling for coal abrasive index: Unveiling influential factors through Shallow and Deep Neural Networks. Fuel 2024, 374, 132319. [Google Scholar] [CrossRef]
- Chen, Y.; Khandelwal, M.; Onifade, M.; Zhou, J.; Lawal, A.I.; Bada, S.O.; Genc, B. Predicting the hardgrove grindability index using interpretable decision tree-based machine learning models. Fuel 2025, 384, 133953. [Google Scholar] [CrossRef]
- Bandopadhyay, A. A study on the abundance of quartz in thermal coals of India and its relation to abrasion index: Development of predictive model for abrasion. Int. J. Coal Geol. 2010, 84, 63–69. [Google Scholar] [CrossRef]
- Alekhnovich, A.N.; Artemieva, N.V.; Bogomolov, V.V. Definition and Assessment of Coal Abrasivity. Power Technol. Eng. 2021, 55, 96–102. [Google Scholar] [CrossRef]
- Wells, J.; Wigley, F.; Foster, D.; Gibb, W.; Williamson, J. The relationship between excluded mineral matter and the abrasion index of a coal. Fuel 2004, 83, 359–364. [Google Scholar] [CrossRef]
- Nahvi, S.; Shipway, P.; McCartney, D. Effects of particle crushing in abrasion testing of steels with ash from biomass-fired powerplants. Wear 2009, 267, 34–42. [Google Scholar] [CrossRef]
- Hower, J.C.; Finkelman, R.B.; Eble, C.F.; Arnold, B.J. Understanding coal quality and the critical importance of comprehensive coal analyses. Int. J. Coal Geol. 2022, 263, 104120. [Google Scholar] [CrossRef]
- Vilakazi, L.; Madyira, D. Estimation of gross calorific value of coal: A literature review. Int. J. Coal Prep. Util. 2024, 45, 390–404. [Google Scholar] [CrossRef]
- Grzegorzek, W.; Adamecki, D.; Głuszek, G.; Lutyński, A.; Kowol, D. Technique to Investigate Pulverizing and Abrasive Performance of Coals in Mineral Processing Systems. Energies 2021, 14, 7300. [Google Scholar] [CrossRef]
- Peisheng, L.; Youhui, X.; Dunxi, Y.; Xuexin, S. Prediction of grindability with multivariable regression and neural network in Chinese coal. Fuel 2005, 84, 2384–2388. [Google Scholar] [CrossRef]
- Tshiongo, N.; Mulaba-Bafubiandi, A. South African coal and its abrasiveness index determination: An account of challenges. In Proceedings of the Southern African Universities Engineering Conference (SAUPEC), Johannesburg, South Africa, 24–26 January 2013; pp. 288–293. [Google Scholar]
- Höök, M.; Aleklett, K. A review on coal-to-liquid fuels and its coal consumption. Int. J. Energy Res. 2010, 34, 848–864. [Google Scholar] [CrossRef]
- Deepa, G.; Niranjana, A.; Balu, A. A hybrid machine learning approach for early cost estimation of pile foundations. J. Eng. Des. Technol. 2025, 23, 306–322. [Google Scholar] [CrossRef]
- Abdelfattah, E.; Joshi, S. Comparison of Machine Learning Classification and Clustering Algorithms for TV Commercials Detection. IEEE Access 2023, 11, 116741–116751. [Google Scholar] [CrossRef]
- Yang, B.; Armaghani, D.J.; Fattahi, H.; Afrazi, M.; Koopialipoor, M.; Asteris, P.G.; Khandelwal, M. Optimized Random Forest Models for Rock Mass Classification in Tunnel Construction. Geosciences 2025, 15, 47. [Google Scholar] [CrossRef]
- Chia, Y.H.; Armaghani, D.J.; Lai, S.H. Predicting Soil Compression Index Using Random Forest and Gradient Boosting Tree. In Proceedings of the Chinese Institute of Engineers (CIE), the Hong Kong Institute of Engineers (HKIE), and the Institution of Engineers Malaysia (IEM) Tripartite Seminar, Taipei, Taiwan, 1 November 2023; Volume 1. [Google Scholar]
- He, B.; Armaghani, D.J.; Lai, S.H.; Mohamad, E.T. Application of an expert extreme gradient boosting model to predict blast-induced air-overpressure in quarry mines. In Applications of Artificial Intelligence in Mining, Geotechnical and Geoengineering; Elsevier: Amsterdam, The Netherlands, 2024; pp. 269–289. [Google Scholar] [CrossRef]
- ASTM D-2013; Standard Practice for Preparing Coal Samples for Analysis. ASTM: West Conshohocken, PA, USA, 2013.
- ASTM D5142; Standard Test Methods for Proximate Analysis of the Analysis Sample of Coal and Coke by Instrumental Procedures. ASTM: West Conshohocken, PA, USA, 1998.
- ASTM D5373-14; Standard Test Methods for Determination of Carbon, Hydrogen, and Nitrogen in Analysis Samples of Coal and Carbon in Analysis Samples of Coal and Coke. ASTM: West Conshohocken, PA, USA, 2014.
- ISO 19579: 2006; Solid Mineral Fuels Determination of Sulphur by IR spectrometry. ISO: Geneva, Switzerland, 2006.
- ASTM D5865-04; Standard Test Method for Gross Calorific Value of Coal and Coke. ASTM: West Conshohocken, PA, USA, 2004.
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. August. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).