Comparison of MLR, MNLR, and ANN Models for Estimation of Young’s Modulus (E50) and Poisson’s Ratio (υ) of Rock Materials Using Non-Destructive Measurement Methods
Abstract
1. Introduction
2. Previous Studies
3. Materials and Methods
3.1. Materials
3.2. Sonic Wave Velocity (Vp and Vs) Tests
3.3. Shore Hardness Tests
3.4. The Stress-Strain Tests to Determine E50 and υ Values
4. Results and Discussion
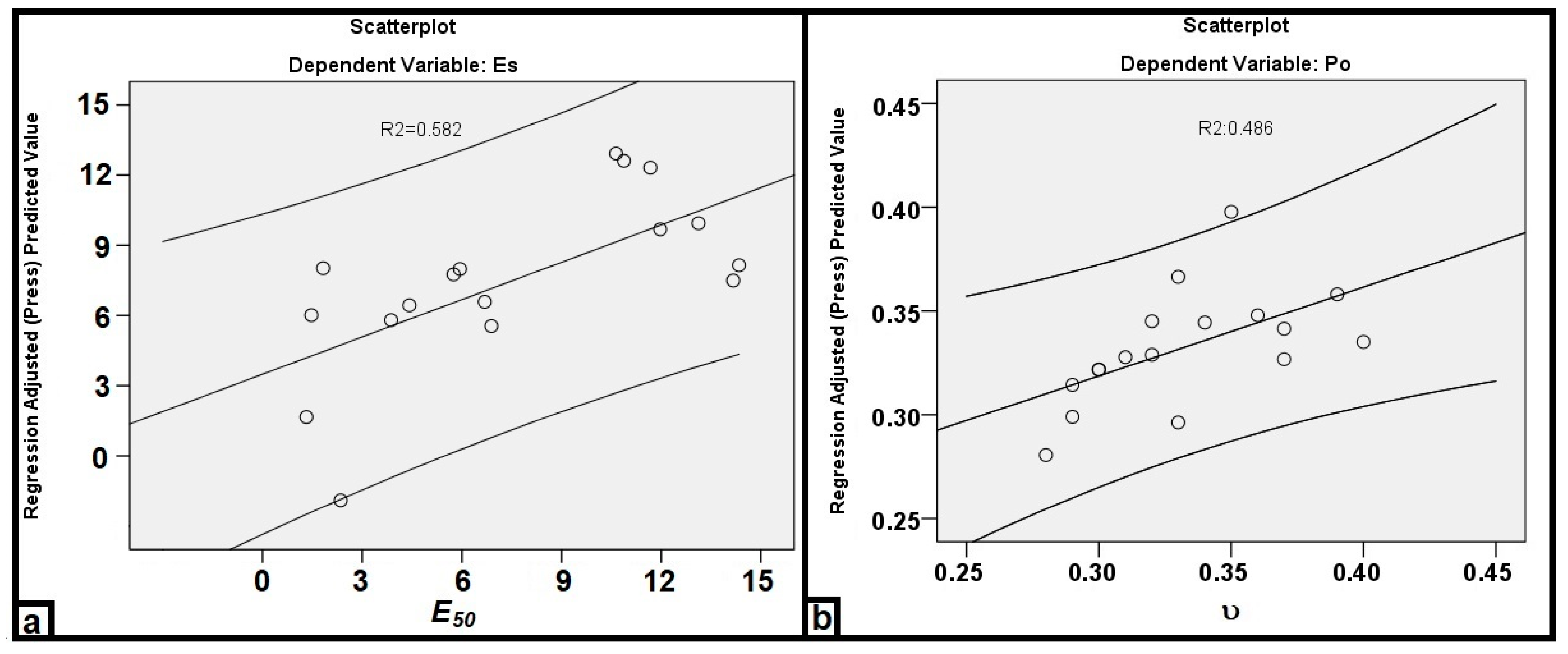
4.1. MLR and MNLR Analysis
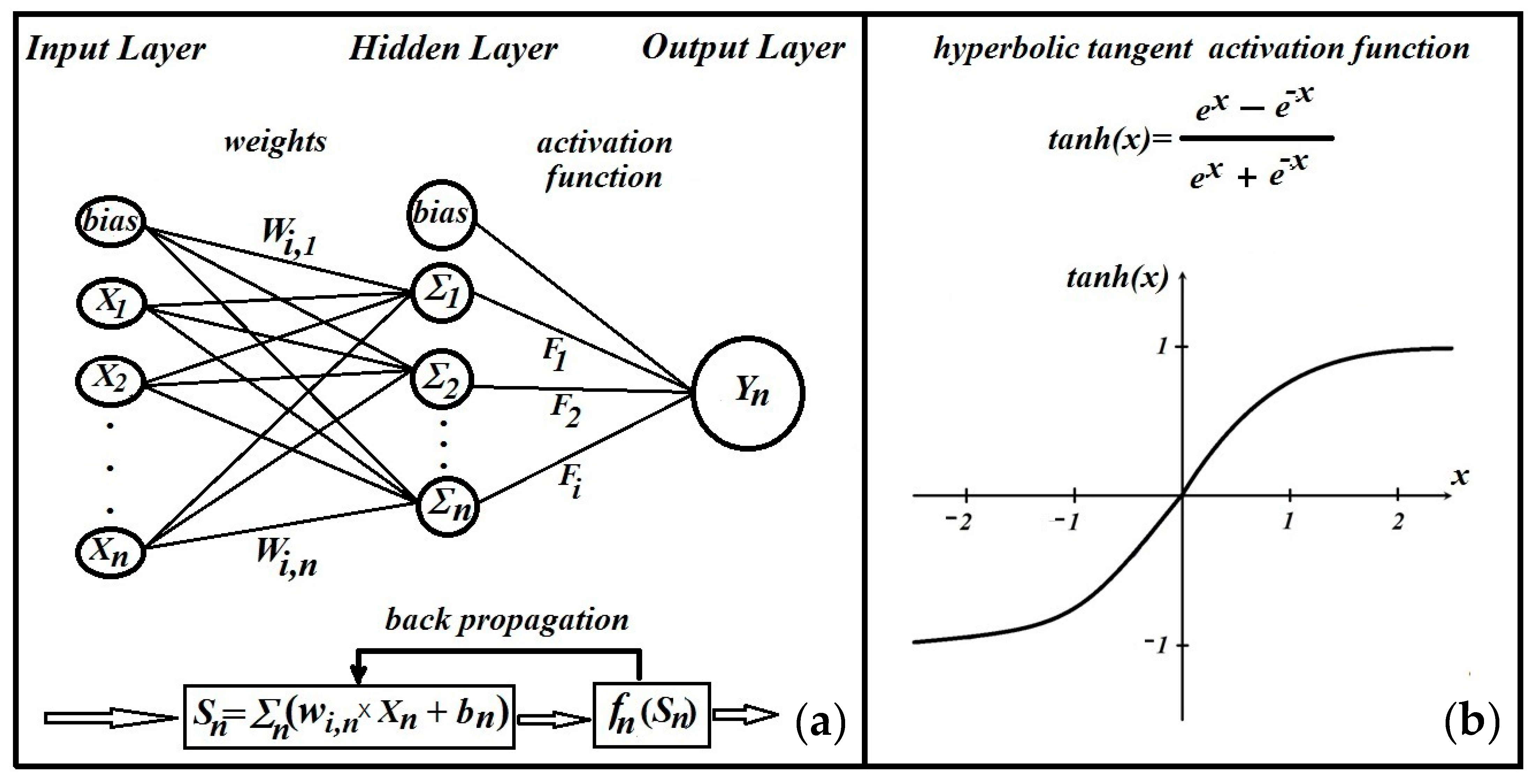
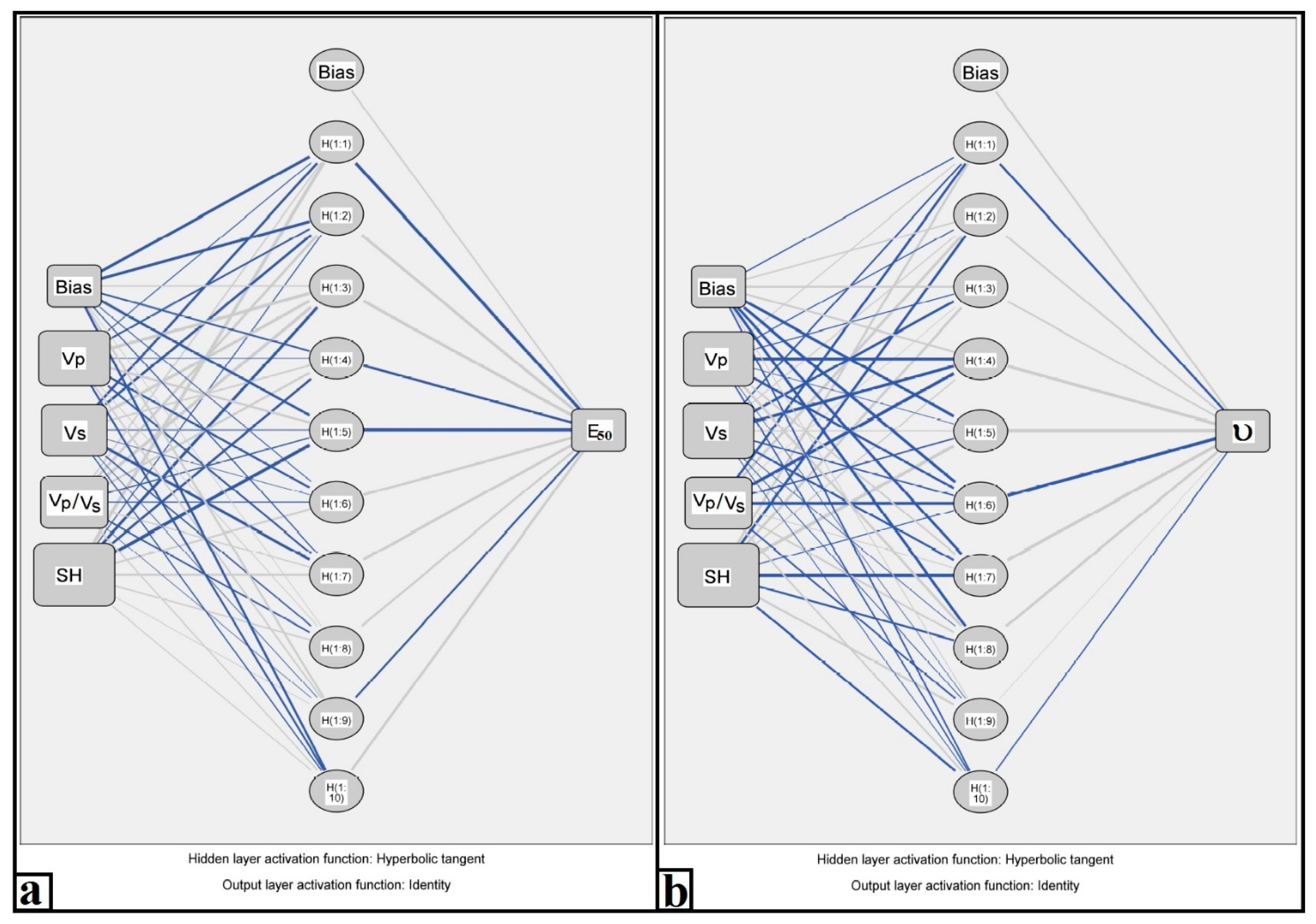
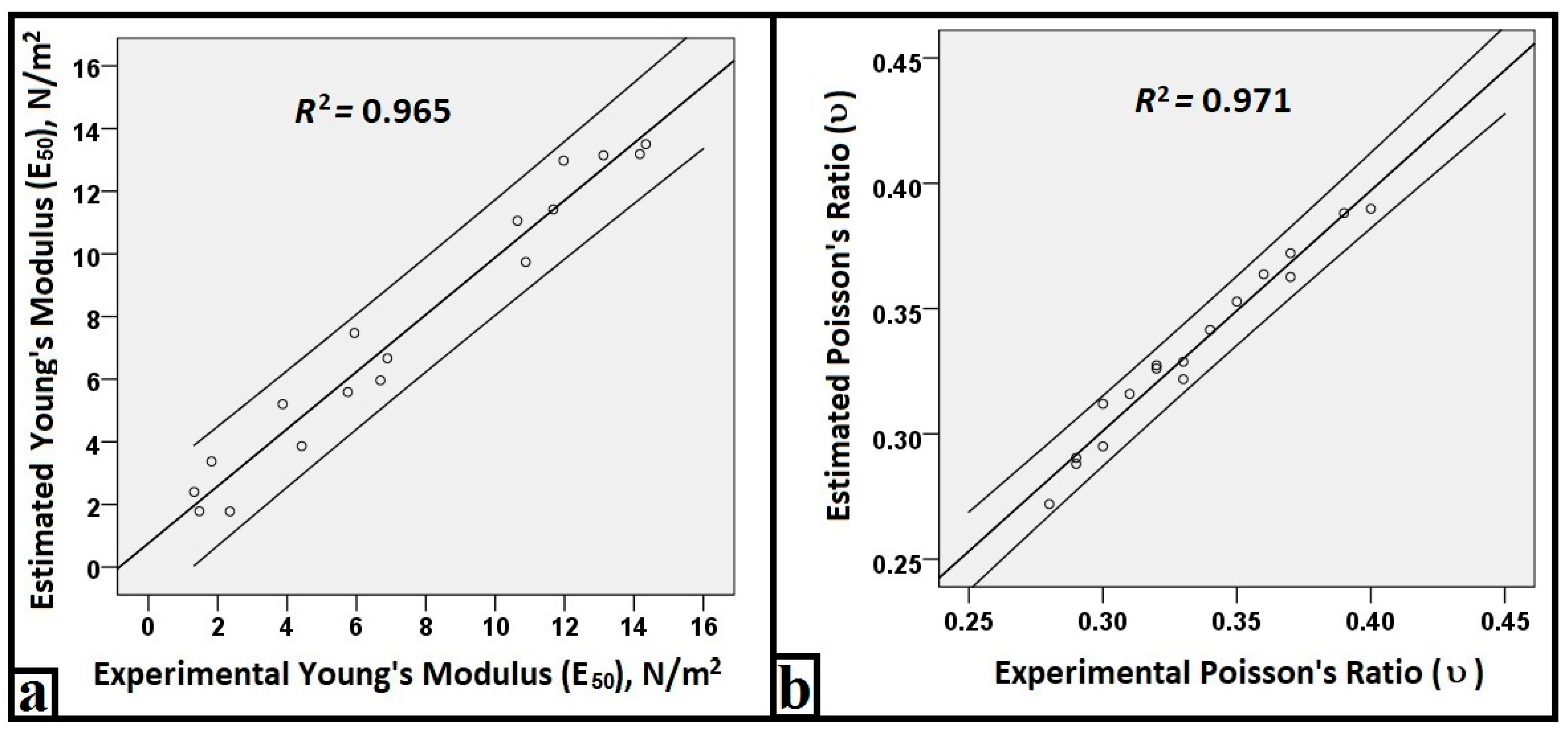
4.2. ANN Analysis
4.3. Comparison of Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ISRM. Rock Characterization, Testing and Monitoring, ISRM Suggested Methods; International Society for Rock Mechanic: Lisbon, Portugal, 1981; p. 211. [Google Scholar]
- ASTM. Soil and Rock Building Stones: Annual Book of ASTM Standards; ASTM Publication: Philadelphia, PA, USA, 1984; Volume 4.08. [Google Scholar]
- Ghafoori, M.; Rastegarnia, A.; Lashkaripour, G.R. Estimation of static parameters based on dynamical and physical properties in limestone rocks. J. Afr. Earth Sci. 2018, 137, 22–31. [Google Scholar] [CrossRef]
- Van Heerden, W.L. General relations between static and dynamic moduli of rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 381–385. [Google Scholar] [CrossRef]
- Pappalardo, G. Correlation between P-wave velocity and physical-mechanical properties of intensely jointed dolostones, Peloritani mounts, NE Sicily. Rock Mech. Rock Eng. 2015, 48, 1711–1721. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Z. The ultrasonic P-wave velocity-stress relationship of rocks and its application. Bull. Eng. Geol. Environ. 2016, 76, 661–669. [Google Scholar] [CrossRef]
- King, M.S. Static and dynamic properties of rocks from the Canadian Shield. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 237–245. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mohamad, E.T.; Momeni, E.; Monjezi, M.; Narayanasamy, M.S. Prediction of the strength and elasticity modulus of granite through an expert artificial neural network. Arab. J. Geosci. 2016, 9, 48. [Google Scholar] [CrossRef]
- Teymen, A. Statistical models for estimating the uniaxial compressive strength and elastic modulus of rocks from different hardness test methods. Heliyon 2021, 7, e06891. [Google Scholar] [CrossRef]
- Khandelwal, M. Correlating P-wave velocity with the physic-mechanical properties of different rocks. Pure Appl. Geophys. 2013, 170, 507–514. [Google Scholar] [CrossRef]
- Raj, K.; Pedram, R. Correlations between direct and indirect strength test methods. Int. J. Min. Sci. Technol. 2015, 25, 355–360. [Google Scholar]
- Sachpazis, C.I. Correlating Schmidt hardness with compressive strength and Young’s modulus of carbonate rocks. Bull. Int. Assoc. Eng. Geol. 1990, 42, 75–83. [Google Scholar] [CrossRef]
- Yilmaz, I.; Sendir, H. Correlation of Schmidt hardness with unconfined compressive strength and Young’s modulus in gypsum from Sivas (Turkey). Eng. Geol. 2002, 66, 211–219. [Google Scholar] [CrossRef]
- Hoek, E.; Diederichs, M.S. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Isik, N.S.; Ulusay, R.; Doyuran, V. Deformation modulus of heavily jointed–sheared and blocky greywackes by pressure meter tests: Numerical, experimental and empirical assessments. Eng. Geol. 2008, 101, 269–282. [Google Scholar] [CrossRef]
- Palchik, V. On the ratios between elastic modulus and uniaxial compressive strength of heterogeneous carbonate rocks. Rock Mech. Rock Eng. 2011, 44, 121–128. [Google Scholar] [CrossRef]
- Alemdag, S.; Gurocak, Z.; Gokceoglu, C. A simple regression based approach to estimate deformation modulus of rock masses. J. Afr. Earth Sci. 2015, 110, 75–80. [Google Scholar] [CrossRef]
- Feng, X.; Jimenez, R. Estimation of deformation modulus of rock masses based on Bayesian model selection and Bayesian updating approach. Eng. Geol. 2015, 199, 19–27. [Google Scholar] [CrossRef]
- Sonmez, H.; Gokceoglu, C.; Nefeslioglu, H.A.; Kayabasi, A. Estimation of rock modulus: For intact rocks with an artificial neural network and for rock masses with a new empirical equation. Int. J. Rock Mech. Min. Sci. 2006, 43, 224–235. [Google Scholar] [CrossRef]
- Yasar, E.; Erdogan, Y. Estimation of rock physicomechanical properties using hardness methods. Eng. Geol. 2004, 71, 281–288. [Google Scholar] [CrossRef]
- Shalabi, F.I.; Cording, E.J.; Al-Hattamleh, O.H. Estimation of rock engineering properties using hardness tests. Eng. Geol. 2007, 90, 138–147. [Google Scholar] [CrossRef]
- Karakus, M.; Kumral, M.; Kilic, O. Predicting elastic properties of intact rocks from index tests using multiple regression modeling. Int. J. Rock Mech. Min. Sci. 2005, 42, 323–330. [Google Scholar] [CrossRef]
- Kahraman, S.; Yeken, T. Determination of physical properties of carbonate rocks from P-wave velocity. Bull. Eng. Geol. Environ. 2008, 67, 277–281. [Google Scholar] [CrossRef]
- Sharma, P.K.; Singh, T.N. A correlation between P-wave velocity, impact strength index, slake durability index and uniaxial compressive strength. Bull. Eng. Geol. Environ. 2008, 67, 17–22. [Google Scholar] [CrossRef]
- Yagiz, S. P-wave velocity test for assessment of geotechnical properties of some rock materials. Bull. Mater. Sci. 2011, 34, 947–953. [Google Scholar] [CrossRef]
- Concu, G.D.; Nicolo, B.; Valdes, M. Prediction of building limestone physical and mechanical properties by means of ultrasonic P-wave velocity. Sci. World J. 2014, 2014, 508073. [Google Scholar] [CrossRef] [PubMed]
- Korkanc, M.; Solak, B. Estimation of engineering properties of selected tuffs by using grain/matrix ratio. J. Afr. Earth Sci. 2016, 120, 160–172. [Google Scholar] [CrossRef]
- Stan-Kłeczek, I. The study of the elastic properties of carbonate rocks on a base of laboratory and field measurement. Acta Montan. Slovaca 2016, 21, 76–83. [Google Scholar]
- Huang, Y.; Wänstedt, S. The introduction of neural network system and its applications in rock engineering. Eng. Geol. 1998, 49, 253–260. [Google Scholar] [CrossRef]
- Meulenkamp, F.; Alvarez-Grima, M. Application of neural networks for the prediction of the unconfined compressive strength (UCS) from Equotip hardness. Int. J. Rock Mech. Min. Sci. 1999, 36, 29–39. [Google Scholar] [CrossRef]
- Baykasoglu, A.; Gullu, H.; Canakcı, H.; Ozbakır, L. Prediction of compressive and tensile strength of limestone via genetic programming. Expert Syst. Appl. 2008, 35, 111–123. [Google Scholar] [CrossRef]
- Zorlu, K.; Gokceoglu, C.; Ocakoglu, F.; Nefeslioglu, H.A.; Acikalin, S. Prediction of uniaxial compressive strength of sandstones using petrography-based models. Eng. Geol. 2008, 96, 141–158. [Google Scholar] [CrossRef]
- Dehghan, S.; Sattari, G.H.; Chehreh, C.S.; Aliabadi, M.A. Prediction of unconfined compressive strength and modulus of elasticity for travertine samples using regression and artificial neural. New Min. Sci. Technol. 2010, 20, 41–46. [Google Scholar]
- Jang, H.; Topal, E. Optimizing over break prediction based on geological parameters comparing multiple regression analysis and artificial neural network. Tunn. Undergr. Space Technol. 2013, 38, 161–169. [Google Scholar] [CrossRef]
- Momeni, E.; Armaghani, D.J.; Hajihassani, M.; Amin, M.F.M. Prediction of uniaxial compressive strength of rock samples using hybrid particle swarm optimization-based artificial neural networks. Measurement 2015, 60, 50–63. [Google Scholar] [CrossRef]
- Mottahedi, A.; Sereshki, F.; Ataei, M. Development of overbreak prediction models in drill and blast tunneling using soft computing methods. Eng. Comput. 2018, 34, 45–58. [Google Scholar] [CrossRef]
- ASTM D7012-14e1; Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures. American Society for Testing and Materials International: West Conshohocken, PA, USA, 2017.
- ASTM D2845-08; Standard Test Method for Laboratory Determination of Pulse Velocities and Ultrasonic Elastic Constants of Rock (Withdrawn 2017). American Society for Testing and Materials International: West Conshohocken, PA, USA, 2008. [CrossRef]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E.; Keys, D.A. Applied Geophysics; Cambridge University Press: Cambridge, UK, 1976. [Google Scholar]
- Tumac, D.; Bilgin, N.; Feridunoglu, C.; Ergin, H. Estimation of rock cuttability from Shore hardness and compressive strength properties. Rock Mech. Rock Eng. 2007, 40, 477–490. [Google Scholar] [CrossRef]
- ISRM. Suggested methods for determining hardness and abrasiveness of rocks, Part 3. In Rock Characterization, Testing and Monitoring; ISRM Suggested Methods; Brown, E.T., Ed.; Pergamon: Oxford, UK, 1981; pp. 101–103. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2004. [Google Scholar]
- Paulson, D.S. Handbook of Regression and Modelling; Chapman & Hall/CRC: Taylor & Francis Group: Boca Raton, FL, USA, 2007. [Google Scholar]
- Bilgili, M.; Ozgoren, M. Daily total global solar radiation modeling from several meteorological data. Meteorol. Atmos. Phys. 2011, 112, 125–138. [Google Scholar] [CrossRef]
- Hair, J.F.J.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Multivariate Data Analysis, 5th ed.; Prentice Hall PTR: New York, NY, USA, 1998. [Google Scholar]
- Jain, A.K.; Mao, J.; Mohiddin, K.M. Artificial neural networks: A tutorial. Comp. IEEE 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Schalkoff, R.J. Artificial Neural Network; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]

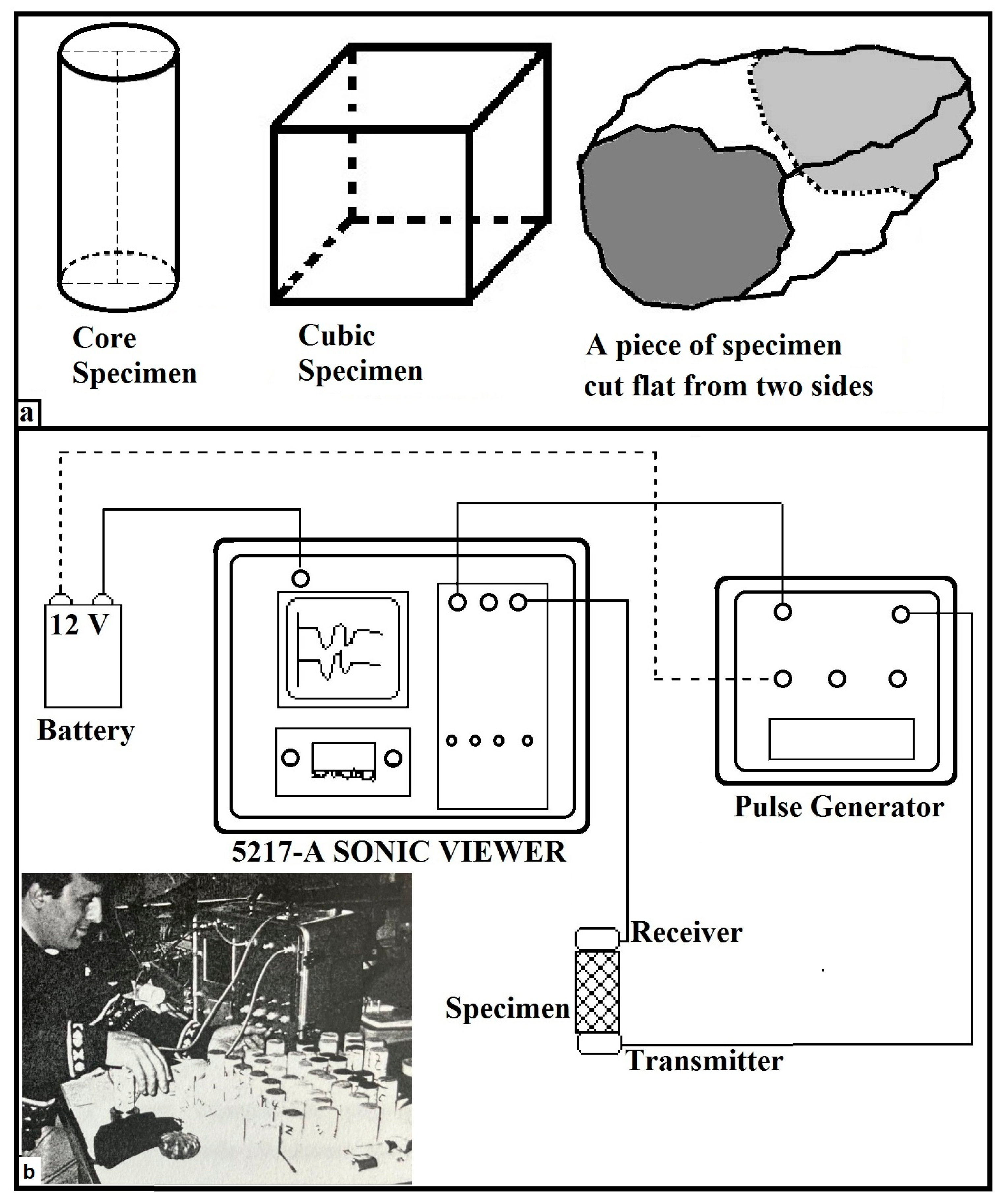


| No. | Description | Geological Origin | Mineralogical Properties |
|---|---|---|---|
| 1 | Limestone-1 | Sedimentary | 50% clay content |
| 2 | Limestone-2 | Sedimentary | very low porosity, sandy limestone texture |
| 3 | Limestone-3 | Sedimentary | micritic texture, fracture filling calcite, and contains a small amount of opaque minerals |
| 4 | Limestone-4 | Sedimentary | sparitic and homogenously textured |
| 5 | Siltstone | Sedimentary | contains 60% quartz |
| 6 | Green-Marl | Sedimentary | contains a small amount of silica |
| 7 | Gypsum | Sedimentary | less opaque and subhedral minerals |
| 8 | Barite | Sedimentary | 15% anhedral particle, may be subject to tectonism, a hydrothermally deposited ore |
| 9 | Feldspar | Metamorphic | coarse crystalline albite mineral, contains 50% quartz minerals |
| 10 | Marble | Metamorphic | contains equidimensional and anhedral calcite crystals |
| 11 | Trass-1 | Igneous-Volcanic | contains amphibole, sanidine, and biotite |
| 12 | Trass-2 | Igneous-Volcanic | contains 50% quartz minerals |
| 13 | Andesite-1 | Igneous-Volcanic | porphyritic, altered |
| 14 | Andesite-2 | Igneous-Volcanic | porphyritic, less altered |
| 15 | Galena | Mafic/Ultramafic-Igneous ore | also contains pyrite and chalcopyrite |
| 16 | Sulfide ore | Mafic/Ultramafic-Igneous ore | contains galena, pyrite, chalcopyrite, and quartz |
| 17 | Chromite | Mafic/Ultramafic-Igneous ore | contains 80% chromite, olivine, and serpentine |
| Sample Number | Number of Cores Used for Each Sample | E50 (N/m2) | υ | Vp (m/s) | Vs (m/s) | Vp/Vs | ρd (t/m3) | SH |
|---|---|---|---|---|---|---|---|---|
| 1 | 12 | 1.47 | 0.39 | 3064 | 1635 | 1.87 | 2.21 | 20.95 |
| 2 | 12 | 5.94 | 0.31 | 4532 | 2448 | 1.85 | 2.51 | 34.66 |
| 3 | 12 | 11.97 | 0.29 | 6023 | 2657 | 2.27 | 2.80 | 55.03 |
| 4 | 12 | 10.88 | 0.30 | 6697 | 2792 | 2.40 | 2.94 | 67.05 |
| 5 | 11 | 4.42 | 0.32 | 3541 | 1968 | 1.80 | 2.31 | 32.31 |
| 6 | 9 | 6.89 | 0.33 | 3217 | 1785 | 1.80 | 2.31 | 32.31 |
| 7 | 12 | 1.82 | 0.37 | 5088 | 2246 | 2.27 | 2.62 | 8.40 |
| 8 | 9 | 13.12 | 0.33 | 4110 | 1989 | 2.07 | 2.42 | 29.25 |
| 9 | 9 | 2.35 | 0.40 | 1997 | 1124 | 1.78 | 2.00 | 65.00 |
| 10 | 12 | 10.64 | 0.37 | 5975 | 2947 | 2.03 | 2.79 | 53.64 |
| 11 | 10 | 3.87 | 0.35 | 2688 | 1552 | 1.74 | 2.14 | 38.55 |
| 12 | 9 | 1.32 | 0.36 | 2327 | 1265 | 1.84 | 2.07 | 13.00 |
| 13 | 12 | 5.75 | 0.34 | 4433 | 2390 | 1.86 | 2.49 | 65.93 |
| 14 | 12 | 6.69 | 0.32 | 4481 | 2233 | 2.01 | 2.46 | 82.85 |
| 15 | 9 | 14.34 | 0.28 | 4927 | 2488 | 1.98 | 2.58 | 31.46 |
| 16 | 9 | 14.17 | 0.30 | 4725 | 2576 | 1.84 | 2.55 | 45.38 |
| 17 | 9 | 11.67 | 0.29 | 4866 | 2332 | 2.11 | 2.57 | 39.45 |
| Standard deviation | 4.50 | 0.04 | 1288 | 511 | 0.19 | 0.07 | 19.79 |
| Model | Input Combination | Output | R2 | RMSE | MAE |
|---|---|---|---|---|---|
| ANN-1 | Vp, Vs, Vp/Vs, ρd, SH | E50 (N/m2) υ | 0.891 0.961 | 1.490 0.007 | 0.947 0.005 |
| ANN-2 | Vp, Vs, Vp/Vs, SH | E50 (N/m2) υ | 0.965 0.971 | 0.883 0.006 | 0.699 0.004 |
| ANN-3 | Vp, Vs, ρd, SH | E50 (N/m2) υ | 0.925 0.956 | 1.252 0.008 | 1.037 0.006 |
| ANN-4 | Vp, Vs, Vp/Vs, ρd | E50 (N/m2) υ | 0.896 0.953 | 1.478 0.008 | 1.106 1.106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deniz, O.T.; Deniz, V. Comparison of MLR, MNLR, and ANN Models for Estimation of Young’s Modulus (E50) and Poisson’s Ratio (υ) of Rock Materials Using Non-Destructive Measurement Methods. Mining 2024, 4, 642-656. https://doi.org/10.3390/mining4030036
Deniz OT, Deniz V. Comparison of MLR, MNLR, and ANN Models for Estimation of Young’s Modulus (E50) and Poisson’s Ratio (υ) of Rock Materials Using Non-Destructive Measurement Methods. Mining. 2024; 4(3):642-656. https://doi.org/10.3390/mining4030036
Chicago/Turabian StyleDeniz, Orcun Tugay, and Vedat Deniz. 2024. "Comparison of MLR, MNLR, and ANN Models for Estimation of Young’s Modulus (E50) and Poisson’s Ratio (υ) of Rock Materials Using Non-Destructive Measurement Methods" Mining 4, no. 3: 642-656. https://doi.org/10.3390/mining4030036
APA StyleDeniz, O. T., & Deniz, V. (2024). Comparison of MLR, MNLR, and ANN Models for Estimation of Young’s Modulus (E50) and Poisson’s Ratio (υ) of Rock Materials Using Non-Destructive Measurement Methods. Mining, 4(3), 642-656. https://doi.org/10.3390/mining4030036







