The Influence of Explosive and Rock Mass Properties on Blast Damage in a Single-Hole Blasting

Abstract

In rock blasting for mining production, stress waves play a major role in rock fracturing, along with explosive gases. Better energy distribution improves fragmentation and safety, lowers production costs, increases productivity, and controls ore losses and dilution. Blast outcomes vary significantly depending on the choice of the explosive and the properties of the rock mass encountered. This study analyzes the effects of rock mass and explosive properties on blast outcomes via numerical simulation using data from the case study, and later validates the simulation results from the field blast fragmentation. The findings suggest that, for a given set of rock properties, the choice of explosive has a major influence on the resulting fragmentation. Strong explosives (high VOD and detonation pressure) favor large fracture extents in hard rocks, while weaker explosives offer a better distribution of explosive energy and fractures. The presence of rock structures such as rock contacts and joints influences the propagation of stress waves and fractures depending on the structures’ material properties, the intensity and orientations, and the direction and strength of the stress wave. When the stress wave encounters a contact depending on its direction, it is enhanced when traveling from soft to hard and attenuates in the opposite direction. The ability of the stress wave to cause fracturing on the opposite side of the contact depends on the intensity of the transmitted wave and the strength of the rock. Transmitted wave intensity is a function of the strength of the incident wave and the impedance difference between the interface materials. The presence of joints in the rock mass affects the propagation of the stress wave, mainly depending on the infill material properties and the angle at which the stress wave approaches the joint. Less compressible, higher stiffness joints transmit more energy. More energy is also transmitted in the areas where the stress wave hits the joint perpendicularly. Joints parallel to the free face offer additional fracturing on the opposite side of the joint. Other parameters, such as the joint width, continuity, fracture frequency, and the distance from the charge, enhance the effects. To achieve effective fragmentation, the blast design should mitigate the effect of variability in the rock mass via explosive selection and pattern design to ensure adequate energy distribution within the limits of geometric design.

1. Introduction

Drilling and blasting are common operations used to fragment and facilitate rock excavation in mining and civil works. The theory of rock fracture and fragmentation due to blasting suggests an overall combined damage mechanism, where intensity, propagation, and interaction of stress waves are responsible for initially fracturing the rock (conditioning). At the same time, the ensuing gas pressure predominantly effects fragmentation breakage and displacement beyond the immediate blasthole region. While the crushed zone surrounding the blasthole is formed due to higher compressive stresses after the stress wave travels through a distance and the rock yields, the tangential stress changes from compressive to tensile, forming radial cracks in the fracture zone [1]. The crushed and fracture zones (crack zones) are the areas of focus in rock fragmentation by blasting.

It is commonly observed that under 10% of broken volume breaks in shear due to compression, while the remaining more than 90% is broken by tensile stresses [2]. While the prior is responsible for crushed zone formation and preconditioning the rock, the latter extends the fractures in the fracture zone. They both contribute to overall rock damage. The further the stress wave travels radially outwards, its amplitude decreases, and it becomes an elastic wave that can deform but not fracture the rock, instigating ground vibrations. The size of the crushed zone can be two to five times the blasthole radius. Meanwhile, the fracture zone can extend to a distance of 20 to 60 times the radius. The size of these zones varies vastly depending on explosive strength and encountered rock mass strength and structural properties.

Damage zones around a single-hole blast have been studied by several researchers experimentally and using numerical models [3,4,5,6,7,8]. These studies observed that several factors influence the extent of damage zones, the main ones being the explosive strength (determined using the velocity of detonation (VOD), density, and detonation pressure) and rock mass strength (uniaxial compressive strength, tensile strength, Young’s modulus, and Poisson ratio). The rock mass is heterogeneous and anisotropic, with various structures cross cutting the mass, altering the distribution of explosive energy and fractures, and ultimately, the extent of damage zones. Studies on the influence of structural properties [9,10,11,12,13] indicate that the presence of interfaces as rock contacts, fractures, joints, etc., may result in partial propagation, reflection, or total arrest of the stress waves and cracks in variable proportions depending on the properties of structures and strength of the stress wave. This complicates the blasting process and blast outcomes.

Regarding the blasting process in variable rock masses where the stress wave passes through rock media with different physical and mechanical properties, Zhang [7] developed the transmission and reflection coefficients of the stress wave from theoretical studies. Chen et al. [14] found that the incident angle greatly influences how the stress wave interacts with the interface and the stress fields at the crack tip. Xu et al. [15] determined experimentally that the stress wave reflects on the joint surface and is concentrated on the crack tip of the joint for the perpendicular joints. Zhu [16] observed from experiments and numerical modelling that the cracks always propagate perpendicular to the joint surface.

These studies provide meaningful insight into the influence of various parameters on the blast outcomes. From our review, it is clear that the explosive and rock mass strength determine the fracture mechanics and extent of damage in blasting. It is also clear that interfaces in the rock formation influence stress wave and fracture distribution in the rock mass. These studies provide a general outlook; little work has been performed on the influence of various explosive and rock mass properties and, more specifically, on the influence of rock contacts’ and joints’ properties on the blasting process and the outcomes. Such analysis is valuable in improving the accuracy of models to predict blast outcomes and in improving blast designs.

Rock fragmentation via blasting is a complex non-linear process involving several parameters [17]. In recent years, with improved computer power, researchers have used artificial intelligence (AI) and machine learning (ML) techniques to improve predictions of blast outcomes with limited input parameters. Nguyen et al. [18] explored the use of multiple linear regression (MLR) analysis and an artificial neural network (ANN) to predict the tunnel area formed after blasting from the specific charge, the blast design, and the properties of the rock mass (rock mass rating). Amoako et al. [17] achieved improved prediction of fragmentation from blasting using a multilayered artificial neural network (ANN) and support vector regression (SVR) techniques.

Due to data analysis limitations, the complexity of the process, and the rock mass, numerical modelling has been a valuable tool in investigating stress wave behavior and the response of rock material to blasting loads and predicting outcomes. Numerical simulations provide a better insight into fragmentation under variable conditions in a more simplified and controlled environment. Zhu et al. [1] used AUTODYN 2D to investigate blasting-induced crack initiation and propagation in rocks. Torres et al. [19] used the Blo-up numerical model to optimize fragmentation from blasting in a copper mine. Xie et al. [20] used the finite element simulation (FEM) with the dynamic constitutive model in LS-DYNA to analyze damage mechanisms and optimize the cut blast design in various in situ stresses.

The FEM is widely used in blasting simulations, due to its ability to track the growth and nucleation of cracks in a brittle material, such as a rock, from the established damage evolution laws [21]. The RHT constitutive material model introduced by Riedel et al. [22] and implemented by Borrvall and Riedel [23] in LS-DYNA has features capable of modelling the dynamic behavior of concrete and is vastly used in simulating rock fragmentation via blasting [24,25,26].

This study investigates the influence of variable explosives and rock properties on blast-induced damage numerically in LS-DYNA. The study is divided into two parts: in the first part, the blast-induced damage distribution in a full-size bench model is investigated, including the role of free faces in enhancing fragmentation. The numerical model uses data from an existing mine, verified and validated by comparing the results with the site measurements and numerical estimations of the same data. In the second part, two-dimensional (2D) models are developed and used to analyze the effects of variable explosive properties, rock mass strength, and structural properties on the blast outcomes. The results from the simulation are compared with the field blast to provide an understanding of the variability of the obtained fragmentation. The outcomes of this study provide insight into the blasting process. They can be useful in improving blast fragmentation prediction models and guiding blast design for various rock mass and explosive properties.

2. Numerical Modelling and Verification

Most blast-induced fragmentation studies are based on two-dimensional (2D) analysis. Although 2D models simplify the computation process and provide a significant understanding of fragmentation, they do not capture the spatial stress distribution and blast damage in the three-dimensional (3D) setup. In this study, both 2D and 3D numerical simulation models are used in various applications.

LS-DYNA, a nonlinear transient finite element code with an explicit integration scheme capable of implementing dynamic problems, is used to model the blasting process [27]. LS-DYNA can successfully model the interaction between the solid material (rock) and fluid and gas flow (explosion gases) using the Lagrangian algorithm and arbitrary Lagrangian–Eulerian (ALE), incorporate coupling between Lagrangian and ALE interfaces and apply boundary conditions to restrict elements’ movements as needed.

Two main damage models commonly used to simulate the damage evolution of rock mass under blasting loads in LS-DYNA are the Holomquist–Johnson–Cook (HJC) model [28] and the Riedel–Hiermaier–Thoma (RHT) model [22]. In the study conducted by Wang et al. [24], the RHT model was observed to define the damage distribution in the rock better and describe the formation of the crushed zone and propagation of radial tensile cracks than the HJC model. Therefore, the RHT model is used as the constitutive model in this study.

2.1. The RHT Material Model

The RHT material model is an advanced brittle plasticity model for impulsive and dynamic loadings of brittle materials such as concrete, rock, or metals. In the RHT material model, the shear and pressure components are coupled. A Mie–Gruneisen equation describes the pressure with a polynomial Hugoniot curve that accounts for porous compaction in Equation (1): B₀ and B₁ are material constants estimated as B₀ = B₁ = 2S − 1. α_o is the initial porosity; ρ_o is the rock density; μ is the volumetric strain; and A₁, A₂, and A₃ are Hugoniot polynomial coefficients [23]. The coefficients A₁ to A₃ can be estimated using the rock density, initial porosity, bulk sound speed, and rock material constant S, using momentum and mass conservation equations as described by Xie et al. [20]. S is the slope of the linear relationship between the shock velocity and particle velocity. For most rocks, S ranges between 1.0 and 1.7, and for sulphide rocks between 1.2 to 1.4 [29].

$$P=\frac{1}{\alpha }\left(\left(B_o+B_1\mu \right){\alpha }_o{\rho }_{o}e+A_1\mu +A_2{\mu }^2+A_3{\mu }^3\right)$$

(1)

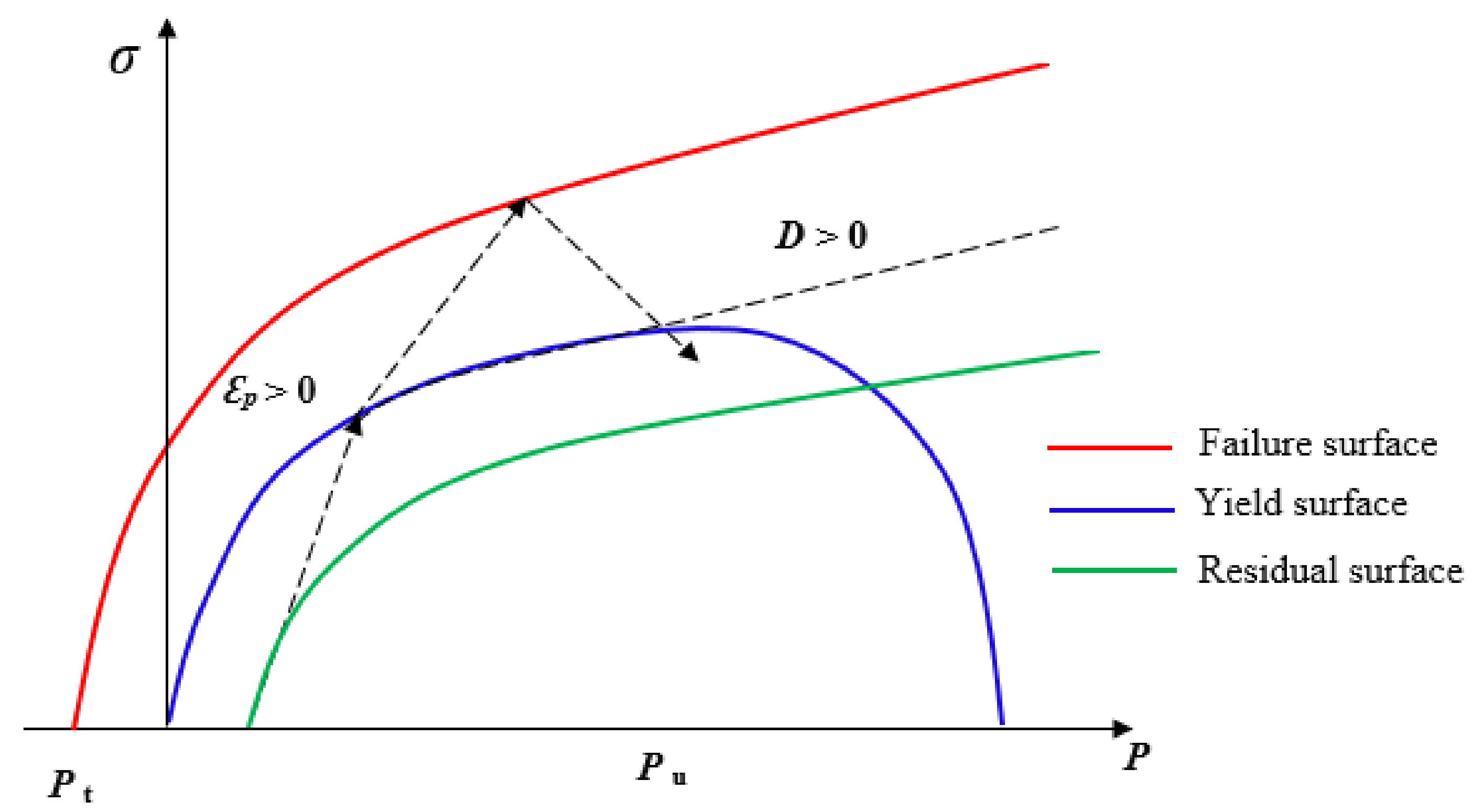
Three limit surfaces define the stress state of the material in the RHT strength model: the initial elastic yield surface, the residual friction surface, and the failure surface, which depend on the hydrostatic pressure. The surfaces represent the reduction in material strength in different meridians and the strain rate effect. Surface material failure is achieved when its ultimate compressive, shear, or tensile strength is reached. Figure 1 illustrates an example of static compressive meridian surfaces; P_t is the pressure at time and P_u is the current pore crush pressure. Pore crushing usually begins when the stress level reaches 2/3 of the UCS. In the figure, the model is elastic until it reaches the initial yield surface, beyond which plastic strain prevails. When stress reaches the failure surface, damage strain accumulation governs damage evolution. The damage variable of the RHT model (D) is calculated using Equation (2), where ${\epsilon }_m^P$ is the accumulated plastic strain and ${\epsilon }_f^P$ the plastic strain failure. D varies from 0 to 1; 0 represents undisturbed material and 1 is a fully damaged material. More information about the RHT model can be found in Borrvall and Riedel [23].

$$D={\displaystyle \sum \frac{\Delta {\epsilon }_m^P}{{\epsilon }_f^P}}$$

(2)

The RHT model has 37 parameters that need to be obtained or estimated from the rock’s physical and mechanical properties. Properties such as the density, uniaxial compressive strength, bulk modulus, and elastic shear modulus are obtained from the laboratory physical and mechanical experiments. Parameters such as Hugoniot polynomial coefficients A₁, A₂, and A₃, crush pressure (P_crush), compressive and tensile strain rate dependence exponents, etc., are dependent on rock physical and mechanical properties and can be estimated from the relationships presented by Borrvall and Riedel [23] and Xie et al. [20]. Other parameters, such as the yield surface parameters ($G_c^{\ast }$ and $G_t^{\ast }$), reduction factor in shear modulus XI, and minimum damaged residual strain ${\epsilon }_m^P$ are insensitive to simulation results and were taken from the reference values suggested by Borrvall and Riedel [23].

The RHT model was calibrated from the banded iron formation rock (BIF) studied by Dotto et al. [8] from Nyankanga Pit; Geita Gold Mine in Tanzania. The parameters calibrated for the RHT model are listed in

Table 1. RHT Model parameters for BIF.

Parameter (Unit)	Value	Parameter (Unit)	Value
Density, RO (kg/m3)	2680	Comp. strain rate dependence exp, $B_c$	0.0104
Elastic shear modulus, SHEAR (GPa)	38.62	Tensile strain rate dependence expo, $B_t$	0.0137
Unit conversion factor, ONEMPA	0	Pressure influence on plastic flow tension, PTF	0.001
Eroding plastic strain, EPSF ()	2	Compr. yield surface parameter, $G_c^{\ast }$	0.53
Parameter for polyn. EOS (Pore crush), B0	1.22	Tensile yield surface parameter, $G_t^{\ast }$	0.7
Parameter for polyn. EOS (Pore crush), B1	1.22	Shear modulus reduction factor, XI, ξ	0.5
Parameter for polyn. EOS, T1 (GPa)	58.22	Damage parameter, D1	0.04
Failure surface parameter, A	1.95	Damage parameter, D2	1
Failure surface parameter, N	0.6	Minimum damage residual strain	0.015
Compressive strength, $f_c$ (MPa)	126.02	Residual surface parameter, Af	0.61
Relative shear strength, $F_t^{*}$	0.18	Residual surface parameter, Nf	1.6
Relative tensile strength, $F_s^{*}$	0.11	Gruneisen gamma, Γ	0
Lode angle dependency factor, Q0	0.68	Hugoniot polynomial coefficient, A1 (GPa)	58.22
Lode angle dependency factor, B	0.0105	Hugoniot polynomial coefficient, A2 (GPa)	81.51
Parameter for polyn. EOS, T2 (GPa)	0	Hugoniot polynomial coefficient, A3 (GPa)	30.28
Reference compressive strain rate, ${\epsilon }_0^c$	3 × 10−5	Crush pressure, Pcrush (MPa)	84.01
Reference Tensile strain rate, ${\epsilon }_0^t$	3 × 10−6	Compaction pressure, Pcomp (GPa)	6
Break compressive strain rate, ${\epsilon }_c^{*}$	3 × 1025	Porosity exponent, NP, γ	3
Break tensile strain rate, ${\epsilon }_t^{*}$	3 × 1025	Initial porosity, ${\alpha }_o$	1

.

2.2. Explosive Properties and Parameters

Upon explosive detonation in the blasthole, the chemical reaction transforms the explosive material into explosion gases at very high pressure and temperature. There are different ways blast loads can be introduced into a simulation model. One way is using the high explosive burn material and Jones–Wilkins–Lee equation of state (JWL EOS) to model explosive charge detonation. The JWL EOS is a high-energy combustion model that can reliably predict higher explosion pressures. The model defines the pressure of detonation products P_cj using Equation (3) [30], where A, B, R₁, R₂, and ω are material constants, E is detonation energy per unit volume, and V₁ is the relative specific volume of detonation products:

$$P_{cj}=A\left(1-\frac{\omega }{R_1{V}_1}\right)e^{-R_1{v}_1}+B\left(1-\frac{\omega }{R_2{V}_1}\right)e^{-R_2{V}_1}+\frac{\omega E}{V_1}$$

(3)

The explosive used is a specially manufactured emulsion by ORICA; Fortis Extra [31], with properties summarized in

Table 2. Explosive (Fortis Extra) properties.

Explosive Property (Units)	Density (g/cm3)	Minimum Diameter (mm)	VOD (km/s)	Relative Effective Energy (REE), (%)
Value	1.10–1.25	64	4.1–6.7	151–189

. The actual field measurements were performed to determine the explosive’s VOD and density and estimate P_cj. Based on the similar ranges of the VOD and E₀, the parameters for the JWL Model constants for emulsion were adapted from a similar emulsion explosive E682 calibrated by Hansson [32] from the cylinder expansion test, as seen in

Table 3. Explosive parameters for simulation.

Explosive Type	Density (kg/m3)	VOD (m/s)	Pcj (GPa)	A (GPa)	B (GPa)	R1	R2	ꞷ	Eo (kJ/cm3)	vo
E682/FortisE	1207	4789	6.926	276.2	8.44	5.2	2.1	0.5	3.87	0

.

2.3. Simulation Model Preparation, Verification, and Validation

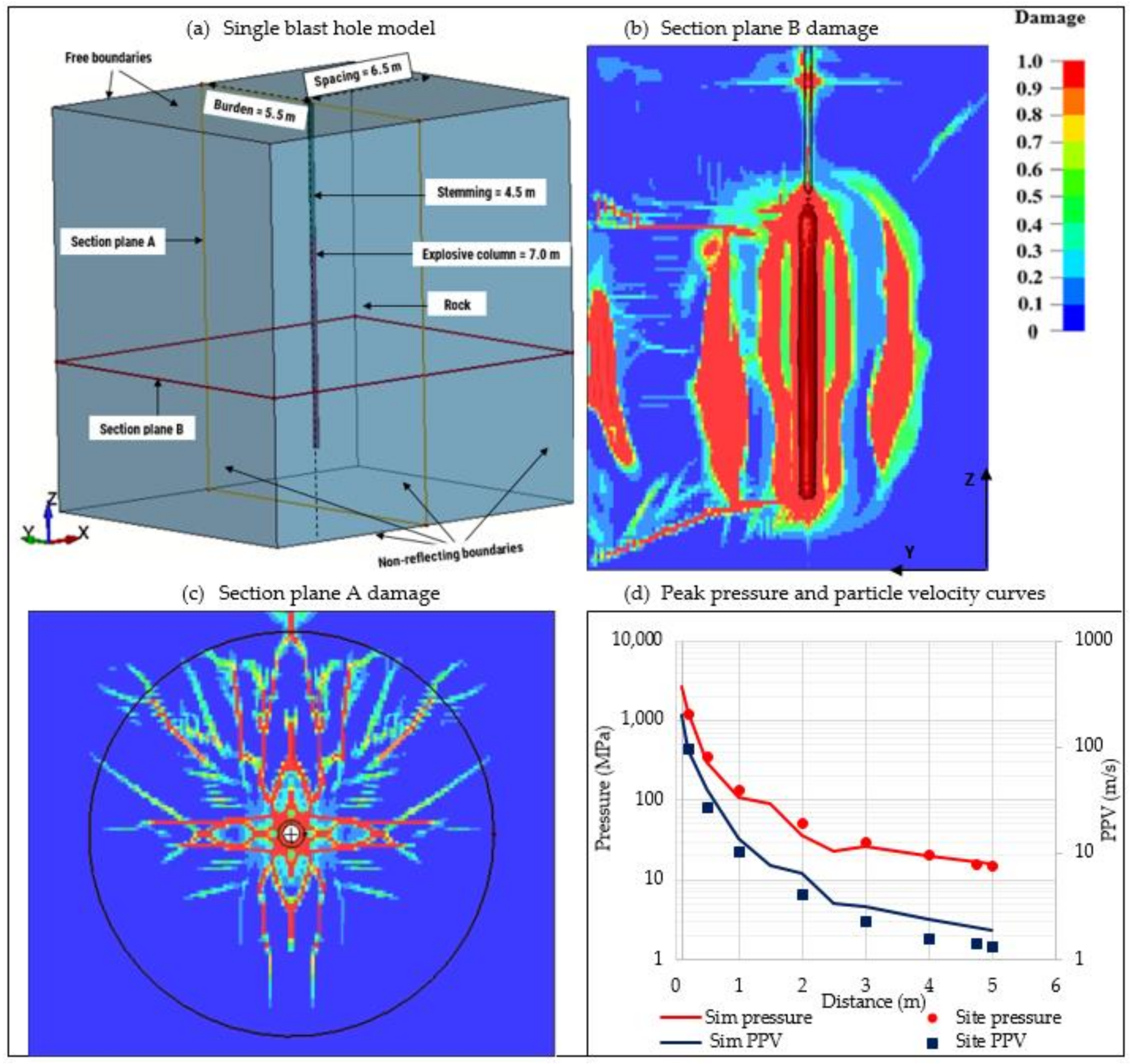
The numerical models were created and executed using LS-DYNA Version: smp s R11.1 on a Dell Precision 7810 with two Intel (R) Xeon (R) eight-core CPUs running at 2.40 GHz and equipped with 32 GB RAM. Figure 2a,

Table 4. Model settings.

Model Settings
Part	Item	Material	EOS	Part Type	Coupling
1	Explosive	High explosive burn	JWL	Solid ALE	Constrained Lagrange in solid
2	Rock	RHT	N/A	Solid Lagrangian

and

Table 5. Model parameters.

Parameter (Units)	Value
Burden (m)	5.5
Spacing (m)	6.5
Blasthole radius (mm)	101.5
Bench height (m)	10
Blastole depth (m)	11.5
Charge column (m)	7.0
Stemming height (m)	4.5
Element size (mm)	3 to 8

illustrate the settings and parameters for a bench-scale single-blasthole model of an intact rock. The model adopts the dimensions of the blast pattern used in the Nyankanga pit, where the burden and spacing are 5.5 m and 6.5 m, respectively; the bench height is 10 m with a 1.5 m sub-drill. The blasthole diameter is 203 mm and a coupled charge is adopted, where the diameter of the charge is the same as the blasthole. The size of the elements ranges from 3 mm close to the blasthole and increases gradually to 8 mm. Non-reflecting boundaries are set on the four sides to simulate infinite rock medium on respective sides and two sides are left as free boundaries along the burden and the top of the bench to allow stress wave reflection. The simulation is run for 2.5 ms.

The simulation results show the damage zones from the vertical plane section A (Figure 2b) and horizontal plane section B (Figure 2c) which is 3 m from the bottom of the blasthole. The crushed zone is represented by the circular red contour around the charge, and the fracture zone is defined by the cracks propagating from the crushed zone. Spalling occurs as seen on top of Figure 2b,c from the free faces propagating inwards. The initial crushed zone is 0.184 m at 0.7 ms, almost twice the blasthole radius; it extends to 0.3 mm at 2.5 ms. The fracture zone is 5 m. The maximum borehole pressure recorded is 2828 MPa, and the peak pressure and peak particle velocity (PPV) at the end of the crushed zone are 1280 MPa, and 95.2 m/s, respectively. Pressure at the end of the fractured zone is 15.97 MPa along the burden (free boundary) and 18.82 MPa along the spacing. PPV is 4.37 m/s on the burden and 1.9 m/s along spacing.

To investigate the validity and applicability of the simulation results, they are compared with the field measurements and estimations from analytical models obtained by Dotto et al. [8] in

Table 6. Simulation results validation.

Approach	rc (m)	Pe (MPa)	ue (m/s)	rf (m)	Pf (Mpa)	uf (m/s)
Study approach	0.169	1543.27	74.23	5.25	14.69	1.25
SWT	0.194	1260.88	98.24	4.75	15.85	1.23
HEL	0.173	1473.89	114.84	-	-	-
Numerical modelling	0.182	1280.00	95.2	5.00	15.97	1.9
Far-field monitoring	0.169	592.82	50.63	5.25	13.82	1.25
Standard error	0.01	70.30	8.34	0.11	0.46	0.15

; r_c and r_f are the radius of the crushed zone and fracture zone. P_e, P_f, u_e, and u_f are the peak pressures and the peak particle velocities at the end of the crushed and fracture zone, respectively. From the visual comparison and the standard error calculation, it is evident that the simulation results are similar to the field and analytical approach results except for the far-field monitoring, which underestimates the pressure and PPV near the blasthole. Likewise, when comparing the field measurements obtained by Dotto et al. [8] to the pressure and PPV curves obtained from the simulation in Figure 2d, they agree well, indicating that the simulation results are feasible.

3. Factors Influencing Damage/Fragmentation around a Single Blasthole

Several factors influence the blast outcomes. This study covers the influence of variable explosive strengths (VOD, density, and detonation pressure), rock strengths (variable UCS, Tensile strength, Young’s modulus, and Poisson ratio), and structural properties, specifically the rock contacts, and rock joints’ parameters (the joint’s width and infill material, distance from the blasthole, orientation, and the fracture frequency). The cases are studied by numerical simulation of a single blasthole in a 2D model. The diameter of the explosive is 203 mm, and the rock is 5.5 by 5.5 m; the size of the elements is the same as in the previous model.

3.1. Variable Explosive and Rock Properties

ANFO and emulsion are the commonly used commercial explosives in civil and mining applications, depending on the energy requirements and the water/moisture content in the blastholes. JWL parameters for emulsion are presented in Table 3, and similar parameters for ANFO were adopted from Sanchidrián et al. [33] in

Table 7. ANFO JWL parameters.

Explosive Type	Density (kg/m3)	VOD (m/s)	Pcj (GPa)	A (GPa)	B (GPa)	R1	R2	ꞷ	Eo (GPa)	vo
ANFO	902	4426	4.503	207.79	2.91	5.91	1.08	0.4	2.29	0

.

Four cases are studied for the two types of explosives and the two rock types. The first rock is BIF with properties listed in Table 1; this study considers it a hard rock. The second rock is sandstone with RHT material parameters calibrated from the experiment results by Jeong and Jeon [34] in

Table 8. Sandstone’s physical and mechanical properties.

Density (kg/m3)	UCS (MPa)	Tensile Strength (MPa)	Young Modulus (GPa)	Poisson Ratio	P-Wave Velocity
2400	88	0.1xUCS	25	0.3	2589

. The actual values for the RHT model are shown in the

Table A1. Sandstone RHT parameters.

Density, RO (kg/m3)	2400	Comp. strain rate exp., BETAC	0.026
Elastic shear modulus, SHEAR (GPa)	9.8	Tens. strain rate exp., BETAT	0.007
Unit conversion factor, ONEMPA	0	Pressure influence in tension, PTF	0.001
Eroding plastic strain, EPSF ()	2	Comp. yield surface par, GC	0.53
Par for polynomial EOS (pore crush), B0	1.2	Tensile yield surface par, GT	0.7
Par for polynomial EOS (pore crush), B1	1.2	Shear modulus reduction factor, XI	0.5
Par for polynomial EOS, (bulk mod) T1 (GPa)	12.87	Damage parameter, D1	0.04
Failure surface parameter, A	1.6	Damage parameter, D2	1
Failure surface parameter, N	0.6	Min damage residual strain, EPM	0.015
Compressive strength, FC (MPa)	88	Residual surface parameter, AF	0.61
Relative shear strength, FS	0.1	Residual surface parameter, NF	1.6
Relative tensile strength, FT	0.1	Gruneisen gamma, GAMMA	0
Lode angle dependency factor, Q0	0.68	Hug. polynomial coefficient, A1 (GPa)	12.87
Lode angle dependency factor, B	0.05	Hug. polynomial coefficient, A2 (GPa)	18.02
Par for polynomial EOS, (bulk mod) T2 (GPa)	0	Hug polynomial coefficient, A3 (GPa)	6.69
Reference compressive strain rate, EOC	3.00 × 10−5	Crush pressure, PEL (MPa)	58.67
Reference Tensile strain rate, EOT	3.00 × 10−6	Compaction pressure, PCO (GPa)	6
Break compressive strain rate, EC	3.00 × 1025	Porosity exponent, NP	3
Break tensile strain rate, ET	3.00 × 1025	Initial porosity, ALPHA	1

. The explosive strength parameters mentioned above, and the values used in this study were used as criteria to categorize emulsion as high explosive and ANFO as low explosive.

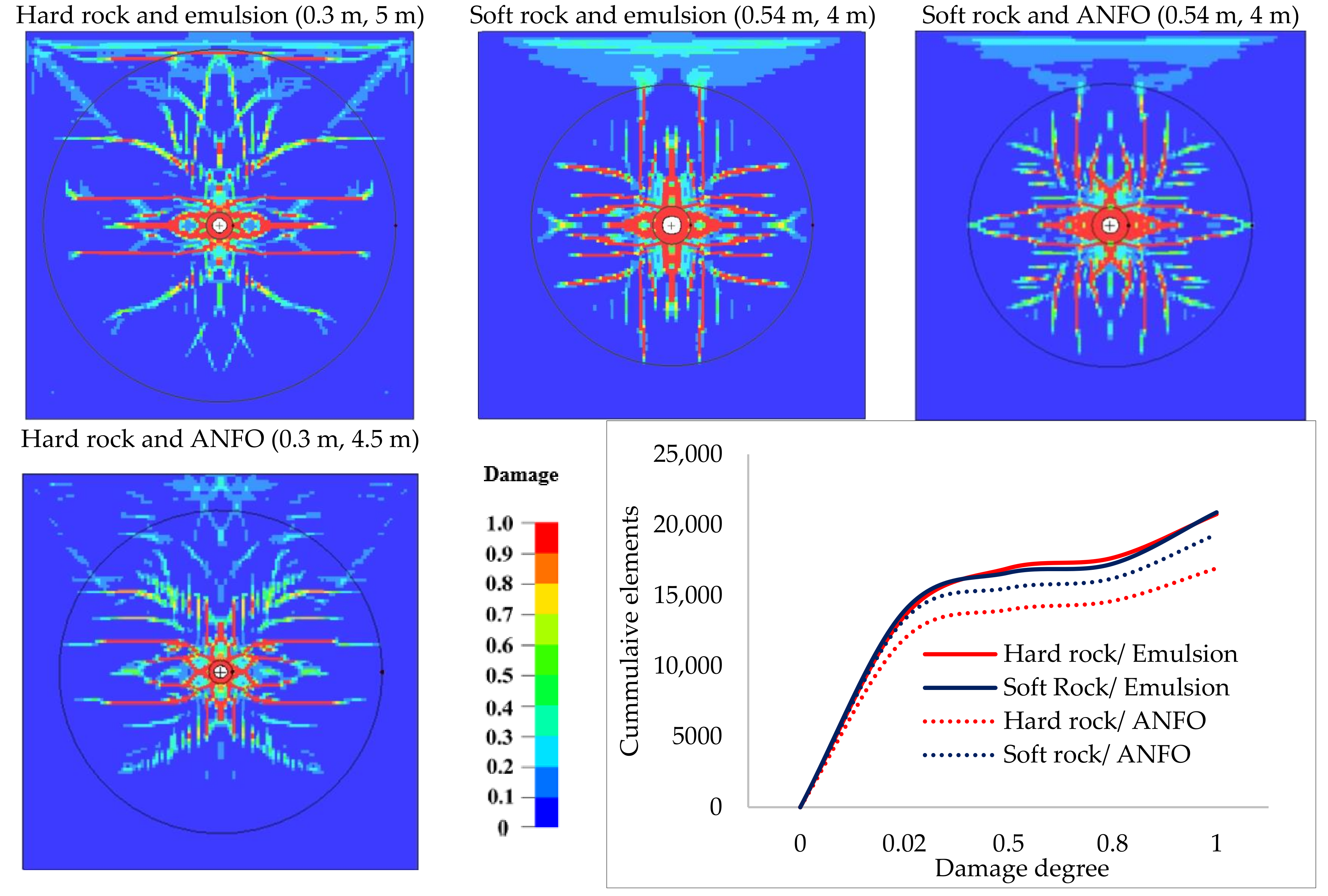
The four scenarios evaluated the influence of explosive properties on the formation of damage zones on the two rock types. Figure 3 shows the peak pressure and PPV profiles for the four scenarios evaluated. The pressure generated is higher with the high-strength explosive and hard rock. The peak pressure attenuates faster in a soft rock. The highest PPV is observed with high-strength explosive and the soft rock; it attenuates faster and all curves converge to 10 m/s at 3 m except for the hard rock/low-strength explosive which is consistently low.

As illustrated in Figure 4, due to high confinement and strength, the crushed zone formed in hard rock/emulsion is small, 0.3 m, and the fractured zone extends over a greater distance (5 m). When ANFO is used the fractured zone is reduced to 4.5 m along with the overall damage intensity. Conversely, on soft rock, the crushed zone formed is bigger, 0.54 m, but with less confinement (high PPV), the fractured zone is reduced to 4 m for both explosives. The damage zones extents on the soft rock do not change with a change in explosive, although within the same boundaries, the damage contours and curves in Figure 4 indicate higher damage intensity when the emulsion is used. In all cases, further fracturing is observed on the free face side (more with emulsion). The distribution of energy and, as a result, fractures is better when ANFO is used.

3.2. Influence of Rock Contacts on Fracture Distribution

The natural rock mass is heterogeneous and usually consists of layers with different rock compositions, properties, thicknesses, etc., making their mechanical properties different from a homogeneous rock mass. The contact between soft rock and hard rock in blasting causes wave dissipation at the interface and hence variable stress wave attenuations from the intact rock. Studies on the behavior of the transmitted wave through interfaces with different impedances show that the wave can either be attenuated or enhanced depending on the direction of the wave.

In this study, two rock contact scenarios are evaluated in a 2D model; the first is the contact between “hard-to-soft” and “soft-hard” at 1.5 m from the blasthole. The second scenario is “hard-soft-hard” and “soft-hard-soft” with interfaces at 1.5 and 2.5 m from the blasthole. Monitoring points are set at 1 m, 2 m, and 3 m distances (M₁, M₂, and M₃) as illustrated in Figure 5.

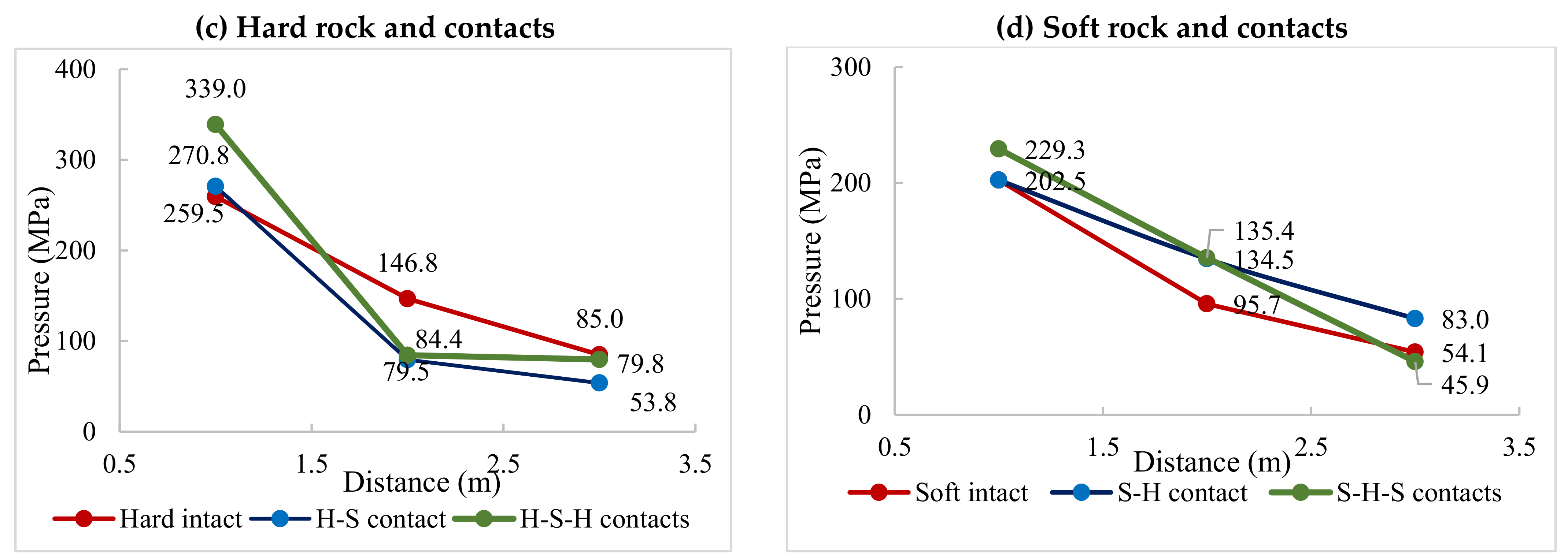
Results indicate that the pressure/stress is enhanced through a “soft-to-hard” interface and on the contrary attenuates through a “hard-to-soft” interface. On the latter, the pressure is reflected at the interface resulting in double peaks on the incident side as seen in Figure 6a. On multiple contacts, energy transmission and reflection across the joints follow the same trend although depending on the interface; for example, comparing “hard-to-soft-to-hard” (HSH) in Figure 6a,b, the pressure on the soft rock at 2 m increases in Figure 6b due to an increase in joint stiffness causing an increase in the pressure transmitted to the hard rock at 3 m distance. Figure 6c,d show that there is a level of enhancement when the stress wave travels from H-S-H and larger attenuations when traveling from S-H-S.

Although the pressure is enhanced on the “soft-to-hard” interface, it is hardly above the hard rock strength, and the cracks are terminated at the contact except for the reflection at the free face; the opposite is true for the “hard-to-soft” interface where the pressure attenuates but still higher than the soft rock strength and the cracks propagate as seen in Figure 7a,b. Overall, the likelihood of a stress wave causing fracturing beyond the interface depends on the impedance difference between the material on the opposite sides of the interface, the direction, and the strength of the incident wave.

3.3. Joint Parameters and Their Influence on Blast Damage

The most common features encountered in the rock mass are the joints formed by brittle fractures of rock, usually by tensile stress acting on a solid rock. The joints can be void or filled with various materials such as clay, sand, etc. When the rock fractures and somehow becomes displaced, it forms a fault in which two rock types come into contact as a scenario in Section 3.2. The presence of joints and their properties influence the overall rock strength, its interaction with the explosive energy, and the overall fragmentation. Understanding such influences is important in optimizing blast designs to achieve operations efficiency and productivity in mining. This study covers the influence of the joint’s infill material, the width and persistence, distance from the charge, and orientation relative to the free face. It also covers the influence of multiple joints considering fracture frequency and variable orientations.

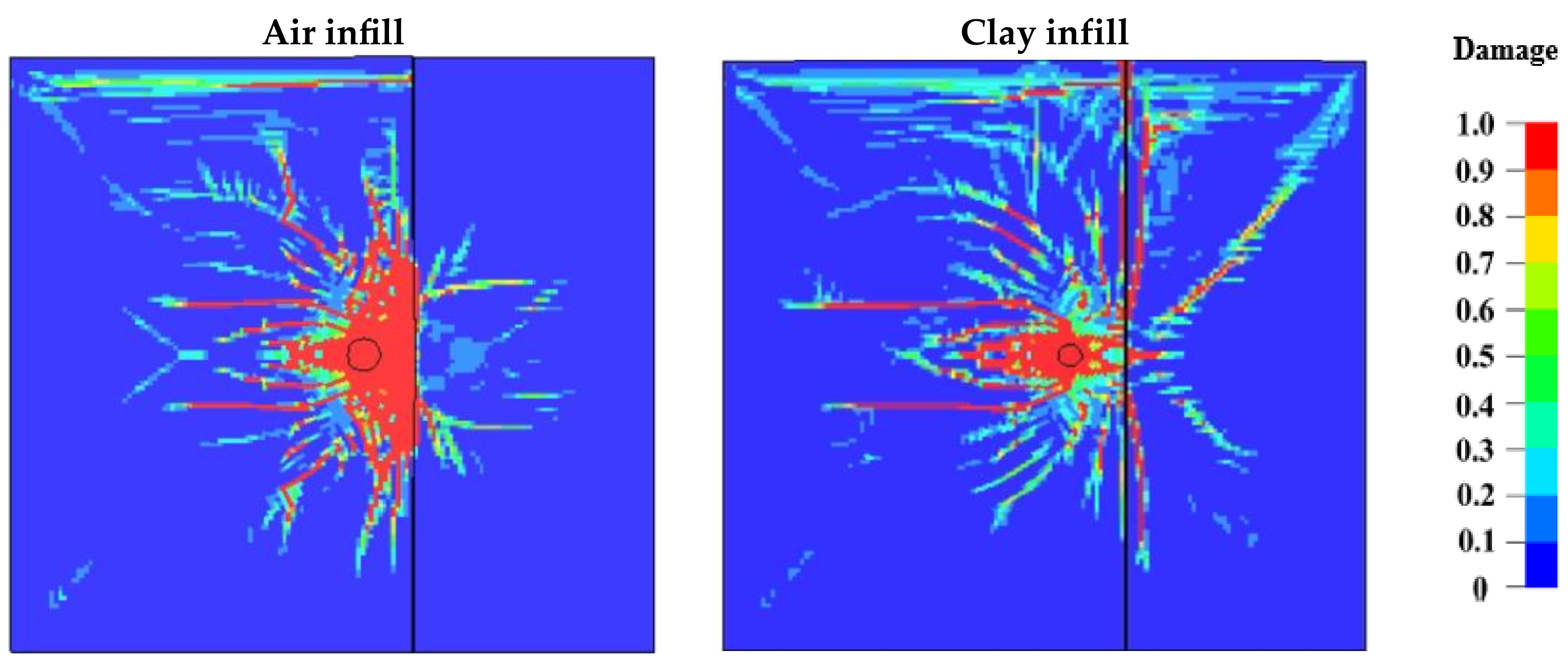
The effect of joints infill material is analyzed through simulations of void joints (air-filled joints) and joints filled clay material. Air is modeled as NULL material and ALE part with properties described in

Table 9. Air properties.

Density (kg/m3)	C4	C5	C6	Eo (MPa)	Vo
1.29	0.4	0.4	0	0.5	1

, while the clay infill is modeled using the plastic kinematic material model as a Lagrangian part with properties detailed in

Table 10. Clay infill properties.

Density (kg/m3)	Young’s Modulus (GPa)	Poisson’s Ratio	Yield Stress, (MPa)	Tangent Modulus, (GPa)	Hardening Parameter	Failure Strain, FS
1600	5	0.35	0.4	4	0	0.5

. The joint is 3 mm wide and 1 m from the blasthole; the surrounding rock is BIF.

The results indicate that partial reflection and transmission occur depending on the joint properties when the stress wave encounters the joint. As for the infill material, as illustrated in Figure 8, more energy is reflected on the void joints, causing excessive failure on the incident side and less fracturing on the opposite side.

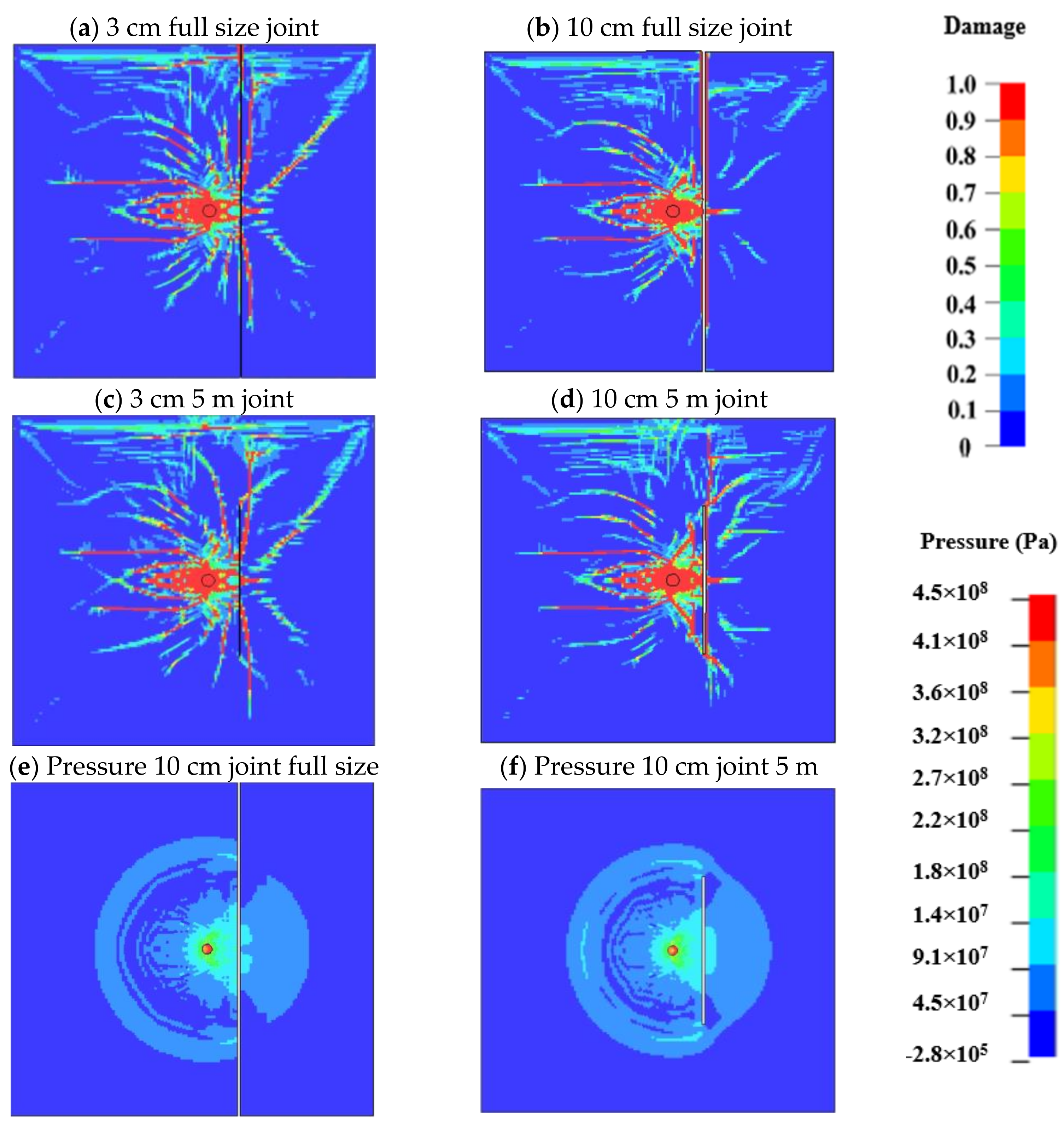
Using clay as the infill material and BIF as the main rock, several other joint parameters are evaluated for their influence on the blasting fragmentation. Figure 9a,b illustrate damage distribution for variable joint widths; 3 and 10 mm and Figure 9c,d persistence where the joint length is changed from full-size length cutting across the bench to 5 m for both cases. With increasing joint width, the fractures on the opposite side of the joint decrease significantly, more energy is reflected causing the increased size of the crushed zone, and significant energy is absorbed in joint deformation, also seen on the rock/joint interface (Figure 9b), significantly reducing the strength of the wave transmitted through the joint.

When the compressive wave reaches the joint interface, the stiffness of the joint increases at a rate that depends on the joint thickness and the normal stress. For the same infill material and normal stress, smaller joints have higher specific stiffness growth than wider joints. An increase in joint stiffness increases the joint’s transmission coefficient. For the same joint properties and orientation, fracturing is favored by discontinuous joints by the formation of new fractures from stress concentration on the cracks/joint tips and uninterrupted energy transmission on the rock bridges, as illustrated by the pressure contours taken at 0.6 ms on a full-size joint and 5 m joint in Figure 9e,f.

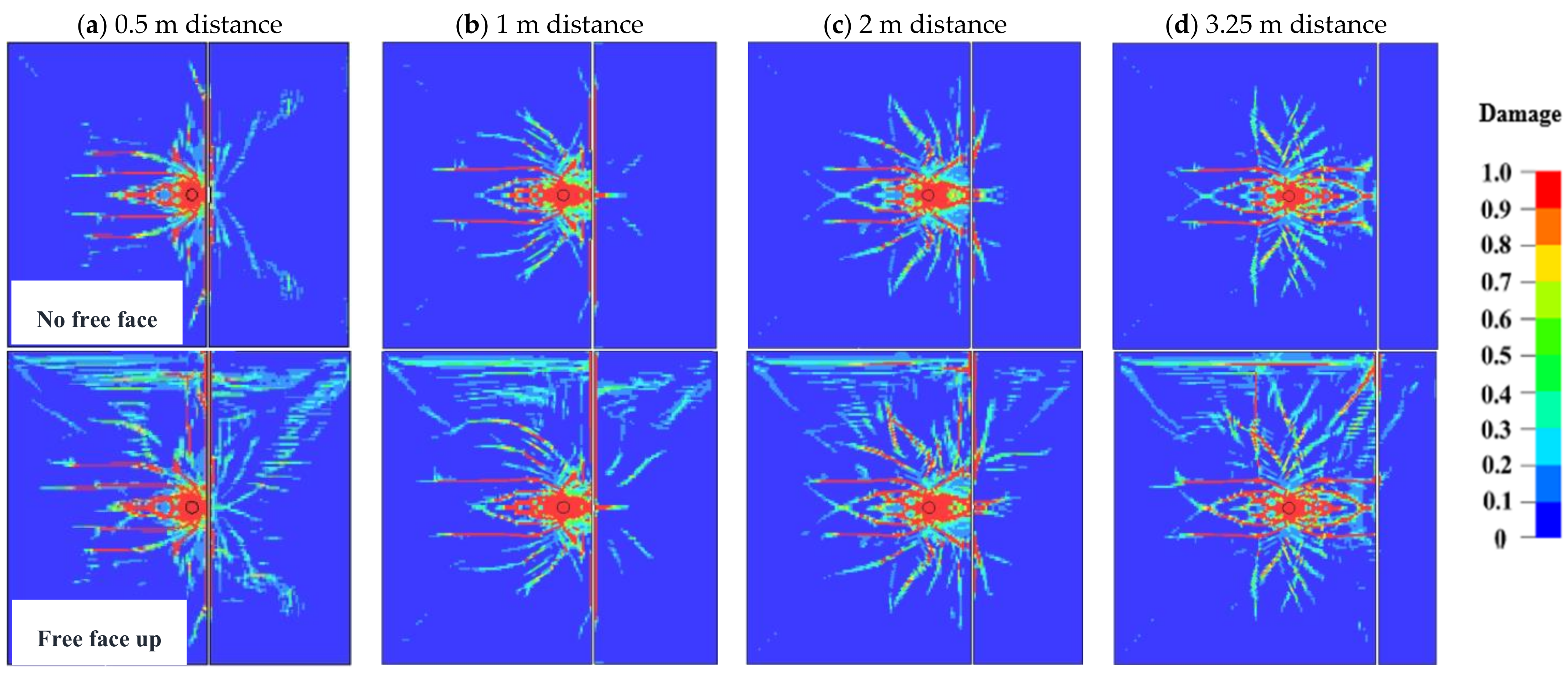
Fragmentation distribution in the rock mass depends on the strength and direction of the stress wave and hence is affected by the distance from the charge to the joint and its orientation relative to the direction of the wave and relative to the free face. Several scenarios are assessed for each case with and without a free face; the distance from the charge varies between 0.5 m, 1 m, 2 m, and 3.5 m, and joint orientation between 0, 15, 45, 60, and 90 degrees relative to the free face.

Figure 10a–d shows damage distribution for variable distance simulations. Fragmentation increases with the wave reflection at the free face in all cases where the free face is used. Fracture patterns generated for various distances indicate that the closer the joint is to the blasthole more energy is reflected and used up on joint deformation, causing less fracturing on the opposite side, as with 0.5 and 1 m distance joints.

Unlike the 1 m distance, when the joint is at 0.5 m, the high energy associated with closeness to the blast influences sufficient energy transmission across the joint, causing fracturing on the opposite side with additional enhancement from the free face. Wave energy reflection and joint deformation decrease with distance increase, hence increasing fracturing for 2 m joint. At 3.25 m the stress wave has attenuated, and fracturing does not occur on the opposite side of the joint except for the enhancement caused by the reflected wave at the free face in Figure 10d.

The orientation of the joints and the free face influences the direction and propagation of cracks as illustrated in Figure 11a–d. Cracks propagation beyond the joint depends on the angle at which the stress wave hits the joints. Regardless of the joint orientation, in the areas where the joints are hit perpendicularly or near perpendicular, the wave becomes transmitted, and cracks propagate through the joint as observed in the 30° orientation. Further burden fracturing depends on the energy reflected at the free face. Energy reflection is limited to the portion that is close to the free face when the joint is perpendicular to the free face as seen with a 90° joint. Since the joint orientation does not favor further cracking from wave reflection at the free face, fragmentation on the opposite side of a vertical joint is significantly reduced (Figure 11d).

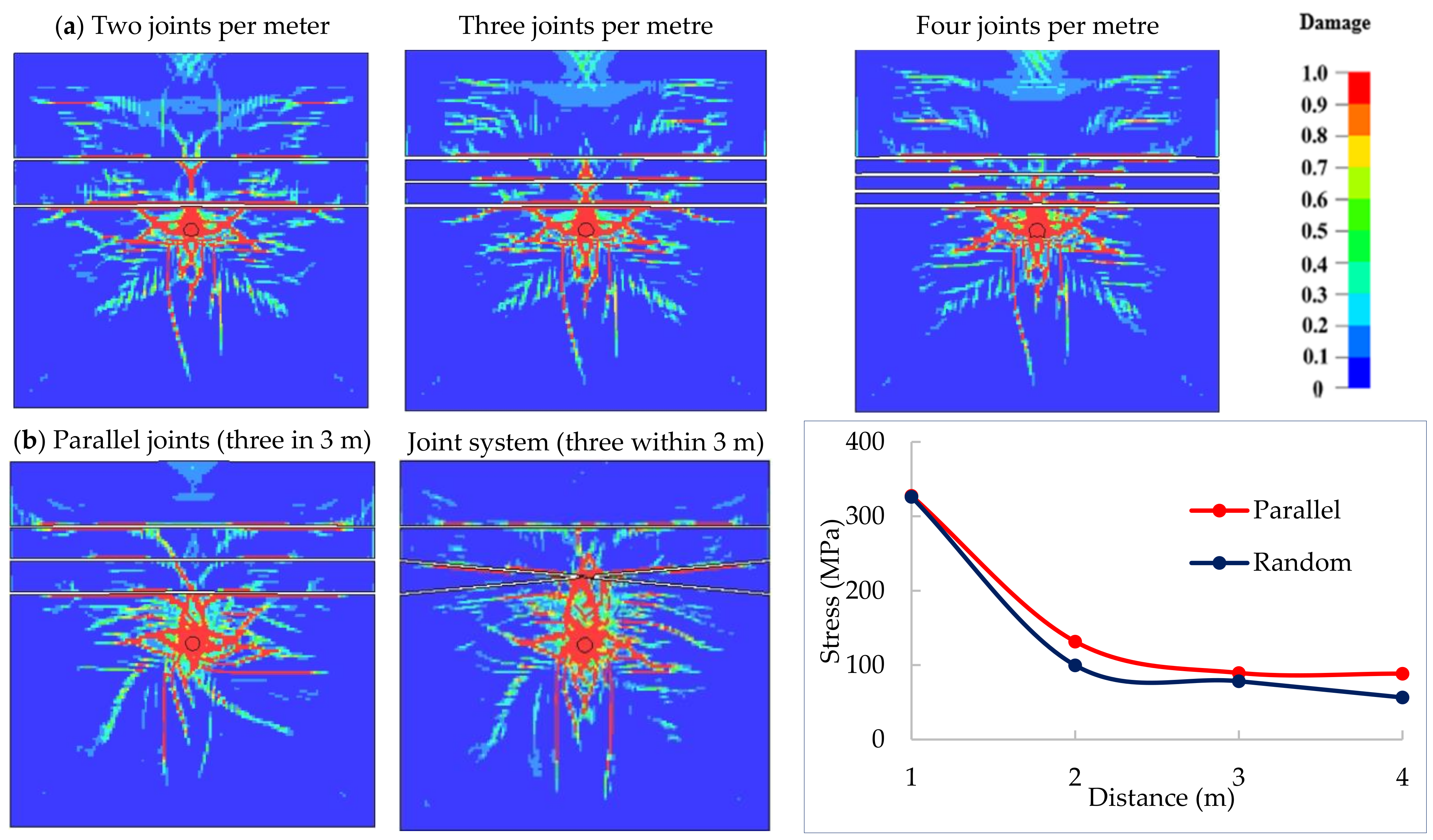
Joints usually occur in multiples, evenly spaced, with the same orientation and physical properties forming a joint set. When two or more joint sets intersect, they form a joint system which is a common feature in the rock mass. The spacing between the joints (fracture frequency), orientations, and intersections affect the fracture distribution from blasting. The analysis is presented in Figure 12.

Investigation of the effect of joint frequency was conducted from three scenarios with two, three, and four joints per meter. The simulation results show that increased joint frequency reduces the burden cracking significantly as illustrated in Figure 12a. With the increase in joint frequency, the wave goes through multiple partial reflections and transmissions, weakening the wave strength. Similarly, joint deformation consumes wave energy, and with the increase in joint frequency, this occurs multiple times, contributing to weakening the stress wave and lessening the fracturing of the burden.

The analysis of the joint system (randomness) with three parallel joints and three intersecting joints all within 3 m width in Figure 12b, shows better energy transfer in parallel than random joints indicated by the least fracturing on the opposite side of the joints. The figure also shows the peak stress monitored in four locations for the two cases where the wave is observed to attenuate more rapidly with random/intersecting joints.

4. Summary and Discussion

4.1. Analysis Summary

Section 3 covers the analysis of several factors influencing blast outcomes, mainly explosive strength, intact rock strength, and structural properties. From the analysis of explosive energy and rock strength, it has been observed that high-energy explosives offer a larger extent of fracturing. In contrast, the low-strength explosive offers a better energy distribution. The extent of fracturing in soft rock does not improve with increasing explosive energy due to less confinement associated with low strength and higher deformations. It requires more energy to fracture a hard rock; therefore, the damage extent decreases when low-strength explosive is used on the hard rock.

The contacts between soft and hard can enhance or attenuate the stress wave depending on the impedance difference and the direction of the wave. The same trend is observed with multiple contacts; however, depending on the properties of the contact materials and the distance between the contacts, the attenuations or enhancement can vary significantly.

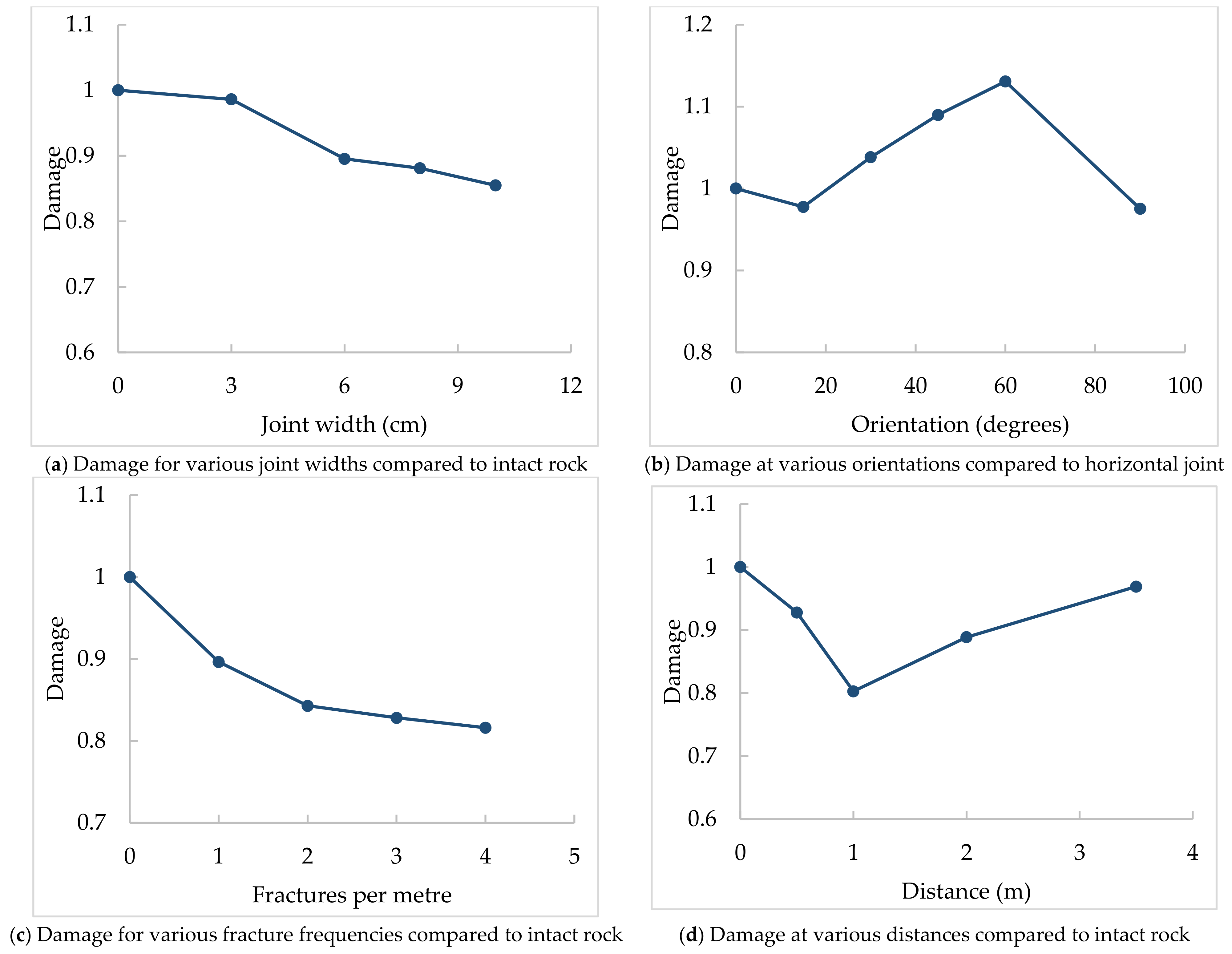
Variable joint parameters influence the fragmentation differently, as summarized in Figure 13. The figure compares the number of damaged elements in various structural properties to those in the intact rock (represented as damage = 1).

The type of joint infill material and the width influence the transmission of the energy and crack propagation across the joint due to materials impedance difference and joint stiffness. Empty joints reflect most of the energy. On wider joints, in addition to energy reflection, more energy is absorbed in joint deformation. Joint persistence determines the surface area in which the joint affects the stress wave. Discontinuous joints favor more fragmentation over continuous joints from blast energy by offering rock bridges for stress wave and cracks propagation, and from the stress concentration on the joints tips where fractures are initiated.

Joint orientation affects the distribution of explosive energy and cracks. Stress waves and cracks can easily propagate in the areas where the wave hits the joint perpendicularly or near perpendicularly. In this case, angled joints become favorable in energy and crack propagation. Further cracking on the opposite side of the joint occurs from the wave reflection at the free face making the perpendicular joints to the free face at a disadvantage.

When the joint is very close to the blasthole, the high-intensity stress wave overcomes losses from reflection and joint deformation, allowing some wave transmission and crack formation across the joint. As the distance increases, the energy attenuates, less is transmitted, and fewer fractures are formed beyond the joint. When the joint is the furthest and the stress wave has weakened, very little to no fractures form beyond the joint.

Joints usually appear in a family with similar properties and orientations, forming joint sets and systems. The comparison of the fracture frequency analysis indicates a consistent decrease in energy transmission and crack formation with increased fracture frequency. Parallel joints offer better energy transmission than randomly oriented (intersected) joints for an equal number of joints.

4.2. The Field Analysis and Model Validation

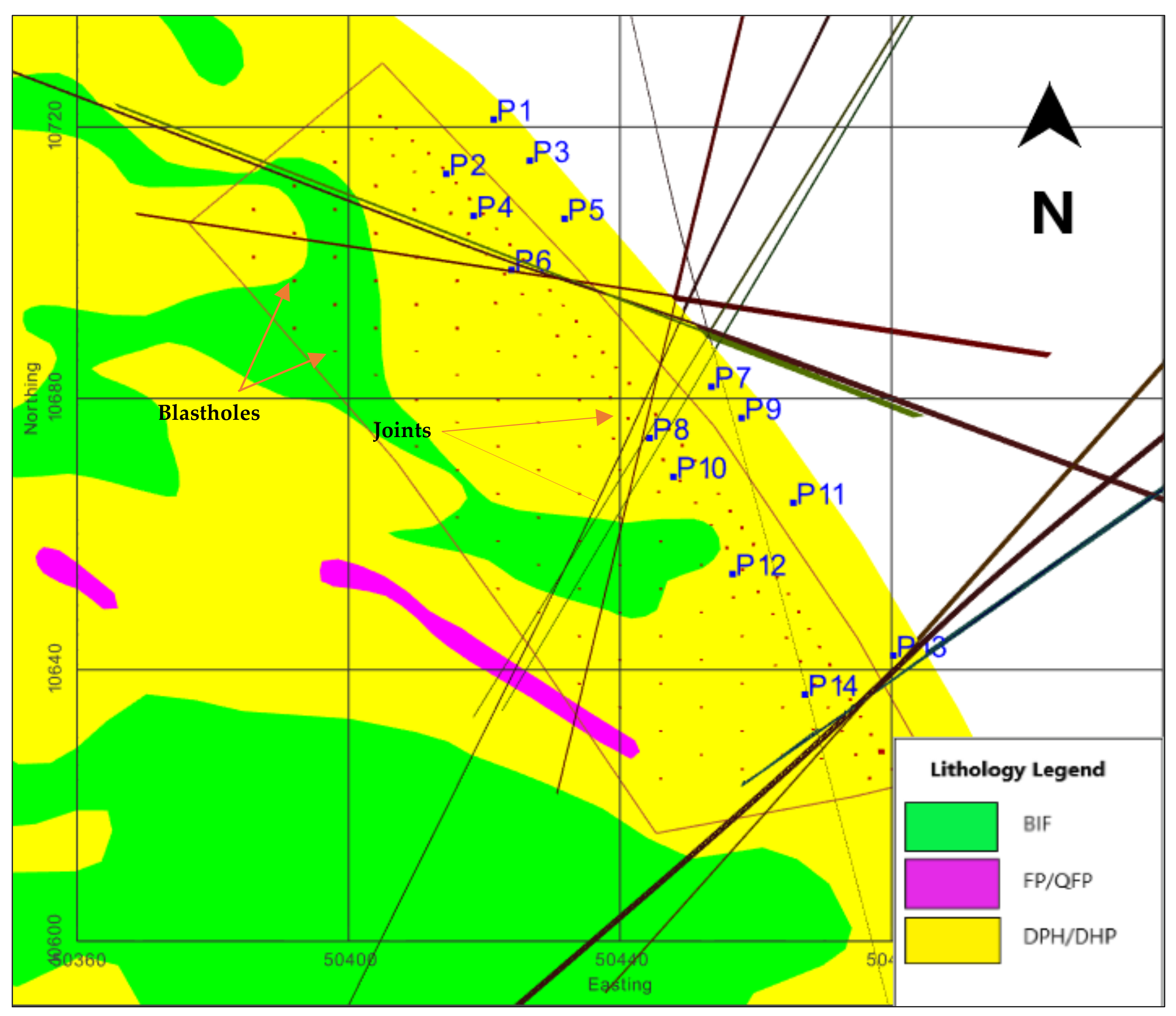
Dotto et al. [8] conducted pit wall mapping and fragmentation analysis in locations P1 to P14 (see Figure 14) and established the location and orientation of the joints relative to the blastholes and the resulting fragmentation after blasting. The pit lithology was a combination of mainly BIF, plagioclase-rich diorite (DPH), or hornblende-rich diorite (DHP), which are categorized as a hard rock having UCS of 110 MPa and tensile strength of 15.2 MPa [8]. Mapping was performed using a combination of stereo photograph analysis (Sirovision) and line mapping, while fragmentation was estimated using muck-pile image analysis using Wip-frag IOS version 3.3.38.0 software [35].

From the mapping and fragmentation analysis, the average in situ block size (B50), the average fragmentation (X₅₀), and the block reduction factor (BRF) were estimated as seen in

Table 11. Block reduction factor calculations.

Muckpile Point	Distance from BH, (m)	Intact Rock Size (B50), (m)	Charge (kg)	SD (m/kg0.5)	PPV (m/s)	Average Frag. (X50)	BRF (B50/X50)
P2	2.48	1.04	73.24	0.29	1.37	129.14	8.09
P4	2.17	1.68	73.24	0.25	1.58	237.42	7.07
P8	0.8	0.67	210	0.06	8.25	73.67	9.12
P6	2.8	2.38	210	0.19	2.12	267.09	8.89
P10	1.27	2.26	210	0.09	5.00	103.97	21.72
P12	1.65	1.42	210	0.11	3.76	87.98	16.16
P14	1.99	1.30	210	0.14	3.07	184.40	7.07

and Figure 15. Based on the fragmentation analysis, the general trend indicates an increase in the average fragmentation size with the burden distance. P8 has the smallest fragmentation size and is the closest to the blasthole (0.8 m). Although multiple random joints cross (see Figure 14), they are very close to the blasthole within the high-intensity stress wave zone. P6 is the furthest from the blasthole. It has several joints at random orientations crossing the burden, resulting in coarser fragmentation, similar to the scenario presented in Figure 12b.

P10 and P12 are almost a quarter burden distance from the blasthole, with fewer to no significant joints between the blasthole and the monitoring point. Medium-size fragmentation is observed in both cases. Although P10, which is closer to the blasthole, has a slightly bigger average fragmentation (103.97 mm) as opposed to P12 (87.98 mm), it has a higher size reduction factor (22) as compared to P12 (16). The similarity between simulation and the blasting fragmentation on the increase in the fragmentation (reduced damage) with the distance and the role of multiple joints on the redistribution of stress wave and cracks indicate that the simulation results are feasible. These results can also be valid in soft rock application if the impedance difference between the rock and joint material is significant.

5. Conclusions

This study conducted a numerical simulation of the effects of explosive strength, rock strength, and structural properties on rock damage in a single blasthole. The field input parameters and fragmentation results were used to prepare and validate the models. The conclusions drawn from the analysis are as follows:

• The RHT model can be used to describe the blast process and evaluate the impact of variable input parameters.
• The choice of explosive for the rock type greatly influences the blast outcomes. From the analysis, the strong explosives offer longer extended fractures while the less strong explosives offer better fractures distribution. With soft rock, the extent of fractures does not improve with stronger explosives; instead, it increases the damage intensity within the same boundaries. Using a weaker explosive on harder rock reduces the extent of fractures.
• The analysis of the structural properties shows the similarity in the behavior of the stress wave and crack propagation at the interface due to the impedance difference between the materials, the intensity, and the direction of the wave. When the stress wave travels from the soft to hard rock, it is enhanced and attenuated when it travels in the opposite direction, similar to the cracks. The same is expected with multiple interfaces, although the outcomes may vary depending on the thickness of rock layers.
• The joints influence the stress wave and fracture propagation differently depending on the properties of the infill material, the width and continuity of the joints, the distance from the charge, the number of joints within the burden distance, and their orientations. Regardless of the case, the stress wave on the opposite side of the joint needs to be higher than the rock strength to guarantee fracturing; this includes the wave reflected at the free face.

Understanding the blasting input parameters and how they affect energy and fracture propagation is important in ensuring effective blast designs. Since the geology, the rock, and structural properties cannot be changed; their influence can be mitigated by the choice of explosive, geometric design of the pattern, initiation delays, and firing sequence, among others. Usually, blasting in mining and civil works involves several holes. The study of a single blasthole provides an understanding of the fracture process to aid design modifications in multi-hole blasting. As an extension to this work, the influence of structural properties in a multi-hole setup will be investigated with design considerations to improve fragmentation.