A Case Study of Incorporating Variable Recovery and Specific Energy in Long-Term Open Pit Mining
Abstract
1. Introduction
2. State of the Art
2.1. Lerchs–Grossmann
2.2. Integrated Optimization
2.2.1. Particularities of the Mathematical Steps
2.2.2. Mathematical Formulations of Integrated Optimization
2.2.3. Improvements and Innovations in Integrated Optimization Approach
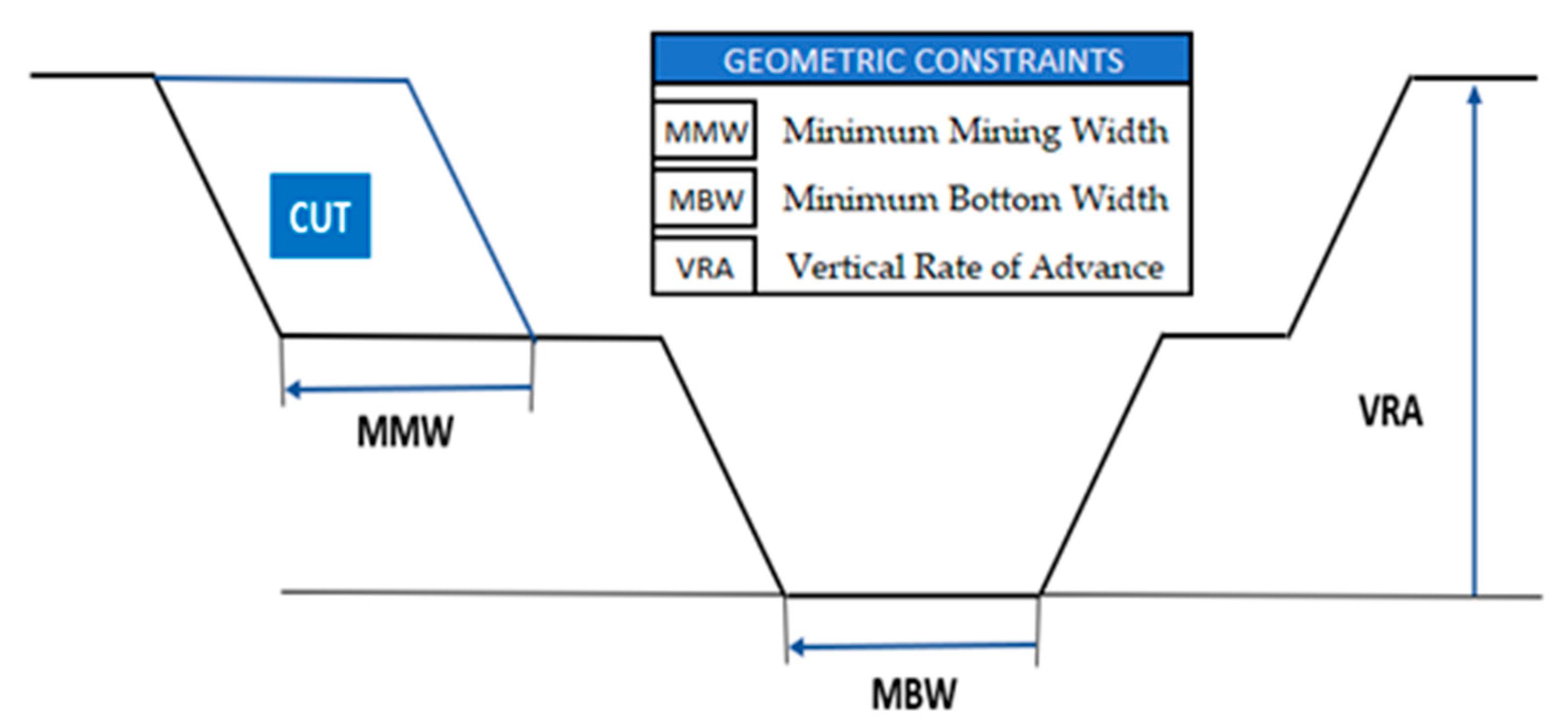
2.3. Geometric Constraints
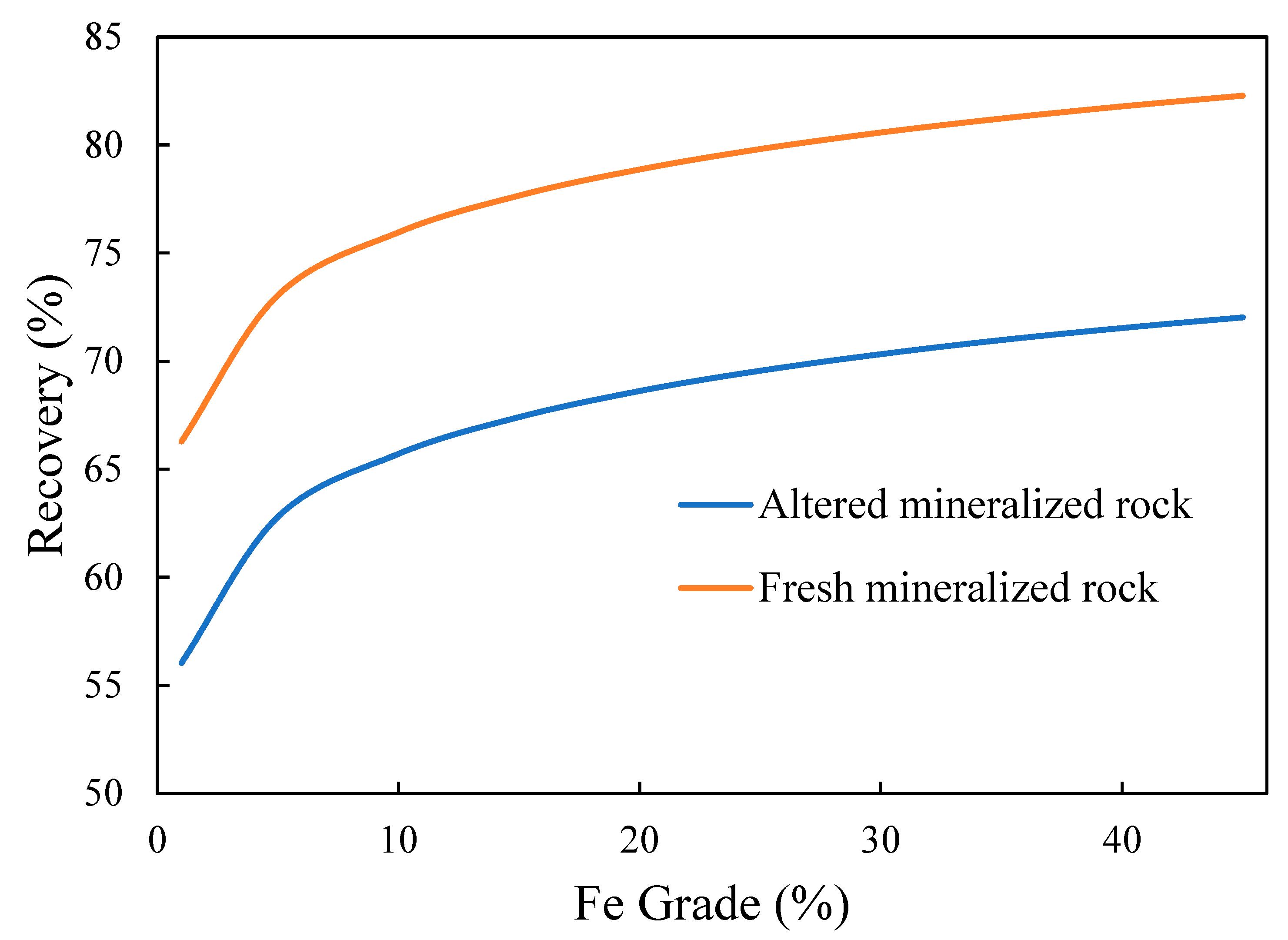
2.4. Geometallurgy Applied to Mine Planning
3. Materials and Methods
3.1. Block Model
3.1.1. General Information
3.1.2. Geometallurgical Parameters
3.2. Scenarios
3.2.1. Base Case (BC) and GeoMet1 Scenarios
3.2.2. GeoMet2 Scenario
3.3. Software for Integrated Optimization
3.4. Block Economic Value
4. Results and Discussion
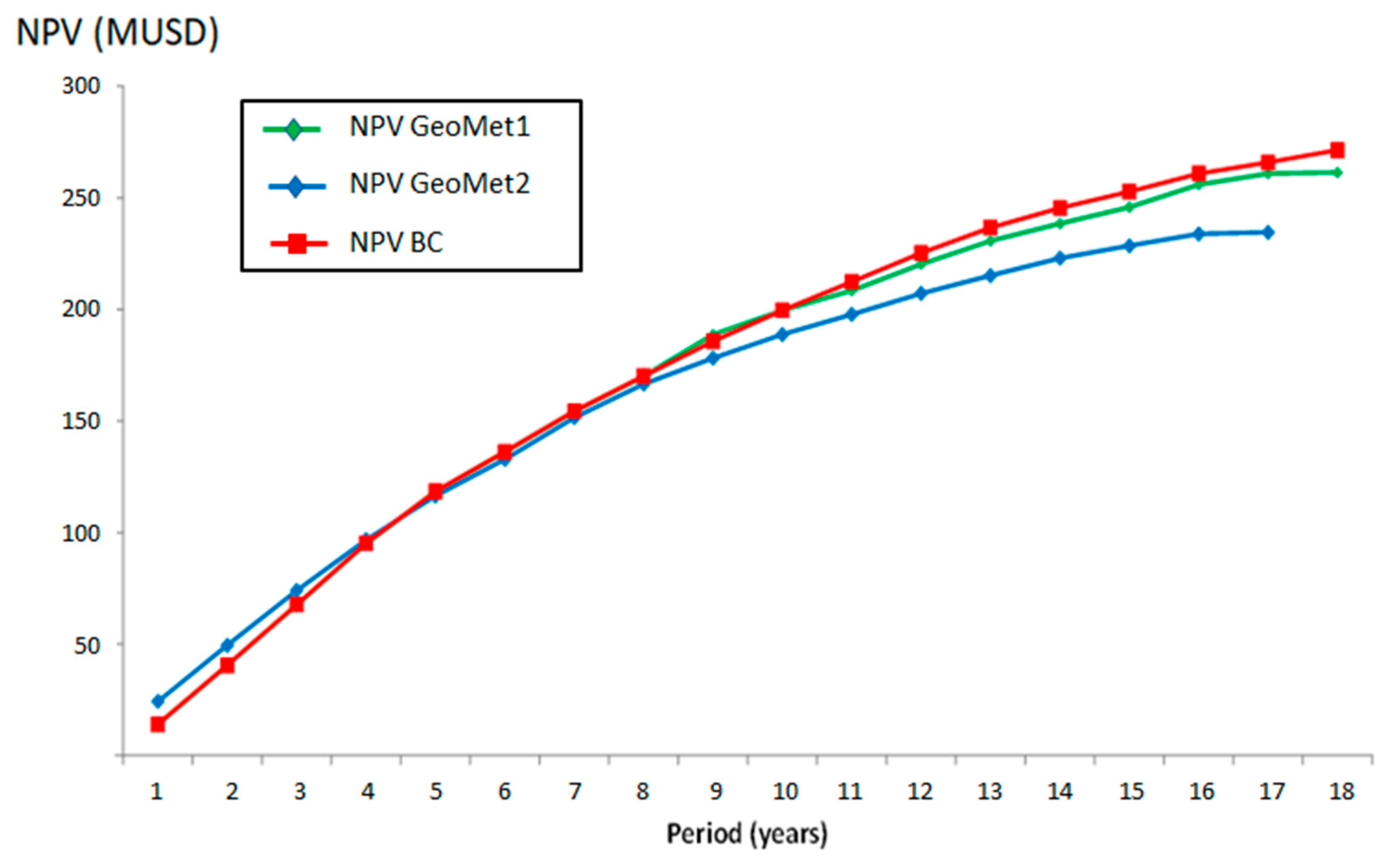
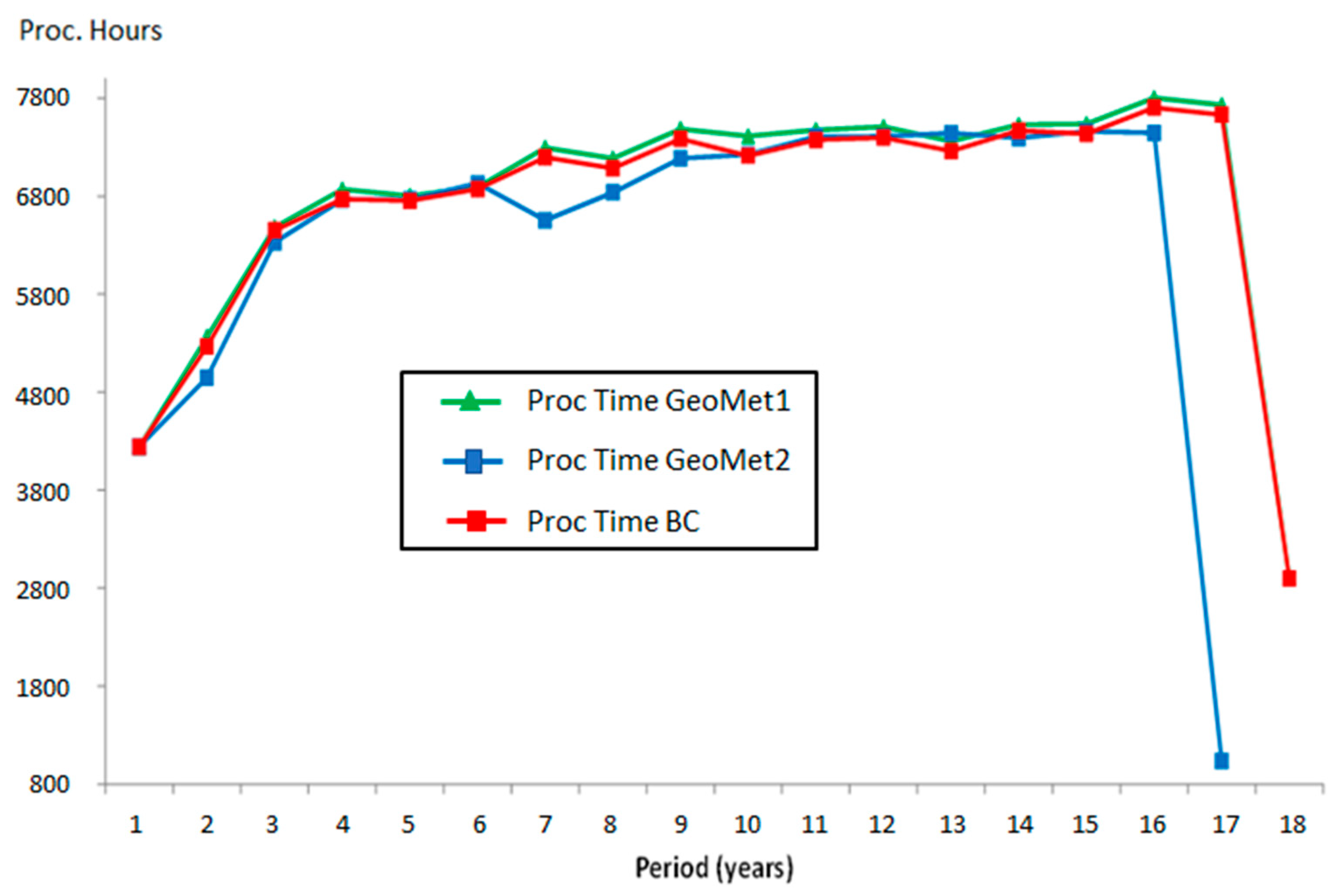
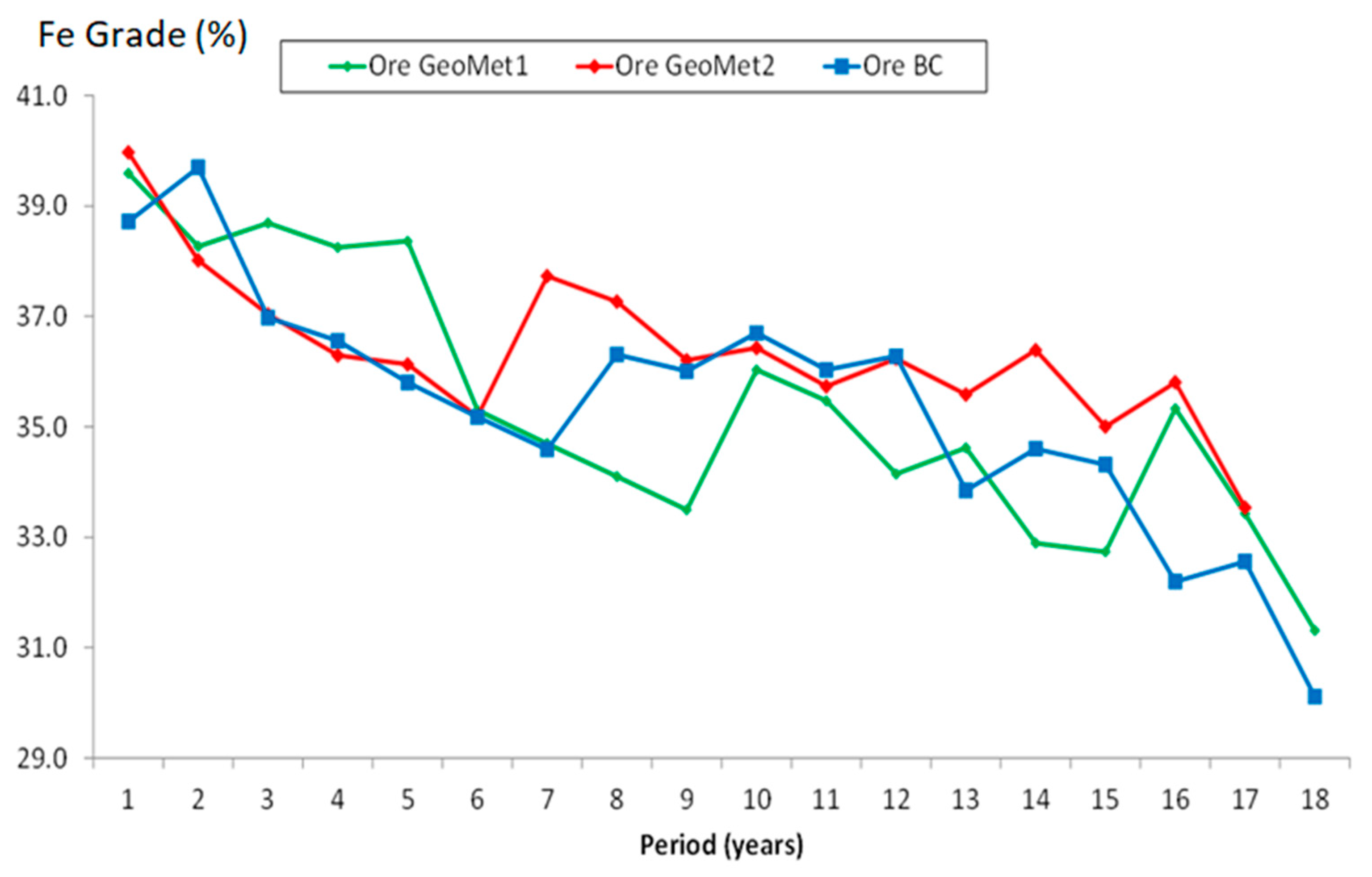
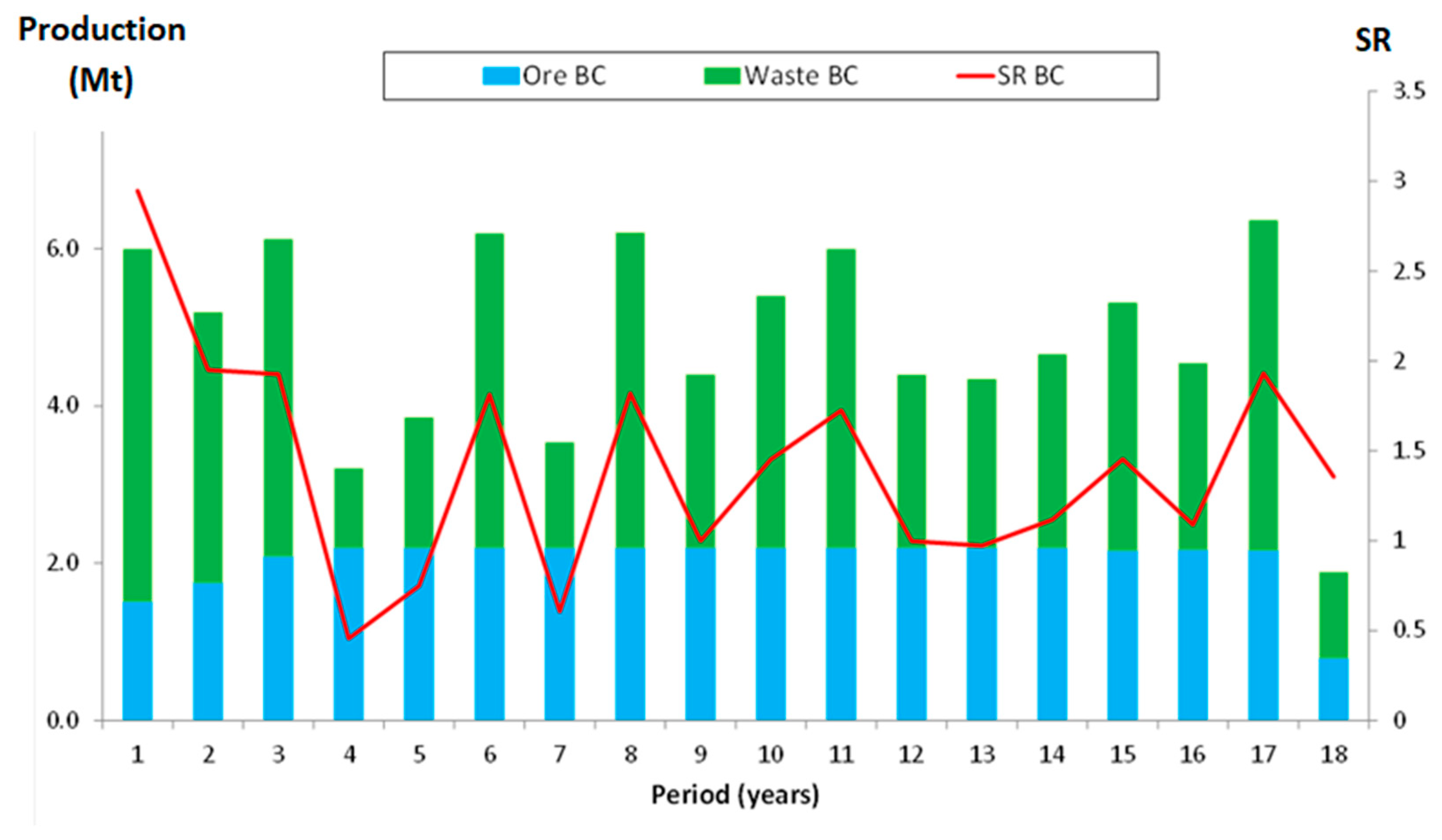
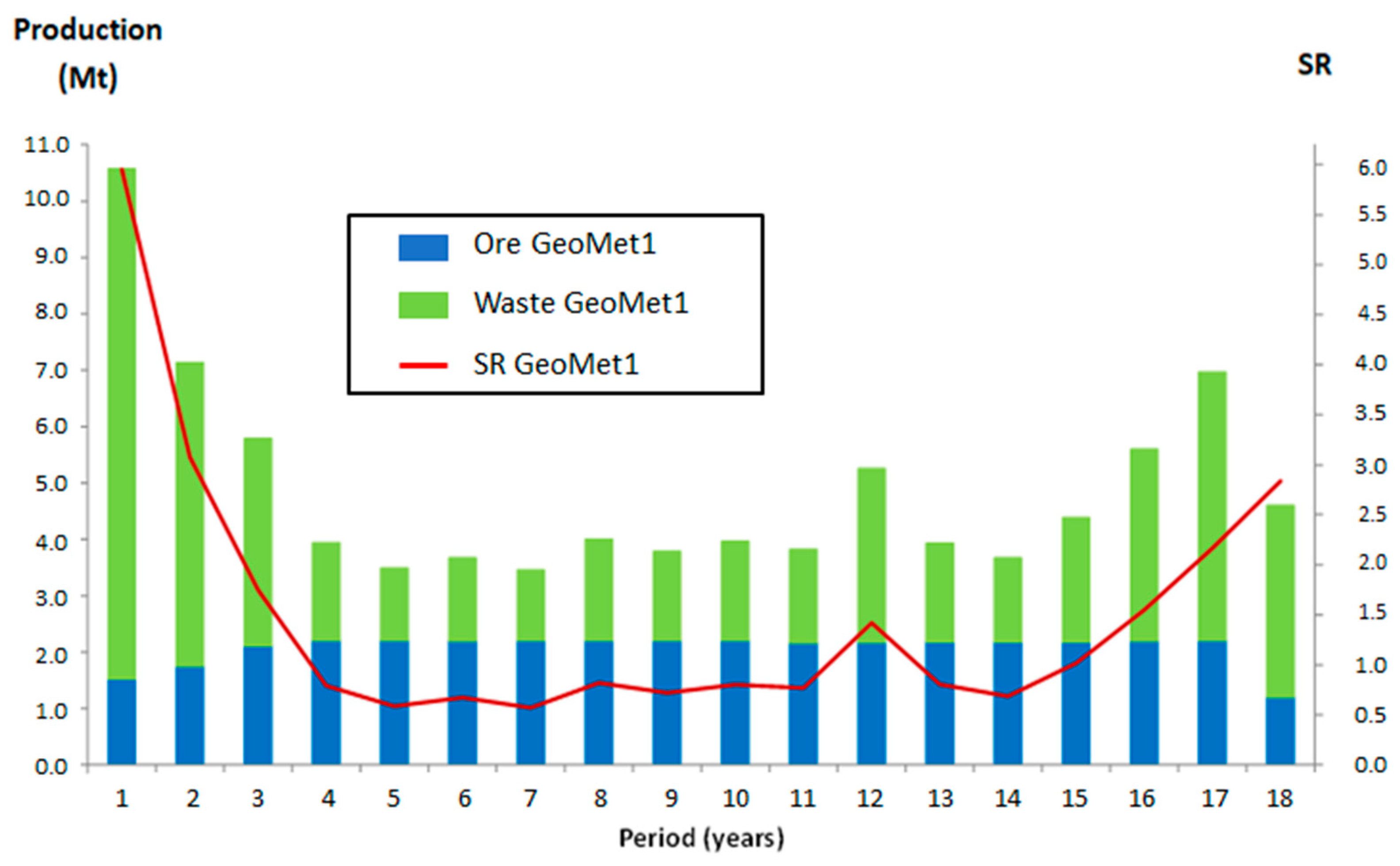
4.1. Global Results
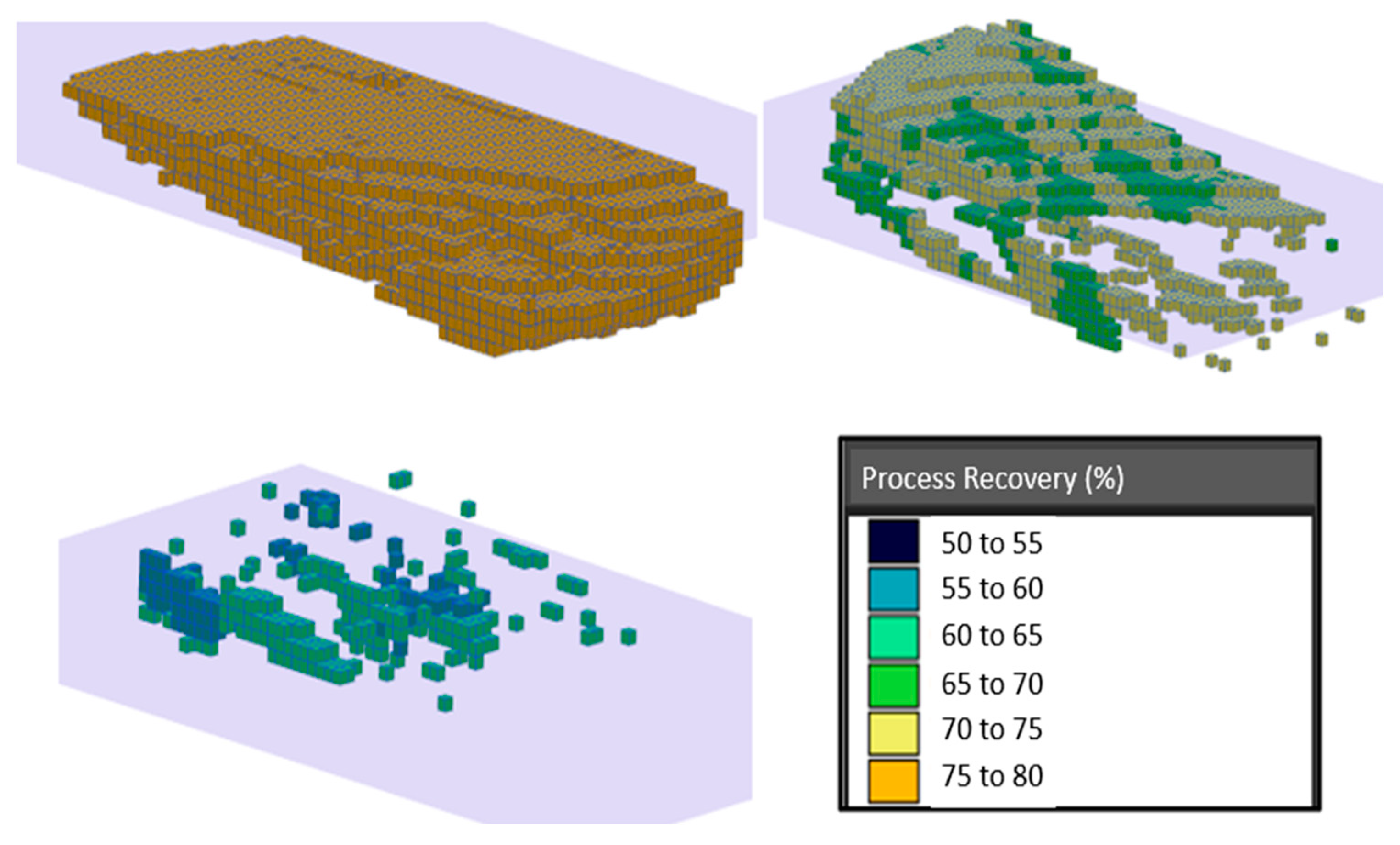
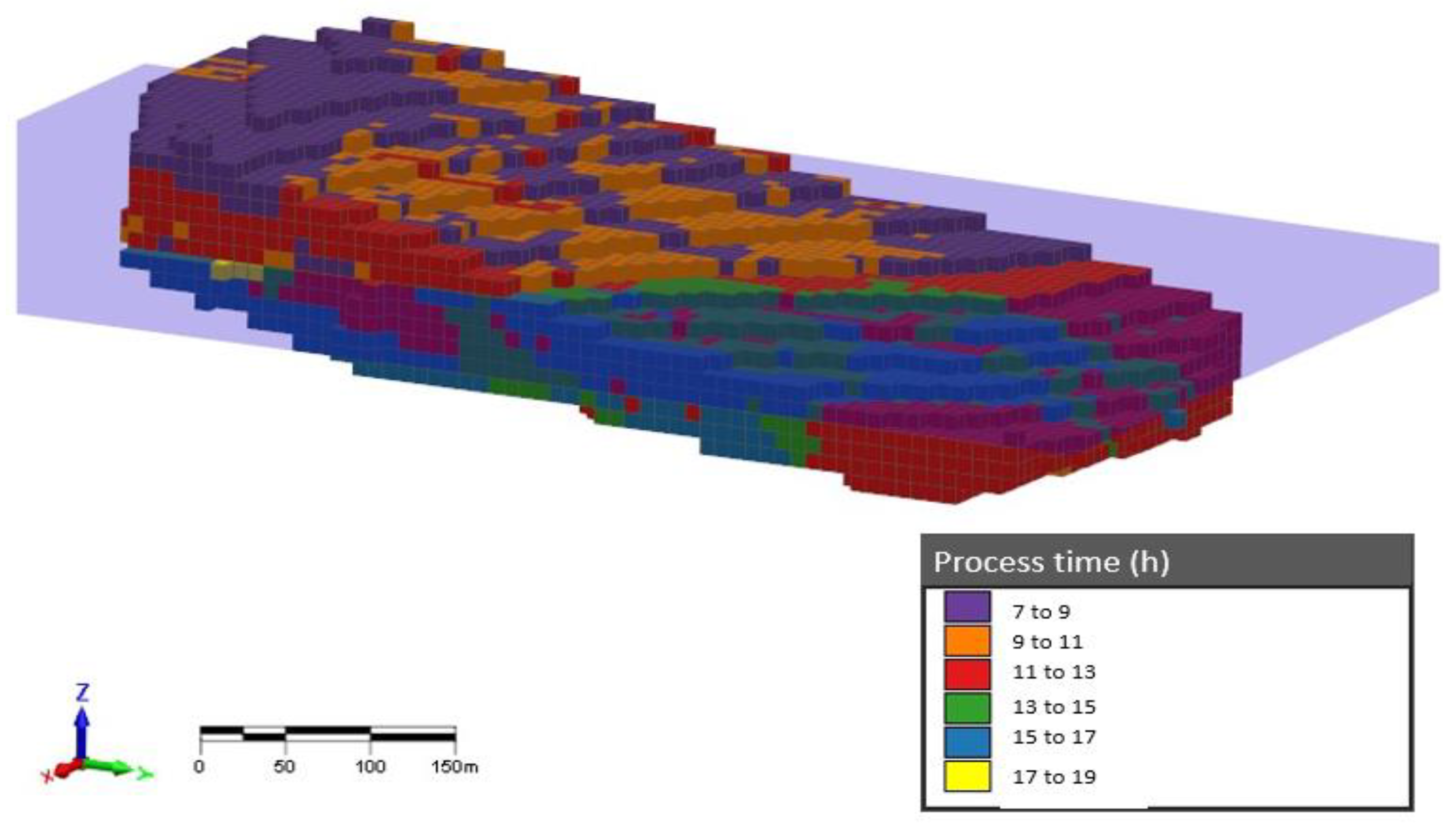
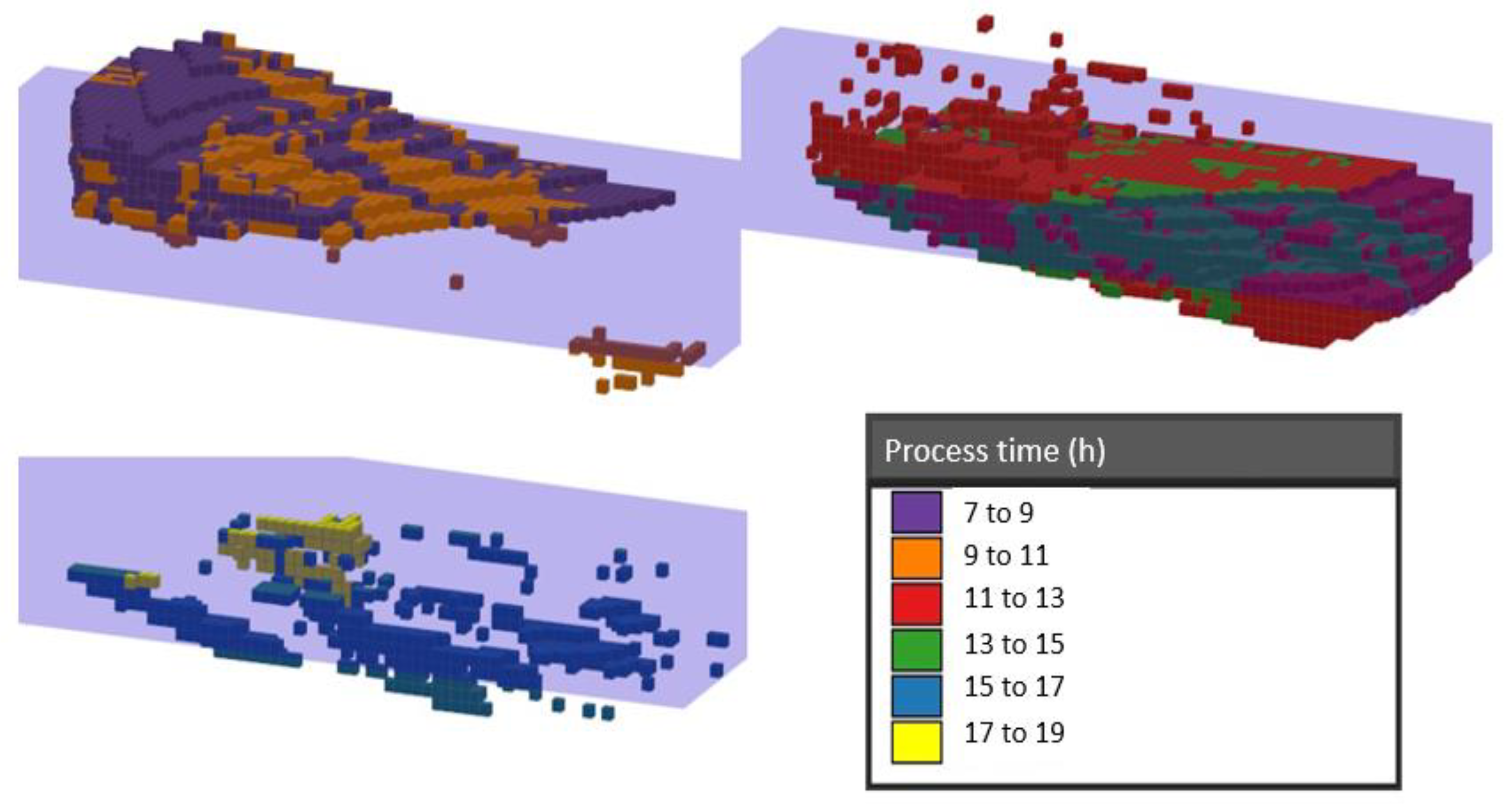
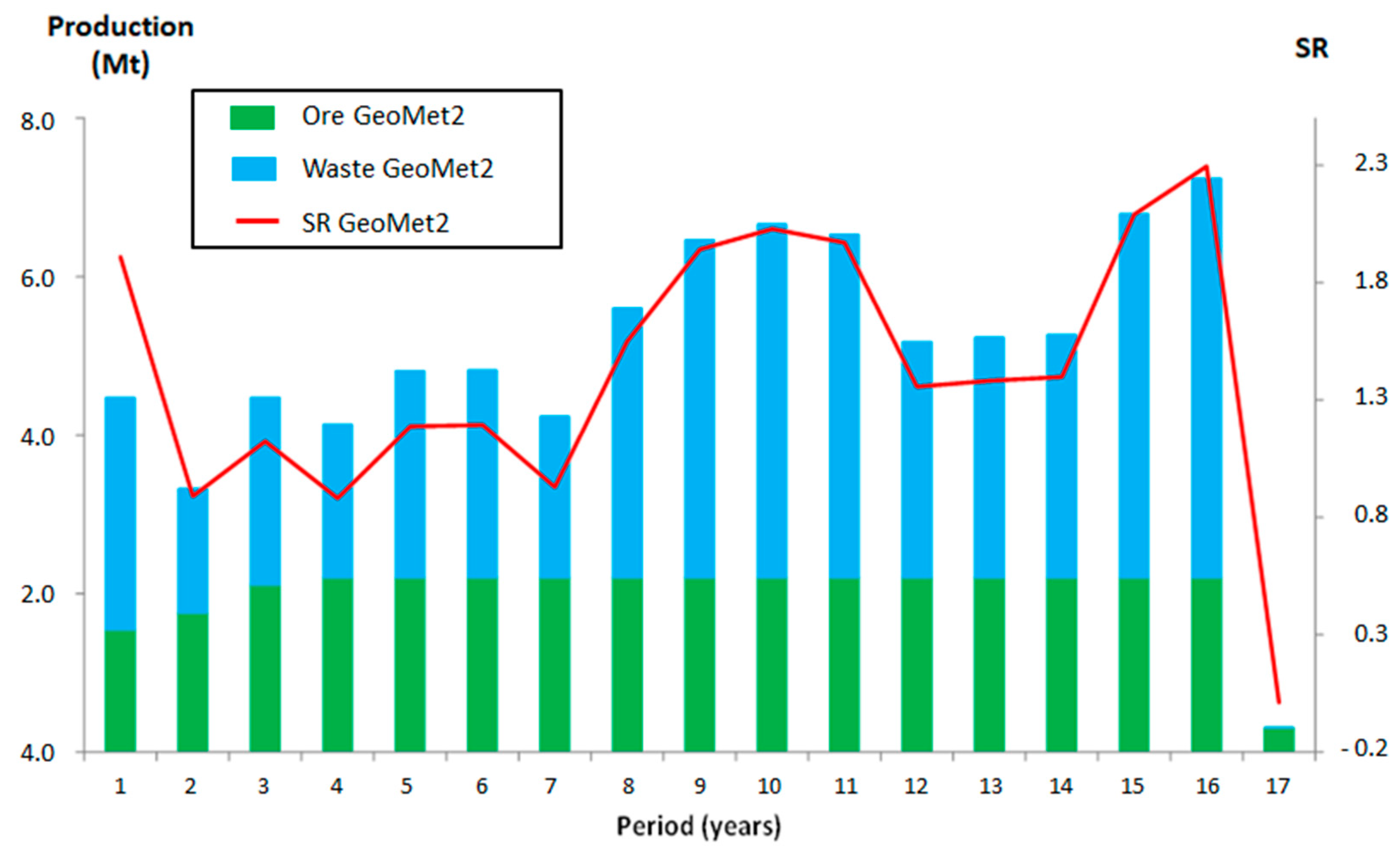
4.2. Graphical Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hustrulid, W.; Kuchta, M. Open Pit Mine—Planning & Design, 2nd ed.; Balkema: Rotterdam, The Netherlands, 2006. [Google Scholar]
- Whittle, D.; Whittle, J.; Wharton, C.; Hall, G. Strategic Mine Planning, 8th ed.; Gemcom Software International Inc.: Vancouver, BC, Canada, 2005. [Google Scholar]
- Poniewierski, J. Block Model Knowledge for Mining Engineers—An Introduction; Deswik Technical Report; Deswik: Brisbane, Australia, 2019. [Google Scholar]
- Lishchuk, V. Geometallurgical Programs—Critical Evaluation of Applied Methods and Techniques. Licentiate Thesis, Department of Civil, Environmental and Natural Resources Engineering, Luleå University of Technology, Luleå, Sweden, 2016. [Google Scholar]
- Dominy, S.C.; O’Connor, L.; Parbhakar-Fox, A.; Glass, H.J.; Purevgerel, S. Geometallurgy—A Route to More Resilient Mine Operations. Minerals 2018, 8, 560. [Google Scholar] [CrossRef]
- Elkington, T.; Durham, R. Integrated open pit pushback selection and production capacity optimization. J. Min. Sci. 2011, 47, 177–190. [Google Scholar] [CrossRef]
- Lerchs, H.; Grossmann, I.F. Optimum design of open pit mines. In Proceedings of the Joint CORS and ORSA Conference, Montreal, QC, Canada, 27–29 May 1964; pp. 17–24. [Google Scholar]
- Johnson, T.B. Optimum Open Pit Mine Production Scheduling. Master’s Thesis, Operations Research Department, University of California, Berkeley, CA, USA, 1968; 120p. [Google Scholar]
- Ota, R.R.M.; Martinez, L.A. SimSched Direct Block Scheduler: A new practical algorithm for the open pit mine production scheduling problem. In Proceedings of the Conference APCOM 2017, Golden, CO, USA, 1–8 July 2017. [Google Scholar]
- MiningMath. MiningMath’s Knowledge Base. Available online: https://knowledge.miningmath.com/ (accessed on 1 January 2022).
- Newman, A.M.; Rubio, E.; Caro, R.; Weintraub, A.; Eurek, K. A Review of Operations Research in Mine Planning. Interfaces 2010, 40, 222–245. [Google Scholar] [CrossRef]
- Fathollahzadeh, K.; Mardaneh, E.; Cigla, M.; Asad, M.W.A. A mathematical model for open pit mine production scheduling with Grade Engineering and stockpiling. Int. J. Min. Sci. Technol. 2021, 31, 717–728. [Google Scholar] [CrossRef]
- Pell, R.; Tijsseling, L.; Palmer, L.W.; Glass, H.J.; Yan, X.; Wall, F.; Zeng, X.; Li, J. Environmental optimisation of mine scheduling through life cycle assessment integration. Resour. Conserv. Recycl. 2019, 142, 267–276. [Google Scholar] [CrossRef]
- Chaves, L.S.; Carvalho, L.A.; Souza, F.R.; Nader, A.S.; Ortiz, C.E.A.; Torres, V.F.N.; Câmara, T.R.; Napa-García, G.F.; Valadão, G.E.S. Analysis of the impacts of slope angle variation on slope stability and NPV via two different final pit definition techniques. REM Int. Eng. J. 2020, 73, 119–126. [Google Scholar] [CrossRef]
- Torres, V.F.N.; Nader, A.S.; Ortiz, C.E.A.; Souza, F.R.; Burgarelli, H.R.; Chaves, L.S.; Carvalho, L.A. Classical and stochastic mine planning techniques, state of the art and trends. REM Int. Eng. J. 2018, 71, 289–297. [Google Scholar] [CrossRef]
- Souza, F.R.; Burgarelli, H.R.; Nader, A.S.; Ortiz, C.E.A.; Chaves, L.S.; Carvalho, L.A.; Torres, V.F.N. Direct block scheduling technology: Analysis of Avidity. REM Int. Eng. J. 2018, 71, 97–104. [Google Scholar] [CrossRef]
- Mckee, D.J. Understanding Mine to Mill; The Cooperative Research Centre for Optimising Resource Extraction (CRC ORE): Brisbane, Australia, 2013. [Google Scholar]
- Deutsch, J.L. Multivariate Spatial Modeling of Metallurgical Rock Properties. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of Alberta, Edmonton, AB, Canada, 2015. [Google Scholar]
- Gomes, R.B.; De Tomi, G.; Assis, P.S. Mine/Mill production planning based on a Geometallurgical Model. REM Int. Eng. J. 2016, 69, 213–218. [Google Scholar] [CrossRef]
- Macfarlane, A.S.; Williams, T.P. Optimizing value on a copper mine by adopting a geometallurgical solution. J. S. Afr. Inst. Min. Metall. 2014, 114, 929. [Google Scholar]
- Morales, N.; Seguel, S.; Cáceres, A.; Jélvez, E.; Alarcón, M. Incorporation of Geometallurgical Attributes and Geological Uncertainty into Long-Term Open-Pit Mine Planning. Minerals 2019, 9, 108. [Google Scholar] [CrossRef]
- Dunham, S.; Vann, J. Geometallurgy, Geostatistics and Project Value: Does Your Block Model Tell You What You Need to Know? Australasian Institute of Mining and Metallurgy Publication Series; AusIMM: Melbourne, Australia, 2007; pp. 189–196. [Google Scholar]
- Kumhal, M. Incorporating geo-metallurgical information into mine production scheduling. J. Oper. Res. Soc. 2011, 62, 60–68. [Google Scholar]
- Lishchuck, V.; Koch, P.; Lund, C.; Lamberg, P. The Geometallurgical Framework. Malmberget and Mikheevskoye Case Studies. Min. Sci. 2015, 22, 57–66. [Google Scholar]
- Reis, C.; Arroyo, C.; Curi, A.; Zangrandi, M. Impact of bulk density estimation in mine planning. Min. Technol. 2021, 130, 60–65. [Google Scholar] [CrossRef]
- Wambeke, T.; Elder, D.; Miller, A.; Benndorf, J.; Peattie, R. Real-time reconciliation of a geometallurgical model based on ball mill performance measurements—A pilot study at the Tropicana gold mine. Min. Technol. 2018, 127, 115–130. [Google Scholar] [CrossRef]
- Nunes, R.A.; De Tomi, G.; Allan, B.; Bezerra, E.B.; Silva, R.S. An integrated pit-to-plant approach using technological models for strategic mine planning of copper and gold deposits. REM Int. Eng. J. 2019, 72, 307–313. [Google Scholar] [CrossRef]
- Rodrigues, R.S.; Bonfioli, L.E.; Mapa, P.S.; Pinto, L.A. Development of a Mathematical Model to Determine the Grinding Energy Requirement of the Iron Ore Reserve of SAMARCO Mineração S.A. In Proceedings of the 44th Seminar on Reduction of Iron Ore and Raw Materials, Belo Horizonte, Brazil, 15–18 September 2014. [Google Scholar]
- King, G.S.; MacDonald, J.L. The business case for early-stage implementation of geometallurgy—An example from the Productora Cu-Au-Mo deposit, Chile. In Proceedings of the International Geometallurgy Conference, Perth, Australia, 15–16 June 2016; Australasian Institute of Mining and Metallurgy: Melbourne, Australia, 2016; pp. 125–133. [Google Scholar]
- Carrasco, P.; Chilès, J.P.; Séguret, S.A. Additivity, Metallurgical Recovery and Grade. In Proceedings of the 8th international Geostatistics Congress, Santiago, Chile, 1–5 December 2008. [Google Scholar]
- WHEATON. Wheaton Precious Metals. In Technical Report—Salobo III Expansion. Salobo Copper-Gold Mine Carajás, Pará State, Brazil; WHEATON: Vancouver, BC, Canada, 2019. [Google Scholar]
- Rodrigues, R.S. Geometallurgy in Iron Ore: Predictability Model of the Behavior of Itabiritic Ores in the Concentration Process mainly by Mineralogical Characterization. Ph.D. Thesis, Federal University of Minas Gerais, Belo Horizonte, Brazil, 2021. (In Portuguese). [Google Scholar]
- Delphos Mining Planning Laboratory. Available online: https://delphoslab.cl/index.php/software-es/41-delphos-open-pit-planner-doppler (accessed on 2 January 2023).
- Mariz, J.L.V.; Cavalcante, M.S.; Rocha, S.S.; Barros, F.B.M.; Souza, J.C.; Assis, A.A.A. Comparison between Economic Evaluation Tools on Dimensioning of Equipment for Mine. In Proceedings of the 20° Mining Symposium ABM Week, São Paulo, Brazil, 1–3 October 2019. [Google Scholar]


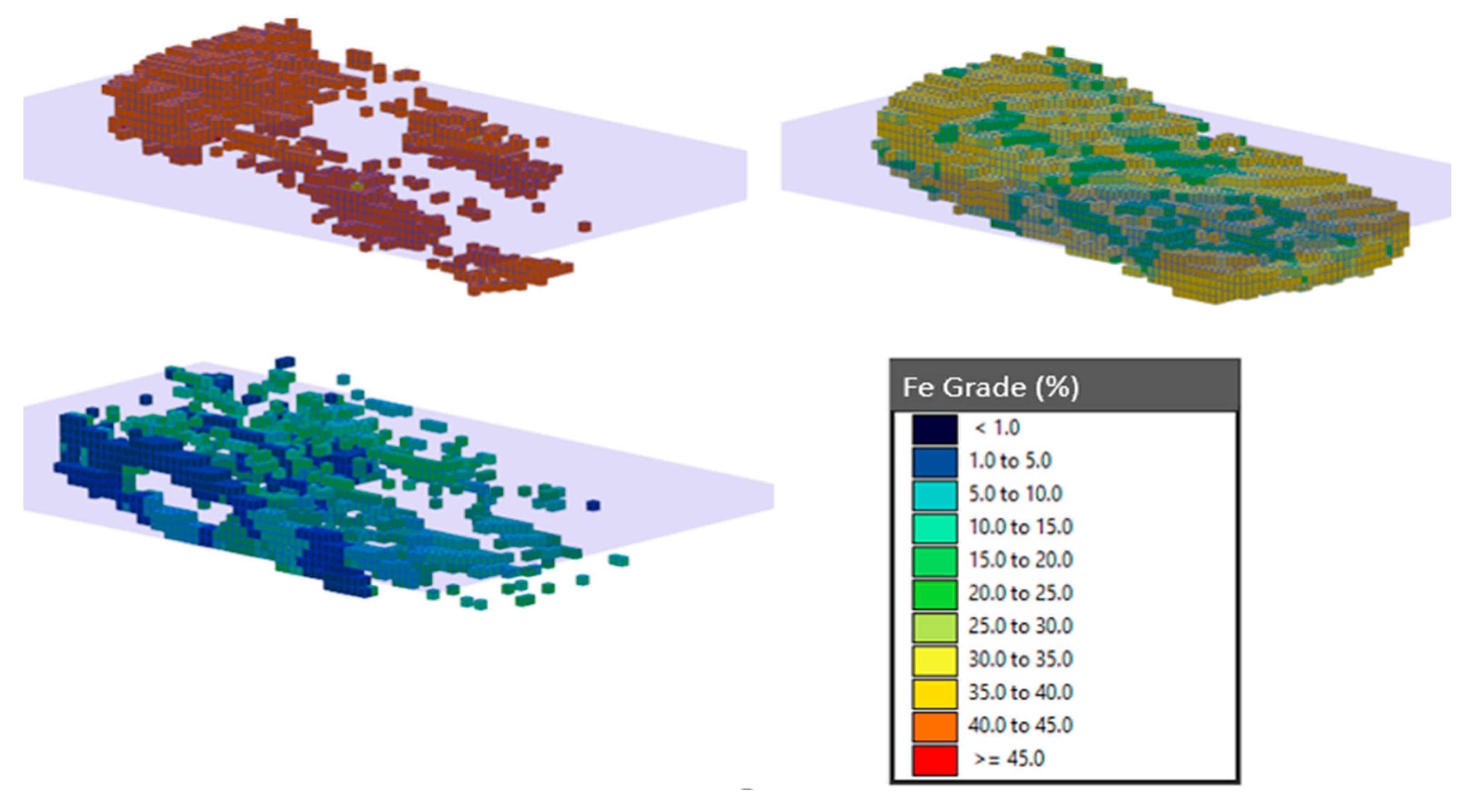

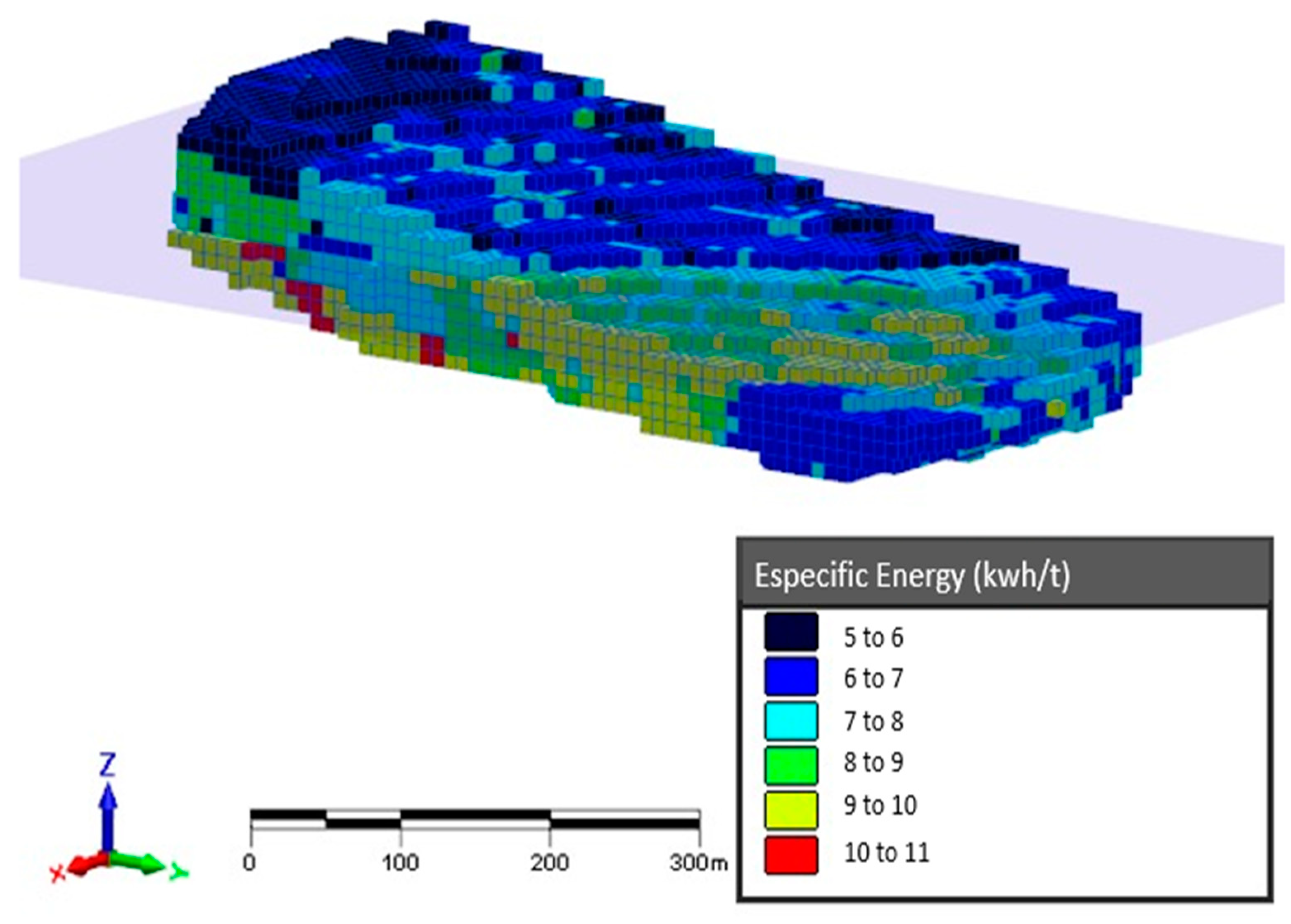

| Typology | Slope Angle (°) | Density (t/m3) |
|---|---|---|
| Altered host rock | 50 | 2.5 |
| Fresh host rock | 55 | 2.7 |
| Altered mineralized rock | 60 | 3.0 |
| Fresh mineralized rock | 65 | 3.5 |
| Parameters | BC | GeoMet1 |
|---|---|---|
| MMW (m) | 30 | 30 |
| MBW (m) | 30 | 30 |
| VRA (m) | 140 | 140 |
| Discount rate (%) | 10 | 10 |
| Interval of Fe grades on the process plant feed (%) | 30 to 40 | 30 to 40 |
| Maximum annual processing time at the plant (hours) | 7884 | 7884 |
| Maximum mine tonnage handled per year (t) | 10,000,000 | 10,000,000 |
| Maximum processing tonnages—first year: 70% (t) | 1,540,000 | 1,540,000 |
| Maximum processing tonnages—second year: 80% (t) | 1,760,000 | 1,760,000 |
| Maximum processing tonnages—third year: 95% (t) | 2,110,000 | 2,110,000 |
| Maximum processing tonnages—after ramp-up (t) | 2,200,000 | 2,200,000 |
| Recovery (%) | 78 | Variable |
| Process cost (USD/t) | 15 | 15 |
| Selling Price (USD/t) | 120.00 | 120.00 |
| Mine Cost (USD/t) | 2.00 | 2.00 |
| Lithology | Processing Time (h) | Process Cost (USD/t) |
|---|---|---|
| Altered mineralized rock | 8.90 | 12.06 |
| Fresh mineralized rock | 12.28 | 16.63 |
| Global values | 11.07 | 15.00 |
| Response Parameter | BC | GeoMet1 | GeoMet2 | Var. BC/GeoMet1 (%) | Var. BC/GeoMet2 (%) |
|---|---|---|---|---|---|
| Software running time (s) | 228.76 | 225.22 | 217.36 | −1.55 | −4.98 |
| Number of periods (years) | 18 | 18 | 17 | 0.00 | −5.56 |
| NPV (MUSD) | 271.42 | 261.42 | 234.59 | −3.68 | −13.57 |
| ANPV (MUSD) | 27.64 | 26.62 | 23.93 | −3.68 | −13.41 |
| % Compliance in the ramp-up—year 1 (%) | 98.57 | 98.70 | 99.94 | 0.13 | 1.39 |
| % Compliance in the ramp-up—year 2 (%) | 99.86 | 99.43 | 99.89 | −0.43 | 0.03 |
| % Compliance in the ramp-up—year 3 (%) | 91.62 | 99.91 | 99.91 | 9.04 | 9.05 |
| % Compliance—average after the ramp-up | 99.66 | 99.48 | 99.93 | −0.18 | 0.27 |
| Global Ore Production (Mt) | 36.86 | 37.24 | 34.29 | 1.03 | −6.97 |
| Average annual production of Ore (Mt) | 2.03 | 2.07 | 2.02 | 1.91 | −0.49 |
| Global Waste Production (Mt) | 50.65 | 50.82 | 51.30 | 0.34 | 1.28 |
| Stripping Ratio—global average of the project | 1.37 | 1.36 | 1.50 | −0.39 | 9.20 |
| Annual average of plant processing time (hours) | 6912.01 | 6998.48 | 6434.09 | 1.25 | −6.91 |
| Average ore Fe grade (%) | 35.36 | 35.37 | 36.38 | 0.04 | 2.88 |
| Average waste Fe grade (%) | 1.4900 | 1.4632 | 2.5700 | −1.80 | 72.48 |
| Constraint Relaxation Occurrence | None | None | None | None | None |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mata, J.F.C.d.; Nader, A.S.; Mazzinghy, D.B. A Case Study of Incorporating Variable Recovery and Specific Energy in Long-Term Open Pit Mining. Mining 2023, 3, 367-386. https://doi.org/10.3390/mining3020022
Mata JFCd, Nader AS, Mazzinghy DB. A Case Study of Incorporating Variable Recovery and Specific Energy in Long-Term Open Pit Mining. Mining. 2023; 3(2):367-386. https://doi.org/10.3390/mining3020022
Chicago/Turabian StyleMata, Jônatas Franco Campos da, Alizeibek Saleimen Nader, and Douglas Batista Mazzinghy. 2023. "A Case Study of Incorporating Variable Recovery and Specific Energy in Long-Term Open Pit Mining" Mining 3, no. 2: 367-386. https://doi.org/10.3390/mining3020022
APA StyleMata, J. F. C. d., Nader, A. S., & Mazzinghy, D. B. (2023). A Case Study of Incorporating Variable Recovery and Specific Energy in Long-Term Open Pit Mining. Mining, 3(2), 367-386. https://doi.org/10.3390/mining3020022








