A Framework for Open-Pit Mine Production Scheduling under Semi-Mobile In-Pit Crushing and Conveying Systems with the High-Angle Conveyor
Abstract
:1. Introduction
2. Literature Review
3. Methodology
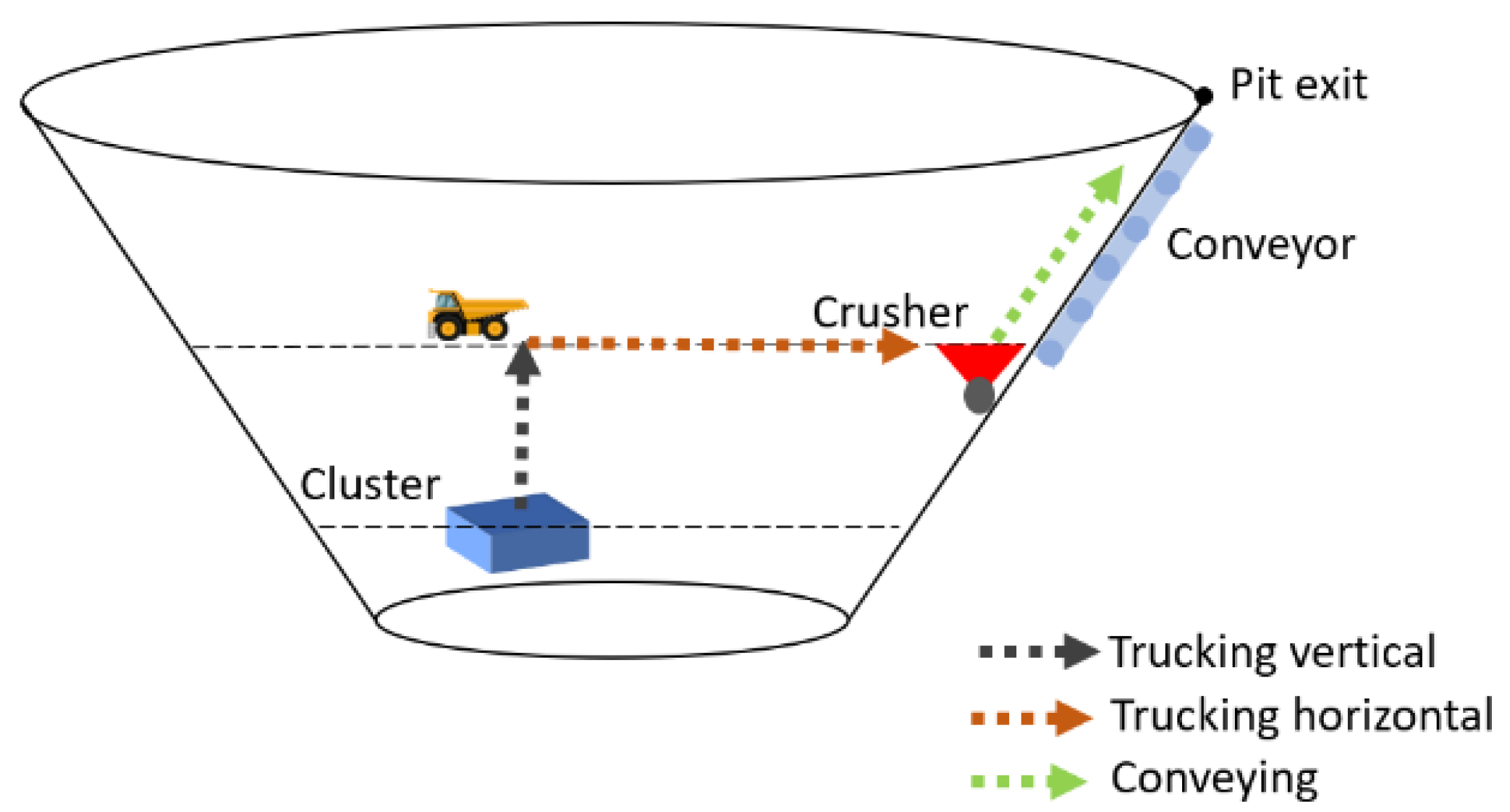
3.1. Theoretical Framework
- (a)
- All the economic and technical parameters used as inputs of this model are known and deterministic
- (b)
- The HAC is fixed on one side of the final pit wall throughout the mine life; however, this system can be extended to deeper levels by connecting another conveyor flight
- (c)
- The proposed model only considers material handling cost up to the pit rim. The ex-pit facilities’ location (i.e., waste dump, stockpile, and processing plant) and the material handling costs from the pit exit to the final destinations are not considered in this model. It should be noted that these costs can be added as a fixed cost for each scenario separately.
- (d)
- The HAC is used to transfer both ore and waste; therefore, parallel conveyors should be installed to move materials.
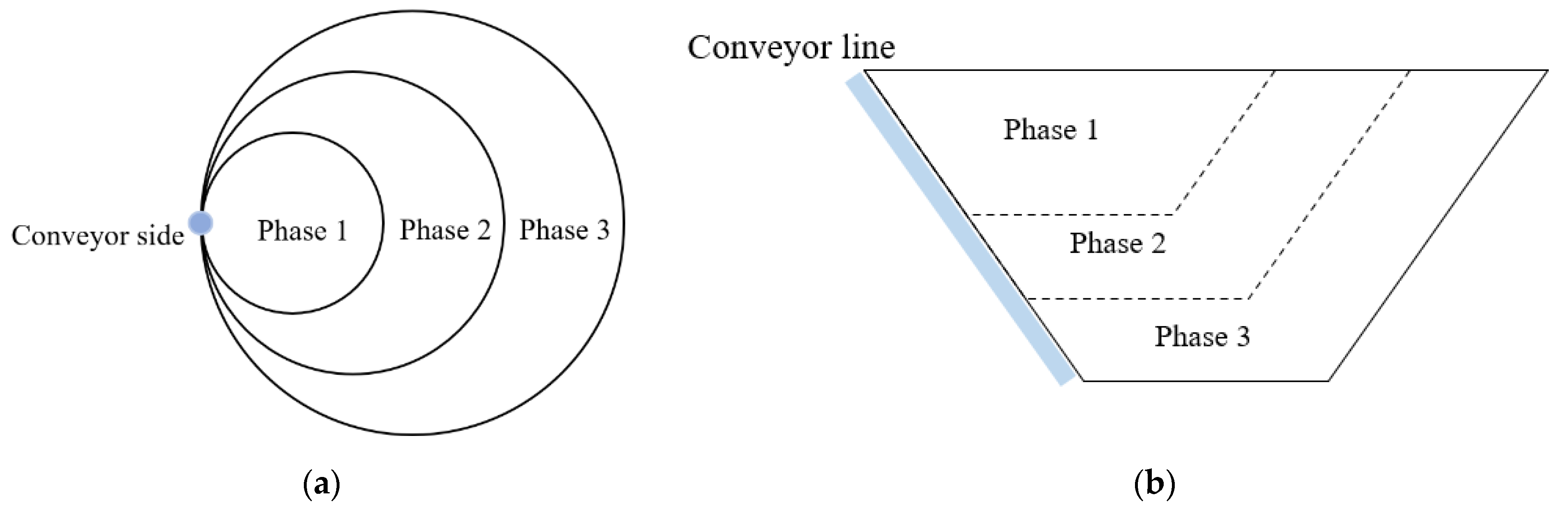
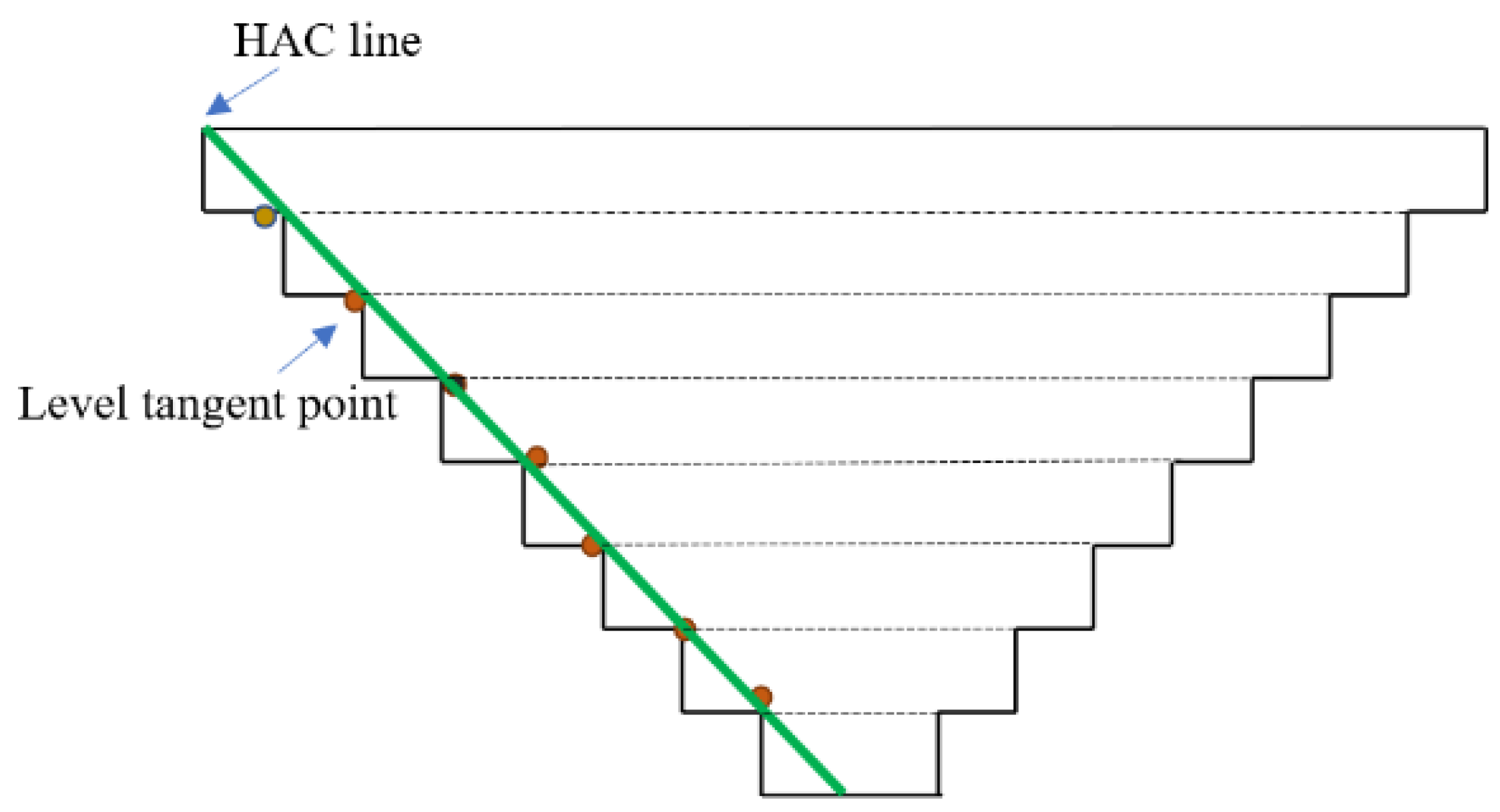
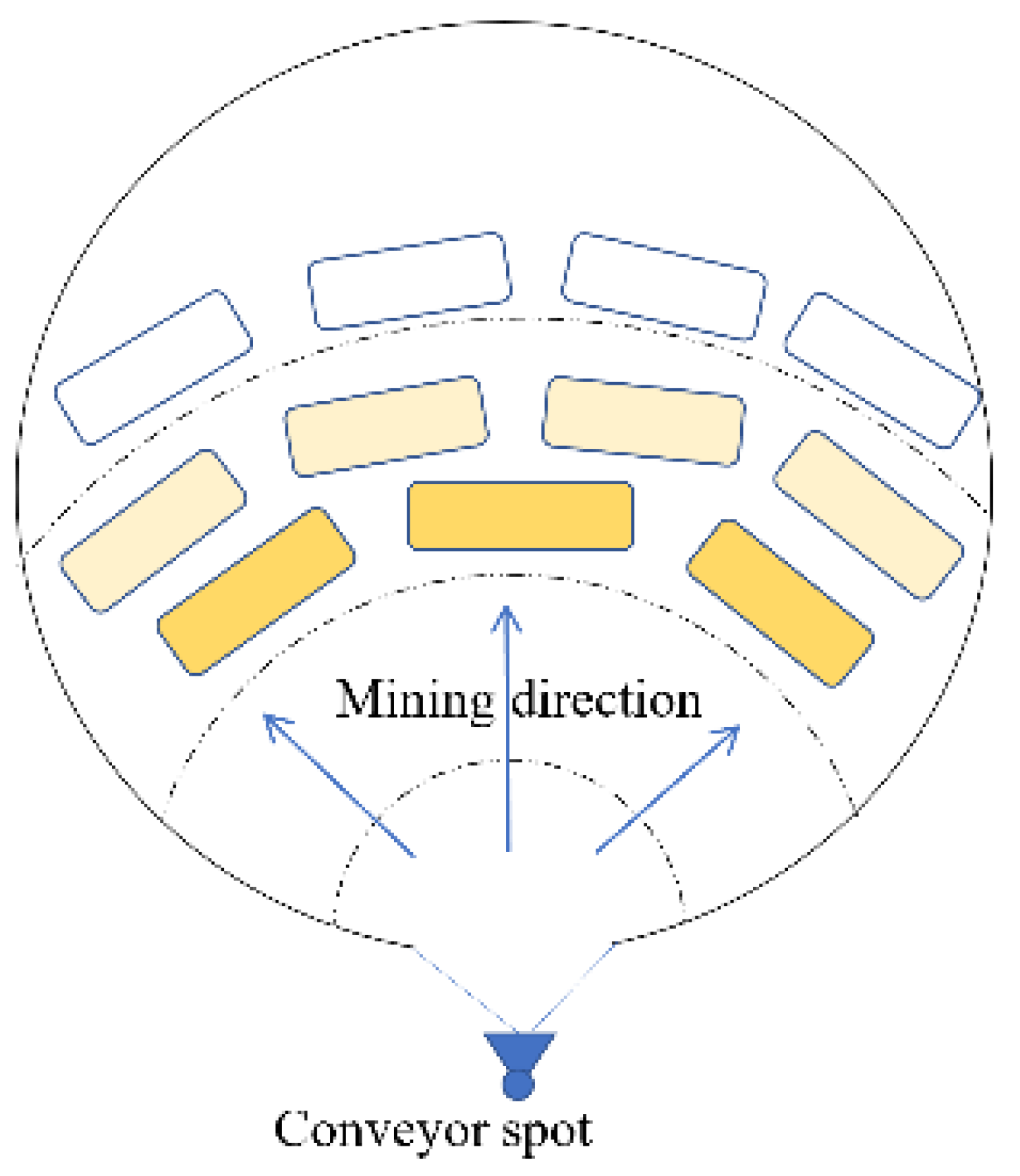
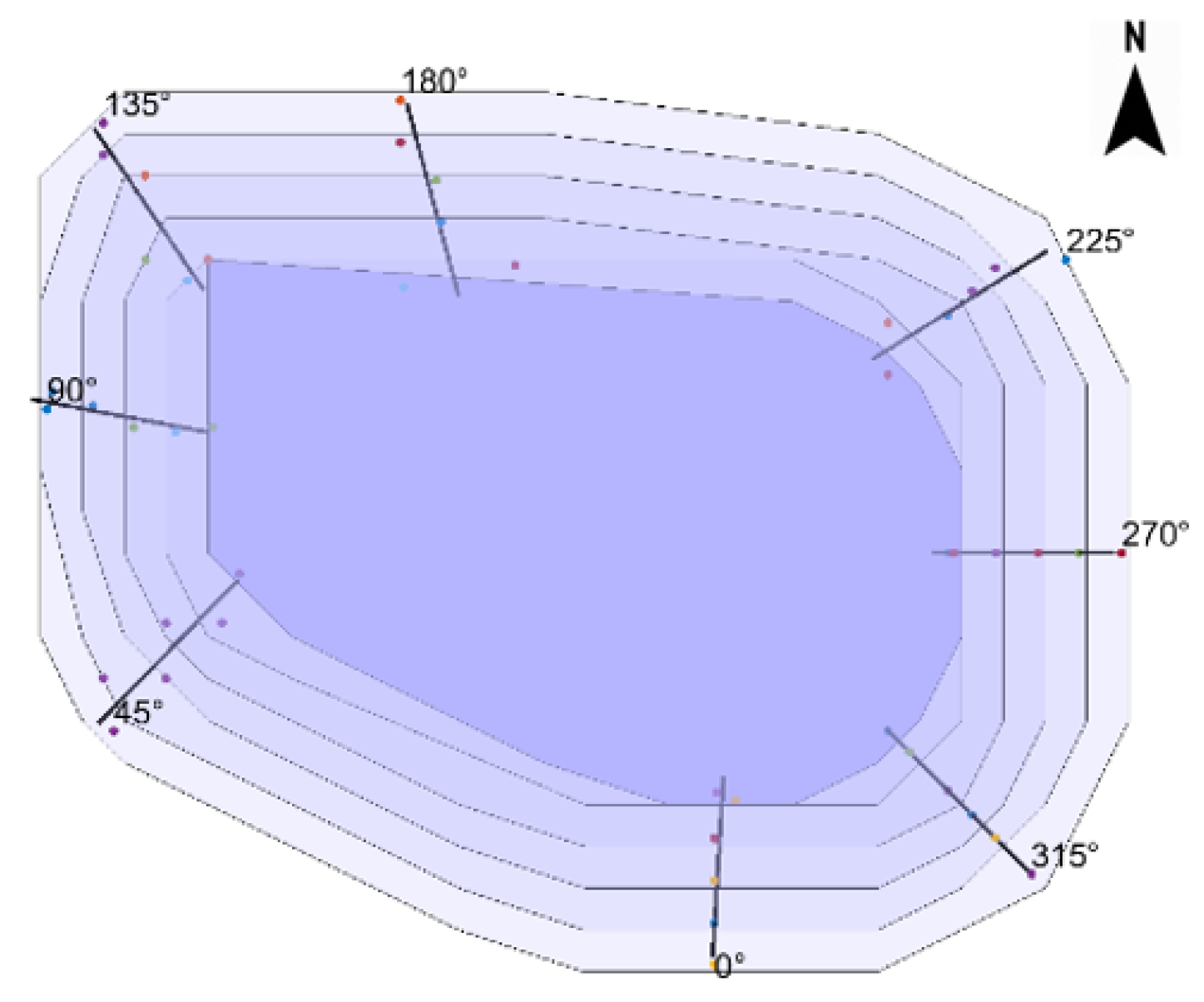
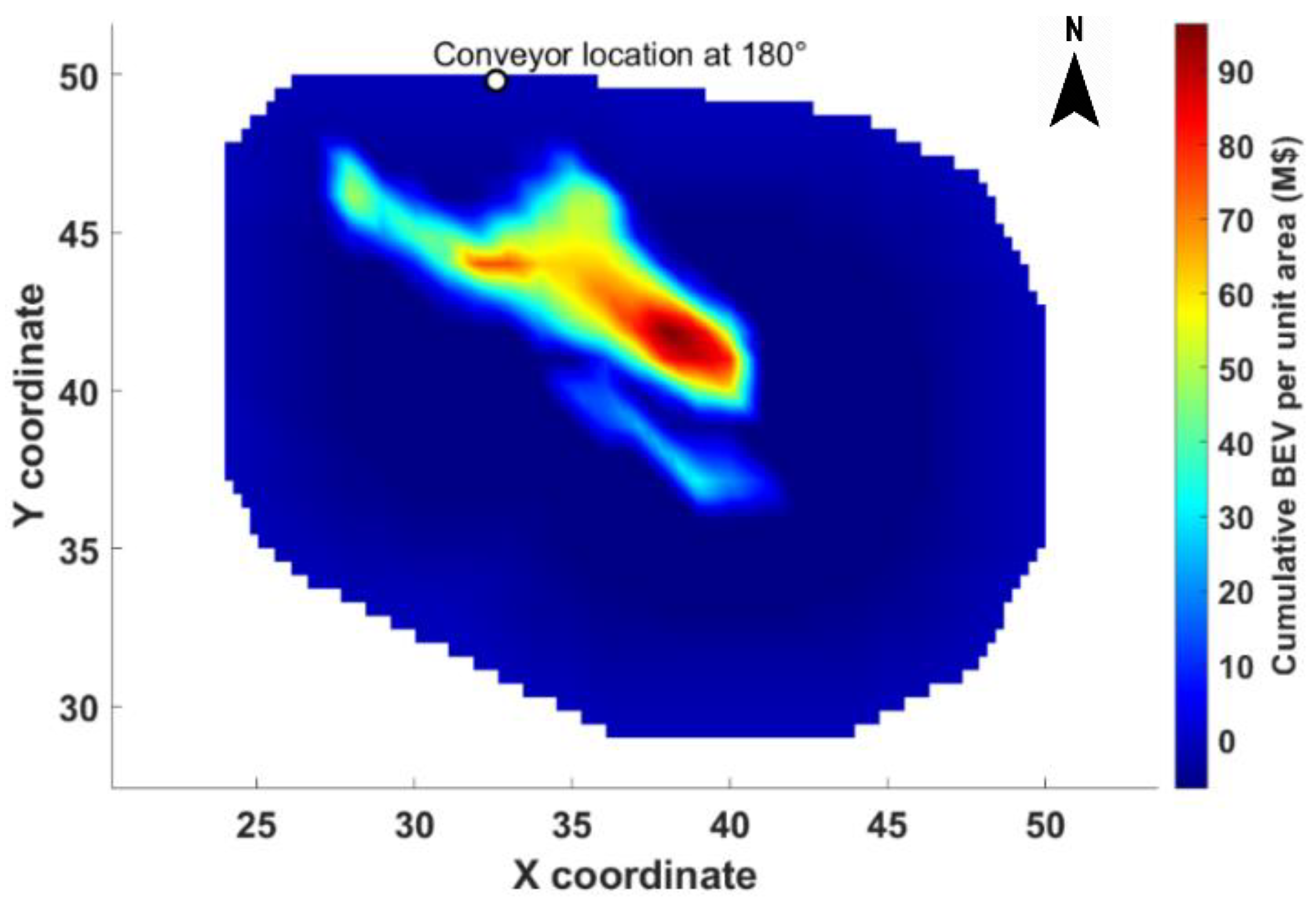
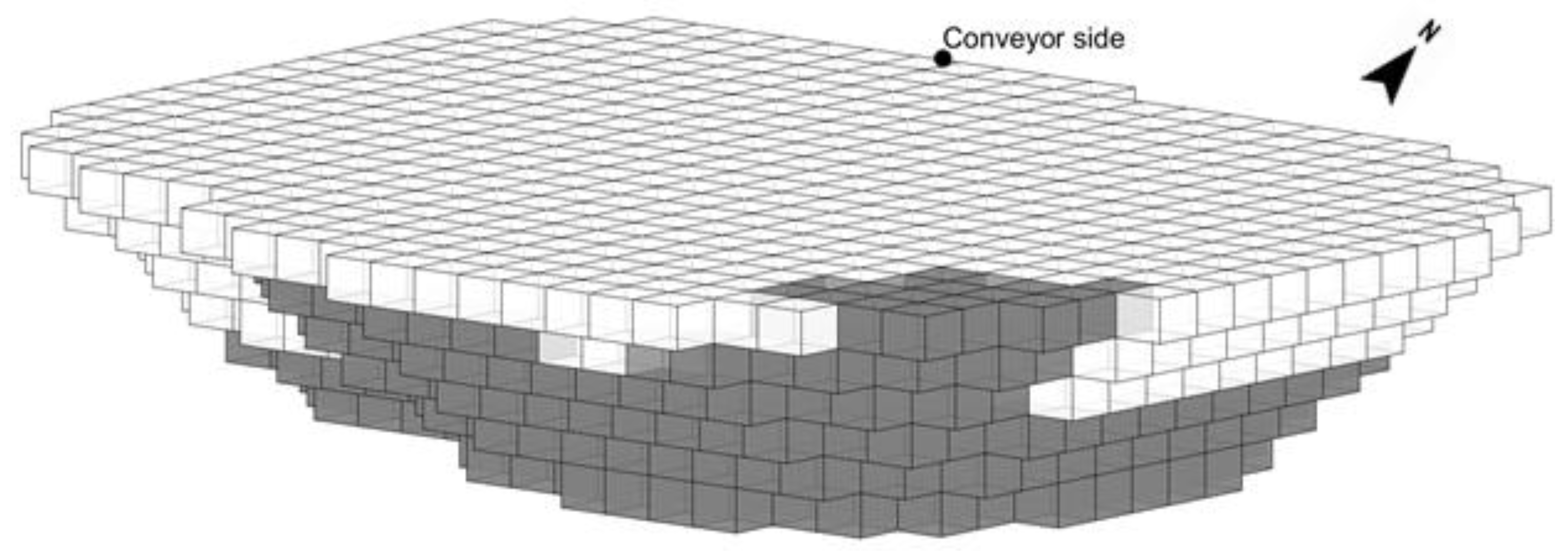
3.2. Determination of the HAC Location
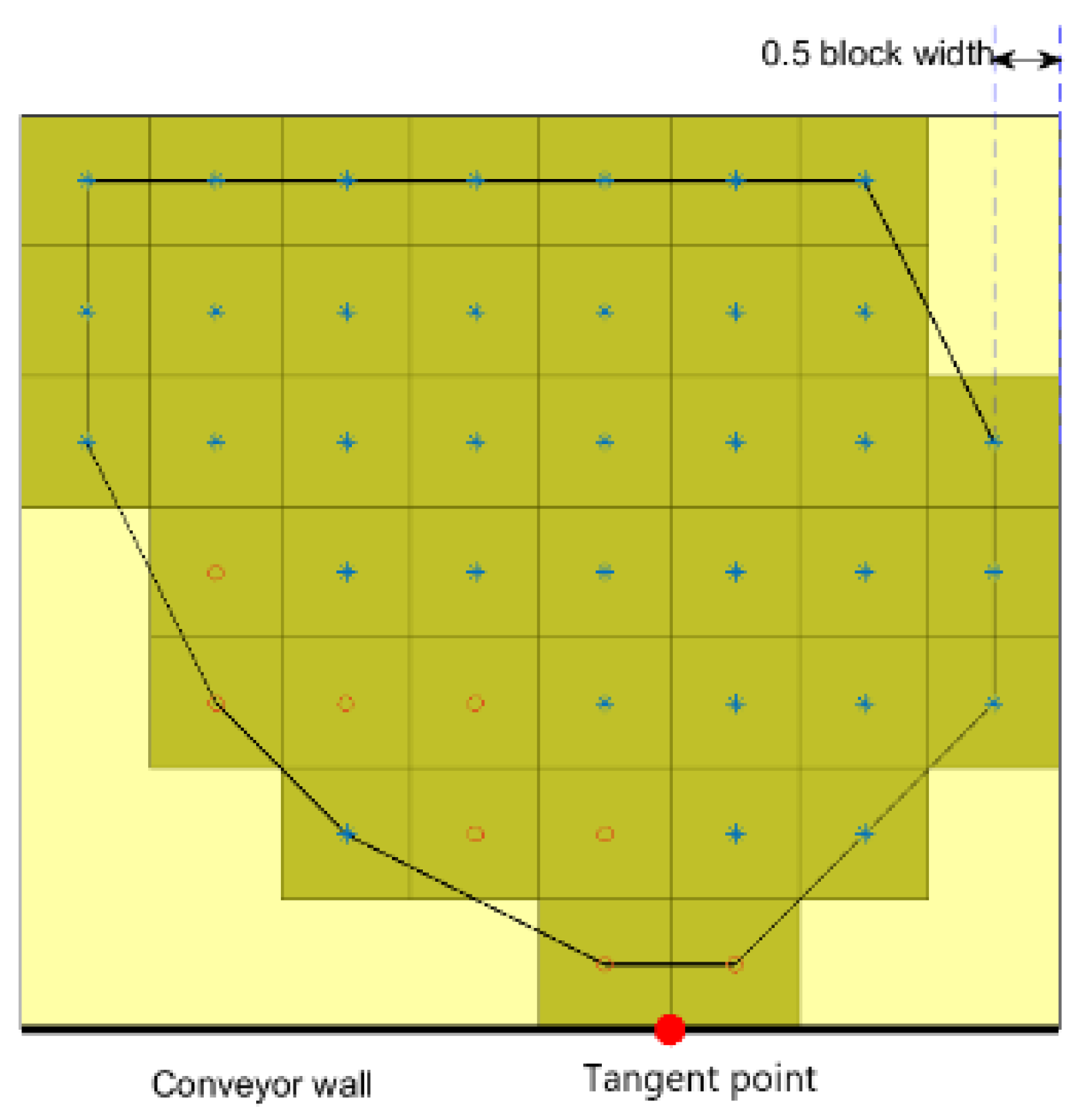
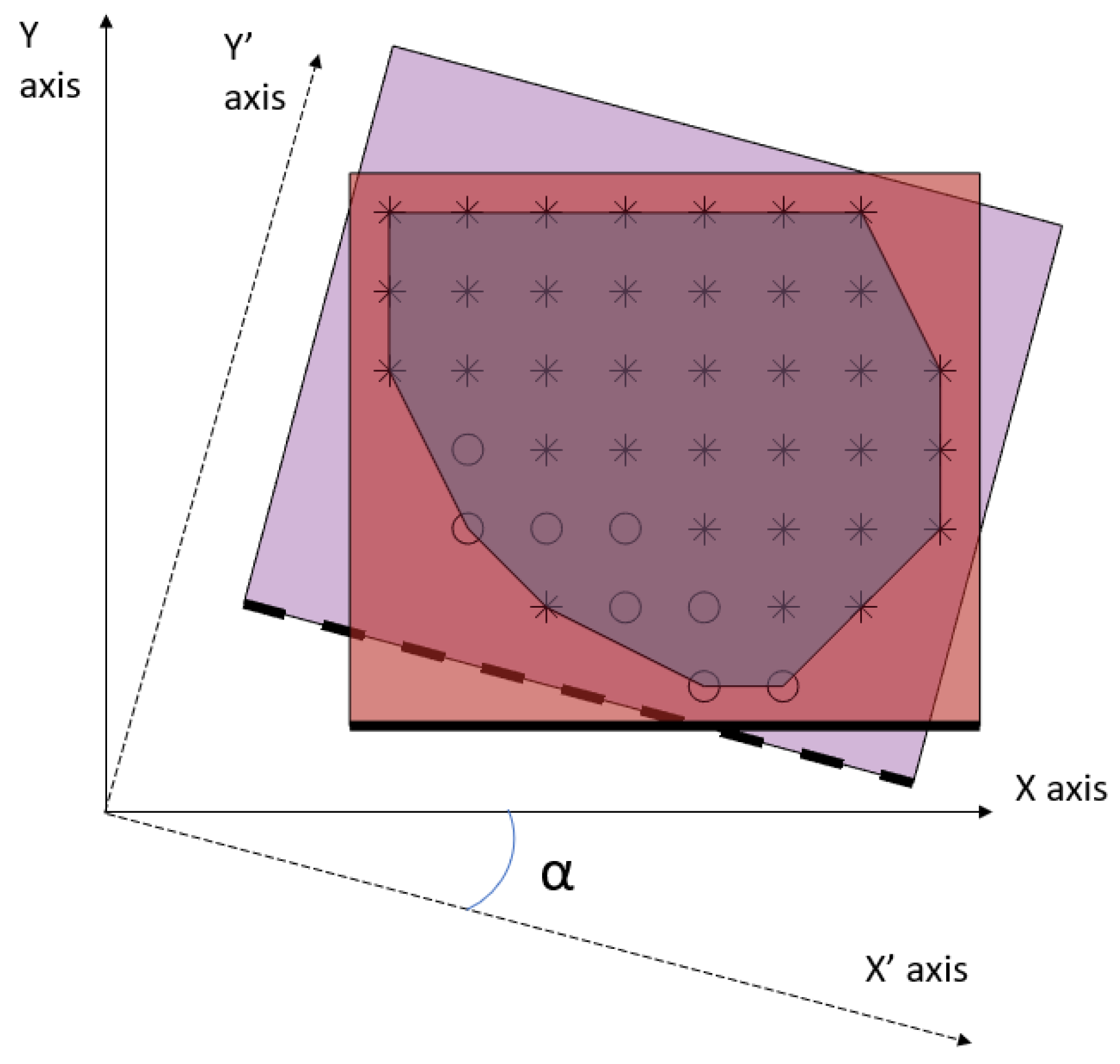
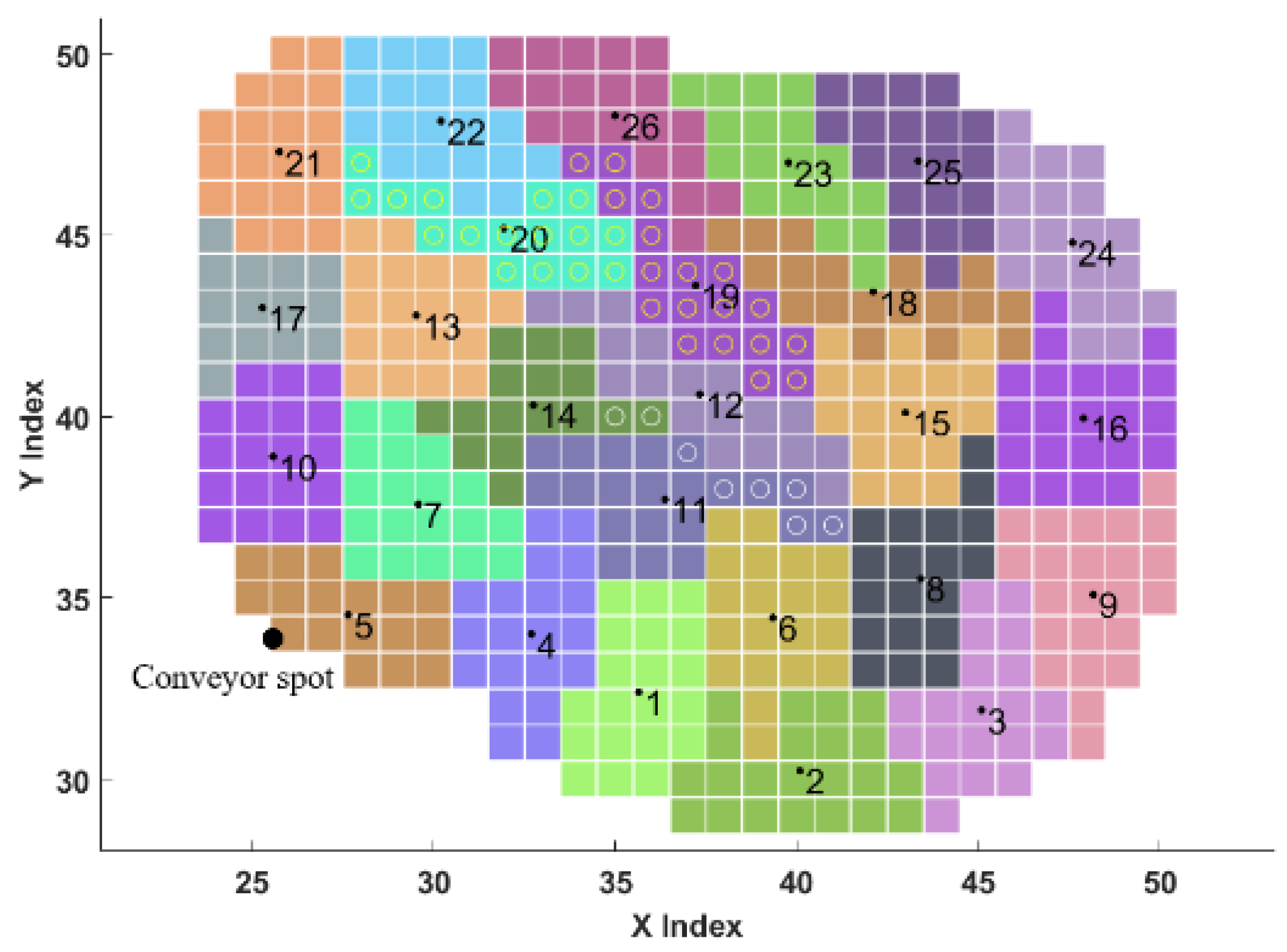
3.3. Hierarchical Agglomerative Clustering
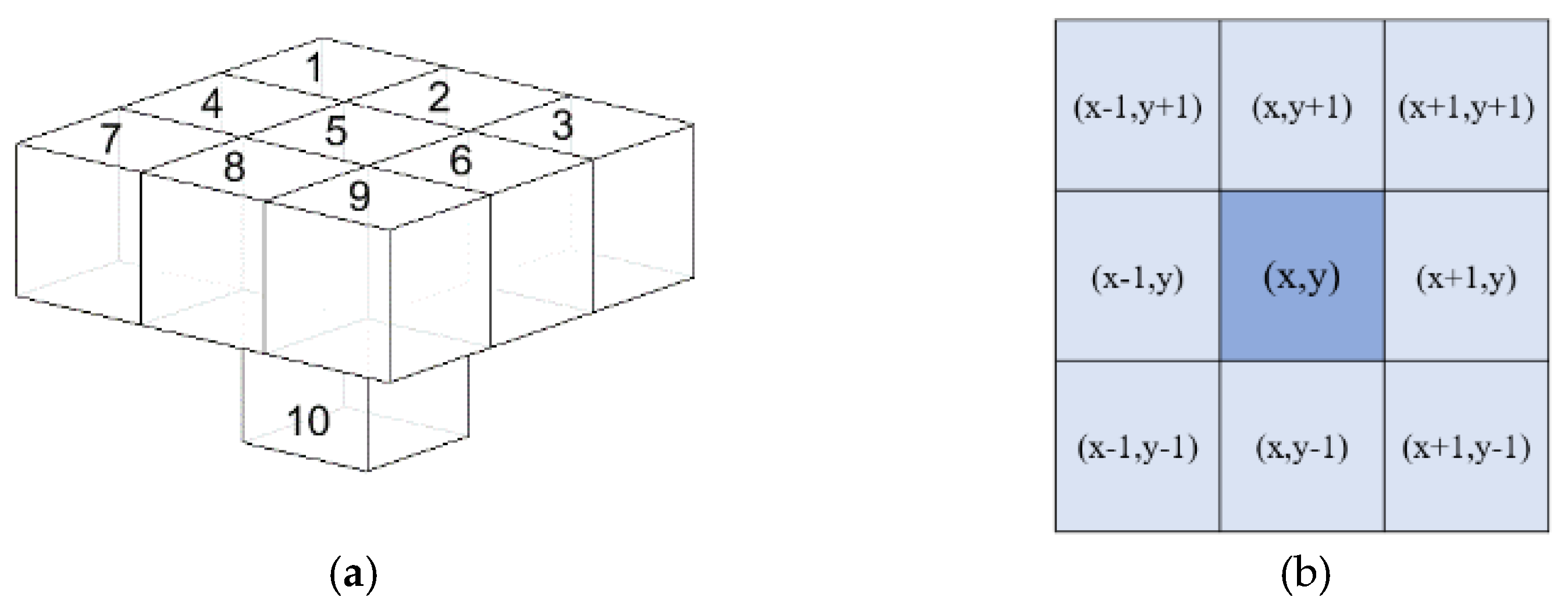
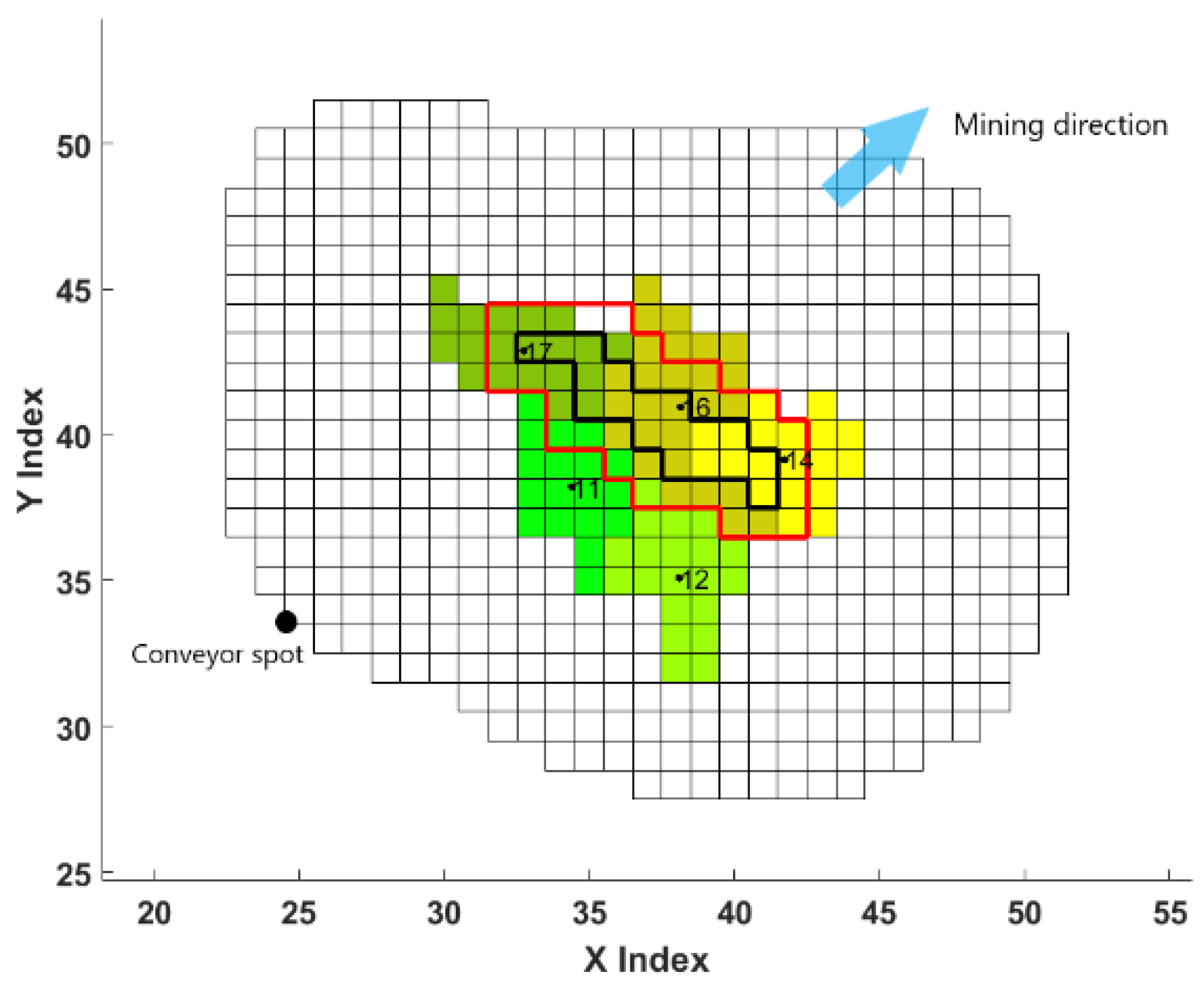
3.4. Cluster Precedence Relationships
- Cluster’s centroid is inside the red boundary (clusters 14, 16, and 17)
- Cluster is partly inside the boundary, and the conveyor is closer to the cluster’s centroid than to the centroid of the target cluster (clusters 11, 12, and 17)
- The portion of the cluster inside the red boundary is greater than 40%.
3.5. Material Handling Costs
4. Integer Linear Programming (ILP) Model
4.1. Objective Function
4.2. Constraints
- Mining and processing capacity
- Blending grade
- Reserves
- Precedence
- Material flow control
- Crusher location and relocation control
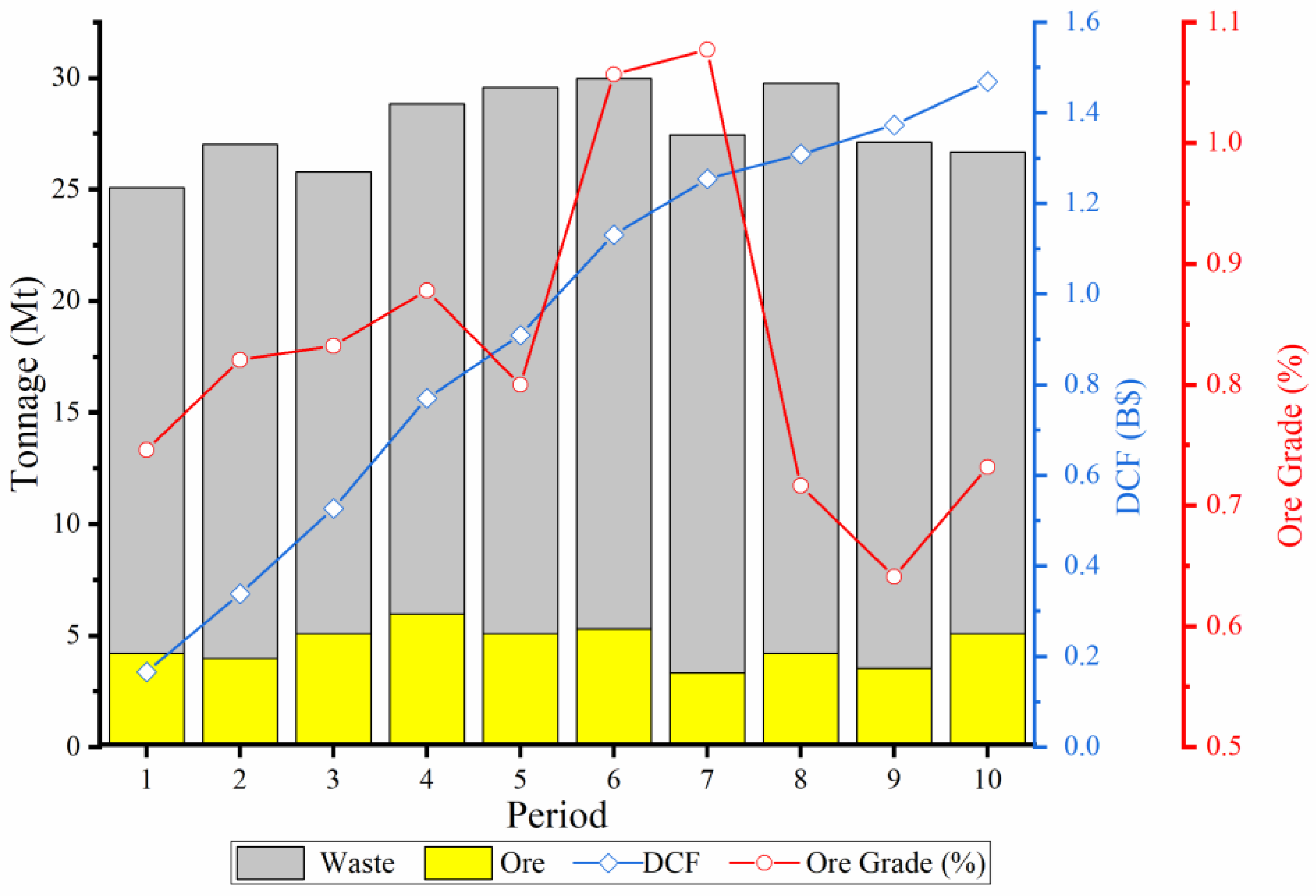
5. Case Study and Discussion of Results
6. Conclusions
- Proposing a mathematical model for making the production scheduling and crusher location-relocation simultaneously
- Incorporating the material handling costs and crusher relocation costs in the NPV maximization
- Developing a conveyor location optimization framework by generating various conveyor lines around the UPL and finding the optimum based on the NPV comparison
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ritter, R. Contribution to the Capacity Determination of Semi-Mobile in-Pit Crushing and Conveying Systems. Ph.D. Thesis, Technische Universität Bergakademie Freiberg, Freiberg, Germany, 2016. [Google Scholar]
- Paricheh, M.; Osanloo, M.; Rahmanpour, M. A heuristic approach for in-pit crusher and conveyor systems time and location problem in large open-pit mining. Int. J. Min. Reclam. Environ. 2018, 32, 35–55. [Google Scholar] [CrossRef]
- Demirel, N.; Gölbaşı, O. Preventive replacement decisions for dragline components using reliability analysis. Minerals 2016, 6, 51. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, H.; Maghaminik, A. Equipment replacement decision in mine based on decision tree algorithm. Sci. Rep. Resour. 2016, 1, 187–194. [Google Scholar]
- Osanloo, M.; Paricheh, M. In-pit crushing and conveying technology in open-pit mining operations: A literature review and research agenda. Int. J. Min. Reclam. Environ. 2019, 34, 430–457. [Google Scholar] [CrossRef]
- Czaplicki, J.M. Shovel-Truck Systems: Modelling, Analysis and Calculations; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Darling, P. SME Mining Engineering Handbook; SME: Denver, CO, USA, 2011; Volume 1. [Google Scholar]
- Nehring, M.; Knights, P.F.; Kizil, M.S.; Hay, E. A comparison of strategic mine planning approaches for in-pit crushing and conveying, and truck/shovel systems. Int. J. Min. Sci. Technol. 2018, 28, 205–214. [Google Scholar] [CrossRef]
- Bernardi, L.; Kumral, M.; Renaud, M. Comparison of fixed and mobile in-pit crushing and conveying and truck-shovel systems used in mineral industries through discrete-event simulation. Simul. Model. Pract. Theory 2020, 103, 102100. [Google Scholar] [CrossRef]
- Santos, J.; Frizzell, E. Evolution of sandwich belt high-angle conveyors. CIM Bull. 1983, 576, 51–66. [Google Scholar]
- Tutton, D.; Streck, W. The application of mobile in-pit crushing and conveying in large, hard rock open pit mines. In Proceedings of the Mining Magazine Congress, Niagara-on-the-Lake, ON, Canada, 8–9 October 2009. [Google Scholar]
- Sturgul, J.R. How to determine the optimum location of in-pit movable crushers. Int. J. Min. Geol. Eng. 1987, 5, 143–148. [Google Scholar] [CrossRef]
- Peng, S.; Zhang, D. Computer simulation of a semi-continuous open-pit mine haulage system. Int. J. Min. Geol. Eng. 1988, 6, 267–271. [Google Scholar] [CrossRef]
- Konak, G.; Onur, A.; Karakus, D. Selection of the optimum in-pit crusher location for an aggregate producer. J. South. Afr. Inst. Min. Metall. 2007, 107, 161–166. [Google Scholar]
- Rahmanpour, M.; Osanloo, M.; Adibee, N. An approach to determine the location of an in pit crusher in open pit mines. In Proceedings of the 23rd International Mining Congress and Exhibition of Turkey, IMCET 2013, Antalya, Turkey, 16–19 April 2013. Chamber of Mining Engineers of Turkey. [Google Scholar]
- Paricheh, M.; Osanloo, M.; Rahmanpour, M. In-pit crusher location as a dynamic location problem. J. South. Afr. Inst. Min. Metall. 2017, 117, 599–607. [Google Scholar] [CrossRef]
- Abbaspour, H.; Drebenstedt, C.; Paricheh, M.; Ritter, R. Optimum location and relocation plan of semi-mobile in-pit crushing and conveying systems in open-pit mines by transportation problem. Int. J. Min. Reclam. Environ. 2018, 33, 297–317. [Google Scholar] [CrossRef]
- Hay, E.; Nehring, M.; Knights, P.; Kizil, M.S. Ultimate pit limit determination for semi mobile in-pit crushing and conveying system: A case study. Int. J. Min. Reclam. Environ. 2019, 1–21. [Google Scholar] [CrossRef]
- Jimenez Builes, C.A. A Mixed-Integer Programming Model for an In-Pit Crusher Conveyor Location Problem. Masters’s Thesis, École Polytechnique de Montréal, Montréal, QC, Canada, 2017. [Google Scholar]
- Paricheh, M.; Osanloo, M. Concurrent open-pit mine production and in-pit crushing–conveying system planning. Eng. Optim. 2020, 52, 1780–1795. [Google Scholar] [CrossRef]
- Samavati, M.; Essam, D.; Nehring, M.; Sarker, R. Production planning and scheduling in mining scenarios under IPCC mining systems. Comput. Oper. Res. 2020, 115, 104714. [Google Scholar] [CrossRef]
- Deutsch, M. The Angle Specification for GSLIB Software. Deutsch, J.L., Ed.; Geostatistics Lessons. 2015. Available online: https://geostatisticslessons.com/lessons/anglespecification (accessed on 5 February 2021).
- Eivazy, H.; Askari-Nasab, H. A mixed integer linear programming model for short-term open pit mine production scheduling. Min. Technol. 2012, 121, 97–108. [Google Scholar] [CrossRef]
- Tabesh, M.; Askari-Nasab, H. Two-stage clustering algorithm for block aggregation in open pit mines. Min. Technol. 2011, 120, 158–169. [Google Scholar] [CrossRef]
- de Werk, M.; Ozdemir, B.; Ragoub, B.; Dunbrack, T.; Kumral, M. Cost analysis of material handling systems in open pit mining: Case study on an iron ore prefeasibility study. Eng. Econ. 2017, 62, 369–386. [Google Scholar] [CrossRef]
- MATLAB. 9.7.0.1190202 (R2019b); The MathWorks Inc.: Natick, MA, USA, 2018. [Google Scholar]
- IBM; IBM ILOG CPLEX Optimization Studio. CPLEX User’s Manual 12; IBM Corporation: Armonk, NY, USA, 2011; pp. 1–148. [Google Scholar]




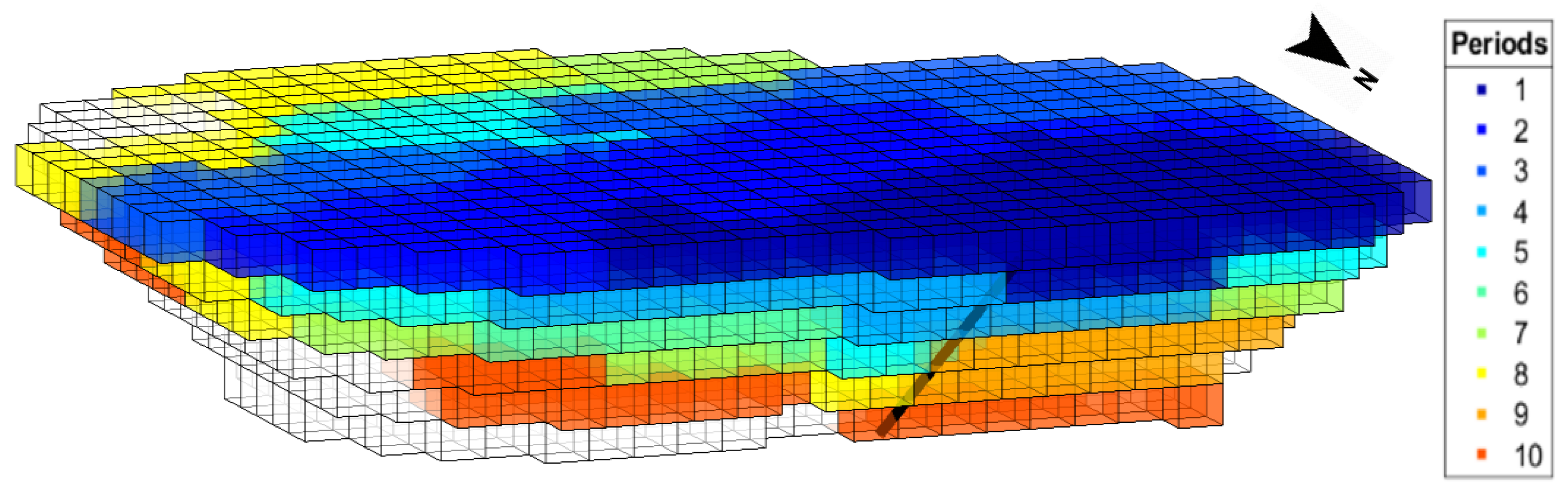
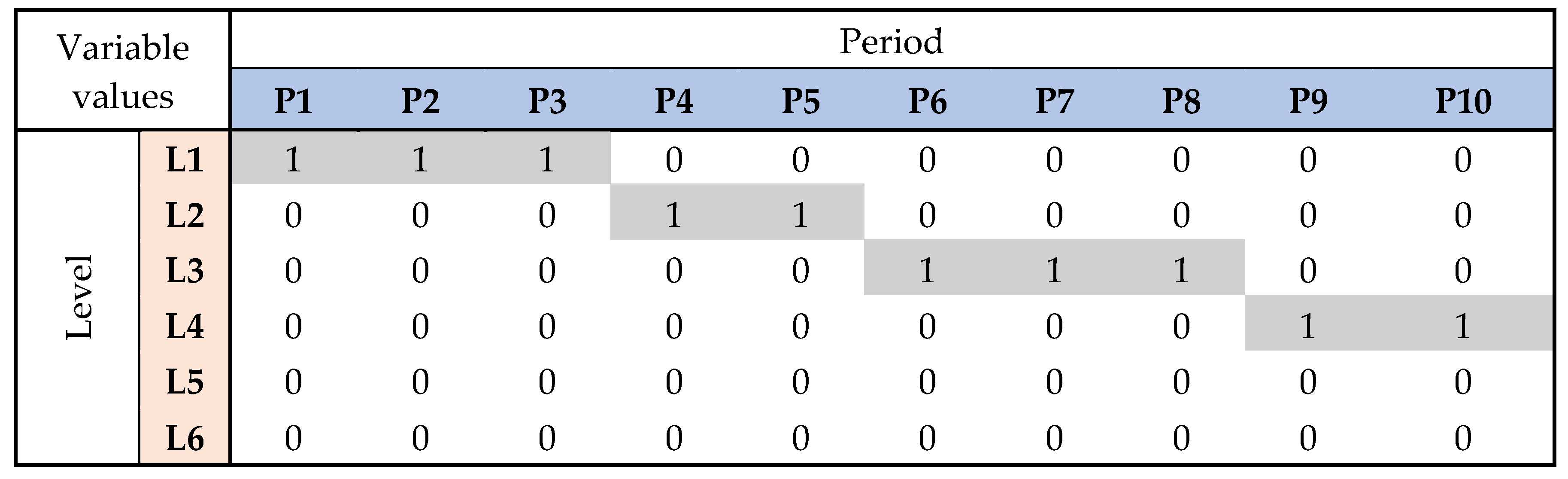
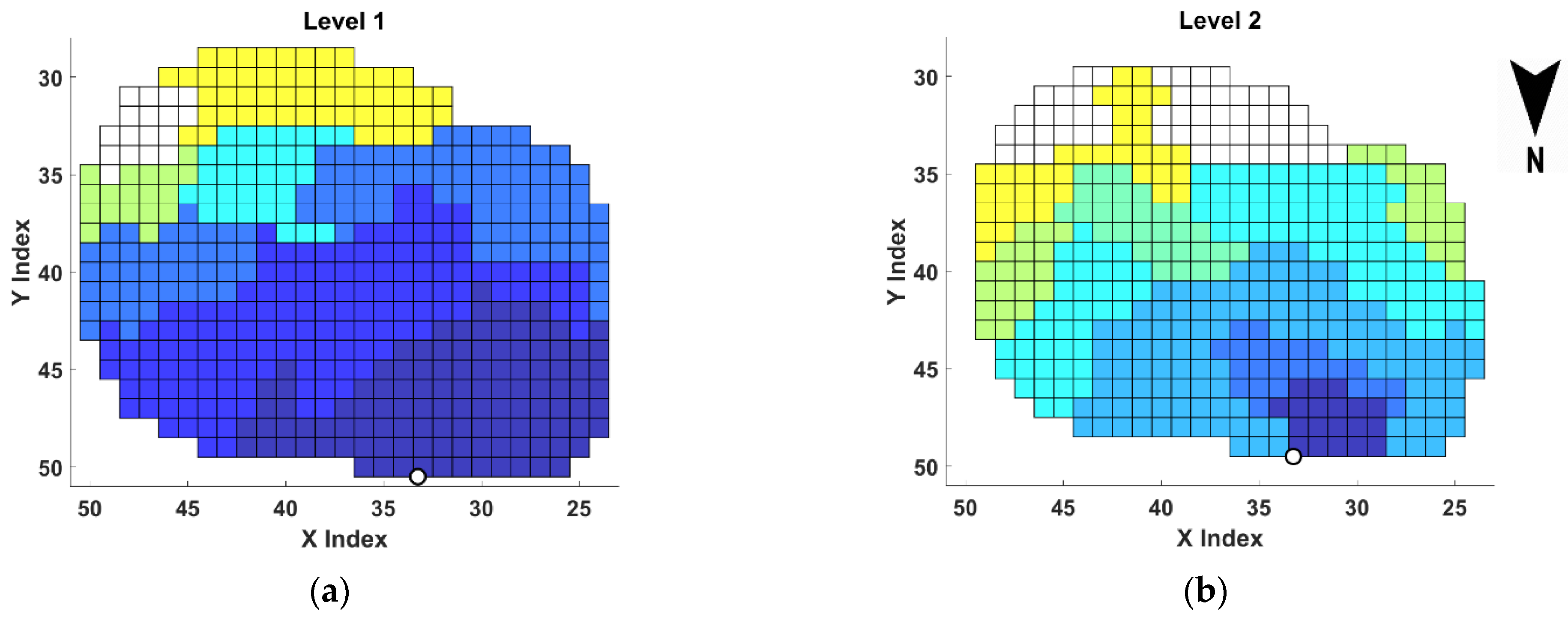
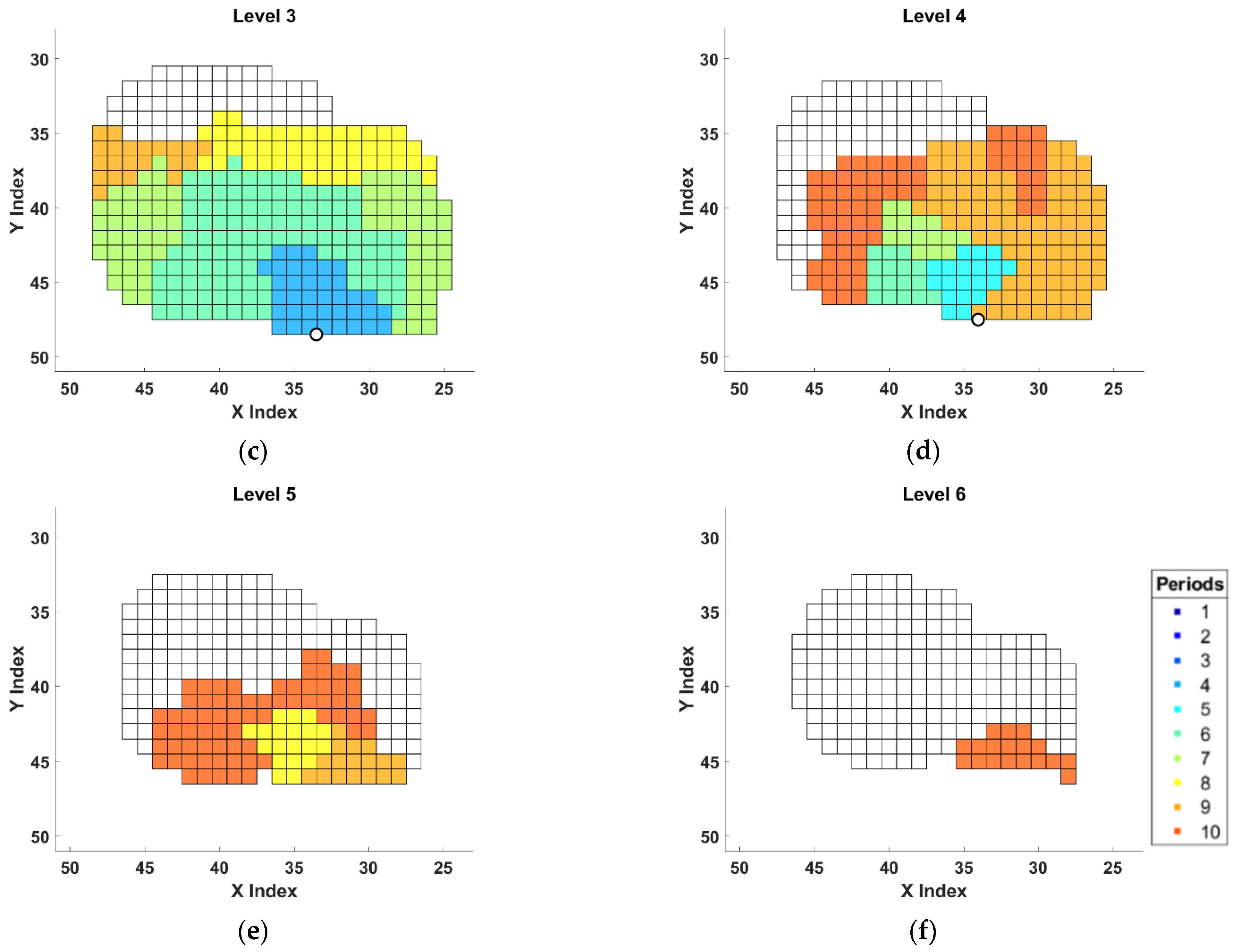
| Sets | |
|---|---|
| Set of clusters in the model | |
| Set of waste blocks in cluster i | |
| Set of ore blocks in cluster i | |
| For each cluster i, there is a set of immediate predecessors that must be extracted before extraction of cluster i | |
| Indices | |
| Index for clusters | |
| Index for pit levels | |
| Index for scheduling periods | |
| Parameters | |
| Total number of clusters | |
| Total number of levels | |
| T | Number of scheduling periods |
| Discount rate | |
| The undiscounted economic value of cluster i | |
| The tonnage of block b | |
| The total tonnage of waste in cluster i | |
| The total tonnage of ore material in cluster i | |
| Grade of ore block b | |
| The average grade of ore material in cluster i | |
| Pct | Price per unit of product sold in period t |
| Selling cost per unit of product | |
| Cost of mining a ton of waste | |
| Cost of mining a ton of ore | |
| Cost of processing a ton of ore | |
| R | The recovery rate for ore material |
| Discounted transportation cost for cluster i sent to crusher j in period t | |
| Material handling cost per unit weight of cluster i to crusher j | |
| Discounted crusher relocation cost at period t | |
| The minimum period interval for crusher relocation | |
| The horizontal distance from the centroid of cluster i to the crushing station j | |
| The vertical distance from cluster i to the crushing station j (truck hauling) | |
| The vertical distance from crushing station j to the pit exit (conveying) | |
| Unit truck horizontal hauling cost per ton per meter | |
| Unit truck vertical hauling cost per ton per meter | |
| CC | Unit conveyor vertical lifting cost per ton per meter |
| Upper bound of mining capacity in period t | |
| Lower bound of mining capacity in period t | |
| Upper bound of processing capacity in period t | |
| Lower bound of processing capacity in period t | |
| Upper bound on allowable average grade of processed ore in period t | |
| Lower bound on allowable average grade of processed ore in period t | |
| Decision variables | |
| Binary variable equal to 1 if cluster i is mined in period t; 0 otherwise | |
| Binary variables equal to 1 if the precedent clusters are all cleared for cluster i; 0 otherwise | |
| Binary variables denoting if cluster i is crushed at level j in period t | |
| Binary variables equal to 1 if the crusher is in level j in period t; 0 otherwise | |
| Binary variables equal to 1 if the crusher is relocated to level j in period t; 0 otherwise | |
| Rock Type | Density (ton/m−3) | Average Grade (%) | Tonnage (Mt) | Number of Blocks |
|---|---|---|---|---|
| Mineralized Zone 1 (MZ1) | 2.10 | 1.836 | 2.94 | 14 |
| Mineralized Zone 2 (MZ2) | 2.10 | 0.822 | 44.73 | 213 |
| W (waste) | 1.80 | 0 | 320.22 | 1779 |
| Number of Blocks | Number of Clusters | Total Tonnage (Mt) | Ore Tonnage (Mt) | Average Ore Grade (%) | |
|---|---|---|---|---|---|
| Level 1 | 498 | 25 | 91.36 | 9.28 | 0.81 |
| Level 2 | 426 | 22 | 78.24 | 8.79 | 0.90 |
| Level 3 | 356 | 20 | 65.56 | 8.45 | 0.94 |
| Level 4 | 294 | 15 | 54.56 | 8.34 | 0.86 |
| Level 5 | 238 | 13 | 44.36 | 8.03 | 0.78 |
| Level 6 | 194 | 10 | 36.31 | 7.51 | 0.76 |
| Category | Parameter | Quantity |
|---|---|---|
| Economic factors | Reference mining cost * ($/t) | 1.5 |
| Ore processing cost ($/t) | 3.06 | |
| Recovery (%) | 90 | |
| Cu price ($/t) | 7,936 | |
| Selling cost ($/t) | 0 | |
| Discount rate (%) | 8 | |
| Transportation costs | Horizontal trucking cost ($/km·t) | 0.2 |
| Conveyor vertical lifting cost ($/level·t) | 0.3 | |
| Vertical trucking cost ($/level·t) | 1.2 [25] | |
| Crusher relocation cost ($/time) | 1,000,000 [17] | |
| Production | Upper mining capacity (Mt/year) | 30 |
| Lower mining capacity (Mt/year) | 25 | |
| Upper processing capacity (Mt/year) | 6 | |
| Lower processing capacity (Mt/year) | 4 | |
| Upper ore blending grade (%) | 1.0 | |
| Lower ore blending grade (%) | 0.5 | |
| Mine life (years) | 10 | |
| Clustering | Maximum number of the blocks | 25 |
| Minimum number of the blocks | 15 | |
| 1 | ||
| 0.2 | ||
| 1 | ||
| 0.2 | ||
| Others | Minimum crusher relocation interval (year) | 2 |
| Rotation Angle (°) | Total Tonnage (Mt) | Ore Tonnage (Mt) | Total Stripping Ratio | NPV (B$) | Average Ore Grade (%) |
|---|---|---|---|---|---|
| 0 | 287.02 | 34.48 | 7.32 | 1.023 | 0.877 |
| 45 | 258.05 | 41.33 | 5.24 | 1.204 | 0.828 |
| 90 | 258.79 | 42.43 | 5.10 | 1.232 | 0.859 |
| 135 | 286.17 | 46.17 | 5.20 | 1.432 | 0.838 |
| 180 | 277.23 | 45.75 | 5.06 | 1.468 | 0.833 |
| 225 | 292.08 | 43.32 | 5.74 | 1.306 | 0.882 |
| 270 | 278.11 | 36.91 | 6.54 | 1.118 | 0.893 |
| 315 | 282.10 | 35.14 | 7.03 | 0.932 | 0.876 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Pourrahimian, Y. A Framework for Open-Pit Mine Production Scheduling under Semi-Mobile In-Pit Crushing and Conveying Systems with the High-Angle Conveyor. Mining 2021, 1, 59-79. https://doi.org/10.3390/mining1010005
Liu D, Pourrahimian Y. A Framework for Open-Pit Mine Production Scheduling under Semi-Mobile In-Pit Crushing and Conveying Systems with the High-Angle Conveyor. Mining. 2021; 1(1):59-79. https://doi.org/10.3390/mining1010005
Chicago/Turabian StyleLiu, Dingbang, and Yashar Pourrahimian. 2021. "A Framework for Open-Pit Mine Production Scheduling under Semi-Mobile In-Pit Crushing and Conveying Systems with the High-Angle Conveyor" Mining 1, no. 1: 59-79. https://doi.org/10.3390/mining1010005
APA StyleLiu, D., & Pourrahimian, Y. (2021). A Framework for Open-Pit Mine Production Scheduling under Semi-Mobile In-Pit Crushing and Conveying Systems with the High-Angle Conveyor. Mining, 1(1), 59-79. https://doi.org/10.3390/mining1010005







