Mathematization Through Application and Common Sense: Motivating Intellectual Activities of Schoolchildren with Digital Tools
Abstract
1. Introduction
2. Materials and Methods
3. Computer Tools for Interiorization and Partnership
4. Construct–Test–Explore Problem Solving and Number Theory with Digital Tools
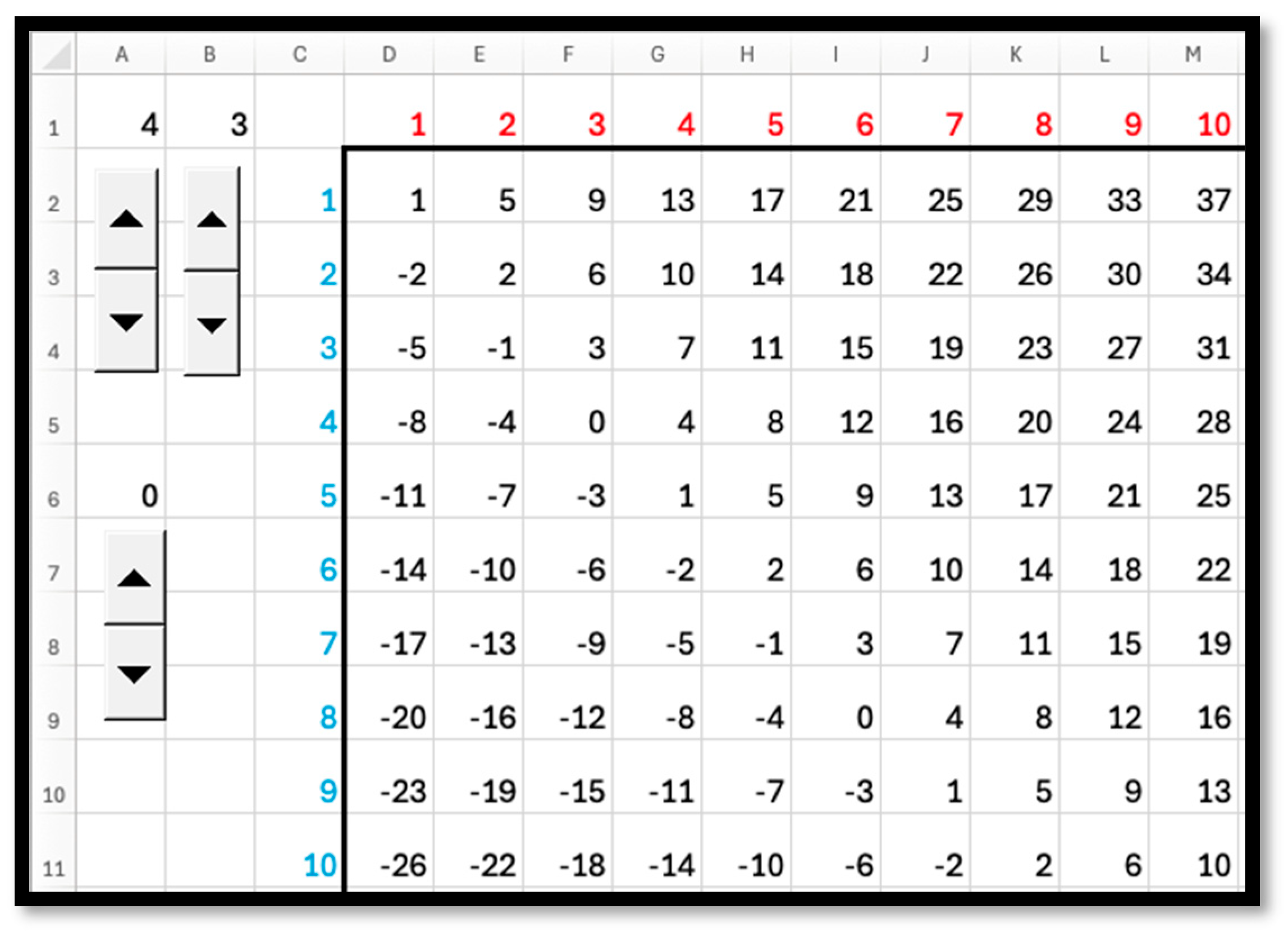
4.1. From NP Problems to Mathematical Competitions
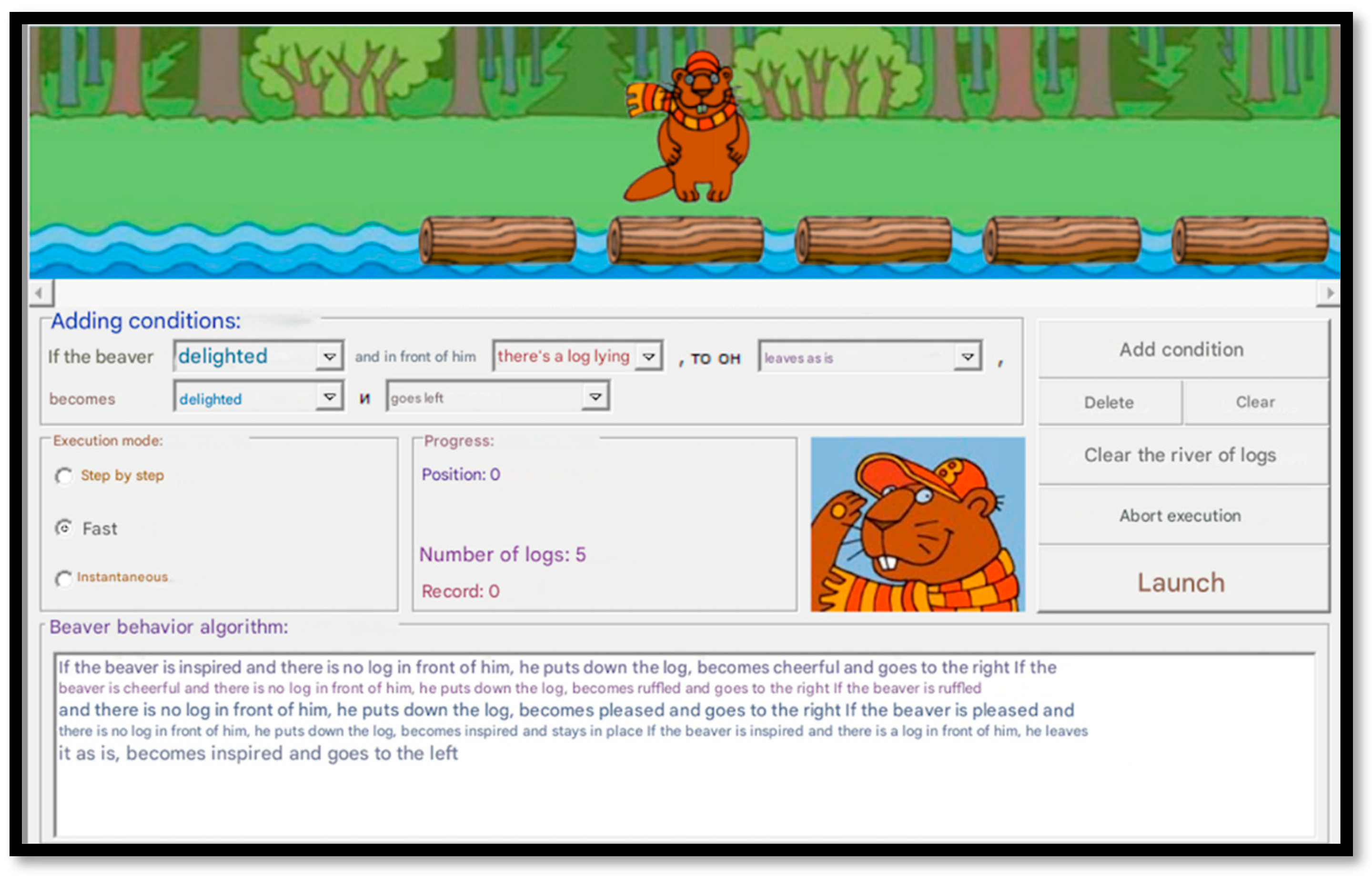
4.2. The “Busy Beaver” Problem
4.3. The “Clock” Problem
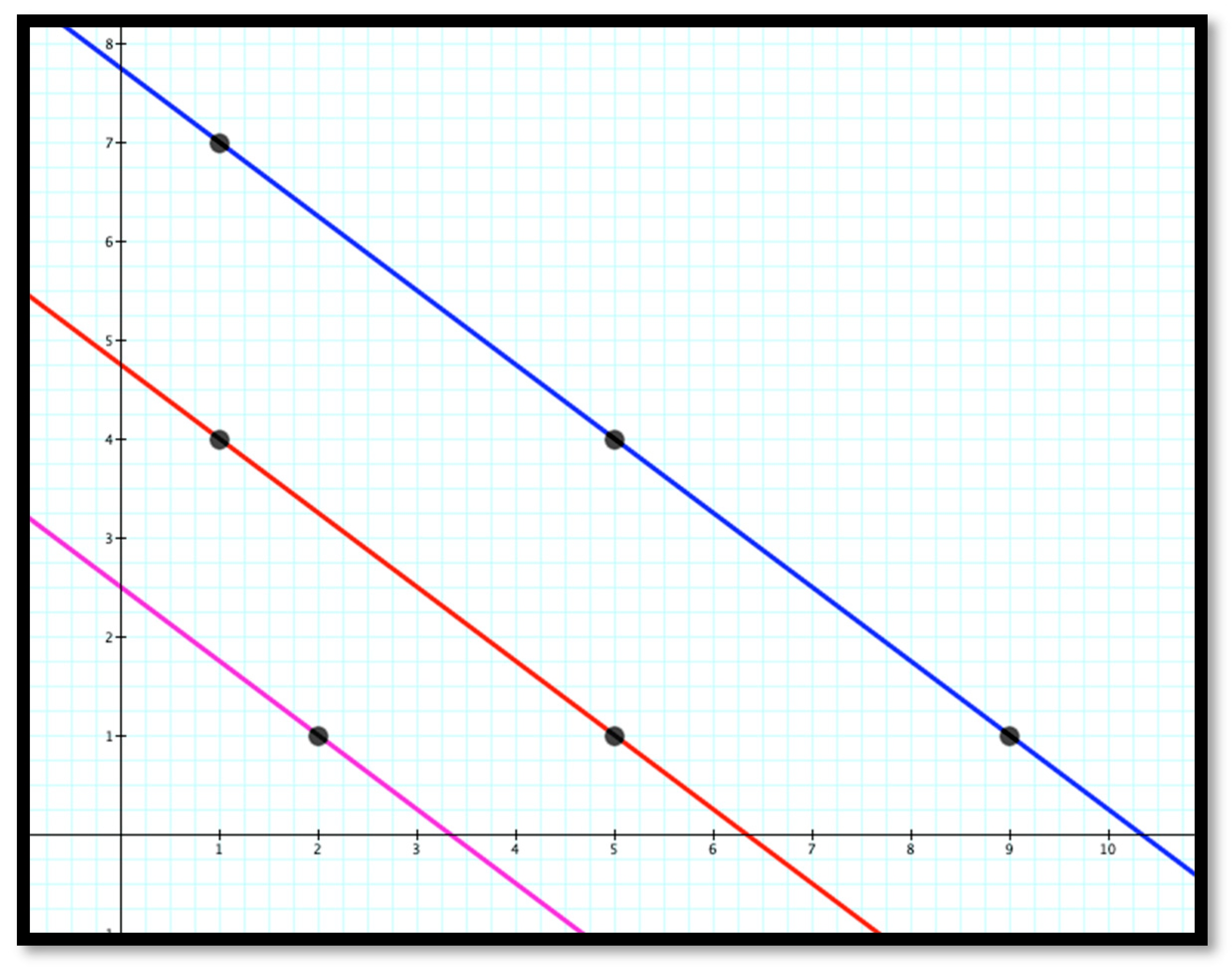
4.4. Exploring Papert’s Foreword Comment Using Multiple Digital Tools
5. Digital Problem Solvers
6. Wise Tasks Type Systems
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Freudenthal, H. Major problems of mathematics education. Educ. Stud. Math. 1981, 12, 133–150. [Google Scholar] [CrossRef]
- Fey, J.T. Technology and mathematics education: A survey of recent developments and important problems. Educ. Stud. Math. 1989, 20, 237–272. [Google Scholar] [CrossRef]
- Kaput, J.J.; Thompson, P.W. Technology in mathematics education research: The first 25 years in the JRME. J. Res. Math. Educ. 1994, 25, 676–684. [Google Scholar]
- Papert, S. An Exploration in the Space of Mathematics Educations. Int. J. Comput. Math. Learn. 1996, 1, 95–123. [Google Scholar] [CrossRef]
- Tall, D. Cognitive development in advanced mathematics using technology. Math. Educ. Res. J. 2000, 12, 210–230. [Google Scholar] [CrossRef]
- Kaput, J.J.; Noss, R.; Hoyles, C. Developing new notations for a learnable mathematics in the computational era. In Handbook of International Research on Mathematics Education, 2nd ed.; Lawrence Erlbaum: London, UK, 2008; pp. 693–715. [Google Scholar]
- Freiman, V.; Kadijevich, D.; Kuntz, G.; Pozdnyakov, S.; Stedøy, I. Technological environments beyond the classroom. In Challenging Mathematics in and Beyond the Classroom; Barbeau, E.J., Taylor, P.J., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 97–131. [Google Scholar]
- Naftaliev, E.; Yerushalmy, M. Guiding explorations: Design principles and functions of interactive diagrams. Comput. Sch. 2013, 30, 61–75. [Google Scholar] [CrossRef]
- Winkel, B. Computers have taken us to the brink in mathematics… and we have balked. Comput. Sch. 2013, 30, 148–171. [Google Scholar] [CrossRef]
- Freiman, V.; Tassell, J.L. Leveraging Mathematics Creativity by Using Technology: Questions, Issues, Solutions, and Innovative Paths. In Creativity and Technology in Mathematics Education; Freiman, V., Tassell, J., Eds.; Springer: Cham, The Netherlands, 2018; Volume 10, pp. 3–29. [Google Scholar]
- Pozdniakov, S.; Freiman, V. Technology-supported innovations in mathematics education during the last 30 years: Russian perspective. ZDM Math. Educ. 2021, 53, 1499–1513. [Google Scholar] [CrossRef]
- Abramovich, S. Revisiting mathematical problem solving and posing in the digital era: Toward pedagogically sound uses of modern technology. Int. J. Math. Educ. Sci. Technol. 2014, 45, 1034–1052. [Google Scholar] [CrossRef]
- Abramovich, S. Computational triangulation in mathematics teacher education. Computation 2023, 11, 31. [Google Scholar] [CrossRef]
- Vygotsky, L.; Luria, R. Tool and Symbol in Child Development. In The Vygotsky Reader; van der Veer, R., Valsiner, J., Eds.; Wiley-Blackwell: Hoboken, NJ, USA, 1994; pp. 99–174. [Google Scholar]
- Vygotsky, L.S. Thinking and speech. In The Collected Works of L. S. Vygotsky; Rieber, R.W., Carton, A.S., Eds.; Plenum Press: New York, NY, USA, 1987; Volume 10, pp. 39–285. [Google Scholar]
- Papert, S. Teaching children thinking. Program. Learn. Educ. Technol. 1972, 9, 245–255. [Google Scholar] [CrossRef]
- Papert, S. Computers and Powerful Ideas. In Mindstorms—Children; Basic Books Inc: New York, NY, USA, 1980. [Google Scholar]
- Harel, I.E.; Papert, S.E. Constructionism; Ablex Publishing: New York, NY, USA, 1991. [Google Scholar]
- Walker, S. Culturally significant artifacts and their relationship to tradition and sustainability. In Culturally Significant Designs, Products and Practices; Walker, S., Evans, M., Cassidy, T., Jung, J., Twigger Holroyd, A., Eds.; Bloomsbury: New York, NY, USA, 2018; pp. 39–48. [Google Scholar]
- Kaire, S. Significant artifacts in schools: Teacher and pupil perspectives. J. Educ. Cult. Soc. 2016, 7, 131–149. [Google Scholar] [CrossRef]
- Hung, D. Situated cognition and problem-based learning: Implications for learning and instruction with technology. J. Interact. Learn. Res. 2002, 13, 393–414. [Google Scholar]
- Downes, S. Connectivism. Asian J. Distance Educ. 2022, 17, 58–87. [Google Scholar]
- Levey, S. Universal design for learning. J. Educ. 2023, 203, 479–487. [Google Scholar] [CrossRef]
- Levin, I.; Semenov, A.I.; Gorsky, M. Smart learning in the 21st century: Advancing constructionism across three digital epochs. Educ. Sci. 2025, 15, 45. [Google Scholar] [CrossRef]
- Santos-Trigo, M.; Moreno-Armella, L.; Camacho-Machín, M. Problem solving and the use of digital technologies within the Mathematical Working Space framework. ZDM Math. Educ. 2016, 48, 827–842. [Google Scholar] [CrossRef]
- Steffe, L.P. Constructivism in Education; Gale, J., Ed.; Lawrence Erlbaum: Mahwah, NJ, USA, 1995. [Google Scholar]
- Allen, A. An introduction to constructivism: Its theoretical roots and impact to contemporary education. J. Learn. Des. Leadersh. 2022, 1, 1–11. [Google Scholar]
- Wolfram Alpha. Software for Technical Computation; Wolfram Research: Champaign, IL, USA, 2004. [Google Scholar]
- Avitzur, R. Graphing Calculator, Version 4.0; Pacific Tech: Atlanta, GA, USA, 2011.
- Gershenfeld, N. From Personal Computers to Personal Fabrication. In The Coming Revolution on Your Desktop; Basic Books Inc: New York, NY, USA, 2005. [Google Scholar]
- Hohenwarter, M. GeoGebra. Available online: http://geogebra.org (accessed on 25 August 2025).
- Jackiw, N. The Geometer’s Sketchpad. Available online: https://www.dynamicgeometry.com (accessed on 16 August 2025).
- Desmos. Available online: www.desmos.com (accessed on 25 August 2025).
- Leont’ev, A.N. Deyatelnost, Soznanie i Lichnost [Activity, Consciousness, and Personality]; Pedagogika: Moscow, Russia, 1983; Volume 2. [Google Scholar]
- Schwartz, J.L.; Yerushalmy, M. The Geometric Supposer; Computer Program; Sunburst Communications: New York, NY, USA, 1985. [Google Scholar]
- Laborde, J.M. CABRI Geometry; Computer Program; Brooks-Cole Publishing Co.: New York, NY, USA, 1985. [Google Scholar]
- Akimushkin, V.A.; Maytarttanakhon, A.; Pozdnyakov, S.N. Olympiad in Theoretical Computer Science and Discrete Mathematics. In Informatics in Schools: Curricula, Competences, and Competitions; Dolinšek, V., Lazar, T., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9378, pp. 94–105. [Google Scholar]
- Vavilov, N.A. Computers as novel mathematical reality: I. A Personal Account. Comput. Tools Educ. 2020, 2, 5–26. (In Russian) [Google Scholar] [CrossRef]
- Vavilov, N.A. Computers as novel mathematical reality. IV. Goldbach Problem. Comput. Tools Educ. 2021, 4, 5–7. (In Russian) [Google Scholar] [CrossRef]
- Vavilov, N.A. Computers as Novel Mathematical Reality. VI. Fermat Numbers and Their Relatives. Comput. Tools Educ. 2022, 4, 5–67. (In Russian) [Google Scholar] [CrossRef]
- Abramovich, S. From Counting to Computing: Ideas for Mathematics Education in Information Age; Emerald Publishing: Leeds, UK, 2025. [Google Scholar]
- Posov, I.A. Busy beaver. Comput. Tools Educ. 2007, 2, 51–55. (In Russian) [Google Scholar]
- Lagaris, J.C. The 3x + 1 problem: An overview. In The Ultimate Challenge: The 3x + 1 Problem; Lagaris, J.C., Ed.; The American Mathematical Society: Providence, RI, USA, 2010; pp. 3–29. [Google Scholar]
- Arnold, V.I. Experimental Mathematics; Fazis: Moscow, Russia, 2005. (In Russian) [Google Scholar]
- Borwein, J.M. The experimental mathematics: The pleasure of discovery and the role of proof. Int. J. Comput. Math. Learn. 2005, 10, 75–108. [Google Scholar]
- Pollak, H. On some of the problems of teaching applications of mathematics. Educ. Stud. Math. 1968, 1, 24–30. [Google Scholar] [CrossRef]
- Leikin, R. Exploring mathematical creativity using multiple solution tasks. In Creativity in Mathematics and the Education of Gifted Students Rotterdam; Leikin, R., Berman, A., Koichu, B., Eds.; Sense Publisher: Rotterdam, The Netherlands, 2009; Volume 9, pp. 129–145. [Google Scholar]
- Lyness, R.C. Applied mathematics in English schools. Educ. Stud. Math. 1968, 1, 98–104. [Google Scholar] [CrossRef]
- Maitarattanakon, A. Information Technologies in Organizing Distance Competitions in Mathematics and Computer Science. Ph.D. Dissertation, Far Eastern Federal University, Vladivostok, Russia, 2022. [Google Scholar]
- Cooney, T.J. Considering the paradoxes, perils, and purposes of conceptualizing teacher development. In Making Sense of Mathematics Teacher Education; Lin, F.L., Ed.; Springer: Dordrecht, The Netherlands, 2001; pp. 9–31. [Google Scholar]
- Harrison, H.; Nettleton, T. Principles of Engineering Mechanics; Elsevier Science: Oxford, UK, 2012. [Google Scholar]
- Canobi, K.H. Children’s profiles of addition and subtraction understanding. J. Exp. Child Psychol. 2005, 92, 220–246. [Google Scholar] [CrossRef]
- Kublanovskij, S.I.; Matiyasevich, Y.V. Artificial intelligence in mathematics—Universal Mathematical Solver. Comput. Tools Educ. 2003, 2, 49–55. [Google Scholar]
- Abramovich, S. Do computers enable mathematical problem solving or just make it “easy”? Comput. Tools Educ. 2016, 2, 45–54. [Google Scholar]
- Bogdanov, M.S. Automation of checking solutions to problems based on a formal description of their conditions. Comput. Tools Educ. 2006, 4, 51–57. [Google Scholar]
- Perchenok, O.V.; Pozdnyakov, S.N.; Posov, I.A. Automation of checking solutions of geometric problems to describe their conditions in a subject-oriented language. Comput. Tools Educ. 2012, 1, 31–38. [Google Scholar]
- Zaykov, D.; Pozdniakov, S. Wise Tasks Graphs System. In Proceedings of the Polynomial Computer Algebra 2022, Euler International Mathematical Institute, St. Petersburg, Russia, 2–7 May 2022. [Google Scholar]
- Minsky, M. The Society of Mind; Simon and Schuster: New York, NY, USA, 1986. [Google Scholar]
- Pozdniakov, S. Proceedings of the PME and Yandex Russian Conference: Technology and Psychology for Mathematics Education; SU HSE Publishing House: Moscow, Russia, 2019. [Google Scholar]
- DiSessa, A.A. Bird’s Eye Conceptual Change. In International Handbook of Research on Conceptual Change, 2nd ed.; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Lavrenov, A.; Tolkacheva, E.; Pozdniakov, S. Computational “Accompaniment” of the Introduction of New Mathematical Concepts. Computation 2023, 11, 194. [Google Scholar] [CrossRef]

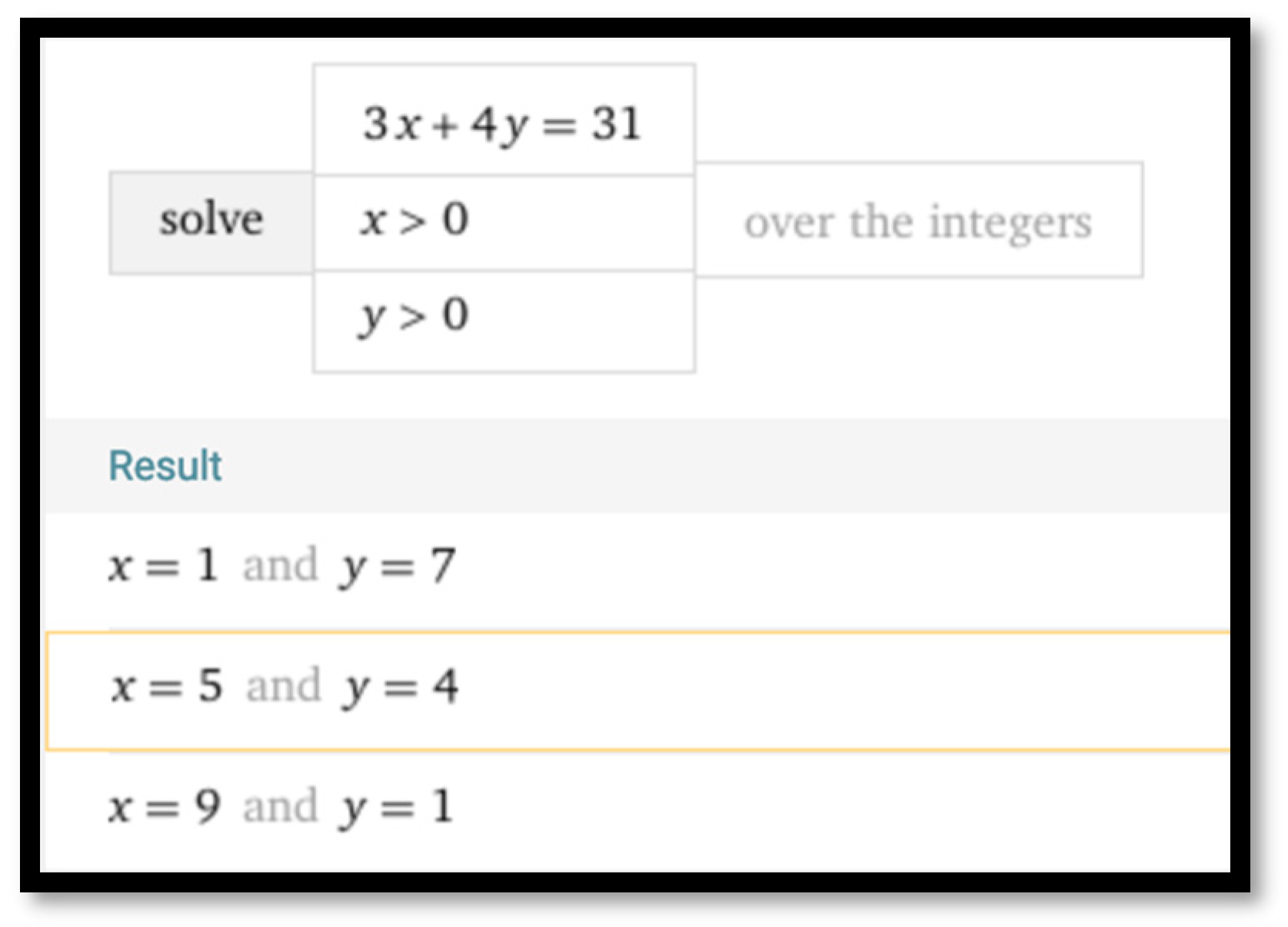

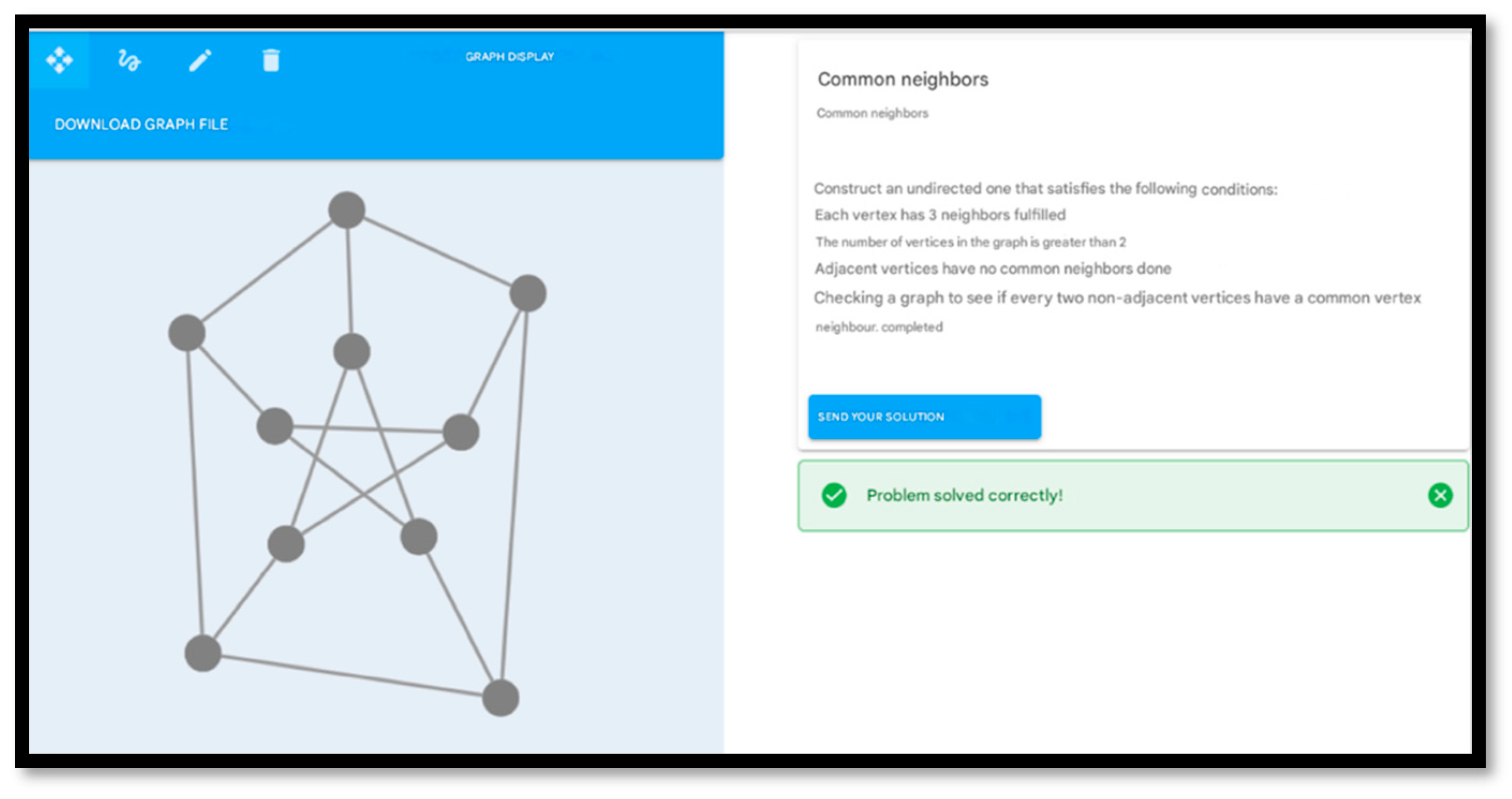
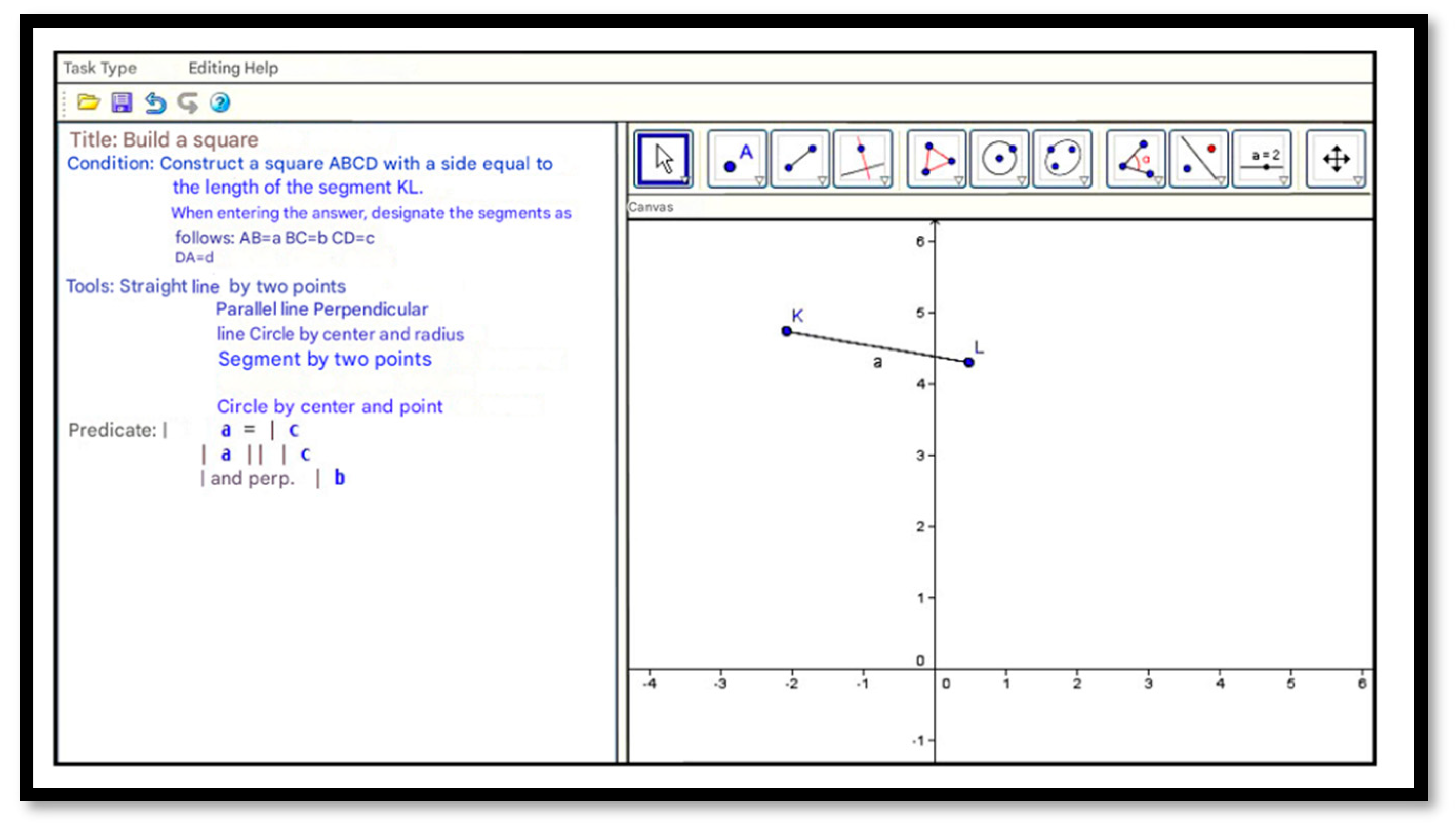
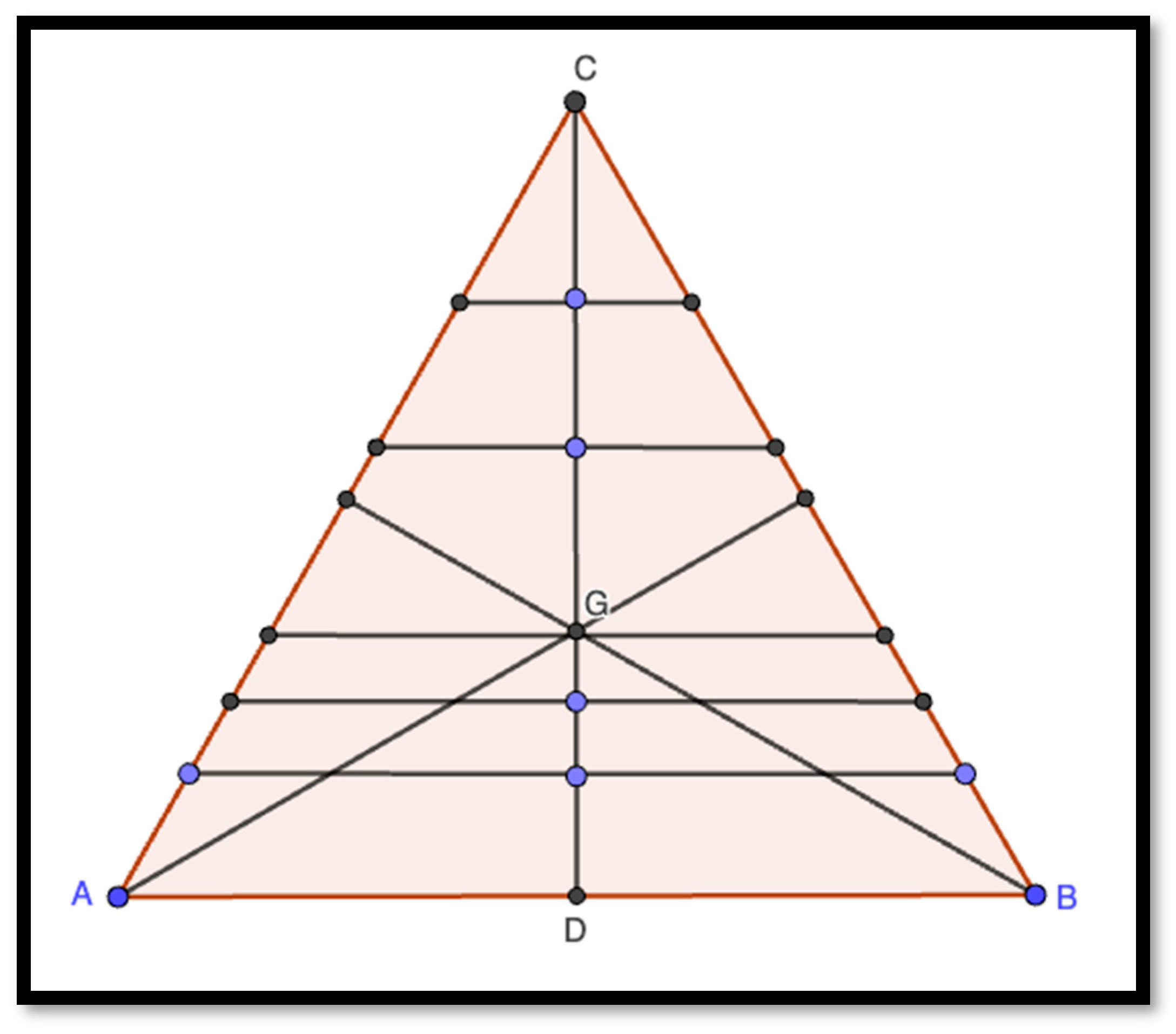

| Software | Educational Uses | Cost | Free On-Line | Used in the Paper |
|---|---|---|---|---|
| Wolfram Alpha https://wolframalpha.com (accessed on 25 August 2025) | Computational knowledge engine | PRO versions (for everyone, students, educators) | Available | Advanced symbolic computations |
| The Graphing Calculator (version 4.1(5), 2018, Pacific Tech, El Cerrito, CA, USA) | Computer graphing | License required | Paid | Digital fabrication and graphing |
| Desmos | Computer graphing | Free | Available | Not used |
| GeoGebra (version 4.2, 2025, GeoGebra GmbH, Linz, Austria) | Dynamic geometry constructions | Free | Available | Wise Tasks Geometry Center of gravity construction |
| The Geometer’s Sketchpad | Dynamic geometry constructions | License required | Paid | Not used |
| Excel spreadsheet (version 16.100.2, Microsoft Corporation, Redmond, WA, USA) | Multiple | Part of Microsoft Office package | Free for students | Numeric modeling and data analysis |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abramovich, S.; Malyutin, E.; Pozdniakov, S. Mathematization Through Application and Common Sense: Motivating Intellectual Activities of Schoolchildren with Digital Tools. Digital 2025, 5, 41. https://doi.org/10.3390/digital5030041
Abramovich S, Malyutin E, Pozdniakov S. Mathematization Through Application and Common Sense: Motivating Intellectual Activities of Schoolchildren with Digital Tools. Digital. 2025; 5(3):41. https://doi.org/10.3390/digital5030041
Chicago/Turabian StyleAbramovich, Sergei, Egor Malyutin, and Sergei Pozdniakov. 2025. "Mathematization Through Application and Common Sense: Motivating Intellectual Activities of Schoolchildren with Digital Tools" Digital 5, no. 3: 41. https://doi.org/10.3390/digital5030041
APA StyleAbramovich, S., Malyutin, E., & Pozdniakov, S. (2025). Mathematization Through Application and Common Sense: Motivating Intellectual Activities of Schoolchildren with Digital Tools. Digital, 5(3), 41. https://doi.org/10.3390/digital5030041








