A Robust Hybrid CNN–LSTM Model for Predicting Student Academic Performance
Abstract
1. Introduction
- We developed a hybrid deep learning model that combines CNN and LSTM to enhance predictive accuracy in student performance.
- We improved data preprocessing by implementing strategies to address key challenges such as data imbalance and missing values.
- We incorporated advanced optimization and regularization techniques for improved prediction accuracy.
- We compared our model to others, including some of the highest-rated models in the literature.
2. Related Works
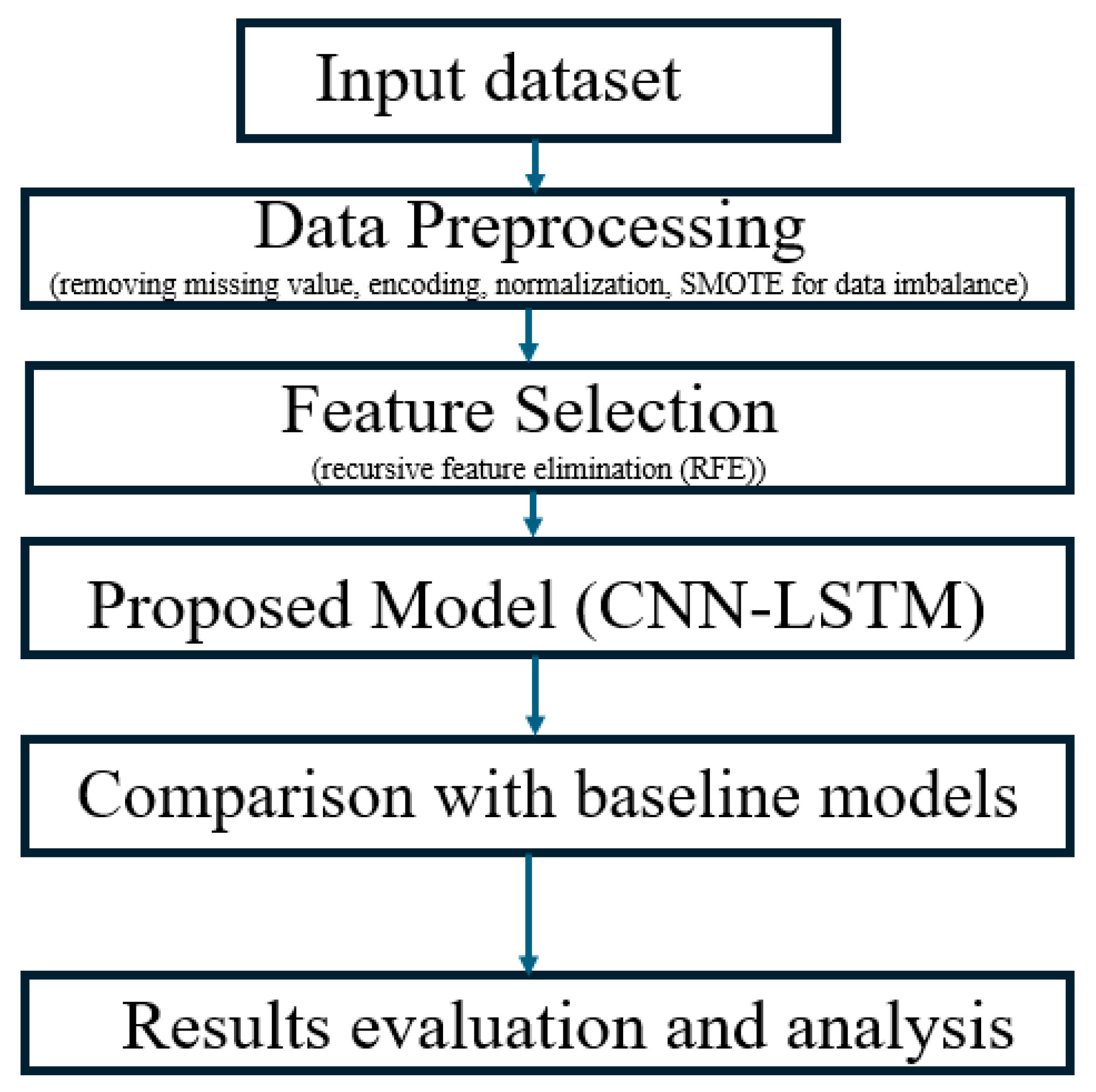
3. Materials and Methods
3.1. Description of the Datasets
3.1.1. Open University Learning Analytics Dataset (OULAD)
3.1.2. Western Ontario University (WOU) Dataset
3.2. Data Preprocessing
3.3. Proposed CNN–LSTM Model
3.3.1. Convolutional Neural Network (CNN)
3.3.2. Long Short-Term Memory (LSTM) Network
3.4. Model Tuning
3.5. Baseline Methods
| Algorithm 1: CNN–LSTM Model |
| Split data into training and testing sets: Input: x_train.shape [1] Output: Metrics Initialization: Define sequential model: model = Sequential () Add Conv1D, (filters, kernel size, activation, MaxPooling1D, LSTM, dropout, Dense) Model Compile optimizer, learning rate, epochs, batch size For epochs = 1 to n do while train model validate model monitor = ‘loss’ adjust loss function using categorical cross-entropy end while end for Evaluate Model Perform prediction using the model Calculate metrics |
3.6. Performance Metrics
3.6.1. Accuracy
3.6.2. Precision
3.6.3. Recall (Sensitivity)
3.6.4. F-Score
4. Results and Discussion
4.1. Proposed CNN–LSTM Model Performance Using the OULAD Dataset
4.2. Proposed CNN–LSTM Model’s Performance Using the WOU Dataset
4.3. Proposed Model Training and Prediction Time
4.4. Significant Test Results Interpretation
4.5. Proposed Model Performance Comparison with Results from Similar Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional neural network |
| EDM | Educational data mining |
| DL | Deep learning |
| DNN | Deep neural network |
| LSTM | Long short-term memory |
| OULAD | Open University Learning Analytics Dataset |
| WOU | Western Ontario University |
References
- Pelima, L.R.; Sukmana, Y.; Rosmansyah, Y. Predicting university student graduation using academic performance and machine learning: A systematic literature review. IEEE Access 2024, 12, 23451–23465. [Google Scholar] [CrossRef]
- Angeioplastis, A.; Aliprantis, J.; Konstantakis, M.; Tsimpiris, A. Predicting Student Performance and Enhancing Learning Outcomes: A Data-Driven Approach Using Educational Data Mining Techniques. Computers 2025, 14, 83. [Google Scholar] [CrossRef]
- Ashish, L.; Anitha, G. Transforming Education: The Impact of ICT and Data Mining on Student Outcomes. In Proceedings of the 2024 7th International Conference on Circuit Power and Computing Technologies (ICCPCT), Kollam, India, 8–9 August 2024; Volume 1, pp. 675–683. [Google Scholar]
- Malik, S.; Patro, S.G.K.; Mahanty, C.; Hegde, R.; Naveed, Q.N.; Lasisi, A.; Buradi, A.; Emma, A.F.; Kraiem, N. Advancing Educational Data Mining for Enhanced Student Performance Prediction: A Fusion of Feature Selection Algorithms and Classification Techniques with Dynamic Feature Ensemble Evolution. Sci. Rep. 2025, 15, 8738. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.; Ray, S.; Khan, M.T.; Nawaz, A. Student Performance Prediction with Decision Tree Ensembles and Feature Selection Techniques. J. Inf. Knowl. Manag. 2025, 24, 2550016. [Google Scholar] [CrossRef]
- Rogers, J.K.; Mercado, T.C.; Cheng, R. Predicting Student Performance Using Moodle Data and Machine Learning with Feature Importance. Indones. J. Electr. Eng. Comput. Sci. 2025, 37, 223–231. [Google Scholar] [CrossRef]
- Mohammad, A.S.; Al-Kaltakchi, M.T.; Alshehabi Al-Ani, J.; Chambers, J.A. Comprehensive evaluations of student performance estimation via machine learning. Mathematics 2023, 11, 3153. [Google Scholar] [CrossRef]
- Bisri, A.; Heryatun, Y.; Navira, A. Educational Data Mining Model Using Support Vector Machine for Student Academic Performance Evaluation. J. Educ. Learn. (EduLearn) 2025, 19, 478–486. [Google Scholar] [CrossRef]
- Badal, Y.T.; Sungkur, R.K. Predictive modelling and analytics of students’ grades using machine learning algorithms. Educ. Inf. Technol. 2023, 28, 3027–3057. [Google Scholar] [CrossRef]
- Pu, H.; Fan, M.; Zhang, H.; You, B.; Lin, J.; Liu, C.; Zhao, Y.; Song, R. Predicting academic performance of students in Chinese-foreign cooperation in running schools with graph convolutional network. Neural Comput. Appl. 2021, 33, 637–645. [Google Scholar]
- Poudyal, S.; Mohammadi-Aragh, M.J.; Ball, J.E. Prediction of student academic performance using a hybrid 2D CNN model. Electronics 2022, 11, 1005. [Google Scholar] [CrossRef]
- Wang, X.; Yu, X.; Guo, L.; Liu, F.; Xu, L. Student performance prediction with short-term sequential campus behaviors. Information 2020, 11, 201. [Google Scholar] [CrossRef]
- Mengash, H.A. Using data mining techniques to predict student performance to support decision making in university admission systems. IEEE Access 2020, 8, 55462–55470. [Google Scholar] [CrossRef]
- Asselman, A.; Khaldi, M.; Aammou, S. Enhancing the prediction of student performance based on the machine learning xgboost algorithm. Interact. Learn. Environ. 2023, 31, 3360–3379. [Google Scholar] [CrossRef]
- Turabieh, H.; Azwari, S.A.; Rokaya, M.; Alosaimi, W.; Alharbi, A.; Alhakami, W.; Alnfiai, M. Enhanced harris hawks optimization as a feature selection for the prediction of student performance. Computing 2021, 103, 1417–1438. [Google Scholar] [CrossRef]
- Yousafzai, B.K.; Khan, S.A.; Rahman, T.; Khan, I.; Ullah, I.; Ur Rehman, A.; Baz, M.; Hamam, H.; Cheikhrouhou, O. Student-performulator: Student academic performance using hybrid deep neural network. Sustainability 2021, 13, 9775. [Google Scholar] [CrossRef]
- Mahareek, E.A.; Desuky, A.S.; El-Zhni, H.A. Simulated annealing for svm parameters optimization in student’s performance prediction. Bull. Electr. Eng. Inform. 2021, 10, 1211–1219. [Google Scholar] [CrossRef]
- Yağcı, M. Educational data mining: Prediction of students’ academic performance using machine learning algorithms. Smart Learn. Environ. 2022, 9, 11. [Google Scholar] [CrossRef]
- Keser, S.B.; Aghalarova, S. Hela: A novel hybrid ensemble learning algorithm for predicting academic performance of students. Educ. Inf. Technol. 2022, 27, 4521–4552. [Google Scholar] [CrossRef]
- Alarape, M.A.; Ameen, A.O.; Adewole, K.S. Hybrid students’ academic performance and dropout prediction models using recursive feature elimination technique. In Advances on Smart and Soft Computing; Springer: Singapore, 2022; pp. 93–106. [Google Scholar]
- Kuzilek, J.; Hlosta, M.; Zdrahal, Z. Open University learning analytics dataset. Sci. Data 2017, 4, 170171. [Google Scholar] [CrossRef]
- Jin, L.; Wang, Y.; Song, H.; So, H.J. Predictive Modelling with the Open University Learning Analytics Dataset (OULAD): A Systematic Literature Review. In Proceedings of the International Conference on Artificial Intelligence in Education, Recife, Brazil, 8–12 July 2024; Springer Nature: Cham, Switzerland, 2024; pp. 477–484. [Google Scholar]
- Injadat, M.; Moubayed, A.; Nassif, A.B.; Shami, A. Systematic ensemble model selection approach for educational data mining. Knowl.-Based Syst. 2020, 200, 105992. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, C.; Mukherjee, T.; Pasiliao, E. Feature representations using the reflected rectified linear unit (RReLU) activation. Big Data Min. Anal. 2020, 3, 102–120. [Google Scholar] [CrossRef]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent neural networks: A comprehensive review of architectures, variants, and applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Adefemi Alimi, K.O.; Ouahada, K.; Abu-Mahfouz, A.M.; Rimer, S.; Alimi, O.A. Refined LSTM Based Intrusion Detection for Denial-of-Service Attack in Internet of Things. J. Sens. Actuator Netw. 2022, 11, 32. [Google Scholar] [CrossRef]
- Shiri, F.M.; Perumal, T.; Mustapha, N.; Mohamed, R. A comprehensive overview and comparative analysis on deep learning models: CNN, RNN, LSTM, GRU. arXiv 2023, arXiv:2305.17473. [Google Scholar]
- Fang, W.; Chen, Y.; Xue, Q. Survey on research of RNN-based spatio-temporal sequence prediction algorithms. J. Big Data 2021, 3, 97. [Google Scholar] [CrossRef]
- Gaur, D.; Kumar Dubey, S. Development of activity recognition model using lstm-rnn deep learning algorithm. J. Inf. Organ. Sci. 2022, 46, 277–291. [Google Scholar]



| Article | Model | Performance (Acc) |
|---|---|---|
| Hai-tao et al. [10] | Graph CNN | 81.5% |
| Poudyal et al. [11] | CNN | 88% |
| Wang et al. [12] | SVM and RNN | 86.9% |
| Mengash et al. [13] | ANN, DT, SVM, NB | 79% |
| Asselman et al. [14] | RF, Adaboost, XGBoost | 78.25%, 78.30%, and 78.75% |
| Turabieh et al. [15] | Harris Hawks Optimization (HHO) Algorithm and Layered RNN | 92% |
| Yousafzai et al. [16] | Attention based-BILSTM | 90.16% |
| Mahareek et al. [17] | SVM | 67.77% |
| Yağcı et al. [18] | SVM, NB, KNN, LR, RF | 70% |
| Keser et al. [19] | GB, XGB, LGB | 96.6% and 91.2% |
| Alarape et al. [20] | SVM and NB | 92.73% and 89.09% |
| Module | Domain | Presentations | Students |
|---|---|---|---|
| AAA | Social Sciences | 2 | 748 |
| BBB | Social Sciences | 4 | 7909 |
| CCC | STEM | 2 | 4434 |
| DDD | STEM | 4 | 6272 |
| Parameters | Configuration/Value |
| Learning rate | 0.001 |
| Number of epochs | 10 |
| Batch sizes | 32 |
| Activation function | ReLU and Softmax |
| Loss function | Categorical cross-entropy |
| Optimization algorithm | Adam optimizer |
| Hyperparameter optimization | Random search |
| Dropout rate | 0.5 |
| Regularization techniques | Dropout technique |
| Model | Accuracy | Precision | Recall | F-Score |
|---|---|---|---|---|
| DNN | 92.20 | 91.70 | 92.00 | 91.90 |
| CNN | 96.10 | 96.13 | 96.01 | 95.19 |
| LSTM | 97.62 | 97.61 | 97.62 | 97.61 |
| CNN–LSTM | 98.93 | 98.93 | 98.93 | 98.93 |
| Model | Accuracy | Precision | Recall | F-Score |
|---|---|---|---|---|
| DNN | 86.52 | 88.84 | 86.38 | 87.59 |
| CNN | 92.20 | 91.80 | 92.00 | 91.90 |
| LSTM | 96.00 | 97.45 | 96.00 | 92.60 |
| CNN–LSTM | 98.82 | 97.53 | 97.61 | 97.56 |
| Model | Training Time (s) | Prediction Time (s) |
|---|---|---|
| DNN | 0.10 | 0.09 |
| CNN | 0.12 | 0.08 |
| LSTM | 0.14 | 0.08 |
| CNN–LSTM | 0.14 | 0.06 |
| Model | Accuracy | 95% Confidence Interval |
|---|---|---|
| DNN | 92.20 | [90.9%, 93.5%] |
| CNN | 96.10 | [95.1%, 97.0%] |
| LSTM | 97.62 | [96.9%, 98.3%] |
| CNN–LSTM | 98.93 | [98.5%, 99.3%] |
| Articles | Model | Accuracy (%) | Precision (%) | Recall (%) | F-Score (%) |
|---|---|---|---|---|---|
| [10] | GCNN | 81.5 | - | - | - |
| [13] | ANN | 79.22 | 81.44 | 78.03 | 79.70 |
| [16] | BiLSTM-AM | 90.16 | 90 | 90 | 90 |
| [19] | GB, XGBoost, and LightGBM | 92.40, 94.13, 89.07 | - | - | 92.32, 94.00, 88.91 |
| [11] | CNN | 88 | - | - | - |
| [12] | SVM-RNN | 86.90 | - | 81.57 | - |
| [18] | NN and RF | 74.6 | 74.8 | 74.6 | 72.3 |
| Our Work | DNN | 92.20 | 91.70 | 92.00 | 91.90 |
| CNN | 96.10 | 96.13 | 96.01 | 95.19 | |
| LSTM | 97.62 | 97.61 | 97.62 | 97.61 | |
| CNN–LSTM | 98.93 | 98.93 | 98.93 | 98.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adefemi, K.O.; Mutanga, M.B. A Robust Hybrid CNN–LSTM Model for Predicting Student Academic Performance. Digital 2025, 5, 16. https://doi.org/10.3390/digital5020016
Adefemi KO, Mutanga MB. A Robust Hybrid CNN–LSTM Model for Predicting Student Academic Performance. Digital. 2025; 5(2):16. https://doi.org/10.3390/digital5020016
Chicago/Turabian StyleAdefemi, Kuburat Oyeranti, and Murimo Bethel Mutanga. 2025. "A Robust Hybrid CNN–LSTM Model for Predicting Student Academic Performance" Digital 5, no. 2: 16. https://doi.org/10.3390/digital5020016
APA StyleAdefemi, K. O., & Mutanga, M. B. (2025). A Robust Hybrid CNN–LSTM Model for Predicting Student Academic Performance. Digital, 5(2), 16. https://doi.org/10.3390/digital5020016






