Physics Guided Neural Networks with Knowledge Graph

Abstract

Over the past few decades, machine learning (ML) has demonstrated significant advancements in all areas of human existence. Machine learning and deep learning models rely heavily on data. Typically, basic machine learning (ML) and deep learning (DL) models receive input data and its matching output. Within the model, these models generate rules. In a physics-guided model, input and output rules are provided to optimize the model’s learning, hence enhancing the model’s loss optimization. The concept of the physics-guided neural network (PGNN) is becoming increasingly popular among researchers and industry professionals. It has been applied in numerous fields such as healthcare, medicine, environmental science, and control systems. This review was conducted using four specific research questions. We obtained papers from six different sources and reviewed a total of 81 papers, based on the selected keywords. In addition, we have specifically addressed the difficulties and potential advantages of the PGNN. Our intention is for this review to provide guidance for aspiring researchers seeking to obtain a deeper understanding of the PGNN.

1. Introduction

A hybrid modeling technique called physics-guided neural network (PGNN) uses data and physical knowledge to train machine learning (ML) models, especially neural networks. The goal of classical machine learning, particularly data-driven models, is to derive correlations and patterns directly from the data. These data-driven models, however, tend to be inconsistent and data-hungry [1].

There are two methods for incorporating physics into a machine-learning model. Firstly, enhance the input data by using feature engineering techniques, which include estimating extra features based on principles derived from physics theory. Secondly, include a physical inconsistency term into the loss function to serve as a regularization mechanism, imposing penalties on physically inconsistent predictions. The integration of these methodologies results in the development of a unique algorithm called physics-guided neural network (PGNN). PGNNs can achieve generalization more effectively since physics models are not as dependent on individual data distributions. Furthermore, PGNNs provide a valuable contribution to the current endeavors in Explainable AI (XAI) by generating findings that are both physically consistent and easily understandable, hence improving the interpretability of the model. Because of the PGNN’s influence on model optimization and adaptability in the domain, we have decided to do this review. A sample figure shows in  Figure 1 as PGNN structure.

By fusing data-driven methods with the advantages of physics-driven models, PGNN aims to overcome this. A PGNN is created when ML models are trained using a combination of physical and mathematical information [2]. The goal of incorporating physics-based limitations, formulas, or concepts into the learning process is to improve the interpretability, dependability, and performance of the model.

In certain cases, data-driven models could perform better than physics-driven models, although they might not be consistent or might need a lot of data [3]. PGNN aims to combine data and physics expertise to provide the best of both worlds. This works especially well in situations when gathering a lot of training data is difficult or costly.

There are two steps [4] in the process of using a physics-guided neural network (PGNN). First, they build hybrid physics–data (HPD) models, which are hybrid models made by fusing neural networks with physics-based models. Second, the learning goal of the neural network is trained using physics-based loss functions that are created using scientific knowledge.

Physics-guided neural network (PGNN) models are a cutting-edge deep learning technique that integrates physics ideas into neural network topologies [5]. PGNNs create a new way of doing things called theory-guided data science. This is different from traditional black-box algorithms because it tries to limit and explain model predictions from a physics point of view [6]. PGNNs combine scientific knowledge with data science techniques to eliminate physical disparities and bridge the gap between empirical data and theoretical understanding.

Creating a PGNN requires three essential steps:

• To construct a hybrid system, physics-based model knowledge and neural networks are combined.
• The learning aim of the neural network is achieved by using scientific knowledge as a physics-based loss function.
• Optimizing empirical loss and physical consistency in model training.

PGNNs leverage physical principles to overcome the limitations of either data-driven or strictly physical models. They embed physics-based equations into the loss function to guarantee that model predictions adhere to accepted physical boundaries. By combining theoretical concepts with actual data, PGNNs increase generalization performance and provide interpretable model outputs, facilitating communication between data scientists and domain specialists.

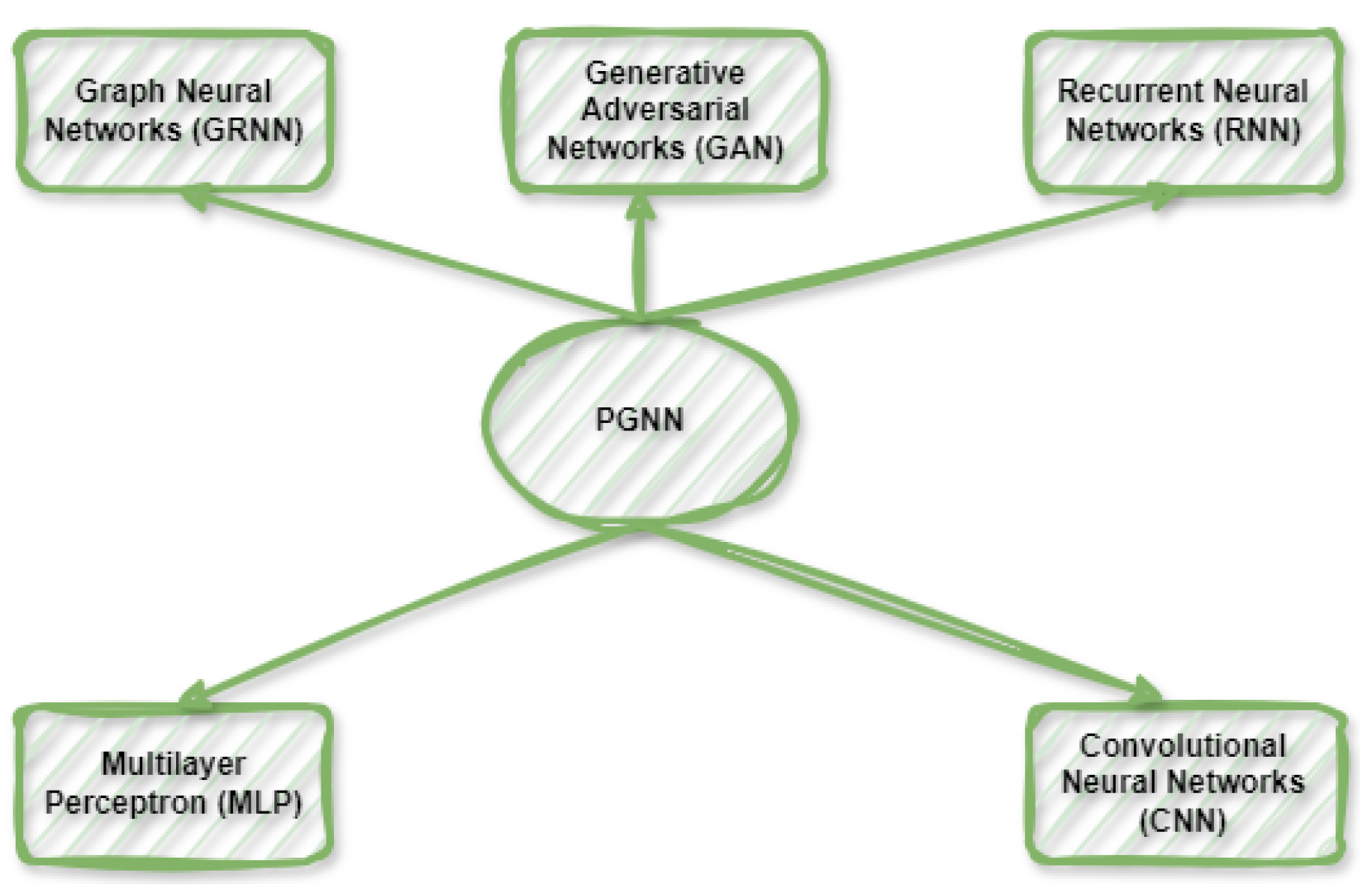
2. Type of PGNN

Physics-guided neural networks (PGNNs) utilize supervised deep learning (DL) models to incorporate the known physics of a phenomenon. Extraction of intricate features from carefully controlled experiments or computer simulations allows for this. PGNNs employ various neural network topologies [7]. A figure illustrating the types of PGNN is shown below in Figure 2.

The intelligent combination of these diverse neural network types enhances the model’s capability to identify and convey intricate links present in the data. PGNNs can quickly learn and use the physical rules that govern the observed events by combining different neural network topologies [8].

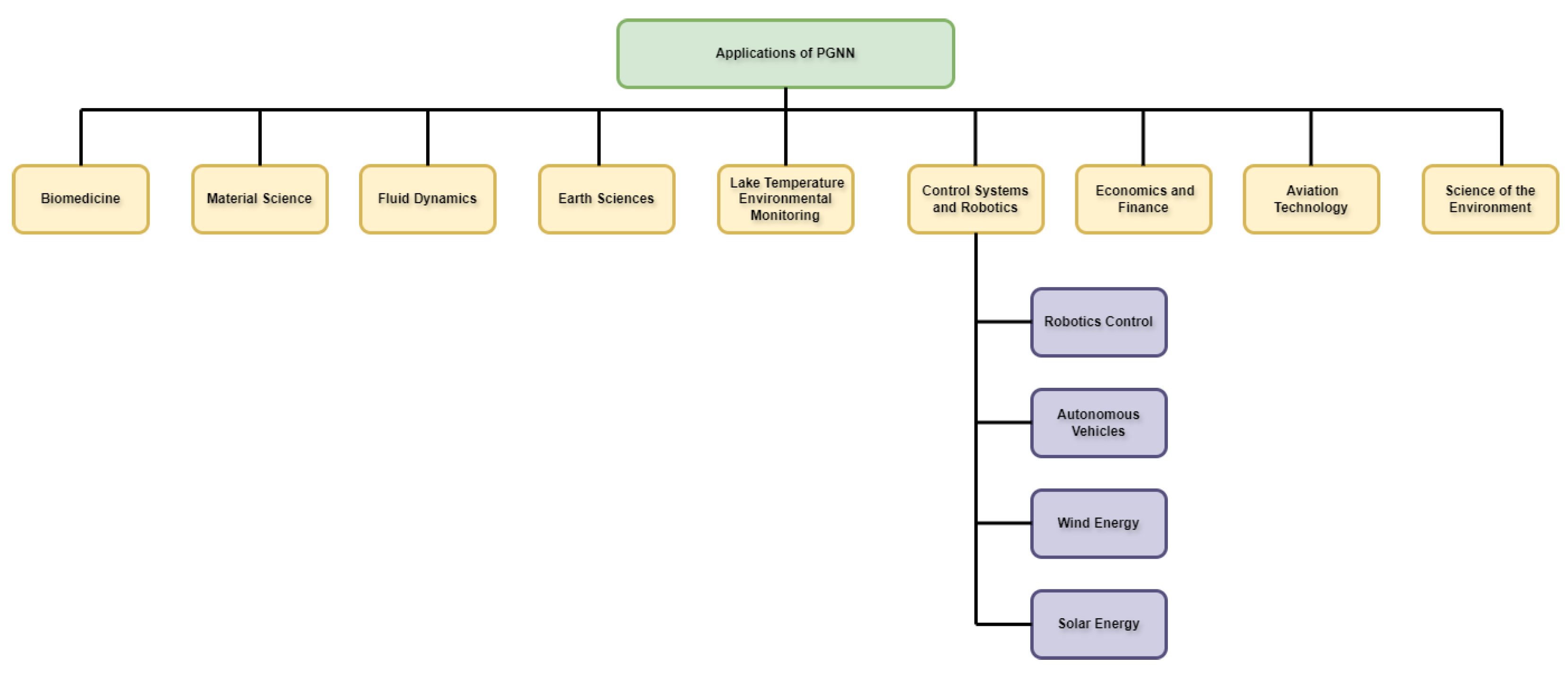
3. Application of PGNN

PGNN has a huge application area. An example of an application is provided in Figure 3.

3.1. Biomedicine

• Drug discovery using predictive modeling.
• Using medical data to forecast patient outcomes.
• Medical diagnostics and image analysis [3].

3.2. Material Science

• Forecasting characteristics and actions of materials.
• Increasing the rate of material discovery.
• Enhancing the methods for synthesizing materials.

3.3. Fluid Dynamics

• Fluid flow pattern modeling and prediction [9].
• Heat transfer and turbulence simulation.
• Creating more aerodynamically efficient systems.

3.4. Earth Sciences

• Forecasting the effects of climate change.
• Examining and simulating geological mechanisms.
• Examining how environments impact ecosystems.

3.5. Lake Temperature Environmental Monitoring

• Monitoring and predicting the temperature of lakes [4].
• Comprehending the effects of global warming on aquatic environments.

3.6. Control Systems and Robotics

• Robotics control: To improve motion planning and control tactics, PGNNs may be used in robotic control systems.
• Autonomous vehicles: By taking into account environmental influences and physical limitations, PGNNs help forecast and optimize the behavior of autonomous vehicles [10].
• Wind energy: PGNNs help maximize energy efficiency in wind turbine installation and design.
• Solar energy: By predicting solar panel performance in response to environmental conditions, PGNNs may help maximize the harvesting of solar energy [11].

3.7. Economics and Finance

• Stock market prediction: By combining market dynamics and economic concepts, PGNNs are utilized to model and forecast stock market movements.
• Financial risk management: By taking into account the influence of several economic aspects, PGNNs help improve risk assessment models in finance.
• Image reconstruction: By combining physical limitations, PGNNs used in computer vision may enhance image reconstruction, producing sharper and more accurate pictures.
• 3D object identification: By using physical characteristics and limitations throughout the learning process, PGNNs help with 3D object identification.

3.8. Aviation Technology

• Structural health monitoring: to guarantee dependability and safety, PGNNs are able to forecast and track the structural health of aircraft and spacecraft components [12].
• Flight control systems: by taking system dynamics and aerodynamics into account, PGNNs help to optimize flight control systems [12].

3.9. Science of the Environment

• Air quality prediction: pollutant emissions, weather patterns, and geographic characteristics are among the variables that PGNNs are utilized to model and forecast air quality.
• Ecological modeling: by forecasting how changes in the environment would affect biodiversity, PGNNs help model ecological systems.

It is important to note that PGNNs are not only used in these fields; in fact, scientists are always looking into new ones where physics-based modeling and neural networks may work together to provide more insightful and accurate predictions. PGNNs’ multidisciplinary character enables them to be used to a wide range of scientific and engineering issues involving the interaction of intricate data patterns and physical rules.

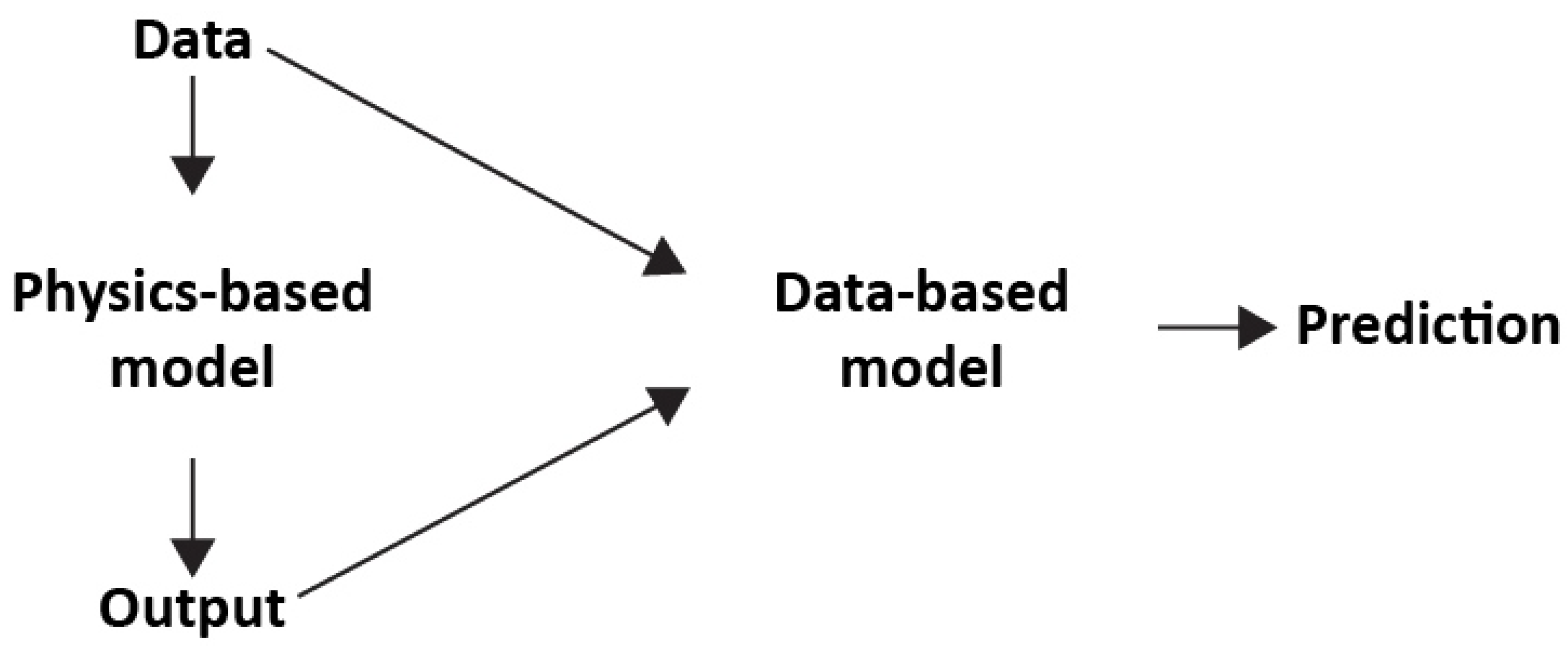
4. Constructing Hybrid Physics–Data Models

There are two main steps in physics-guided neural networks (PGNN): (a) creating hybrid models that combine physics-based models and neural networks; these are called hybrid physics data (HPD) models; and (b) using scientific knowledge as physics-based loss functions in the learning process of neural networks.

Constructing hybrid physics–data models begins with a predictive learning scenario where a set of input drivers, D, are physically linked to a target variable, Y. Typically, a neural network model, $f_{\mathrm{NN}}:D\to Y$, is trained over a dataset to estimate the target variable, $\widehat{Y}$. Alternatively, a physics-based numerical model, $f_{\mathrm{PHY}}:D\to Y$, can simulate the target variable, $Y_{\mathrm{PHY}}$, based on its physical associations with the input drivers. However, calibrating physics-based models often demands laborious parameter adjustments using observational data, and $Y_{\mathrm{PHY}}$ might offer an incomplete depiction of the target variable due to simplified or missing physics, leading to discrepancies with observations. Consequently, the fundamental aim of HPD modeling is to amalgamate $f_{\mathrm{PHY}}$ and $f_{\mathrm{NN}}$ to mitigate their inherent shortcomings and exploit the information from both physics and data.

A key equation in constructing this model is

$$f_{\mathrm{HPD}}:X=[D,Y_{\mathrm{PHY}}]\to Y,$$

where the input X consists of both the observed drivers D and the simulated physics-based outputs $Y_{\mathrm{PHY}}$.

This hybrid physics–data model (HPD) learns the mapping from the combined input $[D,Y_{\mathrm{PHY}}]$ to the target variable Y. The physics-based output $Y_{\mathrm{PHY}}$ is crucial for injecting physical knowledge into the learning process. This enables the model to correct any potential biases or errors in the pure physics model and improve generalization through the data-driven learning provided by the neural network. The HPD model may predict $\widehat{Y}=Y_{\mathrm{PHY}}$, assuming the physics-based model is accurate and $Y_{\mathrm{PHY}}$ fits well with the observations of Y. However, the HPD model, $f_{\mathrm{HPD}}$, has the capacity to adjust for any systematic errors in $Y_{\mathrm{PHY}}$ by extracting intricate features from the space of input drivers. This process bridges knowledge gaps and enhances the overall model performance.

Through the combined use of data-driven neural networks and physics-based simulations, HPD models are able to provide predictions that are more resilient to physical limitations and flexible enough to be applied to actual data.

5. Enhancing Model Training with Physics-Based Loss Functions

In traditional HPD model training, model complexity is controlled while the empirical loss of the model’s predictions $\widehat{Y}$ on the training set is minimized. However, the size of the labeled training set, which is often restricted in scientific situations, limits the efficacy of this strategy. Furthermore, models educated just on empirical loss could not follow the laws of physics. In order to solve this, data science models are guided toward physically compatible answers via the use of physics-based loss functions.

Equations $G(Y,Z)=0$ and $H(Y,Z)\le 0$ represent the physical connections the target variable Y has with other physical variables Z. These equations, which can involve either partial differentials or algebraic operations, illustrate essential principles of physics. $Loss.P_{HY}$, a physics-based loss function, assesses whether model predictions $\widehat{Y}$ contradict certain physics-based equations:

$$Loss.P_{HY}\left(\widehat{Y}\right)=\left|\right|G(\widehat{Y},Z){\left|\right|}_2+\mathrm{ReLU}\left(H(\widehat{Y},Z)\right)$$

where $\mathrm{ReLU}(.)$ represents the rectified linear unit function. The term $G(\widehat{Y},Z)$ expresses equality-based physical relationships, while $H(\widehat{Y},Z)\le 0$ represents inequality constraints. The term $|G(\widehat{Y},Z){|}^2$ penalizes deviations of the model predictions $\widehat{Y}$ from the physical equality constraints. The term $\mathrm{ReLU}\left(H(\widehat{Y},Z)\right)$ enforces inequality constraints, ensuring that only positive violations contribute to the loss, thereby guiding the model to stay within physically valid regions.

Unlike traditional loss functions, $Loss.P_{HY}$ can be computed without requiring actual observations of the target variable, Y, allowing its evaluation on unlabeled data instances. This ability to assess $Loss.P_{HY}$ on unlabeled data makes it a powerful tool for guiding the model to adhere to physical laws even in cases with sparse or incomplete data.

Minimizing empirical loss, model complexity, and physical inconsistency is the overall learning goal of PGNN, which incorporates $Loss.P_{HY}$ as follows:

$$arg\underset{f}{min}\mathrm{Loss}(\widehat{Y},Y)+\lambda R\left(f\right)+{\lambda }_{\mathrm{PHY}}Loss.P_{HY}\left(\widehat{Y}\right)$$

Here, the following is true:

• $\mathrm{Loss}(\widehat{Y},Y)$ represents the empirical loss, typically a mean squared error or cross-entropy, which measures how closely the model predictions $\widehat{Y}$ match the actual target Y from the data.
• $R\left(f\right)$ is a regularization term that controls model complexity, preventing overfitting.
• The hyper-parameter ${\lambda }_{\mathrm{PHY}}$ determines the relative importance of reducing physical inconsistency compared with minimizing empirical loss and model complexity.

By ensuring that model outputs conform to established physical laws, PGNNs can achieve superior generalization, even in scenarios with limited or incomplete training data. Moreover, the model’s outputs are comprehensible to subject matter experts, thereby promoting scientific advancement. To minimize this objective, various optimization techniques, including stochastic gradient descent (SGD) and its variants, can be utilized, employing automated differentiation for efficient gradient computation.

6. How PGNNs Work

Physics-guided neural networks (PGNNs) use a hybrid technique to improve prediction accuracy while maintaining compatibility with well-established scientific principles. Specifically, they integrate neural networks with models based on physics. The elements and functionality of PGNNs are described in this synopsis.

6.1. Components

• Physics-based models: These simulations of physical processes, such as heat transport, fluid dynamics, or quantum mechanics, incorporate domain-specific information.
• Neural networks: Neural networks are universal function approximators that are capable of learning complex mappings between input characteristics and predicted outputs.

6.2. Hybrid Setup

PGNNs use a hybrid framework consisting of the following components:

• Observational features and physics-based simulations: PGNNs use both empirical data and results from physics-based simulations, making the most of each knowledge source.
• Neural network architecture: Integrate with the combined input of simulated outputs and observational characteristics, a customized neural network architecture is created. This allows the model to provide predictions that combine theoretical understanding with empirical observations.
• Physics-based loss functions: The neural network’s learning goal incorporates these loss functions. They improve accuracy and consistency by directing the training process to generate predictions that comply with accepted physics rules by encoding well-known physical principles.

PGNNs provide predictions that are correct and based on basic scientific principles by combining the explanatory power of physics-based models with the adaptability of neural networks. Concerning established physics, this integration allows PGNNs to address a broad spectrum of challenging issues in several domains.

7. Comparison with Other Approaches

In order to accomplish this integration, we clarify three [7] different frameworks.

Table 1. Comparison of PgNN, PiNN, and PeNN Frameworks.

Aspect	PGNN	PiNN	PENN
Definition	Neural networks that incorporate physical principles into their training to model complex phenomena.	Designed to solve PDEs by incorporating physical laws into the training process.	Combines the strengths of PgNN and PiNN, allowing hard-encoded prior knowledge while being adaptable to physical scenarios.
Applications	Structural analysis, topology optimization, health condition assessment, fluid mechanics, solid mechanics, etc.	Fluid mechanics, fluid dynamics, neural particle methods. Advanced variants include PhySRNet, PDDO-PiNN, PiELM, DPiNN, and PiNN-FEM for computational mechanics.	Effective in modeling complex material responses and damage, as well as in extrapolation tasks.
Advantages	Can effectively utilize sparse data and incorporate physical constraints to model complex phenomena.	Can deduce governing equations and unknown boundary conditions, improving predictive capabilities.	Demonstrates superior performance in accuracy and computational efficiency compared with PgNN and PiNN.
Limitations	Statistics-based training, sparse datasets, interpolation issues, boundary condition challenges, resolution-dependent, average solutions, diversity struggles.	Training complexity, convergence issues, generalization limitations, high computational cost, inverse problem difficulty.	Geometry restrictions, overfitting, training complexity, implementation difficulty, memory cost, initial setup.
Experimental Case Study	Tadesse et al. [13] predicted mid-span deflections in composite bridges using ANN with a maximum RMSE of 3.79%. Hung et al. [14] applied ANN to predict the ultimate load factor in a non-linear steel truss with high accuracy.	Cheng and Zhang [15] developed Res-PiNN for fluid simulation with superior results over traditional PiNN. Lou et al. [16] applied PiNN to inverse multiscale flow modeling.	You et al. [17] introduced IFNO for material response modeling, outperforming FNO in hyperelastic and brittle materials. Dulny et al. [18] combined NeuralODE with the Method of Lines for PDE problems but faced limitations with elliptical second-order PDEs.
Model Flexibility	Limited flexibility, mainly for graph-structured problems.	High flexibility, effective across multiple physics domains.	Specialized for implicit modeling of complex material behavior.
Performance and Accuracy	Stable and accurate in graph-related domains but less effective in continuous fields.	Enhanced PiNN variants (e.g., Res-PiNN) show improved accuracy in handling complex phenomena.	IFNO outperforms traditional methods in material modeling but struggles with elliptical PDEs.
Capabilities
Speed Improvement	✓	✓	✓
Easy Network Training	✓	×	×
Training Without Labeled Data	×	✓	×
Physics-Based Loss Function	×	✓	✓
Continuous Solutions	×	✓	✓
Spatiotemporal Interpolation	×	✓	✓
Physics Encoding	×	×	✓
Operator Learning	×	×	✓
Continuous-Depth Models	×	×	✓
Spatiotemporal Extrapolation	×	×	✓
Solution Transferability	×	×	✓

are physics-guided neural networks (PgNN), physics-informed neural networks (PiNN), and physics-encoded neural networks (PeNN).

PGNN

Physics-guided neural networks (PgNNs) are deep learning models that incorporate physical principles from experiments, laws, or differential equations into their training process, enhancing their performance in solving complex scientific problems. By combining data-driven approaches with established physical laws, PgNNs integrate various neural architectures, including Multilayer Perceptrons (MLPs), Convolutional Neural Networks (CNNs), and Graph Neural Networks (GNNs), to accelerate simulations, particularly in computational fluid dynamics (CFD) and material design. While PgNNs require substantial computational resources for training, they offer significantly faster and more efficient simulations once trained.

PgNNs have been successfully applied across several domains, particularly in areas like mesh generation, optimization, scientific computing, structural analysis, topology optimization, health condition assessment, fluid mechanics, solid mechanics, etc. For instance, in fluid mechanics, PgNNs have reduced the computation time required for solving Navier–Stokes equations and predicting fluid dynamics [19]. Deep learning models like STENCIL-NET have shown [20] to improve adaptive discretization for complex equations, boosting both speed and accuracy.

In material design, trained PgNN models predict optimal designs without the need for iterative processes, drastically reducing computation time. Various researchers have proposed advanced architectures that further enhance these capabilities. For example, Saurabh et al. [21] developed a two-stage approach using a CNN-based encoder–decoder and conditional GAN to find near-optimal topological designs, while Banga et al. introduced a 3D CNN that reduced topology optimization time by 40% with 96% accuracy. Baker et al. [22] combined low-resolution GAN with SRGAN for high-resolution topology solutions in heat transfer structures, offering further improvements in computational efficiency.

Moreover, PgNNs have been applied in inverse design problems, where models predict structures with optimal mechanical properties. PgNNs have also been integrated into multiscale simulations, replacing traditional solvers like Finite Element Methods (FEM) to speed up macro-scale simulations by bypassing lower-scale calculations.

Despite their advantages, PgNNs face challenges such as overfitting and computational demands during training. While methods exist to mitigate overfitting, prediction accuracy can still suffer when tested outside the training dataset. However, studies consistently show PgNNs’ potential as either standalone surrogate models or integrated with conventional solvers like FEM, offering a powerful tool for faster, more accurate scientific computing in fields ranging from fluid dynamics to material design.

8. Review Method

This review paper is based on PGNN between 2021 and 2024. We used a systemic analysis for this publication. Systematic reviews help to gather information. The process that we used to conduct is the systematic review process. There are more than 16,000 peer-reviewed publications in this research. For primary analysis, we have chosen limited papers. Our systematic review was conducted in ten steps, as shown in Figure 4.

8.1. Research Question

This survey aims to provide answers to the following PGNN research questions:

PGNN integrates neural networks with physics-based constraints. The ensuing RQs serve as guiding our questions:

RQ1: How to enhance the loss function in PGNN?

Problem: The loss function in PGNN plays a critical role in balancing physical constraints with data-driven learning. Enhancing this function could improve the model’s predictive accuracy by capturing more intricate physical relationships. Current research focuses on refining the loss function to minimize errors and improve PGNN performance. Researchers have likely refined the model’s loss function to improve approaches. We are examining these progressions in the current state of PGNN.

RQ2: What are the application domains in PGNN?

Problem: A significant challenge lies in identifying the specific fields where PGNN can be most effectively applied. The integration of physics into machine learning offers potential in various domains, but understanding which fields benefit the most from PGNN is crucial. PGNN may have proven useful in several scientific and technical fields. We have identified these areas and revealed the flexibility and effectiveness of PGNN.

RQ3: How does PGNN help build correlations using a knowledge graph?

Problem: PGNN has the potential to use knowledge graphs to establish meaningful correlations through structured data. Understanding how PGNN utilizes these graphs to form accurate connections is crucial for improving prediction accuracy. By examining this inquiry, we can determine how PGNNs use structured data to improve their ability to make accurate connections.

RQ4: What are the research challenges?

Problem: PGNN faces several challenges, including scalability, interpretability, robustness, and generalization. Overcoming these issues is essential for enhancing the model’s performance and expanding its applicability to diverse fields. Addressing this question enables us to identify issues for potential research over PGNN. These challenges might encompass scalability, interpretability, robustness, and generalization. Researchers can devise innovative strategies for these obstacles.

8.2. Keyword Selection

To gather a thorough set of publications about physics-guided neural networks (PGNN), keyword searches were used on search engines like Google Scholar. It is advised to use the following keywords:

• Physics Guided Neural Network,
• PGNN,
• Physics Informed Neural Network,
• PINN,
• PHynet,
• Semi-Supervised Graph Neural Network,
• PGDL, and
• PeNN.

We create search queries that yield relevant articles using suitable connectors for these keywords.

8.3. Collection of Documents and Filtering (Inclusion/Exclusion Criteria)

We have collected documents from several databases using our search strategy. We search, filter the results by inclusion and exclusion criteria, and then choose the articles most relevant to our review.

The inclusion criteria are defined in response to the study’s research goals and scope. We include publications that discuss the physics of guided neural networks and their approaches.

The exclusion criteria are intended to exclude research that does not accord with the goal or methodology of PGNN. For example, we exclude works that do not discuss PGNN models.

After applying these inclusion and exclusion criteria, we pick papers most relevant to the PGNN research subject and study scope. These chosen articles serve as the foundation for the following phases of the review process, such as bibliometric analysis, document examination, and discussion of results.

8.4. Source Material and Search Strategy

Our literature search encompassed various technical conferences/journals, including ACM, Elsevier, IEEE, Springer, Wiley, and Google Scholar. The time period of our investigation spanned from 2021 to 2024.

We reviewed the abstracts of the identified papers and filtered them based on our inclusion and exclusion criteria. Through this process, we set to 81 publications. These studies are summarized in

Table 2. Search engines and number of primary studies.

Search Engine	Primary Studies
ACM Digital Library	7
Elsevier ScienceDirect	11
IEEEXplore Digital Library	4
Springer Online Library	35
Wiley InterScience	13
Google Scholar	11
Total	81

. Although our search may not have captured all papers, we believe it accurately reflects the current trends.

8.5. Analysis Data Collection and Database Selection

In this section, we examined all 81 published papers to address our research inquiries. We have collected information relevant to our research inquiries, including the paper’s summary, references, type, contribution, application domains, loss function and enhanced loss function techniques, evaluation details, and suggested challenges. The collection and publication of all data are documented in https://shorturl.at/i6idF (accessed on 21 May 2024). During our investigations, we conducted a comprehensive evaluation and analysis of each document to authenticate and validate the information collected from them. In our search for documentation, we found many papers but chose only those that were open-access and relevant to our study,

Table 3. Search engines used and number of results.

Search Engine	Search Queries	Results	Primary Studies
ACM Digital Library	acmdlTitle, recordAbstract, author keyword:“physics guided neural network” Or“physics Informed neural network”	130,654	7
Elsevier ScienceDirect	pub-date > 2021 and pub-date < 2024 and TITLE-ABSTR-KEY(“physics guided neural network”) or TITLE-ABSTR-KEY(“PGNN”) or TITLE-ABSTR-KEY(“PINN”)[All Sources(Computer Science)]	35	11
IEEEXplore Digital Library	((((“Document Title”:“PGNN”) OR “Abstract”:“PGNN”) OR “Author Keywords”:“PGNN”) OR ((“Document Title”:“physics guided neural network”) OR “Abstract”:“physics guided neural network”) OR “Author Keywords”:“physics guided neural network”) OR ((“Document Title”:“physics informed neural network”) OR “Abstract”:“physics informed neural network”) OR “Author Keywords”:“physics informed neural network”)) and refined by Year: 2021–2024	251	4
Springer Online Library	“PGNN” OR “physics guided neural network” OR “physics informed neural network” within 2021–2024	161	35
Wiley InterScience	“PGNN” in Article Titles OR “physics guided neural network” in Abstract OR “physics informed neural network” in Keywords between years 2021–2024	1477	13
Google Scholar	“PGNN” “physics guided neural network” “physics informed neural network”, None of the words: “Physics” “Physics guided Deep Learning”,“PHynet”, “Semi-Supervised Graph Neural Network”, “PGDL”, Date filter: 2021–2024	2280	11

.

8.6. Publication and Citation Frequency

PGNN (physics-guided neural networks) and PINN (physics-informed neural networks) have gained significant attention and application in recent years due to a rising interest. Consequently, there has been a substantial rise in the number of papers and patents associated with PGNN and PINN. The number of articles, patents, and citations associated with PGNN and PINN over time would most likely be shown in Figure 5. We use ’Dimensions’ (https://www.dimensions.ai/) to search for ’PGNN’ in our annual review. We have collected data from 2015 to 2024.

This number would most likely indicate that there has been an increase in interest in PGNN and PINN over time, as an increasing number of researchers are incorporating these methodologies into their work and expanding upon the findings of prior studies.

In general, the trends are becoming an increasingly significant part of developing and implementing PGNN or PINN.

8.7. Bibliography Analysis Using Knowledge Graph

Using BERT embeddings, we have built a knowledge graph, Figure 6, from the abstract of the reviewed literature by a series of discrete stages. Initially, for each word in the abstracts, we computed BERT embeddings using the BERT tokenizer and “bert-base-uncased”. Each word was tokenized, the tokenized input was fed into the BERT model, and the token was extracted as the pooled output. These mappings, which link each word to its matching BERT vector, are kept in dictionaries.

We next determined the word embedding pairs’ cosine similarity. Establishing the semantic connections between words depends critically on this similarity metric. Making use of these parallels, we build a knowledge network. We divided the abstracts into words and made a blank graph. To the graph, we add every word as a node. We next include edges between each pair of nodes, where the weight of each edge indicates how similar the words are that are connected. By this procedure, the abstract information may be seen and understood analytically since nodes stand in for words and edge weights for the strength of their semantic connections.

The KG image Figure 6 was added to help graphically illustrate how a knowledge graph based on the abstracts we reviewed utilizing BERT embeddings may be constructed and analyzed. The graph, in which each node represents a word and the edges between them show the degree of similarity based on cosine distance, shows the semantic relationships between important concepts. These knowledge graphs give an organized picture of the semantic connections among concepts, which improves the learning process of models such as physics-guided neural networks (PGNNs). Even with sparse labeled data, a model can obtain deeper contextual information by capturing these linkages through KGs, which enhances generalization and interpretability. The edge weights, which represent an additional layer of semantic similarity, may provide the PGNN models with a more comprehensive grasp of the relationships between various features, which can aid in the model’s ability to identify patterns and connections in the data. Consequently, KGs can greatly enhance a model’s capacity to examine and comprehend intricate links across a variety of domains, in addition to acting as warehouses of organized knowledge.

Our incorporation algorithm is provided below in Algorithm 1.

Algorithm 1 Constructing a knowledge graph from abstracts using BERT embeddings.

Require: Abstracts Abstracts Ensure:  Knowledge graph G  1: Load the BERT tokenizer and model from pre-trained “bert-base-uncased”  2: Tokenize the abstracts into words and store them in $words$  3: Initialize an empty dictionary $word\_embeddings$  4: for each word $word$ in $words$ do  5:     Tokenize $word$ using the BERT tokenizer  6:     Obtain BERT embedding for $word$ by feeding tokenized input into BERT model  7:     Extract the pooled output (representation of [CLS] token) and store in $word\_embeddings\left[word\right]$  8: end for  9: Initialize an empty graph G 10: for each word $word$ in $words$ do 11:     Add $word$ as a node in G 12: end for 13: for each pair of words $(wor{d}_i,wor{d}_j)$ in $words$ do 14:     Compute the cosine similarity between $word\_embeddings\left[wor{d}_i\right]$ and $word\_embeddings\left[wor{d}_j\right]$ 15:     Add an edge between $wor{d}_i$ and $wor{d}_j$ in G with weight equal to their similarity 16: end for 17: return  G

8.8. Document Analysis

This part presents a summary of the past surveys in the literature.

In their paper, Huang et al. [23] introduced a physics-guided neural network (PGNN) for reconstructing channeled spectropolarimeter (CSP) data. By incorporating the physical model of CSP into the network, they improved accuracy and achieved lower RMSE compared with other methods. Similarly, Wu et al. [24] developed a physics-informed neural network for predicting milling surface roughness. On the other hand, Daw et al. [4] combined physics-based models with neural networks to advance scientific discovery. Their hybrid models merge physics-based simulations with observational data, showing superior accuracy and consistency in lake temperature modeling.

Similarly, Kumar et al. [9] presented the Herschel Bulkley Network (HB-Net) for modeling non-Newtonian fluid flow, which enhances the ability to capture complex rheological phenomena. Another significant contribution is from Li et al. [12], who developed a hybrid CNN-PGNN framework for dynamic fault detection in aeroengine control systems by combining deep learning with physics-based models. Similarly, Daw et al. [4] proposed a comprehensive PGNN framework that integrates neural networks with physics-based models to improve scientific modeling. Likewise, Muralidhar et al. [25] developed PhyNet, a deep learning network for drag force prediction that integrates physics into its design.

We review some papers on graph-based methods where according to [26], LightGCL is a graph-contrastive learning model that uses Singular Value Decomposition (SVD) to enhance training efficiency and minimize bias and noise. LightGCL outperformed 16 advanced models in five datasets, notably in sparse data circumstances. Candidate-aware Graph Contrastive Learning for Recommendation (CGCL) [27] improves node embeddings in sparse interaction graphs by using semantically analogous contrastive pair embeddings, outperforming DNN, GNN, and GCL methods. Similarly, HOPE [28] introduces a high-order graph ODE approach for analyzing high-order correlations in dynamic systems, proving effective for long-term forecasting. Scorpius et al. [29] use LLMs to create toxic abstractions, risking scientific knowledge graph integrity. In another work [30], a graph-based disentangled representation learning model is presented that improves context-specific citation production using citation graphs for relevance. Moreover, Wei Ju et al. [31] analyze GCL methodology and applications in drug discovery, recommender systems, and traffic forecasting, dividing augmentation techniques into rule-based and learning-based methods. Lastly, Wei Ju et al. [32] explore GNN challenges in practical applications, including imbalance, noise, privacy, and OOD instances to improve GNN robustness and reliability in bioinformatics and finance.

9. PGNN Equations

The interaction between physics and neural networks is captured via equations used in PGNN. A simplified representation is as follows:

Relation 1.

Given input features Y and physics-based features Z we have

$$G(Y;Z)=0$$

Relation 2.

The physics-based prediction at the next time step $(n+1)$ is

$${\widehat{Y}}_{n+1}^{\left(PB\right)}=Y_n+hf(t_{n+1},{\widehat{Y}}_{n+1}^{\left(k\right)},U_n)$$

The following information is here:

• h represents the time step $(t_{n+1}-t_n)$.
• ${\widehat{Y}}_{n+1}^{\left(k\right)}$ is the neural network prediction at time step $(n+1)$.
• $U_n$ denotes any additional physics-based inputs.

10. Description, Benefits, and Applications of Key Concepts

Physics-guided neural networks (PGNNs) merge the interpretability of physical principles with the adaptability of deep learning, resulting in enhanced prediction accuracy and reliability also established physical laws to inform and constrain the neural network’s. Some key concepts are provided below in a

Table 4. Descriptions, Benefits, and applications of key concepts.

Keyword	Description	Benefits	Applications
PGNN	Physics-guided neural network (PGNN) is a neural network architecture that includes ideas from physics into its design and training process. The purpose of this integration is to enhance the model’s performance, interpretability, and generalization by using the underlying physical laws, restrictions, or relationships present in the data. PGNNs are especially valuable in scientific and technical fields where comprehending fundamental physical events is essential for precise forecasting and decision-making. Some examples of these fields include fluid dynamics, material science, and structural mechanics.	Enhanced efficiency and comprehension by using ideas derived from physics  − Enhanced generalization resulting from an understanding of the fundamental physical principles at play	− Computational fluid dynamics  − Material science  − Structural mechanics
Physics-Informed Neural Network	A physics-informed neural network (PINN) is a kind of neural network model that incorporates the understanding of physics principles directly into its structure or training process. These networks use physics-based constraints or equations to direct their learning process, allowing them to more effectively capture fundamental physical correlations and enhance their ability to make accurate predictions, particularly in situations when data are few or unreliable. Physics-informed neural networks (PINNs) have diverse applications in computational physics, medical imaging, and environmental modeling.	− Improved forecasting precision using physics-based limitations  − Enhanced efficiency in situations with sparse or erratic data	− Computational physics  − Medical imaging  − Environmental modeling
Physics-Guided Deep Learning	A method known as “physics-guided deep learning” involves augmenting or guiding deep learning algorithms using physics-derived concepts. Deep learning models may now take use of established physical laws, restrictions, or correlations to enhance their robustness, interpretability, and performance thanks to this integration. These models may become more broadly applicable by adding knowledge of physics, particularly in fields where physical principles control the underlying events. Applications for physics-guided deep learning may be found in astronomy, geophysics, and biophysics, among other scientific fields.	− Improved efficiency and durability by using laws of physics  − Generalization in physics-governed domains	− Astronomy  − Geophysics  − Biophysics
Semi-Supervised Graph Neural Network	A Semi-Supervised Graph Neural Network (SSGNN) is a neural network architecture especially tailored for tackling semi-supervised learning tasks on data organized as graphs. Graph neural networks (GNNs) expand conventional neural network designs to process data formatted as graphs, enabling them to capture relational information and connections among data points in a graph. SSGNNs, in the context of semi-supervised learning, use both labeled and unlabeled data to enhance model performance and generalization. They are used in many fields, such as social network analysis, recommendation systems, and biological network analysis.	− Enhanced model efficacy by using both annotated and unannotated data  − Efficient encoding of information on data organized as graphs	− Social network analysis  − Recommendation systems  − Biological network analysis

.

11. Distinctive Characteristics and Advantages of PGNNs

Physics-guided neural networks (PGNNs) blend deep learning with physical principles, allowing for more accurate modeling of complex systems. By integrating existing knowledge of physics into their training, they produce predictions that are both understandable and consistent with physical laws. PGNNs are also effective in situations with limited data, making them useful in fields where experimental information is not readily available. Some are discussed below:

• Hybridization: Physics-guided neural networks (PGNNs) integrate neural networks with physics-based information, resulting in a potent fusion. This integration enables PGNNs to harness the advantages of both methodologies, leading to models that are more resilient and easier to comprehend.
• Enhanced generalizability: By integrating physical constraints into the learning process, PGNNs exhibit improved capacity to apply learned knowledge to new contexts, particularly when dealing with limited data. This feature allows PGNNs to achieve high performance on data that has not been previously seen and to make accurate predictions beyond the data used for training.
• Application in multiscale multi-physics phenomena: PGNNs are very effective in speeding up the numerical simulation of intricate systems that exhibit both multiscale and multi-physics phenomena. Their capacity to accurately represent the complex interplay between many physical phenomena makes them indispensable in modeling and forecasting the behavior of such systems.
• Future research opportunities: Future research possibilities arise from the use of PGNNs, providing prospects to investigate several facets of their use and advancement. Potential areas for additional investigation are the examination of causal links, the enhancement of algorithms to achieve better performance, and the integration of deep learning solvers with scientific models. These research areas show potential for enhancing the capabilities and uses of PGNNs in many sectors.

Because they combine neural networks with information from physics, PGNNs have unique benefits that make them perfect for solving difficult scientific and engineering problems. They provide a viable route for future study and application development due to their adaptability and room for further advancement.

11.1. Limitation of PGNN

Despite their potential, PgNNs face several limitations:

• Statistics-based training: The main limitation of PgNNs is that their training process is solely based on statistical correlations in data. As a result, their outputs may not fully adhere to underlying physical laws and could violate them in certain cases [33].
• Sparse training data: PgNNs struggle when the training dataset is sparse, which is often the case in scientific fields. Sparse data leads to failure in extrapolating predictions outside the scope of the training data, making the models less effective in real-world applications [34].
• Interpolation issues: Even for inputs within the sparse training datasets, PgNN predictions may be inaccurate, especially in complex, non-linear problems. PgNNs have difficulty interpolating across a wide range of physical parameters, such as different Reynolds numbers in fluid dynamics [19].
• Boundary and initial condition problems: PgNNs may not fully satisfy the boundary and initial conditions under which the training data were generated. As these conditions vary from problem to problem, the training process becomes prohibitively costly, especially for inverse problems [35].
• Resolution invariance: PgNN-based models are not resolution-invariant by design, meaning that models trained at one resolution cannot be easily applied to problems at different resolutions [36].
• Averaging effects: During training, PgNNs may treat minor variations in the functional dependencies between input and output as noise, which can result in averaged solutions. While the model performs optimally over the entire dataset, individual case predictions may be suboptimal [37].
• Complex dataset handling: PgNNs struggle when the training dataset is diverse, i.e., when there are drastically different interdependencies between input and output pairs. To address this, increasing the model size may help, but it requires more data and makes training costlier and, in some cases, impractical [35].
• Scaling to larger systems: As systems grow more complex, scaling PGNNs becomes computationally expensive, making it difficult to apply them to large-scale problems [38].
• Data quality and quantity: PGNNs rely heavily on high-quality, complete datasets. Incomplete or noisy data can lead to poor performance, and obtaining clean data is often costly and challenging [35].
• Balancing physics constraints and flexibility: It is difficult to find the right balance between adhering to physical laws and allowing flexibility in data-driven learning. Too much focus on physics constraints can limit the learning process, while too much flexibility can lead to physically inaccurate results [39].
• Slower performance: PGNNs can be computationally slower than traditional methods due to the complex optimization process needed to balance physics constraints with data-driven learning [40].

To address these limitations, PgNNs can be further constrained by governing physical laws, reducing the need for large datasets and improving their generalization capabilities.

11.2. Challenge of PGNN

Several unresolved research challenges arise from this survey, whether from recurring issues found in the examined studies or gaps in the existing literature. These challenges address Research Question RQ4:.

1.

Challenge 1: Integration of Multiple Laws of Physics

The incorporation of numerous physics principles into Physics-Guided Neural Networks (PGNNs) offers potential advantages, but it also poses some difficulties. To maximize the performance of PGNN, it is necessary to solve open challenges such as comparing various integration techniques, giving heuristics for their application, and defining the combinability and order of physics laws [25,41,42,43,44].

2.

Challenge 2: Instructions for Creating Efficient PGNN Models

It is crucial to establish standards for creating physics-guided neural networks (PGNNs) that are successful. Although multiple PGNN designs can tackle different challenges, their efficacy may differ. Systematic methodologies and guidelines are required to develop PGNN models, which provide a comprehensive and sequential approach suitable for both experienced practitioners and novices. The current understanding of good PGNN design is often both complimentary and conflicting, suggesting a lack of defined principles [45,46,47,48,49].

3.

Challenge 3: Balancing Physics-Based Constraints with Data-Driven Flexibility

A key challenge in PGNNs is maintaining a balance between applying physics rules and allowing flexibility for data-driven learning. If too much focus is placed on the physics constraints, the model may struggle to learn effectively from data. On the other hand, if the model is too flexible, it may break important physical laws. Recent studies suggest [39] that a balanced approach for vapor compression systems using two methods:

(a)

Modular model implementation: Data-driven models for individual components are built separately and integrated, allowing flexibility and reuse across different systems.

(b)

Physical conservation enforcement: Physical laws like mass and energy conservation are enforced, ensuring accuracy while maintaining the efficiency of data-driven techniques.

11.3. Discussion the Future Research Direction of PGNN

Physics-informed neural networks (PINNs) have reached their limitations, prompting researchers to investigate physics-guided neural networks (PGNNs) and their pros and cons. By addressing several PINN difficulties, PGNNs may improve projected accuracy and generalization. However, a recent study examines PGNN methodology limits. Studying PGNN durability across datasets, their ability to handle complex systems, and their interpretability in actual situations are important. The research community studies and tests PGNNs in various scientific and technological sectors to improve their understanding and application.

Improve [7] PGNN, PiNN, and PeNN for convergence, quicker training, accuracy, and generalization with sparse datasets. Improve flexibility to multi-dimensional, multi-physics, and different governing equations.

The method presented in [50] is beneficial for data-driven parametric differential equation solutions and discoveries. Data-driven issue discovery for deterministic and probabilistic ODE solutions will be developed from this technique. Reference [51] discusses training algorithms that restore physical causality in PGNN, PiNN, and PeNN models, resulting in predictions that are more accurate and consistent.

Early hyperparameter sensitivity is a limitation of the hybrid technique. Despite employing auxiliary planes, bad parameter initialization might impede training. More initial hyperparameters will be optimized in future studies.

PGNN, PiNN, and PeNN may address more engineering challenges by applying them to complicated anisotropic materials, multiscale multi-physics phenomena, and structural health monitoring [52].

The cPINNs [53] developed by may parallelize, reducing training costs, but they cannot compute parallelly. CPINNs may be parallelized in future studies.

The goal of the research community’s efforts in these areas is to improve our knowledge and ability to use PGNNs in a variety of scientific and technical fields.

12. Conclusions

Physics-guided neural networks (PGNNs) offer a revolutionary synergy between conventional physics-based modeling and neural networks. This hybrid method overcomes the drawbacks of strictly data-driven models and improves interpretability, generalizability, and scientific consistency.

In future work, we will integrate state-of-the-art graph contrastive learning techniques into PGNNs to improve representation learning and model accuracy. Additionally, we will optimize the tuning of GNN layers to further enhance the balance between data-driven learning and physical laws.

PGNNs have a substantial impact on a variety of scientific fields and have shown to be superior, particularly in situations when there is a lack of data. As PGNNs continue to develop, new applications are being investigated, interpretability is being improved, and this indicates that machine learning will continue to lead to innovative approaches to the understanding of physical events.