FPGA Design Integration of a 32-Microelectrodes Low-Latency Spike Detector in a Commercial System for Intracortical Recordings

Abstract

Numerous experiments require low latencies in the detection and processing of the neural brain activity to be feasible, in the order of a few milliseconds from action to reaction. In this paper, a design for sub-millisecond detection and communication of the spiking activity detected by an array of 32 intracortical microelectrodes is presented, exploiting the real-time processing provided by Field Programmable Gate Array (FPGA). The design is embedded in the commercially available RHS stimulation/recording controller from Intan Technologies, that allows recording intracortical signals and performing IntraCortical MicroStimulation (ICMS). The Spike Detector (SD) is based on the Smoothed Nonlinear Energy Operator (SNEO) and includes a novel approach to estimate an RMS-based firing-rate-independent threshold, that can be tuned to fine detect both the single Action Potential (AP) and Multi Unit Activity (MUA). A low-latency SD together with the ICMS capability, creates a powerful tool for Brain-Computer-Interface (BCI) closed-loop experiments relying on the neuronal activity-dependent stimulation. The design also includes: A third order Butterworth high-pass IIR filter and a Savitzky-Golay polynomial fitting; a privileged fast USB connection to stream the detected spikes to a host computer and a sub-milliseconds latency Universal Asynchronous Receiver-Transmitter (UART) protocol communication to send detections and receive ICMS triggers. The source code and the instruction of the project can be found on GitHub.

1. Introduction

Intracortical microelectrode arrays enable the possibility to read the small amplitude signals–microvolts to millivolts range–of one of the most complex systems: The brain. Each electrode, which is only a few micrometers in width, allows reading the extracellular depolarization from a population of neurons in the proximity of its metallic surface [1,2,3,4]. Usually, multiple microelectrodes are arranged on a probe with one or more shanks, with a channel count increased up to hundreds or even thousands [5,6,7]. These microelectrodes can be also used to inject a variable current or voltage to evoke a physiological response from neurons in a sphere centered on the stimulating channels [8,9]. In order to process the information that relies behind the voltage fluctuations detected by the sensing spots on the probes, the acquired signal must be digitally sampled with a frequency high enough to discern the activity up to the fast depolarization of a single neuron, called Action Potential (AP) or spike, and Multi Unit Activity (MUA). MUA is the faster cumulative and overlapping signal propagated by multiple neurons close enough to the electrode to be sensed but too far to be singularly distinguished [10]. To accurately reconstruct this activity, as short as 1 ms, the samples must be collected at a sampling frequency that can easily go up to 30–40 kHz. Given the large number of channels featured by the most recent probes [4,11,12], the number of samples generated per second can be difficult to process in real-time, precluding experiments where the latency in the activity events recognition is crucial. For example, when dealing with spike dependent closed-loop experiments for brain computer interfacing involving IntraCortical MicroStimulation (ICMS) [13,14], keeping the feedback timing in a biologically acceptable range can be a critical step [15,16,17]. Traditional processing of the information is subjected to the USB communication latency necessary to transfer the samples in chunks from the acquisition system to a computer, where the samples processing is in turn conditioned by the operating system scheduler, blocking calls and computer performances. Altogether, these constrains cause tens of milliseconds of delay from the sampling of the neural activity to its elaboration and interpretation.

This paper aims to overcome these limitations presenting a digital Spike Detector (SD) running in the recording system’s FPGA, that elaborates the neural activity received directly from the headstage, which samples the signals acquired by the microelectrodes without intermediate steps. The headstage, mounted on the top of the probe, embeds up to two chips each managing 16 electrodes and including a Low Noise Amplifier (LNA), a 16-bit Analog-to-Digital Converter (ADC), high-pass and low-pass filters, and stimulation circuitry. Processing the data in-place on the recording system allows evaluating the digitalized signal point-by-point with the lowest latency from the ADC, and communicating the temporal and spatial firing information of each of the 32 channels in less than 1 ms from the maximum negative peak of the spikes. The project has been integrated in the open-source Hardware Description Language (HDL) code and acquisition software RhythmStim from Intan Technologies (Los Angeles, California, USA) and deployed on the RHS stimulation/recording controller (Figure 1) from the same company. The logic managing the sampling and data transmission has been added aside, creating a new dedicated pipeline to process the raw data stream acquired by the 32 channels headstage without reducing the original functionalities. The spike detection pipeline starts without any buffering system when receiving a new sample, guaranteeing the lowest latency from digitalization to processing. The SD presented in this work wants to improve the method included in the system by default, that works in detecting when the first order high-pass filtered signal crosses a threshold set by the user on a subset of a monitored channel, raising the signal from one of the mapped digital output of the system. This work aims to improve the detection accuracy of the system, despite the good noise performance at the high frequencies, to detect both APs and MUAs. Our experiments found the instrument noise at the high frequency of AP and MUA to be about 10 µV RMS during neuronal inactivity, that makes it trivial to detect APs that can reach amplitudes down to −150 µV when neurons are close to the electrode surface (see Section 2.1.1 and Result). Unfortunately, in many experiments, these strong signals represent a minority, most of the signals originate from neurons that are far from the electrodes, leading to MUAs of about 15 µV RMS and a Signal-to-Noise Ratio (SNR) of 3.5 dB once the signal is filtered (see Results section). Hence, the need for a more powerful tool which is able to accurately detect both the AP and MUA events. The presented SD design includes:

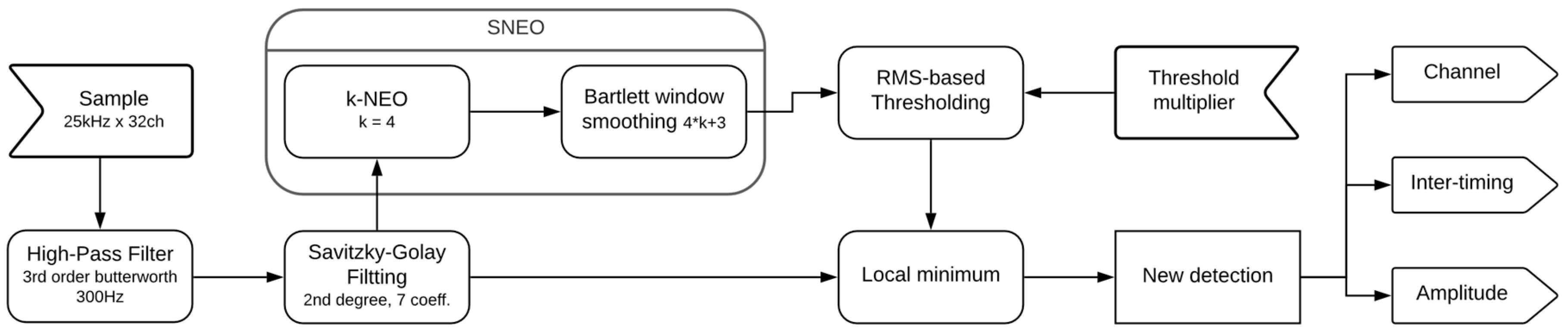
• A third order Butterworth high-pass Infinite Input Response (IIR) filter with a cutoff frequency of 300 Hz and a Savitzky-Golay smoothing filter [18], fitting the high-pass filtered signal with a second degree polynomial.
• A point-by-point signal energy estimation using the SNEO [19], that aggregates both the frequency and the amplitude of the voltage fluctuations in a series of samples that can be compared with a threshold.
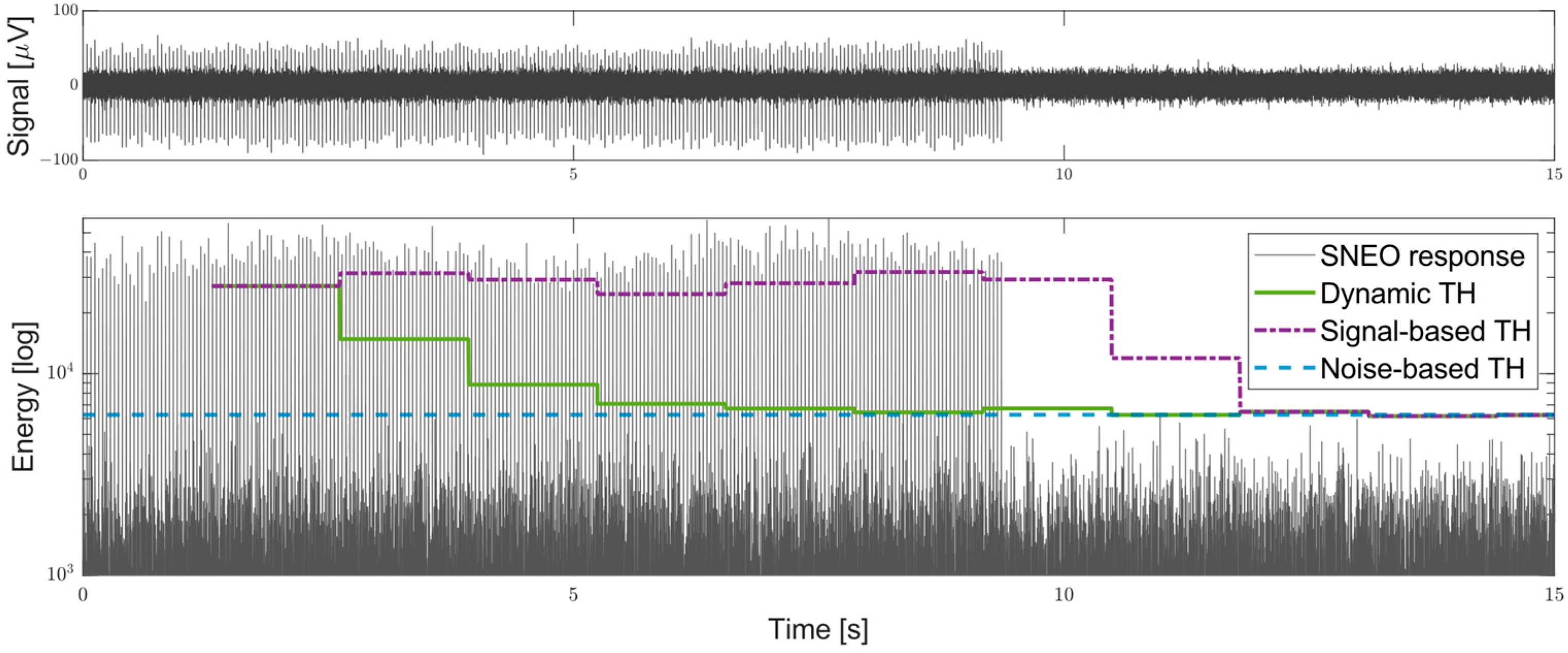
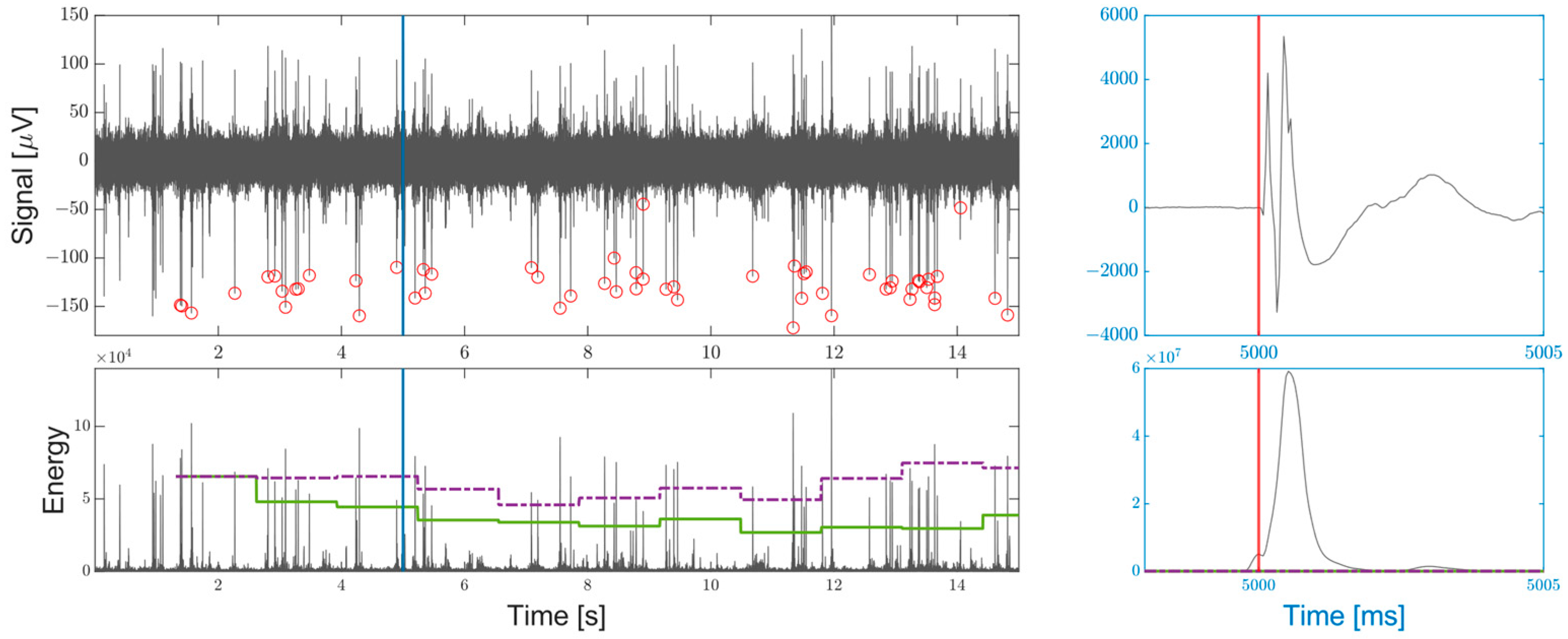
• A novel dynamic threshold per-channel estimation based on the Root Mean Square (RMS) of the SNEO output that accommodates any drift of the probe or changes in the signal quality, that rapidly converges to a firing-independent value close to an ideal threshold based only on the noise energy. The threshold can be adjusted by the user, to open the detection of both the single AP and MUA.
• A post-ICMS blind window of a user-defined duration, to prevent the detection of false positives following the high increase in the signal power due to the artifact induced by the injection of a current.
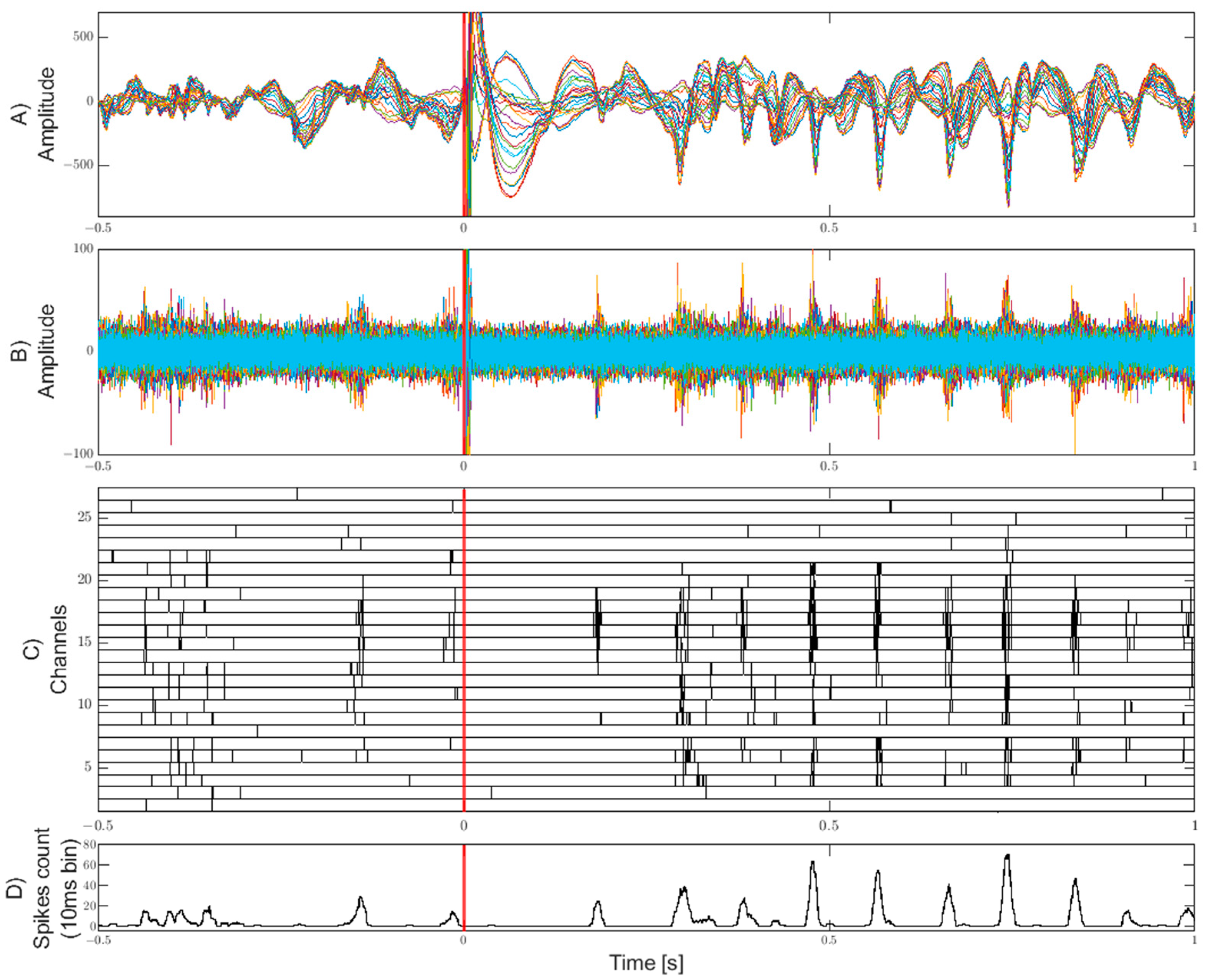
• The capability to stream the amplitude, the channel, and the timing of each detected spikes via the USB to the host computer, and, simultaneously, via the UART protocol to any other connected device with sub-milliseconds latency. By the UART command, it is also possible to trigger the ICMS set from the host application.

The software application on the host computer used to manage the connection, the recording, and the setting of the stimulation/recording controller system has been extended to manage the new functionalities. A new dedicated window to manage the SD has been created to show a real-time raster plot of the spiking activity of each channel and to allow adjusting the threshold multiplier and the artifact blinding duration during the experiment to improve the SD performances. Through the application, the system can be also connected to the network to stream the spikes details to a specified IP address over the UDP protocol. Finally, channels can be excluded from the spike detection so that they are not sent via both UART and UDP. The system has been tested with in vivo experiments on a rat barrel cortex and it is currently used in our laboratory for closed-loop experiments of ICMS. Examples of the system output on APs and MUAs detection are highlighted in the Results section.

2. Materials and Methods

2.1. Design Algorithms

The digital implementation of the SD relies on an algorithmic processing that can be split in six major steps: High-pass filtering, Savitzky-Golay fitting, SNEO, threshold estimation, detection, and local minimum finder. These core parts are here described, together with the parameters used for an implementation running with a sampling frequency of 25 kHz for each of the 32 channels. The input is assumed as a matrix where the first index indicates the electrode number, or channel, while the second index reports the sampled amplitude of the signal. The information to extract from the signals is given by the index where the spiking events are detected for each channel and the corresponding amplitude. The output then is a sparse matrix with the input shape, containing the negative amplitude of the filtered signal where a spike is detected. The parameters—length of the Savitzky-Golay window, $k$ of SNEO and the threshold multiplier—are tuned both by simulation and experimentally to achieve the better accuracy. Synthetic datasets are created as shown in Figure 3, with spikes templates of different amplitudes and SNRs inserted in the known positions. In this case, the accuracy focuses on the single AP detection and is calculated from the ratio between the correctly detected events and the sum of the total events and the false positives. The results achieved varying the parameters of the algorithm are then compared to maximize the accuracy. The analysis is not shown here for the sake of brevity, but the method follows what was reported in a previous work [20]. Acquisitions from experiments are then used to fine tune what has been found by the simulation, where it is possible to evaluate also the MUA detection.

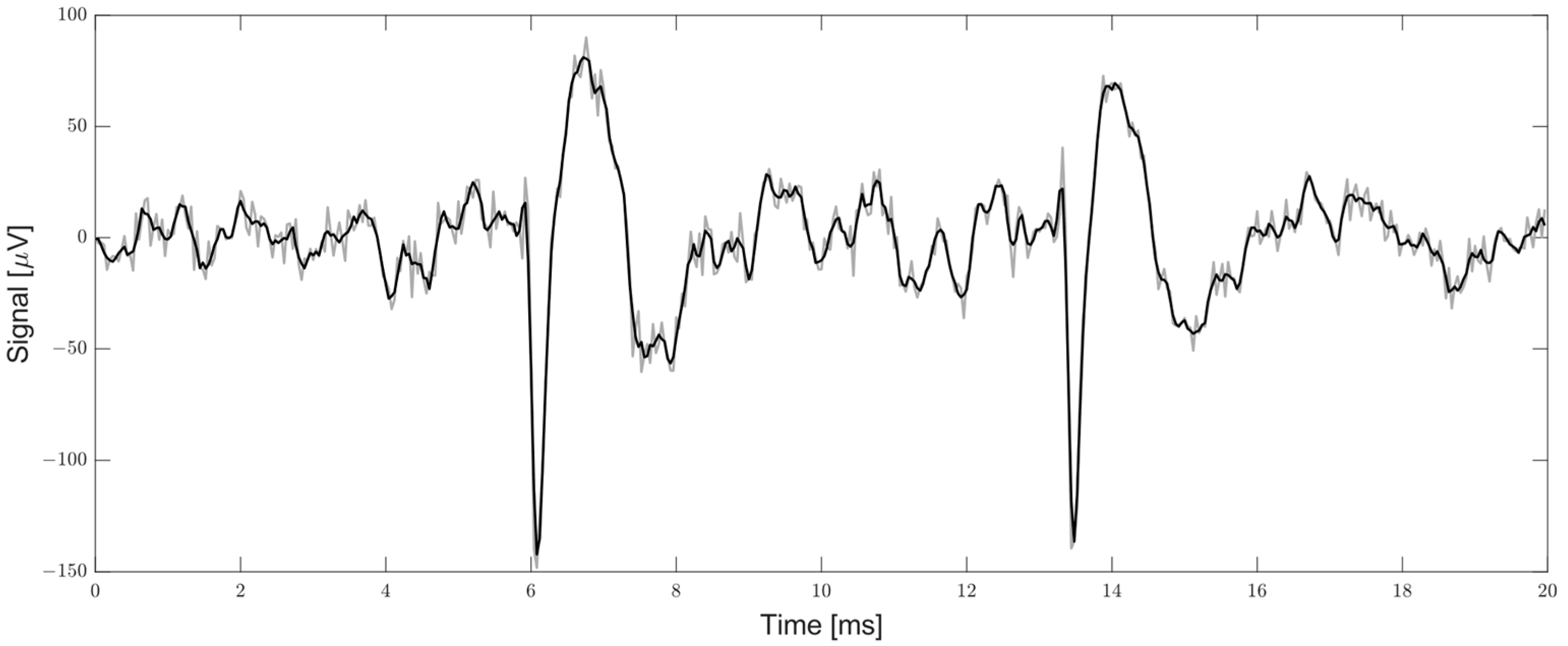
2.1.1. High-Pass and Savitzky-Golay Filtering

When dealing with signals such as APs and MUA characterized by high frequency features, the first step of the processing chain is to high-pass filter the signal, to exclude the Local Field Potential (LFP) from the further analysis, to remove the predominant low frequency components of the signal below 300 Hz. Here, a third order IIR Butterworth filter is used, to remove the low frequency changing features of the LFP, offset, and off-band noise. The filter coefficients in

Table 1. Coefficients for the third order Infinite Input Response (IIR) filter (a and b), and for the Savitzky-Golay (SG) fitting.

Mask	0	1	2	3	4	5	6
a	0.9274	−2.7821	2.7821	−0.9274	\	\	\
b	1	−2.8492	2.7096	−0.8600	\	\	\
SG	−0.0952	0.1429	0.2857	0.3333	0.2857	0.1429	−0.0952

are computed using MATLAB and are used to implement the IIR filter with a cutoff frequency of 300 Hz. The filtering step is immediately followed by the smoothing Savitzky-Golay filter, used to fit the last seven points of the high-pass filtered signal with a second order polynomial at each iteration. The signal is convoluted by the seven coefficients mask shown in Table 1, providing a cutoff frequency of −3 dB at 3 kHz. This results in less sharp high frequency changes, increasing the SNEO performances as demonstrated in [21]. A fitting example of an extracellular signal is shown in Figure 2.

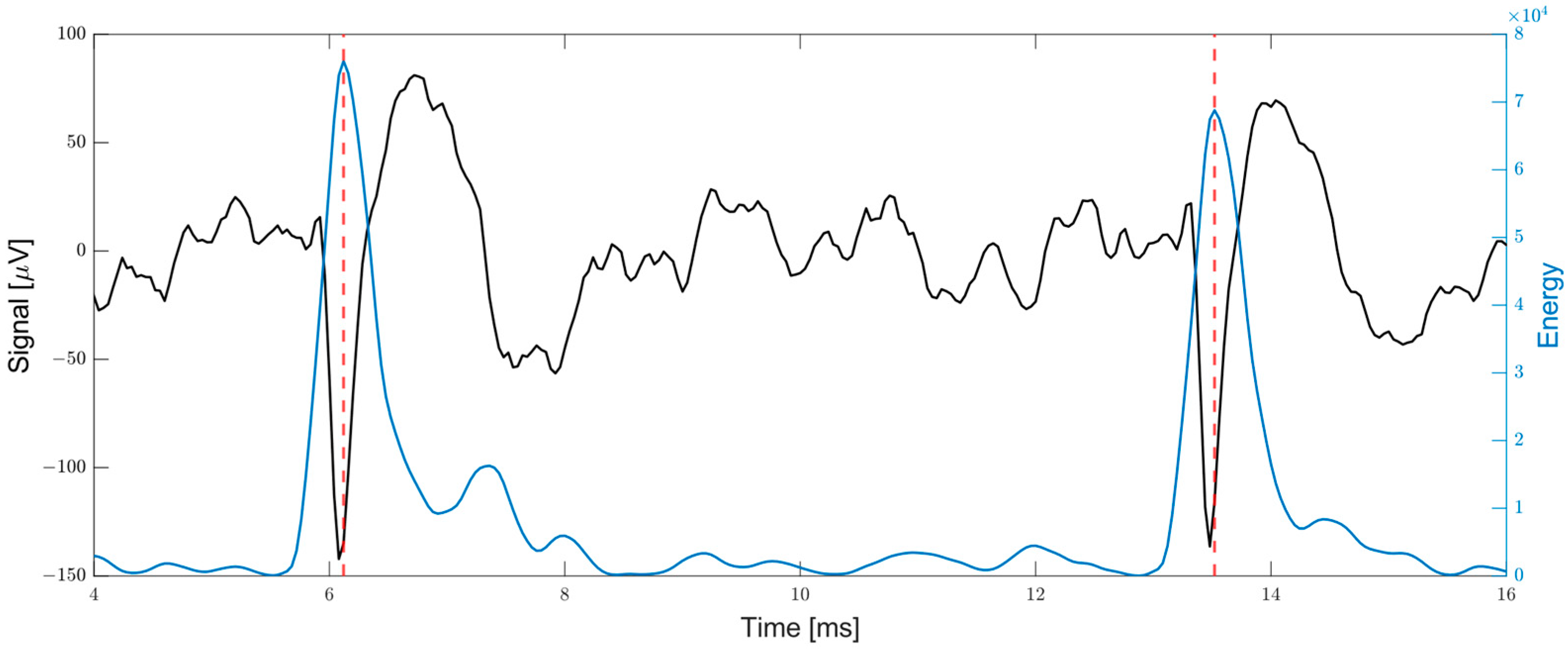
2.1.2. Smoothed Nonlinear Energy Operator and Threshold

The k NEO, on which the SNEO is based, gives an instantaneous estimation of the energy contained in a signal oscillation. Thanks to the energy dependent answer, the SNEO became widely used for the spike detection task and is still one of the preferred spike detector operators when going on real-time processing [22,23,24,25]. It fits very well to a real-time and low-latency application since it does not require any training phase and has a small footprint on the resource usage nevertheless the good performances, as proved and compared in [20]. This operator strictly relies on a parameter called $k$, which depends on the sampling frequency and the average spike duration. Given the sampling frequency of 25 kHz, the average spike duration, and the experimental tuning, the $k$ parameter value achieving the best accuracy results in detection has been found to be 4. After computing the nonlinear energy response of the filtered signal $s$ of each channel $ch$, the SNEO makes it smoother with a Bartlett window $BW$ of a size $4·k + 1$ (Equation (1)).

$$\begin{gathered} kNEO\left(ch,t\right)=s{\left(ch,t\right)}^2-s\left(ch,t+k\right)·s\left(ch,t-k\right) \forall t :t\in \left\{1,\dots ,signal length\right\} \\ SNEO=kNEO\otimes BW\left(4·k+1\right) \end{gathered}$$

(1)

The result returned by the application of the SNEO is now compared with a pre-defined threshold which must be set to a value accurate enough to discern the physiological events from the signal noise. A fixed value for the threshold can sensibly reduce the detection performances, since each channel has its own Signal-to-Noise Ratio (SNR) level that can be also subjected to changes caused by probe drifts. A threshold value based on the SNEO output distribution can adaptively adjust the detection level of each individual channel for the entire duration of the recording. The median is the most reliable option to find an effective threshold using a scaling value, but unfortunately it does not fit well in a real-time hardware implementation pipeline. For this reason, this work relies on the RMS of the signal, multiplied by a scaling factor $C$ to find an accurate threshold which is constantly updated over a window of samples—here called timeframe, $tf$—long enough to provide a correct and stable trend. However, when using the RMS to find the threshold, it must be considered that the SNEO is a nonlinear operator and the high SNEO energy response to a spike will highly affect the RMS value. Being the firing rate intrinsically non-constant, the RMS output can be sensibly affected with different intensities from timeframe to timeframe and therefore, it cannot be simply accounted in reducing the threshold multiplier C by a constant fraction. To mitigate this problem, this paper presents a new approach for the threshold estimation. The signal in each timeframe is compared with the threshold based on the RMS of the prior timeframe. Therefore, the new RMS value can be computed for every timeframe by replacing the samples exceeding the threshold with the RMS from the previous timeframe, to exclude the contribution of the spikes energy from the estimation. Using this approach, the RMS usually converges in a maximum of five iterations to a value close to the RMS value of the noise energy only, independently from the spike amplitude and firing rate, as shown in Figure 3. According to this, stimulation artifacts, which could increase the threshold far over the correct level, are also rejected from the RMS estimation. The threshold multiplier $C$, scaling the RMS value, is chosen by experimental results: A value about 5.5 is used for the MUA detection and a greater value up to 18 is used to detect a clear single AP.

$$Th\left(ch,tf\right)= C\ast RMS\left(s\left(ch, t\right)\right) \forall t :t\in tf$$

(2)

2.1.3. Spike Detection and Local Minimum Finder

For each new sample, the SNEO output is computed and compared with the two previous samples searching for a local maximum, and with the threshold found in the previous RMS timeframe (Equation (3)). It must be considered that a peak in the SNEO output can be not precisely aligned with the peak in the filtered signal. In fact, depending also on the filtering [26], the positive rebound following the negative spike peak can reach a prominent amplitude in the transition from the negative and the positive phase of the spike, developing enough energy to shift the SNEO output peak (Figure 4). Therefore, if the output is a local maximum and is also greater than the threshold, the algorithm searches for the minimum value among the previous samples of the filtered signal, within a window wide as the Bartlett window, which is used to smooth the SNEO. Once the minimum is found, the index will represent the spike temporal information, while the value will be the spike amplitude (Equation (4)).

$$Peaks\left(ch, t\right)= True if\{ \begin{array}{c}SNEO\left(ch,t-1\right)\ge Th\left(ch,tf\right), where tf\ni t\\ SNEO\left(ch,t\right)\le SNEO\left(ch,t-1\right)> SNEO\left(ch,t-2\right)\end{array}$$

(3)

$$Spike\left(ch, t^{\prime }\right)=\min \left(s\left(ch,t^{\prime }\right)\right) \forall t^{\prime } :t-4\ast k+1\le t^{\prime }\le t \& Peaks\left(ch, t\right)=True$$

(4)

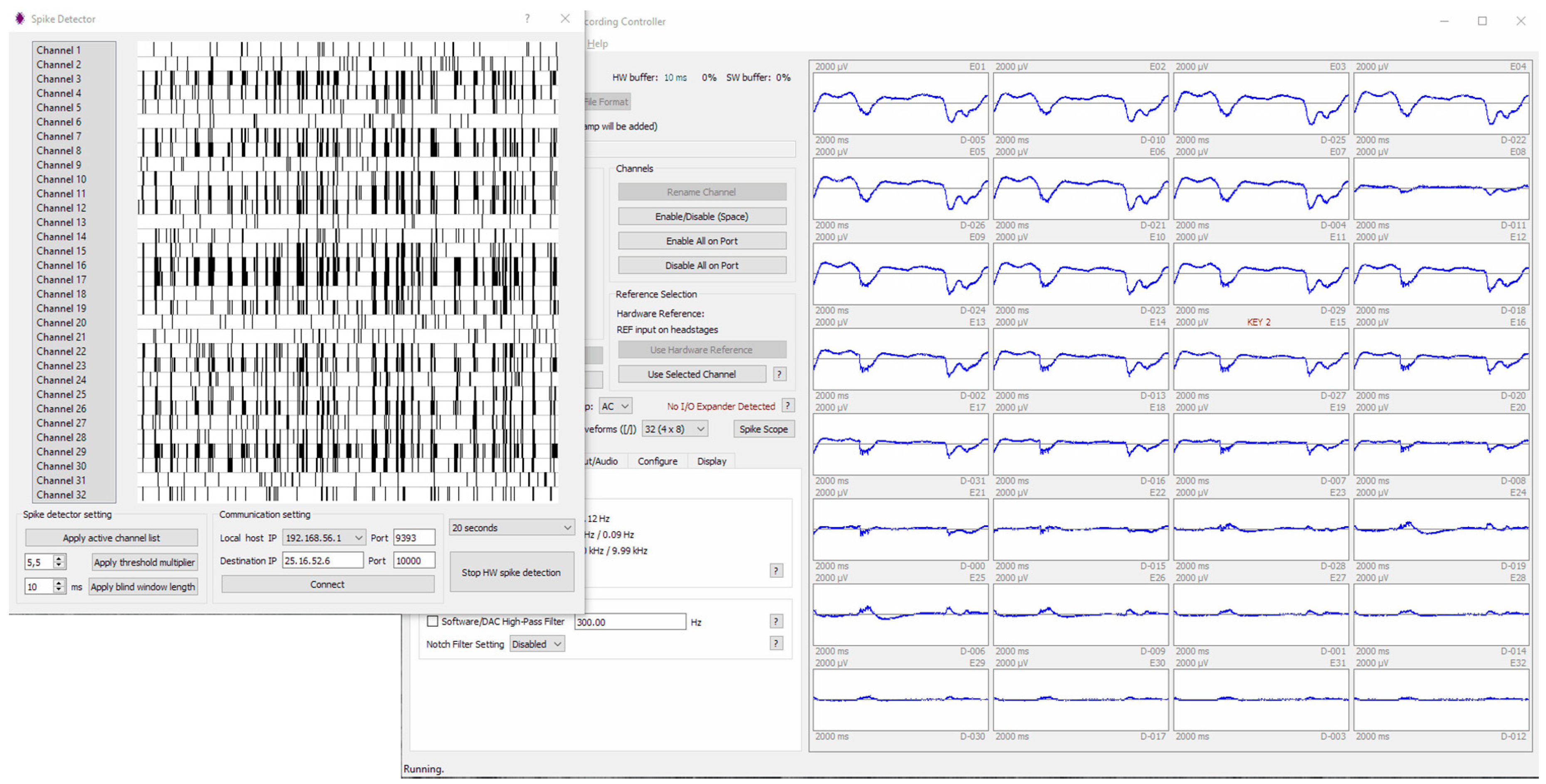
2.2. Design Implementation

The algorithms presented in Section 2.1 have been described in an HDL language to be implemented on the Opal Kelly XEM6010-LX45 board mounting the Xilinx Spartan-6 XC6SLX45-2 FPGA. This board is mounted by default by the Intan RHS stimulation/recording controller and together with the RhythmStim design provides the interface between a host computer and the headstages (up to 4). Each headstage is connected through a Serial Peripheral Interface (SPI) cable to the recording system, used to communicate simultaneously two digitalized samples. The RhythmStim allows acquiring the data for both visualization and recording on the host computer application. The application is used to set the filters on the headstages and to program the latter to stimulate a channel with a user-defined current shape based on different external trigger sources connected to the recording system. The RhythmStim hardware part manages the samples acquisition from each channel at a constant frequency of 20, 25, or 30 kHz and the electrical ICMS when it is triggered. In a high-level overview, the system continuously loops over 20 action slots: The last four slots are used to start and stop the ICMS and to set the parameters of the headstages, while in the other first 16 slots, a 32-bit command is sent via SPI to sample a different pair of channels. The headstage answers after a delay of two slots with a pair of values of 32-bit, each containing in the 16 Most Significant Bits (MSBs) the sampled value, stored with a positive offset of 32,768, where the least significant bit of the value corresponds to 0.195 µV. The pair is written in the RAM of the Opal Kelly board (Portland, Oregon, USA), which is used as a buffer for the asynchronous USB communication with the host application. The design has been modified to write the 16 MSBs of both the samples pair, received from the headstage connected to the system port D, also in a 64-bit width First In First Out (FIFO), filling the other 32 bits with a system timestamp representing the number of samples acquired. The FIFO crosses the domain clock and provides to the SD the values at the working frequency of 100 MHz. Here, the SD pipeline begins, whose main steps of the process are described in Figure 5.

The values are read as soon as the FIFO is not empty, and the two samples are converted in two’s complement removing the positive offset of 32,768. The SD design is split into different HDL components described in the next subsections. These components are orchestrated by a main design that allows the various output to flow from one component to the next, keeping the channel and the samples count. The samples pair is processed sequentially through the pipeline shown in Figure 6, one sample immediately after the other. The processing is tuned for a sampling frequency of 25 kHz. The SD can work also with a 16 channels headstage, since the second value of each samples pair will simply have a constant value of 0. As the main design rules, the operations are performed in the integer domain. Where a division is required, it is constrained to a power of two, to be performed as a bit-shift operation—a 0.5 rounding precision is achieved performing the $n$ bit-shifting operation on the value summed to $2^{n-1}$—. All the components work in time division multiplexing over the 32 channels, storing each channel state. The HDL part of the project has been developed on the Xilinx ISE Design Suite 14.7. The pseudocode of the components can be found in Appendix A.

2.2.1. Filter

Direct and direct-transposed from I and II have been simulated for the FPGA integer-based implementation of the third order IIR filter. Using the direct-transposed form I (Figure 7), the state variables of the filter did not saturate, and the filter remained stable despite the rounding error on the output, avoiding using a cascade of second order filters. Being the coefficients real numbers close to the 0 value, the error introduced by the rounding would be disastrous. To overcome this problem working in the integer domain, the coefficients are scaled by a factor big enough to reduce the rounding error to a negligible one. This scaling factor is chosen as a power of 2, to be then removed from the filter output with a bit-shift operation. The filter form fits well to the DSP48A1 multiplier/adder of the Spartan-6, that provides a signed multiplication of 18-bit per operand, followed by a 48-bit adder. Two DSPs are used to create a 35 × 18-bit fully pipelined multiplier with a 48-bit adder after the multiplication stage. The six filter state variables of the 32 channels are stored in a 48-bit width BRAM, where the state variables of each channel are mapped. A scaling factor of $2^{15}$ is chosen to scale the filter coefficients to fit the 18-bit signed input of the multiplier being sure to not exceed the $\pm 2^{17}$ limit. In

Table 2. Coefficients for the third order IIR filter scaled by the scaling factor of $2^{15}$ and the percentage error introduced from the integer rounding.

	Coefficients				Rounding Error (%)
	0	1	2	3	0	1	2	3
a	30.388	−91.163	91.163	−30.388	0.0021	0.0010	0.0010	0.0021
b	32.768	−93.364	88.789	−28.180	0	0.0009	0.0001	0.0008

, the integer coefficients are shown with the percentage rounding error. For each new sample to filter, the sum of the 16-bit value of the new sample with the state $s_4\left(n\right)$ is tied in the input on the 35-bit multiplicand port. This value is reduced by the scaling factor and is resized to 35 bits without losing any information. The filter coefficients are given sequentially on the 18-bit multiplier port and the corresponding channel state variable is given on the 48-bit sum port to compute all the new state values. The filter output, reduced by the scaling factor, can be safely resized to 16 bits. Even if it is smaller on average compared to the input, the output bit width is kept the same since an eventual stimulation artifact can cause the signal to span on the entire range even after the filtering.

2.2.2. Savitzky-Golay Fitting

The Savitzky-Golay fitting consists in a convolution of a mask of seven coefficients with the last seven samples of the channel. Similarly to the high-pass filter, the seven coefficients of the second grade polynomial fitting are multiplied by a scaling factor. The coefficients can safely be scaled by a factor of $2^{18}$, without exceeding the signed range of an 18-bit word. The last seven values of each channel are stored in a 16-bit width BRAM. The last six samples are ordered in BRAM by channel (i.e., ch1-sample1, …, ch1-sample6, …, ch32-sample1, ch32-sample 6) to be linearly indexed. The convolution exploits the DSP48A1, configured in an 18 × 18-bit multiply and accumulate mode. Each sample is extracted sequentially from the BRAM and is multiplied by its respective coefficient with the DSP multiplier, the result is then accumulated in the 48-bit register. Each sample, when read from the BRAM, is re-inserted as one position delayed—except for the sixth which is discarded—and the new sample is inserted first, to achieve the behavior of a shift register. The accumulation register is reset to a value of $2^{17}$ before receiving any new samples, to account for the 0.5 rounding of the bit shift division used to remove the scale factor from the convolution output. The average error introduced by the rounding after the scaling is 0.0004%.

2.2.3. Smoothed Nonlinear Energy Operator

The operations of the SNEO component involve two DSP48A1 configured in a 35 × 18-bit fully pipelined multiply and accumulate mode and a 35-bit width BRAM. The component receives three samples depending on the SNEO $k$ parameter, to compute the new signal energy value of a 35-bit width as shown in the first row of Equation (1). Both the BRAM organization and convolution with the Bartlett window are implemented as in the Savitzky-Golay component, but with a convolution length of 17. The multiplier input of 35-bit is required due to the energy value width. The Bartlett window is scaled by a factor of $2^{16}$, introducing an average error of 0.0025%. Therefore, the accumulation register starts from a value of $2^{15}$ for the bit shift 0.5 rounding.

2.2.4. Energy RMS and Threshold

This component provides a threshold based on the RMS estimation of the SNEO output to each channel. The RMS is computed incrementally, accumulating the square of the 32-bit energy values of a timeframe. To compute the square of the value, a 35 × 35-bit multiplier based on a single DSP48A1 slice is used. The cumulative sum of the 32 channels is stored in an 85-bit width BRAM. The last thresholds found for each channel and the last 32 RMS values from the previous timeframe are also stored in two 35-bit width BRAM. This allows comparing the energy value with the channel threshold before accumulating it and, in case it is greater, to replace its value with the last RMS value. A counter keeps the number of samples processed and after a timeframe of $2^{15}$ samples, the square root of the accumulated squared sum is computed with the abacus algorithm, returning an integer approximation of the solution in a variable number of iterations. The result is multiplied by the user-selected multiplier and is stored in the thresholds BRAM.

2.2.5. Local Minimum Finder and Spike Output

Whenever a spike is detected, the minimum is found cycling through the last 17 samples of the filtered signal of the channel, stored in a 16-bit width BRAM, to find the maximal negative amplitude. The final timestamp is computed as the difference from the position of the minimum value and the current timestamp, while the amplitude is the minimum value. The timestamp, the amplitude, and the channel of the detected spike are inserted in two different FIFOs. The first is used to cross the clock domain to match the USB communication frequency. Amplitude (16-bit), channel number (8-bit), threshold multiplier (8-bit), and timestamp (32-bit) are written concatenated in the FIFO, which keeps the data count and, thanks to the different aspect-ratio, provides the data in a 16-bit word to the logic managing the USB data transfer. The data count helps a fast transfer of the data to the host PC, as explained in the next subsection. The second FIFO has an 8-bit width, and the timestamp (27-bit) channel number (5-bit), and amplitude (16-bit) of the spike are written in little-endian byte order. This FIFO is used to manage the data transfer via the UART protocol from a GPIO on the high-speed port on the back of the recording system. Data is read and transferred at 8-bit at a BAUD rate that can be customized in the design.

2.2.6. Software Integration

The open-source software of the RhythmStim for the host computer has been modified (with Qt 5.15.1) to support the new features introduced in the acquisition system. By default, the software manages the data transfer from the acquisition system to the computer thanks to the USB communication provided by the PipeOut construct, of the Opal Kelly board and manages the transfer of data via USB. On the HDL side, the PipeOut is instantiated on a specific endpoint, an address, and it is interfaced with the read-side of a 16-bit width FIFO. At this point, the data contained in the FIFO can be retrieved with an API call on the host side, specifying the endpoint and the length of the transfer in bytes. A PipeOut is instantiated in the RhythmStim design connected to the Opal Kelly RAM to manage and buffer the recording transfer. A second PipeOut has been added to bypass the RAM buffering and to provide the spikes information with a lower latency. While the first PipeOut continues to stream the buffered data in big chunks, the software runs a secondary thread polling the new PipeOut for new data every millisecond. The FIFO connected to the PipeOut provides to the software the count of words that it contains. Whenever the software notices that this count is greater than 0, it reads from the PipeOut all the spikes contained in the FIFO. The words counter is given to the host by the WireOut construct of the Opal Kelly, that thanks to an endpoint exposes FPGA variables of 32 bits via USB through an API. The spikes acquired by the software can be streamed via the UDP protocol to any user-defined IP address. The packet is formed by four integers of 4 bytes in Big-Endian order which are, ordered in an array position from 0 to 3: Zero, timestamp, amplitude, and channel. If the acquisition system is saving data on the disk, the detected spikes are also stored in a file separated from the main record. Thanks to the WireIn constructs, used to show variables from the software to the FPGA, the user can control the digital SD through the software to run or stop it, to set the threshold multiplier (in 0.5 step), the blind window length (to stop the detection for a few ms after a stimulation command), and the channels whose outputs have to be active. These parameters are exposed to the user with a dedicated application window reachable from the main window of the RhythmStim application, also showing a real time raster plot of the spiking activity (Figure 8).

2.3. Animals and Surgical Procedure

The experiments shown in the Results section are recorded from the barrel cortex of anesthetized rats belonging to the Wistar strain, which are maintained under standard environmental conditions in the animal research facility of the Department of Biomedical Sciences of the University of Padua. All the procedures are approved by the local Animal Care Committee (OPBA) and the Italian Ministry of Health (authorization number 522/2018-PR). Young adult P28–P32 rats (being P0 the day of birth) of both genders and with body weight between 90 and 120 g are anesthetized with an intra-peritoneal induction dose of Urethane (0.15/100 g body weight), followed by a single additional dose (0.015/100 g body weight). Each animal is positioned on a stereotaxic instrument and the head is fixed by teeth- and ear-bars. After a sub-cutaneous injection of Carprofen painkiller (Rimadyl; 10 µL/100 g body weight), an anterior-posterior opening in the skin is made in the center of the head and a dedicated window in the skull is drilled over the somatosensory barrel cortex at stereotaxic coordinates −1 ÷ −4 AP, +4 ÷ +8 ML referred to as bregma [27,28], and the linear probe (E32+R-65-S1-L6 NT IrOx; Atlas Neuroengineering, Figure 9) is then inserted orthogonal to the cortical surface in the middle of the window at coordinates −2.5 AP, +6 ML. As a reference for the recording/stimulation, the depth is set at 0 when the electrode proximal to the chip tip touches the cortical surface. The neuronal activity is recorded by the 32 electrodes from the entire barrel cortex (from 0 to −1750 µm), which is constantly bathed in Krebs’ solution (in mM: NaCl 120, KCl 1.99, NaHCO₃ 25.56, KH₂PO₄ 136.09, CaCl₂ 2, MgSO₄ 1.2, glucose 11). An Ag/AgCl electrode bathed in the extracellular solution in proximity of the probe is used as a reference.

3. Results

The SD has been tested on both simulations and different in vivo experiments collected in our laboratory from the barrel cortex of six different rats. The experimental protocol consists of a 5 min recording where 28 cathodic to anodic (negative to positive) ICMSs of 50 µA amplitude and 200 µs duration per phase have been delivered every 10 s from the fifteenth electrode. Figure 10 shows the performances of the SD on 15 s around one of the given ICMS of a channel recording a strong spiking signal. The threshold multiplier is set to a value of 18 to focus on the detection of the single unit AP. Note that the first spikes are lost due to the threshold initialization. The threshold fluctuation depends on the MUAs energy around the APs, that being undetected (as expected), influences the RMS level. Anyway, the fluctuation is small compared to the energy developed by the spikes and the threshold remains closer to what would be the noise-based value, allowing for an accuracy greater than that achievable with the firing-dependent threshold. The accuracy achieved on the entire acquisition of 5 min is 92%, with 1369 spikes detected out of 1429 and 58 false negatives. The accuracy, once again, has been defined as the ratio between the correct detection and the sum of the total spikes and the false positives.

The off-line analysis performed on our experiments showed that APs were found on a reduced subset of channels. Since the probe used in this study is not a high-density one (65 µm pitch), the probability to get close to multiple neurons with the electrodes surface is low, resulting in only one or two channels acquiring strong APs. On the six experiments, spikes with a strong negative peak below −70 µV were not present in any channels in two experiments, on two channels in three experiments, and only on a single channel in a single experiment. This is the reason behind the need of an accurate MUA detection. Unfortunately, the SD performances for MUA detection are difficult to properly evaluate on simulation. MUAs are generated by a simultaneous activity of large populations of neurons spatially distributed and interconnected, a behavior which is difficult to emulate reliably to create a synthetic dataset. Therefore, here MUAs are quantified on the information provided on in vivo experiments. A MUA detection example from a channel without neurons close enough to the electrode to allow distinguishing single unit APs can be seen in Figure 11. The RMS multiplier used to find the threshold must be set to a value significantly lower than that used for the single AP detection and here is set to 5.5. A more stable threshold compared to that of the single AP detection can be observed, which is due to the fact that the MUA contribution is excluded from the RMS estimation, while MUA fluctuations in the AP detection were treated as noise. The results are a smoother threshold change between the different timeframes and the capability to also accurately detect the smaller fluctuation at the beginning and end of MUAs.

The ICMS experiments allowed evoking a response both in the LFP and in the high frequency domain and thus, to perform a comparison with the MUA detection. A stereotyped response, as shown in Figure 12, has been evoked and therefore, detected reliably in the six in vivo experiments for 12, 20, 26, 27, 27, and 28 trials out of the 28 given stimuli. On all the trials where a response was visible in the LFP domain, the SD highlighted MUAs correspond to the LFP negative peaks. Figure 12 shows an example of a stereotyped evoked response where MUAs are detected in the channels near the stimulation site after a silent period of 170 ms from the ICMS and further expands rhythmically in repetitions spreading across multiple channels of the linear probe. Before the stimulation, in comparison, the detected activity shows some spurious unsynchronized spiking activity.

The clock cycles required for each component of the design to output the result are reported in

Table 3. Clock cycles required by the design components to provide the output.

Component	Clock Cycles to Output	Notes
Samples preprocessing	7	cross-clock and samples format
High-pass filter	11	complete the filter state after 17
Savitzky-Golay fitting	15	8 + mask length
SNEO	34	18 + 4 * k (k = 4)
Thresholding	5
Local minimum	20	4 $\ast$ k + 4 (k = 4)
Samples postprocessing	4	writing to output FIFOs
Threshold estimation 1	11	the square root and eight more cycles are required every $2^{15}$ samples
Total	96	One hundred and twenty-five cycles are available between the two samples

¹ Threshold estimation does not influence the total cycles count since no other components wait for its output.

, where the latency of each pipeline component is evaluated, from the samples acquisition of the main RhythmStim loop to the writing of the results in the output FIFOs. The cycles required are intrinsically dependent on the parameters $k$ of the SNEO, that in this design is assumed to be 4.

Table 4. Logic utilization of designs.

Logic	Default	Custom	Increment	Available
Slice register	8883	13,770	4887	54,576
Slice LUT	17,775	23,065	5290	27,288
BRAM16	69	76	7	116
BRAM8	0	15	15	232
DSP48A1	8	19	11	58

compares the FPGA logic consumed by the Intan RhythmStim design by default without any addition and the logic used after the modified implementation, highlighting the amount of space left available on the FPGA for eventual further development of other functionalities. This led to a power consumption reported by the Xilinx XPower Analyzer of the design modified with the SD of 1.002 W, with an increment of 0.096 W over the default design consumption of 0.906 W.

4. Discussion

The first design constraint of the system is the sub-millisecond latency between a neuronal spike peak in the biological domain and its detection and digital communication. The latency of the system can be calculated from Table 3. Each of the 16 pairs of samples is acquired at 25 kHz, thus the total system sampling rate is 400 kHz. Considering the SD working frequency of 100 MHz, each pair disposes of 250 clock cycles to be elaborated, hence 125 cycles for each sample. The design requires 96 clock cycles to process a single sample, that results in about 1 µs of processing time. The detection can be algorithmically found after only 14 samples from a spike peak, since the k NEO output evaluates the energy of the central sample in the $2k+1$ window and in turn the smoothing refers to the central energy value of the Bartlett window of $4k+1$, where $k=4$. Considering the processing time and the channels sampling period of 40 µs, the time required to detect a spike is about half-millisecond. The communication latency depends on the UART baud rate: Assuming a rate of 230,400, 6 bytes can be transferred in less than 240 µs. This satisfies the initial constraint of the sub-millisecond processing time from a spike peak to its propagation for a fast and reliable closed-loop system design. Obviously, the time required to transfer the spikes information via the USB to the host computer is affected by different factors as mentioned in the introduction, but considering the privileged USB communication and the 1 ms polling by the host application, the spike reception latency will be of a few milliseconds at most. The second constraint was to have a higher system accuracy compared to the SD included in the default RhythmStim design. The SD accuracy of this work allows detecting the single unit APs with a great precision up to 92%, with a reduced number of false positives and without false detections during the post-ICMS artifact. Furthermore, the SD can be used to provide a precise firing profile of MUAs, that due to the low SNR are difficult to correctly recognize with a standard threshold crossing approach. The firing-independent threshold helps in this by providing a stable threshold value, especially when detecting MUAs, and it has the valuable advantage to avoid the hand-tuning of the threshold for each channel, an important limitation of the default SD. As already mentioned, our recording from the rat barrel cortex showed strong APs—with a similar shape—only on few channels per records, while MUAs were recorded by most of the channels. For this reason, a spike sorter has not been included in the design.

Table 5. Comparison of this work with other works including the default spike detector of the Intan RHS stimulation/recording system.

	This Work	Default	[29]	[24]	[30]
AP detection accuracy (%)	92	N/A	90.7	80–96 1	N/A
Latency (ms)	~0.5	0.2	0.3–0.8	1.96	0.1
Supported channels	32	8	8	1	32
Automatic threshold	✓	✗	✗	✓	✓
Stimulation artifact dealing	✓	✗	✓	✗	✗
MUA detection	✓	~	✓	✗	✗
Sorting	✗	✗	✗	✓ 2	✓ 2
UDP spike communication	✓	✗	✗	✗	✗
Use Intan RHS	✓	✓	✓	✓ 3	✓ 3
Code availability	✓	✓	✓	✗	✓

¹ On spike sorting; ² off-line clustering with template matching; ³ headstage only.

shows a comparison with other similar recent works. Work from Murphy, M. at al. [29] is the most similar, being developed on the same recording system, while works from Wang, P.K. et al. [24] and Luan, S. et al. [30] use only the same headstage. Particularly, the latter is a battery-powered standalone platform that logs data on a SD card and therefore, could be considered belonging to another category of devices.

5. Conclusions

In this work, a design for an embedded low latency reliable SD for the Intan Technologies RHS stimulation/recording controller, able to detect AP and MUA on up to 32 channels, has been presented. The implementation consists of a third order high-pass digital IIR filter, a Savitzky-Golay polynomial fitting, a SNEO, and a continuously updated firing-rate-independent threshold and allows dealing with the stimulation artifact, avoiding the detection of false positives. Particularly, the threshold computation is based on an RMS estimation that rejects the spikes energy, approximating the recording real noise. This allowed reaching an accuracy of the 92% for the single AP detection and a precise firing profiling of MUAs. The design requires a total of less than half-millisecond from a spike peak for the detection and the communication of the spike details via the UART protocol. Simultaneously, the detections details are also sent via a privileged USB connection to the RHS Stimulation/Recording application, where a newly developed interface allows configuring the spike detector to show the real-time raster plot of the activity detected and to send through the network the detection information via the UDP protocol.

This design is currently used in our laboratory for the purpose of the SYNCH project. This project aims to create a hybrid system where a neural network in the rat brain is interconnected by neuromorphic synapses to an on-chip silicon neural network of spiking neurons, to enable the co-evolution of connectivity and the co-processing of information by the two. Therefore, the modified system presented in this work is used to recognize the spiking activity of the neurons population to be given in the input to the artificial network. This processes the information and interacts and influences the biological network through ICMS.

The design works out-of-the-box with the Intan RHS stimulation/recording controller, but it has been encapsulated and parametrized to make it easily adapted to other platforms, and it can be modified and scaled both in the capabilities and number of supported channels. The elaboration throughput, if required, can be increased by running the different components of the pipeline in parallel, allowing to start the processing of a new sample before the previous has been completed. The source code of the project can be found on GitHub (www.github.com/Tiax93/RhythmStim-SNEO).