Improving Generalized Discrete Fourier Transform (GDFT) Filter Banks with Low-Complexity and Reconfigurable Hybrid Algorithm
Abstract
1. Introduction
2. Methodology
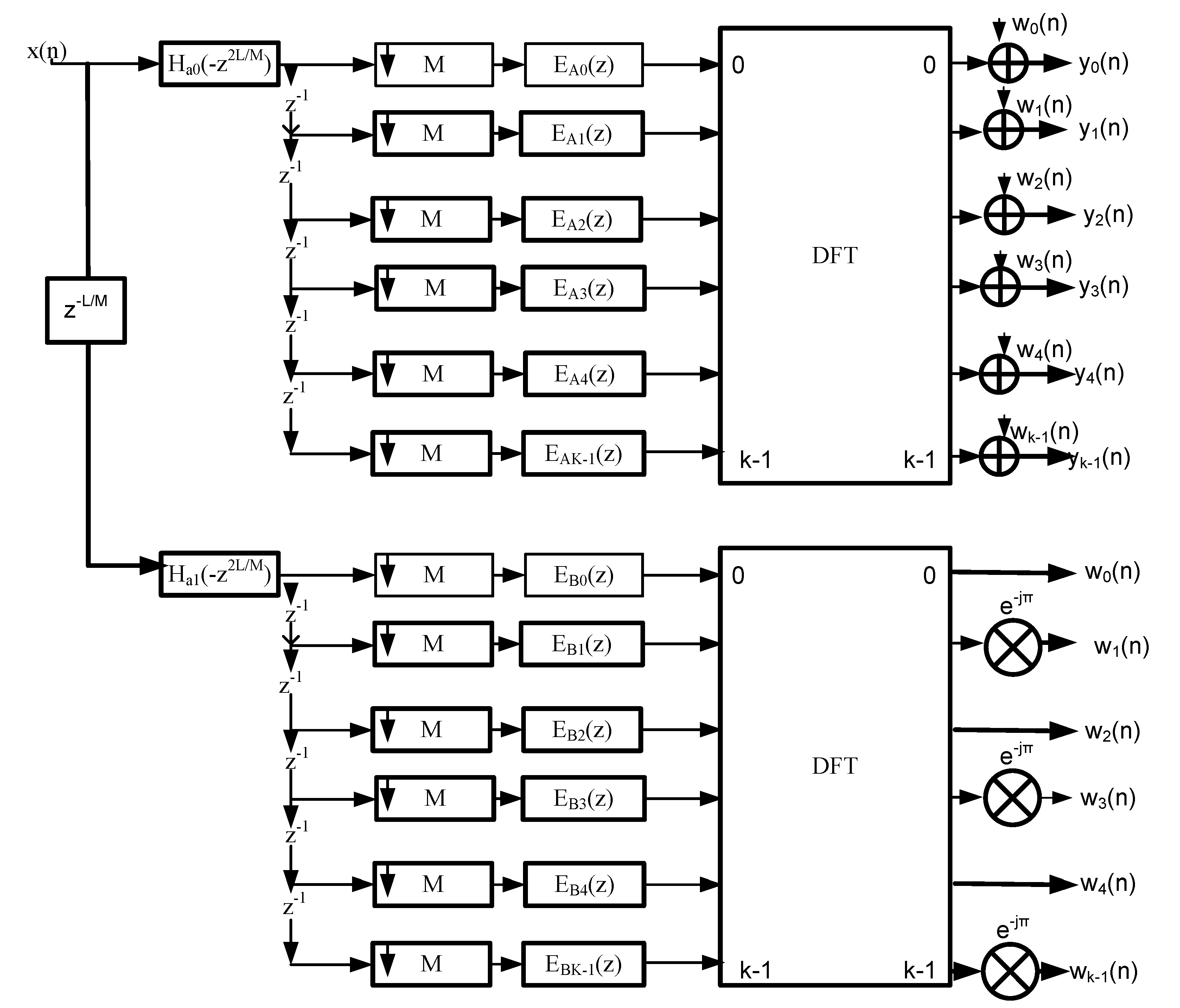
2.1. Proposed Hybrid Generalized Discrete Fourier Transform (HGDFT-FB)
2.1.1. Proposed Design Steps
- Normalise all the channel bandwidths (BWs), such that the and transition bandwidth specifications range from 0 to 1; 1 corresponds to , where is the sampling frequency.
- Calculate each channel stopband frequency, such that .
- Calculate the modal bandwidth such that = GCD/2. This corresponds to the modal stopband frequency.
- Calculate the decimation factor M of the masking filter using the formula M=. The interpolated factor is calculated using the formula , where is the stopband frequency for each channel. Thus, the fractional rate for the masking filter can be calculated as .
- Calculate the decimator factor of the complementary filter using the formula . The interpolated factor is calculated using the formula . Thus, the fractional rate for complementary filter can be calculated as .
- Determine the transition bandwidth for the masking and complementary filters, , such that = , where is the fractional rate for masking or complementary filter.
- Determine the base modal or complementary modal TBW as= min. This corresponds to the modal transition width.
- Calculate the modal, masking, and complementary passband widths using = .
- Determine the passband edge and stopband edge of the modal or prototype filter, masking, and complementary filter, using Table 2, where m = for the masking filter and m = for the complementary filter.
- Find the stopband ripple using = .
- The modal passband peak ripple is calculated as: = min().
- The cutoff frequency of the prototype and masking filter are calculated using Table 2.
- Determine the prototype filter order and the individual channel filter order using the Bellanger formula N = [58].
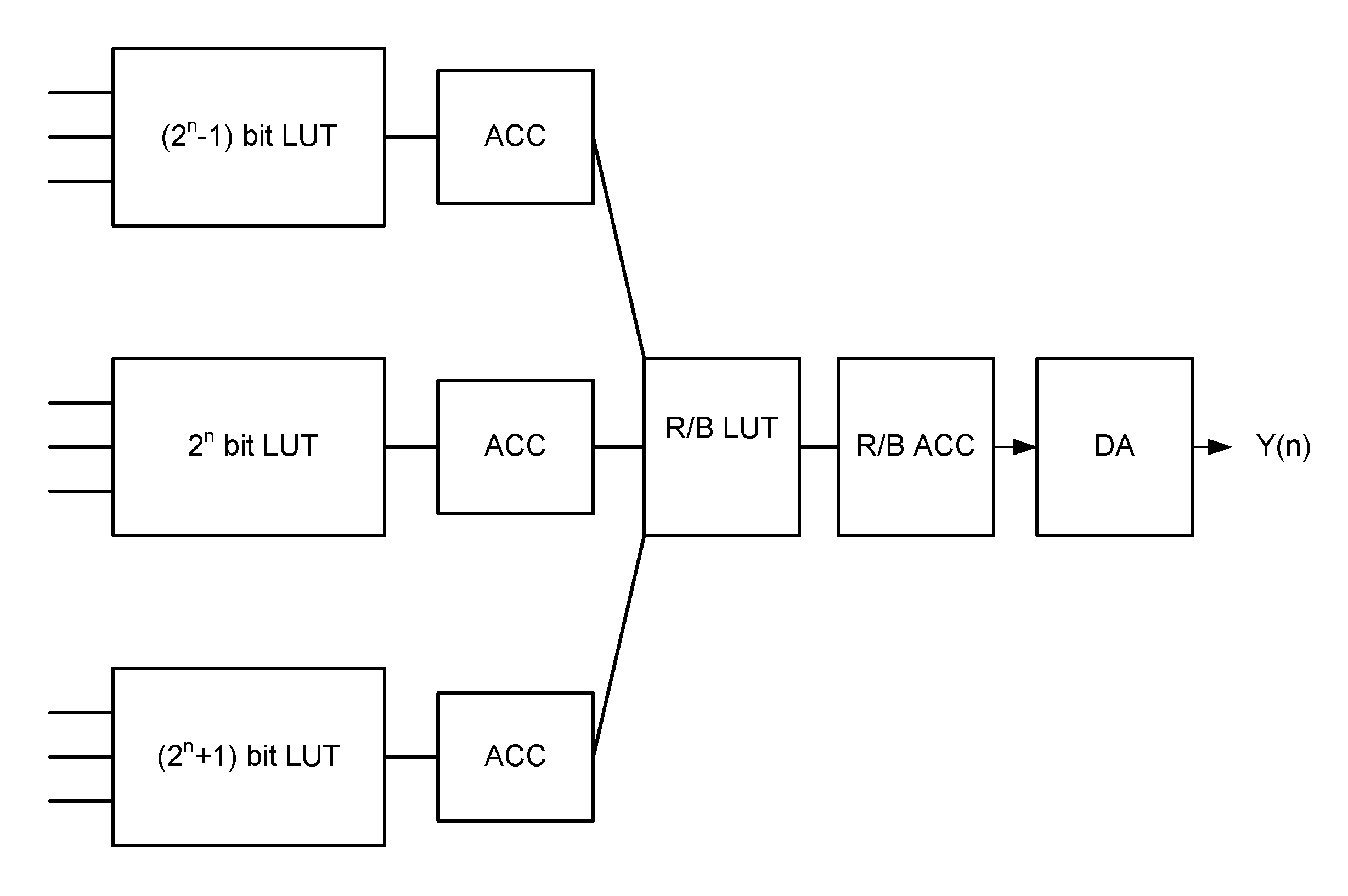
2.2. Improving HGDFT with Parallel Distributed Arithmetic-Based Residual Number System (PDA-RNS)
2.2.1. Application of HGDFT with PDA-RNS Filter Bank to Non-Uniform Channels: BT, ZIGBEE, WCDMA
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Boucheret, M.L.; Mortensen, I.; Favaro, H. Fast convolution filter banks for satellite payloads with on-board processing. IEEE J. Sel. Areas Commun. 1999, 17, 238–248. [Google Scholar] [CrossRef]
- Lillington, J. Comparison of wideband channelisation architectures. In Proceedings of the International Signal Processing Conference (ISPC), Dallas, TX, USA, 31 March–3 April 2003. [Google Scholar]
- Deshmukh, T.P.; Deshmukh, P.; Dakhole, P. Design of cyclotomic Fast Fourier Transform architecture over Galois field for 15 point DFT. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; pp. 607–611. [Google Scholar]
- Diniz, P.S.; Da Silva, E.A.; Netto, S.L. Digital Signal Processing: System Analysis and Design; Cambridge University Press: Cambridge, UK, 2010; pp. 259–299. [Google Scholar]
- Navarro, A.P. Overlapped polyphase DFT modulated filter banks applied to TETRA/TEDS SDR base station channelization. In Proceedings of the Royal Irish Academy Communication and Radio Science Colloquium, Dublin, Ireland, 21–22 April 2010. [Google Scholar]
- Tietche, B.H.; Romain, O.; Denby, B. Sparse channelizer for FPGA-based simultaneous multichannel DRM30 receiver. IEEE Trans. Consum. Electron. 2015, 61, 151–159. [Google Scholar] [CrossRef]
- Duhamel, P.; Vetterli, M. Fast Fourier transforms: A tutorial review and a state of the art. Signal Process. 1990, 19, 259–299. [Google Scholar] [CrossRef]
- Crochiere, R.E.; Rabiner, L.R. Multirate Digital Signal Processing, 1983; Pretice Hall: Upper Saddle River, NJ, USA, 1987; pp. 127–192. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Abu-Al-Saud, W.A.; Stuber, G.L. Efficient wideband channelizer for software radio systems using modulated PR filterbanks. IEEE Trans. Signal Process. 2004, 52, 2807–2820. [Google Scholar] [CrossRef]
- Kalathil, S.; Elias, E. Non-uniform cosine modulated filter banks using meta-heuristic algorithms in CSD space. J. Adv. Res. 2015, 6, 839–849. [Google Scholar] [CrossRef]
- Blok, M. Fractional delay filter design for sample rate conversion. In Proceedings of the 2012 Federated Conference on Computer Science and Information Systems (FedCSIS), Wroclaw, Poland, 9–12 September 2012; pp. 701–706. [Google Scholar]
- Valimaki, V.; Haghparast, A. Fractional delay filter design based on truncated Lagrange interpolation. IEEE Signal Process. Lett. 2007, 14, 816–819. [Google Scholar] [CrossRef]
- Karp, T.; Fliege, N.J. MDFT filter banks with perfect reconstruction. In Proceedings of the ISCAS’95-International Symposium on Circuits and Systems, Seattle, WA, USA, 30 April–3 May 1995; Volume 1, pp. 744–747. [Google Scholar]
- Farrow, C.W. A continuously variable digital delay element. In Proceedings of the 1988 IEEE International Symposium on Circuits and Systems, Espoo, Finland, 7–9 June 1988; pp. 2641–2645. [Google Scholar]
- Kuldeep, B.; Kumar, A.; Singh, G. Design of quadrature mirror filter bank using Lagrange multiplier method based on fractional derivative constraints. Eng. Sci. Technol. Int. J. 2015, 18, 235–243. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P. Multirate Systems and Filter Banks; Pearson Education: Tamil Nadu, India, 1993. [Google Scholar]
- Brannon, B.; Efstathiou, D.; Gratzek, T. A look at software radios: Are they fact or fiction? Electron. Des. 1998, 46, 117–122. [Google Scholar]
- Chang, Z.; Vinod, A.; Meher, P. Reconfigurable architectures for low complexity software radio channelizers using hybrid filter banks. In Proceedings of the 2006 10th IEEE Singapore International Conference on Communication Systems, Singapore, 30 October–1 November 2006; pp. 1–5. [Google Scholar]
- Harris, F.; McGwier, R. A receiver structure that performs simultaneous spectral analysis and time series channelization. In Proceedings of the SDR’09 Technical Conference and Product Exposition, Washington, DC, USA, 1–4 December 2009. [Google Scholar]
- Navarro, Á.P. Channelization for Multi-Standard Software-Defined Radio Base Stations. Ph.D. Thesis, National University of Ireland Maynooth, Maynooth, Ireland, 2011. [Google Scholar]
- Palomo-Navarro, Á.; Farrell, R.J.; Villing, R. Combined FRM and GDFT filter bank designs for improved nonuniform DSA channelisation. Wirel. Commun. Mob. Comput. 2016, 16, 1440–1456. [Google Scholar] [CrossRef]
- Sudharman, S.; Rajan, A.D.; Bindiya, T. Design of a Power-Efficient Low-Complexity Reconfigurable Non-maximally Decimated Filter Bank for High-Resolution Wideband Channels. Circuits Syst. Signal Process. 2019, 38, 2703–2735. [Google Scholar] [CrossRef]
- Ambede, A.; Smitha, K.; Vinod, A.P. Flexible low complexity uniform and nonuniform digital filter banks with high frequency resolution for multistandard radios. IEEE Trans. Very Large Scale Integr. Syst. 2014, 23, 631–641. [Google Scholar] [CrossRef]
- Lovina, P.; Manjusha, K.A. SDR Applications using VLSI Design of Reconfigurable Devices. IJSRST 2018, 4, 1148–1153. [Google Scholar]
- Peng, X.; Li, J.; Zhou, X.; Lin, Q.; Chen, Z. Analysis and design of M-channel hybrid filter bank with digital calibration. IEEE Access 2018, 6, 24606–24616. [Google Scholar] [CrossRef]
- Badave, S.; Bhalchandra, A. Critical Path Reduction of Distributed Arithmetic Based FIR Filter. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 71–78. [Google Scholar] [CrossRef][Green Version]
- Singh, S.; Saini, S. Performance Analysis of FIR Filter Using Distributed Arithmetic. Glob. J. Comput. Technol. 2017, 5, 310–313. [Google Scholar]
- Naik, N.S.; Gupta, K.A. An efficient reconfigurable FIR digital filter using modified distribute arithmetic technique. arXiv 2017, arXiv:1704.08526. [Google Scholar]
- Yoo, H.; Anderson, D.V. Hardware-efficient distributed arithmetic architecture for high-order digital filters. In Proceedings of the (ICASSP’05) IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 23–23 March 2005; Volume 5, pp. 5–125. [Google Scholar]
- White, S.A. Applications of distributed arithmetic to digital signal processing: A tutorial review. IEEE Assp Mag. 1989, 6, 4–19. [Google Scholar] [CrossRef]
- Chen, C.C.; Lin, T.J.; Liu, C.W.; Jen, C.W. Complexity-aware design of a DA-based FIR filters. In Proceedings of the 2004 IEEE Asia-Pacific Conference on Circuits and Systems, Tainan, Taiwan, 6–9 December 2004; Volume 1, pp. 445–448. [Google Scholar]
- Longa, P.; Miri, A. Area-efficient FIR filter design on FPGAs using distributed arithmetic. In Proceedings of the 2006 IEEE International Symposium on Signal Processing and Information Technology, Vancouver, BC, Canada, 27–30 August 2006; pp. 248–252. [Google Scholar]
- Iruleswari, M.; Sheela Merlin, M.; Jeyapaul Murugan, A. Design and Implementation of distributed arithmetic technique based FIR filter using lookup table. Int. J. Innov. Res. Sci. Eng. Technol. 2016, 5, 3480–3488. [Google Scholar]
- Roy, K.J.; Ramya, R. Low-Power And Low-Area Adaptive FIR Filter Based on Distributed Arithmetic and LMS Algorithm. IJSRP 2014, 4, 1–5. [Google Scholar]
- Kalaiyarasi, D.; Reddy, T.K. Design and implementation of least mean square adaptive FIR filter using offset binary coding based distributed arithmetic. Microprocess. Microsyst. 2019, 71, 102884. [Google Scholar] [CrossRef]
- Bindiya, T.S.; Kumar, V.S.; Elias, E. Design of low power and low complexity multiplier-less reconfigurable non-uniform channel filter using genetic algorithm. Glob. J. Res. Eng. 2012, 12, 7–19. [Google Scholar]
- Bindiya, T.; Elias, E. Modified metaheuristic algorithms for the optimal design of multiplier-less non-uniform channel filters. Circuits Syst. Signal Process. 2014, 33, 815–837. [Google Scholar] [CrossRef]
- Srinivasa Reddy, K.; Sahoo, S.K. An approach for fixed coefficient RNS-based FIR filter. Int. J. Electron. 2017, 104, 1358–1376. [Google Scholar] [CrossRef]
- Andraos, S.; Ahmad, H. A new efficient memoryless residue to binary converter. IEEE Trans. Circuits Syst. 1988, 35, 1441–1444. [Google Scholar] [CrossRef]
- Molahosseini, A.S.; Navi, K. New arithmetic residue to binary converters. IJCSES 2007, 1, 296. [Google Scholar]
- Premkumar, A.B. An RNS to binary converter in a three moduli set with common factors. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1995, 42, 298–301. [Google Scholar] [CrossRef]
- Premkumar, A.B.; Bhardwaj, M.; Srikanthan, T. High-speed and low-cost reverse converters for the (2n − 1, 2n, 2n + 1) moduli set. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1998, 45, 903–908. [Google Scholar] [CrossRef]
- Vun, C.H.; Premkumar, A.B.; Zhang, W. A new RNS based DA approach for inner product computation. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2139–2152. [Google Scholar] [CrossRef]
- Živaljević, D.; Stamenković, N.; Stojanović, V. Digital filter implementation based on the RNS with diminished-1 encoded channel. In Proceedings of the 2012 35th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 3–4 July 2012; pp. 662–666. [Google Scholar]
- Vergos, H.T.; Efstathiou, C. A unifying approach for weighted and diminished-1 modulo 2 n+1 addition. IEEE Trans. Circuits Syst. II Express Briefs 2008, 55, 1041–1045. [Google Scholar] [CrossRef]
- Singh, R.; Mishra, R. Design and Simulation of Diminished-One Modulo 2n+ 1 Adder Using Circular Carry Selection. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011. [Google Scholar]
- Mohan, P.A. Evaluation of fast conversion techniques for binary-residue number systems. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1998, 45, 1107–1109. [Google Scholar] [CrossRef]
- Skavantzos, A.; Abdallah, M. Implementation issues of the two-level residue number system with pairs of conjugate moduli. IEEE Trans. Signal Process. 1999, 47, 826–838. [Google Scholar] [CrossRef]
- Conway, R.; Nelson, J. Fast converter for 3 moduli RNS using new property of CRT. IEEE Trans. Comput. 1999, 852–860. [Google Scholar] [CrossRef]
- Gbolagade, K.A.; Voicu, G.R.; Cotofana, S.D. An Efficient FPGA Design of Residue-to-Binary Converter for the Moduli Set. IEEE Trans. Very Large Scale Integr. Syst. 2011, 19, 1500–1503. [Google Scholar] [CrossRef]
- Hiasat, A. A Residue-to-Binary Converter for the Extended Four-Moduli Set. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 2188–2192. [Google Scholar] [CrossRef]
- Ambede, A.; Shreejith, S.; Vinod, A.P.; Fahmy, S.A. Design and realization of variable digital filters for software-defined radio channelizers using an improved coefficient decimation method. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 59–63. [Google Scholar] [CrossRef]
- Mahesh, R.; Vinod, A.P.; Lai, E.M.; Omondi, A. Filter bank channelizers for multi-standard software defined radio receivers. J. Signal Process. Syst. 2011, 62, 157–171. [Google Scholar] [CrossRef]
- Sakthivel, V.; Elias, E. Low complexity reconfigurable channelizers using non-uniform filter banks. Comput. Electr. Eng. 2018, 68, 389–403. [Google Scholar]
- Devi, P.K.; Bhuvaneshwaran, R. FPGA implementation of coefficient decimated polyphase filter bank structure for multistandard communication receiver. J. Theor. Appl. Inf. Technol. 2014, 64, 298–306. [Google Scholar]
- Cappello, S.; Cardarilli, G.; Di Nunzio, L.; Fazzolari, R.; Re, M.; Albicocco, P. Flexible channel extractor for wideband systems based on polyphase filter bank. J. Theor. Appl. Inf. Technol. 2017, 95, 3841–3850. [Google Scholar]
- Bellanger, M. On computational complexity in digital filters. In Proceedings of the European Conference on Circuit Theory and Design, Hague, The Netherlands, 25–28 August 1981; pp. 58–63. [Google Scholar]



| Channelisation Technique | Computational Load | Reconfigurability |
|---|---|---|
| Per Channel [1,2,3] | Very High | Bad |
| Binary Approach [4] | High | Bad |
| DFT [5] | Very High | Bad |
| DFT (poly-phase) [6,7,8,9] | High | Bad |
| EMFB [10,11] | Low | Bad |
| FPCC [12,13,14,15] | Low | Bad |
| QMFB [16,17] | High | Bad |
| TQMB [18] | High | Good |
| GDFT [5] | High | Good |
| HTQMB [19,20] | High | Good |
| PGDFT [10,21] | High | Good |
| RGDFT [10,22] | High | Good |
| FRM [22,53] | High | Good |
| CDM 1 and 11 [23,24,25,26] | Low | Bad |
| MCD 1 and 11 [23,24,25,26] | Low | Bad |
| ICDM 1 and 11 | Low | Bad |
| Parameter | Case 1 | Case 2 |
|---|---|---|
| = | = | |
| = | = | |
| = | = | |
| = | = |
|
Filter Bank |
Stopband Frequency () |
Passband Frequency () |
Stopband Attenuation () |
Passband Ripples () |
Filter Length | |
|---|---|---|---|---|---|---|
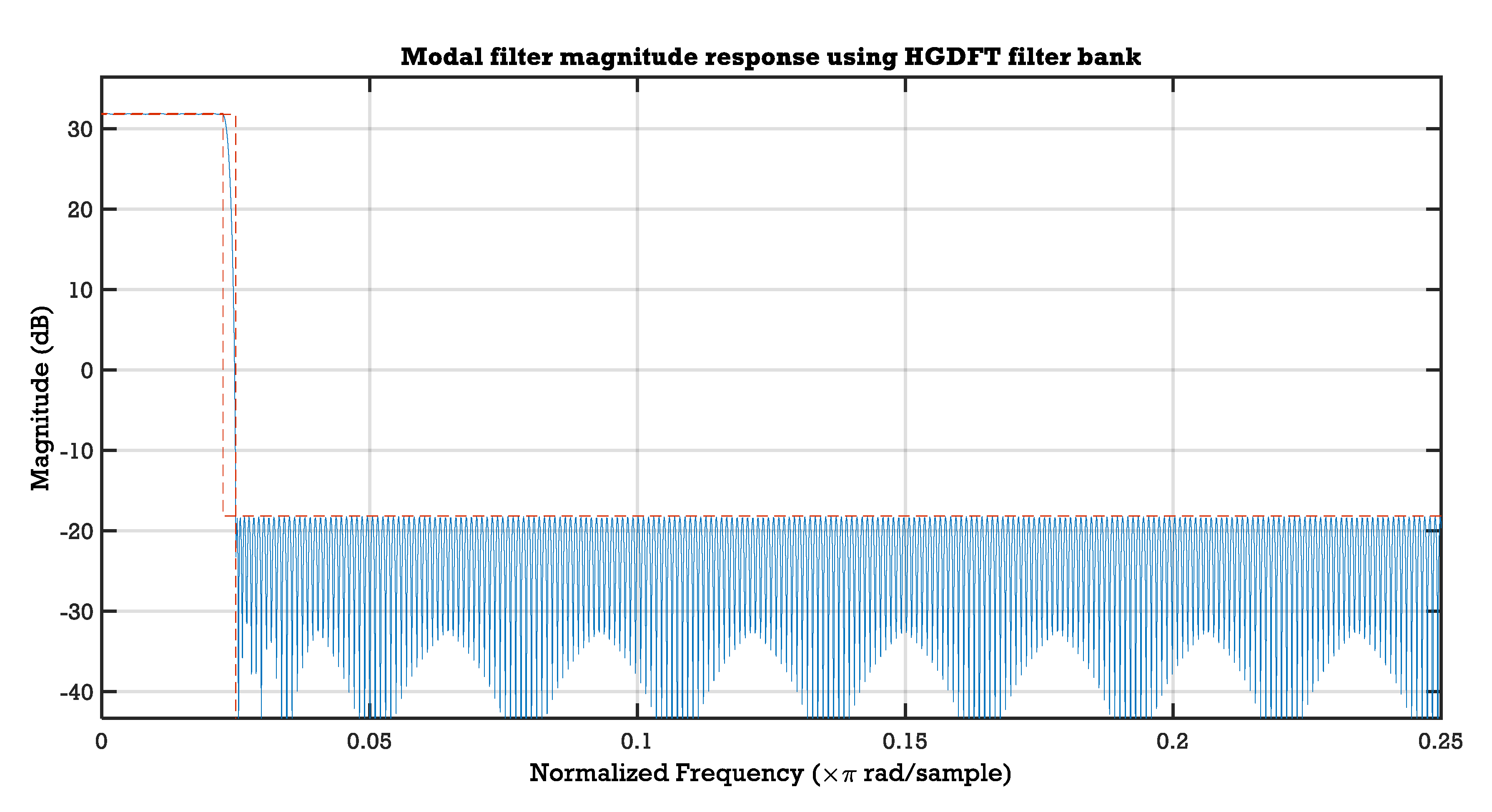
| Modal filter, | 0.025 | 0.022625 | 0.1 | −50 | 196 | |
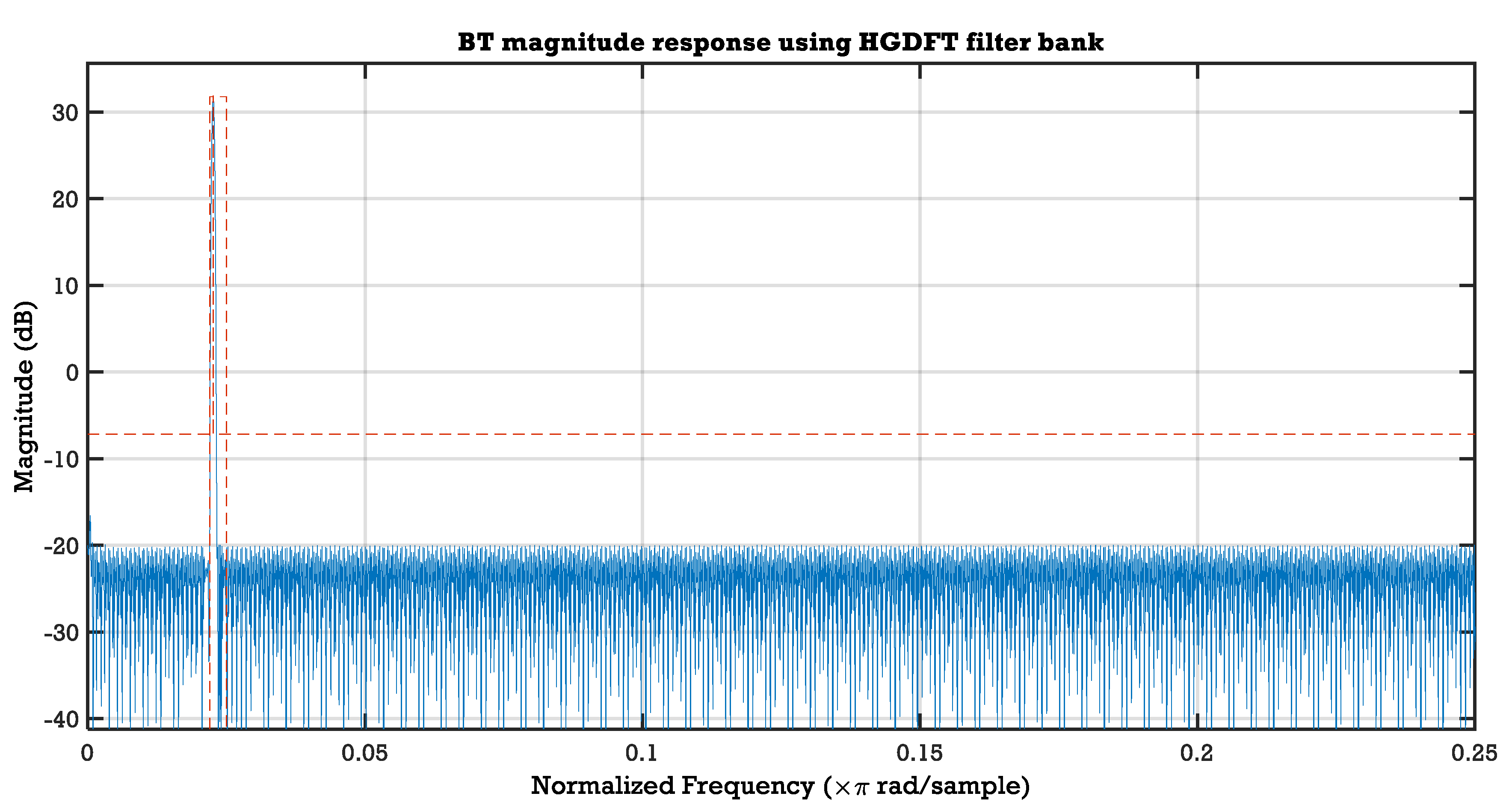
| Bluetooth, | 0.025 | 0.0224 | 0.0975 | −39 | 159 | |
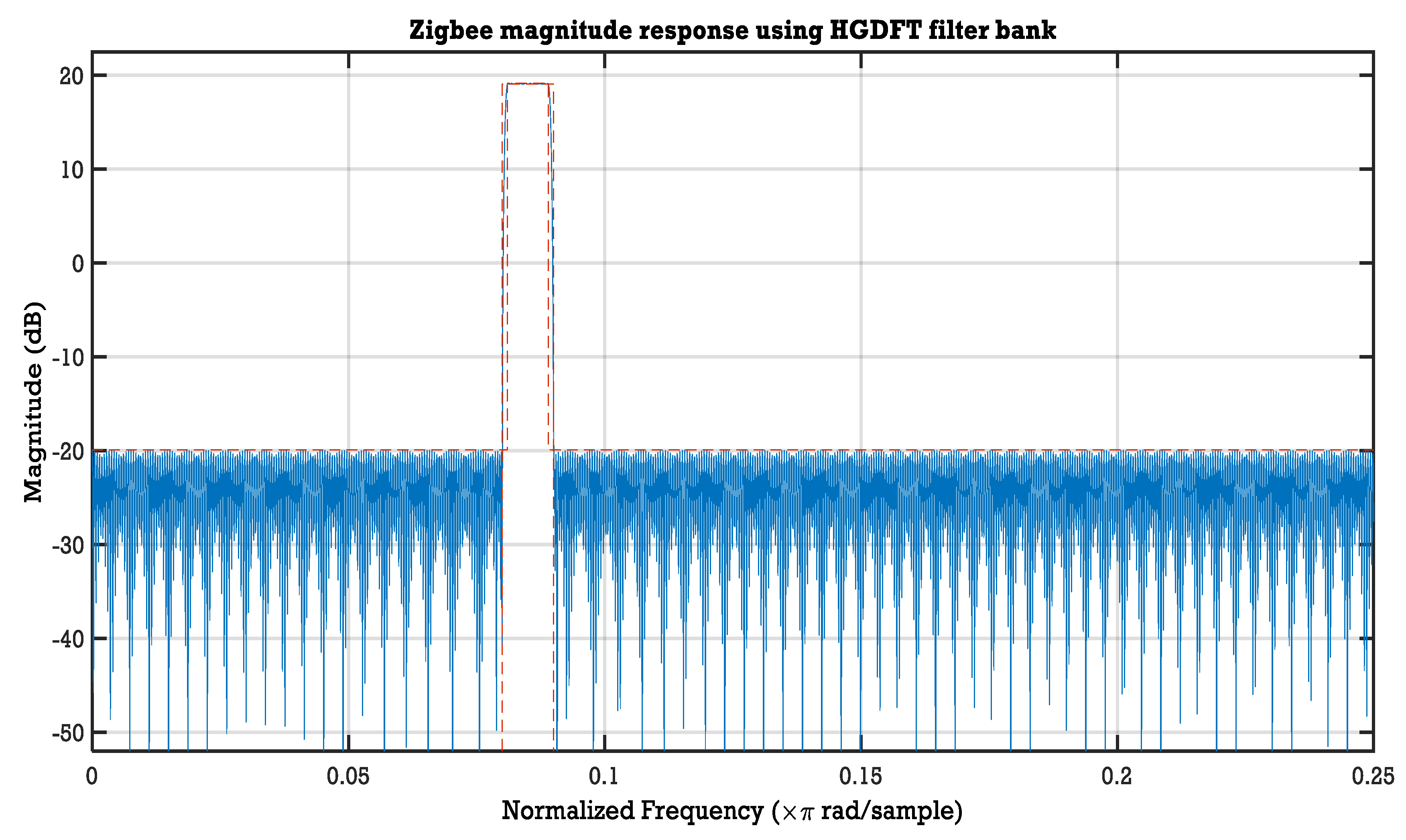
| Zigbee, | 0.1 | 0.089 | 0.09 | −39 | 34 | |
| WCDMA, | 0.2 | 0.125 | 0.0875 | −48.25 | 13 |
| Filter Specification | Sampling Frequency (MHz) | Channel Bandwidth (MHz) | Transition Bandwidth (kHz) | Passband Ripples (dB) | Stopband Ripples (dB) |
|---|---|---|---|---|---|
| Bluetooth | 40 | 1 | 50 | 0.1 | −40 |
| Zigbee | 40 | 4 | 200 | 0.1 | −40 |
| WCDMA | 40 | 5 | 500 | 0.1 | −55 |
| Filter Bank | Passband Frequency () | Stopband Frequency () | Stopband Attenuation () | Passband Ripples () | Filter Length | |
|---|---|---|---|---|---|---|
| Modal filter, | 0.027307 | 0.02269 | 0.1 | −50 | 209 | |
| Bluetooth, | 0.027307 | 0.02269 | 0.092 | −36.92 | 150 | |
| Zigbee, | 0.1080 | 0.0911 | 0.088 | −35.5 | 37 | |
| WCDMA, | 0.2 | 0.125 | 0.0875 | −48.25 | 13 |
| Filter Bank | Filter Order | Total Number of Multiplication | ||
|---|---|---|---|---|
| Modal filter | 405 | - | - | 320 |
| BT | - | 159 | 150 | 156 |
| Zigbee | - | 34 | 37 | 37 |
| WCDMA | - | 13 | 13 | 13 |
| Filter Bank | Filter Order | Total Number of Multiplication | ||
|---|---|---|---|---|
| CDFB [54] | 3089 | 400 | - | 1745 |
| ICDM FB [53] | 2929 | 160 | - | 1545 |
| NU-MDFT FB [55] | 187 | 430 | 469 | 1090 |
| Proposed HGDFT filter bank Bank | 320 | 104 | 102 | 526 |
| Filter | Input Bits | Passband Filter PB Ripples(dB) | Stopband Attenuation | No of Adders | Amp-Litude Distor-Tion |
|---|---|---|---|---|---|
| Prototype filter | 8-bits | 3.360 | 11.204 | 0.20 | |
| 12-bits | 0.087 | 48.146 | 391 | 0.205 | |
| 16-bits | 0.09 | 48.146 | 0.19 | ||
| Bluetooth | 8-bits | 3.457 | 10.532 | 0.05 | |
| 12-bits | 0.094 | 42.818 | 150 | 0.054 | |
| 16-bits | 0.022 | 43.062 | 0.047 | ||
| Zigbee filter | 8-bits | 0.089 | 39.095 | 0.164 | |
| 12-bits | 0.088 | 39.094 | 34 | 0.164 | |
| 16-bits | 0.089 | 39.094 | 0.164 | ||
| WCDMA | 8-bits | 0.146 | 43.638 | 0.28 | |
| 12-bits | 0.068 | 50.314 | 13 | 0.276 | |
| 16-bits | 0.068 | 50.34 | 0.27 |
| Parameter | NU-MDFT Continous Coefficients | HGDFT with PDA-RNS | NU-MDFT CSD with Pareto ABC [55] | NU-MDFT SID-CSE [55] |
|---|---|---|---|---|
| Total slices | 2507 | 941 | 2406 | 1633 |
| Slice LUTs | 8694 | 2073 | 8950 | 5901 |
| Flip flops | 10,313 | 2338 | 8980 | 5911 |
| Total Power (mW) | 1865 | 333.53 | 1751 | 1281 |
| Total Delay (ns) | 45.125 | 3.328 | 3.75 | 2.6 |
| Parameter | SDR in [56] | SDR Channelizer in [57] |
SDR Channelizer Using NU MDFT FB [55] |
Proposed HGDFT with PDA-RNS FB |
|---|---|---|---|---|
| Slice Registers | 15,295 out of 58,880 | 29,797 out of 301,440 | 5880 out of 597,200 | 2279 out of 23,9616 |
| Slice LUTs | 14,726 out of 58,880 | 21,169 out of 150,720 | 5901 out of 298,600 | 2022 out of 119,808 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otunniyi, T.O.; Myburgh, H.C. Improving Generalized Discrete Fourier Transform (GDFT) Filter Banks with Low-Complexity and Reconfigurable Hybrid Algorithm. Digital 2021, 1, 1-17. https://doi.org/10.3390/digital1010001
Otunniyi TO, Myburgh HC. Improving Generalized Discrete Fourier Transform (GDFT) Filter Banks with Low-Complexity and Reconfigurable Hybrid Algorithm. Digital. 2021; 1(1):1-17. https://doi.org/10.3390/digital1010001
Chicago/Turabian StyleOtunniyi, Temidayo O., and Hermanus C. Myburgh. 2021. "Improving Generalized Discrete Fourier Transform (GDFT) Filter Banks with Low-Complexity and Reconfigurable Hybrid Algorithm" Digital 1, no. 1: 1-17. https://doi.org/10.3390/digital1010001
APA StyleOtunniyi, T. O., & Myburgh, H. C. (2021). Improving Generalized Discrete Fourier Transform (GDFT) Filter Banks with Low-Complexity and Reconfigurable Hybrid Algorithm. Digital, 1(1), 1-17. https://doi.org/10.3390/digital1010001






