Characterisation of Omicron Variant during COVID-19 Pandemic and the Impact of Vaccination, Transmission Rate, Mortality, and Reinfection in South Africa, Germany, and Brazil
Abstract
1. Introduction
2. Material and Methods
2.1. Mathematical Model
2.2. Numerical Simulations
2.3. Data Sources
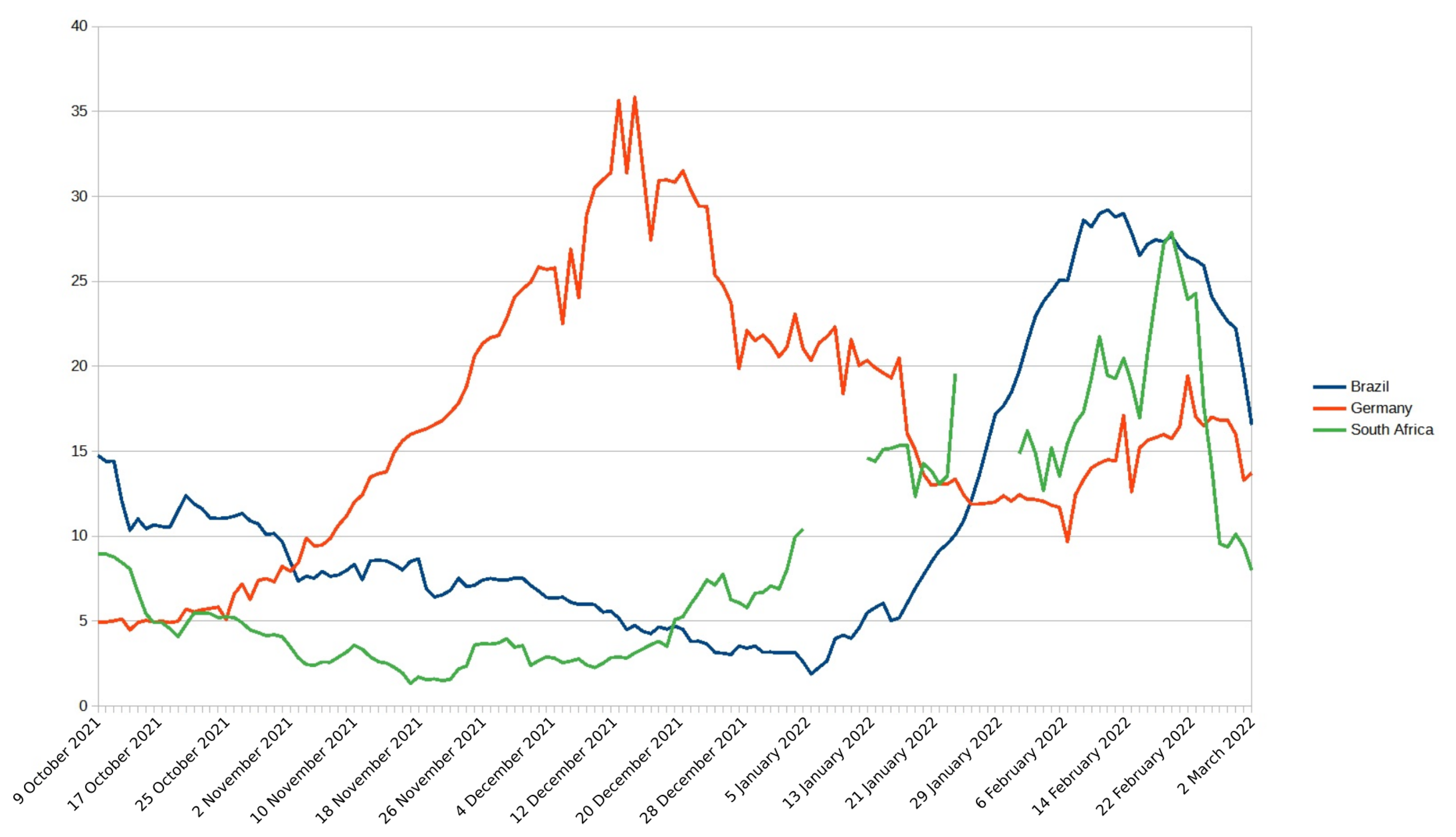
3. Results
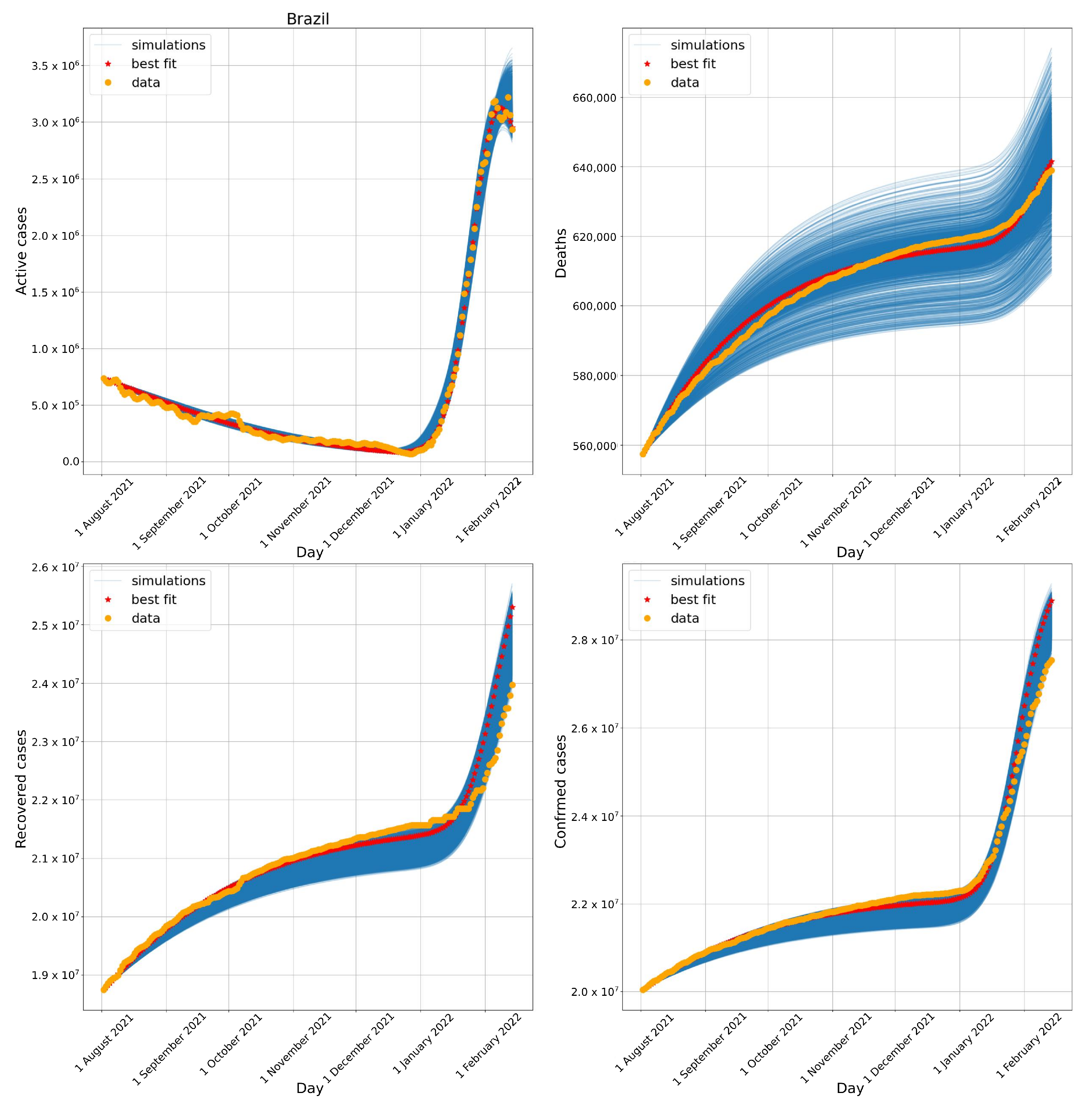
3.1. Brazil
3.2. South Africa
3.3. Germany
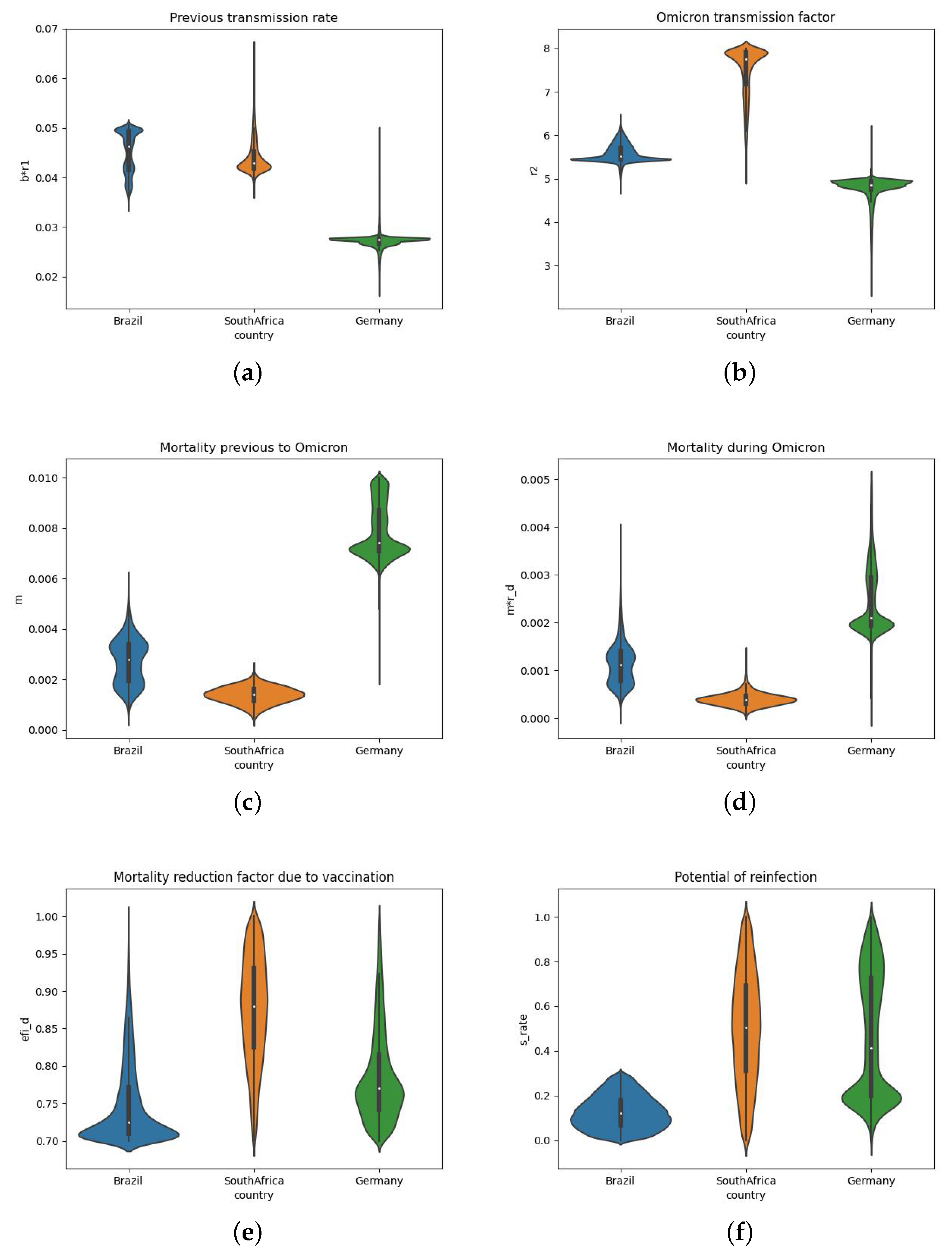
3.4. Estimated Parameters for the Three Different Countries
4. Discussion
5. Limitations and Future Works
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. WHO Timeline—COVID-19. 27 April 2020. Available online: https://www.who.int/news/item/27-04-2020-who-timeline—covid-19 (accessed on 3 February 2021).
- Our World in Data. Coronavirus Pandemic (COVID-19). Available online: https://ourworldindata.org/coronavirus. (accessed on 15 February 2022).
- Li, X.; Mukandavire, C.; Cucunubá, Z.M.; Londono, S.E.; Abbas, K.; Clapham, H.E.; Jit, M.; Johnson, H.L.; Papadopoulos, T.; Vynnycky, E.; et al. Estimating the health impact of vaccination against ten pathogens in 98 low-income and middle-income countries from 2000 to 2030: A modelling study. Lancet 2021, 397, 398–408. [Google Scholar] [CrossRef]
- Davies, N.G.; Abbott, S.; Barnard, R.C.; Jarvis, C.I.; Kucharski, A.J.; Munday, J.D.; Pearson, C.A.; Russell, T.W.; Tully, D.C.; Washburne, A.D.; et al. Estimated transmissibility and impact of SARS-CoV-2 lineage B. 1.1. 7 in England. Science 2021, 372, eabg3055. [Google Scholar] [CrossRef]
- Ong, S.W.X.; Chiew, C.J.; Ang, L.W.; Mak, T.M.; Cui, L.; Toh, M.P.H.S.; Lim, Y.D.; Lee, P.H.; Lee, T.H.; Chia, P.Y.; et al. Clinical and virological features of SARS-CoV-2 variants of concern: A retrospective cohort study comparing B.1.1.7 (Alpha), B.1.315 (Beta), and B.1.617.2 (Delta). Clin. Infect. Dis. 2021, ciab721. [Google Scholar] [CrossRef] [PubMed]
- Salleh, M.Z.; Derrick, J.P.; Deris, Z.Z. Structural evaluation of the spike glycoprotein variants on SARS-CoV-2 transmission and immune evasion. Int. J. Mol. Sci. 2021, 22, 7425. [Google Scholar] [CrossRef]
- Sanches, P.R.; Charlie-Silva, I.; Braz, H.L.; Bittar, C.; Calmon, M.; Rahal, P.; Cilli, E.M. Recent advances in SARS-CoV-2 Spike protein and RBD mutations comparison between new variants Alpha (B. 1.1. 7, United Kingdom), Beta (B. 1.351, South Africa), Gamma (P. 1, Brazil) and Delta (B. 1.617. 2, India). J. Virus Eradic. 2021, 7, 100054. [Google Scholar] [CrossRef]
- Abu-Raddad, L.J.; Chemaitelly, H.; Ayoub, H.H.; Yassine, H.M.; Benslimane, F.M.; Al Khatib, H.A.; Tang, P.; Hasan, M.R.; Coyle, P.; AlMukdad, S.; et al. Severity, Criticality, and Fatality of the Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) Beta Variant. Clin. Infect. Dis. 2021, ciab909. [Google Scholar] [CrossRef] [PubMed]
- Faria, N.R.; Mellan, T.A.; Whittaker, C.; Claro, I.M.; Candido, D.D.S.; Mishra, S.; Crispim, M.A.; Sales, F.C.; Hawryluk, I.; McCrone, J.T.; et al. Genomics and epidemiology of the P. 1 SARS-CoV-2 lineage in Manaus, Brazil. Science 2021, 372, 815–821. [Google Scholar] [CrossRef]
- Planas, D.; Veyer, D.; Baidaliuk, A.; Staropoli, I.; Guivel-Benhassine, F.; Rajah, M.M.; Planchais, C.; Porrot, F.; Robillard, N.; Puech, J.; et al. Reduced sensitivity of SARS-CoV-2 variant Delta to antibody neutralization. Nature 2021, 596, 276–280. [Google Scholar] [CrossRef]
- Dougherty, K.; Mannell, M.; Naqvi, O.; Matson, D.; Stone, J. SARS-CoV-2 B. 1.617. 2 (Delta) variant COVID-19 outbreak associated with a gymnastics facility—Oklahoma, April–May 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 1004. [Google Scholar] [CrossRef]
- Singh, J.; Rahman, S.A.; Ehtesham, N.Z.; Hira, S.; Hasnain, S.E. SARS-CoV-2 variants of concern are emerging in India. Nat. Med. 2021, 27, 1131–1133. [Google Scholar] [CrossRef]
- World Health Organization. WHO Director-General’s Opening Remarks at the Media Briefing on COVID-19. 30 July 2021. Available online: https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19-30-july-2021 (accessed on 29 September 2021).
- Tegally, H.; Wilkinson, E.; Giovanetti, M.; Iranzadeh, A.; Fonseca, V.; Giandhari, J.; Doolabh, D.; Pillay, S.; San, E.J.; Msomi, N.; et al. Detection of a SARS-CoV-2 variant of concern in South Africa. Nature 2021, 592, 438–443. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.J.; Guo, H.; Luo, G. Omicron variant (B. 1.1. 529) of SARS-CoV-2, a global urgent public health alert! J. Med. Virol. 2022, 94, 1255–1256. [Google Scholar] [CrossRef]
- Furushima, D.; Kawano, S.; Ohno, Y.; Kakehashi, M. Estimation of the basic reproduction number of novel influenza A (H1N1) pdm09 in elementary schools using the SIR model. Open Nurs. J. 2017, 11, 64. [Google Scholar] [CrossRef] [PubMed]
- Gaudart, J.; Ghassani, M.; Mintsa, J.; Rachdi, M.; Waku, J.; Demongeot, J. Demography and diffusion in epidemics: Malaria and black death spread. Acta Biotheor. 2010, 58, 277–305. [Google Scholar] [CrossRef] [PubMed]
- Chowell, G.; Tariq, A.; Hyman, J.M. A novel sub-epidemic modeling framework for short-term forecasting epidemic waves. BMC Med. 2019, 17, 164. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thoracic Dis. 2020, 12, 165. [Google Scholar] [CrossRef]
- Li, L.; Yang, Z.; Dang, Z.; Meng, C.; Huang, J.; Meng, H.; Wang, D.; Chen, G.; Zhang, J.; Peng, H.; et al. Propagation analysis and prediction of the COVID-19. Infect. Dis. Model. 2020, 5, 282–292. [Google Scholar] [CrossRef]
- Caetano, C.; Morgado, M.L.; Patrício, P.; Pereira, J.F.; Nunes, B. Mathematical Modelling of the Impact of Non-Pharmacological Strategies to Control the COVID-19 Epidemic in Portugal. Mathematics 2021, 9, 1084. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S.; Nieto, J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals 2020, 139, 110049. [Google Scholar] [CrossRef]
- Makhoul, M.; Ayoub, H.H.; Chemaitelly, H.; Seedat, S.; Mumtaz, G.R.; Al-Omari, S.; Abu-Raddad, L.J. Epidemiological impact of SARS-CoV-2 vaccination: Mathematical modeling analyses. Vaccines 2020, 8, 668. [Google Scholar] [CrossRef]
- Rodrigues, R.F.; Silva, A.R.D.; Fonseca Vieira, V.D.; Xavier, C.R. Optimization of the choice of individuals to be immunized through the genetic algorithm in the sir model. In Proceedings of the International Conference on Computational Science and Its Applications, Melbourne, VIC, Australia, 2–5 July 2018; Springer: Cham, Switzerland, 2018; pp. 62–75. [Google Scholar]
- Vespignani, A.; Pastor-Satorras, R.; Van Mieghem, M.; Castellano, C. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar]
- Piontti, A.P.Y.; Gomes, M.F.D.C.; Samay, N.; Perra, N.; Vespignani, A. The infection tree of global epidemics. Netw. Sci. 2014, 2, 132–137. [Google Scholar] [CrossRef]
- Nowzari, C.; Preciado, V.M.; Pappas, G.J. Optimal resource allocation for control of networked epidemic models. IEEE Trans. Control Netw. Syst. 2015, 4, 159–169. [Google Scholar] [CrossRef]
- Nadini, M.; Rizzo, A.; Porfiri, M. Epidemic spreading in temporal and adaptive networks with static backbone. IEEE Trans. Netw. Sci. Eng. 2018, 7, 549–561. [Google Scholar] [CrossRef]
- Eames, K.; Keeling, M. Networks and epidemic models. J. R. Soc. Interface 2005, 2, 295–307. [Google Scholar]
- Lin, F.; Muthuraman, K.; Lawley, M. An optimal control theory approach to non-pharmaceutical interventions. BMC Infect. Dis. 2010, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Tulu, T.W.; Tian, B.; Wu, Z. Modeling the effect of quarantine and vaccination on Ebola disease. Adv. Diff. Equ. 2017, 2017, 178. [Google Scholar] [CrossRef]
- Bar-On, Y.M.; Goldberg, Y.; Mandel, M.; Bodenheimer, O.; Freedman, L.; Kalkstein, N.; Mizrahi, B.; Alroy-Preis, S.; Ash, N.; Milo, R.; et al. Protection of BNT162b2 vaccine booster against covid-19 in Israel. N. Engl. J. Med. 2021, 385, 1393–1400. [Google Scholar] [CrossRef] [PubMed]
- Levine-Tiefenbrun, M.; Yelin, I.; Katz, R.; Herzel, E.; Golan, Z.; Schreiber, L.; Wolf, T.; Nadler, V.; Ben-Tov, A.; Kuint, J.; et al. Decreased SARS-CoV-2 viral load following vaccination. Nat. Med. 2021, 27, 790–792. [Google Scholar] [CrossRef]
- Borse, R.H.; Shrestha, S.S.; Fiore, A.E.; Atkins, C.Y.; Singleton, J.A.; Furlow, C.; Meltzer, M.I. Effects of vaccine program against pandemic influenza A (H1N1) virus, United States, 2009–2010. Emerg. Infect. Dis. 2013, 19, 439. [Google Scholar] [CrossRef]
- Nguyen, C.; Carlson, J.M. Optimizing real-time vaccine allocation in a stochastic SIR model. PLoS ONE 2016, 11, e0152950. [Google Scholar] [CrossRef] [PubMed]
- Reis, R.F.; de Melo Quintela, B.; de Oliveira Campos, J.; Gomes, J.M.; Rocha, B.M.; Lobosco, M.; dos Santos, R.W. Characterization of the COVID-19 pandemic and the impact of uncertainties, mitigation strategies, and underreporting of cases in South Korea, Italy, and Brazil. Chaos Solitons Fractals 2020, 136, 109888. [Google Scholar] [CrossRef] [PubMed]
- Reis, R.F.; Oliveira, R.S.; Quintela, B.D.; Campos, J.D.O.; Gomes, J.M.; Rocha, B.M.; Lobosco, M.; Santos, R.W.D. The Quixotic Task of Forecasting Peaks of COVID-19: Rather Focus on Forward and Backward Projections. Front. Public Health 2021, 9, 168. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, R.S.; Xavier, C.R.; da Fonseca Vieira, V.; Rocha, B.M.; Reis, R.F.; de Melo Quintela, B.; Lobosco, M.; dos Santos, R.W. How Fast Vaccination Can Control the COVID-19 Pandemic in Brazil? In Proceedings of the Computational Science—ICCS 2021, Krakow, Poland, 16–18 June 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 497–510. [Google Scholar] [CrossRef]
- Xavier, C.R.; Oliveira, R.S.; da Fonseca Vieira, V.; Rocha, B.M.; Reis, R.F.; de Melo Quintela, B.; Lobosco, M.; dos Santos, R.W. Timing the race of vaccination, new variants, and relaxing restrictions during COVID-19 pandemic. J. Comput. Sci. 2022, 61, 101660. [Google Scholar] [CrossRef] [PubMed]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Lei, C.L.; Ghosh, S.; Whittaker, D.G.; Aboelkassem, Y.; Beattie, K.A.; Cantwell, C.D.; Delhaas, T.; Houston, C.; Novaes, G.M.; Panfilov, A.V.; et al. Considering discrepancy when calibrating a mechanistic electrophysiology model. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190349. [Google Scholar] [CrossRef]
- Worldometers. COVID-19 Coronavirus Pandemic. 2020. Available online: https://www.worldometers.info/coronavirus/. (accessed on 15 February 2022).
- Ulloa, A.C.; Buchan, S.A.; Daneman, N.; Brown, K.A. Estimates of SARS-CoV-2 Omicron Variant Severity in Ontario, Canada. JAMA 2022, 327, 1286–1288. [Google Scholar] [CrossRef]
- Wolter, N.; Jassat, W.; Walaza, S.; Welch, R.; Moultrie, H.; Groome, M.; Amoako, D.G.; Everatt, J.; Bhiman, J.N.; Scheepers, C.; et al. Early assessment of the clinical severity of the SARS-CoV-2 omicron variant in South Africa: A data linkage study. Lancet 2022, 399, 437–446. [Google Scholar] [CrossRef]
- Ferguson, N.; Ghani, A.; Hinsley, W.; Volz, E. Report 50: Hospitalisation Risk for Omicron Cases in England; Report; Imperial College London: London, UK, 2021. [Google Scholar] [CrossRef]




| Parameters | Brazil | South Africa | Germany |
|---|---|---|---|
| b | 0.049745 | 0.083456 | 0.098533 |
| m | 0.002223 | 0.001614 | 0.007456 |
| 0.999733 | 0.503252 | 0.279499 | |
| 37.611357 | 27.571859 | 27.361629 | |
| 43.476986 | 7.465598 | 25.647412 | |
| 5.422328 | 7.993557 | 4.961679 | |
| 139.978414 | 86.668599 | 65.600770 | |
| 21.272066 | 34.562475 | 17.164128 | |
| 6.305544 | 4.653837 | 11.486396 | |
| 18.950821 | 33.184733 | 27.741349 | |
| 11.803360 | 9.761925 | 10.689566 | |
| 0.052279 | 0.019445 | 0.241283 | |
| 0.702603 | 0.753452 | 0.761646 | |
| 0.133930 | 0.419652 | 0.211434 | |
| 0.410348 | 0.283680 | 0.278265 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro Xavier, C.; Sachetto Oliveira, R.; da Fonseca Vieira, V.; Lobosco, M.; Weber dos Santos, R. Characterisation of Omicron Variant during COVID-19 Pandemic and the Impact of Vaccination, Transmission Rate, Mortality, and Reinfection in South Africa, Germany, and Brazil. BioTech 2022, 11, 12. https://doi.org/10.3390/biotech11020012
Ribeiro Xavier C, Sachetto Oliveira R, da Fonseca Vieira V, Lobosco M, Weber dos Santos R. Characterisation of Omicron Variant during COVID-19 Pandemic and the Impact of Vaccination, Transmission Rate, Mortality, and Reinfection in South Africa, Germany, and Brazil. BioTech. 2022; 11(2):12. https://doi.org/10.3390/biotech11020012
Chicago/Turabian StyleRibeiro Xavier, Carolina, Rafael Sachetto Oliveira, Vinícius da Fonseca Vieira, Marcelo Lobosco, and Rodrigo Weber dos Santos. 2022. "Characterisation of Omicron Variant during COVID-19 Pandemic and the Impact of Vaccination, Transmission Rate, Mortality, and Reinfection in South Africa, Germany, and Brazil" BioTech 11, no. 2: 12. https://doi.org/10.3390/biotech11020012
APA StyleRibeiro Xavier, C., Sachetto Oliveira, R., da Fonseca Vieira, V., Lobosco, M., & Weber dos Santos, R. (2022). Characterisation of Omicron Variant during COVID-19 Pandemic and the Impact of Vaccination, Transmission Rate, Mortality, and Reinfection in South Africa, Germany, and Brazil. BioTech, 11(2), 12. https://doi.org/10.3390/biotech11020012






