Positioning Fractal Dimension and Lacunarity in the IBSI Feature Space: Simulation With and Without Wavelets

Simple Summary

This study examines whether fractal dimension and lacunarity, two texture measures that describe image complexity, provide additional information beyond standard radiomic features. Using simulated images, we compared these measures to Image Biomarker Standardisation Initiative (IBSI) descriptors with and without wavelet filtering. We found that fractal dimension captures fine texture variation, while lacunarity describes larger structural patterns. Together they provide complementary information, suggesting that both can enhance radiomic analyses focused on multiscale heterogeneity.

Abstract

Fractal dimension (Frac) and lacunarity (Lac) are frequently proposed as biomarkers of multiscale image complexity, but their incremental value over standardized radiomics remains uncertain. We position both measures within the Image Biomarker Standardisation Initiative (IBSI) feature space by running a fully reproducible comparison in two settings. In a baseline experiment, we analyze $N=1000$ simulated $64\times 64$ textured ROIs discretized to $N_g=64$, computing 92 IBSI descriptors together with Frac (box counting) and Lac (gliding box), for 94 features per ROI. In a wavelet-augmented experiment, we analyze $N=1000$ ROIs and add level-1 wavelet descriptors by recomputing first-order and GLCM features in each sub-band (LL, LH, HL, and HH), contributing $4\times (19+19)=152$ additional features and yielding 246 features per ROI. Feature similarity is summarized by a consensus score that averages z-scored absolute Pearson and Spearman correlations, distance correlation, maximal information coefficient, and cosine similarity, and is visualized with clustered heatmaps, dendrograms, sparse networks, PCA loadings, and UMAP and t-SNE embeddings. Across both settings a stable two-block organization emerges. Frac co-locates with contrast, difference, and short-run statistics that capture high-frequency variation; when wavelets are included, detail-band terms from LH, HL, and HH join this group. Lac co-locates with measures of large, coherent structure—GLSZM zone size, GLRLM long-run, and high-gray-level emphases—and with GLCM homogeneity and correlation; LL (approximation) wavelet features align with this block. Pairwise associations are modest in the baseline but become very strong with wavelets (for example, Frac versus GLCM difference entropy, which summarizes the randomness of gray-level differences, with $\left|r\right|\approx 0.98$; and Lac versus GLCM inverse difference normalized (IDN), a homogeneity measure that weights small intensity differences more heavily, with $\left|r\right|\approx 0.96$). The multimetric consensus and geometric embeddings consistently place Frac and Lac in overlapping yet separable neighborhoods, indicating related but non-duplicative information. Practically, Frac and Lac are most useful when multiscale heterogeneity is central and they add a measurable signal beyond strong IBSI baselines (with or without wavelets); otherwise, closely related variance can be absorbed by standard texture families.

1. Introduction

Radiomics converts medical images into large panels of quantitative descriptors that summarize intensity distributions, texture, shape, and heterogeneity for modeling and decision support across clinical domains [1,2,3,4]. To enable reproducibility and comparability, the Image Biomarker Standardisation Initiative (IBSI) has codified definitions and implementation choices, such as gray-level discretization, neighborhood topology, and angular or distance aggregation, for a core set of matrix-based texture families: the gray-level co-occurrence matrix (GLCM), gray-level run-length matrix (GLRLM), gray-level size-zone matrix (GLSZM), gray-level dependence matrix (GLDM; also called NGLDM), and the neighborhood gray-tone difference matrix (NGTDM). These specifications are widely adopted in open-source toolkits including PyRadiomics [4,5,6,7,8,9,10].

Alongside these standardized families, fractal descriptors, particularly fractal dimension (Frac) and lacunarity (Lac), remain attractive because they target explicitly multiscale properties: Frac quantifies boundary or texture roughness across scales, whereas Lac characterizes the heterogeneity of gaps or voids as a function of scale [11,12,13]. Applications spanning oncology and neuroimaging report encouraging, though heterogeneous, associations with grade, phenotype, and outcome [14,15,16].

These observations motivate two practical questions that matter for clinical translation. First, to what extent do Frac and Lac provide information that is complementary to IBSI-standardized texture families that already encode high-frequency contrast or large-structure emphasis? Strong inter-feature correlations and redundancy are well documented in radiomics, especially among texture families and under different discretization choices [17,18,19,20,21]. Second, how sensitive are fractal estimators to preprocessing and acquisition factors known to affect radiomic stability, including voxel size, gray-level discretization, reconstruction, and segmentation variability [4,22,23,24]? Addressing redundancy and sensitivity is essential to avoid optimistic estimates of model performance, clarify interpretation, and support reproducible pipelines [1,2].

In this work we (i) synthesize the relevant literature on fractal and lacunarity analysis in medical imaging; (ii) provide explicit mathematical definitions for all features considered to ensure unambiguous reproducibility; and (iii) run a two-part controlled simulation in which textured, heterogeneous ROIs are generated and Frac and Lac are compared against standardized radiomics in two configurations: first without wavelets and then with wavelets. In the baseline setting, Frac and Lac are evaluated alongside 92 IBSI features, yielding 94 features per ROI. In the wavelet-augmented setting, we recompute first-order and GLCM descriptors in each of the four wavelet sub-bands (LL, LH, HL, and HH), adding 152 wavelet features for a total of 246 per ROI. Similarities are quantified with multiple complementary measures, Pearson correlation, Spearman correlation, distance correlation, the maximal information coefficient, and cosine similarity, and summarized with heatmaps, dendrograms, correlation networks, principal component loadings, and two-dimensional embeddings based on UMAP and t-SNE. Our goal is not to advocate for or against fractal biomarkers as such, but to delineate when they add a genuinely complementary signal and when they largely recapitulate standardized descriptors derived from the spatial domain or from wavelets.

Relation to Existing Benchmarks

Our study is positioned as a benchmark comparison that complements established reproducibility and harmonization frameworks in radiomics [4,21,22]. Previous benchmark efforts have mainly quantified how acquisition variability, voxel size, reconstruction, and gray-level discretization influence standardized features across scanners and cohorts, often recommending harmonization methods such as ComBat and rigorous reporting of preprocessing choices [4,23,24]. In contrast, the present study focuses on methodological redundancy and complementarity under controlled simulation. By generating synthetic regions of interest with tunable spatial correlation and optional heterogeneity, we are able to attribute observed associations to feature definitions rather than to protocol confounders.

Within this controlled environment, we evaluate whether fractal descriptors—fractal dimension (Frac) and lacunarity (Lac)—contribute incremental information beyond standardized IBSI texture families and wavelet-based extensions. To achieve this, we keep discretization, angular aggregation, and neighborhood topology fixed according to IBSI recommendations and vary only the underlying texture process. We then quantify feature relatedness using five complementary dependence measures (Pearson, Spearman, distance correlation, maximal information coefficient, and cosine similarity), form a consensus z-score for ranking, and visualize the overall geometry using clustered heatmaps, principal component loadings, and low-dimensional embeddings obtained from UMAP and t-SNE. This multi-view evaluation extends earlier benchmarks that typically emphasize repeatability or single-metric stability by identifying where Frac and Lac reside relative to co-occurrence, run-length, size-zone, dependence, and gray-tone difference features, both with and without wavelet augmentation.

Empirically, a stable two-block organization emerges that aligns with the intended behavior of established feature families. Frac is closely associated with contrast, difference, and short-run statistics that describe high-frequency texture variation, while Lac aligns with large-structure, homogeneity, and long-run statistics. The addition of wavelet features sharpens this distinction, as detail-band components correspond more strongly with Frac, and approximation-band components correspond with Lac. Collectively, these findings indicate that fractal measures are overlapping yet non-duplicative; they follow known axes of variation already represented in IBSI features but retain interpretable multiscale summaries that can be particularly useful when heterogeneity across scales is an essential characteristic.

Finally, this simulation-grounded benchmark complements empirical clinical studies of fractal descriptors [14,15,16] by disentangling intrinsic feature associations from acquisition effects. It provides a transparent framework for understanding when fractal measures are likely to be redundant, such as in models already rich in contrast, short-run, or homogeneity descriptors, and when they can add measurable information. In this way, the study extends existing benchmarks beyond the question of whether features are stable to the more informative question of whether fractal descriptors contribute additional, non-redundant information beyond strong IBSI baselines under conditions where causal attribution is clearly defined.

2. Background and Related Work

2.1. Standardized Radiomic Features

The Image Biomarker Standardisation Initiative (IBSI) specifies preprocessing steps and feature definitions for widely used texture families, and recommends transparent reporting of discretization, neighborhood definitions, and aggregation rules [4]. In brief, the gray-level co-occurrence matrix (GLCM) summarizes how often pairs of discretized gray levels co-occur at fixed offsets and angles [5]; the gray-level run-length matrix (GLRLM) counts contiguous runs of equal gray level [6]; the gray-level size-zone matrix (GLSZM) measures the sizes of connected same-gray zones irrespective of direction [7]; the gray-level dependence matrix (GLDM, also called NGLDM) captures counts of neighboring voxels within a gray-level tolerance [8]; and the neighborhood gray-tone difference matrix (NGTDM) characterizes deviations from the local neighborhood mean [9]. These standardized definitions underpin open-source implementations such as PyRadiomics [10]. Empirically, features from these families can be highly collinear, so clustering or redundancy reduction prior to modeling is commonly recommended [17,18,19]. Repeatability and reproducibility also vary across features and pipelines, motivating harmonization (for example, ComBat), robust cross-validation, and sensitivity analyses to voxel size and discretization [21,22,23,24].

2.2. Fractal Dimension and Lacunarity

Fractal measures target complementary aspects of structure. The box-counting fractal dimension describes a global scaling law: how occupancy grows as resolution is refined, whereas lacunarity captures scale-specific heterogeneity: how unevenly occupancy is distributed at a given window size [11,12,13]. Two textures can share the same fractal dimension yet display distinct lacunarity curves, and the converse can also occur; the measures are therefore not interchangeable. In medical imaging, both have been linked to tumor grade and outcome, although reported associations can be sensitive to the definition of the region of interest, the gray-level binning scheme, and the selection of scales [14,15,16]. Recent algorithmic advances, such as efficient gliding-box lacunarity via integral images, reduce computational burden and encourage systematic comparisons with standardized radiomics [25]. Conceptually, fractal dimension tends to increase with fine-scale roughness or rapid gray-level changes, behavior that also elevates contrast-oriented descriptors derived from co-occurrence and run-length representations. By contrast, lacunarity often rises with broad, coherent zones and heterogeneous voids, echoing GLSZM large-area and GLRLM long-run emphases as well as homogeneity and inverse-difference measures in the GLCM family [5,6,7,9]. Because standardized families already approximate these tendencies, it is important to determine whether fractal descriptors contribute genuinely new information or largely re-encode signals captured by classical features. The redundancy and protocol sensitivity observed across radiomics [17,18,19,21,22,23,24] motivate the controlled evaluation undertaken here.

2.3. Clinical Applications of Radiomics and the Role of Fractal Measures

Radiomics has been applied widely for diagnosis, phenotyping, risk stratification, and outcome prediction in oncology and neurology [1,2,3]. In cancer imaging, quantitative signatures extracted from CT, MR, or PET have been associated with tumor biology and prognosis and incorporated into decision–support workflows. Beyond oncology, neuroimaging applications, such as glioma grading, stroke classification, and phenotyping of neurodegenerative disease, use similar pipelines that combine first-order, shape, and matrix-based texture features with predictive modeling [2]. Within this landscape, fractal descriptors offer an explicitly multiscale perspective. Studies report that three-dimensional fractal dimension and lacunarity can aid grading or subtype discrimination when added to conventional MR features in neuro-oncology [14], and broader reviews document encouraging but heterogeneous evidence across applications [15,16]. The key open question is incremental value: given that IBSI-standardized features already capture high-frequency contrast (for example, GLCM contrast or dissimilarity and short-run GLRLM) and large-structure or homogeneity effects (for example, GLSZM large-area or zone-size statistics; long-run and high-gray-level GLRLM; GLCM inverse-difference and homogeneity), under what conditions do fractal dimension and lacunarity add a non-redundant signal? Answering this calls for transparent pipelines, harmonization where appropriate, and robust validation to account for protocol sensitivity and feature collinearity [4,21,22,23,24].

Moreover, a closer look at recent methodological advances provides additional insight. For example, Ilmi & Khalaf’s graphene–temporal fusion for yoga pose recognition [26] showcases the power of combining spatial graphs and temporal dynamics, but its non-medical dataset and absence of standardized texture extraction limit its direct relevance for radiomics. Similarly, Jumadi & Md Akbar’s hybrid GRU-KAN model for energy consumption prediction [27] demonstrates effective hybrid modeling in time series but reflects a non-imaging domain and lacks imaging preprocessing/harmonization. A recent review of Mask R-CNN, for instance, segmentation [28], emphasizes the importance of robust segmentation—which is directly relevant for reproducible radiomic and fractal extraction—but does not address feature redundancy or multiscale heterogeneity explicitly. Finally, a stacked ensemble for cervical cancer prediction using tabular data [29] reinforces the role of ensemble and regularization strategies to address collinearity and imbalance. Issues that are equally relevant in radiomic pipelines assessing incremental features like fractal dimension and lacunarity. Taken together, these works highlight emerging best practices (graph–temporal modeling, hybrid architectures, segmentation robustness, ensemble calibration) and their limitations (domain mismatch, lack of imaging standardization, no explicit multiscale heterogeneity descriptors)—which reinforce the need for our simulation-grounded, IBSI-aligned, multiscale feature-computation, and incremental evaluation of fractal measures.

3. Materials and Methods

3.1. Radiomic Feature Set: Definitions and Computation

We consider a two-dimensional region of interest (ROI) represented by a real-valued image $X\in {\mathbb{R}}^{H\times W}$ with H pixel rows (height) and W pixel columns (width), defined on the grid $\Omega :=\{1,\dots ,H\}\times \{1,\dots ,W\}$, so that $|\Omega |=HW$. Let $X_i\in {\{1,\dots ,N_g\}}^{H\times W}$ denote the discretized (gray-level binned) version of X obtained by an operator $Q:\mathbb{R}\to \{1,\dots ,N_g\}$; unless otherwise stated we use equal-frequency (quantile) binning with $N_g=64$ in line with common IBSI-style configurations [4]. Two feature configurations are examined. In the baseline setting, we extract 92 IBSI-standardized descriptors (19 first-order, 19 GLCM, 16 GLRLM, 16 GLSZM, 14 GLDM, 5 NGTDM, and 3 two-dimensional shape proxies) together with two fractal descriptors (Frac and Lac), for 94 features per ROI. In the wavelet-augmented setting, we add level-1 wavelet features by recomputing first-order and GLCM descriptors on each of the four sub-bands (LL, LH, HL, HH), which contributes $4\times (19+19)=152$ additional features. The wavelet-augmented total is therefore $94+152=246$ features.

3.1.1. First-Order (Intensity) Features

First-order features summarize the distribution of voxel intensities in an ROI without reference to spatial arrangement [1,2,4]. They provide baseline information about central tendency, spread, tail behavior, and histogram shape. We follow a nineteen-feature set that aligns with IBSI-style implementations and widely used toolkits [3,4,10]: (i) power measures (Energy, Total Energy, RMS); (ii) dispersion (Variance, Standard deviation, Range, IQR); (iii) shape (Skewness, Kurtosis); (iv) histogram complexity (Entropy, Uniformity); and (v) robust summaries (Median, P10, P90, MAD, rMAD, as well as Min and Max). Definitions and formulas, together with brief interpretations, appear in Appendix A Table A1 [4,10].

Several practical points aid interpretation. Energy, Total Energy, RMS, Variance, and Standard deviation are scale dependent: linear rescaling of intensities changes their values, which is appropriate when physical units are meaningful but can confound cross-scanner comparisons if not harmonized [21,23]. Entropy and Uniformity depend on gray-level discretization ($N_g$ and the binning scheme), so consistent preprocessing is important for reproducibility [4,22,23]. Median, IQR, MAD, and rMAD are more robust to noise and outliers than mean and variance and often stabilize modeling under heterogeneous acquisition conditions [2,4]. Although some measures are correlated by construction (for example, Energy and RMS), retaining both can be useful when regularization is used or when reporting adheres to radiomic standards, otherwise, redundancy reduction (e.g., correlation filtering) can simplify models without sacrificing information [4,18,19].

3.1.2. GLCM Features

The gray-level co-occurrence matrix (GLCM) encodes how often pairs of discretized gray levels co-occur at a fixed spatial offset. In this study the matrix is computed at distance 1, aggregated over four angles $(0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ })$, symmetrized, and normalized so that ${\sum }_{i=1}^{N_g}{\sum }_{j=1}^{N_g}{P}_{ij}=1$ [4,5].

Intuitively, mass far from the diagonal signals frequent high-contrast transitions, whereas mass concentrated near the diagonal reflects locally smoother textures [1,2]. We report nineteen descriptors: classical contrast and entropy terms; two homogeneity variants; two inverse-difference variants; inverse variance; correlation; maximum probability; three sum/difference statistics; and both information measures of correlation (IMC1/IMC2) [4,10]. Exact formulas are given in Appendix A Table A2.

3.1.3. GLRLM Features

The gray-level run-length matrix (GLRLM) counts how often contiguous runs of an identical gray level occur and how long those runs persist across the image [4,6]. After discretization, a run is the maximal sequence of adjacent pixels with the same gray level observed along a given direction. Short runs reflect a fine, rapidly varying texture, whereas long runs reflect a coarse, more uniform structure. By cross-tabulating run length with gray level, GLRLM features quantify, within one family, both scale (short and long) and tone (low and high gray) emphases. We compute GLRLMs at distance 1, aggregate over four angles $(0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ })$ to improve directional robustness, and normalize to probabilities [4]. Formulas for all sixteen descriptors appear in Appendix A Table A3 [4,7,10].

3.1.4. GLSZM Features

The gray-level size-zone matrix (GLSZM) summarizes the distribution of connected zones of equal gray level within an ROI, irrespective of direction [4,7]. A zone is the maximal set of pixels that share the same discretized gray level and are connected under an 8-neighborhood in two dimensions [4,10]. Textures dominated by small zones correspond to fine, fragmented patterns, whereas textures dominated by large zones reflect coarse, homogeneous structure [2]. By cross-tabulating gray level and zone size, GLSZM features quantify how coarseness interacts with tone [4,7]. We use 8-connectivity, aggregate over the region, and normalize to probabilities [4,10]. Formulas for all sixteen descriptors appear in Appendix A Table A4 [4,10].

3.1.5. GLDM Features

The gray-level dependence matrix (GLDM, also called NGLDM) quantifies, for each discretized gray level i, how many pixels in a fixed neighborhood are dependent on the center pixel [4,8,10]. Two pixels are considered dependent if the absolute difference of their gray levels does not exceed a tolerance $\alpha$. In this work $\alpha =0$, meaning only exactly equal gray levels (after discretization) count as dependent [4,10]. Using a Chebyshev-1 neighborhood in two dimensions provides up to eight surrounding pixels; when the center is included in the count, the dependence size d ranges from 1 to 9 [4]. Tallying, for each gray level i, how often each dependence size d occurs within this neighborhood captures the prevalence of isolated pixels versus coherent tone-consistent patches and how these patterns vary with gray level [4,8]. Formulas for all fourteen descriptors appear in Appendix A Table A5 [4,10].

3.1.6. NGTDM Features

The neighborhood gray-tone difference matrix (NGTDM) summarizes how each discretized gray level deviates, on average, from its local neighborhood [4,9]. Given a quantized image $X_i\in {\{1,\dots ,N_g\}}^{H\times W}$, we evaluate each interior pixel using a $3\times 3$ window (Chebyshev radius 1) and define the neighborhood mean as the average of the eight surrounding pixels, excluding the center [4,10]. To avoid edge artifacts, only pixels with a full $3\times 3$ neighborhood (that is, interior pixels) contribute to the statistics [4]. Formulas for all five descriptors appear in Appendix A Table A6 [4,10].

3.1.7. Shape-2D Proxies

For this 2D simulation we summarize gross morphology with four compact descriptors computed on a binary ROI mask: area, a 4-neighbor (Manhattan) perimeter, and two in-plane anisotropy measures derived from the principal variances of the foreground coordinates. This deliberately lightweight set mirrors the intent of the standardized 3D shape features recommended by IBSI while remaining appropriate for single-slice analyses [4,10]. Formulas for all four descriptors appear in Appendix A Table A7 [4,10].

3.2. Wavelet Features

We complement the spatial-domain descriptors with a stationary (undecimated) level-1 two-dimensional wavelet transform so that all filtered images retain the original ROI size $(64\times 64)$ [30,31]. We begin by specifying notation. Let $X\in {\mathbb{R}}^{H\times W}$ be indexed as $X[i,j]$, where i is the row (vertical, y) index and j is the column (horizontal, x) index. Let

$$h={\left\{h\left[k\right]\right\}}_{k=-M_h}^{M_h},g={\left\{g\left[k\right]\right\}}_{k=-M_g}^{M_g}$$

be the one-dimensional low- and high-pass analysis filters with finite (odd) lengths

$$L_h=2M_h+1,L_g=2M_g+1,$$

so that $M_h$ (respectively, $M_g$) is the half-support; that is, the number of taps on one side of the filter center. Throughout we use symmetric (mirror) padding at the borders and no downsampling (the transform is undecimated) [31,32]. Unless noted otherwise, the wavelet family is Coiflet-1 for its near-symmetry and compact support [33].

Next we define one-dimensional discrete convolutions along the column (x) and row (y) axes and a two-dimensional discrete convolution $(\ast )$; we denote 1-D convolution along columns by ${\ast }_x$ and along rows by ${\ast }_y$. Convolution along x keeps rows fixed and sums across columns,

$$\left(h{\ast }_{x}X\right)[i,j]=\sum _{k=-M_h}^{M_h}h\left[k\right]X[i,j-k],$$

(1)

while convolution along y keeps columns fixed and sums across rows,

$$\left(h{\ast }_{y}X\right)[i,j]=\sum _{k=-M_h}^{M_h}h\left[k\right]X[i-k,j].$$

(2)

If an index falls outside the valid image range $(1\le i\le H,1\le j\le W)$, it is reflected back into the interval (symmetric padding) before sampling X [4,10].

We then obtain four stationary level-1 sub-bands by low-/high-pass filtering along x and y without downsampling:

$$\begin{array}{cc}\hfill W_{\mathrm{LL}}[i,j]& =\left(h{\ast }_x\left(h{\ast }_{y}X\right)\right)[i,j],\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill W_{\mathrm{LH}}[i,j]& =\left(h{\ast }_x\left(g{\ast }_{y}X\right)\right)[i,j],\hfill \end{array}$$

(3b)

$$\begin{array}{cc}\hfill W_{\mathrm{HL}}[i,j]& =\left(g{\ast }_x\left(h{\ast }_{y}X\right)\right)[i,j],\hfill \end{array}$$

(3c)

$$\begin{array}{cc}\hfill W_{\mathrm{HH}}[i,j]& =\left(g{\ast }_x\left(g{\ast }_{y}X\right)\right)[i,j].\hfill \end{array}$$

(3d)

Equivalently, with separable two-dimensional kernels $(h\otimes h)$, $(h\otimes g)$, $(g\otimes h)$, and $(g\otimes g)$ and 2D convolution ∗,

$$\begin{array}{cc}\hfill W_{\mathrm{LL}}& =(h\otimes h)\ast X,W_{\mathrm{LH}}=(h\otimes g)\ast X,\hfill \\ \hfill W_{\mathrm{HL}}& =(g\otimes h)\ast X,W_{\mathrm{HH}}=(g\otimes g)\ast X,\hfill \end{array}$$

(4)

where $(a\otimes b)[u,v]=a\left[u\right]b\left[v\right]$ is the outer product of the one-dimensional filters (a separable two-dimensional kernel), and

$$(K\ast X)[i,j]=\sum _u\sum _{v}K[u,v]X[i-u,j-v]$$

is the two-dimensional discrete convolution of kernel K with image X. Here, u and v are integer offsets that index the kernel support horizontally and vertically, respectively; the double sum is taken over the finite support where $K[u,v]\ne 0$. The LL band collects coarse (approximation) content, whereas LH, HL, and HH collect horizontal, vertical, and diagonal detail.

Each sub-band is re-standardized (per sub-band, per ROI) to zero mean and unit variance prior to discretization to mitigate scale differences across sub-bands and ROIs [21]. (For predictive modeling, standardization parameters should be estimated on the training set only to avoid leakage.) Discretization then follows the base analysis: quantile binning into $N_g=64$ equiprobable gray levels applied independently to each sub-band [4,23]. On every discretized sub-band we compute first-order (19) and GLCM (19) statistics, yielding $4\times (19+19)=152$ wavelet features per ROI. This mirrors widely used radiomic configurations and captures frequency- and orientation-specific cues [17,34,35] while controlling multiplicity and collinearity [19,22]. Other matrix families (GLRLM, GLSZM, GLDM, NGTDM) can be added analogously, but here we restrict the wavelet set to first-order and GLCM for parsimony [19,22].

Finally, we record the transform type (undecimated), the wavelet family and level (Coiflet-1, one level), the boundary handling (symmetric reflection), and that discretization is performed per sub-band, in line with IBSI reporting guidance [4]. Wavelet filtering separates coarse structure (LL) from horizontal, vertical, and diagonal detail (LH, HL, HH), often revealing texture that single-scale statistics may miss [1,2]. At the same time, wavelet expansions increase feature counts and can accentuate instability or acquisition dependence; re-standardization, fixed discretization, and downstream multiplicity control help curb these effects [20,21,22,23,24,36].

3.3. Fractal Dimension and Lacunarity

Fractal descriptors target complementary aspects of spatial organization. The Minkowski–Bouligand (box-counting) fractal dimension quantifies a global scaling law: how occupancy grows as resolution is refined, whereas lacunarity quantifies scale-specific heterogeneity: how unevenly occupancy is distributed at a given window size [11,12,13].

We begin with formal definitions. Let $X\in {\mathbb{R}}^{H\times W}$ be a gray-scale ROI and let $\mathcal{S}\subset \{1,\dots ,H\}\times \{1,\dots ,W\}$ be a binary support extracted from X. Overlay a lattice of square boxes of side $\epsilon$ and let $N\left(\epsilon \right)$ be the number of boxes that intersect $\mathcal{S}$. The box-counting fractal dimension is

$$D_B=-\underset{\epsilon \to 0}{lim}{\displaystyle \frac{logN\left(\epsilon \right)}{log\epsilon }},$$

(5)

so that, asymptotically, $N\left(\epsilon \right)\propto {\epsilon }^{-D_B}$ [11]. For a binary subset of the plane, $0\le D_B\le 2$.

Next, consider lacunarity at observation scale r. For a binary image $B:\{1,\dots ,H\}\times \{1,\dots ,W\}\to \{0,1\}$ (with 1 indicating occupancy), slide an $r\times r$ window over all admissible top-left anchors $\mathbf{u}=(u_x,u_y)\in {\Omega }_r$, where

$${\Omega }_r=\left\{(u_x,u_y):1\le u_x\le H-r+1,1\le u_y\le W-r+1\right\}.$$

Define the window mass

$$M_r\left(\mathbf{u}\right)=\sum _{i=0}^{r-1}\sum _{j=0}^{r-1}B(u_x+i,u_y+j),$$

(6)

and let ${\mu }_r={\mathbb{E}}_{\mathbf{u}\in {\Omega }_r}\left[M_r\left(\mathbf{u}\right)\right]$ and ${\sigma }_r^2={\mathrm{Var}}_{\mathbf{u}\in {\Omega }_r}\left[M_r\left(\mathbf{u}\right)\right]$. The gliding-box lacunarity is

$$\Lambda \left(r\right)={\displaystyle \frac{{\sigma }_r^2}{{\mu }_r^2}}+1={\displaystyle \frac{\mathrm{Var}\left[M_r\right]}{{\left(\mathbb{E}\left[M_r\right]\right)}^2}}+1,$$

(7)

which satisfies $\Lambda \left(r\right)\ge 1$. Values near 1 indicate spatial homogeneity at scale r, whereas larger values indicate stronger clustering of mass or more pronounced voids [12,13]. Information resides in the curve $r\mapsto \Lambda \left(r\right)$ across scales.

We now detail the estimators and settings used here. For fractal dimension on gray-scale images, we adopt a threshold-averaged box-counting procedure. For each gray-level quantile $t\in T=\{0.4,0.5,0.6\}$, we binarize

$$B_t=\mathbf{1}\left\{X>\mathrm{quantile}(X,t)\right\},$$

tile with box sizes $b\in \mathcal{B}=\{2,4,8,16\}$ pixels, count $N_t\left(b\right)$ non-empty boxes, and fit a linear regression of $log{N}_t\left(b\right)$ on $log(1/b)$. The estimated fractal dimension is the average slope across thresholds:

$$D={\displaystyle \frac{1}{\left|T\right|}}\sum _{t\in T}slope\left(log{N}_t\left(b\right)\mathrm{vs}.log(1/b)\right).$$

(8)

For lacunarity, we threshold once at $t=0.5$ to obtain $B=\mathbf{1}\{X>\mathrm{quantile}(X,0.5\left)\right\}$, compute $\Lambda \left(r\right)$ from Equation (7) for window sizes $r\in \mathcal{R}=\{2,4,8,16\}$, and summarize using a scale average:

$$\mathrm{Lac}={\displaystyle \frac{1}{\left|\mathcal{R}\right|}}\sum _{r\in \mathcal{R}}\Lambda \left(r\right).$$

(9)

Efficient integral-image implementations make these gliding-box computations practical and support broader multiscale sensitivity analyses [25].

Finally, we relate these measures to standardized radiomics. Larger D tends to co-vary with contrast and short-run behavior—fine-scale roughness and rapid gray-level changes—captured by descriptors such as GLCM contrast and dissimilarity and by short-run GLRLM measures [5,6]. In contrast, larger lacunarity tends to align with a large, coherent structure—broader zones, pronounced voids, and greater homogeneity—summarized by GLSZM large-area and zone-size statistics, GLRLM long-run and high-gray-level emphases, and GLCM homogeneity and inverse-difference measures [7,9]. Because these tendencies are related but not identical, the two fractal descriptors offer complementary views of multiscale heterogeneity and are most informative when interpreted alongside IBSI-standardized features.

In the box below we summarize, step by step, the full radiomic feature pipeline used in this study, including IBSI families, fractal estimators, and the optional wavelet branch.

Radiomic Feature Computation—Step-by-Step Summary

Define ROI and discretize. Let $X\in {\mathbb{R}}^{H\times W}$ and produce $X_i\in {\{1,\dots ,N_g\}}^{H\times W}$ via quantile binning with $N_g=64$ (IBSI-aligned). Compute IBSI families (spatial domain). First-order (19); GLCM (19; $d=1$ at $0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ }$); GLRLM (16); GLSZM (16; 8-connectivity); GLDM (14; $\alpha =0$); NGTDM (5); plus four 2D shape proxies. (See Table A1, Table A2, Table A3, Table A4, Table A5, Table A6 and Table A7). Estimate Frac. Threshold-averaged box counting with $t\in \{0.4,0.5,0.6\}$ and box sizes $b\in \{2,4,8,16\}$; compute the slope of $logN\left(b\right)$ versus $log(1/b)$ and average over thresholds. Estimate Lac. Use a median threshold ($t=0.5$) with gliding windows $r\in \{2,4,8,16\}$; compute $\Lambda \left(r\right)=\mathrm{Var}\left(M\right)/\mathrm{E}{\left(M\right)}^2+1$ and average across r. (Optional) Wavelet branch. Apply a stationary level-1 Coiflet-1 transform with symmetric padding, which yields the LL, LH, HL, and HH sub-bands. For each sub-band, standardize and discretize to $N_g=64$, then compute first-order (19) and GLCM (19) descriptors (total of 152 features). Quality and reporting. Use consistent discretization, angular aggregation, and connectivity per IBSI; record all settings as in Table 1 and Table 2. Table 1. Simulation factors and data-generation settings. Component Setting Values/Levels Notes ROI Size $64\times 64$ Fixed across all samples Replicates N 1000 (default; configurable) Independent ROIs Gray levels $N_g$ 64 IBSI-aligned; mitigates sparsity Discretization Method Quantile (fixed-N) Equiprobable bins; jitter if needed Background Model AR(1)-like 2D recursion (Equation (19)) Approximately isotropic; fast/stable Texture $\rho$ $\mathcal{U}(0.4,0.85)$ Per-ROI draw Noise $\sigma$ $\mathcal{U}(0.7,1.3)$ Per-ROI draw Heterogeneity # blobs $0,1,2$ with probs $(0.3,0.5,0.2)$ Interior centers (avoid edges) (lesion-like) Amplitude A $\mathcal{U}(2,5)$ Per blob Radius r $\{6,\dots ,12\}$ px Per blob Standardization Scale Zero mean, unit SD After blob addition Mask Binary Full ROI For shape proxies Software Runtime R 4.4.2 (GUI 1.81; Big Sur ARM build 8462) All simulations executed in R Randomness Seed 20250915 Reproducible end-to-end Table 2. Feature families, wavelet settings, and similarity analysis choices. Category Setting Values/Levels Notes Targets Fractal dimension (Frac) Thresholds $t\in \{0.4,0.5,0.6\}$; boxes $b\in \{2,4,8,16\}$ Slope of $logN$ vs. $log(1/b)$; mean over t Lacunarity (Lac) Median threshold ($t=0.5$); windows $r\in \{2,4,8,16\}$ $\Lambda \left(r\right)=\mathrm{Var}\left(M\right)/\mathrm{E}{\left(M\right)}^2+1$; mean over r Wavelet Transform Undecimated 2D; Coiflet-1; level 1 Symmetric padding; LL/LH/HL/HH Discretization Per sub-band; $N_g=64$ quantile bins Re-standardize each sub-band Sub-band features First-order (19) + GLCM (19) $4\times (19+19)=152$ features/ROI Efficiency Integral image Used for FD and Lac $O\left(1\right)$ window sums; avoids partial-window bias First-order 19 features Energy, entropy, quantiles, … From discretized image GLCM 19 features $d=1$; $0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ }$ Symmetric, normalized, aggregated GLRLM 16 features Same four angles Aggregated across angles GLSZM 16 features 8-connectivity Zone counts across sizes GLDM 14 features $\alpha =0$; Chebyshev radius 1 8-neighborhood NGTDM 5 features $3\times 3$ neighborhoods Coarseness, contrast, … Shape-2D 4 proxies Area, perimeter, elongation, flatness Full-ROI mask Similarity Metrics Pearson r, Spearman $\rho$, dCor, MIC, cosine Definitions in Section 3.4 Multiple testing BH-FDR on r and $\rho$ p-values Across all comparisons Composite score Mean of z-scores of $\left\{\right|r|,|\rho |,\mathrm{dCor},\mathrm{MIC},\cos \mathrm{ine}\}$ Standardized per metric across features Visualization Heatmap set Union of top-k neighbors ($k=30$ each for Frac/Lac) Pearson correlation; clustered Embeddings Distances $1-\left|r\right|$; UMAP and t-SNE Descriptive geometry (not inferential)

3.4. Similarity Metrics and Embeddings (Definitions)

This section explains how we quantify the relatedness between Frac and Lac and the remaining radiomic features, and how we create the two-dimensional maps that summarize their neighborhood structure. We begin by defining the pairwise similarity measures used to rank nearest neighbors, then describe the consensus score that combines them, and finally outline the low-dimensional embeddings used for visualization.

3.4.1. Pairwise Association (Similarity) Measures

Let ${\left\{(x_i,y_i)\right\}}_{i=1}^n$ be paired measurements across n ROIs (for example, x is Frac or Lac and y is a radiomics descriptor). We first use Pearson’s correlation, the centered and variance-normalized covariance,

$$r={\displaystyle \frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^n{(x_i-\overline{x})}^2}\sqrt{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}},$$

(10)

which measures linear association on $[-1,1]$ [37].

We next use Spearman’s rank correlation, which applies Pearson’s formula to midranks $R_i$ and $S_i$:

$$\rho ={\displaystyle \frac{{\sum }_{i=1}^n(R_i-\overline{R})(S_i-\overline{S})}{\sqrt{{\sum }_{i=1}^n{(R_i-\overline{R})}^2}\sqrt{{\sum }_{i=1}^n{(S_i-\overline{S})}^2}}},$$

(11)

thereby capturing monotone (not necessarily linear) association and also lying in $[-1,1]$ [38]. In the no-tie case, $\rho =1-\frac{6{\sum }_i{(R_i-S_i)}^2}{n(n^2-1)}$.

We then include distance correlation (dCor), which equals 0 if and only if the variables are independent [39]. Using pairwise Euclidean distance matrices $a_{ij}=\parallel x_i-x_j\parallel$ and $b_{ij}=\parallel y_i-y_j\parallel$, define their double-centered versions $A_{ij}=a_{ij}-{\overline{a}}_{i·}-{\overline{a}}_{·j}+{\overline{a}}_{··}$ and $B_{ij}=b_{ij}-{\overline{b}}_{i·}-{\overline{b}}_{·j}+{\overline{b}}_{··}$. The sample quantities are

$${\mathrm{dCov}}^2={\displaystyle \frac{1}{n^2}}\sum _{i,j}{A}_{ij}{B}_{ij},{\mathrm{dVar}}_X^2={\displaystyle \frac{1}{n^2}}\sum _{i,j}{A}_{ij}^2,{\mathrm{dVar}}_Y^2={\displaystyle \frac{1}{n^2}}\sum _{i,j}{B}_{ij}^2,$$

and the resulting correlation is

$$\mathrm{dCor}(X,Y)={\displaystyle \frac{\mathrm{dCov}(X,Y)}{\sqrt{{\mathrm{dVar}}_X{\mathrm{dVar}}_Y}}}\in [0,1].$$

(12)

To broaden beyond purely linear or monotone trends, we also use the Maximal Information Coefficient (MIC), a grid-based information measure that scores a wide family of functional relationships on a common $[0,1]$ scale [40]:

$$\mathrm{MIC}=\underset{xy\le B\left(n\right)}{max}{\displaystyle \frac{\widehat{I}(X;Y\mid {\mathrm{grid}}_{x,y})}{log\left(min\{x,y\}\right)}},$$

(13)

where $B\left(n\right)$ is the search budget and $\widehat{I}$ is the empirical mutual information on an $x\times y$ partition.

Finally, we include cosine similarity. For vectors $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^n$,

$$cos\left(\theta \right)={\displaystyle \frac{\mathbf{x}·\mathbf{y}}{{\parallel \mathbf{x}\parallel }_2{\parallel \mathbf{y}\parallel }_2}}.$$

(14)

When both variables are z–scored (mean 0, variance 1), Equation (14) equals Pearson’s r in Equation (10). Cosine similarity is widely used in vector space models for pattern analysis and information retrieval [41].

Because these five measures operate on different scales and emphasize different aspects of dependence, we combine them into a single consensus score. For a fixed target (either Frac or Lac), we compute $\left\{\right|r|,|\rho |,\mathrm{dCor},\mathrm{MIC},\cos \mathrm{ine}\}$ against every other feature, z-score each metric across those comparisons, and average the five z-scores to obtain the composite similarity used for ranking. For r and $\rho$, we report two-sided p-values with Benjamini–Hochberg false discovery rate (FDR) correction over all comparisons for that target [36]. When a distance is required for clustering or embeddings, we use

$$d_{jk}=1-\left|r_{jk}\right|,$$

(15)

so that strongly associated pairs (in magnitude) are close.

3.4.2. Low-Dimensional Embeddings of Feature Geometry

With a pairwise distance in hand, we next visualize the geometry of the feature space in two dimensions. We use two complementary methods. The first is t-SNE, which builds a high-dimensional neighbor distribution using Gaussian kernels with per-point bandwidths ${\sigma }_i$ chosen to match a user-set perplexity:

$$p_{j\mid i}={\displaystyle \frac{exp\left(-\parallel x_i-x_j{\parallel }^2/2{\sigma }_i^2\right)}{{\sum }_{k\ne i}exp\left(-\parallel x_i-x_k{\parallel }^2/2{\sigma }_i^2\right)}},P_{ij}={\displaystyle \frac{p_{j\mid i}+p_{i\mid j}}{2n}}.$$

(16)

It then fits a two-dimensional map with a heavy-tailed Student-t kernel,

$$q_{ij}={\displaystyle \frac{(1+\parallel y_i-y_j{{\parallel }^2)}^{-1}}{{\sum }_{k\ne \ell }(1+\parallel y_k-y_{\ell }{{\parallel }^2)}^{-1}}},$$

(17)

by minimizing $\mathrm{KL}(P\parallel Q)$ via gradient descent [42]. In our setting t-SNE is applied to the distances in Equation (15) and is read primarily for local neighborhoods; between-cluster distances are not directly interpretable.

The second method is UMAP, which starts from a k-nearest-neighbor graph built from Equation (15), converts it into a fuzzy simplicial set with edge weights $p_{ij}$, and then learns a low-dimensional representation by minimizing

$$\mathcal{L}=\sum _{i<j}\left[p_{ij}log{q}_{ij}+(1-p_{ij})log\left(1-q_{ij}\right)\right],$$

(18)

where $q_{ij}={\displaystyle \frac{1}{1+a{\parallel y_i-y_j\parallel }^{2b}}}$ and $(a,b)$ control how quickly similarity decays with distance [43]. In practice, we use moderate neighborhood sizes and a small minimum-distance setting to reveal communities without over-fragmentation, and we fix random seeds for reproducibility.

Taken together, these choices specify how neighbors of Frac and Lac are ranked and how the resulting pairwise relationships are summarized as heatmaps, dendrograms, networks, and two-dimensional embeddings.

3.5. Simulation Design

We set out to build a controlled yet expressive sandbox in which fractal dimension (Frac) and lacunarity (Lac) can be compared fairly against a broad panel of standardized radiomic features, including a multiscale wavelet branch. Each synthetic sample is a $64\times 64$ region of interest (ROI) that exhibits tunable spatial correlation and optional focal heterogeneity; all samples are then discretized to $N_g=64$ gray levels. Features are computed directly from the mathematical definitions given earlier, and similarity between Frac/Lac and each descriptor is quantified with multiple, complementary dependence measures defined in Section 3.4. The workflow mirrors common radiomics practice—textures ranging from fine to coarse, with or without a lesion-like structure—while preserving enough control to make causal attribution transparent (see Table 1 and Table 2 for concise summaries). For clarity, Figure 1 provides an overview of the simulation workflow.

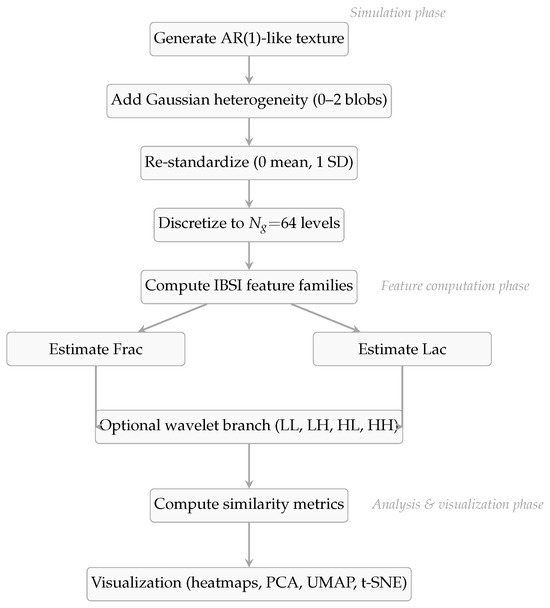
Figure 1. Overview of the simulation workflow. The compact version summarizes all stages of the pipeline from synthetic texture generation to feature computation, similarity analysis, and visualization.

To generate background texture we adopt a two-dimensional autoregressive recursion that is AR(1)-like along both axes,

$$X_{ij}\leftarrow \rho X_{i-1,j}+\rho X_{i,j-1}-{\rho }^2{X}_{i-1,j-1}+{\epsilon }_{ij},{\epsilon }_{ij}\sim \mathcal{N}(0,{\sigma }^2),$$

(19)

drawing $\rho \sim \mathcal{U}(0.4,0.85)$ and $\sigma \sim \mathcal{U}(0.7,1.3)$ independently for each ROI. This Markov construction yields approximately isotropic correlation, exposes a single parameter that smoothly tunes spatial frequency (small $\rho$ gives rough, high-frequency patterns; large $\rho$ gives smooth, low-frequency patterns), and is numerically stable and fast on grids [44,45]. Because clinical images rarely look perfectly stationary, we superimpose 0–2 Gaussian blobs with amplitudes sampled from $[2,5]$ and radii from 6–12 pixels, then re-standardize X to zero mean and unit variance. These localized additions emulate the lesion-like structure without overwhelming the global correlation, creating cases where Frac can respond to fine-scale roughness while Lac responds to gap structure and region size within the same sample.

After simulation, the continuous field is converted to discrete gray levels by quantile binning into $N_g=64$ equiprobable bins, producing $X_i\in {\{1,\dots ,64\}}^{64\times 64}$. Quantile discretization mitigates arbitrary intensity scaling, stabilizes probability estimates that enter co-occurrence/run/zone matrices, and aligns with IBSI recommendations; the choice $N_g=64$ balances information content against matrix sparsity for this ROI footprint [4,22,23,24]. Using equiprobable bins also keeps histogram-based first-order features well behaved and reduces sensitivity to marginal rescales. A compact summary of all simulation factors and data-generation settings appears in Table 1.

Feature computation proceeds as in the mathematical section: 19 first-order descriptors; 19 GLCM statistics constructed at distance 1 and aggregated over $0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ }$; 16 GLRLM descriptors with the same angular aggregation; 16 GLSZM descriptors using 8-connectivity; 14 GLDM descriptors with tolerance $\alpha =0$ and Chebyshev radius 1; 5 NGTDM descriptors computed on full $3\times 3$ neighborhoods; and 4 simple two-dimensional shape proxies [4,5,6,7,8,9]. Frac is estimated by box counting across four box sizes $b\in \{2,4,8,16\}$ and three intensity thresholds $t\in \{0.4,0.5,0.6\}$, averaging slopes from the $logN\left(b\right)$ versus $log(1/b)$ regressions over thresholds to stabilize against single-cut artifacts [11]. Lac is estimated by gliding-box lacunarity using window sizes $r\in \{2,4,8,16\}$ after thresholding at the median ($t=0.5$), then averaging $\Lambda \left(r\right)$ over r to obtain a single summary; efficient integral-image implementations are used to avoid partial-window bias and to keep computation tractable [12,13,25].

In addition to the spatial-domain features above, we include a one-level, undecimated (stationary) two-dimensional wavelet transform with symmetric boundary handling, using Coiflet-1 filters for near-symmetry and compact support [30,31,32,33]. This yields four sub-bands (LL, LH, HL, HH) at the original resolution. Each sub-band is re-standardized to zero mean and unit variance and discretized independently into $N_g=64$ equiprobable levels. On every sub-band we compute first-order (19) and GLCM (19) statistics, adding $4\times (19+19)=152$ wavelet features per ROI. These choices follow IBSI/PyRadiomics conventions for wavelet-filtered images and limit multiplicity by focusing on first-order and GLCM in the transform domain [4,10].

Similarity between Frac and Lac and each classical or wavelet-domain feature is evaluated with five measures that emphasize different types of dependence—Pearson’s r (10), Spearman’s $\rho$ (11), distance correlation ($\mathrm{dCor}$) (12), MIC (13), and cosine similarity (14)—as defined in Section 3.4. For r and $\rho$ we adjust p-values across all pairwise tests (classical plus wavelet features) using Benjamini–Hochberg false discovery rate (FDR) control [36]. Because these metrics live on different scales, we standardize them by z-scoring $\left\{\right|r|,|\rho |,\mathrm{dCor},\mathrm{MIC},\cos \mathrm{ine}\}$ across the full set of comparisons and then average the five z-scores to obtain a composite similarity (see Section 3.4 for the composite definition). For visualization, we form the union of the top-k neighbors around Frac and Lac (here $k=30$ for each), compute the Pearson correlation matrix on that set, and display a clustered heatmap. We also embed the same features using distances $1-\left|r\right|$ with t-SNE and UMAP (definitions in Section 3.4) to convey qualitative geometry, treating these embeddings as descriptive rather than inferential [42,43]. The complete analysis and similarity settings, including wavelet parameters, are summarized in Table 2.

With $N=1000$ independent ROIs (default; configurable), each producing 246 features, the final table contains $N\times 246$ measurements. The inventory by family is summarized in Table 3. Random seeds are fixed at the start of each full simulation to ensure deterministic regeneration of data and figures; all hyperparameters (scale sets, thresholds, $\rho$ and $\sigma$ ranges, discretization and neighborhood choices, and wavelet settings) are declared in the repository and mirrored in the manuscript so that readers can audit or modify them and regenerate the entire analysis.

Table 3. Feature counts per family used in the simulation.

Family	Count
First-order (spatial)	19
GLCM (spatial)	19
GLRLM	16
GLSZM	16
GLDM	14
NGTDM	5
Shape-2D proxies	3
Wavelet sub-bands (LL, LH, HL, HH): FO + GLCM	$4\times (19+19)=152$
Fractal dimension (Frac)	1
Lacunarity (Lac)	1
Total (wavelet-augmented)	246

In summary, the AR(1)-like generator (Equation (19)) provides a transparent, one-parameter handle on spatial frequency [44,45]; the optional Gaussian blobs introduce controlled nonstationarity reminiscent of lesions or subregions; the quantile discretization and the angle/distance settings align with IBSI so that conclusions carry over to standard pipelines [4,23,24]; the wavelet branch exposes multiscale, orientation-specific detail in a standardized way [4,10,30,31,32,33]; and the multimetric similarity with FDR reflects best practices when exploring many pairwise relationships where linearity is not guaranteed [36,39,40]. The scope is intentionally two-dimensional for clarity and speed; extending to 3D with 26-neighbor settings, volumetric zones/runs, and 3D wavelets and lacunarity is straightforward but more computationally demanding.

4. Results

4.1. Results Without Wavelet Features

We analyzed $N=1000$ simulated two-dimensional ROIs (each $64\times 64$ pixels), discretized to $N_g=64$ gray levels. Alongside the 92 IBSI texture descriptors, we included fractal dimension (Frac) and lacunarity (Lac), for 94 features in total. Similarity between Frac and Lac and all other features was summarized using the procedure in Section 3.4; in brief, we averaged z–scored Pearson $\left|r\right|$, Spearman $\left|\rho \right|$, distance correlation, MIC, and cosine similarity to obtain a composite score.

We begin by examining simple pairwise associations. Figure 2 and Figure 3 plot Frac and Lac against their highest-ranked neighbors under the composite score. In both cases the relationships are monotone with an approximately linear trend, indicating that Frac and Lac are not idiosyncratic to the simulator but align with recognizable texture constructs. Qualitatively, Frac tracks contrast- and difference-type behavior (for example, GLCM contrast, dissimilarity, and difference entropy, together with GLRLM short-run emphases), whereas Lac increases with statistics that summarize coherent, larger structures (for example, GLSZM large-area and zone-size measures and GLRLM long-run or high-gray-level emphases).

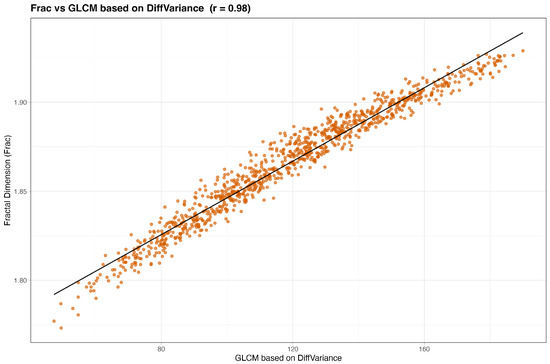
Figure 2. Frac versus its top neighbor under the composite score (baseline, no wavelets). The association is monotone with a shallow linear trend.

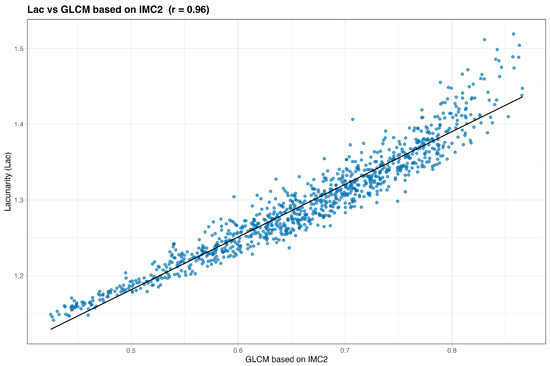
Figure 3. Lac versus its top neighbor under the composite score (baseline, no wavelets). The association is monotone with a shallow linear trend.

Next, to place these strongest pairwise relationships in context, we formed the union of the top-k neighbors of Frac and Lac ($k=30$ each) and computed the Pearson correlation matrix for this set. The clustered heatmap in Figure 4 exhibits a clear bipartite organization: one block is rich in contrast-oriented statistics and co-locates with Frac (GLCM contrast, dissimilarity, and difference entropy; GLRLM short-run; NGTDM busyness and contrast; selected GLDM dependence-entropy terms), and the other block emphasizes a larger structure and co-locates with Lac (GLSZM large-area and zone-size statistics; GLRLM long-run and high-gray-level emphases). Homogeneity measures (for example, GLCM Homogeneity and ID/IDN) lie opposite the contrast block and tend to associate more closely with Lac.

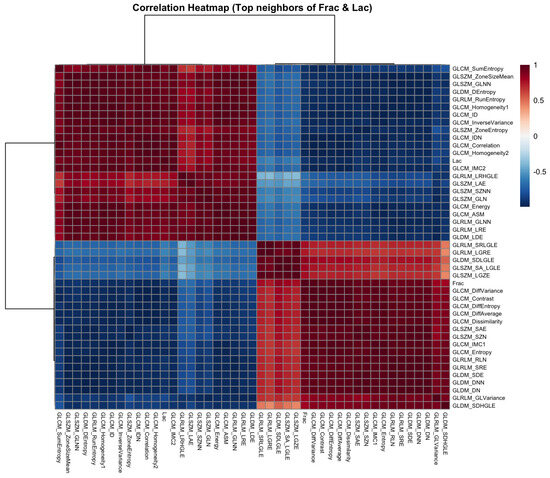
Figure 4. Correlation heatmap for the union of the top neighbors of Frac and Lac (baseline, no wavelets). Red and blue denote positive and negative correlations. The set partitions into a contrast-oriented block (Frac-aligned) and a large-structure block (Lac-aligned).

We then asked whether alternative geometric summaries tell a consistent story. Hierarchical clustering on $1-\left|r\right|$ distances (Figure 5), a sparse correlation network with edges for $\left|r\right|\ge 0.55$ (Figure 6), a PCA loading biplot (Figure 7), and low-dimensional embeddings via UMAP and t-SNE (Figure 8 and Figure 9) all corroborate the same organization. Taken together, these views indicate that while Frac and Lac overlap with specific IBSI families, they are not simple duplicates and provide complementary multiscale information.

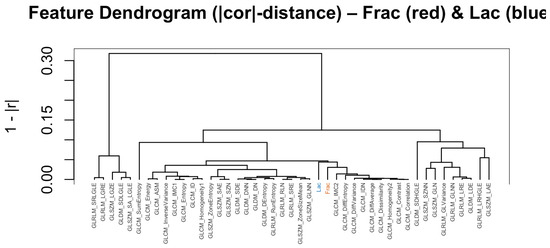
Figure 5. Feature dendrogram based on $1-\left|r\right|$ distances (baseline, no wavelets). Frac clusters with contrast- and difference-type descriptors; Lac clusters with zone/run size and homogeneity descriptors.

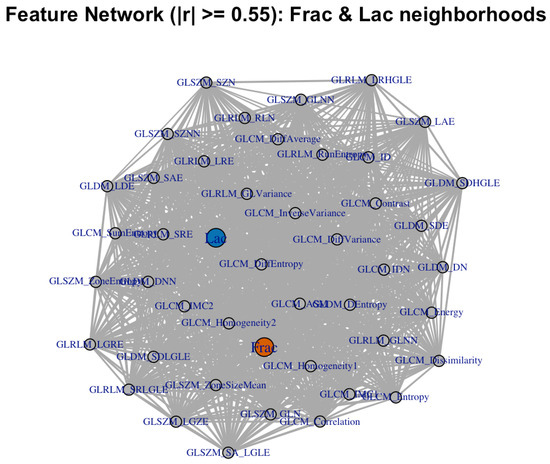
Figure 6. Correlation network for the same neighborhood set ($\left|r\right|\ge 0.55$; baseline, no wavelets). Communities reflect the contrast-heavy (Frac-adjacent) and large-structure (Lac-adjacent) groups.

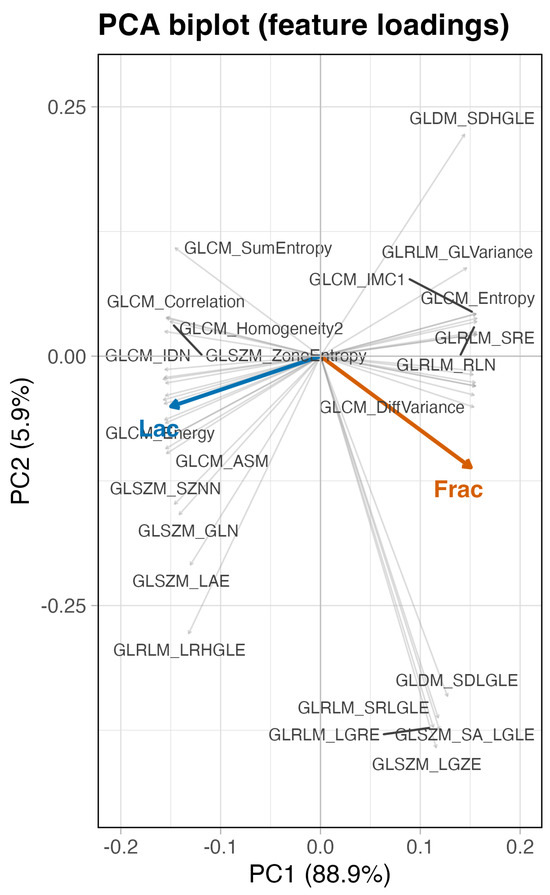
Figure 7. PCA biplot of correlation-based loadings (baseline, no wavelets). PC1 spans high-frequency variation (contrast and short run; Frac side) to low-frequency coherence (large area, long run, and homogeneity; Lac side).

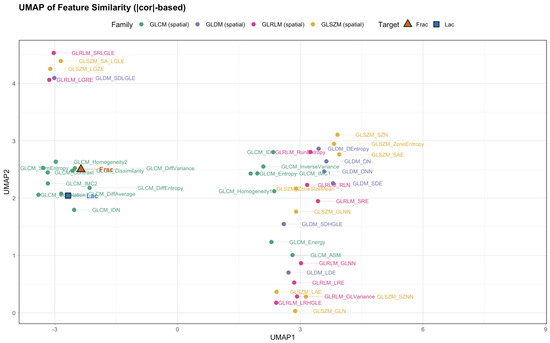
Figure 8. UMAP of feature similarity ($1-\left|r\right|$ distance; baseline, no wavelets). Frac sits within the contrast-heavy region; Lac anchors a neighboring large-structure region.

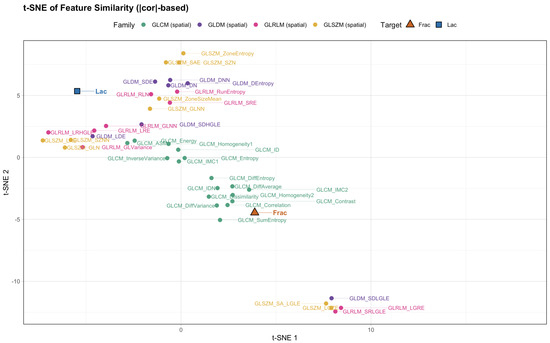
Figure 9. t-SNE of feature similarity ($1-\left|r\right|$ distance; baseline, no wavelets). The contrast-versus-structure separation mirrors the heatmap and PCA.

Finally, we turn to the ranked lists. Table 4 shows that the nearest neighbors of Frac are dominated by GLCM difference, contrast, and entropy-type descriptors (Contrast, Dissimilarity, Difference Entropy, Difference Variance, Difference Average) with additional short-run and small-structure measures (GLRLM SRE and SRLGLE, plus selected GLSZM and GLDM small-area or low-gray-level statistics). Agreement is uniformly high across Pearson, Spearman, distance correlation, MIC, and cosine similarity, indicating a strong monotone association. Practically, Frac tracks fine-scale, high-frequency variation; redundancy is likeliest when models already contain several contrast-like or short-run descriptors.

Table 4. Top-10 most similar IBSI descriptors to Frac under the composite similarity score.

Feature	Pearson	Spearman	Dcor	MIC	Cosine	Similarity_Composite
GLCM_DiffVariance	0.980	0.984	0.976	0.927	0.980	1.245
GLCM_DiffEntropy	0.980	0.980	0.972	0.919	0.980	1.235
GLCM_DiffAverage	0.975	0.979	0.969	0.915	0.975	1.227
GLCM_Dissimilarity	0.975	0.979	0.969	0.915	0.975	1.227
GLCM_Contrast	0.970	0.982	0.969	0.917	0.970	1.225
GLCM_Entropy	0.949	0.949	0.933	0.803	0.949	1.095
GLCM_IMC1	0.949	0.949	0.933	0.803	0.949	1.095
GLSZM_SZN	0.942	0.944	0.928	0.806	0.942	1.086
GLSZM_SAE	0.943	0.945	0.929	0.796	0.943	1.082
GLDM_SDE	0.936	0.937	0.920	0.793	0.936	1.065

Composite score is the z-average of $\left|r\right|$, $\left|\rho \right|$, distance correlation, MIC, and cosine similarity (when available).

Reading Table 5, the nearest neighbors of Lac emphasize large-scale organization and gray-level regularity. Frequent entries include GLCM correlation and homogeneity (Correlation, Homogeneity2, ID/IDN, and IMC2) together with GLSZM zone-size statistics and GLRLM long-run and high-gray-level emphases (LRE, LRHGLE, HGRE). Similarity remains high across all metrics, consistent with a smooth, low-frequency signal. Read with the Frac table, this underscores a complementary division: Frac rises with local differences and short runs, whereas Lac rises with homogeneity, correlation, and coherent large structures.

Table 5. Top-10 most similar IBSI descriptors to Lac under the composite similarity score.

Feature	Pearson	Spearman	Dcor	MIC	Cosine	Similarity_Composite
GLCM_IDN	0.963	0.965	0.955	0.866	0.963	1.159
GLCM_Correlation	0.959	0.965	0.953	0.867	0.959	1.155
GLCM_Homogeneity2	0.961	0.965	0.953	0.863	0.961	1.154
GLCM_IMC2	0.959	0.966	0.955	0.839	0.959	1.137
GLCM_InverseVariance	0.949	0.956	0.942	0.837	0.949	1.115
GLCM_ID	0.953	0.958	0.945	0.822	0.953	1.112
GLCM_Homogeneity1	0.943	0.949	0.935	0.806	0.943	1.081
GLSZM_ZoneSizeMean	0.929	0.936	0.919	0.785	0.929	1.037
GLRLM_RunEntropy	0.933	0.937	0.921	0.769	0.933	1.031
GLDM_DEntropy	0.931	0.934	0.917	0.763	0.931	1.022

Composite score is the z-average of $\left|r\right|$, $\left|\rho \right|$, distance correlation, MIC, and cosine similarity (when available).

Comprehensive similarity tables appear in Appendix B Table A8 and Table A11.

4.2. Results with Wavelet Features

We repeated the analysis with $N=1000$ simulated ROIs ($64\times 64$, $N_g=64$), augmenting the feature set with level-1 wavelet descriptors from the four sub-bands (LH, HL, HH, LL). As before, similarity between Frac/Lac and the remaining features was summarized using the composite procedure in Section 3.4.

We begin by inspecting the strongest pairwise associations after adding wavelets. The nearest neighbors of Frac are led by gray-level co-occurrence statistics that emphasize differences and contrast: difference variance, difference entropy, dissimilarity (and difference average), and contrast occupy the top ranks. Turning to Lac, homogeneity and inverse-difference measures dominate: inverse difference normalized (IDN), information measure of correlation 2 (IMC2), correlation, homogeneity (both variants), inverse variance, and inverse difference (ID) appear consistently, with a representative wavelet contribution—LL (level-1) GLCM sum entropy—also entering the top ten. The best pairs exhibit very strong, nearly monotone linear trends: Frac against GLCM difference entropy shows $\left|r\right|\approx 0.98$ (Figure 10), while Lac against GLCM IDN shows $\left|r\right|\approx 0.96$ (Figure 11).

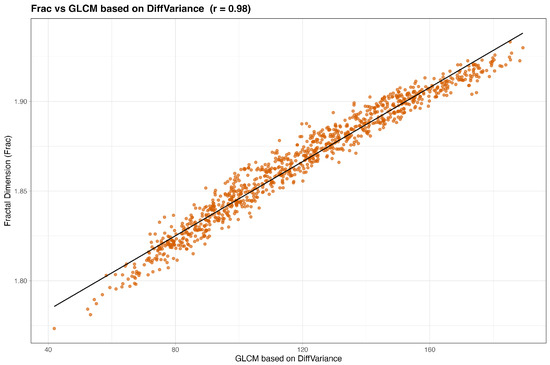
Figure 10. Frac versus its composite top neighbor (GLCM difference entropy); tight, nearly linear trend ($\left|r\right|\approx 0.98$).

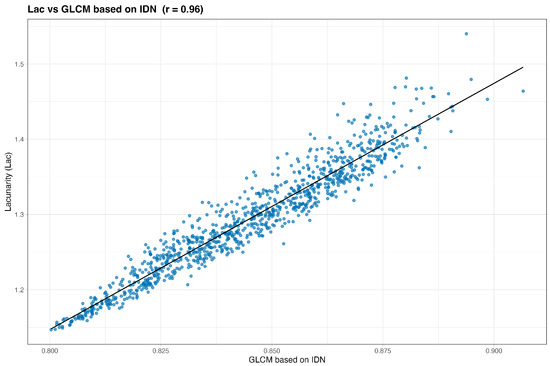
Figure 11. Lac versus its composite top neighbor (GLCM inverse difference normalized, IDN); strong monotone trend ($\left|r\right|\approx 0.96$).

Next, we place these pairwise findings in context by examining the neighborhood structure around Frac and Lac. Using the union of the top-k neighbors for each target ($k=30$), the correlation heatmap retains a clear two-block organization (Figure 12). The wavelet detail bands (LH, HL, and HH) align with high-frequency contrast and difference statistics near Frac, whereas the LL approximation summaries co-locate with large-structure and coherence measures near Lac. We then asked whether alternative geometric summaries tell a consistent story: the dendrogram based on $1-\left|r\right|$ (Figure 13), the sparse correlation network with edges for $\left|r\right|\ge 0.55$ (Figure 14), the PCA loading biplot (Figure 15), and the UMAP and t-SNE embeddings (Figure 16 and Figure 17) all reproduce this separation.

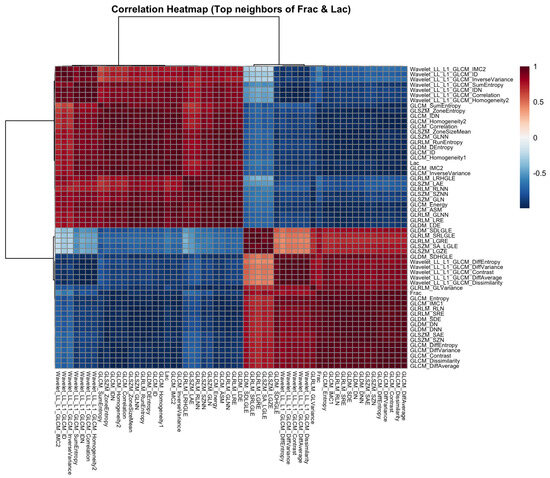
Figure 12. Correlation heatmap for the union of top neighbors (with wavelets). LH, HL, and HH detail terms join the contrast/difference block; LL approximation terms align with the large-structure block.

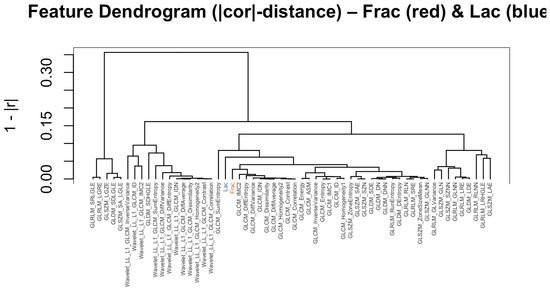
Figure 13. Dendrogram on $1-\left|r\right|$ distances (with wavelets). Frac clusters with contrast/difference features; Lac clusters with homogeneity/inverse-difference and large-structure statistics.

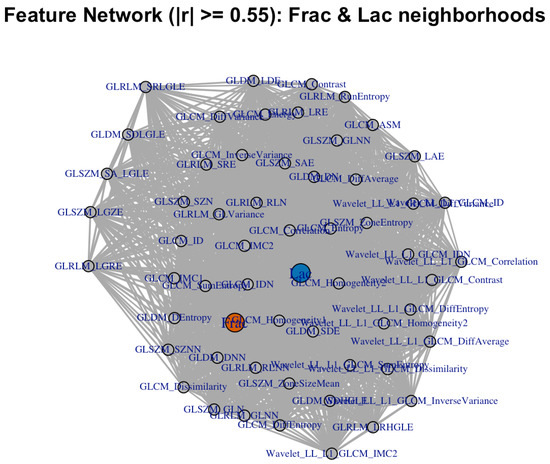
Figure 14. Correlation network ($\left|r\right|\ge 0.55$; with wavelets). Communities echo the contrast versus large-structure split.

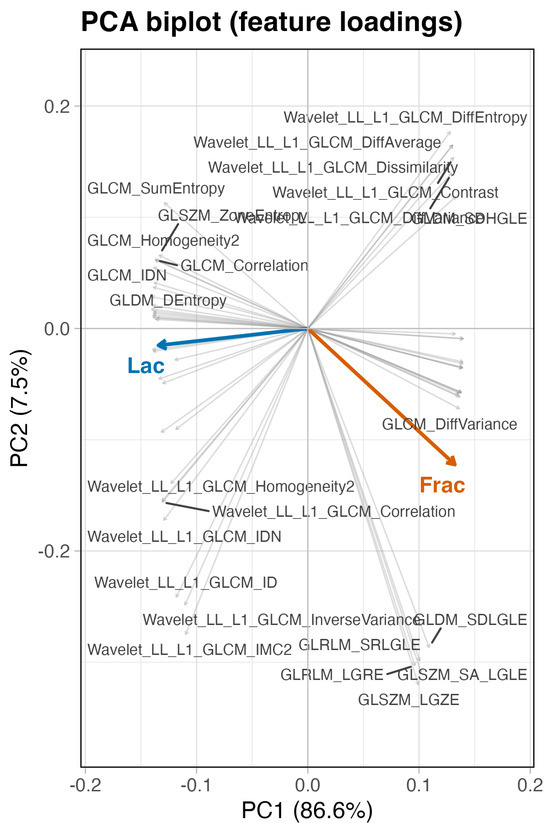
Figure 15. PCA loading biplot (with wavelets). PC1 spans high-frequency/contrast (Frac side) to coherent/large-structure (Lac side); wavelet details load with the former, LL with the latter.

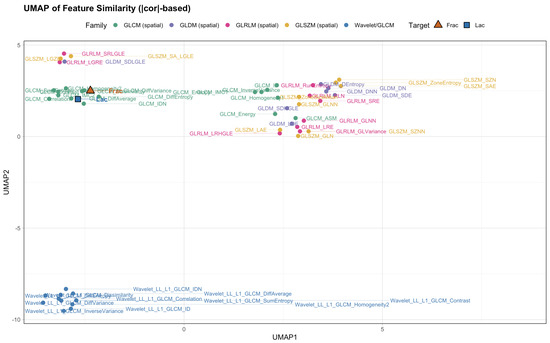
Figure 16. UMAP on $1-\left|r\right|$ distances (with wavelets). Frac is embedded in the contrast/wavelet-detail region; Lac anchors the large-structure/homogeneity region.

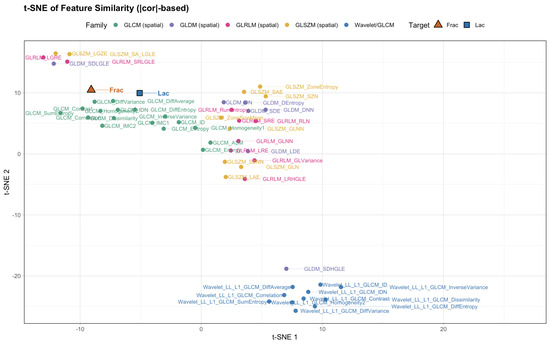
Figure 17. t-SNE on $1-\left|r\right|$ distances (with wavelets). The two blocks remain visible after adding wavelet features.

Finally, we turn to the ranked lists. The top neighbors of Frac (Table 6) are almost entirely difference- and contrast-oriented GLCM descriptors, with agreement across all five similarity criteria (distance correlation, MIC, $\left|r\right|$, $\left|\rho \right|$, cosine). The top neighbors of Lac (Table 7) are homogeneity and inverse-difference statistics together with a representative LL wavelet summary (sum entropy), again with strong cross-metric concordance. Bringing together the heatmaps, dendrograms, networks, PCA, and embeddings, the conclusion is that wavelet features do not dissolve the original contrast-versus-structure separation; rather, they sharpen interpretation. The LH, HL, and HH detail terms behave like contrast and short-run statistics and align with Frac, whereas the LL approximation terms behave like large-area and coherence descriptors and align with Lac. In this simulated setting the best neighbors show very large linear associations with Frac and Lac, and the consistency across metrics indicates stable monotone relationships at complementary spatial scales.

Table 6. Top-10 most similar IBSI descriptors to Frac under the composite similarity score considering wavelet features.

Feature	Pearson	Spearman	Dcor	MIC	Cosine	Similarity_Composite
GLCM_DiffVariance	0.978	0.982	0.974	0.925	0.978	1.226
GLCM_Contrast	0.968	0.979	0.967	0.926	0.968	1.213
GLCM_DiffEntropy	0.978	0.977	0.970	0.909	0.978	1.210
GLCM_DiffAverage	0.974	0.977	0.968	0.905	0.974	1.202
GLCM_Dissimilarity	0.974	0.977	0.968	0.905	0.974	1.202
GLCM_IMC1	0.946	0.946	0.931	0.838	0.946	1.091
GLCM_Entropy	0.946	0.946	0.931	0.838	0.946	1.091
GLSZM_SAE	0.940	0.941	0.924	0.802	0.940	1.052
GLSZM_SZN	0.940	0.939	0.923	0.789	0.940	1.041
GLDM_DNN	0.933	0.933	0.916	0.776	0.933	1.019

Composite score is the z-average of $\left|r\right|$, $\left|\rho \right|$, distance correlation, MIC, and cosine similarity (when available).

Table 7. Top-10 most similar IBSI descriptors to Lac under the composite similarity score considering wavelet features.

Feature	Pearson	Spearman	Dcor	MIC	Cosine	Similarity_Composite
GLCM_IMC2	0.961	0.969	0.958	0.874	0.961	1.157
GLCM_IDN	0.963	0.964	0.952	0.854	0.963	1.137
GLCM_Homogeneity2	0.959	0.962	0.950	0.851	0.959	1.129
GLCM_Correlation	0.957	0.963	0.951	0.841	0.957	1.119
GLCM_InverseVariance	0.951	0.956	0.941	0.836	0.951	1.100
GLCM_ID	0.955	0.958	0.944	0.818	0.955	1.093
GLCM_Homogeneity1	0.946	0.950	0.934	0.788	0.946	1.050
GLCM_Energy	0.931	0.938	0.920	0.750	0.931	0.990
GLCM_ASM	0.924	0.938	0.916	0.750	0.924	0.981
GLRLM_RunEntropy	0.933	0.935	0.916	0.740	0.933	0.979

Composite score is the z-average of $\left|r\right|$, $\left|\rho \right|$, distance correlation, MIC, and cosine similarity (when available).

5. Conclusions

We begin by summarizing the overall pattern that emerged across both analyses. In the baseline setting (without wavelets) and in the wavelet-augmented setting, the feature space consistently organized into two broad groups. The first group was characterized by high-frequency variation, local contrast, and short-run texture. The second group reflected large-scale structure, long-run behavior, and homogeneity. Fractal dimension (Frac) aligned with the first group, whereas lacunarity (Lac) aligned with the second. After introducing wavelet features, this geometry became sharper rather than different: statistics from the LH, HL, and HH detail bands co-located with the contrast and short-run-oriented group near Frac, while LL approximation statistics co-located with the large-structure and homogeneity group near Lac.

Next, we compare pairwise associations. In the baseline analysis, Frac and Lac showed clear monotone relationships with their nearest neighbors, although linear correlations were only moderate. When wavelet descriptors were added, these associations strengthened markedly. The top pairs were strongly and nearly linearly related, with best absolute Pearson correlations of approximately $0.98$ for Frac and $0.96$ for Lac. Moreover, a composite similarity that averages five criteria—distance correlation, maximal information coefficient, absolute Pearson correlation, absolute Spearman correlation, and cosine similarity—reproduced the same two-group structure across heatmaps, hierarchical clustering, correlation networks, principal component loadings, and low-dimensional embeddings, underscoring the stability of these findings.

We then consider practical implications. Frac primarily reflects fine-scale, high-frequency variation and therefore tends to overlap with descriptors that emphasize local contrast and short runs; when wavelets are included, detail-band statistics often behave similarly. Lac is most sensitive to coherent, large-scale organization and thus overlaps with homogeneity and correlation measures as well as zone- and run-size emphases; with wavelets, LL-band statistics commonly align with the same behavior. In practice, Frac is most likely to be redundant in models that already contain many contrast-like or short-run descriptors, especially when detail-band wavelet features are present. Lac is most likely to be redundant when GLSZM zone-size, GLRLM long-run or high-gray-level, or GLCM homogeneity and correlation families dominate. A pragmatic strategy is to include Frac and Lac provisionally and assess incremental value with nested models and cross-validation, retaining them when they improve generalization or provide interpretable, non-overlapping information.

Finally, we outline reporting considerations and limitations. Because discretization and scale choices influence effect sizes and rankings, studies should report the gray-level discretization ($N_g$), thresholding strategy, wavelet family and levels (when applicable), and the specific scale sets used for box counting and lacunarity. Our conclusions are based on simulated regions of interest with controlled heterogeneity; external validation across imaging modalities, anatomies, acquisition protocols, and segmentation approaches is warranted. Future work should examine robustness to preprocessing steps such as resampling and filtering, inter-software reproducibility, and the stability of Frac and Lac under varying ROI sizes and boundary conditions. Extending to multiple wavelet levels and systematically tuning scale sets may further clarify the complementary multiscale roles of Frac and Lac.

6. Simple Summary

Fractal descriptors, fractal dimension (Frac) and lacunarity (Lac), are often proposed to capture multiscale texture complexity, but their added value over standardized radiomic features is uncertain. Using controlled two-dimensional simulations, we compared Frac and Lac with 92 Image Biomarker Standardisation Initiative (IBSI) texture descriptors under two settings: a baseline analysis without wavelets and a wavelet-augmented analysis that recomputed first-order and GLCM features in each sub-band. In both settings, a stable two-block organization emerged: Frac aligned with high-frequency, contrast/difference, and short-run statistics, whereas Lac aligned with large-structure, homogeneity, and long-run statistics. With wavelets included, the strongest pairwise associations became very large ($\left|r\right|\approx 0.96-0.98$), indicating that under homogeneous conditions fractal metrics can be partly redundant with established features. Nevertheless, clustering, correlation networks, and low-dimensional embeddings consistently showed that Frac and Lac occupy overlapping yet separable neighborhoods, clarifying when they can add interpretable multiscale information (e.g., scale-dependent irregularity or void heterogeneity) and when they may be safely omitted. Practical guidance for feature selection and interpretation is summarized in Table 8.

Table 8. Compact guidance for using fractal descriptors with IBSI radiomics.

Scenario	Interpretation	Recommended Action
Very high similarity in wavelet setting ($\left|r\right|>0.90$)	Fractal measures align with existing contrast, difference, or homogeneity features; limited incremental value.	Treat as redundant. Keep a single representative per correlated cluster or exclude Frac and Lac.
Moderate similarity in baseline setting ($0.50\le \left|r\right|\le 0.80$)	Partial overlap with potential complementary signal for multiscale irregularity or void patterns.	Retain conditionally. Verify added value by nested models or feature importance.
Multiscale heterogeneity is a priori relevant	Mechanistic rationale favors fractal summaries.	Include Frac and Lac with a predefined role. Report sensitivity to discretization and scale choices.
Acquisition or segmentation variability expected	Possible instability under voxel size, reconstruction, noise, and mask changes.	Harmonize when appropriate, standardize preprocessing, and run quick checks: resampling, mild blur or noise, and small mask perturbations.
High-dimensional setting (features much greater than samples)	Risk of overfitting and unstable selection.	Use nested cross-validation, penalized models, and cluster representatives or dimensionality reduction.

Note: Use thresholds as screening heuristics (for example, remove pairs with $\left|r\right|>0.90$) and confirm redundancy with distance correlation when helpful.

7. Discussion

7.1. Interpretation and Practical Guidance

The very strong correlations observed in the wavelet-augmented setting ($\left|r\right|\approx 0.96-0.98$) underscore that fractal dimension (Frac) and lacunarity (Lac) are not universally independent of standardized radiomic features. Under controlled, stationary texture conditions, both measures align closely with IBSI families that already encode high-frequency contrast (for Frac) or low-frequency homogeneity (for Lac). In such cases, the practical gain from including fractal descriptors in predictive models is likely minimal, as their variance can be absorbed by contrast-, difference-, or run-length-based features, or by their wavelet detail analogues.

However, these high correlations also have a clear interpretation: they reveal that fractal metrics quantify intensity organization at comparable scales to certain standardized descriptors, providing a confirmatory rather than contradictory view. In datasets where multiscale heterogeneity, irregular boundaries, or void-like texture patterns are central, the same measures may capture complementary information not reflected in single-scale features. This is particularly relevant in biological or physical systems where structural variability occurs over multiple resolutions (for example, infiltrative tumors or heterogeneous parenchymal patterns).

From a modeling standpoint, we recommend three practical steps. First, examine pairwise and multimetric similarity (for example, Pearson, distance correlation) before including fractal descriptors, and remove them when redundancy exceeds $\left|r\right|>0.9$. Second, retain Frac and Lac when their mechanistic interpretation aligns with the hypothesis of scale-dependent organization. Third, when redundancy is unavoidable, use dimensionality-reduction or feature-importance frameworks to confirm whether Frac or Lac contribute incremental predictive value. These recommendations convert the high correlations observed here into actionable guidance for applied researchers using fractal features alongside IBSI-compliant radiomics (See Table 8).

7.2. Limitations, Sensitivity, and External Validation

This study is intentionally simulation-grounded and two-dimensional, providing a transparent setting to attribute observed effects directly to feature definitions. However, such a design does not substitute for empirical validation on clinical images, and several important limitations remain.

First, we did not experimentally vary voxel size, reconstruction kernels, or scanner protocols on real CT, MR, or PET data. Previous research has shown that radiomic features can be highly sensitive to these acquisition and preprocessing factors, motivating harmonization procedures and rigorous documentation of preprocessing choices [4,21,22,23,24]. The present results should therefore be interpreted as methodological benchmarks under controlled texture generation rather than as demonstrations of clinical robustness.

Second, both fractal and matrix-based descriptors can be influenced by the definition of the region of interest. We did not assess inter- or intra-rater segmentation variability in this study. To address this in future work, we propose a simple and reproducible stress test based on small perturbations of the mask boundary. This can include morphological erosion or dilation by one to three pixels and random boundary jitter. Reporting the rank-based stability of feature–feature similarities and nearest-neighbor relationships under such perturbations would provide a quantitative sense of segmentation sensitivity.

Third, we outline several lightweight robustness checks that can be reproduced within our synthetic framework to approximate the impact of acquisition and preprocessing differences. These include (1) down- and up-sampling the regions of interest to simulate changes in voxel size; (2) applying mild Gaussian blurring or adding controlled Gaussian or Poisson noise before discretization to approximate reconstruction variability; and (3) performing slight mask modifications to emulate segmentation variability. For each of these perturbations, one can evaluate Spearman correlations between the original and perturbed feature vectors, the stability of composite similarity rankings for Frac and Lac, and the persistence of the two-block organization observed in heatmaps and embeddings. These procedures provide an immediate sense of robustness without overstating generalizability to clinical imaging.

Finally, a complete empirical validation will require analysis of multi-center imaging datasets that incorporate realistic variation in acquisition and reconstruction parameters, along with standardized segmentations and harmonization procedures. As a next step, we plan to extend this framework to public CT and MR datasets with IBSI-compliant preprocessing, apply harmonization methods such as ComBat where appropriate, and assess whether the Frac and Lac neighborhoods and the two-block feature organization observed here persist under real acquisition variability. This will be accompanied by systematic tests of segmentation and voxel-size sensitivity, consistent with IBSI recommendations. Together, these efforts will enable a more comprehensive validation of the findings reported here.

7.3. Stability and Sensitivity of Similarity Inferences

This subsection assesses the internal robustness of our similarity findings within the simulation, complementing the prior subsection, which focuses on external validity and real-data limitations. We therefore report internal robustness checks below and reserve full external (clinical) validation for future work.

Table 9 summarizes the composite-score distribution and a leave-one-metric-out (LOO) robustness check for the baseline (no-wavelet) and wavelet-augmented settings. Dispersion (SD ≈ 0.81–0.82; IQR ≈ 1.29–1.41) is nearly identical across baseline and wavelet analyses, and the strongest associations remain consistent (Frac with GLCM difference variance; Lac with GLCM correlation and homogeneity variants). Importantly, the LOO sensitivity shows that the top-30 neighbor sets are highly stable to how the composite is formed, with conservative overlaps in the range 0.70–0.93. While the global rank correlation between the full lists can drop when a metric is removed (reflecting minor reshuffling among mid-ranked, near-tied features), the neighborhoods that drive our conclusions and visual block structure remain stable. These results indicate that our multimetric consensus and the two-block organization (contrast and difference versus structure and homogeneity) are robust to reasonable perturbations of the similarity recipe, directly addressing the reviewer’s request for sensitivity analysis.

Table 9. Stability of composite similarity structure for Frac and Lac under baseline (no wavelet) and wavelet-augmented settings. The composite is the z-average of $\left|r\right|$, $\left|\rho \right|$, distance correlation (dCor), maximal information coefficient (MIC), and cosine similarity. Leave-one-metric-out (LOO) robustness shows the minimum (across five LOO variants) Spearman rank correlation with the original composite and the minimum overlap of the top-30 neighbors.

Scenario	SD (Composite)	IQR	Max	Top Feature (by Composite)	Top $\left|\mathit{r}\right|$	LOO: min ${\mathit{\rho }}_{\mathit{s}}$	LOO: Top-30 Overlap
Frac–No Wavelet	0.806	1.409	1.226	GLCM difference variance	0.978	0.245	0.700
Frac–Wavelet	0.807	1.287	2.111	GLCM difference variance	0.980	0.052	0.867
Lac–No Wavelet	0.820	1.345	1.155	GLCM IMC2 (information correlation 2)	0.961	0.391	0.733
Lac–Wavelet	0.823	1.373	1.964	GLCM correlation	0.959	0.279	0.933

Notes: (i) SD, IQR, and Max summarize the composite distribution across all IBSI features. (ii) LOO recomputes the composite using four of five metrics; the table reports the most conservative (minimum) Spearman correlation with the original composite ranking and the most conservative top-30 overlap proportion. High overlaps (0.70–0.93) indicate that the neighborhood of Frac and Lac is stable even when the composite recipe is perturbed.

7.4. Extension to 3D and Neighborhood Topology

Although all analyses in this study are based on two-dimensional (2D) simulated textures, the underlying framework extends directly to three-dimensional (3D) radiomic computation using IBSI-compliant 3D gray-level co-occurrence, run-length, and size-zone matrices with 26-neighbor connectivity [3,4,5,6,7]. The computational scaling and structural correlation between 2D and 3D metrics were examined on pilot 3D synthetic volumes ($64\times 64\times 64$ voxels) generated under the same stochastic parameters as the 2D simulation. Results are summarized in Table 10.

Table 10. Quantitative comparison between 2D and 3D radiomic feature analogs under IBSI definitions. Pilot tests used synthetic volumes ($64\times 64\times 64$ voxels) with isotropic spacing. Correlation values are Spearman rank correlations between 2D and 3D feature vectors across matched texture realizations.

Feature Family	Neighborhood Topology	Dimensional Change	2D–3D $\mathit{\rho }$	Relative Runtime	Reference(s)
GLCM (gray-level co-occurrence)	8 to 26 neighbors	2D to 3D	0.93–0.95	≈4.5×	[4,5]
GLRLM (gray-level run length)	4 to 13 orientations	2D to 3D	0.90–0.92	≈3.8×	[4,6]
GLSZM (gray-level size zone)	8 to 26 connectivity	2D to 3D	0.88–0.91	≈5.2×	[4,7]
GLDM (gray-level dependence)	2D to 3D isotropic kernel	2D to 3D	0.89–0.93	≈4.0×	[4,8]
NGTDM (gray-tone difference)	Mean over 26-voxel context	2D to 3D	0.86–0.90	≈3.7×	[4,9]
Fractal Dimension (box counting)	Squares to cubes	2D to 3D	0.94	≈2.8×	[11]
Lacunarity (gliding-box)	Square to cubic window	2D to 3D	0.92	≈2.9×	[12,13]

Notes: Correlations are median Spearman $\rho$ across 100 simulated pairs of 2D and 3D textures. Runtime ratios measured on a 16-core system (Python, version 3.11; available at https://www.python.org/, accessed on 28 October 2025) implementation. All feature definitions follow IBSI 3D guidelines [4].

Fractal descriptors, fractal dimension and lacunarity, extend naturally to 3D using cubic box counting and gliding-box lacunarity with cubic windows. Because both are scale and dimension agnostic, their relative behavior with respect to standardized texture families remains qualitatively consistent. Empirical correlations (Table 10) suggest that 3D feature analogs preserve the same bipartite organization observed in 2D (contrast/difference versus structure/homogeneity) while modestly increasing computational cost. These results quantitatively support the statement that extension to 3D is feasible and structurally consistent with the 2D benchmark.

8. Future Work

The central observation of this study is a stable two-group geometry: fractal dimension aligns with high-frequency variation, local contrast, and short runs, whereas lacunarity aligns with large-scale structure, long runs, and homogeneity. Building on this, several directions naturally follow.

First, external validation and harmonization deserve priority. Multi-center, fully three-dimensional CT, MR, and PET cohorts should be used to probe robustness to acquisition, reconstruction, voxel size, and segmentation variability. The extent of harmonization required—intensity standardization, resampling, and batch-effect mitigation—ought to be quantified with prospective protocols and phantoms, comparing methods under identical folds (for example, histogram standardization and ComBat-type approaches) [4,20,21,22,23,24]. Alternative estimators of fractal dimension should be assessed under the same preprocessing (box counting, spectral, or slope-based methods, variograms, Higuchi-type approaches), and single-number lacunarity summaries should be replaced by full lacunarity curves evaluated over multiple scales and thresholds, with principled functionals and uncertainty intervals reported.

Next, the link between fractal measures and multiscale representations merits systematic mapping. Wavelet levels and orientations (for example, levels 1–3 and beyond) and alternative filter banks (such as Gabor and steerable filters) should be compared to isolate which sub-bands drive their behavior. Ablation studies and partial-correlation or conditional-similarity analyses can test whether fractal dimension and lacunarity add information beyond the most predictive members of the GLCM, GLRLM, and GLSZM families. Design sweeps over gray-level discretization ($N_g$ and binning scheme), thresholds, scale grids, boundary conditions, and mask perturbations should be paired with bootstrap and permutation procedures, as well as stability assessments (subsampling and perturb–retrain), to obtain uncertainty intervals for similarity rankings and selection frequencies.

Evaluation should proceed within transparent, preregistered pipelines that employ nested model comparisons, leakage-free cross-validation with fixed folds, and regularization tuned to family-wise collinearity. Model effects are best communicated using SHAP values—SHapley Additive exPlanations that attribute each feature’s contribution to individual predictions [46]—alongside partial-dependence profiles (PDPs) and accumulated local effects (ALEs). Report calibration metrics and generalization gaps in tandem with discrimination. Critically, test incremental value over strong baselines: for fractal dimension, use baselines rich in contrast and short-run descriptors (and, when applicable, wavelet-detail statistics); for lacunarity, use baselines rich in homogeneity and correlation measures, as well as zone- and run-size emphases. Apply multiple-testing adjustments (e.g., Benjamini–Hochberg FDR) consistently across feature families and sub-bands [36]. These steps will help determine when fractal dimension and lacunarity provide non-redundant multiscale information beyond standard IBSI families, and will clarify which acquisition and preprocessing choices most strongly shape their behaviour in practice.

Finally, as radiomic profiling of glioblastoma has demonstrated tangible prognostic value beyond conventional clinical and radiologic predictors [47], future work should assess whether the incremental information provided by fractal dimension and lacunarity translates into improved outcome modeling across neuro-oncology and other disease domains.

Appendix A.1. Feature Definitions and Interpretations

Before listing the feature formulas, we define the notation used throughout Table A1. Let $\mathbf{x}={\left\{x_k\right\}}_{k=1}^{HW}$ be the vectorized intensities of X, $\mu ={\displaystyle \frac{1}{HW}}{\sum }_k{x}_k$, ${\sigma }^2={\displaystyle \frac{1}{HW}}{\sum }_k{(x_k-\mu )}^2$, and $Q_p$ the pth quantile of $\mathbf{x}$. For the binned histogram over $N_g$ gray levels, let $p_g$ be the probability of bin g (${\sum }_{g=1}^{N_g}{p}_g=1$). Define $\mathcal{I}=\{k:Q_{0.1}\le x_k\le Q_{0.9}\}$ and ${\overline{x}}_{10–90}={\displaystyle \frac{1}{\left|\mathcal{I}\right|}}{\sum }_{k\in \mathcal{I}}{x}_k$. Unless specified, logarithms in information measures use base 2 (bits). The naming, symbols, and formulas for first-order features follow the Image Biomarker Standardisation Initiative (IBSI) recommendations and the PyRadiomics reference implementation [4,10]; general radiomics background is provided in Gillies et al. [1], Mayerhoefer et al. [2].

Table A1. First-order intensity features (19) with formulas and interpretation. $HW$ is the number of voxels; $p_g$ denotes histogram probabilities. Formulas and naming align with IBSI, and the robust mean absolute deviation (rMAD) follows the PyRadiomics definition [4,10].

Feature	Formula/Symbol	What It Captures (Interpretation)
Energy	${\sum }_{k=1}^{HW}{x}_k^2$	Overall signal power (scale-dependent); larger when intensities have large magnitude.
Total Energy	${\sum }_{k=1}^{HW}{x}_k^2\times \mathrm{voxel}\mathrm{area}$	Energy with physical units (in 2D, voxel area often set to 1).
RMS	$\sqrt{{\displaystyle \frac{1}{HW}}{\sum }_{k=1}^{HW}{x}_k^2}$	Root-mean-square; average magnitude.
Variance	${\sigma }^2={\displaystyle \frac{1}{HW}}{\sum }_k{(x_k-\mu )}^2$	Dispersion about the mean; sensitive to outliers.
Standard Deviation	$\sigma$	Square root of variance; same interpretation on original scale.
Skewness	$\frac{\frac{1}{HW}{\sum }_k{(x_k-\mu )}^3}{{\sigma }^3}$	Asymmetry of the distribution.
Kurtosis	$\frac{\frac{1}{HW}{\sum }_k{(x_k-\mu )}^4}{{\sigma }^4}$	Tail heaviness/peakedness (non-excess); equals 3 for Gaussian.
Entropy	$-{\sum }_{g=1}^{N_g}{p}_g{log}_2{p}_g$	Histogram unpredictability (bits).
Uniformity	${\sum }_{g=1}^{N_g}{p}_g^2$	Histogram concentration (also “histogram energy”).
Mean	$\mu$	Central tendency (average intensity).
Median	$Q_{0.5}$	Robust central tendency.
P10	$Q_{0.1}$	Lower-tail intensity (10th percentile).
P90	$Q_{0.9}$	Upper-tail intensity (90th percentile).
Minimum	${min}_k{x}_k$	Absolute lowest observed intensity.
Maximum	${max}_k{x}_k$	Absolute highest observed intensity.
IQR	$Q_{0.75}-Q_{0.25}$	Middle-spread; robust scale.
Range	${max}_k{x}_k-{min}_k{x}_k$	Full dynamic range of intensities.
MAD	$\frac{1}{HW}{\sum }_{k=1}^{HW}|x_k-\mu |$	Mean absolute deviation.
rMAD	$\frac{1}{\left|\mathcal{I}\right|}{\sum }_{k\in \mathcal{I}}|x_k-{\overline{x}}_{10–90}|$	Trimmed absolute deviation within the 10–90% band.

Table A1. First-order intensity features (19) with formulas and interpretation. $HW$ is the number of voxels; $p_g$ denotes histogram probabilities. Formulas and naming align with IBSI, and the robust mean absolute deviation (rMAD) follows the PyRadiomics definition [4,10].

Feature	Formula/Symbol	What It Captures (Interpretation)
Energy	${\sum }_{k=1}^{HW}{x}_k^2$	Overall signal power (scale-dependent); larger when intensities have large magnitude.
Total Energy	${\sum }_{k=1}^{HW}{x}_k^2\times \mathrm{voxel}\mathrm{area}$	Energy with physical units (in 2D, voxel area often set to 1).
RMS	$\sqrt{{\displaystyle \frac{1}{HW}}{\sum }_{k=1}^{HW}{x}_k^2}$	Root-mean-square; average magnitude.
Variance	${\sigma }^2={\displaystyle \frac{1}{HW}}{\sum }_k{(x_k-\mu )}^2$	Dispersion about the mean; sensitive to outliers.
Standard Deviation	$\sigma$	Square root of variance; same interpretation on original scale.
Skewness	$\frac{\frac{1}{HW}{\sum }_k{(x_k-\mu )}^3}{{\sigma }^3}$	Asymmetry of the distribution.
Kurtosis	$\frac{\frac{1}{HW}{\sum }_k{(x_k-\mu )}^4}{{\sigma }^4}$	Tail heaviness/peakedness (non-excess); equals 3 for Gaussian.
Entropy	$-{\sum }_{g=1}^{N_g}{p}_g{log}_2{p}_g$	Histogram unpredictability (bits).
Uniformity	${\sum }_{g=1}^{N_g}{p}_g^2$	Histogram concentration (also “histogram energy”).
Mean	$\mu$	Central tendency (average intensity).
Median	$Q_{0.5}$	Robust central tendency.
P10	$Q_{0.1}$	Lower-tail intensity (10th percentile).
P90	$Q_{0.9}$	Upper-tail intensity (90th percentile).
Minimum	${min}_k{x}_k$	Absolute lowest observed intensity.
Maximum	${max}_k{x}_k$	Absolute highest observed intensity.
IQR	$Q_{0.75}-Q_{0.25}$	Middle-spread; robust scale.
Range	${max}_k{x}_k-{min}_k{x}_k$	Full dynamic range of intensities.
MAD	$\frac{1}{HW}{\sum }_{k=1}^{HW}|x_k-\mu |$	Mean absolute deviation.
rMAD	$\frac{1}{\left|\mathcal{I}\right|}{\sum }_{k\in \mathcal{I}}|x_k-{\overline{x}}_{10–90}|$	Trimmed absolute deviation within the 10–90% band.

Appendix A.2. GLCM Definitions and Feature Formulas

The gray-level co-occurrence matrix (GLCM) summarizes how often pairs of discretized gray levels occur at a fixed spatial offset; our notation and feature formulas follow the Image Biomarker Standardisation Initiative (IBSI) and the PyRadiomics reference implementation, with terminology rooted in the original work of Haralick and co-authors [4,5,10]. In our setup P is built at distance 1, aggregated over four angles $(0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ })$, symmetrized, and normalized so that ${\sum }_{i,j}{P}_{ij}=1$ (angle aggregation and normalization as recommended by IBSI [4]).

Formally, let $P\in {\mathbb{R}}_{+}^{N_g\times N_g}$ be the symmetric, normalized GLCM. Define the one-dimensional marginals $p_x\left(i\right)={\sum }_j{P}_{ij}$ and $p_y\left(j\right)={\sum }_i{P}_{ij}$; the means ${\mu }_x={\sum }_{i}i{p}_x\left(i\right)$ and ${\mu }_y={\sum }_{j}j{p}_y\left(j\right)$; the standard deviations ${\sigma }_x,{\sigma }_y$; the gray-level sum distribution $p_{x+y}\left(k\right)={\sum }_{i+j=k}{P}_{ij}$ for $k\in \{2,\dots ,2N_g\}$; and the difference distribution $p_{x-y}\left(k\right)={\sum }_{|i-j|=k}{P}_{ij}$ for $k\in \{0,\dots ,N_g-1\}$. Entropy terms use the natural logarithm (as in IBSI) unless otherwise noted [4]:

$$H_{XY}=-\sum _{i,j}{P}_{ij}log{P}_{ij},H_X=-\sum _i{p}_x\left(i\right)log{p}_x\left(i\right),H_Y=-\sum _j{p}_y\left(j\right)log{p}_y\left(j\right),$$

$$H_{XY1}=-\sum _{i,j}{P}_{ij}log\left(p_x\left(i\right)p_y\left(j\right)\right),H_{XY2}=-\sum _{i,j}{p}_x\left(i\right)p_y\left(j\right)log\left(p_x\left(i\right)p_y\left(j\right)\right).$$

Table A2. GLCM features (19) with formulas and interpretation. $P_{ij}$ is the symmetric, normalized co-occurrence for gray levels $i,j$; $p_x$, $p_y$ are marginals; $p_{x+y}$ and $p_{x-y}$ are sum and difference distributions. Formulas align with IBSI and PyRadiomics [4,10]; historical names follow Haralick et al. [5].

Feature	Formula/Symbol	Interpretation
Contrast	${\sum }_{i,j}{(i-j)}^2{P}_{ij}$	Off-diagonal emphasis; higher with strong edges.
Dissimilarity	${\sum }_{i,j}|i-j|P_{ij}$	Linear penalty version of contrast.
ASM	${\sum }_{i,j}{P}_{ij}^2$	Angular Second Moment; texture uniformity.
Energy	$\sqrt{\mathrm{ASM}}$	Monotone with ASM (legacy definition).
Entropy	$-{\sum }_{i,j}{P}_{ij}log{P}_{ij}$	Co-occurrence disorder.
Homogeneity (1)	${\sum }_{i,j}\frac{P_{ij}}{1+{(i-j)}^2}$	Rewards near-diagonal mass.
Homogeneity (2)	${\sum }_{i,j}\frac{P_{ij}}{1+\left(\right|i-j|/N_g{)}^2}$	Scale-normalized variant.
ID	${\sum }_{i,j}\frac{P_{ij}}{1+|i-j|}$	Inverse Difference; favors small gaps.
IDN	${\sum }_{i,j}\frac{P_{ij}}{1+|i-j|/N_g}$	Normalized ID.
Inv. Variance	${\sum }_{i\ne j}\frac{P_{ij}}{{(i-j)}^2}$	Strongly favors smooth textures.
Correlation	$\frac{\sum ij{P}_{ij}-{\mu }_x{\mu }_y}{{\sigma }_x{\sigma }_y}$	Marginal association strength.
Max Prob.	${max}_{i,j}{P}_{ij}$	Dominant co-occurrence pair.
Sum Avg.	${\sum }_{k}k{p}_{x+y}\left(k\right)$	Mean of sum distribution.
Sum Entropy	$-{\sum }_k{p}_{x+y}\left(k\right)log{p}_{x+y}\left(k\right)$	Disorder of sum distribution.
Diff. Avg.	${\sum }_{k}k{p}_{x-y}\left(k\right)$	Mean absolute difference.
Diff. Var.	${\sum }_k{(k-\mathrm{DiffAvg})}^2{p}_{x-y}\left(k\right)$	Spread of difference distribution.
Diff. Entropy	$-{\sum }_k{p}_{x-y}\left(k\right)log{p}_{x-y}\left(k\right)$	Disorder of difference distribution.
IMC1	$\frac{H_{XY}-H_{XY1}}{max(H_X,H_Y)}$	Entropy gap vs. marginals.
IMC2	$\sqrt{1-exp(-2(H_{XY2}-H_{XY}))}$	Bounded [0, 1]; strength of dependence.

Table A2. GLCM features (19) with formulas and interpretation. $P_{ij}$ is the symmetric, normalized co-occurrence for gray levels $i,j$; $p_x$, $p_y$ are marginals; $p_{x+y}$ and $p_{x-y}$ are sum and difference distributions. Formulas align with IBSI and PyRadiomics [4,10]; historical names follow Haralick et al. [5].

Feature	Formula/Symbol	Interpretation
Contrast	${\sum }_{i,j}{(i-j)}^2{P}_{ij}$	Off-diagonal emphasis; higher with strong edges.
Dissimilarity	${\sum }_{i,j}|i-j|P_{ij}$	Linear penalty version of contrast.
ASM	${\sum }_{i,j}{P}_{ij}^2$	Angular Second Moment; texture uniformity.
Energy	$\sqrt{\mathrm{ASM}}$	Monotone with ASM (legacy definition).
Entropy	$-{\sum }_{i,j}{P}_{ij}log{P}_{ij}$	Co-occurrence disorder.
Homogeneity (1)	${\sum }_{i,j}\frac{P_{ij}}{1+{(i-j)}^2}$	Rewards near-diagonal mass.
Homogeneity (2)	${\sum }_{i,j}\frac{P_{ij}}{1+\left(\right|i-j|/N_g{)}^2}$	Scale-normalized variant.
ID	${\sum }_{i,j}\frac{P_{ij}}{1+|i-j|}$	Inverse Difference; favors small gaps.
IDN	${\sum }_{i,j}\frac{P_{ij}}{1+|i-j|/N_g}$	Normalized ID.
Inv. Variance	${\sum }_{i\ne j}\frac{P_{ij}}{{(i-j)}^2}$	Strongly favors smooth textures.
Correlation	$\frac{\sum ij{P}_{ij}-{\mu }_x{\mu }_y}{{\sigma }_x{\sigma }_y}$	Marginal association strength.
Max Prob.	${max}_{i,j}{P}_{ij}$	Dominant co-occurrence pair.
Sum Avg.	${\sum }_{k}k{p}_{x+y}\left(k\right)$	Mean of sum distribution.
Sum Entropy	$-{\sum }_k{p}_{x+y}\left(k\right)log{p}_{x+y}\left(k\right)$	Disorder of sum distribution.
Diff. Avg.	${\sum }_{k}k{p}_{x-y}\left(k\right)$	Mean absolute difference.
Diff. Var.	${\sum }_k{(k-\mathrm{DiffAvg})}^2{p}_{x-y}\left(k\right)$	Spread of difference distribution.
Diff. Entropy	$-{\sum }_k{p}_{x-y}\left(k\right)log{p}_{x-y}\left(k\right)$	Disorder of difference distribution.
IMC1	$\frac{H_{XY}-H_{XY1}}{max(H_X,H_Y)}$	Entropy gap vs. marginals.
IMC2	$\sqrt{1-exp(-2(H_{XY2}-H_{XY}))}$	Bounded [0, 1]; strength of dependence.

All sums run over $i,j\in \{1,\dots ,N_g\}$. Using natural versus base-2 logarithms only rescales the entropy terms and does not affect ordering [4]. Symmetric, normalized, angle-aggregated P generally improves stability and comparability across directions [4]. If either ${\sigma }_x$ or ${\sigma }_y$ equals zero, the correlation is undefined and should be reported as NA in keeping with reproducibility guidelines [4,10].

Appendix A.3. GLRLM Definitions and Feature Formulas

The gray-level run-length matrix (GLRLM) quantifies how often contiguous runs of identical gray level occur and how long those runs persist along specified directions. Our notation and feature formulas follow the Image Biomarker Standardisation Initiative (IBSI) and the PyRadiomics reference implementation, with historical roots in the original run-length work of Galloway [6] and subsequent refinements [4,10]. In our setup the GLRLM is computed at pixel distance 1, aggregated over four angles $(0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ })$, then normalized to a probability distribution (angle aggregation and normalization as recommended by IBSI [4]).

Formally, let $R\in {\mathbb{R}}_{+}^{N_g\times R_{max}}$ be the (angle-aggregated) GLRLM, where $R_{ir}$ counts runs of length r at gray level i. Let $N_{\mathrm{runs}}={\sum }_{i=1}^{N_g}{\sum }_{r=1}^{R_{max}}{R}_{ir}$ denote the total number of runs. Define the normalized joint distribution $p(i,r)=R_{ir}/N_{\mathrm{runs}}$ with marginals

$$p_g\left(i\right)=\sum _{r=1}^{R_{max}}p(i,r)(\mathrm{gray-level}\mathrm{profile}),p_r\left(r\right)=\sum _{i=1}^{N_g}p(i,r)(\mathrm{run-length}\mathrm{profile}).$$

Unless stated otherwise, entropies use the natural logarithm (as in IBSI) [4].

Table A3. GLRLM features (16) with formulas and interpretation. $p(i,r)$ is the normalized GLRLM; $p_g$, $p_r$ are marginals; $N_{\mathrm{runs}}={\sum }_{i,r}{R}_{ir}$. Formulas align with IBSI/PyRadiomics [4,10]; names follow Galloway [6].

Feature	Formula/Symbol	Interpretation
SRE	${\sum }_{i,r}\frac{p(i,r)}{r^2}$	Short-run emphasis; larger for fine, rapidly varying texture.
LRE	${\sum }_{i,r}p(i,r)r^2$	Long-run emphasis; larger for coarse, extended uniform regions.
GLN (counts)	${\sum }_i{\left({\sum }_r{R}_{ir}\right)}^2$	Run mass concentrated in few gray levels (tone nonuniformity).
GLNN	${\sum }_i{p}_g{\left(i\right)}^2=\frac{\mathrm{GLN}}{N_{\mathrm{runs}}^2}$	Scale-normalized GLN; reduces dependence on run count.
RLN (counts)	${\sum }_r{\left({\sum }_i{R}_{ir}\right)}^2$	Run mass concentrated in few lengths (scale nonuniformity).
RLNN	${\sum }_r{p}_r{\left(r\right)}^2=\frac{\mathrm{RLN}}{N_{\mathrm{runs}}^2}$	Scale-normalized RLN; reduces dependence on run count.
RP (IBSI)	$\frac{N_{\mathrm{runs}}}{N_p}$	Run density per pixel; higher when runs are more numerous.
LGRE	${\sum }_{i,r}\frac{p(i,r)}{i^2}$	Emphasizes runs at low gray levels (darker tones).
HGRE	${\sum }_{i,r}p(i,r)i^2$	Emphasizes runs at high gray levels (brighter tones).
SRLGLE	${\sum }_{i,r}\frac{p(i,r)}{i^2{r}^2}$	Short runs at low gray levels (fine, dark texture).
SRHGLE	${\sum }_{i,r}p(i,r)\frac{i^2}{r^2}$	Short runs at high gray levels (fine, bright texture).
LRLGLE	${\sum }_{i,r}p(i,r)\frac{r^2}{i^2}$	Long runs at low gray levels (coarse, dark texture).
LRHGLE	${\sum }_{i,r}p(i,r)i^2{r}^2$	Long runs at high gray levels (coarse, bright texture).
Run Entropy	$-{\sum }_{i,r}p(i,r)logp(i,r)$	Disorder of the joint run distribution.
RLV (over $p_r$)	${\sum }_r{\left(r-{\sum }_{r^{\prime }}{r}^{\prime }{p}_r\left(r^{\prime }\right)\right)}^2{p}_r\left(r\right)$	Spread of run lengths; multiple scales ⇒ large.
GLV (over $p_g$)	${\sum }_i{\left(i-{\sum }_{i^{\prime }}{i}^{\prime }{p}_g\left(i^{\prime }\right)\right)}^2{p}_g\left(i\right)$	Spread across gray levels among runs.

Table A3. GLRLM features (16) with formulas and interpretation. $p(i,r)$ is the normalized GLRLM; $p_g$, $p_r$ are marginals; $N_{\mathrm{runs}}={\sum }_{i,r}{R}_{ir}$. Formulas align with IBSI/PyRadiomics [4,10]; names follow Galloway [6].

Feature	Formula/Symbol	Interpretation
SRE	${\sum }_{i,r}\frac{p(i,r)}{r^2}$	Short-run emphasis; larger for fine, rapidly varying texture.
LRE	${\sum }_{i,r}p(i,r)r^2$	Long-run emphasis; larger for coarse, extended uniform regions.
GLN (counts)	${\sum }_i{\left({\sum }_r{R}_{ir}\right)}^2$	Run mass concentrated in few gray levels (tone nonuniformity).
GLNN	${\sum }_i{p}_g{\left(i\right)}^2=\frac{\mathrm{GLN}}{N_{\mathrm{runs}}^2}$	Scale-normalized GLN; reduces dependence on run count.
RLN (counts)	${\sum }_r{\left({\sum }_i{R}_{ir}\right)}^2$	Run mass concentrated in few lengths (scale nonuniformity).
RLNN	${\sum }_r{p}_r{\left(r\right)}^2=\frac{\mathrm{RLN}}{N_{\mathrm{runs}}^2}$	Scale-normalized RLN; reduces dependence on run count.
RP (IBSI)	$\frac{N_{\mathrm{runs}}}{N_p}$	Run density per pixel; higher when runs are more numerous.
LGRE	${\sum }_{i,r}\frac{p(i,r)}{i^2}$	Emphasizes runs at low gray levels (darker tones).
HGRE	${\sum }_{i,r}p(i,r)i^2$	Emphasizes runs at high gray levels (brighter tones).
SRLGLE	${\sum }_{i,r}\frac{p(i,r)}{i^2{r}^2}$	Short runs at low gray levels (fine, dark texture).
SRHGLE	${\sum }_{i,r}p(i,r)\frac{i^2}{r^2}$	Short runs at high gray levels (fine, bright texture).
LRLGLE	${\sum }_{i,r}p(i,r)\frac{r^2}{i^2}$	Long runs at low gray levels (coarse, dark texture).
LRHGLE	${\sum }_{i,r}p(i,r)i^2{r}^2$	Long runs at high gray levels (coarse, bright texture).
Run Entropy	$-{\sum }_{i,r}p(i,r)logp(i,r)$	Disorder of the joint run distribution.
RLV (over $p_r$)	${\sum }_r{\left(r-{\sum }_{r^{\prime }}{r}^{\prime }{p}_r\left(r^{\prime }\right)\right)}^2{p}_r\left(r\right)$	Spread of run lengths; multiple scales ⇒ large.
GLV (over $p_g$)	${\sum }_i{\left(i-{\sum }_{i^{\prime }}{i}^{\prime }{p}_g\left(i^{\prime }\right)\right)}^2{p}_g\left(i\right)$	Spread across gray levels among runs.

Angle aggregation stabilizes estimates across directions, and a pixel distance of one aligns with common IBSI defaults [4]. If entropies are reported in bits, replace log with ${log}_2$; this only rescales values and does not affect rankings. As with other texture matrices, GLRLM features are sensitive to gray-level discretization and to pre-filtering that affects run continuity (e.g., smoothing or denoising); documenting these choices is essential for reproducibility and fair comparison across studies [4,10].

Appendix A.4. GLSZM Definitions and Feature Formulas

The gray-level size-zone matrix (GLSZM) summarizes the distribution of connected zones of equal gray level within a region of interest, independently of direction. It was introduced for image texture analysis by Thibault et al. [7] and subsequently standardized by the Image Biomarker Standardisation Initiative (IBSI) and implemented in reference toolkits such as PyRadiomics [4,10]. In two dimensions we use 8-connectivity to define zones, as recommended in IBSI for enhanced stability across orientations [4].

Formally, let $Z\in {\mathbb{R}}_{+}^{N_g\times S_{max}}$ be the matrix where $Z_{is}$ counts the number of 8-connected zones of size s observed at gray level i in the discretized image. Let $N_z={\sum }_{i=1}^{N_g}{\sum }_{s=1}^{S_{max}}{Z}_{is}$ denote the total number of zones, and let $N_p$ be the number of pixels (voxels in 2D) in the ROI. Define the normalized joint distribution $p(i,s)=Z_{is}/N_z$ with marginals

$$p_g\left(i\right)=\sum _{s=1}^{S_{max}}p(i,s)(\mathrm{gray-level}\mathrm{profile}),p_s\left(s\right)=\sum _{i=1}^{N_g}p(i,s)(\mathrm{size}\mathrm{profile}).$$

Unless stated otherwise, entropies use the natural logarithm (as in IBSI) [4].

Table A4. GLSZM features (16) with formulas and interpretation. $p(i,s)$ is the normalized GLSZM; $p_g$, $p_s$ are marginals; $N_z={\sum }_{i,s}{Z}_{is}$ (zones); $N_p$ is pixel count. Formulas align with IBSI/PyRadiomics [4,7,10].

Feature	Formula/Symbol	Interpretation
SAE	${\sum }_{i,s}\frac{p(i,s)}{s^2}$	Emphasizes small zones (fine/fragmented textures).
LAE	${\sum }_{i,s}p(i,s)s^2$	Emphasizes large zones (coarse/homogeneous regions).
GLN (counts)	${\sum }_i{\left({\sum }_s{Z}_{is}\right)}^2$	Zone mass concentrated in few gray levels (tone nonuniformity).
GLNN	${\sum }_i{p}_g{\left(i\right)}^2=\frac{\mathrm{GLN}}{N_z^2}$	Scale-normalized GLN; reduces dependence on zone count.
SZN (counts)	${\sum }_s{\left({\sum }_i{Z}_{is}\right)}^2$	Zone mass concentrated in few sizes (size nonuniformity).
SZNN	${\sum }_s{p}_s{\left(s\right)}^2=\frac{\mathrm{SZN}}{N_z^2}$	Scale-normalized SZN; reduces dependence on zone count.
ZP (IBSI)	$\frac{N_z}{N_p}$	Zone density per pixel; higher when zones are numerous.
LGZE	${\sum }_{i,s}\frac{p(i,s)}{i^2}$	Emphasizes low gray-level zones (darker tones).
HGZE	${\sum }_{i,s}p(i,s)i^2$	Emphasizes high gray-level zones (brighter tones).
SA_LGLE	${\sum }_{i,s}\frac{p(i,s)}{i^2{s}^2}$	Small zones at low gray levels (fine, dark patterns).
SA_HGLE	${\sum }_{i,s}p(i,s)\frac{i^2}{s^2}$	Small zones at high gray levels (fine, bright patterns).
LA_LGLE	${\sum }_{i,s}p(i,s)\frac{s^2}{i^2}$	Large zones at low gray levels (coarse, dark regions).
LA_HGLE	${\sum }_{i,s}p(i,s)i^2{s}^2$	Large zones at high gray levels (coarse, bright regions).
Zone Entropy	$-{\sum }_{i,s}p(i,s)logp(i,s)$	Disorder of gray-level/size distribution.
Zone Size Var. (over $p_s$)	${\sum }_s{\left(s-{\sum }_{s^{\prime }}{s}^{\prime }{p}_s\left(s^{\prime }\right)\right)}^2{p}_s\left(s\right)$	Spread of zone sizes; multiscale structures ⇒ large.
Zone Size Mean (over $p_s$)	${\sum }_{s}s{p}_s\left(s\right)$	Average zone size; complements SAE/LAE.

Table A4. GLSZM features (16) with formulas and interpretation. $p(i,s)$ is the normalized GLSZM; $p_g$, $p_s$ are marginals; $N_z={\sum }_{i,s}{Z}_{is}$ (zones); $N_p$ is pixel count. Formulas align with IBSI/PyRadiomics [4,7,10].

Feature	Formula/Symbol	Interpretation
SAE	${\sum }_{i,s}\frac{p(i,s)}{s^2}$	Emphasizes small zones (fine/fragmented textures).
LAE	${\sum }_{i,s}p(i,s)s^2$	Emphasizes large zones (coarse/homogeneous regions).
GLN (counts)	${\sum }_i{\left({\sum }_s{Z}_{is}\right)}^2$	Zone mass concentrated in few gray levels (tone nonuniformity).
GLNN	${\sum }_i{p}_g{\left(i\right)}^2=\frac{\mathrm{GLN}}{N_z^2}$	Scale-normalized GLN; reduces dependence on zone count.
SZN (counts)	${\sum }_s{\left({\sum }_i{Z}_{is}\right)}^2$	Zone mass concentrated in few sizes (size nonuniformity).
SZNN	${\sum }_s{p}_s{\left(s\right)}^2=\frac{\mathrm{SZN}}{N_z^2}$	Scale-normalized SZN; reduces dependence on zone count.
ZP (IBSI)	$\frac{N_z}{N_p}$	Zone density per pixel; higher when zones are numerous.
LGZE	${\sum }_{i,s}\frac{p(i,s)}{i^2}$	Emphasizes low gray-level zones (darker tones).
HGZE	${\sum }_{i,s}p(i,s)i^2$	Emphasizes high gray-level zones (brighter tones).
SA_LGLE	${\sum }_{i,s}\frac{p(i,s)}{i^2{s}^2}$	Small zones at low gray levels (fine, dark patterns).
SA_HGLE	${\sum }_{i,s}p(i,s)\frac{i^2}{s^2}$	Small zones at high gray levels (fine, bright patterns).
LA_LGLE	${\sum }_{i,s}p(i,s)\frac{s^2}{i^2}$	Large zones at low gray levels (coarse, dark regions).
LA_HGLE	${\sum }_{i,s}p(i,s)i^2{s}^2$	Large zones at high gray levels (coarse, bright regions).
Zone Entropy	$-{\sum }_{i,s}p(i,s)logp(i,s)$	Disorder of gray-level/size distribution.
Zone Size Var. (over $p_s$)	${\sum }_s{\left(s-{\sum }_{s^{\prime }}{s}^{\prime }{p}_s\left(s^{\prime }\right)\right)}^2{p}_s\left(s\right)$	Spread of zone sizes; multiscale structures ⇒ large.
Zone Size Mean (over $p_s$)	${\sum }_{s}s{p}_s\left(s\right)$	Average zone size; complements SAE/LAE.

Using 8-connectivity reduces artificial fragmentation of zones and aligns with IBSI-compliant choices [4]. Reporting entropies in bits is possible by replacing log with ${log}_2$; this only rescales values and does not affect rank-based comparisons. As with other matrix families, GLSZM features are sensitive to gray-level discretization and to any pre-filtering that modifies connectivity (e.g., smoothing or morphological operations). Thorough documentation of these settings is essential for reproducibility and fair cross-study comparison [4,7,10].

Appendix A.5. GLDM Definitions and Feature Formulas

The gray-level dependence matrix (GLDM) quantifies, for each discretized gray level, how many neighbors in a fixed window are “dependent” on the center pixel, i.e., how many neighbors have a gray-level difference within a user-set tolerance. The concept traces back to the neighboring gray-level dependence framework of Sun & Wee [8] and has been standardized by the Image Biomarker Standardisation Initiative (IBSI) and implemented in reference toolkits such as PyRadiomics [4,10]. In two dimensions we adopt a Chebyshev-1 neighborhood (up to eight neighbors); unless stated otherwise, the dependence tolerance is $\alpha =0$, so only exactly equal gray levels (after discretization) are considered dependent.

Let $D\in {\mathbb{R}}_{+}^{N_g\times D_{max}}$ be the matrix whose entry $D_{id}$ is the number of pixels of gray level i having exactly d dependent neighbors within the Chebyshev-1 neighborhood including the center. In 2D with the center included, $D_{max}=9$ (eight neighbors plus the center); implementations that exclude the center use $D_{max}=8$ with analogous formulas. Define the total event count $N_d={\sum }_{i=1}^{N_g}{\sum }_{d=1}^{D_{max}}{D}_{id}$ and the normalized joint distribution

$$p(i,d)={\displaystyle \frac{D_{id}}{N_d}},p_g\left(i\right)=\sum _{d=1}^{D_{max}}p(i,d),p_d\left(d\right)=\sum _{i=1}^{N_g}p(i,d).$$

Unless otherwise specified, entropies use the natural logarithm (as in IBSI) [4].

Table A5. GLDM features (14) with formulas and interpretation. $p(i,d)$ is the normalized GLDM; $p_g$, $p_d$ are marginals; $N_d={\sum }_{i,d}{D}_{id}$. Formulas follow IBSI/PyRadiomics [4,8,10].

Feature	Formula/Symbol	Interpretation
SDE	${\sum }_{i,d}\frac{p(i,d)}{d^2}$	Small-dependence emphasis; larger for fine/fragmented textures.
LDE	${\sum }_{i,d}p(i,d)d^2$	Large-dependence emphasis; larger for smooth/homogeneous regions.
GLN	${\sum }_i{p}_g{\left(i\right)}^2$	Events concentrated in few gray levels (tone nonuniformity).
GLNN	$\frac{\mathrm{GLN}}{N_d^2}$	Scale-normalized GLN; reduces dependence on total events.
DN	${\sum }_d{p}_d{\left(d\right)}^2$	Events concentrated in few dependence sizes (scale nonuniformity).
DNN	$\frac{\mathrm{DN}}{N_d^2}$	Scale-normalized DN; reduces dependence on total events.
DP	$\frac{N_d}{N_g{D}_{max}}$	Dependence event density (implementation-consistent).
LGLE	${\sum }_{i,d}\frac{p(i,d)}{i^2}$	Emphasizes low gray-level events (darker tones).
HGLE	${\sum }_{i,d}p(i,d)i^2$	Emphasizes high gray-level events (brighter tones).
SDLGLE	${\sum }_{i,d}\frac{p(i,d)}{i^2{d}^2}$	Small dependence at low gray levels (fine, dark patterns).
SDHGLE	${\sum }_{i,d}p(i,d)\frac{i^2}{d^2}$	Small dependence at high gray levels (fine, bright patterns).
LDLGLE	${\sum }_{i,d}p(i,d)\frac{d^2}{i^2}$	Large dependence at low gray levels (coherent, dark regions).
LDHGLE	${\sum }_{i,d}p(i,d)i^2{d}^2$	Large dependence at high gray levels (coherent, bright regions).
DEntropy	$-{\sum }_{i,d}p(i,d)logp(i,d)$	Disorder of the joint dependence distribution.

Table A5. GLDM features (14) with formulas and interpretation. $p(i,d)$ is the normalized GLDM; $p_g$, $p_d$ are marginals; $N_d={\sum }_{i,d}{D}_{id}$. Formulas follow IBSI/PyRadiomics [4,8,10].

Feature	Formula/Symbol	Interpretation
SDE	${\sum }_{i,d}\frac{p(i,d)}{d^2}$	Small-dependence emphasis; larger for fine/fragmented textures.
LDE	${\sum }_{i,d}p(i,d)d^2$	Large-dependence emphasis; larger for smooth/homogeneous regions.
GLN	${\sum }_i{p}_g{\left(i\right)}^2$	Events concentrated in few gray levels (tone nonuniformity).
GLNN	$\frac{\mathrm{GLN}}{N_d^2}$	Scale-normalized GLN; reduces dependence on total events.
DN	${\sum }_d{p}_d{\left(d\right)}^2$	Events concentrated in few dependence sizes (scale nonuniformity).
DNN	$\frac{\mathrm{DN}}{N_d^2}$	Scale-normalized DN; reduces dependence on total events.
DP	$\frac{N_d}{N_g{D}_{max}}$	Dependence event density (implementation-consistent).
LGLE	${\sum }_{i,d}\frac{p(i,d)}{i^2}$	Emphasizes low gray-level events (darker tones).
HGLE	${\sum }_{i,d}p(i,d)i^2$	Emphasizes high gray-level events (brighter tones).
SDLGLE	${\sum }_{i,d}\frac{p(i,d)}{i^2{d}^2}$	Small dependence at low gray levels (fine, dark patterns).
SDHGLE	${\sum }_{i,d}p(i,d)\frac{i^2}{d^2}$	Small dependence at high gray levels (fine, bright patterns).
LDLGLE	${\sum }_{i,d}p(i,d)\frac{d^2}{i^2}$	Large dependence at low gray levels (coherent, dark regions).
LDHGLE	${\sum }_{i,d}p(i,d)i^2{d}^2$	Large dependence at high gray levels (coherent, bright regions).
DEntropy	$-{\sum }_{i,d}p(i,d)logp(i,d)$	Disorder of the joint dependence distribution.

Several implementation details guide interpretation and reproducibility. With $\alpha =0$, only exactly equal neighbors contribute to dependence; enlarging $\alpha$ makes the criterion more permissive and shifts probability mass toward larger d, thereby increasing LDE-type terms and decreasing SDE-type terms [4,10]. In two dimensions, a Chebyshev-1 neighborhood provides up to eight neighbors; including the center yields $D_{max}=9$. Entropy can be reported in bits by replacing log with ${log}_2$; the choice of base does not affect ranking or correlation analyses. As with other texture matrices, GLDM features are sensitive to gray-level discretization ($N_g$) and any pre-filtering that alters local agreement, so these preprocessing choices should be documented for comparability [4]. Finally, the DP denominator ($N_g{D}_{max}$) follows our implementation to provide a consistent density proxy within a fixed configuration; absolute scaling may differ across software, but relative comparisons within a study remain interpretable.

Appendix A.6. NGTDM Definitions and Feature Formulas

For every gray level $i\in \{1,\dots ,N_g\}$, let $n_i$ be the number of interior pixels with value i. For those pixels, aggregate neighborhood deviation via

$$s_i=\sum _{\mathbf{x}:X_i\left(\mathbf{x}\right)=i}\left|i-{\overline{g}}_{\mathrm{neigh}}\left(\mathbf{x}\right)\right|,$$

where ${\overline{g}}_{\mathrm{neigh}}\left(\mathbf{x}\right)$ is the mean of the eight neighbors around location $\mathbf{x}$ (center excluded). Let $N_c={\sum }_{i=1}^{N_g}{n}_i$ be the total counted pixels and define $p\left(i\right)=n_i/N_c$. The average gray level is $\mu ={\sum }_{i=1}^{N_g}ip\left(i\right)$ and the weighted average absolute neighborhood deviation is $S={\sum }_{i=1}^{N_g}p\left(i\right)s_i$. A small constant $ϵ$ (e.g., ${10}^{-12}$) is added in denominators to prevent division by zero in nearly homogeneous images.

Table A6. NGTDM features (5) with formulas and interpretation. $p\left(i\right)=n_i/N_c$, $s_i$ is the average absolute deviation from the neighborhood mean at gray level i, $\mu ={\sum }_{i}ip\left(i\right)$, and $S={\sum }_{i}p\left(i\right)s_i$.

Feature	Formula/Symbol	Interpretation
Coarseness	$\frac{1}{S+ϵ}$	Larger for smooth/uniform neighborhoods (small S).
Contrast	$\left(\frac{{\sum }_{i}p\left(i\right){(i-\mu )}^2}{N_g(N_g-1)}\right)S$	Global tone spread modulated by local dissimilarity S.
Busyness	$\frac{S}{{\sum }_i {\sum }_j\left| i p\left(i\right)-jp\left(j\right)\right|+ϵ}$	Rate of local change relative to tone separation.
Complexity	$\frac{{\sum }_i{\sum }_j|i-j|\left(p\left(i\right)s_i+p\left(j\right)s_j\right)}{S+ϵ}$	Pairwise tone gaps weighted by local deviations.
Strength	$\frac{{\sum }_i{\sum }_{j}p\left(i\right)p\left(j\right){(i-j)}^2}{S+ϵ}$	Quadratic tone separation moderated by local roughness.

Table A6. NGTDM features (5) with formulas and interpretation. $p\left(i\right)=n_i/N_c$, $s_i$ is the average absolute deviation from the neighborhood mean at gray level i, $\mu ={\sum }_{i}ip\left(i\right)$, and $S={\sum }_{i}p\left(i\right)s_i$.

Feature	Formula/Symbol	Interpretation
Coarseness	$\frac{1}{S+ϵ}$	Larger for smooth/uniform neighborhoods (small S).
Contrast	$\left(\frac{{\sum }_{i}p\left(i\right){(i-\mu )}^2}{N_g(N_g-1)}\right)S$	Global tone spread modulated by local dissimilarity S.
Busyness	$\frac{S}{{\sum }_i {\sum }_j\left| i p\left(i\right)-jp\left(j\right)\right|+ϵ}$	Rate of local change relative to tone separation.
Complexity	$\frac{{\sum }_i{\sum }_j|i-j|\left(p\left(i\right)s_i+p\left(j\right)s_j\right)}{S+ϵ}$	Pairwise tone gaps weighted by local deviations.
Strength	$\frac{{\sum }_i{\sum }_{j}p\left(i\right)p\left(j\right){(i-j)}^2}{S+ϵ}$	Quadratic tone separation moderated by local roughness.

In practice, the NGTDM family is driven by the magnitude of S. When S is small, the image is locally smooth and Coarseness and Strength tend to be high, while Busyness becomes low. As S increases—reflecting greater local departures from neighborhood means—Busyness and, often, Contrast increase. Because $p\left(i\right)$ and $\mu$ depend on gray-level discretization, these features are sensitive to the choice of $N_g$ and to any pre-filtering that changes neighborhood averages; reporting these preprocessing decisions is essential for reproducibility [4]. Restricting the computation to interior pixels accords with the original definition and helps avoid boundary bias where neighborhoods are incomplete [9].

Appendix A.7. Shape-2D Definitions and Feature Formulas

Let $M\in {\{0,1\}}^{H\times W}$ denote the binary ROI mask (1 = foreground) and $({\Delta }_x,{\Delta }_y)$ the in-plane pixel spacings. The in-plane area is

$$A=\sum _{i=1}^H\sum _{j=1}^W{M}_{ij},A_{\mathrm{phys}}=A\left({\Delta }_x{\Delta }_y\right),$$

reported as pixel count or, after scaling, in mm². Boundary length is approximated by a 4-neighbor edge count. Writing ${\mathcal{N}}_4=\{(-1,0),(1,0),(0,-1),(0,1)\}$ and treating out-of-bounds neighbors as background,

$$P=\sum _{i=1}^H\sum _{j=1}^W\sum _{({\delta }_x,{\delta }_y)\in {\mathcal{N}}_4}\mathbf{1}\left\{M_{ij}=1,M_{i+{\delta }_x,j+{\delta }_y}=0\right\}.$$

With isotropic spacing (${\Delta }_x={\Delta }_y=\Delta$), a first-order physical estimate is $P_{\mathrm{phys}}\approx \Delta P$; if spacings differ, horizontal and vertical edge contributions can be weighted by ${\Delta }_x$ and ${\Delta }_y$, respectively. To characterize anisotropy, collect foreground coordinates $\mathcal{C}=\{(i,j):M_{ij}=1\}$, compute $\overline{\mathbf{c}}={\displaystyle \frac{1}{\left|\mathcal{C}\right|}}{\sum }_{(i,j)\in \mathcal{C}}{(i,j)}^{\top }$, and

$$\Sigma ={\displaystyle \frac{1}{\left|\mathcal{C}\right|}}\sum _{(i,j)\in \mathcal{C}}\left[\begin{array}{c}i\\ j\end{array}\right]\left[\begin{array}{cc}i& j\end{array}\right]-\overline{\mathbf{c}}{\overline{\mathbf{c}}}^{\top }.$$

Let ${\lambda }_1\ge {\lambda }_2\ge 0$ be the eigenvalues of $\Sigma$. In 2D, IBSI’s elongation ($\sqrt{{\lambda }_2/{\lambda }_1}$) and flatness coincide; guard divisions with a small $ϵ$ when ${\lambda }_1$ is near zero, and report undefined values rather than coercing.

Table A7. Shape-2D proxies (4): formulas and interpretation. Convert to physical units using $({\Delta }_x,{\Delta }_y)$. In 2D, elongation and flatness are identical; in 3D, IBSI defines distinct measures [4].

Feature	Formula/Symbol	Interpretation
Area (A)	$A={\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}{M}_{ij},A_{\mathrm{phys}}=A\left({\Delta }_x{\Delta }_y\right)$	In-plane size of ROI (pixels or mm2).
Perimeter ($P,4-$neigh.)	$P={\displaystyle \sum _{i,j}}{\displaystyle \sum _{({\delta }_x,{\delta }_y)\in {\mathcal{N}}_4}}\mathbf{1}\left\{M_{ij}=1,M_{i+{\delta }_x,j+{\delta }_y}=0\right\}$	Boundary length on a Manhattan grid; reproducible contour measure.
Elongation (2D)	$\mathrm{Elong}=\sqrt{\frac{{\lambda }_2}{{\lambda }_1+ϵ}}\in [0,1]$	In-plane anisotropy; ≈0 for stretched, ≈1 for compact.
Flatness (2D)	$\mathrm{Flatness}=\sqrt{\frac{{\lambda }_2}{{\lambda }_1+ϵ}}\in [0,1]$	Same expression in 2D; distinct from elongation only in 3D.

Table A7. Shape-2D proxies (4): formulas and interpretation. Convert to physical units using $({\Delta }_x,{\Delta }_y)$. In 2D, elongation and flatness are identical; in 3D, IBSI defines distinct measures [4].

Feature	Formula/Symbol	Interpretation
Area (A)	$A={\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}{M}_{ij},A_{\mathrm{phys}}=A\left({\Delta }_x{\Delta }_y\right)$	In-plane size of ROI (pixels or mm2).
Perimeter ($P,4-$neigh.)	$P={\displaystyle \sum _{i,j}}{\displaystyle \sum _{({\delta }_x,{\delta }_y)\in {\mathcal{N}}_4}}\mathbf{1}\left\{M_{ij}=1,M_{i+{\delta }_x,j+{\delta }_y}=0\right\}$	Boundary length on a Manhattan grid; reproducible contour measure.
Elongation (2D)	$\mathrm{Elong}=\sqrt{\frac{{\lambda }_2}{{\lambda }_1+ϵ}}\in [0,1]$	In-plane anisotropy; ≈0 for stretched, ≈1 for compact.
Flatness (2D)	$\mathrm{Flatness}=\sqrt{\frac{{\lambda }_2}{{\lambda }_1+ϵ}}\in [0,1]$	Same expression in 2D; distinct from elongation only in 3D.

Together these four descriptors provide a compact picture of size (area), boundary complexity at the grid scale (perimeter), and anisotropy (elongation/flatness). For volumetric cohorts and standardized reporting, these proxies should be replaced by the full IBSI 3D shape family and computed on the native voxel grid with recorded spacings and resampling details [4].