Characterizing the Early Acidic Response in Advanced Small Modular Reactors Cooled with High-Temperature, High-Pressure Water

Simple Summary

In this brief communication, we aim to underscore the importance of acidic pH levels during the initial stages of radiation exposure in small modular reactors (SMRs) cooled using supercritical water (SCW). Our study focuses on temperatures ranging from 300 to 500 °C at a nominal pressure of 25 MPa and investigates the effects of varying radiation dose rates. In this context, pH values are calculated using both molar and molal concentrations of H₃O⁺. It is important to highlight that under conditions involving substantial temperature changes, such as those encountered in our study, molality offers a more accurate pH determination. Although molarity and molality exhibit discernible differences, a key finding of our research is the consistent observation of a pronounced ‘acid spike’ effect in both cases, which is significantly influenced by dose rate variations. This raises a critical question regarding the dynamics of water chemistry under such extreme conditions: do these transient acidic states foster a corrosive environment that could potentially accelerate the degradation of materials? Addressing this question is crucial, considering its direct impact on the durability and safety of reactor materials. Owing to the specific operating conditions of SMRs cooled using SCW, this work is anticipated to have significant applicability and importance for those involved in the SCW-cooled SMR field.

Abstract

Utilizing Monte Carlo multi-track chemistry simulations along with a cylindrical instantaneous pulse (Dirac) irradiation model, we assessed the initial acidic response in both subcritical and supercritical water under high radiation dose rates. This investigation spans a temperature range of 300 to 500 °C at a nominal pressure of 25 MPa, aligning with the operational conditions anticipated in proposed supercritical water (SCW)-cooled small modular reactors (SCW-SMRs). A pivotal finding from our study is the observation of a significant ‘acid spike’ effect, which shows a notable intensification in response to increasing radiation dose rates. Our results bring to light the potential risks posed by this acidity, which could potentially foster a corrosive environment and thereby increase the risk of accelerated material degradation in reactor components.

1. Introduction

Just as with hydroelectricity, nuclear power has the potential to significantly reduce global greenhouse gas emissions. As such, it is viewed as a promising alternative to fossil fuels in the fight against climate change. This point was emphasized during the ‘IAEA International Conference on Climate Change and the Role of Nuclear Power’, which took place in Vienna, Austria, from 7 to 11 October 2019 [1]. Simultaneously, nuclear energy also addresses the escalating energy demands driven by global population growth and economic expansion. This has prompted increased interest in the development and deployment of innovative nuclear technologies, such as ‘small modular reactors’ (SMRs) [2,3]. These reactors are distinct from traditional large-scale nuclear reactors due to their smaller physical size, reduced power capacity, and a ‘modular’ technology. Over 70 reactor designs are being developed for global commercial deployment, leveraging existing cooling systems from conventional nuclear reactors.

In this study, our focus is on the SMR cooled using supercritical water (SCW), which operates in the temperature range of ~300–500 °C and under a pressure of 25 MPa. This can be seen as a scaled-down, modular counterpart of the supercritical water-cooled reactor (SCWR) that operates between roughly 350 and 625 °C and at 25 MPa. Notably, the SCWR is one of the six advanced nuclear energy systems chosen for further research and development by the ‘Generation IV International Forum’ (GIF) [4,5,6]. A primary water chemistry challenge for all reference SCWR-based SMR designs is understanding and mitigating the impacts of water radiolysis on material performance and the transportation of corrosion products [6]. The chemical species formed during radiolysis, including the hydrated electron (e⁻_aq), the hydrogen atom (H^•), molecular hydrogen (H₂), the hydroxyl radical (^•OH), hydrogen peroxide (H₂O₂), the hydronium ion (H₃O⁺), the hydroxide ion (OH⁻), and the hydroperoxyl/superoxide anion radicals (HO₂^•/O₂^•−) [7,8], are highly reactive with many metal alloys, particularly at the elevated temperatures proposed for SCW reactors. These species have the potential to significantly accelerate the corrosion processes affecting in-core materials, particularly the fuel cladding. This can result in fuel failures, leading to the release of fuel fragments and fission products into the coolant. Additionally, these reactive species can also affect the transport of radioactive material from the core to downstream piping components in the reactor, a phenomenon known as ‘activity transport’. This can lead to a heightened radiation dose for reactor maintenance personnel [6].

Directly measuring the chemistry within reactor cores beyond the critical point of water is exceedingly challenging, if not impossible. This is largely because the SCWR coolant, as it traverses the reactor core, is subjected to an intense radiation field—comprising fast neutrons, recoil protons and oxygen ions, γ-rays, and, in the presence of boron, α-particles, and recoil lithium-7 nuclei. As a consequence, theoretical modeling and computer simulations play a crucial role in quantitatively understanding the effects of water radiolysis and its subsequent influence on materials in both SCWRs and their SMR variants [6].

While many experiments and simulations have been conducted on the radiolytic yields (or G values) of water decomposition products at temperatures up to 350 °C [8], most studies of radiolysis in SCW (ranging from 380 to 800 °C) have primarily been based on modeling (e.g., see [9] and references cited therein). However, recent experimental research conducted at temperatures and pressures exceeding the water critical point (t_c = 373.95 °C and P_c = 22.06 MPa) and reaching up to 500 °C is detailed in a review paper by Lin and Katsumura [10].

Recently, radiolysis modeling in support of SCWR/SCW-SMR development has emphasized the effects of high dose rates on primary radiolytic yields. In fact, in this high-temperature range and especially above t_c (as noted in Sultana et al. [9]), most simulation studies to date have operated under the assumption that the dose rates were sufficiently low to prevent any interaction or overlap between radiation tracks. When operating under these conditions, the chemical impact of the irradiation can be understood as the cumulative effects of individual radiation tracks. In such instances, the radiation quality, often termed the ‘linear energy transfer’ or LET, is viewed as the predominant factor influencing the radiolysis yields [11]. In practice, the radiation dose rates typically found in the cores of current water-cooled reactors are estimated to be between 300 and 2000 Gy/s, which translates to a few 10³ kGy/h [6]. During certain extreme situations—such as severe accidents or emergencies—these radiation fluxes can fluctuate across a much broader spectrum, reaching up to approximately 10¹⁰ Gy/s or even more [12]. At these notably elevated dose rates, the overall spatial and temporal dynamics change considerably due to the overlapping of adjacent radiation tracks that occur shortly following radiation absorption. This overlap results in an increased yield of inter-track, radical-radical reactions [7]. Consequently, there is an increased production of molecular compounds like H₂, H₂O₂, and reformed water, while the proportion of free-radical products diminishes [12].

In our recent research, we investigated the effects of high dose rates on the production of hydronium ions via the very fast pseudo-first-order reaction:

H₂O^•+ + H₂O → H₃O⁺ + ^•OH.

(1)

This reaction occurs within a very short duration of 46 ± 10 fs, as detailed by Loh et al. [13]. It involves the H₂O^•+ cation, which is produced by the ionization of water. Furthermore, we also studied the associated pH values immediately post-irradiation, observing them as a function of time both at 25 °C [14] and under supercritical conditions (400 °C, 25 MPa) [15]. In these studies, we simulated dose–rate effects by varying the number of interactive tracks of 300 MeV monoenergetic incident protons. These protons mimic the low-LET characteristics of ⁶⁰Co γ rays or high-energy electrons (e.g., those in the MeV range) with an LET value of ~0.3 keV/μm at 25 °C and ~0.056 keV/μm at 400 °C, under a pressure of 25 MPa [15]. In all cases we examined, an early and transient, highly acidic pH response, which we have termed an ‘acid spike’ [16], was observed throughout the irradiated volume. Notably, this response showed little dependence on whether oxygen was present or absent. As outlined in previous discussions [15], the source of this acidity is the radiolytic production of H₃O⁺ through reaction (1). This is followed by a charge separation that develops between the more concentrated positive-ion core within the tracks and the displaced ejected electrons in the surrounding medium. These electrons traverse a considerable distance from their initial ionization point to their final resting spot after undergoing thermalization, trapping, and hydration. Given the significant separation between the H₃O⁺, the ^•OH radical, and the e⁻_aq, immediate recombination between them (resulting in H^• and OH⁻) is not feasible. As a result, this charge separation and its accompanying acidity persist temporally until the slow diffusion of H₃O⁺ and ^•OH aligns these species with the distant positions initially occupied by the electrons. Interestingly, this transient acidic milieu, evident immediately post-irradiation at the chemical stage’s onset, was first underscored in the late 1940s [17,18]. Despite several authors providing experimental evidence for this initial acidity [7], such ‘acid-spike’ effects have largely been overlooked in water subjected to ionizing radiation [19].

In expanding upon our earlier calculations, we have assessed the effects of high dose rates on the initial transient yields and concentrations of H₃O⁺ ions produced in the low-LET radiolysis of deaerated, sub- and supercritical water at temperatures of 300, 350, 400, and 500 °C, all under nominal pressure of 25 MPa. As previously noted, these conditions mirror those at the coolant level within the heat transport system of an SCW-SMR.

2. Monte Carlo Multiple Ionization Track Chemistry Simulations

Our approach utilizes a Monte Carlo-based simulation model to investigate the simultaneous input of multiple ionization tracks and their intra- and inter-track interactions [20]. In essence, this model simulates the random irradiation of water through instantaneous pulses of N incident 300 MeV protons. These protons, with nearly linear trajectories, simultaneously strike the water surface perpendicularly within a circle of radius R_o. This results in a cylindrical beam geometry within the water upon entry (refer to Figure 1 of Alanazi et al. [20]). In this geometry, every proton track aligns parallel to the cylinder’s axis throughout the chosen track length for computations. This design is based on the ‘instantaneous pulse’ (or Dirac) model [21], where the pulse duration is considered negligible, meaning all chemical species form instantaneously. Given that the irradiated cylinder is immersed in non-irradiated bulk water, the radiolytic species first generated inside it are not limited to just the cylinder; they gradually diffuse into the boundless surrounding bulk water as time progresses.

In this context, the influence of dose rate can be evaluated by modifying N, alternatively described as the ‘fluence’, which is defined as N/πR_o², with πR_o² representing the area of the cylinder’s circular base. For this research, we conducted calculations using values of N = 1, 10, and 2000. The data obtained for N = 1, signifying no dose–rate effects, were utilized as a reference point. The values of N = 10 and N = 2000 represent dose rates on the magnitude that (1) are common in both conventional and SCW-cooled nuclear reactors, and (2) might be anticipated during specific accident or emergency scenarios (around 10¹⁰ Gy/s) [20]. Time zero was chosen as the moment when the N incident protons make contact with the cylinder’s forefront.

The radiolysis of both subcritical and supercritical water at a high dose rate was modeled in the temperature range of 300–500 °C under a pressure of 25 MPa. This modeling utilized the multi-track chemistry version of our Monte Carlo computer code, IONLYS-IRT [22]. This code has been detailed in previous studies [12,15,20]. It should be noted that the reaction scheme, rate constants, and diffusion coefficients of reactive species used in the program at temperatures of 300 and 350 °C align with those adopted in previous studies [8,9]. Beyond the critical point, specifically at the chosen temperatures for this study (400 and 500 °C at 25 MPa, corresponding to water densities of ρ ≈ 0.16654 and 0.08974 g/cm³, respectively [23]), we used the SCW radiolysis database from Liu et al. [24,25]. In line with earlier assumptions, we posited that the diffusion coefficients for all species scale proportionally to the self-diffusion of compressed SCW [9,26,27]. In our study, we opted to overlook the heterogeneous structural nature of SCW [28]. Instead, we posited that the instantaneous representation of SCW can be perceived as a uniform medium with a mean density equivalent to the bulk water density (ρ).

We carried out all yield calculations by simulating short track segments of 300 MeV incident protons, typically ranging from ~5 to 200 μm, during which the average LET observed in the simulations remained virtually constant. The number of simulated ‘histories’ (essentially the number of pulses, usually between 5 and 100, contingent on the value of N being considered) was selected to guarantee minimal statistical fluctuations in the calculated mean chemical yield values, all while staying within acceptable computational time constraints.

Employing our cylindrical, multi-track irradiation model and assuming a uniform distribution of hydronium ions produced by N incident protons within the considered circular cylinder (1 μm in length and an initial radius R_o of 0.1 μm) [20], we determined the prevailing pH in the irradiated water volume. Assuming that the activity of hydrogen ions can reasonably be well approximated by their concentration, this can be achieved by computing the negative logarithm of the total H₃O⁺ ion concentration:

$$\mathrm{p}\mathrm{H}\left(t\right)\hspace{0.33em}=\hspace{0.33em}-\hspace{0.17em}\mathrm{l}\mathrm{o}{\mathrm{g}}_{10}\left({\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{total}}\left(t\right)\right)$$

(2)

where

$${\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{total}}\left(t\right)\hspace{0.33em}=\hspace{0.17em}{\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{autoprotolysis}}+\hspace{0.33em}{\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{radiolytic}}\left(t\right).$$

(3)

Here, [H₃O⁺]_{autoprotolysis} is the non-radiolytic, pre-irradiation concentration of H₃O⁺ due to water’s autoprotolysis [29], and [H₃O⁺]_radiolytic represents the H₃O⁺ concentration generated radiolytically, as given by [20,30]

$${\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{radiolytic}}\left(t\right)\hspace{0.33em}\hspace{0.17em}\approx \hspace{0.33em}5.3\hspace{0.33em}\times \hspace{0.33em}10^{-\hspace{0.17em}9}\hspace{0.33em}\times \hspace{0.33em}\left(\frac{N\hspace{0.33em}\times \hspace{0.33em}\mathrm{L}\mathrm{E}\mathrm{T}}{R{(t)}^2}\right)\hspace{0.33em}\times \hspace{0.33em}G\left({\mathrm{H}}_3{\mathrm{O}}^{+}\right)\left(t\right)$$

(4)

where [H₃O⁺]_radiolytic is expressed in molarity (moles per liter) or molality (moles per kg), LET is in keV/μm, G(H₃O⁺) denotes the chemical yield of H₃O⁺ in molecule per 100 eV (for conversion into SI units, 1 molecule/100 eV ≈ 0.10364 μmol/J), and

$$R{\left(t\right)}^2\hspace{0.33em}\approx \hspace{0.33em}\hspace{0.17em}{R_{\mathrm{o}}}^2\hspace{0.33em}+\hspace{0.33em}\hspace{0.17em}4Dt$$

(5)

illustrates the variation in R_o over time due to the two-dimensional diffusive expansion of the tracks. In this expression, t stands for time in seconds, and D denotes the average diffusion coefficient for the various track species involved in the simulations.

3. Results and Discussion

Figure 1 illustrates the influence of dose rate on the temporal evolution of the pH values in deaerated, pure water, which has been exposed to 300 MeV proton irradiation at 25 MPa. These pH values are calculated using Equations (2)–(5) based on the molar concentrations of H₃O⁺ (molarity). The figure presents results for two specific N values: panel A for N = 10 and panel B for N = 2000. The conditions examined include both subcritical (300 and 350 °C) and supercritical (400 and 500 °C) temperatures, spanning the time range of 1 ps to 10 μs. Additionally, for comparative purposes, reference curves for single proton irradiation (N = 1) are included, illustrating conditions under which dose–rate effects are non-existent.

As observed, the pH level of the water volume exposed to radiation under supercritical conditions, in the absence of dose–rate effects (when N = 1), remains nearly neutral initially or turns slightly alkaline at ~10 μs. However, when dose–rate effects are taken into account, with N = 10, the pH level experiences a reduction of about one unit, varying between ~5.8 and 6 at around 1 picosecond. In the case where N = 2000, the initial acidic response intensifies, leading the pH to drop to values between ~3.5 and 3.7. When examining subcritical water at 300 and 350 °C, the results are fairly consistent; the pH diminishes at ~1 ps, dropping from 5.6 at N = 1 to 5.2 at N = 10 and further down to 3 at N = 2000. Despite being transient, these initial ‘acid spikes’ continue to occur over durations spanning more than 5 or 6 orders of magnitude, the extent of which depending on the temperature. As illustrated in Figure 1, the acidity is most pronounced when the time frame is less than a few nanoseconds. Within this temporal bracket, the pH remains nearly constant. As time progresses, there is a gradual increment in the pH across all temperature conditions, stabilizing ultimately at a constant value that aligns with the water’s autoprotolysis pH.

Remarkably, Figure 1 highlights that the duration of acidity is significantly shorter at supercritical temperatures compared to subcritical temperatures. This can be explained by the faster charge-recombination reaction:

H₃O⁺ + e⁻_aq → H^• + H₂O

(6)

in irradiated SCW, which is predominantly due to a substantial increase in its rate constant (k) as conditions shift from subcritical to supercritical water. Indeed, within the temperature range under consideration, k(H₃O⁺ + e⁻_aq) experiences a significant increase from ~7.2 × 10¹¹ M⁻¹ s⁻¹ at 300 °C and 1.94 × 10¹² M⁻¹ s⁻¹ at 350 °C [8] to ~1.1 × 10¹³ M⁻¹ s⁻¹ at 400 °C and 3.3 × 10¹³ M⁻¹ s⁻¹ at 500 °C (at a pressure of 25 MPa) [25]. Reaction (6) holds significant importance in irradiated SCW, as it is known to predominantly control the decay kinetics of hydrated electrons at short times [31]. As a result, the prominence of this reaction facilitates a more rapid recombination of e⁻_aq and H₃O⁺ in the supercritical regime, subsequently leading to a swifter depletion of the hydronium ions produced during the initial stages of radiolysis.

A referee correctly pointed out that in situations involving notable temperature variations, like those encountered in this study, a more accurate determination of pH can be achieved by expressing H₃O⁺ concentrations in moles per kilogram (molality) instead of the traditional moles per liter (molarity) approach that was used above. Heeding this critical advice, we re-evaluated the pH values using molality, maintaining the same conditions as those used in Figure 1, where molarity was the basis for pH calculation. The conversion from molarity to molality was accomplished by dividing each molar concentration by the corresponding solution’s density. The densities used were ρ = 0.74302 g/cm³ at 300 °C, 0.62545 g/cm³ at 350 °C, 0.16654 g/cm³ at 400 °C, and 0.08974 g/cm³ at 500 °C, all at 25 MPa [23]. These new findings are illustrated in Figure 2. Our results now demonstrate a more pronounced effect of dose rate on pH levels compared to our previous observations in Figure 1. Specifically, pH levels dropped to around 5 for N = 10, as shown in Figure 2A. Even more notably, for N = 2000, the pH further declined to approximately 2.75, as illustrated in Figure 2B. These changes in pH are consistently observed across a range of temperature conditions. This uniformity in response across different temperatures highlights the robustness of the effect of dose rate on pH during the early stages of radiolysis, specifically within the nanosecond time range.

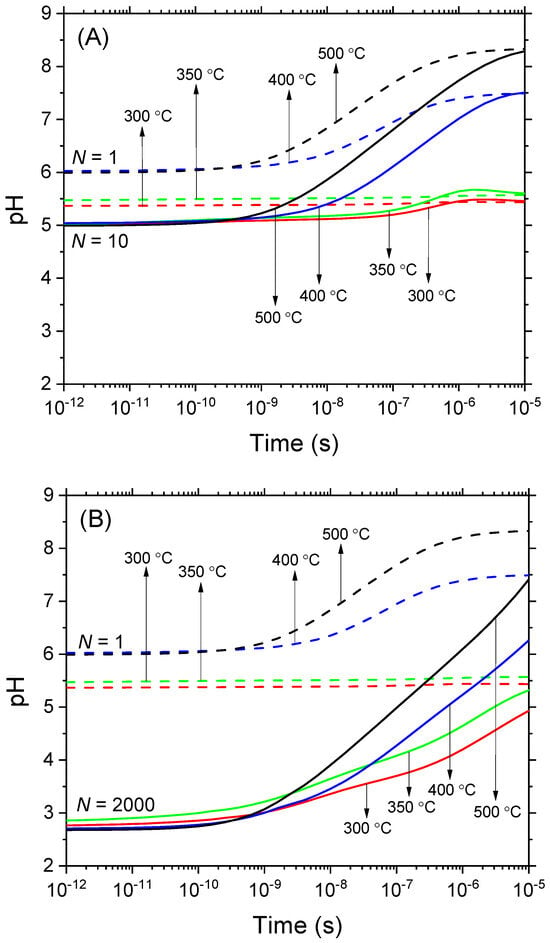
Figure 1. Time evolution of pH deduced from Equations (2)–(5) in deaerated, pure water exposed to N 300 MeV proton irradiation at various temperatures: 300, 350, 400, and 500 °C, all maintained at a constant pressure of 25 MPa. The pH is expressed here in terms of the concentration of H₃O⁺ given in moles per liter (molarity). Two cases are examined, based on the value of N (the number of irradiating protons per pulse) selected to illustrate the effects of dose rate. In (panel A), scenarios with N = 1 (dashed lines) and N = 10 (solid lines) are compared, while in (panel B), the scenarios with N = 1 (dashed lines) and N = 2000 (solid lines) are compared. Data corresponding to N = 1 (i.e., for a single-proton track scenario) represent the absence of dose–rate effects and are presented for comparison. The time interval for this study ranged from 1 ps to 10 μs. The average diffusion coefficient D, which intervenes in the calculations via Equation (5), was set at ~5 × 10⁻⁷ and 12.6 × 10⁻⁷ m² s⁻¹ for temperatures of 400 and 500 °C, respectively [26,27]. Based on molarity, the pH values associated with the autoprotolysis of water were taken to be ~5.6 at 300 °C, 5.8 at 350 °C, 8.3 at 400 °C, and 9.4 at 500 °C [29].

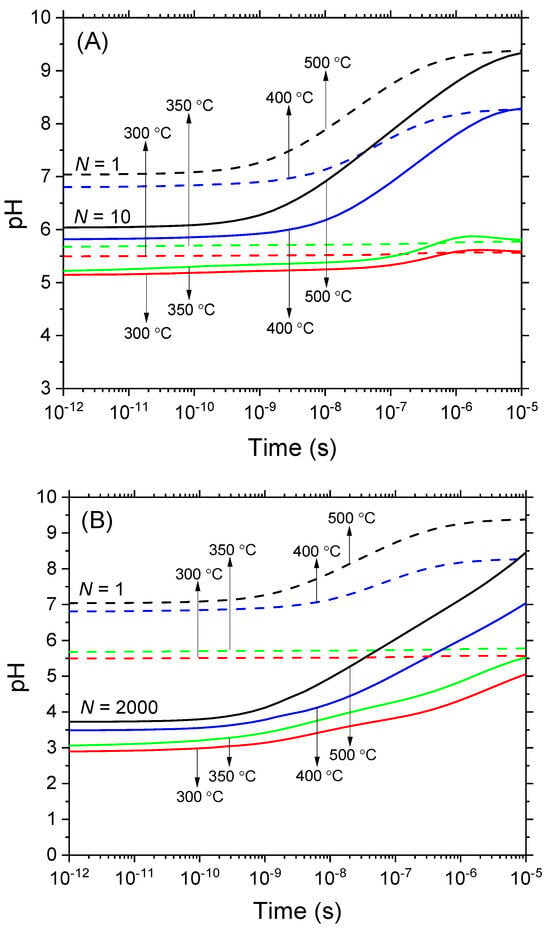
Figure 1. Time evolution of pH deduced from Equations (2)–(5) in deaerated, pure water exposed to N 300 MeV proton irradiation at various temperatures: 300, 350, 400, and 500 °C, all maintained at a constant pressure of 25 MPa. The pH is expressed here in terms of the concentration of H₃O⁺ given in moles per liter (molarity). Two cases are examined, based on the value of N (the number of irradiating protons per pulse) selected to illustrate the effects of dose rate. In (panel A), scenarios with N = 1 (dashed lines) and N = 10 (solid lines) are compared, while in (panel B), the scenarios with N = 1 (dashed lines) and N = 2000 (solid lines) are compared. Data corresponding to N = 1 (i.e., for a single-proton track scenario) represent the absence of dose–rate effects and are presented for comparison. The time interval for this study ranged from 1 ps to 10 μs. The average diffusion coefficient D, which intervenes in the calculations via Equation (5), was set at ~5 × 10⁻⁷ and 12.6 × 10⁻⁷ m² s⁻¹ for temperatures of 400 and 500 °C, respectively [26,27]. Based on molarity, the pH values associated with the autoprotolysis of water were taken to be ~5.6 at 300 °C, 5.8 at 350 °C, 8.3 at 400 °C, and 9.4 at 500 °C [29].

Responding to a concern from another reviewer, it is important to acknowledge that an in-depth understanding of the chemical processes occurring in the coolant as it traverses the reactor core necessitates the consideration of diverse radiation types, a point underscored in the Introduction. In this brief communication, our objective is to present quantitative data pertaining to the scenario where irradiation occurs due to low-LET 300-MeV incident protons. This example provides a clear illustration of how water’s pH might vary in the early stages of radiolysis under varying dose rate conditions, specifically at a nominal pressure of 25 MPa. Our prior studies [16,32,33] have shown that the initial acidic response in water exposed to high-LET radiation is markedly more significant than that observed with low-LET radiation. Conversely, using 300 MeV protons as a representative model to evaluate acidic spikes in SCWRs and SMRs can be seen as a cautious approach, particularly in terms of the actual magnitude of the effect. This method may understate the true extent of the acidity changes, given the specific energy and interaction characteristics of these protons compared to the broader range of radiations encountered in reactor environments. Such an inclusive investigation, accounting for this variety of radiations, could be a subject for future research under specific conditions. Nevertheless, it is important to note that the early acidity levels reported in this study are likely to be even more significant than our current findings suggest.

The current study prompts the question: Can the generation of an early, albeit transitory, ‘acid-spike’ response chemically foster a corrosive environment, potentially accelerating material degradation in proposed SCW-cooled SMRs? Such a scenario becomes especially plausible when radiation tracks materialize near a metal/water interface, given that corrosion is inherently a surface phenomenon. The interaction of H₃O⁺ ions with structural materials has the potential to trigger spontaneous, pH-dependent electrochemical reactions. The occurrence of these reactions could lead to the continuous release of positive metal ions (cations) at the metal’s surface, culminating in the material’s corrosion [6,34]. Notably, an increase in environmental acidity correlates with an accelerated release of metal cations into the solution. This process leaves behind vacancies or defects within the metallic structures, which, over time, could serve as initiation points for ‘stress corrosion cracking’ (SCC) [35]. Even more importantly, once a crack initiates, radiolysis occurring within the crack, particularly at the nanoscale dimensions of the crack tip, coupled with the consequent ‘acid spikes’, can significantly hasten the propagation of the SCC process [36]. Over time, this could culminate in the failure of fuel cladding [6]. Moreover, the continuous liberation of metal ions into the system may pose detrimental effects on non-core components, like heat exchangers, where the accumulation of metal ions can lead to an increase in radioactivity.

4. Conclusions

In this work, we employed Monte Carlo multiple ionization track chemistry simulations to quantitatively assess the initial acidic response in both sub- and supercritical water exposed to high radiation dose rates. This evaluation was specifically carried out at temperatures ranging from 300 to 500 °C and a pressure of 25 MPa, mirroring the typical conditions anticipated in proposed supercritical water-cooled SMRs. pH values were calculated using both molar and molal concentrations of H₃O⁺. Although molarity and molality exhibit discernible differences, a key finding of our research is the consistent observation of a pronounced ‘acid spike’ effect in both cases, which is significantly influenced by dose rate variations. The observed uniformity in response across different temperatures highlights the robustness of the effect of dose rate on pH during the early stages of radiolysis. In this context, our findings highlight the potential risks associated with this acidic environment, which could foster a corrosive environment, subsequently enhancing the likelihood of accelerated material degradation.

Considering the potential implications of such early acidic pH responses, this study underscores the importance of thoroughly investigating the water chemistry in proposed Generation IV SCW-cooled small modular reactors. The results should spur the development of advanced predictive models that specifically address corrosion induced by the ‘acid-spike’ phenomenon. These models would subsequently be validated through new measurements conducted under SCW-SMR conditions.

Additionally, it is imperative to acknowledge that our current analysis of dose–rate effects is based on the utilization of a single Dirac radiation pulse model. This model represents a relatively simplified theoretical approach for exploring dose–rate effects in water radiolysis, but it provides a foundational basis for understanding these complex interactions. Nonetheless, within the core of an SCW-SMR, irradiation occurs continuously, involving numerous consecutive pulses within a given solution volume. Consequently, it becomes vital to enrich our simulations by incorporating a ‘finite’ pulse duration and considering the impact of a pulse train delivered at a specific or even randomly determined repetition frequency. Our laboratory is actively engaged in modeling these additional complex aspects.