Metallic Nanoparticles: A Useful Prompt Gamma Emitter for Range Monitoring in Proton Therapy?
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Geant4 Monte Carlo Simulations
2.1.1. Physics Lists
2.1.2. Geant4 Simulation Geometry
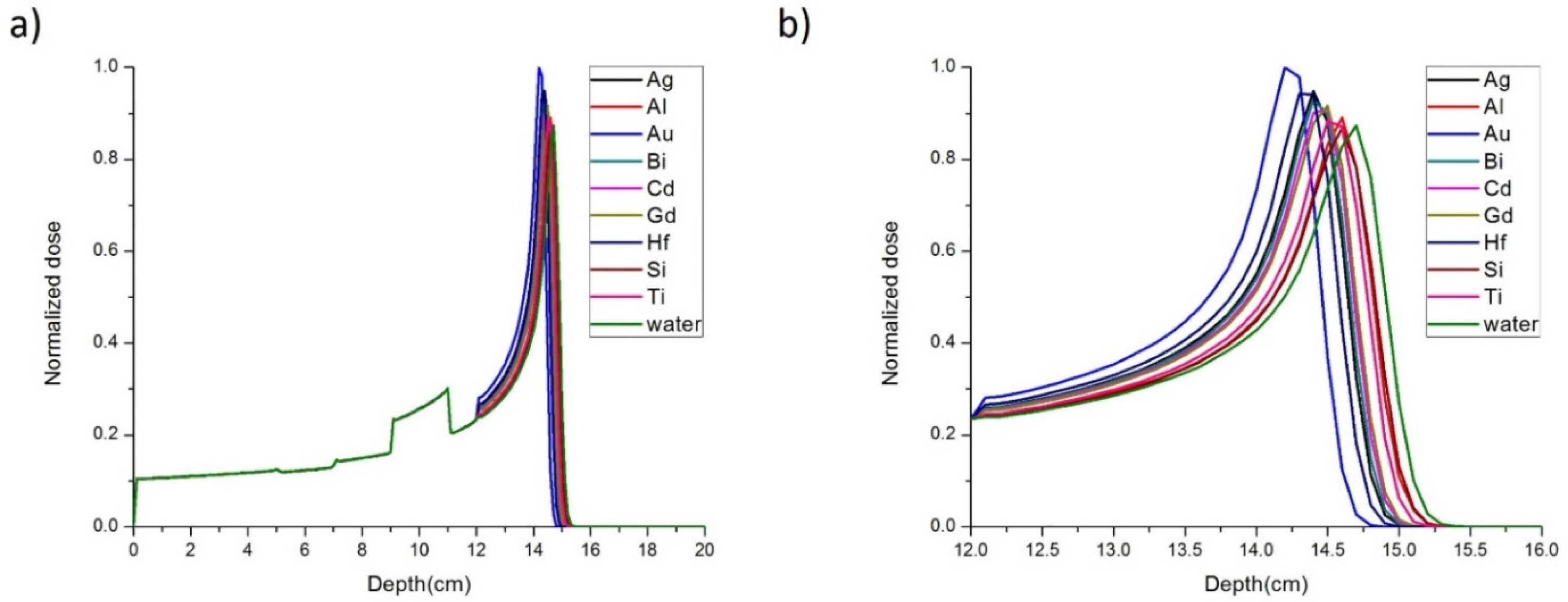
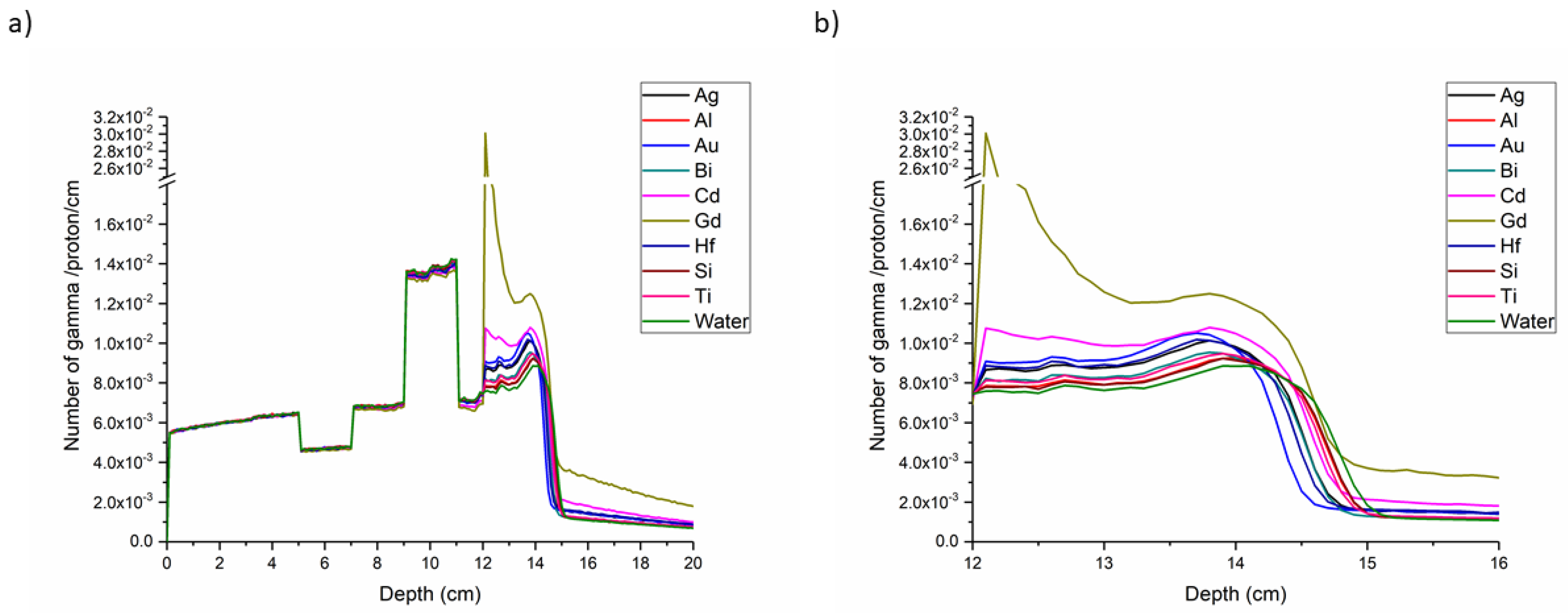
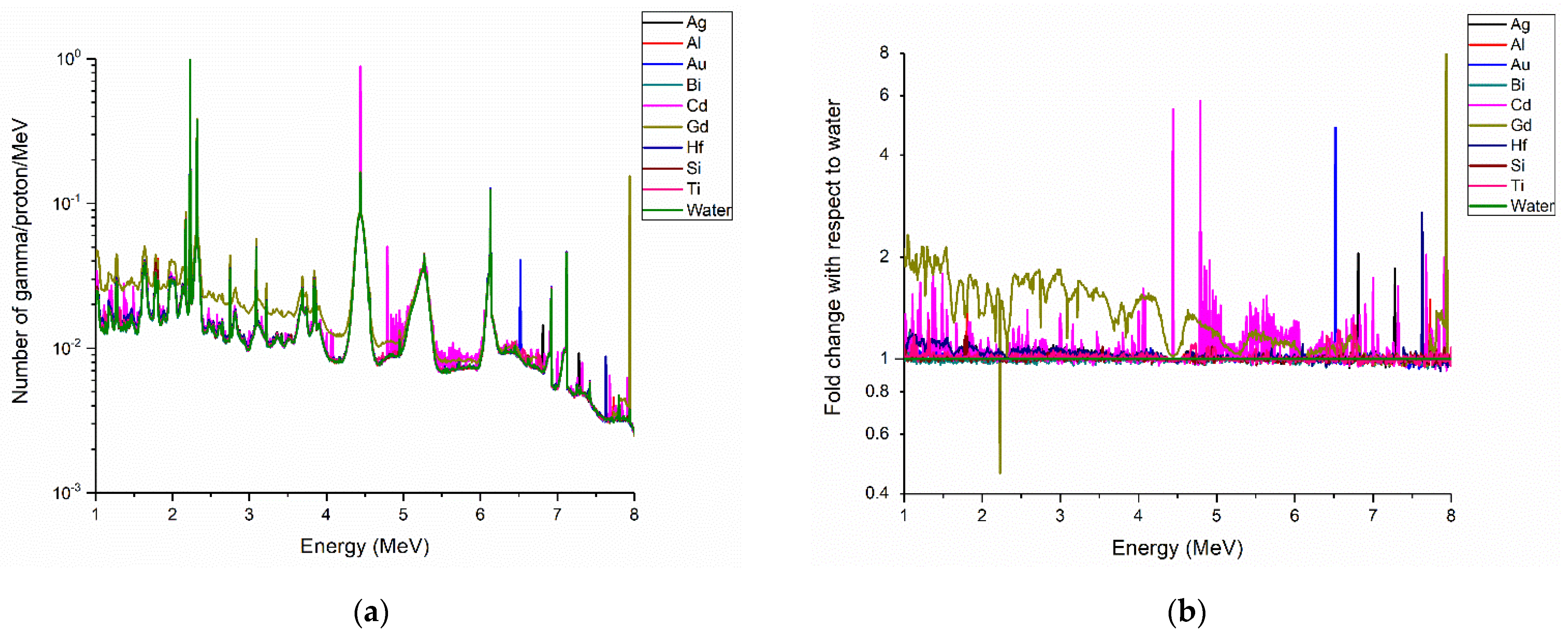
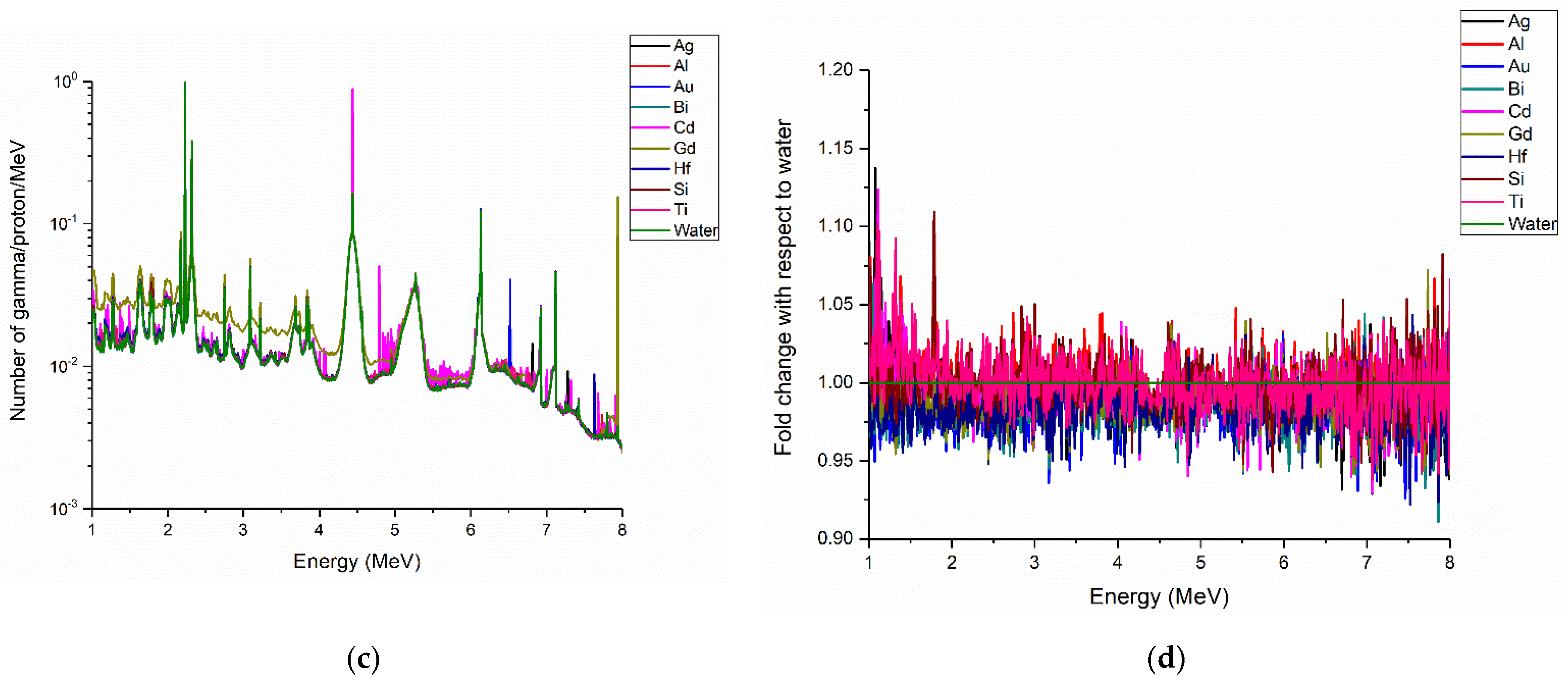
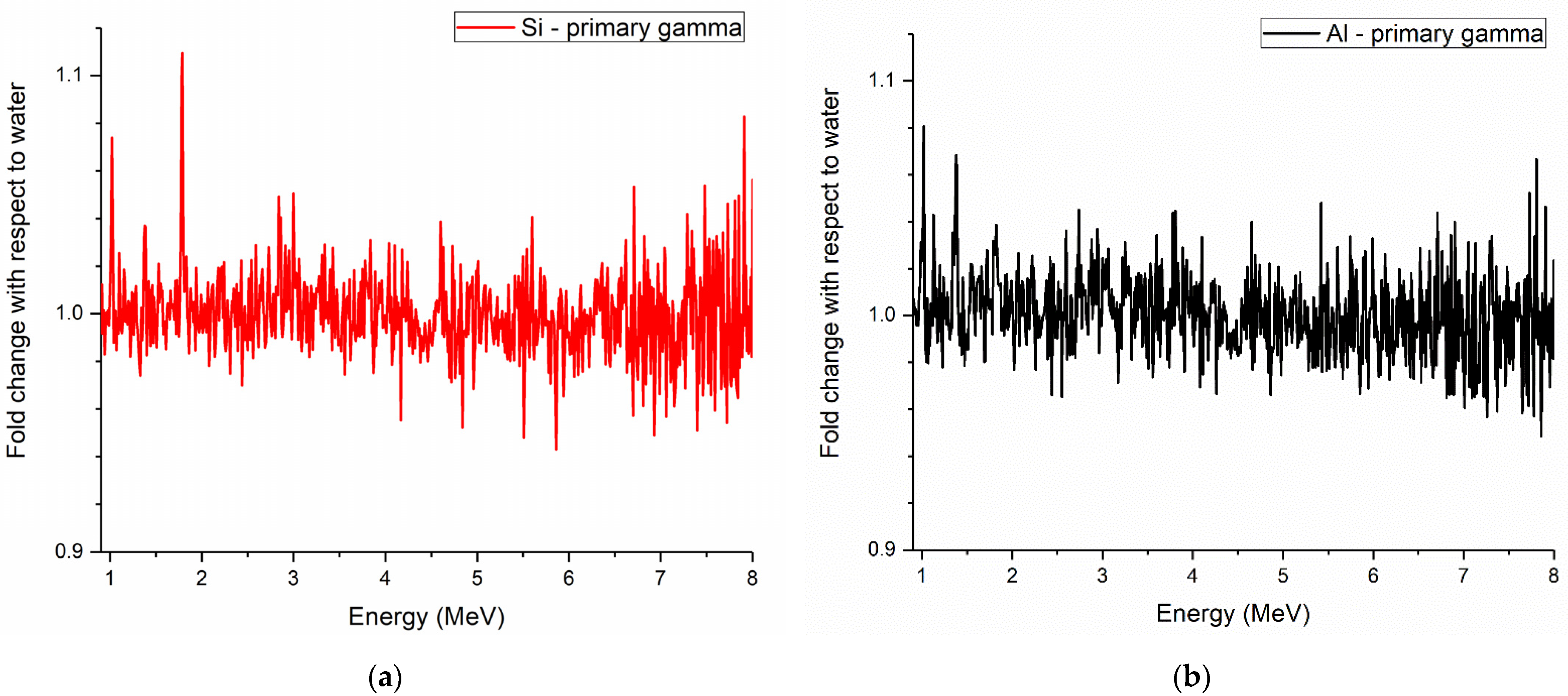
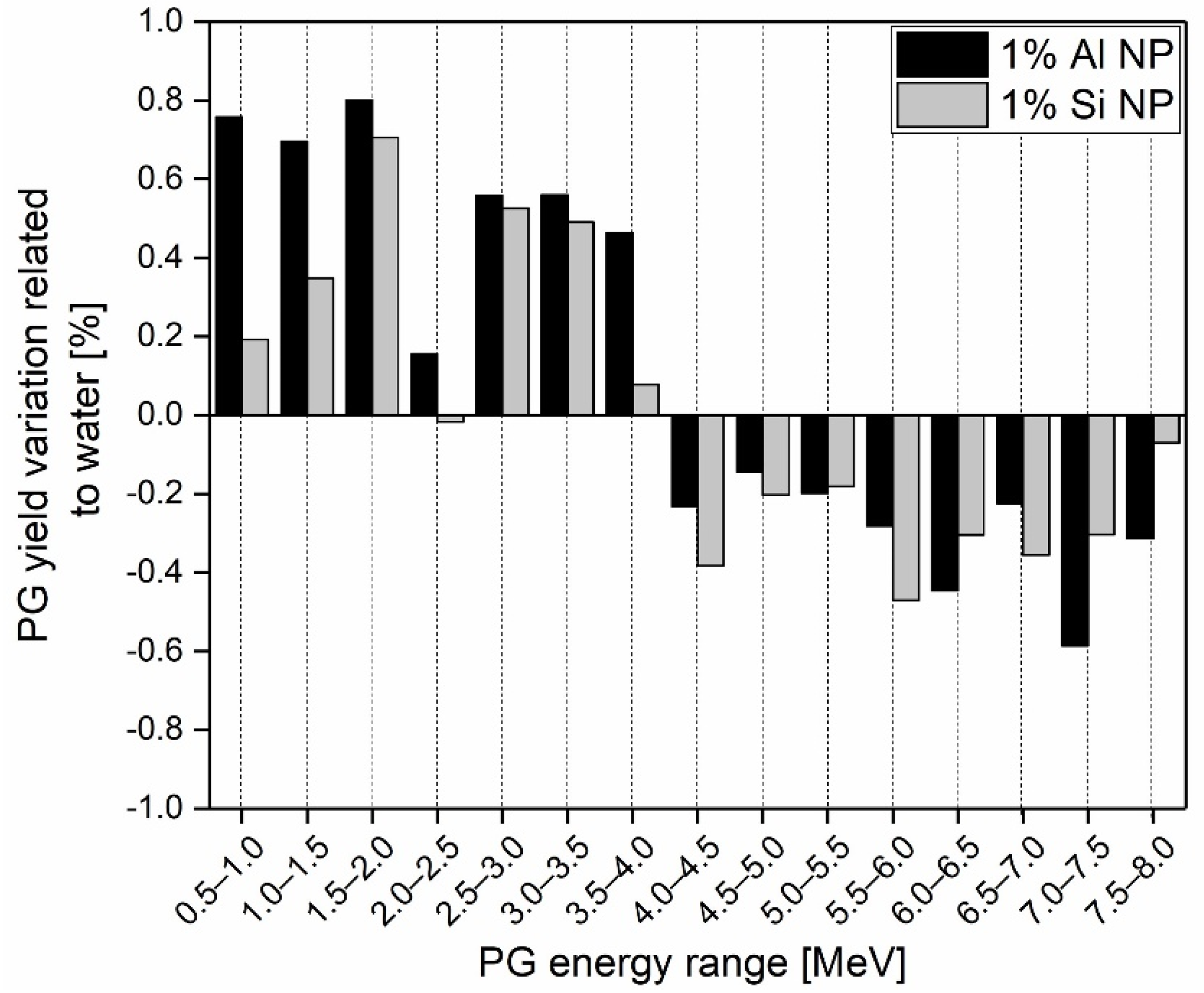
3. Results
Prompt Gamma Enhancement with Nanoparticles
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Paganetti, H. Proton Therapy Physics; CRC Press: Boka Raton, FL, USA, 2018. [Google Scholar]
- Paganetti, H.; Beltran, C.; Both, S.; Dong, L.; Flanz, J.; Furutani, K.; Grassberger, C.; Grosshans, D.R.; Knopf, A.-C.; Langendijk, J.A. Roadmap: Proton therapy physics and biology. Phys. Med. Biol. 2021, 66, 05RM01. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Virshup, G.; Clayton, J.; Zhu, X.R.; Mohan, R.; Dong, L. Theoretical variance analysis of single-and dual-energy computed tomography methods for calculating proton stopping power ratios of biological tissues. Phys. Med. Biol. 2010, 55, 1343. [Google Scholar] [CrossRef]
- Bourque, A.E.; Carrier, J.-F.; Bouchard, H. A stoichiometric calibration method for dual energy computed tomography. Phys. Med. Biol. 2014, 59, 2059. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paganetti, H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys. Med. Biol. 2012, 57, R99. [Google Scholar] [CrossRef]
- Knopf, A.-C.; Lomax, A. In vivo proton range verification: A review. Phys. Med. Biol. 2013, 58, R131. [Google Scholar] [CrossRef]
- Gioscio, E.; Battistoni, G.; Bochetti, A.; de Simoni, M.; Dong, Y.; Fischetti, M.; Mattei, I.; Mirabelli, R.; Muraro, S.; Patera, V. Development of a novel neutron tracker for the characterisation of secondary neutrons emitted in Particle Therapy. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 958, 162862. [Google Scholar] [CrossRef]
- Marafini, M.; Gasparini, L.; Mirabelli, R.; Pinci, D.; Patera, V.; Sciubba, A.; Spiriti, E.; Stoppa, D.; Traini, G.; Sarti, A. MONDO: A neutron tracker for particle therapy secondary emission characterization. Phys. Med. Biol. 2017, 62, 3299. [Google Scholar] [CrossRef] [PubMed]
- Assmann, W.; Kellnberger, S.; Reinhardt, S.; Lehrack, S.; Edlich, A.; Thirolf, P.; Moser, M.; Dollinger, G.; Omar, M.; Ntziachristos, V. Ionoacoustic characterization of the proton Bragg peak with submillimeter accuracy. Med. Phys. 2015, 42, 567–574. [Google Scholar] [CrossRef]
- Jones, K.C. Acoustic-Based Proton Range Verification, Radiation Therapy Dosimetry: A Practical Handbook; CRC Press: Boka Raton, FL, USA, 2021; pp. 443–456. [Google Scholar]
- Ferrero, V.; Fiorina, E.; Morrocchi, M.; Pennazio, F.; Baroni, G.; Battistoni, G.; Belcari, N.; Ciocca, M.; del Guerra, A.; Donetti, M. Online proton therapy monitoring: Clinical test of a Silicon-photodetector-based in-beam PET. Sci. Rep. 2018, 8, 4100. [Google Scholar] [CrossRef]
- Pennazio, F.; Battistoni, G.; Bisogni, M.G.; Camarlinghi, N.; Ferrari, A.; Ferrero, V.; Fiorina, E.; Morrocchi, M.; Sala, P.; Sportelli, G. Carbon ions beam therapy monitoring with the INSIDE in-beam PET. Phys. Med. Biol. 2018, 63, 145018. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Nagao, Y.; Ando, K.; Yamamoto, S.; Toshito, T.; Kataoka, J.; Kawachi, N. Secondary-electron-bremsstrahlung imaging for proton therapy. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 833, 199–207. [Google Scholar] [CrossRef]
- Min, C.-H.; Kim, C.H.; Youn, M.-Y.; Kim, J.-W. Prompt gamma measurements for locating the dose falloff region in the proton therapy. Appl. Phys. Lett. 2006, 89, 183517. [Google Scholar] [CrossRef]
- Martins, P.M.; Bello, R.D.; Seco, J. Prompt Gamma Detection for Proton Range Verification, Radiation Therapy Dosimetry: A Practical Handbook; CRC Press: Boka Raton, FL, USA, 2021; pp. 427–442. [Google Scholar]
- Jongens, Y.; Stichelbaut, F. Verification of the proton beams position in the patient by the detection of prompt gamma-rays emission. In Proceedings of the 39th Meeting of the Particle Therapy Co-Operative Group, San Francisco, CA, USA, 26–29 October 2003. [Google Scholar]
- Richter, C.; Pausch, G.; Barczyk, S.; Priegnitz, M.; Keitz, I.; Thiele, J.; Smeets, J.; Stappen, F.V.; Bombelli, L.; Fiorini, C. First clinical application of a prompt gamma based in vivo proton range verification system. Radiother. Oncol. 2016, 118, 232–237. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Bentefour, E.H.; Janssens, G.; Smeets, J.; Stappen, F.V.; Hotoiu, L.; Yin, L.; Dolney, D.; Avery, S.; O‘Grady, F. Prompt gamma imaging for in vivo range verification of pencil beam scanning proton therapy. Int. J. Radiat. Oncol. Biol. Phys. 2017, 99, 210–218. [Google Scholar] [CrossRef]
- Pinto, M.; Dauvergne, D.; Freud, N.; Krimmer, J.; Létang, J.M.; Testa, E. Assessment of Geant4 prompt-gamma emission yields in the context of proton therapy monitoring. Front. Oncol. 2016, 6, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zarifi, M.; Guatelli, S.; Qi, Y.; Bolst, D.; Prokopovich, D.; Rosenfeld, A. Characterization of prompt gamma ray emission for in vivo range verification in particle therapy: A simulation study. Phys. Med. 2019, 62, 20–32. [Google Scholar] [CrossRef] [Green Version]
- Zarifi, M.; Guatelli, S.; Bolst, D.; Hutton, B.; Rosenfeld, A.; Qi, Y. Characterization of prompt gamma-ray emission with respect to the Bragg peak for proton beam range verification: A Monte Carlo study. Phys. Med. 2017, 33, 197–206. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.a.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G. GEANT4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef] [Green Version]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Penninckx, S.; Heuskin, A.-C.; Michiels, C.; Lucas, S. Gold nanoparticles as a potent radiosensitizer: A transdisciplinary approach from physics to patient. Cancers 2020, 12, 2021. [Google Scholar] [CrossRef]
- Schuemann, J.; Bagley, A.F.; Berbeco, R.; Bromma, K.; Butterworth, K.T.; Byrne, H.L.; Chithrani, B.D.; Cho, S.H.; Cook, J.R.; Favaudon, V. Roadmap for metal nanoparticles in radiation therapy: Current status, translational challenges, and future directions. Phys. Med. Biol. 2020, 65, 21RM02. [Google Scholar] [CrossRef]
- Li, S.; Penninckx, S.; Karmani, L.; Heuskin, A.C.; Watillon, K.; Marega, R.; Zola, J.; Corvaglia, V.; Genard, G.; Gallez, B.; et al. LET-dependent radiosensitization effects of gold nanoparticles for proton irradiation. Nanotechnology 2016, 27, 455101. [Google Scholar] [CrossRef] [PubMed]
- Bolst, D.; Cirrone, G.A.; Cuttone, G.; Folger, G.; Incerti, S.; Ivanchenko, V.; Koi, T.; Mancusi, D.; Pandola, L.; Romano, F. Validation of Geant4 fragmentation for heavy ion therapy. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrometers Detect. Assoc. Equip. 2017, 869, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Jarlskog, C.Z.; Paganetti, H. Physics Settings for Using the Geant4 Toolkit in Proton Therapy. IEEE Trans. Nucl. Sci. 2008, 55, 1018–1025. [Google Scholar] [CrossRef]
- ICRU. 37 Stopping Powers for Electrons and Positrons; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 1984. [Google Scholar]
- Hainfeld, J.; Smilowitz, H.; O’Connor, M.; Dilmanian, F.; Slatkin, D. Gold nanoparticle imaging and radiotherapy of brain tumors in mice. Nanomedicine 2013, 8, 1601–1609. [Google Scholar] [CrossRef] [Green Version]
- Hainfeld, J.F.; Slatkin, D.N.; Smilowitz, H.M. The use of gold nanoparticles to enhance radiotherapy in mice. Phys. Med. Biol. 2004, 49, N309. [Google Scholar] [CrossRef]
- Sung, W.; Schuemann, J. Energy optimization in gold nanoparticle enhanced radiation therapy. Phys. Med. Biol. 2018, 63, 135001. [Google Scholar] [CrossRef]
- Tanaka, T.; Hagiwara, K.; Gazzola, E.; Ali, A.; Ou, I.; Sudo, T.; Das, P.K.; Reen, M.S.; Dhir, R.; Koshio, Y. Gamma-ray spectra from thermal neutron capture on gadolinium-155 and natural gadolinium. Prog. Theor. Exp. Phys. 2020, 2020, 043D002. [Google Scholar] [CrossRef]
- Kozlovsky, B.; Murphy, R.J.; Ramaty, R. Nuclear deexcitation gamma-ray lines from accelerated particle interactions. Astrophys. J. Suppl. Ser. 2002, 141, 523. [Google Scholar] [CrossRef] [Green Version]
- Demortier, G.; Bodart, F. Quantitative analysis of phosphorus by (p,g) reactions—LARN report 711. In Proceedings of the International Meeting on Chemical Analysis by charged Particles Bombardment, Namur, Belgium, 6–8 September 1971. [Google Scholar]
- Verburg, J.M.; Seco, J. Proton range verification through prompt gamma-ray spectroscopy. Phys. Med. Biol. 2014, 59, 7089–7106. [Google Scholar] [CrossRef]
- Pringle, R.; Taylor, H.; Roulston, K. Radiative Capture of Thermal Neutrons by Cd 113. Phys. Rev. 1952, 87, 1016. [Google Scholar] [CrossRef]
- Sadler, G.; Jarvis, O.; van Belle, P.; Pillon, M. Use of the 28Si (n,p) 28Al reaction for the measurement of 14 MeV neutrons from fusion plasmas. Rev. Sci. Instrum. 1990, 61, 3175–3177. [Google Scholar] [CrossRef]
- Mannhart, W.; Schmidt, D. Measurement of the 28Si(n,p), 29Si(n,p) and 30Si(n,α) Cross Sections between 6.9 and 14.0 MeV. J. Nucl. Sci. Technol. 2002, 39, 218–221. [Google Scholar] [CrossRef]
- Golnik, C.; Hueso-González, F.; Müller, A.; Dendooven, P.; Enghardt, W.; Fiedler, F.; Kormoll, T.; Roemer, K.; Petzoldt, J.; Wagner, A. Range assessment in particle therapy based on prompt γ-ray timing measurements. Phys. Med. Biol. 2014, 59, 5399. [Google Scholar] [CrossRef] [PubMed]
- Lopes, P.C.; Clementel, E.; Crespo, P.; Henrotin, S.; Huizenga, J.; Janssens, G.; Parodi, K.; Prieels, D.; Roellinghoff, F.; Smeets, J. Time-resolved imaging of prompt-gamma rays for proton range verification using a knife-edge slit camera based on digital photon counters. Phys. Med. Biol. 2015, 60, 6063. [Google Scholar] [CrossRef] [Green Version]
- Austin, J. Silicon Levels in Human Tissues. In Biochemistry of Silicon and Related Problems; Bendz, G., Lindqvist, I., Runnström-Reio, V., Eds.; Springer: Boston, MA, USA, 1978. [Google Scholar]
- Karmani, L.; Labar, D.; Valembois, V.; Bouchat, V.; Nagaswaran, P.G.; Bol, A.; Gillart, J.; Levêque, P.; Bouzin, C.; Bonifazi, D. Antibody-functionalized nanoparticles for imaging cancer: Influence of conjugation to gold nanoparticles on the biodistribution of 89Zr-labeled cetuximab in mice. Contrast Media Mol. Imaging 2013, 8, 402–408. [Google Scholar] [CrossRef]
- Li, S.; Bouchy, S.; Penninckx, S.; Marega, R.; Fichera, O.; Gallez, B.; Feron, O.; Martinive, P.; Heuskin, A.C.; Michiels, C.; et al. Antibody-functionalized gold nanoparticles as tumor targeting radiosensitizers for proton therapy. Nanomedicine 2019, 14, 317–333. [Google Scholar] [CrossRef]
- Durymanov, M.O.; Rosenkranz, A.A.; Sobolev, A.S. Current Approaches for Improving Intratumoral Accumulation and Distribution of Nanomedicines. Theranostics 2015, 5, 1007–1020. [Google Scholar] [CrossRef] [Green Version]
- Tremi, I.; Spyratou, E.; Souli, M.; Efstathopoulos, E.P.; Makropoulou, M.; Georgakilas, A.G.; Sihver, L. Requirements for Designing an Effective Metallic Nanoparticle (NP)-Boosted Radiation Therapy (RT). Cancers 2021, 13, 3185. [Google Scholar] [CrossRef]
- Heuskin, A.C.; Gallez, B.; Feron, O.; Martinive, P.; Michiels, C.; Lucas, S. Metallic nanoparticles irradiated by low-energy protons for radiation therapy: Are there significant physical effects to enhance the dose delivery? Med. Phys. 2017, 44, 4299–4312. [Google Scholar] [CrossRef]
- Penninckx, S.; Heuskin, A.C.; Michiels, C.; Lucas, S. The role of thioredoxin reductase in gold nanoparticle radiosensitization effects. Nanomedicine 2018, 13, 2917–2937. [Google Scholar] [CrossRef] [PubMed]
- Penninckx, S.; Heuskin, A.C.; Michiels, C.; Lucas, S. Thioredoxin Reductase Activity Predicts Gold Nanoparticle Radiosensitization Effect. Nanomaterials 2019, 9, 295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martins, P.M.; Freitas, H.; Tessonnier, T.; Ackermann, B.; Brons, S.; Seco, J. Towards real-time PGS range monitoring in proton therapy of prostate cancer. Sci. Rep. 2021, 11, 15331. [Google Scholar] [CrossRef] [PubMed]
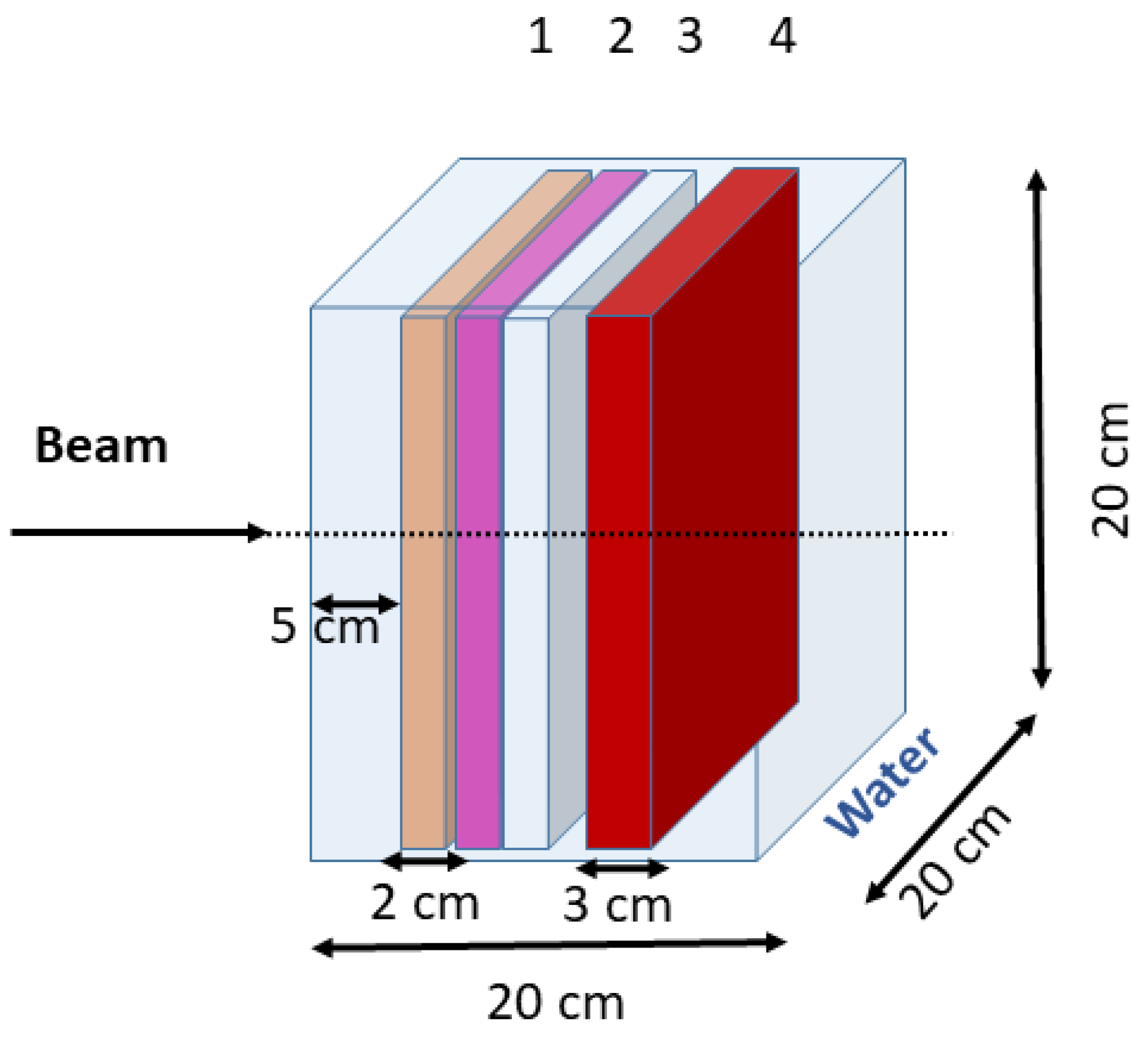
| Material | Density (g/cm3) |
|---|---|
| Adipose tissue | 0.967 |
| Water | 1.000 |
| Muscle | 1.061 |
| Dense bone | 1.575 |
| Element | Longitudinal Beam Range (mm ± 0.1 mm) | Longitudinal PG Range (mm ± 0.1 mm) | Delta (mm ± 0.1mm) |
|---|---|---|---|
| Ag | 145.5 | 143.4 | 2.1 |
| Al | 147.3 | 145.1 | 2.2 |
| Au | 143.7 | 141.8 | 1.9 |
| Bi | 145.7 | 143.5 | 2.2 |
| Cd | 146.0 | 143.8 | 2.2 |
| Gd | 146.2 | 144.0 | 2.2 |
| Hf | 145.0 | 142.9 | 2.1 |
| Si | 147.5 | 145.2 | 2.3 |
| Ti | 146.9 | 144.7 | 2.2 |
| Water | 148.3 | 145.9 | 2.4 |
| Element | Number of Primary PG per Incident Proton | Number of Secondary PG per Incident Proton | Ratio (Primary/Secondary PG) | Fold Change with Respect to Water |
|---|---|---|---|---|
| Ag | 6.72 × 10−4 | 1.73 × 10−4 | 3.88 | 0.86 |
| Al | 6.17 × 10−4 | 1.32 × 10−4 | 4.66 | 1.03 |
| Au | 6.33 × 10−4 | 1.76 × 10−4 | 3.60 | 0.80 |
| Bi | 6.66 × 10−4 | 1.43 × 10−4 | 4.66 | 1.03 |
| Cd | 6.03 × 10−4 | 2.35 × 10−4 | 2.56 | 0.57 |
| Gd | 6.07 × 10−4 | 4.05 × 10−4 | 1.50 | 0.33 |
| Hf | 6.20 × 10−4 | 1.80 × 10−4 | 3.45 | 0.76 |
| Si | 6.24 × 10−4 | 1.30 × 10−4 | 4.79 | 1.06 |
| Ti | 5.84 × 10−4 | 1.42 × 10−4 | 4.10 | 0.91 |
| Water | 5.75 × 10−4 | 1.28 × 10−4 | 4.51 | 1.00 |
| Peaks (MeV) | Prompt Gamma Reactions |
|---|---|
| Water | |
| 1.022 | 16O (p,x) 10B* |
| 1.635 | 16O (p,x) 14N* |
| 2.313 | 16O (p,x) 14N* |
| 2.742 | 16O (p,p’) 16O* |
| 3.684 | 16O (p,x) 13C* |
| 3.853 | 16O (p,x) 13C* |
| 4.438 | 16O (p,x) 12C* |
| 5.240 | 16O (p,x) 15O* |
| 5.269 | 16O (p,x) 15N* |
| 5.298 | 16O (p,x) 15N* |
| 6.129 | 16O (p,p’) 16O* |
| 6.175 | 16O (p,x) 15O* |
| 6.916 | 16O (p,p’) 16O* |
| 7.115 | 16O (p,p’) 16O* |
| Silicon | |
| 1.014 | 28Si (p,x) 27Al* |
| 1.779 | 28Si (p,p’) 28Si* |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penninckx, S.; Hespeels, F.; Smeets, J.; Colaux, J.L.; Lucas, S.; Heuskin, A.-C. Metallic Nanoparticles: A Useful Prompt Gamma Emitter for Range Monitoring in Proton Therapy? Radiation 2021, 1, 305-316. https://doi.org/10.3390/radiation1040025
Penninckx S, Hespeels F, Smeets J, Colaux JL, Lucas S, Heuskin A-C. Metallic Nanoparticles: A Useful Prompt Gamma Emitter for Range Monitoring in Proton Therapy? Radiation. 2021; 1(4):305-316. https://doi.org/10.3390/radiation1040025
Chicago/Turabian StylePenninckx, Sébastien, Félicien Hespeels, Julien Smeets, Julien L. Colaux, Stéphane Lucas, and Anne-Catherine Heuskin. 2021. "Metallic Nanoparticles: A Useful Prompt Gamma Emitter for Range Monitoring in Proton Therapy?" Radiation 1, no. 4: 305-316. https://doi.org/10.3390/radiation1040025
APA StylePenninckx, S., Hespeels, F., Smeets, J., Colaux, J. L., Lucas, S., & Heuskin, A.-C. (2021). Metallic Nanoparticles: A Useful Prompt Gamma Emitter for Range Monitoring in Proton Therapy? Radiation, 1(4), 305-316. https://doi.org/10.3390/radiation1040025