Underground Hydrogen Storage: Steady-State Measurement of Hydrogen–Brine Relative Permeability with Gas Slip Correction

Abstract

Large-scale underground hydrogen storage in saline aquifers requires an understanding of hydrogen–brine two-phase flow properties, particularly relative permeability, which influences reservoir injectivity and hydrogen recovery. However, such hydrogen–brine relative permeability data remain scarce, hindering the predictive modeling of hydrogen injection and withdrawal. In this study, steady-state hydrogen–brine co-injection coreflood experiments were conducted on an Austin Chalk core sample to measure the relative permeabilities. Klinkenberg slip corrections were applied to the gas flow measurements to determine the intrinsic (slip-free) hydrogen permeability. The core’s brine permeability was 13.2 mD, and the Klinkenberg-corrected hydrogen gas permeability was 13.8 mD (approximately a 4.5% difference). Both raw and slip-corrected hydrogen relative permeability curves were obtained, showing that the gas-phase conductivity increased as the water saturation decreased. Gas slippage caused higher apparent gas permeability in the raw data, and slip correction significantly reduced hydrogen relative permeability at lower hydrogen saturations. The core’s irreducible water saturation was 39%, at which point the hydrogen relative permeability reached 0.8 (dropping to 0.69 after slip correction), which is indicative of strongly water-wet behavior. These results demonstrate a measurable impact of gas slippage on hydrogen flow behavior and highlight the importance of accounting for slip effects when evaluating hydrogen mobility in brine-saturated formations.

1. Introduction

The transition to low-carbon energy systems has increased reliance on renewable energy sources, which are inherently intermittent [1,2,3,4]. This intermittency leads to mismatches between the energy supply and demand, necessitating large-scale energy storage solutions [5,6,7]. Hydrogen has emerged as a promising energy carrier for long-term energy storage [8,9]: surplus renewable electricity can be converted into hydrogen via electrolysis and stored for later use [10,11,12,13]. In other words, the hydrogen economy is crucial for integrating high levels of renewable power. Among various hydrogen storage options [14,15], including compressed tanks, liquid hydrogen, and chemically bonded forms, geological storage in underground formations stands out for its potential capacity and economic viability; salt caverns, depleted oil/gas fields, and saline aquifers are all being considered as long-term hydrogen storage options [16,17]. Saline aquifers [18,19], in particular, offer vast storage space and have been proven to be effective for CO₂ sequestration and natural gas storage [20]. Early pilot projects and feasibility studies have begun to demonstrate underground hydrogen storage (UHS) in these formations [21,22]. These geological options are attractive because they can safely accommodate the cushion gas volumes and pressures needed for cyclic hydrogen injection and withdrawal over seasonal or multi-year timeframes [23,24,25,26,27]. Beyond capacity and pressure limits, hydrogen permeation and multiphase transport in porous media strongly influence injectivity, containment, and deliverability. Related studies on depleted gas reservoirs and CO₂-based systems show how pore-scale transport and fluid–rock interactions govern performance and should be considered when assessing UHS in these formations [28,29].

Despite this interest, there remains a notable gap in understanding the fluid-flow characteristics of hydrogen in porous media. Much of the existing multiphase flow knowledge comes from decades of research on oil–water systems in hydrocarbon reservoirs and on CO₂–water systems for carbon storage [18,30]. These studies have established how the relative permeability of oil–water and CO₂–water systems governs the concurrent flow of fluids under reservoir conditions. Relative permeability functions are crucial inputs for reservoir simulations that predict injectivity, containment, and recoverability in UHS systems [20,31,32]. However, hydrogen–brine relative permeability data are extremely scarce. Hydrogen has unique properties like low density, high diffusivity, and non-wetting behavior in water-wet rocks that could lead to different flow behavior compared to natural gas or CO₂ [33]. For large-scale UHS, surface compression systems determine wellhead pressures, injection rates, and round-trip efficiency; recent advances in reciprocating, diaphragm, ionic liquid, liquid piston, and electrochemical compressors are directly relevant to UHS facility design and operation [34]. In particular, liquid piston compressor simulations provide chamber-scale thermodynamic insights and scaling guidance that can reduce thermal losses and compression energy across UHS injection and withdrawal cycles [35,36]. Early modeling studies of UHS, like that of [37,38,39,40], often had to assume relative permeability parameters based on analogs like natural gas, introducing uncertainty in performance predictions.

Because of these unique behaviors, researchers have questioned whether hydrogen flow can be safely approximated by methane analogs. Recent experimental studies provide differing perspectives. Ref. [41] conducted high-pressure experiments in both sandstone and carbonate cores and reported that the hydrogen relative permeability curves are distinct from those of methane and nitrogen and can depend on pressure and salinity. However, remarkably, they also found that in practice, nitrogen behaved so similarly that it “can be used as a proxy gas for hydrogen” in laboratory tests, simplifying experimental work. By contrast, ref. [31] directly compared hydrogen, methane, and nitrogen in the same Bentheimer sandstone core at reservoir conditions and observed nearly identical flow properties for all three gases. Their findings suggest that in some homogeneous rocks, hydrogen’s flow can closely mimic that of methane or nitrogen, whereas in other cases (especially in tight or heterogeneous formations), hydrogen’s low viscosity and slip can cause notable deviations. This divergence highlights the need for direct hydrogen-specific measurements: current UHS simulations still often rely on assumed or methane-based relative permeability models, introducing uncertainty into predictions.

Several review studies have called for better hydrogen–water data. For example, ref. [32] emphasizes that the cyclical injection/withdrawal operations in UHS require “accurate application of hydrogen–water dynamic properties in the simulation process,” including detailed relative permeability and hysteresis characteristics. They and others highlight that neglecting hydrogen’s unique multiphase behavior can significantly alter predicted recovery factors and water production during UHS cycles. In short, the literature makes it clear that hydrogen–brine relative permeability is not yet a solved problem, and that both the shape of the relative permeability curves and the end-point saturations (irreducible water and residual hydrogen) must be quantified to assess hydrogen injectivity, recovery, and cushion gas requirements.

These limited studies give more relevance to the need for further experimental data. In particular, understanding the end-point saturations (residual brine and trapped hydrogen) and the curvature of relative permeability functions for hydrogen–brine systems is vital for evaluating hydrogen recovery efficiency and cushion gas requirements in aquifer storage [5]. In light of these research gaps, the present study aims to experimentally determine the relative permeability of hydrogen and brine in a representative saline aquifer rock. We used a controlled core-flooding experiment with an outcrop core from the Austin Chalk formation [42,43,44] to simulate the drainage process of hydrogen displacing brine, which is analogous to hydrogen injection into an aquifer. The Austin Chalk, a carbonate rock, was selected due to its comparable porosity and irreducible water saturation, S_w,irr, to prolific saline formations, which has been considered for CO₂ storage [45,46,47] and potential UHS [48,49]. By measuring concurrent flow rates of hydrogen and brine at a steady state under various fractional flow conditions, we obtain relative permeability curves for both phases.

Recent hydrogen–brine studies have begun to provide baseline data, but the present work offers clear advancements beyond those. For example, ref. [41] conducted unsteady-state drainage experiments and explored pressure/salinity effects (finding that nitrogen can serve as a proxy gas for hydrogen), while [31] compared hydrogen, methane, and nitrogen in a high-permeability Bentheimer sandstone (observing nearly identical flow properties for all three gases under those conditions). In contrast, our study delivers the first steady-state hydrogen–brine relative permeability measurements on a representative carbonate core with an explicit gas-slip (Klinkenberg) correction. This approach provides a more direct and high-resolution characterization of hydrogen flow behavior without relying on proxy fluids. We ensure the measured gas permeability reflects true intrinsic values by accounting for hydrogen’s slip-flow effects which were not addressed in the prior experiments. In summary, the data presented here extend the current literature by quantifying hydrogen–brine flow in an Austin Chalk carbonate under steady co-injection, including slip-flow analysis, which is a novel improvement over the methods of [31,41].

This study provides a much-needed experimental dataset and insight into hydrogen–brine multiphase flow characteristics. The resulting relative permeability functions offer crucial inputs for UHS reservoir engineering, improving the fidelity of simulations for hydrogen injection and withdrawal cycles. Our findings highlight how hydrogen–brine systems differ from more extensively studied gas–brine systems (such as natural gas–brine or CO₂–brine), which has important implications for designing and operating UHS projects. By quantifying the hydrogen–brine relative permeabilities in a carbonate, the work helps refine predictive models, such as adjusting reservoir simulators that previously relied on methane analogs, and guides future research on multiphase flow in the context of clean energy storage. Ultimately, closing the data gap on hydrogen relative permeability moves us closer to safe and efficient large-scale underground hydrogen storage as part of the clean energy transition.

2. Materials and Methods

2.1. Materials and Equipment

A Teledyne ISCO 500D syringe pump (Teledyne ISCO Inc., Lincoln, NE, USA) was employed for methanol injection during core cleaning, as well as for brine injection in both absolute and relative permeability experiments. Hydrogen injection was performed using a Vindum VP-12K high-pressure metering pump (Vindum Engineering Inc., Sandpoint, ID, USA), which delivers a pulse-free flow with precise control of both rate and pressure. System pressure was maintained using an Equilibar U6L back-pressure regulator (Equilibar LLC, Fletcher, NC, USA). Pressure measurements were recorded upstream and downstream of the core holder, using digital pressure gauges to measure the differential pressure across the core sample. Effluent gas volumes were measured with a Vinci manual gasometer (Vinci Technologies, Nanterre, France), equipped with an airtight floating piston and integrated pressure and temperature readouts.

The core was mounted in a high-pressure core holder rated for 340 atm and 176.7 °C, featuring a rubber sleeve to isolate the pore system from the confining oil. Confining stress was applied via an Enerpac P80 hydraulic hand pump (Enerpac, Menomonee Falls, WI, USA). A Gast rotary vane vacuum pump was used to remove particulates from the core sample prior to testing. Core drying was performed in an Ofite 5-roller oven (OFI Testing Equipment Inc., Houston, TX, USA) with controlled heating and rotation, to ensure uniform drying. All wetted lines and fittings were selected for compatibility with both hydrogen and brine, and all instruments were calibrated prior to testing.

2.2. Austin Chalk Core Sample

A core plug sourced from the Austin Chalk formation was utilized for all experiments in this study.

Table 1. Core properties and dimensions.

Property	Value
Length, cm	15.24
Diameter, cm	2.54
Area, cm2	5.07
Dry Weight, g	154.74
Saturated Weight, g	172.03
Pore Volume, cm3	16.8
Bulk Volume, cm3	77.22
Porosity	0.22
Brine Viscosity, cp	1.1
Hydrogen Viscosity, cp	0.00876
Density of Brine, g/cm3	1.029

summarizes the measured intrinsic properties and dimensions of the core sample used and some properties of the brine and hydrogen. The Austin Chalk is a Late Cretaceous pelagic carbonate unit that extends across the onshore Gulf Coast of Texas, Louisiana, and Mississippi. Regionally, it was deposited on a broad, low-relief marine shelf to ramp, and is stratigraphically bounded by the Eagle Ford Formation below and the lower Taylor or Navarro units above. These relationships make it a key marker for subsurface correlation and sequestration studies [43,50]. Thickness varies significantly along the strike, as chalky beds alternate with marls. At the type locality, thicknesses of approximately 128 m have been reported, with similar variations observed across South and Central Texas, where chalk and marl packages thin and thicken, according to facies and structural controls [42,43].

Lithologically, the Austin Chalk is composed of fine-grained chalk and chalky limestone, dominated by coccolithic nannofossil debris within a micritic matrix. The unit is frequently interbedded with marly chalk and contains bentonitic ash layers. Calcite cementation and the abundance of coccolith plates impart the characteristic white to light-gray, friable fabric that is observed in the core sample. Reservoir quality is influenced by both matrix microporosity and natural fractures, with brittle chalk beds providing fracture networks, and marls functioning as more ductile barriers. This heterogeneity contributes to production variability along the play trend [42,43,51]. For this study, the Austin Chalk core plug was prepared as a cylindrical specimen, measuring 6 inches in length and 1 inch in diameter, as shown in Figure 1. The sample displays the typical chalky fabric with thin marly laminae, as described in the previous literature [43].

2.3. Core Sample and Synthetic Brine Preparation

The core sample was initially cleaned to remove residual fluids and coring contaminants, ensuring that subsequent rock-fluid measurements would reflect the intrinsic properties of the rock. Among common cleaning techniques (solvent, mechanical, ultrasonic [52,53,54]), solvent cleaning with methanol was selected due to its effectiveness in dissolving drilling mud residues, oil-based fluids, paraffins, and salts. Methanol is compatible with most lithologies [55,56] and its low boiling point (64.7 °C) expedites the drying process. The core was placed in the core holder, and methanol was injected at a rate of 0.536 cm³/min to simulate in situ displacement, with injection continuing until the effluent was visually clear. Complete cleaning was achieved after approximately six pore volumes of methanol injection.

To ensure accurate characterization and preserve native wettability, the core was dried in a roller oven that provided uniform heating and continuous rotation. The oven temperature was set to 79.4 °C, exceeding methanol’s boiling point, and the core was removed periodically for weighing. Drying was considered to be complete when the core’s weight stabilized, indicating full solvent removal and a return to its pre-cleaning dry weight. Prior to fluid injection, the core was vacuumed to eliminate trapped air and fine particulates. This was accomplished by placing the core in the core holder, connecting one effluent port to a vacuum pump, and sealing the pump inlet valves and outlet to the back-pressure regulator. The vacuum pump was operated until the upstream pressure stabilized at −0.67 atm for 30 min, establishing a complete vacuum throughout the core before saturation and flooding experiments. Brine was prepared by dissolving the solute described in

Table 2. Solute mass for synthetic brine preparation.

Solute	Mass, g
Sodium Chloride, NaCl	9.890
Magnesium Chloride, MgCl2	1.637
Calcium Chloride, CaCl2	0.447
Sodium Bicarbonate, NaHCO3	0.053
Potassium Chloride, KCl	0.257
Sodium Sulfate, Na2SO4	0.337

in 10 L of deionized water.

This synthetic brine has a total dissolved solids (TDS) content of approximately 1.25 g/L, which is representative of formation water salinity in the Austin Chalk region. Reported formation waters in and around the Austin Chalk typically have a TDS of about 0.8–1.4 g/L and are generally below 2.6 g/L [57,58,59], making our brine composition a realistic proxy.

Table 3. Ionic composition of synthesized brine.

	Ions	mg/L
Cations	Na+	400.46
	Mg2+	41.69
	Ca2+	16.09
	K+	13.43
Anions	Cl−	760.72
	SO42−	22.71
	HCO3−	3.86
Total		1258.97

shows the ionic composition of our synthesized brine.

2.4. Experimental Setup and Design

A core-flooding apparatus was employed to simultaneously inject hydrogen and brine at controlled rates, using the steady-state relative permeability method. The core was mounted in a high-pressure core holder, encased in a rubber sleeve, and subjected to an overburden pressure of 54.4 atm to prevent leakage or fluid bypass along the core edges. Two high-precision pumps were utilized—one dedicated to brine injection and the other to hydrogen gas injection—enabling independent control over the flow rates of each phase. A back-pressure regulator (BPR) was installed at the core outlet to maintain the target downstream fluid pressures, minimize gas expansion, and replicate subsurface reservoir conditions.

For relative permeability measurements, the BPR was utilized to provide back-pressure downstream, while hydrogen exited at a near-atmospheric pressure, via a dedicated gas measurement system. A pressure transducer was positioned at the inlet of the core holder to measure the upstream pressure, P₁, and another was positioned at the outlet of the core holder to measure the downstream pressure, P₂, as shown in Figure 2. Unless otherwise indicated, all pressures in the manuscript are reported as gauge pressures in atm. The volumetric flow rate of hydrogen was measured using a gas flow meter, while brine effluent volumes were collected in a graduated cylinder. A schematic and a photo of the experimental setup, including the injection pumps, pressure gauges, core holder, and measurement devices, are presented in Figure 3 and Figure 4, respectively.

2.5. Absolute Permeability Measurements

Before starting the relative permeability experiments, absolute permeabilities to both brine and hydrogen were measured under single-phase, steady-state flow conditions. For brine, three (3) constant flow rates (1.0, 0.5, and 0.25 cm³/min) were applied sequentially. At each flow rate, injection continued until the differential pressure across the core stabilized. Permeability values were then calculated using Darcy’s law.

For hydrogen, nine upstream pressure set points ranging from 2.4 to 12.9 atm were employed, while the downstream pressure was regulated between approximately 0.3 and 7.8 atm to establish distinct mean flowing pressures within the core. At each pressure set point, the experiment proceeded until a steady-state flow was achieved. The steady state was defined as being achieved when: (i) the differential pressure varied by less than 1% of its mean over two consecutive 30 min windows; and (ii) each phase flow rate differed by less than 3% between the averages of those windows. The hydrogen discharge rate was then measured at near-atmospheric conditions using a gasometer and was subsequently converted to the equivalent volumetric rate at the mean core pressure, using the ideal gas law (Boyle’s law), with a correction for gas compressibility. The apparent gas permeability for each mean pressure condition was calculated using Darcy’s law, generating the dataset required for subsequent Klinkenberg correction.

2.6. Relative Permeability Experiment Design

The core was initially saturated with brine to achieve a baseline of 100% brine saturation. Following saturation, a steady-state co-injection procedure was implemented to gradually displace the brine with hydrogen. We began with a hydrogen injection at 0.2 cm³/min and brine at 0.8 cm³/min. The hydrogen injection rate was incrementally increased in 0.2 cm³/min steps, with a proportional decrease in brine flow, until reaching 0.8 cm³/min hydrogen and 0.2 cm³/min brine (an 80% hydrogen fractional flow).

To further approach the irreducible water saturation, S_w,irr, the brine co-injection rate was reduced to 0.05 cm³/min for the remainder of this step in the experimental procedure. The hydrogen flow rate was progressively increased through a series of higher set points (2, 4, 6, 12, 16, 18, and 20 cm³/min). Each successive increase in hydrogen flow facilitated additional brine production, ultimately lowering the water saturation to approximately 45%. At each flow rate, after reaching steady-state conditions, this was indicated by stable differential pressure and effluent production. Upon achieving equilibrium at each stage, the core was removed from the holder and weighed to determine the remaining brine content by the mass difference.

In the final stage, hydrogen was injected at the maximum flow rate allowed by the pump for four (4) hours while maintaining a constant upstream pressure of 11 atm and a downstream pressure of 1.1 atm. The core was periodically weighed during this extended injection phase, until no further change in mass was recorded, confirming the attainment of S_w,irr. Throughout this phase, hydrogen flow rates were precisely measured using the gasometer.

3. Results and Discussion

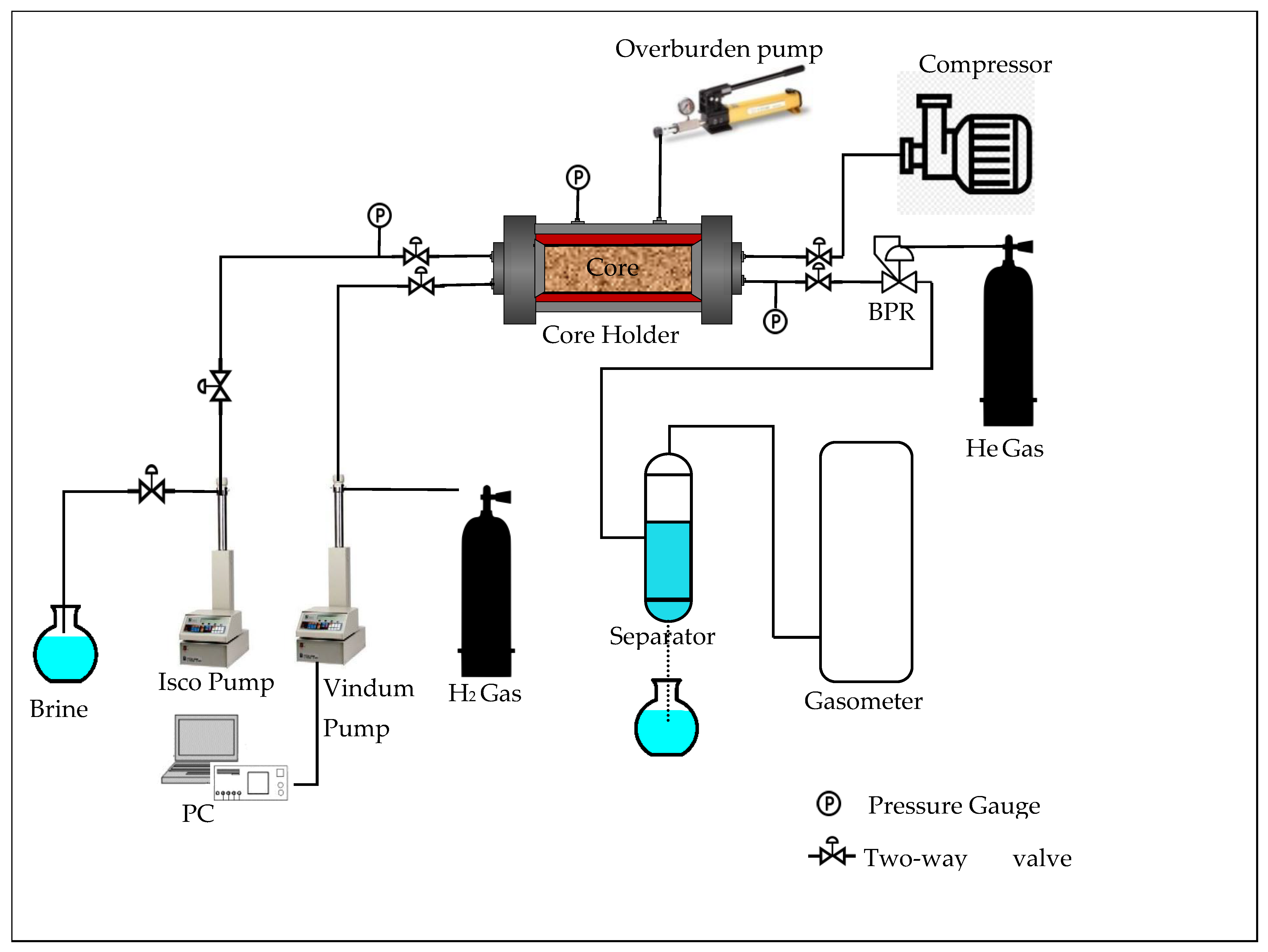
3.1. Brine and Hydrogen Absolute Permeability

The average measured absolute permeability to brine was 13.23 millidarcy (mD), based on steady-state tests conducted at three flow rates (0.25, 0.5, and 1.0 cm³/min). Individual permeability values were highly consistent, ranging from approximately 13.1 to 13.3 mD, and exhibited no significant dependence on the flow rate, as summarized in

Table 4. Brine absolute permeability results.

Brine Flow Rate (ql), cm3/min	Upstream Pressure (P1) atm	Downstream Pressure (P2) atm	Reciprocal of Mean Pressure (1/Pm), atm	Brine Permeability (kw), md
1	4.967	0.823	0.345	13.31
0.5	2.490	0.381	0.696	13.07
0.25	1.279	0.245	1.312	13.33

. This consistency indicates that Darcy’s law was obeyed throughout the experiments and that rate-dependent effects such as turbulence or fines migration were negligible in this regime.

Equation (1) calculates the brine permeability in mD derived from the Darcy equation

$$k_l={\displaystyle \frac{{1000\mu }_l{q}_{l}L}{∆pA}}$$

(1)

where

k_w is the brine permeability in mD.

μ_l is the brine viscosity in cP.

q_l is the brine flow rate at steady state conditions in cc/s.

L is the core length in cm.

P₁ is the upstream pressure in atm.

P₂ is the downstream pressure in atm.

∆P = P₁ − P_2.

A is the cross-sectional area of the porous medium in cm².

The measured brine permeability, k_w (13.23 mD), closely matches the Klinkenberg-corrected gas permeability, k_g* (13.8 mD), with a difference of only about 4.5%. Figure 5 illustrates a strong agreement between the brine-derived permeability and the gas-derived permeability extrapolated to infinite pressure. The minor difference in value (approximately 0.6 mD) falls within the range of experimental uncertainty. These results confirm that, once gas slippage is accounted for, the absolute permeability to gas converges with that of brine, as expected for an ideal single-phase system [60,61,62]. The close correspondence between the brine and slip-corrected gas permeability values demonstrates the validity of the Klinkenberg correction and supports the conclusion that the core’s permeability is an intrinsic property, independent of the fluid phase when slip effects are properly addressed.

Measured hydrogen permeability, k_w, values ranged from 15 mD to 23 mD. We observed a strong trend of decreasing absolute permeability with increasing mean flowing pressure, with the highest permeability recorded at the lowest mean pressure (P_m), as summarized in

Table 5. Hydrogen absolute permeability results.

P1, atm	P2, atm	Pm, atm	1/Pm, atm−1	kg, md
2.291	0.413	1.352	0.740	23.08
3.611	0.510	2.061	0.485	20.82
4.675	0.578	2.627	0.381	18.91
5.798	2.599	4.198	0.238	17.23
7.198	3.568	5.383	0.186	15.87
8.879	4.807	6.843	0.146	15.49
10.571	6.226	8.399	0.119	15.23
12.275	7.334	9.805	0.102	15.11
12.982	7.671	10.326	0.097	15.36

. This pressure dependence is indicative of the Klinkenberg effect: the plot of gas permeability against the reciprocal of mean pressure (1/P_m) shows an almost perfect linear correlation. This behavior reflects the influence of gas slippage along pore walls, which leads to inflated permeability measurements at lower pressures [63,64].

We used Equation (3), derived from Equation (2), to calculate the gas-measured permeability at the mean gas-flowing pressure

$$k_g={\displaystyle \frac{{1000\mu }_{l}L}{(p_1-p_2)A}}\times {\displaystyle \frac{2p_a{q}_1}{(p_1+p_2)}}$$

(2)

$$k_g={\displaystyle \frac{{2000p_a\mu }_g{q}_{g}L}{(p_1^2-p_2^2)A}}$$

(3)

where

q₁ is the brine flow rate at atmospheric pressure in cm³/s.

q_g is the hydrogen flow rate at mean flowing pressure in cm³/s.

k_g is the hydrogen permeability in mD.

μ_g is the hydrogen viscosity in cP.

P₁ is the upstream pressure in atm.

P₂ is the downstream pressure in atm.

P_a is the pressure at which gas flow rate is taken in atm.

Plotting the measured gas permeability, k_g, against 1/P_m revealed a strong linear relationship with an R² of 0.985, as shown in Figure 5. The standard error of the slope is 0.600 mD·atm (13.071 ± 0.600 mD·atm) and the standard error of the intercept is 0.208 mD (13.810 ± 0.208 mD). These standard errors indicate a precise fit with uncertainty that is modest relative to the parameter magnitudes and supports the accuracy and adequacy of the linear Klinkenberg model over our pressure range.

This almost perfect linear fit is consistent with Klinkenberg’s [65] model of gas flow in porous media. The extrapolated interception of the linear fit, 13.8 mD (Figure 5), represents the k_g*, which corresponds to the intrinsic permeability of the core in the absence of gas slippage. Practically, this value reflects the expected liquid-phase permeability at infinite pressure, where slip effects are negligible. The high degree of linearity and the strong R² confirm that gas slippage is the primary factor responsible for the observed pressure dependence of gas permeability in these experiments.

We used the linear form of Klingenberg’s [66] equation, shown in Equation (4), to correct gas slippage in lab-measured gas permeability.

$$k_g=k_w\left(1+{\displaystyle \frac{b}{p_m}}\right)=(1+{\displaystyle \frac{4c\lambda }{r}})$$

(4)

$$P_m={\displaystyle \frac{P_1+P_2}{2}}$$

(5)

where

k_g is the gas permeability.

b is the slip factor.

P_m = mean pressure, Equation (5).

P₁ is the upstream pressure in atm.

P₂ is the downstream pressure in atm.

λ is the mean flow path.

r is the pore-throat radius.

c is a proportional factor.

The relation between k_g and 1/P_m was highly linear, having an R² of 0.985 with random, homoscedastic residuals. A first-order slip correction is theoretically appropriate in the slip-flow regime where the Knudsen number, K_n (λ/r) is small but nonzero. Using a representative hydrogen mean free path, λ, of 100 nm at 1 atm [67], which scales approximately as 1/P_m, and pore-throat radii, r, of 0.5 to 2 μm for chalk [67,68], K_n is in the order of 0.01 to 0.2 across our conditions. This range lies primarily in the slip flow, where the linear term dominates. Consistent with this expectation, augmenting the model with a quadratic, as shown in Equation (6), term c did not improve the goodness of fit or information criteria, and the estimated c was not significant. By contrast, in much lower-permeability rocks or at very low pressures, deviations from linearity can occur. Ref. [60], among others [69,70], developed an improved Klinkenberg model, accounting for non-linear gas slippage in tight cores, showing that the k_g vs. 1/P_m relationship can become curved when K_n is higher. Their analysis indicates that in ultra-tight media, a single b-factor will not suffice, and higher-order terms or pressure-dependent slip coefficients are needed.

$$k_g=k_l\left(1+{\displaystyle \frac{b}{P_m}}+{\displaystyle \frac{c}{P_m^2}}\right)$$

(6)

Non-linear slip effects can be of concern at lower pressures or in much finer throats that drive K_n ≳ 0.1 into the transition regime. Under such conditions, higher-order slip models or pore-scale simulations may be needed. Within the pressure and rock tested here, the linear Klinkenberg correction provides an adequate estimation of gas-slippage.

From the k_g vs. 1/P_m plot, and using Equation (4), we estimated the Klinkenberg correction factor, b at 0.944 atm, shown in Equation (7) as

$$Klinkenberg correction factor, b={\displaystyle \frac{Slope}{Intercept}}={\displaystyle \frac{13.062 (mD.atm)}{13.837 \left(md\right)}}=0.944 \mathrm{a}\mathrm{t}\mathrm{m}$$

(7)

3.2. Hydrogen–Brine Relative Permeability

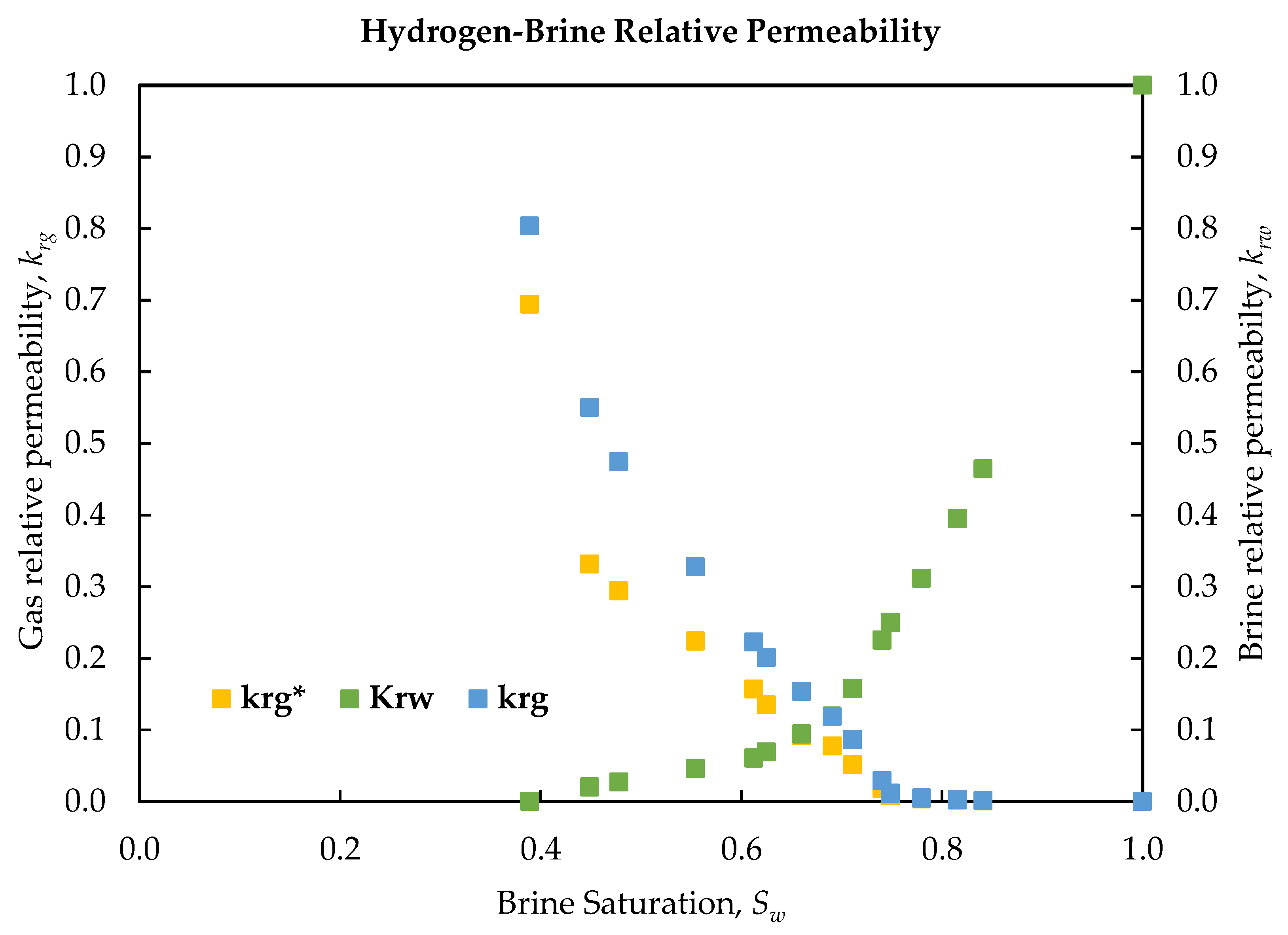
Steady-state relative permeability measurements for the hydrogen–brine system, presented in

Table 6. Data from the hydrogen–brine relative permeability experiment.

ql, cm3/min	qg, cm3/min	P1, atm	P2, atm	Pm, atm	Core Weight, g
0.80	0.20	7.825	0.646	4.236	169.28
0.60	0.40	7.192	0.864	4.028	168.84
0.40	0.60	5.906	0.558	3.232	168.22
0.20	0.80	3.987	0.653	2.320	167.69
0.10	1.00	2.559	0.708	1.633	167.54
0.05	2.00	2.041	0.721	1.381	167.03
0.05	4.00	2.667	0.919	1.793	166.68
0.05	6.00	2.518	0.306	1.412	166.15
0.05	12.00	3.430	0.422	1.926	165.55
0.05	16.00	3.967	0.524	2.246	165.33
0.03	18.00	3.402	0.687	2.045	164.32
0.02	20.00	2.695	0.388	1.541	163.00
0.01	20.00	2.456	0.408	1.432	162.50
0.00	35.00	10.955	1.055	6.005	161.46

, confirm strongly water-wet behavior. Noticeable hydrogen flow began at a S_w of 0.84, where the k_rg was 0.001 and the k_rw had declined markedly to 0.464. S_w,irr was reached at 0.39, at which point the brine became essentially immobile and the gas phase attained its maximum relative permeability of 0.8 (prior to slip correction). These results demonstrate a delayed hydrogen breakthrough, a sharp increase in k_rg with increasing gas saturation, and a high S_w,irr—all characteristic of a strongly water-wet system.

Figure 6 and

Table 7. Relative permeability results at different brine saturations, corrected for gas slippage.

Sw	Pm, atm	krw	krg	krg*	(krg − krg*)
1.00	-	1.000	0.000	0.000	-
0.84	4.236	0.464	0.001	0.001	0.000
0.82	4.028	0.395	0.003	0.002	0.001
0.78	3.232	0.312	0.005	0.004	0.001
0.75	2.320	0.250	0.011	0.008	0.003
0.74	1.633	0.225	0.029	0.018	0.011
0.71	1.381	0.158	0.087	0.051	0.036
0.69	1.793	0.119	0.118	0.077	0.041
0.66	1.412	0.094	0.154	0.092	0.062
0.63	1.926	0.069	0.201	0.135	0.066
0.61	2.246	0.061	0.223	0.157	0.066
0.55	2.045	0.046	0.328	0.224	0.104
0.48	1.541	0.027	0.474	0.294	0.180
0.45	1.432	0.020	0.550	0.332	0.218
0.39	6.005	0.000	0.804	0.694	0.110

present the experimentally determined relative permeabilities for brine and hydrogen, along with the corresponding slip-corrected values. The Klinkenberg slip corrected relative permeability, k_rg*, values were obtained by applying the previously established slip correction factor to the gas-phase permeability at each saturation, thereby estimating the k_rg, as it would be measured at infinite pressure (i.e., in the absence of slippage). At all saturation points, k_rg* is consistently lower than the k_rg, highlighting the elimination of slip-induced overestimation. Notably, the difference between k_rg and k_rg* becomes more pronounced at higher gas saturations (lower S_w), where gas flow rates and Reynolds numbers are elevated and mean pressures are reduced. This systematic discrepancy emphasizes the necessity of accounting for gas slippage during two-phase flow experiments; neglecting this effect would lead to an overestimation of apparent gas mobility under reservoir (liquid-equivalent) conditions. Following correction, the hydrogen relative permeability curve is shifted downward, yielding a more accurate representation of the gas phase’s conductive capacity in the absence of slip effects. Despite this adjustment, the overall shape of the relative permeability curves remains unchanged: the gas curve initiates near zero (0) at high S_w and increases sharply as S_w decreases, while the water curve approaches S_w,irr.

The high endpoint, k_rg, in our H₂-brine data (0.8 at S_w,irr of 0.39, dropping to 0.69 with slip correction) is slightly above the values reported for other gas–water systems. For instance, carbonate core tests in [71] found CO₂ or methane–water’s relative permeabilities maxing out around 0.5–0.6 under similar saturations. Our hydrogen results reach a somewhat higher gas conductivity, which can be attributed to hydrogen’s lower interfacial tension and viscosity. Overall, the shape of the hydrogen relative permeability curve mirrors those documented for methane–brine or air–brine systems in strongly water-wet rocks [72]. This indicates that hydrogen, like other non-wetting gases, must overcome entry pressures and then flow primarily through larger pore channels. One distinction is that hydrogen’s lower interfacial tension against water and lower viscosity can lead to slightly more efficient gas mobility. In fact, comparative analyses suggest that hydrogen may exhibit marginally higher relative permeability than methane at equivalent saturations [41]. This is consistent with our data showing a high k_rg endpoint. However, these differences are subtle and the shape of our relative permeability curve and CH₄-brine relative permeability curves are broadly similar: controlled primarily by rock wettability and pore structure, rather than gas type [73]. Appendix A provides detailed calculations illustrating the estimation of porosity, pore volume, P_m, S_w, k_w, k_g, k_g*, k_rw, k_rg, and k_rg* for a representative flow condition.

3.3. Controls on Flow: Wettability, Solubility, Diffusivity, and Pore Structure

The observed relative permeability trends can be interpreted in light of the core’s pore structure, wettability, and the hydrogen’s fluid properties. The Austin Chalk contains micron to sub-micron scale pores and throats [67,68], which promote extensive capillary trapping of brine. This fine-scale porosity explains the high S_w,irr of 0.39. Water remains in the small pores and grain contacts, even after extensive hydrogen injection. As a result, hydrogen flow is largely confined to larger pore pathways at lower S_w, which limits gas mobility until those larger channels connect. The core’s strongly water-wet nature further delays the hydrogen percolation. Hydrogen, being non-wetting in a water-wet matrix [33], must overcome the entry capillary pressures to move through smaller pores. Once hydrogen pathways form, k_rg rises sharply: a typical behavior of a strongly water-wet system where brine clings to pore walls and hydrogen flows through the central pore regions. The pronounced increase in k_rg to 0.8 as at S_w,irr reflects this behavior, as the water evacuation from the pore centers greatly boosts gas conductivity.

Hydrogen’s molecular characteristics, like low viscosity, small molecular size, and high diffusivity, also influence flow. While bulk-phase diffusion of hydrogen into the brine is minimal due to low solubility under steady-state conditions, the small molecule size manifests in the form of gas slippage. In our tests, at lower pressures, the mean free path of H₂ (approximately 100 nm at 1 atm) became significant relative to the pore-throat sizes, resulting in the Klinkenberg effect. This slip flow enhanced the apparent gas permeability without altering the fundamental shape of the relative permeability curves. In essence, hydrogen’s high diffusivity and molecular free path allowed it to navigate pore walls more freely (increasing flow rates in micro-pores), but it did not change the fact that a water-wet, micro-porous structure governs the saturation at which gas can move through the rock. Hydrogen’s low solubility in brine means essentially all the injected H₂ remains in the gas phase under our conditions. These factors combined (a micro-porous, strongly water-wet matrix and hydrogen’s slip-flow tendency) explain the delayed gas breakthrough and steep k_rg progression observed in our experiments.

Molecular diffusion of hydrogen through water can allow it to penetrate fine-scale stagnant pores or water films, producing a small “tail” of hydrogen presence, even at high water saturations, thus smoothing the k_rw decline. Hydrogen’s tiny molecules also give rise to slip flow along pore walls, effectively reducing viscous drag and enhancing its mobility compared to higher molecular gases [74]. Pore-scale modeling by [38] indicates that hydrogen can diffuse into water-filled micro-porosities more readily than larger gas molecules, although this effect is subtle during active flow. We did not explicitly measure diffusion in our experiments, but qualitatively, if any hydrogen dissolved into the brine or diffused ahead of the displacement front, it could contribute to a smoother decline in k_rw and a small hydrogen presence, even above S_w,irr. Recent pore-scale analyses confirm these effects: when the K_n exceeds 1 × 10⁻³, hydrogen exhibits both bulk slip flow and surface (adsorption) diffusion, so that the classical no-slip Darcy law breaks down. The remaining distinctive features of hydrogen at low S_w, which includes the rapid rise of k_rg and a near-linear k_rg–S_w trend, agree qualitatively with recent models and experiments. For example, ref. [75] shows that hydrogen’s non-wetting relative permeability curve is nearly linear at a high gas saturation. Similarly, ref. [76] reports strong hysteresis in hydrogen–water relative permeability, with significant hydrogen flow persisting into the imbibition regime. The pore-scale phenomena of wall slip and molecular diffusion help explain why hydrogen achieves such high relative permeability in our experiments and why slight departures from methane-analog behavior occur in low-perm pores. The slight deviations observed in the low-saturation end of our hydrogen relative permeability curve can be partly attributed to pore-scale effects like interfacial slip and molecular diffusion. Our slip correction ensured that this did not distort the relative permeability magnitude, but at very low S_w, hydrogen was flowing through the largest pores with high K_n.

3.4. Field-Scale Implications and Reservoir Condition Considerations

The relative permeability curves derived in this work can directly provide input data for UHS models, but certain scaling considerations must be addressed. Our steady-state drainage-relative permeability functions provide input parameters for reservoir simulators, improving predictions of hydrogen injectivity and recovery. For instance, using the measured endpoint k_rg will yield more realistic injectivity estimates than assuming an arbitrary value. Likewise, the high S_w,irr we found implies that a considerable fraction of pore volume will remain occupied by brine, depending on the formation rock, which, in field models, translates to the need for cushion gas and lower working hydrogen capacity. It is important to note that we have characterized only the drainage cycle; during withdrawal (imbibition), relative permeability curves will differ due to hysteresis [32]. Neglecting hysteresis in UHS cycles can lead to optimistic predictions. Bo et al. [39] report that ignoring relative permeability hysteresis can overestimate the annual working gas capacity by up to 34% and the recovered hydrogen volume by 85%.

When utilizing our curves in simulations, one should implement appropriate hysteresis models or imbibition curves to account for the lower gas relative permeability and residual trapping expected in hydrogen production. While our experiments were performed on a homogeneous core in ambient laboratory conditions, reservoirs may exhibit greater heterogeneity, different wettability distributions, and elevated pressures/temperatures. In situ, higher overburden stress could reduce absolute permeability, and any fine-scale heterogeneity or partial wettability changes at the reservoir temperature might lower the effective relative permeability. The slip-corrected hydrogen–brine curves presented here are effectively intrinsic (approximating infinite pressure conditions), which makes them transferable to higher reservoir pressures without further correction for gas slippage. However, reservoir-scale modeling may still require integrating capillary pressure functions and accounting for multi-scale rock features. Nonetheless, the fundamental trends captured, i.e., a strongly water-wet system with a high S_w,irr and rapid rise in k_rg, are expected to remain in similar geologic formations. These experimental flow functions thus serve as a valuable calibration dataset. Based on our data, we anticipate that reservoir conditions would yield slightly lower gas slippage and slightly higher hydrogen diffusivity, but similar relative permeability shapes. History-matching our relative permeability curves in numerical simulations will constrain models of hydrogen plume migration and trapping. In particular, incorporating the measures will improve estimates of injection pressure requirements, working gas fraction, and cushion gas needs. By using laboratory-derived hydrogen–brine relative permeabilities instead of analogs from methane or CO₂, UHS project simulations can achieve greater fidelity in forecasting storage performance under cyclic operations.

Our findings carry important implications for hydrogen containment in UHS. The good news is that the intrinsic permeability of the reservoir rock and the high k_rg at S_w,irr indicate that hydrogen can flow readily through the intended storage formation, supporting efficient injectivity and withdrawal. However, the flip side is that hydrogen’s mobility means that if any unintended pathway exists (fractures, caprock micro-perm, or wellbore leaks), hydrogen could escape more easily than a less mobile fluid. In particular, hydrogen’s high diffusivity and low viscosity raise the risk of leakage through tiny pores or defects that might retain other gases. For instance, our slip-corrected data show that hydrogen moves almost as freely as brine in the rock. Thus, any permeable conduit could transmit hydrogen nearly unhindered, underscoring the need for extremely low-permeability seals. The measured parameters from our work can be used to model worst-case leakage scenarios. The high hydrogen relative permeability in storage conditions also implies that once a crack or pathway opens, hydrogen will preferentially flow through it (being non-wetting and mobile). Therefore, safeguards like multiple sealing layers, active monitoring, and rapid pressure relief are warranted to mitigate leakage risk.

Hydrogen’s high diffusivity poses a long-term leakage concern in UHS. The small hydrogen molecules can gradually migrate through ostensibly tight caprocks and engineered seals over storage timescales [77]. This diffusion-driven loss mechanism may undermine storage integrity, especially in sites with thinner or more porous caprock layers. Hydrogen diffuses very slowly through water-saturated caprocks, with effective diffusivities typically being around 1 × 10⁻¹⁰–1 × 10⁻⁸ m²/s [78], so long-term migration is controlled by molecular diffusion, rather than flow [79]. Despite being slow, diffusion can still move gas appreciable distances over decades. A simple semi-analytical model by [80] shows that diffusivity of approximately 1 × 10⁻⁷ m²/s, which is at the upper end of measured values, would drive on the order of 2.5 m of H₂ penetration per year. Additionally, reservoir simulation by [81] found diffusion-driven plume expansion of H₂ to be a few percent under the ideal conditions and suggested that diffusion flow has a minimal impact on plume migration. Hydrogen can likewise permeate wellbore seals over time. Numerical simulations indicate that hydrogen could fully penetrate a standard 35 cm-thick cement sheath in about a week under dry conditions, due to its small molecular size and high diffusivity [82]. Caprocks strongly suppress flux because low porosity and high tortuosity reduce the effective diffusivity to only a few percent of the bulk value [81], and full brine saturation further slows hydrogen compared with gas-phase diffusion [79]. Cushion gases such as methane or CO₂ can further reduce hydrogen’s effective diffusivity by diluting its partial pressure at the seal and partially blocking pore pathways, so a dense, brine-saturated, low-permeability caprock with cushion gas in the reservoir behaves closely to a diffusion barrier for H₂ over practical storage timescales [83]. These findings show that while caprocks and well seals exhibit ultra-low permeability to convective flow, their ability to halt molecular diffusion of hydrogen is limited. Therefore, diffusion-induced losses must be considered in long-term containment risk assessments.

The plug contained minor laminations (chalk and marl), but it behaved hydraulically homogeneously. Pressure drops were smooth with consistent saturation changes, with no signatures of multi-region flow, such as dual plateaus or abrupt jumps in fractional flow. The thin laminations were parallel to the flow, so the co-injected fluids sampled an average of all layers and the measured relative permeability represents an effective composite. If strong heterogeneity were present, for example, a high-permeability streak or a fracture, we would expect an earlier gas breakthrough or a lower apparent S_w,irr. This was not observed; the breakthrough was gradual and consistent with a uniform water-wet system. The close agreement between k_w and the k_rg* (difference about 4.5%) further indicates an evenly distributed flow. We conclude that core-scale heterogeneity had minimal impact on our results. Field-scale heterogeneity can still influence local behavior, so our curve should be viewed as representative of a homogeneous matrix.

We quantified the force balance in the displacement experiments using the dimensionless capillary number, defined in Equation (8) as

$$N_c={\displaystyle \frac{{\mu }_g{v}_g}{\sigma }}$$

(8)

where

N_c is capillary number.

μ is gas viscosity in Pa∙s.

v_g is superficial (Darcy) velocity in m/s.

σ is interfacial tension in N/m.

For hydrogen in our core, μ is approximately 9 × 10⁻⁶ Pa∙s (0.009 cP) and σ of 0.072 N/m for the H₂—brine system. At the highest gas injection rate of 20 cm³/min, v_g is 6.6 × 10⁻⁴ m/s, which yields N_c on the order of 10 × 10⁻⁷ to 10 × 10⁻⁸. At the lowest gas rate of 0.2 cm³/min, (v_g is 6.6 × 10⁻⁴ m/s), N_c was approximately 10 × 10⁻⁹. These values are several orders of magnitude below the commonly cited threshold N_c value of 2 × 10⁻⁵ required to mobilize a trapped wetting phase. Thus, viscous forces in our tests were too small to overcome the capillary retention of brine. This is consistent with the S_w,irr and indicates a capillary-force dominated regime. The flow rates (0.2 to 20 cm³/min H₂ co-injected with 0.8 to 0.05 cm³/min brine) correspond to interstitial velocities on the order of 10 × 10⁻⁶ to 10 × 10⁻⁴ m/s, which further supports that capillary forces dominated at these flow rates. As a result, hydrogen did not significantly displace brine from smaller pores, because viscous forces were insufficient to overcome capillary trapping, in line with the observed strongly water-wet behavior.

To assess experimental reliability, we quantified uncertainties and checked the repeatability of the measurements. The single-phase permeability tests showed excellent consistency. k_w varied from 13.07 to 13.33 mD across three flow rates (within 2% range), indicating negligible rate-dependent effects and high repeatability. Similarly, the k_r vs. 1/P_m plot was almost perfectly linear with an R² of 0.985, demonstrating minimal scatter in the measured data. Based on equipment precision (pressure transducers ±0.25% F.S., flow measurements ±1%, and balance accuracy ±0.01 g for core mass), we estimate an uncertainty on the order of ±5% in the reported permeability values. Water saturation determinations by core weighing are accurate within approximately ±0.5% of the pore volume, given the small mass increments recorded. The stringent steady-state criteria (change in pressure stability < 1% and flow rate variation < 3% over 30 min intervals) lend confidence that each data point is representative. Overall, the precision and repeatability of these results support their validity for use in further analysis.

4. Conclusions

This study’s steady-state hydrogen–brine core-flood experiments revealed classical water-wet relative permeability behavior, marked by a high S_w,irr of 39%and a sharp increase in hydrogen relative permeability at higher gas saturations. The sharp rise in hydrogen relative permeability with decreasing brine saturation affirms the presence of a strongly water-wet pore structure. This steep rise in gas’ relative permeability at lower S_w confirms a strongly water-wet pore structure, with k_rg* reaching 0.69 at S_w,irr.

A key result was the significant impact of gas slippage on the measured hydrogen permeability. Absolute hydrogen permeabilities at low pressures were notably higher than intrinsic values, highlighting the importance of the Klinkenberg correction. Once slip effects were accounted for, the corrected gas permeability closely matched the liquid-phase (brine) permeability, confirming the need to correct for slippage in order to obtain realistic hydrogen flow estimates. Failing to account for slip would thus cause reservoir simulations to overestimate hydrogen mobility (and injectivity); using slip-corrected relative permeability curves is essential for reliable field-scale predictions.

The slip-corrected relative permeability curves generated in this study are directly applicable to UHS modeling. Relative permeability and capillary pressure are critical inputs for reservoir simulation, with the endpoint hydrogen relative permeability controlling gas injectivity and the residual hydrogen saturation governing recoverable volumes and cushion gas requirements. The empirical flow functions produced here can enhance predictions of UHS injectivity and recovery efficiency at the reservoir scale.

Some limitations should be recognized. Capillary pressure was not measured, so capillary trapping effects were not directly characterized. Experiments were limited to the outcrop core at room temperature and a single drainage cycle, without incorporating reservoir stress, heterogeneity, imbibition, or hysteresis. Future studies will address these gaps by including imbibition and hysteresis tests, direct capillary pressure measurements, and experiments on heterogeneous or field-scale cores. Recent studies have shown that hydrogen can slowly migrate through water-saturated caprock by molecular diffusion. For instance, a semi-analytical model by [67] predicts that cumulative H₂ loss through a shale caprock scales with the square root of time, and is proportional to factors like caprock diffusivity, porosity, and exposed area (simulation future work). To fully address containment, we plan dedicated diffusion experiments in follow-up work. For example, we intend to measure hydrogen’s effective diffusivity through actual caprock samples (shale or evaporite) by performing time-lapse pressure-decay or sorption tests, similar to recent experiments by [82]. Incorporating these data into multiphase flow models will improve the accuracy of hydrogen migration and recovery forecasts for practical UHS applications.