Numerical Investigation of CO₂ Injection Effects on Shale Caprock Integrity: A Case Study of Opalinus Clay

Abstract

Carbon dioxide (CO₂) geosequestration is a critical technology for reducing greenhouse gas emissions, with shale caprocks, such as Opalinus Clay (OPA), serving as essential seals to prevent CO₂ leakage. This study employs computational fluid dynamics and finite element analysis to investigate the hydromechanical behavior of OPA during CO₂ injection, integrating qualitative and quantitative insights. Validated numerical models indicate that capillary forces are the most critical factor in determining the material’s reaction, with an entry capillary pressure of 2–6 MPa serving as a significant threshold for CO₂ breakthrough. The numbers show that increasing the stress loading from 5 to 30 MPa lowers permeability by 0.3–0.45% for every 5 MPa increase. Porosity, on the other hand, drops by 9.2–9.4% under the same conditions. The OPA is compacted, and axial displacements confirm numerical models with an error margin of less than 10%. Saturation analysis demonstrates that CO₂ penetration becomes stronger at higher injection pressures (8–12 MPa), although capillary barriers slow migration until critical pressures are reached. These results demonstrate how OPA’s geomechanical stability and fluid dynamics interact, indicating that it may be utilized as a caprock for CO₂ storage. The study provides valuable insights for enhancing injection techniques and assessing the safety of long-term storage.

1. Introduction

As the global community continues to combat the accelerating threat of climate change, reducing anthropogenic carbon dioxide (CO₂) emissions has become an urgent scientific and political imperative. According to the Intergovernmental Panel on Climate Change (IPCC), limiting global warming to below 2 °C requires dramatic reductions in CO₂ emissions and the deployment of technologies capable of removing CO₂ from the atmosphere [1].

One of the most promising approaches in this context is carbon capture and storage (CCS), a suite of technologies that involve capturing CO₂ from significant point sources, transporting it to a storage site, and injecting it into deep geological formations for long-term isolation from the atmosphere [2,3]. Among the various storage options, saline aquifers, depleted oil and gas fields, and unmineable coal seams have gained particular attention due to their large storage capacities, widespread distribution, and geological characteristics that are favorable for long-term containment [4,5].

A considerable amount of research has been conducted on injecting CO₂ into geological reservoirs. This research has focused on how fluids flow, how they become trapped, and how the rocks respond to the injection [4,6,7]. Bashir et al. [4], for example, provide a detailed examination of the concepts of geological storage of CO₂ and its potential for trapping. Song et al. [6] and Chen et al. [7] discuss the primary geomechanical issues, including changes in stress, reactivation of faults, and maintaining the integrity of the caprock during high-pressure injection. The lack of site-specific or material-specific modeling results has not been considered, such as those involving shale formations like Opalinus Clay.

Recent advances have also highlighted the potential of hydrate-based CO₂ capture and storage, particularly under cold and high-pressure subsurface conditions. Has-sanpouryouzband et al. [6] demonstrated that injecting CO₂-rich flue gas into methane hydrate-bearing sediments can result in over 60% CO₂ capture efficiency through hydrate formation, with performance susceptible to pressure, temperature, and hydrate saturation levels. Building on this, further studies confirmed CO₂ capture efficiencies of up to 92 mol% under optimized conditions, emphasizing the role of sediment type and kinetic factors, as well as the structural evolution of clathrates in selectively trapping CO₂ over N₂ [7]. The results mention the central role of multiphase thermodynamic and kinetic behavior in determining CO₂ sequestration efficiency and system stability, paralleling the significance of the pressure-dependent mechanisms explored in caprock integrity modeling.

Central to the effectiveness and safety of geological CO₂ storage is the integrity of the caprock. The low-permeability geological formation over the storage reservoir prevents CO₂ from rising [6]. Due to their limited permeability and geomechanical robustness, shale formations make good caprocks. CO₂ injection into the subsurface may compromise the physical and mechanical properties of caprocks, affecting their sealing integrity [7]. Understanding the relationship between injected CO₂, pore structure, and caprock mineralogical composition is crucial for assessing the long-term stability of geological carbon dioxide (CO₂) storage sites. Specifically, the clay mineral content (e.g., smectite, illite, kaolinite) influences swelling or shrinkage behavior. The porosity and permeability of carbonate rocks, such as calcite, change in response to acidic conditions. Therefore, mineralogical parameters govern the geochemical reactivity and mechanical strength of the caprock over extended periods.

Shale formations typically consist of fine-grained sedimentary rocks composed predominantly of clay minerals, quartz, carbonates, and organic matter. Their low permeability and high capillary entry pressure make them suitable natural seals [8,9]. However, in response, their behavior under CO₂-rich environments is complex. Exposure to CO₂-saturated brine can induce physical changes such as swelling, shrinkage, or micro-fracturing, as well as chemical alterations, including mineral dissolution, precipitation, and changes in pore structure [10]. These processes can alter the permeability and mechanical strength of the shale, potentially creating pathways for leakage of stored CO₂.

Numerical simulations are crucial for studying CO₂ storage systems. They may evaluate geomechanical coupling processes in geological formations, anticipate subsurface system evolution over decades, and assess risks of leakage and system failure [11,12]. Geomechanical models can simulate stress, strain, and fractures between CO₂, brine, and minerals [13].

Caprock behavior has been studied using continuum-based finite element, finite difference, and discrete fracture network models [14,15]. These models utilize constitutive relationships to explain rock deformation and reactive transport equations for failure criteria, enabling the prediction of fracture initiation and propagation. Integrating these methods—such as finite element models for stress and strain analysis, discrete fracture networks for capturing fracture propagation, and reactive transport models for simulating mineral-fluid interactions—enables a comprehensive understanding of how CO₂ injection affects caprock stability. As a result, this integrated approach helps capture the fluid flow behavior and mechanical deformation, thereby improving the accuracy and risk assessment for long-term storage.

However, the geomechanical characteristics, mineralogy, porosity, permeability, and boundary conditions of the input data determine the reliability of the numerical model. To achieve predictive power, models must be calibrated and tested against laboratory trials, field observations, or pilot projects. The realistic data from site-specific investigations are valuable for model creation and testing [16]. While generic caprock behavior models might be helpful, they fail to capture geological complexity. For instance, a generic model may assume homogeneous permeability or linear elastic behavior across the caprock, which overlooks localized heterogeneities such as bedding planes, variable clay content, or existing microfractures—all of which significantly influence CO₂ migration and mechanical response in real formations. Investigations at individual sites provide a complete understanding of CO₂ injection and storage procedures. They help identify crucial caprock integrity elements in certain formations and establish specialized monitoring, risk assessment, and management techniques.

The Opalinus Clay shale formation has been extensively investigated in Europe, primarily in Switzerland [17]. It is preferable for numerical CO₂ storage impact studies due to the abundance of high-quality, site-specific data on its mineralogy and porosity. This large dataset reduces model uncertainty, making it a vital benchmark for coupled hydromechanical model calibration and validation. The Opalinus Clay is a Middle Jurassic argillaceous formation widely present in the Swiss Plateau and adjacent regions [18]. It typically consists of alternating layers of claystone and marlstone, with dominant clay minerals such as illite, kaolinite, and smectite, along with calcite, quartz, and feldspar. The formation exhibits extremely low permeability (10⁻²¹ to 10⁻¹⁸ m²), high capillary entry pressure, and favorable self-sealing properties [19].

Previous studies on Opalinus Clay have explored its geomechanical behavior and poroelastic properties [20]. Experimental work has examined its swelling and shrinkage potential, as well as fracture propagation under various stress states in CO₂-rich fluids [21]. However, comprehensive numerical investigations into the coupled geomechanical effects of CO₂ injection on Opalinus Clay as a caprock remain limited.

It is essential to understand the strength of Opalinus Clay in storing CO₂, not only for its relevance to future storage projects in Switzerland but also because it serves as a well-characterized analog for other clay-rich formations worldwide. Insights gained from its documented behavior, such as low permeability, self-sealing capacity, and predictable hydromechanical responses, can inform the design, risk assessment, and modeling strategies for similar argillaceous caprocks in regions lacking extensive site-specific data. Few studies have examined the flow behavior and geomechanical interactions between CO₂ and clay-rich caprocks in realistic subsurface conditions [22]. Second, modest mineralogical changes and stress redistribution do not significantly restrict caprock integrity over time.

Numerous numerical studies have focused on sandstone reservoirs and their surroundings [23], whereas claystone caprocks have received less attention [6]. A case study of Opalinus Clay utilizing advanced coupled modeling approaches can provide valuable insights into its effectiveness as a CO₂ seal, considering the importance of site-specific features. This research addresses these deficiencies using a fully coupled computational model that incorporates geomechanical and flow behavior, realistic material properties, and various injection scenarios. It simulates the caprock’s geomechanical integrity over time in response to CO₂ exposure, taking into account changes in pore pressure and stress redistribution.

This study numerically investigates the effects of CO₂ injection on the integrity of the Opalinus Clay caprock and models the associated geomechanical processes. It assesses fracture risks, permeability changes, and mineralogical impacts on sealing capacity. Specifically, it identifies critical failure conditions such as the exceedance of capillary entry pressure, stress-induced fracture initiation, and permeability thresholds beyond which CO₂ may migrate uncontrollably. These factors compromise the caprock’s sealing integrity. The study then develops a validated framework for assessing and evaluating long-term risks at storage sites in shale systems.

2. Governing Equations

This study utilizes a coupled multiphase flow and geomechanics framework to simulate the behavior of Opalinus Clay during CO₂ injection. The model accounts for two immiscible fluid phases (water and CO₂) within a deformable porous medium, applying the principles of mass conservation, Darcy’s law, and poroelasticity, as outlined in COMSOL 6.2 [24].

The general mass conservation equation for each phase (β) is expressed as

$${\displaystyle \frac{\partial }{\partial t}}\left(\phi S_{\beta } {\rho }_{\beta }\right)-\nabla .\left({\rho }_{\beta } u_{\beta }\right)={\Psi }_{\beta }$$

(1)

where φ is the porosity, S is the saturation, $\rho$ is the density (kg/m³), u is the Darcy velocity (m/s), and Ψ represents source or sink term. The Darcy velocity is given by

$$u_{\beta }=-{\displaystyle \frac{k K_{r\beta }}{{\mu }_{\beta }}}{\nabla P}_{\beta }$$

(2)

where $k$ is the intrinsic permeability (mD), $K_r$ is the relative permeability, and P is the fluid pressure (Pa). The source term (${\Psi }_{\beta }$) includes contributions from volumetric strain through the Biot coefficient (${\alpha }_B$), as follows:

$${\Psi }_{\beta }={\rho }_{\beta } {\alpha }_B\left({\displaystyle \frac{\partial {\epsilon }_{vol}}{\partial t}}\right)$$

(3)

where ${\epsilon }_{vol}$ is the volumetric strain. In the present study, the effects of gravity are neglected; therefore, the pressure gradient acts as the sole driving force for oil transport within the core and fracture regions. The Biot modulus (M) and the Biot coefficient (${\alpha }_B$) can be expressed as

$${\displaystyle \frac{\partial }{\partial t}}\left(\phi S_{\beta } {\rho }_{\beta }\right)={\displaystyle \frac{1}{M}}{\displaystyle \frac{\partial \left(S_{\beta } {\rho }_{\beta } p_{\beta }\right)}{\partial t}}$$

(4)

$${\displaystyle \frac{1}{M}}={\displaystyle \frac{\phi }{K_d}}+{\displaystyle \frac{{\alpha }_B-\phi }{K_s}}$$

(5)

where $K_d$ is the drained bulk modulus (MPa), and $K_s$ is the solid bulk modulus (MPa). Substituting Equations (2)–(5) into Equation (1), the governing mass conservation equation can be used for the fully coupled scheme can be expressed as

$$\left({\displaystyle \frac{\phi }{k_d}}+{\displaystyle \frac{{\alpha }_B-\phi }{K_s}}\right){\displaystyle \frac{\partial \left(S_{\beta }{\rho }_{\beta }{p}_{\beta }\right)}{\partial t}}-\nabla .\left({\displaystyle \frac{k_a{Kr}_{\beta }{\rho }_{\beta }}{{\mu }_{\beta }}} {\nabla P}_{\beta }\right)={\rho }_{\beta }{\alpha }_B\left({\displaystyle \frac{\partial {\epsilon }_{vol}}{\partial t}}\right)$$

(6)

where ${\epsilon }_{vol}$ is the volumetric strain for the 2D model in Equation (8) $\left[{\epsilon }_{vol}={\displaystyle \frac{1}{2}}\left[{\left(\nabla d\right)}^2+\nabla d\right] {\epsilon }_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{\partial d}_i}{{\partial x}_j}}+{\displaystyle \frac{{\partial d}_j}{{\partial x}_i}}\right)\right]$ in the form of a strain tensor.

where d is the displacement (mm). The force equilibrium (or solid deformation) can be represented by

$$\nabla .\sigma +\left({\rho }_{\beta } \phi +{\rho }_{\beta }\right) g=0 \text{and} \sigma ={\sigma }^{\prime }-{\alpha }_B P_{\beta } I$$

(7)

where $\sigma$ and ${\sigma }^{\prime }$ are the total and effective stress (MPa), respectively, and I is the second-order identity tensor. The porosity changes within the matrix are analyzed concerning the generated strain, as described by Equation (8) [20], as follows:

$$\phi =1-\left(1-{\phi }_i\right)\mathrm{e}\mathrm{x}\mathrm{p}(-{\epsilon }_{vol})$$

(8)

The porosity (φ) dependent on elastic modulus (E) is considered in the present work and is given in Equation (9) [21], as follows:

$$ln\left({\displaystyle \frac{E}{E_i}}\right)=-d\left({\phi }_i-\phi \right)$$

(9)

As the rock undergoes compression, the ability of multiphase flow through it changes. The permeability of the rock matrix ($k_{mat}$) can be expressed as [22]

$$k_{mat}=k_i{\left\{1\pm {\displaystyle \frac{1}{2}}{\left[{\displaystyle \frac{9\left(1-{\nu }^2\right)}{2}}{\left({\displaystyle \frac{\pi \Delta \sigma }{E}}\right)}^2\right]}^{1/3}\right\}}^2$$

(10)

where $k_i$ is the initial rock matrix permeability (mD), and E is Young’s modulus (GPa) of the rock matrix. The positive sign refers to dilatational loading, and the negative sign corresponds to the compressional loading [25].

The effective viscosity is given in Equation (11), as follows:

$${\mu }_{eff}={\displaystyle \frac{{\rho }_{total}}{\frac{k_{rw}{\rho }_w}{{\mu }_w}-\frac{k_{rg}{\rho }_g}{{\mu }_g}}}$$

(11)

Total density is represented in Equation (12), as follows:

$${\rho }_{total}=S_w{\rho }_w+S_g{\rho }_g$$

(12)

The Brooks and Corey approach models the contact between the rock matrix and the fracture zone [26]. According to this method, the fluid saturation (S) of the phases can be expressed as

$$S_g={\displaystyle \frac{(S_{ig}-S_{rg})}{(1-S_{rg}-S_{rw})}}$$

(13)

$$S_w={\displaystyle \frac{(S_{iw}-S_{rw})}{(1-S_{rg}-S_{rw})}}$$

(14)

where the subscripts i and r represent initial and residual, respectively.

The Brooks and Corey method is used to compute the capillary pressure as a function of water saturation at the fracture matrix interface, which can be expressed as

$$Pc=Pec {S_w}^{-1/{\lambda }_p}$$

(15)

where $Pec$ is the entry capillary pressure (Pa), and ${\lambda }_p$ is the pore size distribution index.

The relative permeability is computed as a function of the water saturation and pore size distribution index (${\lambda }_p$) using the Brooks and Corey method, as expressed below

$$K_{rw}={S_w}^{\left(3+2/{\lambda }_p\right)}$$

(16)

$$K_{rg}={\left(1-S_w\right)}^2\left(1-{S_w}^{\left(1+2/{\lambda }_p\right)}\right)$$

(17)

3. Modeling Workflow and Simulation Parameters

3.1. Description of the Shale Caprock and Parameters

In this research, we investigated shale caprock (Opalinus Clay) using a two-dimensional (2D) core sample [21]. The core sample displays a predominantly uniform composition, primarily comprising clay particles. The characteristics of the core sample were assessed. Initially, the grain density (${\rho }_s$) was determined using the water pycnometer method on material that was crushed and sieved to a particle size of 0.5 mm. The core sample’s bulk density ($\rho$) is determined using the fluid displacement method on a prepared slice. The bulk of the density ($\rho$) is measured to be 2.35 g/cm³.

Table 1. Reservoir rock, fluid, and poroelastic parameters [21].

Properties	Value
Dimensions (x,z)	35 [mm] × 12 [mm]
Rock Density	2330 [kg/m3]
Initial Porosity	0.1
Initial Permeability	2.4 × 10−20 [m2]
Young Modulus	1.36 [GPa]
Poisson ratio	0.44
Initial Pore Pressure	1 [atm]
Water density	1040 kg/m3
Water viscosity	0.0046 [Pa × s]
Entry capillary pressure	5 [Pa]
Pore size distribution index	0.67
Biot-Willis coefficient	0.7
Overburden load	0, 5, 10, 15, 20, 25, 30

displays the corresponding properties related to petrophysics, fluids, and geomechanics.

3.2. Initial Boundary Conditions

The numerical simulation builds upon experimental findings and posits that CO₂ injection leads to the development of upstream pressure, which is countered by water pressure acting in the opposite direction to offset the impact of the CO₂ injection pressure. Initially, the Opalinus Clay (OPA) sample undergoes full water saturation before CO₂ injection to replicate in situ subsurface conditions, where caprocks are typically saturated with water. This ensures a realistic simulation of capillary forces and fluid displacement dynamics, allowing accurate evaluation of entry capillary pressure, mechanical response, and CO₂ migration behavior during injection. To assess the entry capillary pressure and examine the material’s mechanical response, the boundary conditions are implemented using an extra-fine mesh. Then, CO₂ is incrementally injected into the saturated shaly OPA sample from the upstream side, as illustrated in Figure 1.

The simulation initializes with the Opalinus Clay sample fully saturated with water, reflecting the natural in situ state of deep geological formations. CO₂ is introduced from the upstream boundary to replicate subsurface injection scenarios.

Boundary conditions are defined to simulate the replacement of pore water with CO₂ and the subsequent pressurization of the system. The complete scope of this work is shown in

Table 2. The scope of numerical modeling.

Pdownstream (MPa)	Pupstream (MPa)
2	2
2	4
2.3	8
2.7	12
5.4	8

. These specific pressure increments were selected to span both sub-capillary and super-capillary entry thresholds of the OPA sample, allowing for the identification of the critical pressure at which CO₂ begins to penetrate the material. Additionally, they reflect a realistic range of injection pressures encountered in field-scale CO₂ storage operations, ensuring that the results apply to practical scenarios.

The mesh is refined in regions where high gradients are expected to ensure numerical accuracy. CO₂ is modeled in both gaseous and supercritical states, depending on the injection pressure, with temperature held constant to isolate pressure-related effects.

This setup enables the evaluation of caprock integrity through measurable parameters, including displacement, pressure propagation, and saturation distribution, all under realistic stress and flow conditions.

3.3. Numerical Model Implementation

The governing equations were solved using COMSOL Multiphysics 6.1. The model employs the Galerkin finite element method for spatial discretization and a fully implicit Backward Differentiation Formula (BDF) for time integration. A Newton–Raphson iterative scheme is used to resolve nonlinearity, with automatic time stepping controlled by the convergence behavior.

The relative and absolute tolerances for convergence were set to 1 × 10⁻⁶ and 1 × 10⁻⁹, respectively, ensuring high accuracy in both hydraulic and mechanical fields. Mesh independence was verified through a refinement study (described in the Results section), and all simulations were run with adaptive time stepping to maintain numerical stability during periods of rapid saturation and pressure changes.

The solver settings were optimized to handle the strong coupling between pore pressure and deformation, particularly under high capillary gradients near breakthrough.

4. Results and Discussion

In this section, we compare and contrast the different results. First, we measure the entry capillary pressure using results from the CO₂ injection of shaly OPA and compare them to experimental data, with a focus on the sample’s initial saturation. Next, we examine how the CO₂ saturation changes when the pressure upstream in the sample rises. Finally, we discuss how stress affects permeability.

4.1. Entry Capillary Pressure

Figure 2 illustrates the hydraulic response, showing how the recorded capillary pressure changes over time on the downstream side. Initially, as the CO₂ pressure increases to 4 MPa upstream, there is no significant change in the downstream capillary pressure, which remains at 491.73 Pa. This indicates that the material acts as a perfect barrier, preventing CO₂ from passing through and spreading. However, in the next stage, when the upstream CO₂ pressure rises to 8 MPa, the downstream capillary pressure drops to 6.35 Pa, which indicates that something has changed. This drop suggests that the sample’s entry capillary pressure has been exceeded, allowing CO₂ to displace water and flow through the pore network toward the downstream side. As CO₂ penetrates the material, it replaces the wetting phase (water), reducing the capillary forces that initially resisted flow. This displacement of water by the non-wetting CO₂ phase results in a measurable decrease in downstream capillary pressure, indicating the onset of two-phase flow and partial desaturation within the caprock matrix. In the third phase, this trend intensifies as the CO₂ pressure increases to 12 MPa. This causes the capillary pressure downstream to drop even more, down to 5.57 Pa, which is lower than in the previous steps. In the final step, when the injection pressure is lowered to 8 MPa, a slight rise in downstream capillary pressure occurs. Notably, the observed reduction in downstream capillary pressure cannot be attributed to a diffusive flow mechanism within a brief time frame [27].

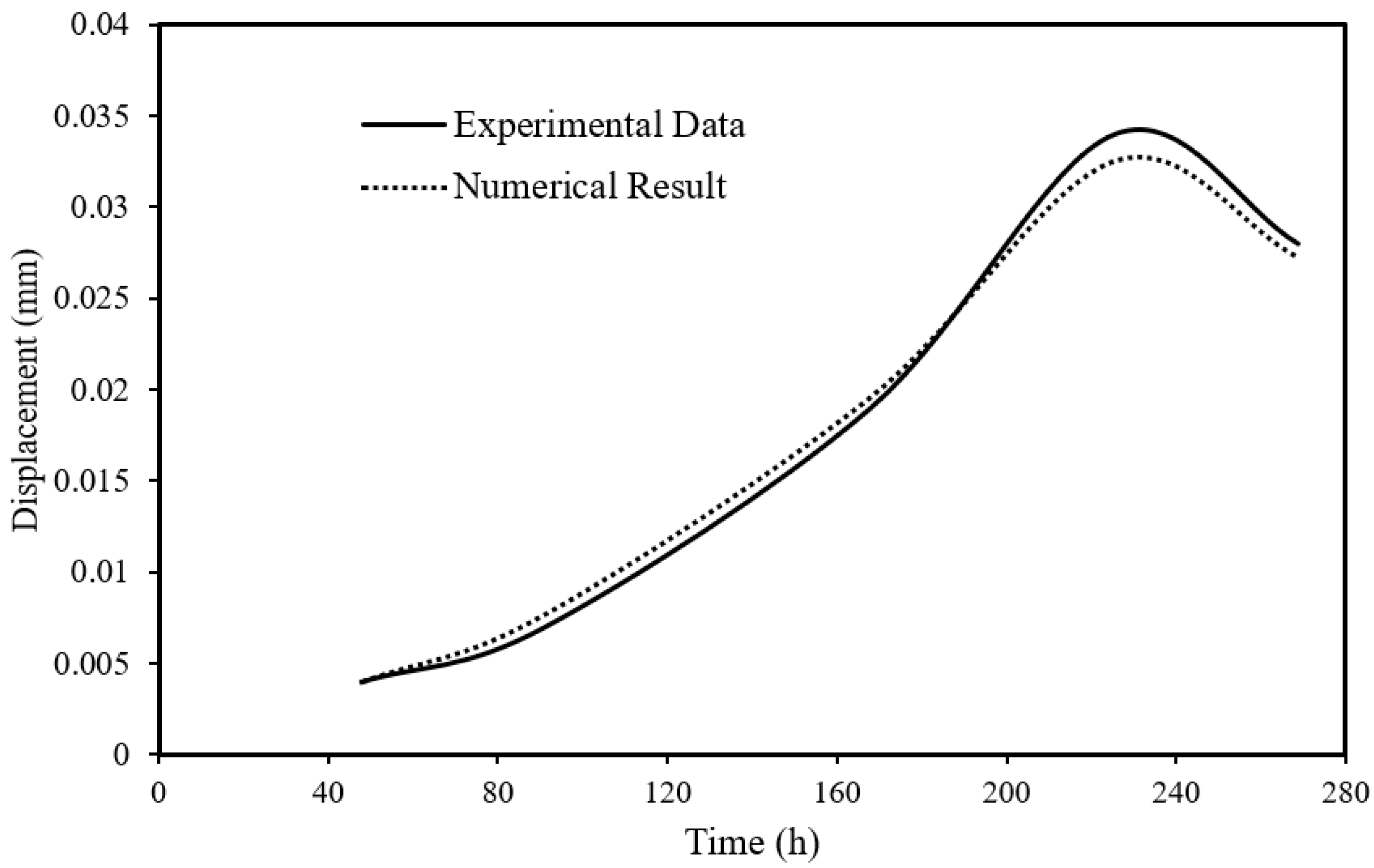
Figure 3 illustrates the numerical mechanical behavior of the sample, as measured by axial displacements and validated against experimental data [21]. The numerical behavior of the shaly OPA results matches the experimental data within a margin of less than 10%. Positive displacements indicate compaction. Each increment in CO₂ pressure at the upstream side results in observable compaction. An immediate displacement occurs upon an increase in CO₂ pressure, followed by delayed compaction at a slower rate. The presence of creep is evident after the CO₂ injection pressure rise, particularly during the initial step (Step 1), in the sample’s response before and after water replacement with CO₂ at a pressure of 2 MPa.

The hydro-mechanical behaviors of Opalinus Clay when CO₂ is injected are closely tied to capillary forces arising within water-saturated samples. In a single-fluid system, increased injection pressure results in material expansion due to a decrease in effective stress. However, when two immiscible fluids, such as CO₂ and water, are present, capillary forces develop at their interface, preventing pressure transmission from the injected fluid to the pore fluid. Instead, these capillary forces generate additional effective stress at the grain scale by pulling water toward pore throats and effectively drawing mineral grains together. This increases intergranular attractive forces, reducing the pore volume and leading to mechanical compaction of the rock matrix even without external loading changes. Capillary forces, roughly estimated using the Young–Laplace equation, are particularly significant in geomaterials such as Opalinus Clay and shales due to their small pore sizes, often in the nanometer range. The extent of capillary force influence during CO₂ injection depends on the saturation levels of CO₂ and water in the sample. If most pores are filled with CO₂, the overall increase in pore pressure from injection predominates over capillary effects.

Before CO₂ penetration into the sample (during Step 2 with an injection pressure of 4 MPa), capillary forces only exerted themselves on the upstream boundary of the sample. These forces adequately counteracted the CO₂ overpressure, resulting in slight material compaction. This capillary barrier effectively prevented CO₂ migration across the sample, with no pressure fluctuations detected downstream. However, upon CO₂ recovery downstream (Step 3, with injection pressure increased to 8 MPa), capillary forces began to manifest within the sample, following pathways that conveyed CO₂ through the material. This phenomenon led to more substantial material compaction during the subsequent steps (Steps 3 and 4, with injection pressures of 8 and 12 MPa, respectively). The observed behavior supports the notion that CO₂ displaced water within the pore space, penetrating the material along localized pathways with lower water retention capacities, resulting in partial desaturation of the sample. The mechanical response in Step 5, when the injection pressure is lowered, further supports this argument. When the pressure of CO₂ decreases, the capillary forces also decrease, causing the sample to expand.

4.2. CO₂ Saturation

Figure 4 depicts the initial phase of gas injection, emphasizing the entry of carbon dioxide (CO₂) into the system under an upstream pressure of 2 MPa. This stage marks the initiation of the CO₂ injection process, which is crucial for various industrial applications, including enhanced oil recovery and carbon capture and storage projects.

It is worth noting that there are no significant changes in CO₂ saturation within the OPA clay during this preliminary phase. This lack of substantial change is due to the fact that the downstream pressure remains constant during the initial injection stage.

The stability of CO₂ saturation levels inside the OPA clay during this period implies that the gas was introduced gradually and deliberately into the system. This controlled method is crucial for effectively monitoring and managing the injection process, leading to optimal performance and adherence to predefined operational criteria.

Figure 5 illustrates the evolution of CO₂ saturation as the upstream pressure rises for 4 MPa, 8 MPa, 12 MPa, and 8 MPa from step 2 to step 5, respectively. It is clear that as the upstream pressure increases to 4 MPa at the second step, the CO₂ saturation in the system slightly rises, indicating that the entry capillary pressure of the sample has been surpassed, allowing CO₂ to penetrate through the sample toward the downstream side. This trend intensifies in the third and fourth steps, as the upstream pressure rises to 8 MPa and 12 MPa, resulting in a more significant increase in upstream pressure than in the previous step, and the CO₂ saturation rises significantly toward the downstream. Upon reducing the upstream pressure back to 8 MPa in the final step, a decrease in the pressure increase at the downstream side is noted, and the CO₂ saturation is also reduced.

As the upstream pressure rises to 4 MPa in the second stage, the CO₂ saturation level increases dramatically. This spike indicates that the sample’s entry capillary pressure has been exceeded, allowing CO₂ to pass through and reach the downstream side. The increase in saturation is slight at this moment, but it is a sign of bigger changes that will happen in the following steps.

As the numerical investigation advances to the third and fourth phases, where the upstream pressure rises to 8 MPa and 12 MPa, respectively, the trend of CO₂ saturation accelerates significantly. The significant increase in upstream pressure compared to the preceding stage causes a noticeable rise in CO₂ saturation toward the downstream side. This event demonstrates how pressure levels influence the extent to which CO₂ can penetrate a sample. It also reflects the importance of adjusting pressure to control gas flow and saturation.

In the last step, lowering the upstream pressure back to 8 MPa reduces the pressure rise on the downstream side, resulting in a decrease in CO₂ saturation. This decrease indicates that gas saturation in the sample is dynamic and fluctuates in response to changes in pressure.

Figure 5 presents the overall view of CO₂ saturation, illustrating how pressure changes and gas flows through the sample in a complex manner. By examining these trends, researchers can gain valuable insights into how gas moves through porous surfaces [28,29]. Understanding how CO₂ saturation changes during the first injection stage provides us with essential information about how gas injection works, which enables us to devise methods to improve its effectiveness and efficiency. By closely monitoring and analyzing the early stages, operators can refine injection procedures, mitigate risks, and optimize environmental outcomes and process efficiency.

4.3. Impact on Permeability

To fully understand the importance of initial sample saturation in measuring sealing capacity, we conducted a strict repeat CO₂ injection using the same shaly OPA sample. This test was performed with a range of stress-loading settings, from 5 MPa to 30 MPa, while maintaining a steady upstream pressure of 12 MPa. This multifaceted investigation addresses an intriguing question regarding material permeability, initially highlighted by Haghi et al. [30], which remains unresolved in the existing literature.

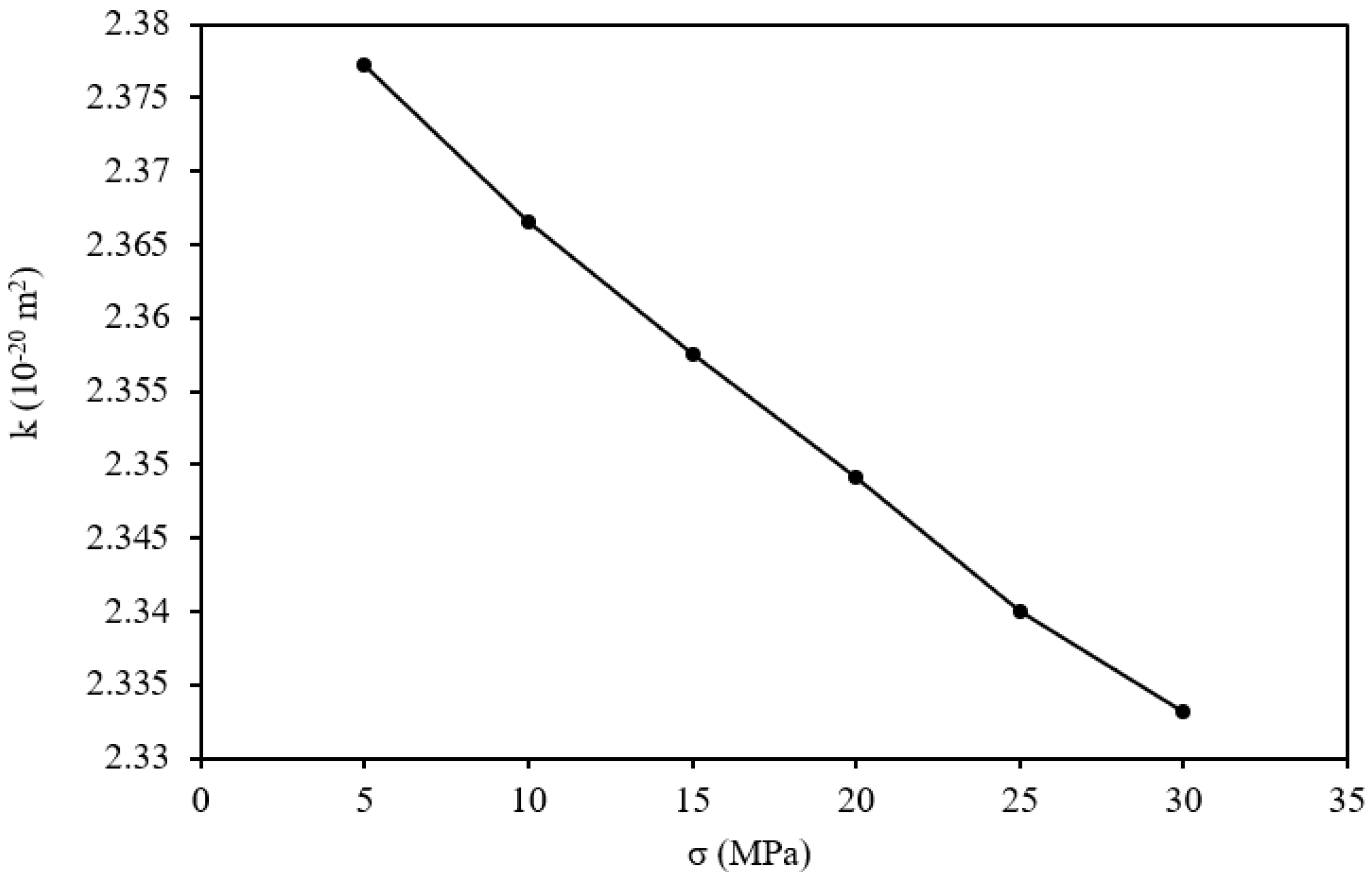
The observed variations in permeability (denoted as k) of the OPA sample as a function of stress loading (σ) are graphically represented in Figure 6. A discernible trend emerges as stress loading increases: the matrix permeability exhibits a discernible, roughly linear decrease. Specifically, under a stress loading of 5 MPa, the permeability registers at 2.377 × 10⁻²⁰ m². With an increase in stress loading to 10 MPa, a marginal reduction in matrix permeability is observed, dropping to 2.367 × 10⁻²⁰ m², representing a decrease of 0.45%. As the stress loading escalates to 15 MPa, the matrix permeability undergoes further diminishment, measuring 2.357 × 10⁻²⁰ m², reflecting a reduction of 0.35%. This downward trend persists with stress loading increments to 20 MPa, 25 MPa, and 30 MPa, resulting in respective permeability decreases of 0.39%, 0.30%, and 0.35%.

Moreover, these results reveal a consequential relationship: the fluid’s capacity to pass through the matrix decreases with a decrease in permeability due to mineralogical alteration processes, such as the dissolution of carbonates (e.g., calcite) and the precipitation of secondary minerals, like clays or silicates, which can either open or clog pore spaces. These chemical changes, coupled with mechanical responses such as compaction, alter pore connectivity and throat size, ultimately reducing overall permeability [31,32]. These results demonstrate how stress alters the permeability of the matrix structure and how such changes affect the flow of fluids within the matrix. This information is essential for determining how well-sealing devices perform under various types of stress and is particularly useful for subsurface engineering projects, such as geological carbon storage.

4.4. Impact on Porosity

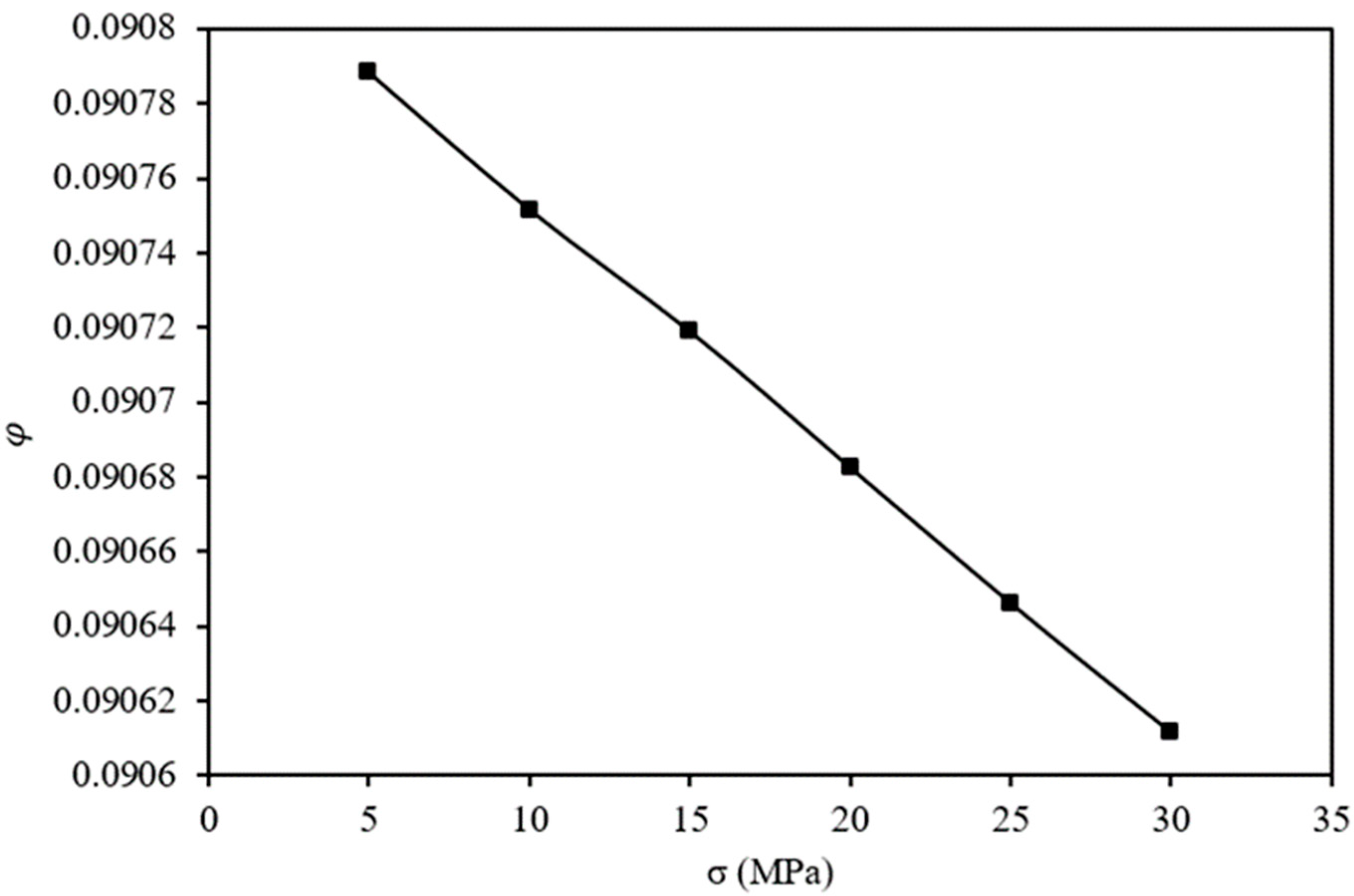
As depicted in Figure 7, stress loading leads to a decrease in porosity. The reduction in porosity follows an approximately linear trend as the stress increases. Specifically, the initial porosity of the OPA reduces by 9.21%, 9.25%, 9.28%, 9.32%, 9.35%, and 9.39% under stress loadings of 5 MPa, 10 MPa, 15 MPa, 20 MPa, 25 MPa, and 30 MPa, respectively.

Stress modifies the porosity of a material, although these changes are not as significant as the changes in permeability that happen under the same loading conditions. Vairogs et al. [33] and Jones and Owens [34] have also reported similar findings in the literature. During the loading process, the volumes of pores and channels undergo reduction, significantly impacting permeability due to channel closure. However, porosity experiences less noticeable alteration since its primary component, pore volume, remains relatively unaffected. Consequently, the stress dependency of porosity is anticipated to be lower than that of permeability.

5. Conclusions

This study used a fully coupled hydro-mechanical model calibrated for Opalinus Clay to investigate the caprock response under varying CO₂ injection pressures. The following key findings emerged from the simulations:

• Capillary entry pressure was observed to be between 4 and 8 MPa, confirming that breakthrough occurs only when the CO₂ pressure exceeds the sealing threshold, which is influenced by the initial water saturation;
• Mechanical compaction occurred due to capillary-induced stress, not just external loading, and this compaction reduced porosity and permeability nonlinearly across the injection stages;
• Sensitivity analysis revealed that increasing the initial permeability by 50% resulted in earlier CO₂ migration and a reduction in sealing time, underscoring the critical role of matrix properties;
• Partial water saturation (≤90%) significantly decreased capillary resistance, enabling earlier breakthrough and enhanced saturation distribution;
• Under anisotropic stress conditions, CO₂ migration patterns became directionally biased, indicating that stress heterogeneity can influence containment performance.

The results offer practical guidance for evaluating caprock reliability under variable geological and operational conditions. The work emphasizes that accurate modeling, grounded in site-specific parameters, is crucial for predicting the long-term integrity of CO₂ storage.