Abstract
In Europe, primary energy consumption in buildings accounts for up to 25–40%, depending on the climate conditions. Space heating and Domestic Hot Water (DHW) contribute significantly to this energy consumption. Among the most common sources for heat generation in these appliances is natural gas. Condensing boilers can surpass the 100% energy performance over the lower heating value, if the operating conditions enable the water vapor in the exhaust gases to condensate. Consequently, optimizing the operating parameters of condensing boilers is necessary to decrease fuel consumption without hindering water heating needs. The present work presents an experimental approach to the operating parameters of a condensing boiler that works with natural gas. The aim is to develop a theoretical model that relates the energy performance to the water temperature set by the final user and the excess air set by the maintenance staff.
1. Introduction
Given the primary energy consumed in buildings [1], the building stock is a key target to improve energy use. The substitution of old boilers that use solid or liquid fossil fuels by condensing boilers fueled by natural gas has noticeably improved the energy performance in water heating, hence the environmental impact [2].
Although increasing the percentage of hydrogen in the natural gas achieves lower CO2 emissions [3], its composition is determined by the supplier and thus cannot be controlled. Condensation of the water vapor in the exhaust gases depends on the water vapor pressure and the saturation vapor pressure at the cooling temperature. Water vapor pressure depends on the atmospheric pressure, the composition of the natural gas used and the excess air in the combustion process. The temperature at which the exhaust gases cool depends on the DHW set temperature and the supply and return water temperatures from the heating system. Consequently, set values of these parameters will be determinants for the boiler performance, hence the fuel consumption. As optimizing the combustion process minimizes the energy consumed to achieve the required heating and DHW needs, this work develops an experimental study to validate a theoretical model that enables identification of the optimal operating parameters. The theoretical model is implemented in Excel. First, total combustion is considered. Operating conditions are then modified to compare the results yielded by the theoretical model to the actual experimental values observed.
2. Materials and Methods
The target natural gas condensing boiler for the experimental tests was a Vaillant Ecotech PLUS. During the tests, DHW was generated at 45 °C set temperature and supply water to the heating system was set at 50 °C. Temperature was measured at the supply tap water temperature, actual DHW temperature, supply and return water temperatures from the heater system and the gas exhaust. Temperature and Relative Humidity were measured at the air inlet to the combustion process. Further measured variables were the gas consumption and the amount of water condensed from the exhaust gases. Figure 1 shows the target condensing boiler and the temperature sensors used at some of the measuring points.

Figure 1.
Views of the (a) condensing boiler, (b) temperature sensors at the water supply and return, (c) temperature measurement at the gas exhaust.
Temperature sensors were Testo Data Loggers, model 175 T2. Air temperature and relative humidity were measured with a Testo Data Logger model 175 H1. The measuring interval and storage cycle was 10s. Figure 2 shows the values registered along a typical day.
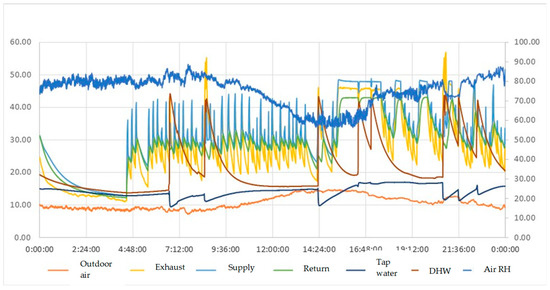
Figure 2.
Experimental values registered during one typical day.
During periods of continuous space heating, it could be observed that the exhaust gas temperature was maintained between the heating system supply and return water temperatures. This demonstrates that the temperature at which the exhaust gases can get cooled is always lower than the supply water for space heating. Although the average temperature of the exhaust gases stays below that water temperature, it can occasionally exceed it due to the boiler start-up.
Besides, an analysis of combustion was performed to determine the exhaust gases composition and the excess air in the combustion process. The results are gathered in Table 1. The analyzer was a TESTO model 330-2 that calculated the boiler performance through the Siegert equation. The average fuel consumption was also measured. Water condensed during five days was weighted, obtaining an average condensing rate of 840 g/Nm3 of natural gas.

Table 1.
Combustion parameters measured.
3. Results and Discussion
A theoretical model is developed to calculate the temperature at which condensation of water vapor in the exhaust gases starts, condensed water mass flow, the condensing boiler energy performance and the energy recovered in the boiler. Parameters studied are fuel mass rate and composition, excess air and ambient air psychrometric conditions.
First, the stoichiometric combustion is calculated assuming a non-fixed composition of the natural gas [4], whose components are: Methane, ethane, propane, n-butane, isobutane, n-pentane, isopentane, hexane, heptane, nitrogen and carbon dioxide. Assuming no unburnt combustibles, stoichiometric oxygen is calculated. Excess air is used to calculate the air rate supplied to the boiler and the composition of the exhaust gases.
Next, an energy balance is constructed in the burner. Provided an adiabatic process, this energy balance provides the Adiabatic Flame Temperature. Assuming steady flow [5], this energy balance is given by Equation (1):
where is the heat losses to the environment (equal to zero, provided an adiabatic process), is the molar rate of the reactants supplied to the burner, is the reactants average isobaric specific heat, is the temperature of the reactants at the burner inlet, is the molar rate of products in the exhaust gases, is the products average isobaric specific heat, is the product temperature (corresponding to the Adiabatic Flame Temperature, provided an adiabatic process), is the molar rate of each reactive component i of the natural gas and is the enthalpy of combustion for each component of the natural gas. Super index N in the summation denotes the number of reactive components considered for the supplied natural gas.
Then, a value for the exhaust gases temperature is set. This value may correspond to a measured, experimental value or rather be an arbitrary temperature. Composition of the exhaust gases enables calculation of the temperature at which water vapor condensation starts (dew point temperature): If this temperature is over that of the exhaust gases, then condensation occurs. Both the dew point temperature and the water molar fraction in the exhaust gases are calculated from the Raoult–Dalton Law (2) and the Antoine Equation (3) [6]:
In Equation (2), is the partial water vapor pressure in the exhaust gases, is the water molar fraction in the exhaust gases, P is the total pressure and is the saturation vapor pressure of water. Concerning Equation (3), T is the absolute temperature in Kelvin, whereas A, B and C are constants dependent on the component. It should be noted that the only possible condensable component considered in the exhaust gases is the water vapor, which has its molar fraction changed as it condenses. The amount of water condensed is calculated through Equation (4):
where is the condensed water molar rate, is the exhaust gases molar rate, is the water molar fraction in the exhaust gases at the burner outlet, and is the water molar fraction in the exhaust gases at the boiler outlet.
Finally, the boiler performance is calculated through the sensible heat transferred from the exhaust gases and the water latent heat ():
where and are the temperatures of the exhaust gases at the burner and at the chimney outlet, respectively, is the natural gas molar flow and is its Lower Heating Value.
Table 2 gathers and compares the results obtained through the theoretical model and the experimental measurements. It must be noted that the theoretical model considered a fixed value of the excess air and composition of the natural gas [4]. The temperature of exhaust gases at the boiler outlet is fixed at 40 °C, considered a more typical value during the steadiest operating periods of the boiler observed in Figure 2. Results provided in Table 2 show slight deviations due to differences in the concentration of carbon dioxide in the exhaust gases, whose cause relies on the unknown actual composition of the natural gas used.

Table 2.
Comparative results obtained through the theoretical model and the experimental study.
Author Contributions
E.V.-G. and D.F.-C. conceived and designed the experiments; E.V.-G. performed the experiments; D.F.-C., J.P.-A. and A.T.-G. analyzed the data; D.F.-C. and A.T.-G. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
This work was supported by the Ente Regional de la Energía of the Regional Government of Castile and Leon [grant number EREN_2019_L2_UVA].
Conflicts of Interest
The authors declare no conflict of interest.
References
- IEA Energy Efficiency 2018—Analysis and Outlooks to 2040; Sixth Edition in the IEA Market Report Series; IEA: Paris, France, 2018; pp. 1–143. [CrossRef]
- Horak, J.; Kubonova, L.; Krpec, K.; Hopan, F.; Kubesa, P.; Motyka, O.; Laciok, V.; Dej, M.; Ochodek, T.; Placha, D. PAH emissions from old and new types of domestic hot water boilers. Environ. Pollut. 2017, 225, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Boulahlib, M.S.; Medaerts, F.; Boukhalfa, M.A. Experimental study of a domestic boiler using hydrogen methane blend and fuel-rich staged combustion. Int. J. Hydrog. Energy 2021, in press. [Google Scholar] [CrossRef]
- Kuczyński, S.; Łaciak, M.; Szurlej, A.; Włodek, T. Impact of Liquefied Natural Gas Composition Changes on Methane Number as a Fuel Quality Requirement. Energies 2020, 13, 5060. [Google Scholar] [CrossRef]
- Smith, R. Chemical Process Design and Integration, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Propierties of Gases and Liquids. McGraw Hill Professional, 2000. Available online: https://www.researchgate.net/file.PostFileLoader.html?id=576b60dc3d7f4b3e0b1acf84&assetKey=AS%3A375993815584769%401466655319665 (accessed on 12 October 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).