A Hybrid Extended Kalman Filter Based on a Parametrized FeedForward Neural Network for the Improvement of the Results of Numerical Wave Prediction Models ^†

Abstract

Aiming to develop a novel optimization model for numerical weather and wave predictions, this study proposes a hybrid approach based on the combination of Artificial Neural Networks (ANNs) and Kalman Filters (KFs). The KF technique uses fixed covariance matrices, which is inappropriate for dynamic conditions where the measurement error varies due to outside factors. This work proposes an alternative method for updating the covariance matrices, depending on a selected parameter that was obtained from a parametrized FeedForward Neural Network. The FeedForward Neural Network is trained for various values of the parameter for a set of historical data to provide the best choice based on a predetermined objective. Following this procedure, the parameter is added to the hybrid Extended Kalman Filter, which improves the direct outputs of numerical forecasts by decoding the systematic error between the model’s direct output and the corresponding observations. The suggested approach was used in a number of time periods in various locations with very promising results.

1. Introduction

Due to numerous important applications, including search and rescue, shipping and renewable energy sources, the necessity for accurate wave predictions has substantially increased. Numerical wave prediction models, which are employed by many operational and research centers, are a trustworthy and effective instrument to reach these goals, as they are fairly successful in simulating global environmental conditions. Nevertheless, when the forecasting concerns a local area of interest, numerical models fail to provide precise forecasts. The main reason for this is the multiparametric nature of the various factors involved, such as the strong dependence on initial and lateral conditions or the parametrization of some atmospheric or wave procedures [1].

The enhancement of the model’s resolution could be a potential solution to these problems, but the success of this strategy is uncertain and at the same time extremely costly, as the computational time will rise dramatically. An alternative approach could be to use post-processing algorithms [1,2,3] to improve the starting conditions based on assimilation systems. These instruments, like ANNs and Kalman Filters, can be used to improve the output generated by statistical models by reducing the systematic error of the simulation. In order to achieve this, a cost function is defined as the “distance” (bias) between the direct output of the model and the actual observations.

Under this framework, we introduce a hybrid Extended Kalman Filter based on a parametrized FeedForward Neural Network (pFFNN) for the prediction of the Significant Wave Height (SWH). In particular, for a set of historical data, the pFFNN is trained for various values of the parameter and the optimal value is added to the hybrid Extended Kalman Filter, which reduces the systematic error between the direct output of the WAM-cycle 4 [4] model and the corresponding observation.

2. Extended Kalman Filter Algorithm

Kalman Filtering (KF) is a recursive prediction algorithm which provides an optimal estimation for an unknown state vector $x_t$ given information about an observable vector $y_t$ based on the assumption that there is a linear correlation between these variables. However, when the dynamics of the model are nonlinear, a different filtering approach is necessary. One such technique is the Extended Kalman Filter, which is an extension of the Kalman Filter through a linearization process based on Taylor’s approximation [5].

To lay the groundwork for the construction of the EKF, we consider a nonlinear system which is described by the following state measurement model:

$$x_t=h_{t-1}\left({t-1,x}_{t-1}\right)+w_{t-1}$$

(1)

$$y_t=g_t\left({t,x}_t\right)+ v_t$$

(2)

where $w_t$ and $v_t$ are independent Gaussian noise processes with zero mean and covariance matrices $Q_{t-1}$ and $R_t$, respectively. The quantities $h_{t-1}(•)$ and $g_t(•)$ are the nonlinear transition matricies functions, which are considered to be $C^1$ and in some cases are time varying.

The fundamental idea behind the Extended Kalman Filter is to linearize the state space model of Equations (1) and (2) each time around the previous or most recent state estimate, which is taken to be either ${\widehat{x}}_{t-1}$ or ${\widehat{x}}_{t/t-1}$ depending on which specific functional is being taken into consideration [5]. The variables ${\widehat{x}}_{t-1}$ and ${\widehat{x}}_{t/t-1}$ express the priori and the posteriori estimate of the state, respectively.

3. Parametrized FeedForward Neural Network

Artificial Neural Networks (ANNs) are adaptable artificial systems that draw inspiration from the processes of the human brain, and are able to rebuild the fuzzy rules that determine the unknown correlation between various variables. The simplest type of ANN is the FeedForward Neural Network, which is a multi-layer network where every neuron in the previous layer connects to each neuron of the next layer [6].

In this study, a parametrized three-level FeedForward Neural Network has been applied in order to determine the optimal parameter $a$, with one hidden layer, twenty neurons, the sigmoid function, $f(x)=\frac{1}{1+e^{-x}}$ as the activation function and one linear output layer. In particular, the network’s direct output is given by:

$$y_{out}=V\ast f(W{\tilde{x}}^T+b_1)+b_2$$

where $W$ is a $d\times m$ matrix, with $m$ being the number of neurons in the hidden layer and $d$ being the size of the input data $\tilde{x}=(x_1,x_2,\dots x_{d-1},\alpha )$. $V$ and $b_1$ are $1\times m$ matrices, while $b_2$ is the (scalar) bias of the output layer.

The pFFNN can be trained for a range of values of the parameter $\alpha$ (here $0\le \alpha \le 1$), enhancing network’s efficiency. The idea behind the application of a parameterized ANN is based on the work of Famelis and Kaloutsa, in which an NN was trained for different values of a parameter in order to determine to what extent this affects the stiffness of the problem [7]. Furthermore, in order to determine the network’s parameters, the Levenberg–Marquardt method was applied as learning a rule.

4. The Proposed Methodology

The Kalman Filtering procedure uses fixed covariance matrices; thus, choosing the quantities $Q_{t-1}$ and $R_t$ is one of the most challenging issues for the filter’s successful implementation.

To avoid this problem, Shahrokh Akhlaghi and Zhenyu Huang [8] proposed an estimating method to adaptably adjust the quantities $Q$ and $R$ at each step of the EKF algorithm, based on:

$$R_t=\alpha R_{t-1}+(1-\alpha )\left({\epsilon }_t{\epsilon }_t^T+G_{t/t-1}{P}_{t/t-1}{G}_{t/t-1}^T\right)$$

and

$$Q_t=\alpha Q_{t-1}+\left(1-\alpha \right)\left({\mathrm{K}}_t{d}_t{d}_t^T{\mathrm{K}}_t^T\right)$$

Their choice was $\alpha =0.3$ for all their tests. Here, the quantity ${\epsilon }_t$ is the residual and can be determined by the difference between the measurement’s actual value and its projected value based on the data provided at step t. On the other hand, $d_t$ is the innovation and expresses the difference between the actual measurement and its predicted value at time t.

However, the choice of the parameter $\alpha$ cannot be independent of the available data, as this loses essential information necessary for the study of dynamical systems. For this reason, aiming to improve the forecasting capabilities of WAM-cycle 4, the proposed methodology implements the parametrized FeedForward Neural Network presented in Section 2 to determine parameter $\alpha$ and therefore to modify the covariance matrices.

More specifically, the available historical data are divided into three sections:

• Data Set1. Train the pFFNN and obtain the parameter $a$.
• Data Set2. Train the hybrid Extended Kalman Filter with the parameter a.

  $$Data Set2=Data Set1+1:DataSet1+range$$
• Data Set3. Forecast using the hybrid Extended Kalman Filter.

  $$Data Set3=Data Set2+1:DataSet2+forecast.$$

For all case studies, $DataSet1=1000$, $range=250$ and $forecast=40$.

Hybrid Extended Kalman Filter

In order to reduce the systematic error of the simulation, we define $y_t$ as the difference between the actual Significant Wave Height and the FeedForward Neural Network’s direct output, which uses as input the previous forecast of the model, with the following form:

$$y_t=m_t\left(t,N_t,{SWH}_{t-1}\right)+v_t.$$

(3)

where $m(•)$ is the nonlinear transition matrix function, while the quantity $N_t$ express a vectorial parameter that needs to be estimated by the filter. Note here that $N_t$ includes the parameters of each layer of the FFNN, i.e., $N_t=[W,V,b_1,b_2]$ and $m_t\left(t,N_t,{SWH}_{t-1}\right)=V\ast f(W\ast {SWH}_{t-1}+b_1)+b_2$, where $f(•)$ is the sigmoid function.

Furthermore, as we lack accurate knowledge about the evolution of the state vector $N_t$ in time, we presume that its change would be random and thus we set the system’s nonlinear transition matrix function $h_{t-1}=1$. Therefore, the state equation for the EKF can be described as follows:

$$N_t=N_{t-1}+w_{t-1}$$

(4)

Combining (3) and (4), we construct the state space model:

$$N_t=N_{t-1}+w_{t-1}$$

$$y_t=m_t(t,N_t,{SWH}_{t-1})+v_t$$

When the dynamic system is defined, the hybrid Extended Kalman Filter follows the following steps:

• Step 1. Initialization. For $t=0$, set

  $${{{\widehat{N}}_0=E\left[N_0\right],\mathrm{P}}_0=E\left[\left(N_0-E\left[N_0\right]\right){\left(N_0-E\left[N_0\right]\right)}^T\right],\mathrm{R}}_0,Q_0$$
• Step 2. Iteration. For $t=\mathrm{1,2},\dots$, compute:
  • The Jacobian matrix of the nonlinear transition function $m(•)$.

    $$F_{t/t-1}={\nabla m}_{t/t-1}|{\widehat{N}}_{t/t-1}$$
  • The Prediction Step.

    $${\widehat{N}}_{t/t-1}={\widehat{N}}_{t-1}$$

    $$P_{t/t-1}=P_{t-1}+Q_{t-1}$$

    $$d_t=y_t-m_t\left({\widehat{N}}_{t/t-1}\right)$$

    $$K_t=P_{t/t-1}{F}_{t/t-1}^T{[F_{t/t-1}{P}_{t/t-1}{F}_{t/t-1}^T+R_t]}^{-1}$$

    $${\widehat{N}}_{t/t}={\widehat{N}}_{t/t-1}+K_t[y_t-m_t({\widehat{N}}_{t/t-1}\left)\right]$$

    $${\epsilon }_t=y_t-m_t\left({\widehat{N}}_{t/t}\right)$$

    $$R_t=\alpha R_{t-1}+(1-\alpha )\left({\epsilon }_t{\epsilon }_t^T+F_{t/t-1}{P}_{t/t-1}{F}_{t/t-1}^T\right)$$

    $$K_t=P_{t/t-1}{F}_{t/t-1}^T{[F_{t/t-1}{P}_{t/t-1}{F}_{t/t-1}^T+R_t]}^{-1}$$

    $$P_{t/t}=[I-K_t{F}_{t/t-1}]P_{t/t-1}$$

    $$Q_t=\alpha Q_{t-1}+(1-\alpha )\left({\mathrm{K}}_t{d}_t{d}_t^T{\mathrm{K}}_t^T\right)$$

    $${\widehat{N}}_{t/t}={\widehat{N}}_{t/t-1}+K_t[y_t-m_t({\widehat{N}}_{t/t-1}\left)\right]$$

5. Case Study

In this section, we compare the results derived from the hybrid Extended Kalman Filter with the tuned parameter $a$ to those obtained by the same filter but with a stable parameter ($a=0.3$). The presented case study concerns data from the area of Lesvos in the Aegean Sea for the period 2010–2012. As training data for the pFFNN, one thousand WAM forecasts were used (DataSet1), while as training data for the hybrid EKF, the next two hundred and fifty model estimations were applied (DataSet2). Finally, in order to validate the performance of the proposed method, the following forty WAM predictions were used (DataSet3).

The values of Bias, Absolute Bias, Root Mean Square Error (Rmse) and Nash–Sutcliffe model efficiency coefficient (Ns) are reported in

Table 1. Aggregate results for the different periods. The historic database contains 1250 observations and 40 correct predictions.

2010	Bias	AbsoluteBias	Rmse	Ns
Model	0.148526	0.189	0.3007057	0.6992427
HybridEKFwithStablePar a = 0.3	0.027886	0.1643306	0.259394	0.7762037
HybridEKFwithTuningPar a = 0.7	0.030033	0.1359092	0.2185181	0.941179
2011	Bias	AbsoluteBias	Rmse	Ns
Model	0.275632	0.2956842	0.4009535	−0.9108604
HybridEKFwithStablePar a = 0.3	0.117658	0.117658	0.3021639	−0.0852406
HybridEKFwithTuningPar a = 0.6	0.023235	0.1586907	0.1962634	0.5421536
2012	Bias	AbsoluteBias	Rmse	Ns
Model	0.208316	0.2834211	0.4355139	−0.172398
HybridEKFwithStablePar a = 0.3	−0.02932	0.2656988	0.3486826	0.2484957
HybridEKFwithTuningPar a = 0.1	−0.00571	0.1414679	0.1940013	0.7673621

. More specifically, the indications “HybridEKFwithStableParameter” and “HybridEKFwithTuning Parameter” express the corresponding results from the proposed methodology, while the indication “Model” presents the direct output of the numerical wave model prior to the use of the method.

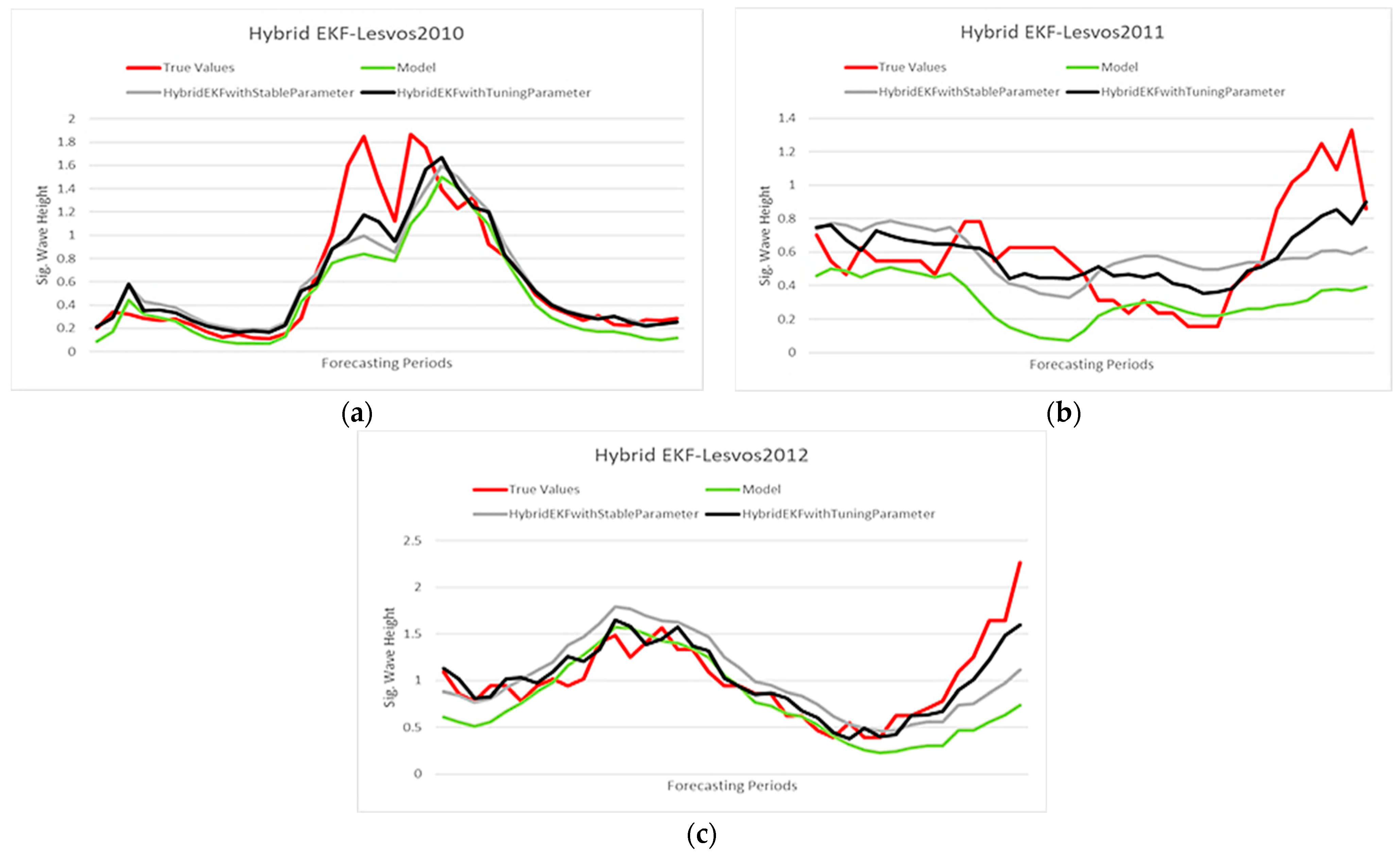
Additionally, time series diagrams per year are included. In particular, the indicator “True Values” expresses the actual observations of the Significant Wave Height, while “Model”, “HybridEKFwithStablePar” and “HybridEKFwithTuningPar” present the results produced from the numerical model before and after the implementation of the method, respectively.

Improving the Forecasting Capabilities-Lesvos Region

As new data for the Significant Wave Height were provided every three hours, our goal was to employ the suggested strategy to improve the wave model predictions for a period of five days.

Analyzing the time series (Figure 1) and Table 1, it is observed that the proposed method enhances the forecasts of the simulation model for all time periods. In particular, the various indicators improved greatly, most of all the Nash–Sutcliffe model efficiency coefficient index (Ns) and the Root Mean Square Error (Rmse).

According to the Ns, the greatest improvement was observed in the period of 2012, which prior to the usage of the method had a negative value ($Ns=-0.172398$), while after the implementation of the hybrid filter with a tuning parameter, the corresponding value increased to $Ns=0.7673621$.

Furthermore, in the same period, the Rmse indicator significantly reduced, as its prior value was $Rmse=0.4355139$, while after the application of the proposed methodology with the adaptive parameter, the corresponding value was $Rmse=0.1940013.$ Additionally, it should be noted that in all cases, the hybrid filter with a fixed parameter improves the model’s performance, but to a lesser extent compared to the adapted parameter filter and therefore it cannot be considered as the optimal choice.

6. Conclusions

In this study, we introduce a hybrid Extended Kalman Filter based on a parametrized FeedForward Neural Network (pFFNN) for the prediction of the Significant Wave Height (SWH). In particular, for a set of historical data, the pFFNN is trained for various values of the parameter and the optimal value is selected. Then, the chosen parameter is used in the Extended Kalman Filter in order to modify the covariance matrices.

The efficiency of the above methodology was evaluated through various time periods, which concerned (among others) the area of Lesvos in the Aegean Sea in 2010–2012. For every case, we compared the hybrid Extended Kalman Filter with a tuned parameter with the corresponding constant parameter filter to determine to what extent the value of the parameter influenced the performance of the proposed methodology.

The hybrid filter significantly improved the forecasting results of the simulation system. More specifically, in all cases, we observed that the hybrid filter based on a tuned parameter provided better results in comparison to those derived from the fixed parameter filter and therefore it is considered the better option to improve the forecasts of the WAM-cycle 4 model.

Finally, the proposed method was also implemented for the Pacific and other Aegean regions with similar success, but the results are not included in this paper. Furthermore, it should be noted that the hybrid approach of ANNs and EKFs is not limited to WAM-cycle 4 applications, but can be extended to other numerical prediction models as well.