Impact of Aerosol Optical Properties, Precipitable Water, and Solar Geometry on Sky Radiances Using Radiative Transfer Modeling †
Abstract
1. Introduction
2. Radiative Transfer Simulations
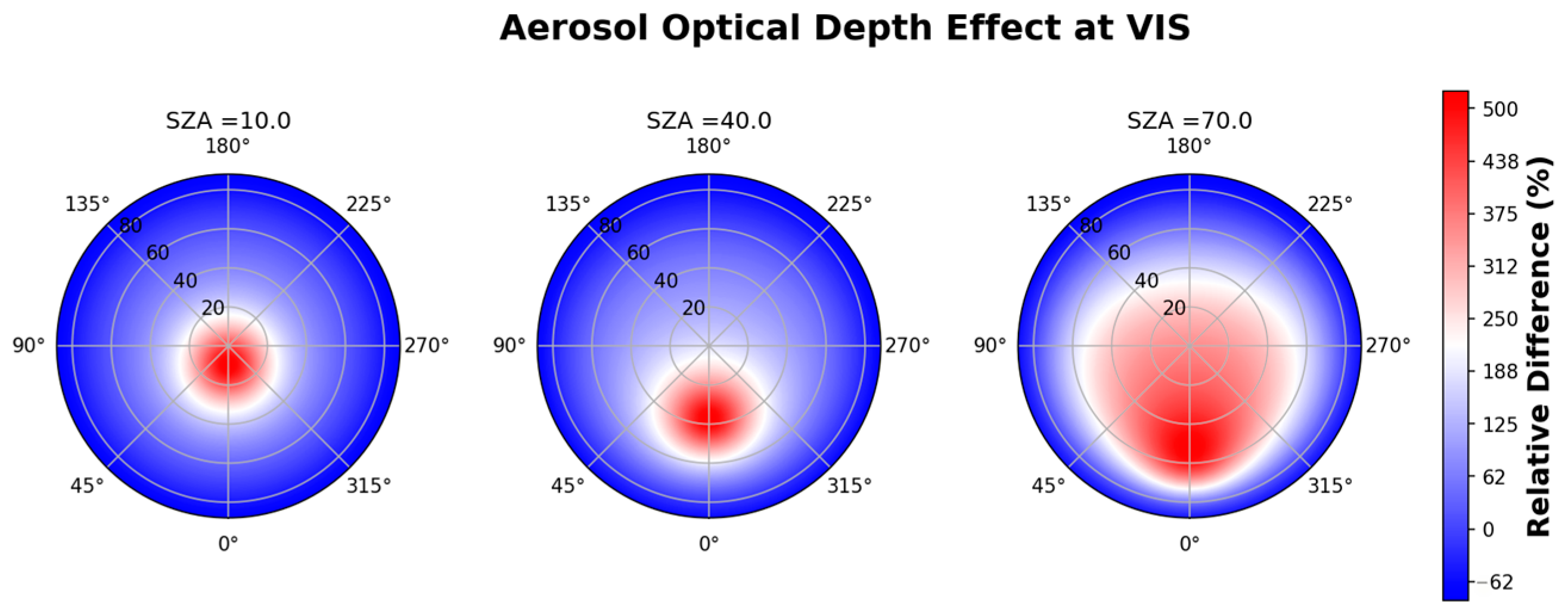
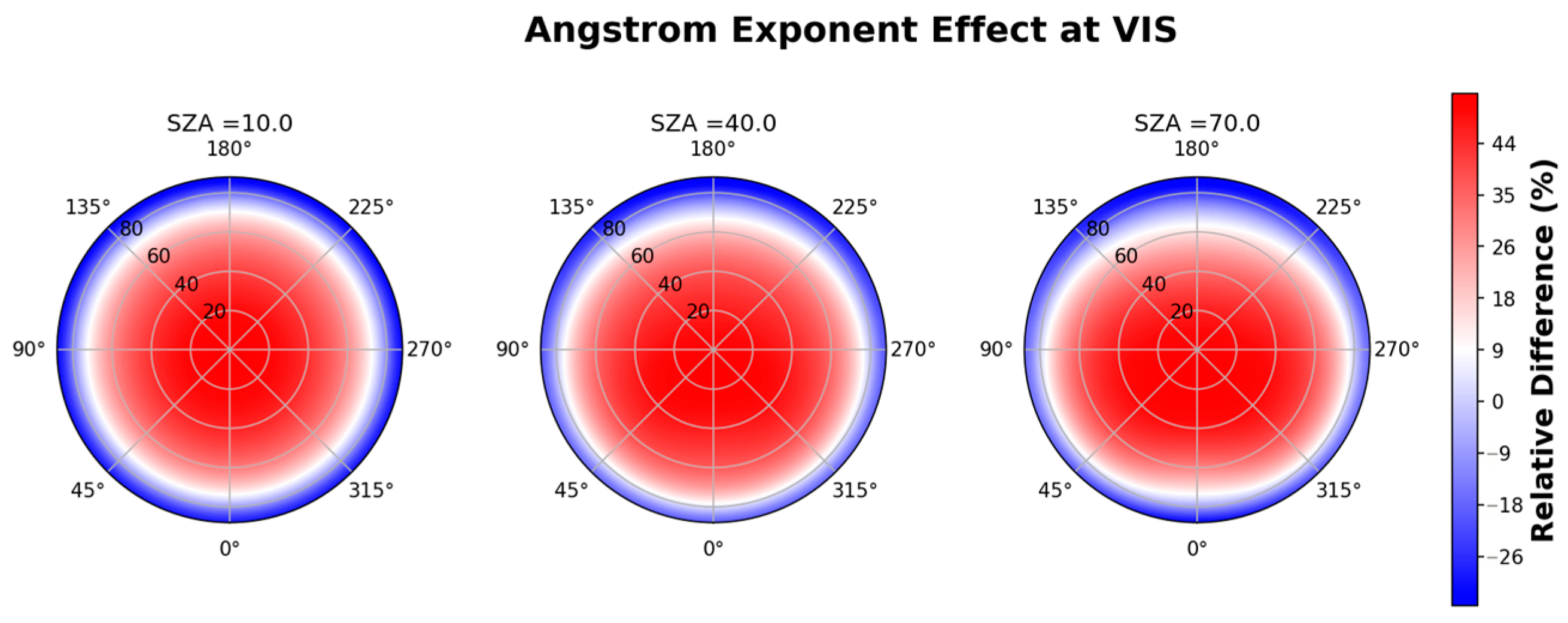
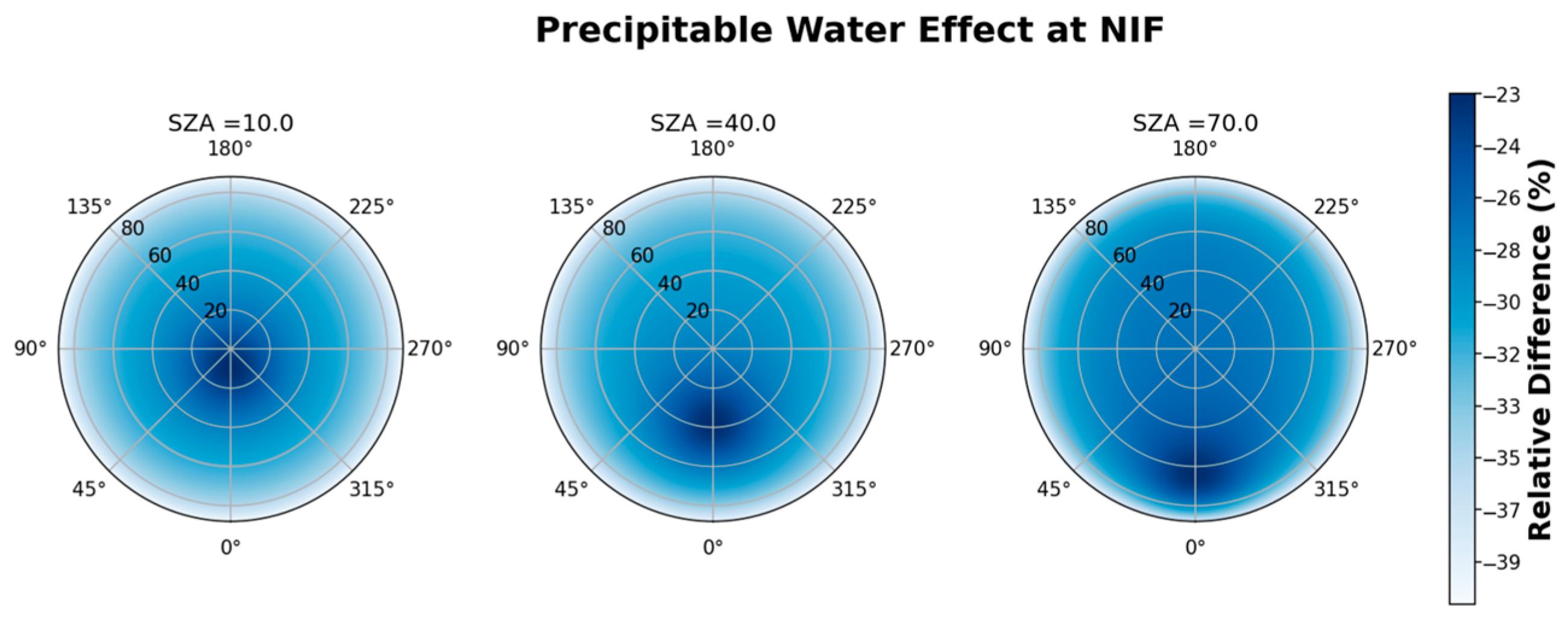
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, D.H.; Lam, J.C. Predicting solar irradiance on inclined surfaces using sky radiance data. Energy Convers. Manag. 2004, 45, 1771–1783. [Google Scholar] [CrossRef]
- Plag, F.; Kröger, I.; Riechelmann, S.; Winter, S. Multidimensional model to correct PV device performance measurements taken under diffuse irradiation to reference conditions. Sol. Energy 2018, 174, 431–444. [Google Scholar] [CrossRef]
- Behrendt, T.; Kuehnert, J.; Hammer, A.; Lorenz, E.; Betcke, J.; Heinemann, D. Solar spectral irradiance derived from satellite data: A tool to improve thin film PV performance estimations? Sol. Energy 2013, 98, 100–110. [Google Scholar] [CrossRef]
- Suzuki, A.; Kobayashi, S. Yearly distributed insolation model and optimum design of a two dimensional compound parabolic concentrator. Sol. Energy 1995, 54, 327–331. [Google Scholar] [CrossRef]
- de Simón-Martín, M.; Díez-Mediavilla, M.; Alonso-Tristán, C. Shadow-band radiometer measurement of diffuse solar irradiance: Calculation of geometrical and total correction factors. Sol. Energy 2016, 139, 85–99. [Google Scholar] [CrossRef]
- Seckmeyer, G.; Schrempf, M.; Wieczorek, A.; Riechelmann, S.; Graw, K.; Seckmeyer, S.; Zankl, M. A Novel Method to Calculate Solar UV Exposure Relevant to Vitamin D Production in Humans. Photochem. Photobiol. 2013, 89, 974–983. [Google Scholar] [CrossRef]
- Allen, S.K.; Barros, V.; Burton, I.; Campbell-Lendrum, D.; Cardona, O.-D.; Cutter, S.L.; Dube, O.P.; Ebi, K.L.; Field, C.B.; Handmer, J.W.; et al. Summary for Policymakers. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptations: Special Report of the Intergovernmental Panel on Climate Change; Field, C., Barros, V., Stocker, T., Dahe, Q., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 3–22. [Google Scholar] [CrossRef]
- Olmo, F.; Quirantes, A.; Lara, V.; Lyamani, H.; Alados-Arboledas, L. Aerosol optical properties assessed by an inversion method using the solar principal plane for non-spherical particles. J. Quant. Spectrosc. Radiat. Transf. 2007, 109, 1504–1516. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from Sun and sky radiance measurements. J. Geophys. Res. Atmos. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
- Tohsing, K.; Klomkliang, W.; Masiri, I.; Janjai, S. An investigation of sky radiance from the measurement at a tropical site. AIP Conf. Proc. 2017, 1810, 080006. [Google Scholar] [CrossRef]
- Wuttke, S.; Seckmeyer, G. Spectral radiance and sky luminance in Antarctica: A case study. Theor. Appl. Clim. 2006, 85, 131–148. [Google Scholar] [CrossRef][Green Version]
- Nakajima, T.; Campanelli, M.; Che, H.; Estellés, V.; Irie, H.; Kim, S.-W.; Kim, J.; Liu, D.; Nishizawa, T.; Pandithurai, G.; et al. An overview of and issues with sky radiometer technology and SKYNET. Atmospheric Meas. Tech. 2020, 13, 4195–4218. [Google Scholar] [CrossRef]
- Kider, J.T.; Knowlton, D.; Newlin, J.; Li, Y.K.; Greenberg, D.P. A framework for the experimental comparison of solar and skydome illumination. ACM Trans. Graph. 2014, 33, 1–12. [Google Scholar] [CrossRef]
- Ricchiazzi, P.J.; Payton, A.; Gautier, C. The Effect of Surface Albedo Heterogeneity on Sky Radiance. In Proceedings of the Tenth ARM Science Team Meeting, San Antonio, TX, USA, 13–17 March 2000. [Google Scholar]
- Tohsing, K.; Schrempf, M.; Riechelmann, S.; Seckmeyer, G. Validation of spectral sky radiance derived from all-sky camera images – A case study. Atmos. Meas. Tech. 2014, 7, 2137–2146. [Google Scholar] [CrossRef]
- Perez, R.; Seals, R.; Michalsky, J. All-weather model for sky luminance distribution—Preliminary configuration and validation. Sol. Energy 1993, 50, 235–245. [Google Scholar] [CrossRef]
- Mardaljevic, J. Sky model blends for predicting internal illuminance: A comparison founded on the BRE-IDMP dataset. J. Build. Perform. Simul. 2008, 1, 163–173. [Google Scholar] [CrossRef]
- Ferraro, V.; Mele, M.; Marinelli, V. Analysis of sky luminance experimental data and comparison with calculation methods. Energy 2012, 37, 287–298. [Google Scholar] [CrossRef]
- Igawa, N. Improving the All Sky Model for the luminance and radiance distributions of the sky. Sol. Energy 2014, 105, 354–372. [Google Scholar] [CrossRef]
- Liang, S.; Lewis, P. A parametric radiative transfer model for sky radiance distribution. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 181–189. [Google Scholar] [CrossRef]
- Gueymard, C.A. Parameterized transmittance model for direct beam and circumsolar spectral irradiance. Sol. Energy 2001, 71, 325–346. [Google Scholar] [CrossRef]
- Kocifaj, M. Angular distribution of scattered radiation under broken cloud arrays: An approximation of successive orders of scattering. Sol. Energy 2012, 86, 3575–3586. [Google Scholar] [CrossRef]
- Kocifaj, M. Unified model of radiance patterns under arbitrary sky conditions. Sol. Energy 2015, 115, 40–51. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Kocifaj, M. Clear-sky spectral radiance modeling under variable aerosol conditions. Renew. Sustain. Energy Rev. 2022, 168. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations - description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannaklis, C.-P.; Logothetis, S.-A.; Salamalikis, V.; Tzoumanikas, P.; Kazantzidis, A. Impact of Aerosol Optical Properties, Precipitable Water, and Solar Geometry on Sky Radiances Using Radiative Transfer Modeling. Environ. Sci. Proc. 2023, 26, 106. https://doi.org/10.3390/environsciproc2023026106
Giannaklis C-P, Logothetis S-A, Salamalikis V, Tzoumanikas P, Kazantzidis A. Impact of Aerosol Optical Properties, Precipitable Water, and Solar Geometry on Sky Radiances Using Radiative Transfer Modeling. Environmental Sciences Proceedings. 2023; 26(1):106. https://doi.org/10.3390/environsciproc2023026106
Chicago/Turabian StyleGiannaklis, Christos-Panagiotis, Stavros-Andreas Logothetis, Vasileios Salamalikis, Panayiotis Tzoumanikas, and Andreas Kazantzidis. 2023. "Impact of Aerosol Optical Properties, Precipitable Water, and Solar Geometry on Sky Radiances Using Radiative Transfer Modeling" Environmental Sciences Proceedings 26, no. 1: 106. https://doi.org/10.3390/environsciproc2023026106
APA StyleGiannaklis, C.-P., Logothetis, S.-A., Salamalikis, V., Tzoumanikas, P., & Kazantzidis, A. (2023). Impact of Aerosol Optical Properties, Precipitable Water, and Solar Geometry on Sky Radiances Using Radiative Transfer Modeling. Environmental Sciences Proceedings, 26(1), 106. https://doi.org/10.3390/environsciproc2023026106





