Abstract
A smart, flexible, fuzzy-based regression is proposed in order to describe non-constant behavior of runoff as a function of precipitation. Hence, for high precipitation, beyond a fuzzy threshold, a conventional linear (precise) relation between precipitation and runoff is established, while for low precipitation, a curve with different behavior is activated. Between these curves and for a runoff range, each curve holds to some degree. Hence, a simplified Sugeno architecture scheme is established on few logical rules. Alternatively, the model can be enhanced by using a combination between the fuzzy linear regression of Tanaka and the aforementioned simplified Sugeno architecture. The training process is achieved based on the Particle Swarm Optimization (PSO) method.
1. Introduction
Due to the complexity and the inherent uncertainty of hydrological processes, it is rather impossible to apply white box (or physical-based) models to treat hydrological phenomena. Among the black box models, which can be used, the least square model is widely used. The scope of the article is to enhance the utility of the regression model by using fuzzy sets and logic. Hence, two models are proposed. The first one is based on the combination between the fuzzy reasoning and the least square method, and the other is based on the couple between the fuzzy reasoning and fuzzy regression.
Firstly, a simple relationship between precipitation and runoff at the annual scale could be successfully described by the law presented in Equation (1):
where is annual runoff in mm, is annual precipitation in mm, and (dimensionless) and (mm) are two parameters that may be estimated through linear regression [1,2]. may be interpreted as a rainfall depth threshold below which the runoff is zero and is a runoff coefficient at the annual scale. For humid climates, where annual precipitation is always greater than the runoff threshold, this simple relation is always valid. However, in certain arid or semi-arid climates, annual precipitation may be lower than the runoff threshold, and this would yield negative runoff, meaning that the relationship may not be valid for low precipitation years. In this work, a solution for this problem is proposed. For a high annual cumulative precipitation, beyond a threshold, a conventional (crisp) relation between precipitation and runoff is established, while for low precipitation, a curve with a lower slope must be derived. Between these curves, and for a precipitation range close to the runoff threshold, each curve holds to some degree. Hence, initially, the conventional regression is used for each area. Furthermore, the use of the fuzzy model proposed by Tanaka is later examined.
A simplified Sugeno architecture scheme is proposed based on only two logical rules. The training process is achieved based on an interplay between the Particle Swarm Optimization (PSO) method and either the conventional least square analysis or the widely used fuzzy regression model of Tanaka. Although there are many examples that illustrate the application of Sugeno Systems to water engineering problems based on the MATLAB toolbox, and even if the errors remain within acceptable range, sometimes the rational and logical basis of the model is ambiguous [3,4]. On the other hand, there are also applications of the if-then systems based on a logical explanation, but these lack a proper training process. The method proposed for the application presented in this work was successfully applied by [3] to assess bedload transport in gravel-bed rivers as a function of discharge. The combined use of the simplified Sugeno architecture with the fuzzy regression is proposed for the first time in this work.
2. Proposed Simplified Reasoning System by Using Crisp Regression
The independent variable (here the annual rainfall) takes only two linguistic values (high and low), which correspond to quantitative fuzzy sets, and hence, only two rules exist. Consequently, there are two areas without uncertainty where only one regression equation is activated. However, between two crisp areas (Figure 1), there is a grey area where both rules are activated to some degree. Based on Figure 1, it is obvious that only two rules were structured, whilst in fact, the grey area is between β1 and β2.
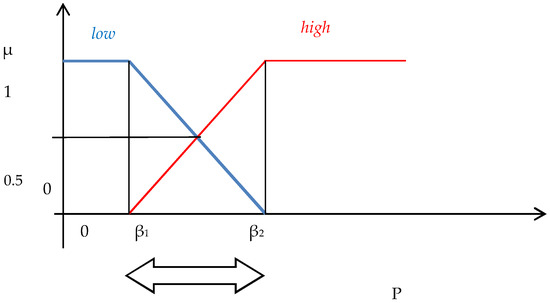
Figure 1.
Proposed simplified architecture of the fuzzy rule-based systems.
In this work, only one independent variable (annual precipitation) appears, P. For given variables β1 and β2, the following membership functions are modulated (Figure 1). From the picture, it is obvious that the following property holds:
As aforementioned, the reasoning consists of two rules:
| IF P (annual precipitation) is low, THEN y (annual Runoff) is | (MODEL 1) |
| IF P (annual precipitation) is high, THEN y (annual Runoff) is |
In this model, the coefficients are crisp numbers, so finally a nonlinear crisp curve is produced as follows:
where are the values of the membership functions of the linguistic terms low and high, respectively (Figure 1). Each rule is activated with respect of the values of the corresponding membership function.
In the case that the thresholds β1 and β2 are known, then the next linear system of algebraic equations is produced [3,4] in order to determine the vector θ:
In which M is the number of data. The superscript for P indicates the examined number of data.
In addition, b is the matrix that contains the values of the measured runoff (dependent variables)
Hence, according to the usual least squares method, the optimal vector θ* can be found:
The coefficient of determination can be adopted to evaluate the proposed model [3,5]:
Hence, if the thresholds β1 and β2 are known, the coefficients of the crisp linear equations can be determined with respect to Equations (3) and (5).
3. Proposed Simplified Architecture of the Fuzzy Rule Based System by Using Fuzzy Regression
The main difference with the previous model is that for each rule, a fuzzy regression is activated. Hence, the model will produce a fuzzy band, where all the data must be included within the produced fuzzy band [6,7]. Therefore, the following rule-based system is produced:
| IF P is low, THEN Annual Runoff, y is | (MODEL 2) |
| IF P is high, THEN Annual Runoff, y is |
In this new model, where the coefficients are fuzzy symmetrical triangular numbers, a nonlinear fuzzy curve is produced. Hence, the problem concludes to the following equation:
The tilde means the fuzziness and the characteristic of these numbers are the central value and the semi-widths. The aforementioned numbers are selected to be fuzzy symmetrical triangular numbers for simplicity reasons [6].
Even if the new proposed model produces more complexity, the proposed model has the advantage that all the data are located within the produced fuzzy estimation of the annual runoff. However, if the produced fuzzy band is large, the proposed model has no practical sense. Hence, the minimization of the width regarding the produced fuzzy estimation of the annual runoff is the key question in order to evaluate the applicability of the model. The mathematical background of the Tanaka model can be found in [6,7].
4. The Proposed Learning Process with the Use of PSO
Particle Swarm Optimization (PSO) is a heuristic, stochastic, global optimization method based on the behavior of the swarm [8]. Each possible solution is called a particle, and the set of potential solutions in each iteration creates the ‘swarm’. A ‘swarm’ has a dimension N’, in which N’ is the number of examined solutions. Each examined solution is made up of D variables, in which D is the dimension of the problem [8]. Here, D = 2; that is, the couple (β1, β2). More details about the method can be found in [8,9,10,11].
Firstly, a swarm of candidate solutions is randomly structured. Each of them contains only the (crisp) values of the β1, β2, which are the aforementioned parameters of the membership functions. Two cases can be distinguished. The first one is the use of crisp regression, and hence, the least square method is activated, whilst the second choice is the use of the fuzzy model of Tanaka. In the case of the Tanaka fuzzy regression being used, for each candidate solution, a linear programming problem is used.
5. Case Study
The proposed method was successfully applied to the basins of two water resource basins in Spain: the Rio Piedras and Rio de Aguas basins. The Piedras River is a coastal river in the southwest of Spain. It drains a contributing basin of 550 km2, running from north to south along 40 km in the Huelva province. The mean annual precipitation is 574 mm/year, and mean annual runoff is 106 mm/year. It is regulated by the Piedras and Los Machos reservoirs, which are operated for water supply and irrigation. The Aguas river is a short coastal river in the south of Spain, running along 65 km through the east of the province of Almería. The contributing basin is 547 km2. The climate is semiarid, with mean annual precipitation of 334 mm/year and mean annual runoff of 41 mm/year.
Based on the proposed adaptive crisp regression between rainfall and runoff, the results are presented in Figure 2 in the case of Rio Piedras.
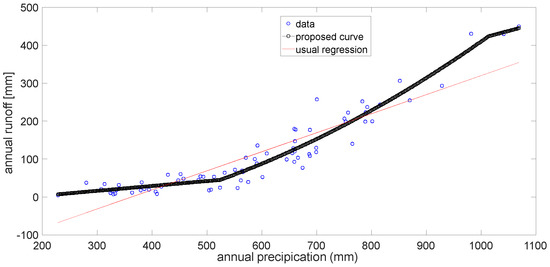
Figure 2.
The proposed method and the conventional regression applied in order to assess a relationship between annual precipitation and runoff in the case of Rio Piedras.
The proposed method recognizes the grey region between regarding the precipitation (524.06, 1013.43); that is, a large non-linear behavior. The produced equation is:
Another important question is the evolution of the swarms. After s significant number of iterations, but not immediately, the convergence of the swarm is obvious (Figure 3).
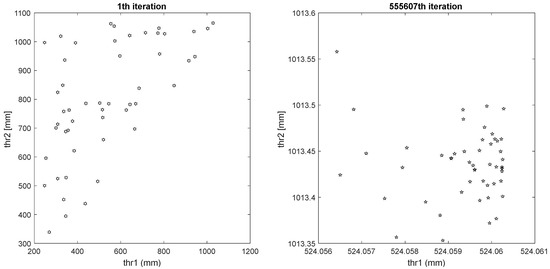
Figure 3.
The evolution of the parameter (β1, β2) after a sufficient number of iterations in the case of Rio Piedra.
The method is also applied in the case of the Rio de Aguas Basin. The results are shown in Figure 4. In both cases, a significant grey zone exists, as can be shown from Figure 2 and Figure 4. The results for the examined cases indicate that the proposed method better simulates the relationship between the annual precipitation and the annual runoff compared to the conventional crisp regression.
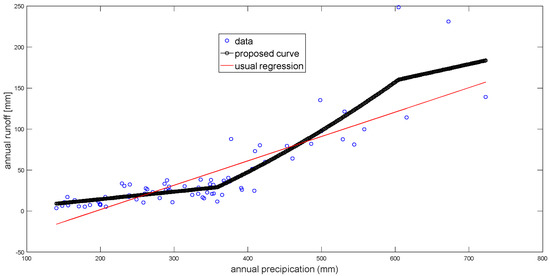
Figure 4.
The proposed method and the conventional regression applied in order to assess a relationship between annual precipitation and runoff in the case of Rio de Aguas.
Next, the proposed fuzzy rules with the simultaneous use of the fuzzy regression model of Tanaka is used in the case of Rio Piedras. The following fuzzy curve is produced (Figure 5):
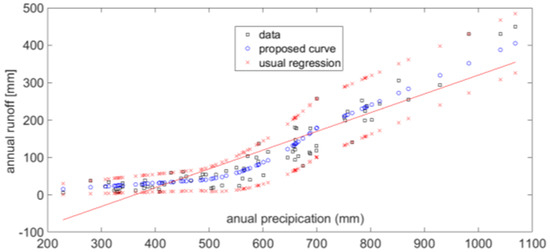
Figure 5.
The proposed method with fuzzy regression curves applied in order to assess a fuzzy relationship between annual precipitation and annual runoff in the case of Rio Piedras.
In the bracket, the first term denotes the central value, and the second term expresses the semi-width. For instance, the fuzzy estimation of the annual runoff in the case that the measured annual runoff is y = 98.8538 mm (in the case of Rio Piedras) is depicted in Figure 6.
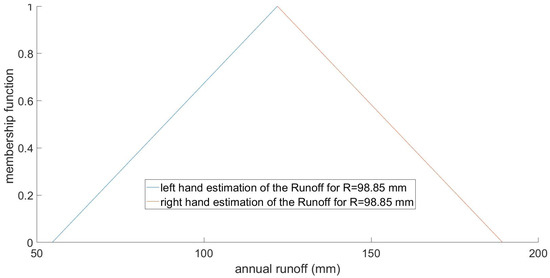
Figure 6.
Fuzzy estimation of the runoff in the case that the annual runoff is y = 98.8538 mm in the case of Rio Piedras.
The main difference between model 1 and model 2 is that in the last model, all the data must be included within the produced fuzzy estimation of the annual runoff. The proposed method is suitable to estimate the annual water yield, but it is not intended to assess the peak flow under a significant rainfall. However, the second model requires more computational time.
Author Contributions
Conceptualization, M.S. and L.G.; methodology, M.S. and L.G.; software, M.S. and L.G.; validation, M.S. and L.G.; formal analysis, M.S. and L.G.; investigation M.S. and L.G.; resources, L.G.; data curation, M.S. and L.G.; writing—original draft preparation, M.S. and L.G.; writing—review and editing, M.S. and L.G.; visualization M.S. and L.G.; supervision, M.S. and L.G.; project administration, M.S. and L.G.; funding acquisition, M.S. and L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data can be found in https://www.miteco.gob.es/es/agua/temas/evaluacion-de-los-recursos-hidricos/evaluacion-recursos-hidricos-regimen-natural/ (accessed on 28 March 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ponce, V.M. Engineering Hydrology: Principles and Practices; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; pp. 66–67. [Google Scholar]
- Spiliotis, M.; Garrote, L. Assessment of a Precipitation-Runoff relation based on a new fuzzy adaptive regression. In Proceedings of the 7th IAHR Europe Congress “Innovative Water Management in a Changing Climate”, Athens, Greece, 7–9 September 2022. [Google Scholar]
- Spiliotis, M.; Kitsikoudis, V.; Hrissanthou, V. Assessment of bedload transport in gravel-bed rivers with a new fuzzy adaptive regression. Eur. Water 2017, 57, 237–244. [Google Scholar]
- Sen, Z. Fuzzy Logic and Hydrological Modelling; Taylor and Francis Group, CRC Press: Boca Raton, FL, USA, 2010; p. 223. [Google Scholar]
- Chen, G.; Pham, T.T. Introduction to Fuzzy Sets, Fuzzy Logic, and Fuzzy Control Systems; CRC Press: Boca Raton, FL, USA, 2001; pp. 89–103. [Google Scholar]
- Tanaka, H. Fuzzy data analysis by possibilistic linear models. Fuzzy Sets Syst. 1987, 24, 363–375. [Google Scholar] [CrossRef]
- Kitsikoudis, V.; Spiliotis, M.; Hrissanthou, V. Fuzzy regression analysis for sediment incipient motion under turbulent flow conditions. Environ. Process. 2016, 3, 663–679. [Google Scholar] [CrossRef]
- Spiliotis, M.; Mediero, L.; Garrote, L. Optimization of Hedging Rules for Reservoir Operation during Droughts Based on Particle Swarm Optimization. Water Resour. Manag. 2016, 30, 5759–5778. [Google Scholar] [CrossRef]
- Parsopoulos, K.E.; Vrahatis, M.N. Recent Approaches to Global Optimization Problems through Particle Swarm Optimization. Nat. Comput. 2002, 1, 235–306. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Simpson, P.K.; Dobbins, R.W. Computational Intelligence PC Tools; Academic Press Professional: Boston, MA, USA, 1996. [Google Scholar]
- Poli, P.; Keenedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).