Fuzzy Analytical Solution for the Case of a Semi-Infinite Unconfined Aquifer †
Abstract
1. Introduction
2. Constructing the Fuzzy Model and Solution
2.1. Crisp Model
2.2. Fuzzy Model
2.3. Solution of the First System
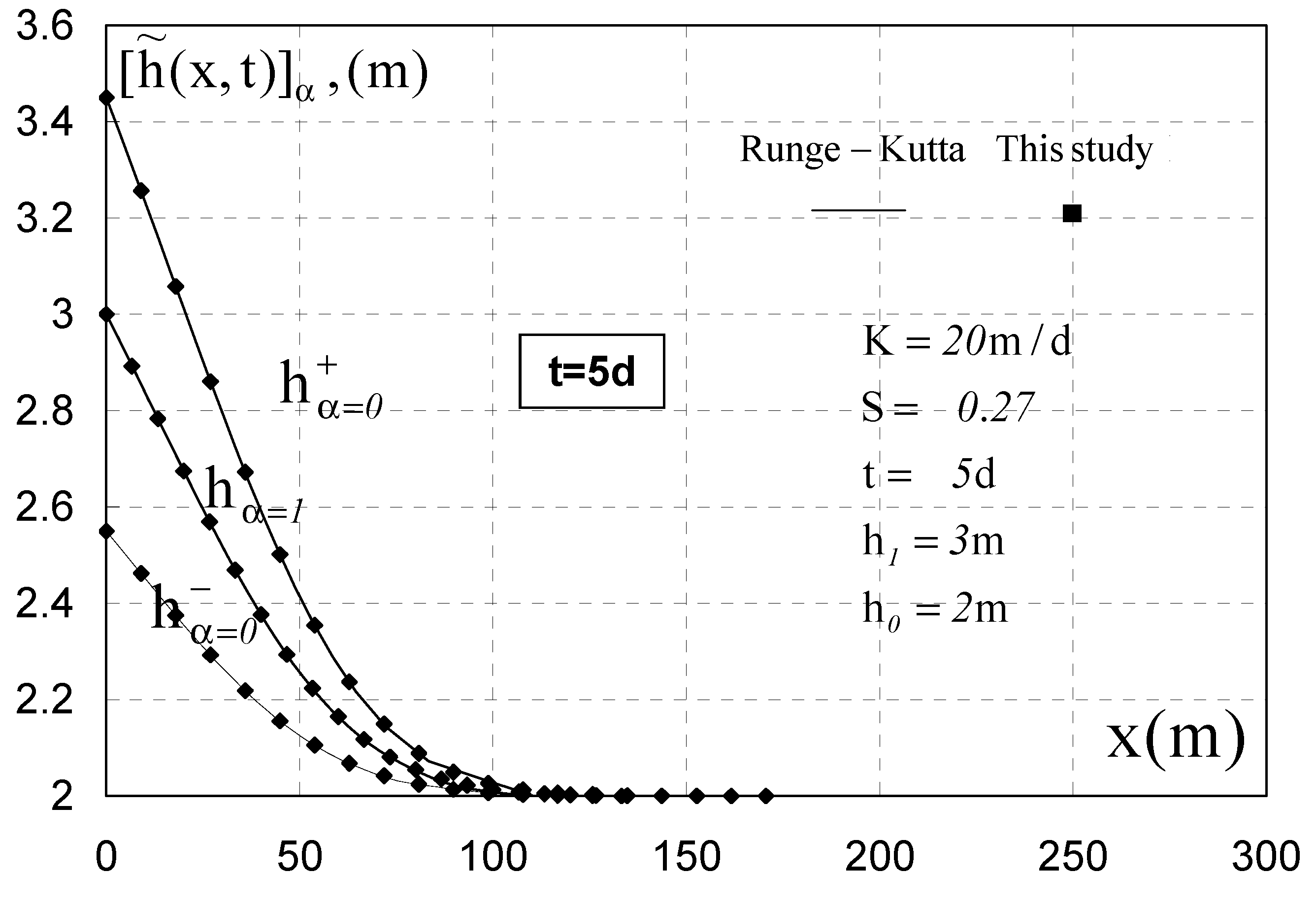
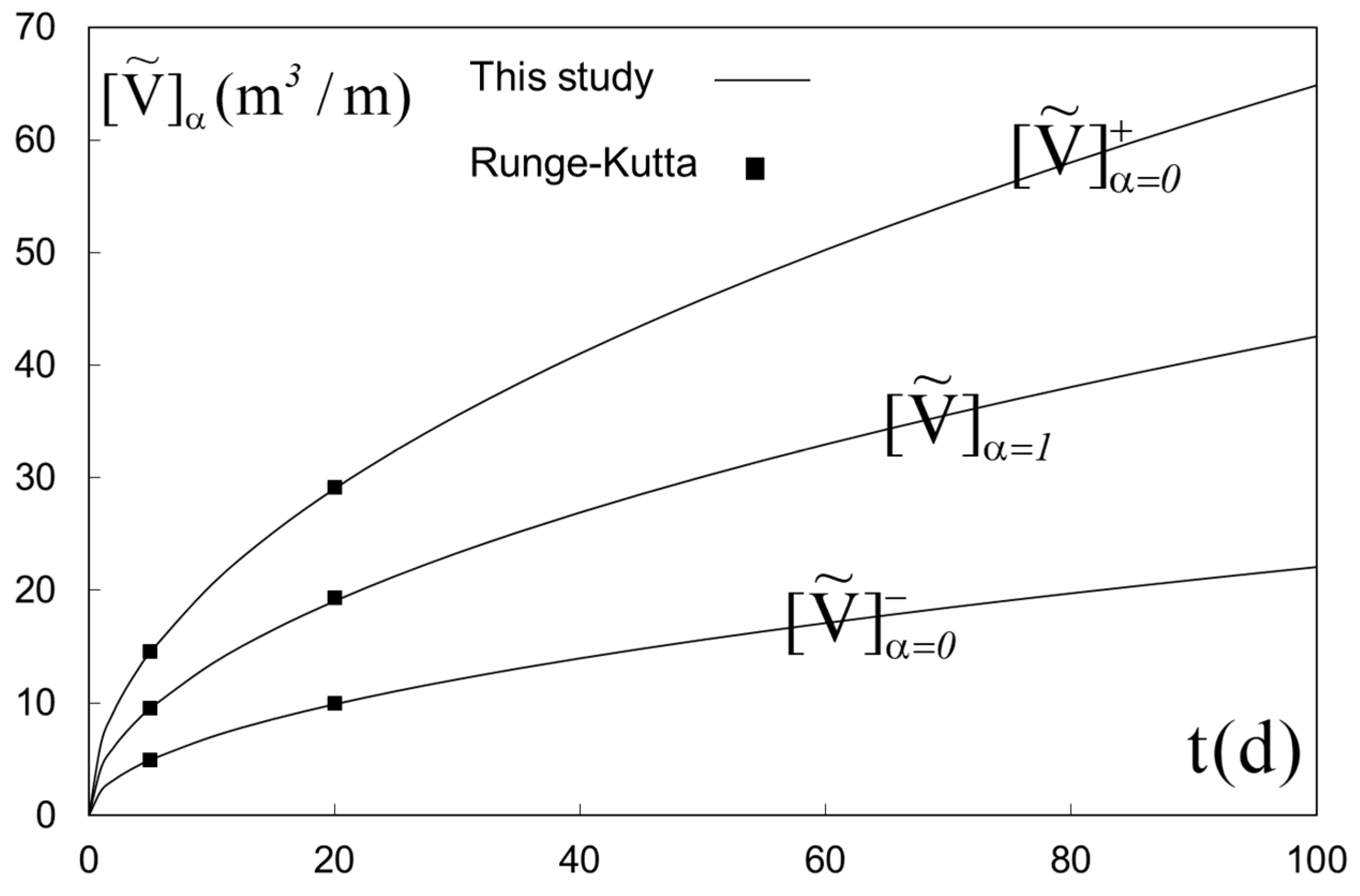
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boussinesq, J. Recherches théoriques sur l’écoulement des nappes d’eau infiltrées dans le sol et sur le débit des sources. J. De Mathématiques Pures Appliquées 1904, 10, 5–78. [Google Scholar]
- Polubarinova-Cochina, P.Y. On unsteady motions of groundwater during seepage from water reservoirs. PMM (Prinkladaya Matematica I Mekhanica) 1949, 13, 2. [Google Scholar]
- Polubarinova-Cochina, P.Y. Theory of Groundwater Movement; Moscow: Gostekhizdat, Old Soviet Union (Now Russia); de Wiest, R.J.M., Translator; Princeton University Press: Princeton, NJ, USA, 1962. (In Russia) [Google Scholar]
- Tolikas, P.K.; Sidiropoulos, E.; Tzimopoulos, C.D. A simple analytical solution for the Boussinesq one-dimensional groundwater flow equation. Water Resour. Res. 1984, 20, 24–28. [Google Scholar] [CrossRef]
- Lockington, D.A. Response of unconfined aquifer to sudden change in boundary head. J. Irrig. Drain. Eng. 1997, 123, 24–27. [Google Scholar] [CrossRef]
- Moutsopoulos, K.N. The analytical solution of the Boussinesq equation for flow induced by a step change of the water table elevation revisited. Transp. Porous Media 2010, 85, 919–940. [Google Scholar] [CrossRef]
- Lockington, D.A.; Parlange, J.Y.; Parlange, M.B.; Selker, J. Similarity solution of the Boussinesq equation. Adv. Water Resour. 2000, 23, 725–729. [Google Scholar] [CrossRef]
- Basha, H.A. Traveling wave solution of the Boussinesq equation for groundwater flow in horizontal aquifers. Water Resour. Res. 2013, 49, 1668–1679. [Google Scholar] [CrossRef]
- Chor, T.; Dias, N.L.; de Zarate, A.R. An exact series and improved numerical and approximate solutions for the Boussinesq equation. Water Resour. Res. 2013, 49, 7380–7387. [Google Scholar] [CrossRef]
- Hayek, M. Accurate approximate semi-analytical solutions to the Boussinesq groundwater flow equation for recharging and discharging of horizontal unconfined aquifers. J. Hydrol. 2019, 570, 411–422. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Papadopoulos, K.; Evangelides, C.; Spyrides, A. Analytical solution of nonlinear Boussinesq equation. Desalination Water Treat. 2022, 24, 1127–1147. [Google Scholar] [CrossRef]
- Chen, Z.-X.; Bodvarsson, G.S.; Witherspoon, E.A.; Yortsos, Y.C. An integral equation formulation for the unconfined flow of groundwater with variable inlet conditions. Transp. Porous Media 1995, 18, 15–36. [Google Scholar] [CrossRef]
- Parlange, J.-Y.; Hogarth, W.L.; Govindaraju, R.S.; Parlange, M.B.; Lockington, D. On an Exact Analytical Solution of the Boussinesq Equation. Transp. Porous Media 2000, 39, 339–345. [Google Scholar] [CrossRef]
- Pistiner, A. Similarity solution to unconfined flow in an aquifer. Transp. Porous Media 2008, 71, 265–272. [Google Scholar] [CrossRef]
- Olsen, J.S.; Telyakovskiy, A.S. Polynomial approximate solutions of a generalized Boussinesq equation. Water Resour. Res. 2013, 49, 3049–3053. [Google Scholar] [CrossRef]
- Bartlett, M.S.; Porporato, A. A Class of exact solutions of the Boussinesq equation for horizontal and sloping aquifers. Water Resour. Res. 2018, 54, 767–778. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Papadopoulos, K.; Evangelides, C.; Papadopoulos, B. Fuzzy solution to the unconfined aquifer problem. Water 2018, 11, 54. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Papadopoulos, K.; Evangelides, C. Fuzzy Solution to the Second Order Unsteady Partial Differential Equation. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2018), Rhodes, Greece, 13–18 September 2018; Volume 2116, pp. 440004-1–440004-5. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965. [Google Scholar] [CrossRef]
- Bhaskar, V.; Lakshikantham, T.; Devi, V. Revisiting fuzzy differential equations. Nonlinear Anal. 2004, 58, 351–358. [Google Scholar]
- Nieto, J.J.; Rodríguez-López, R. Bounded solutions for fuzzy differential and integral equations. Chaos Solitons Fractals 2006, 27, 1376–1386. [Google Scholar] [CrossRef]
- Aminikhah, H. Approximate analytical solution for the one-dimensional nonlinear Boussinesq equation. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 831–840. [Google Scholar] [CrossRef]
- Chen, F.; Qiu, X.; Alattas, K.A.; Mohammadzadeh, A.; Ghaderpour, E. A New Fuzzy Robust Control for Linear Parameter-Varying Systems. Mathematics 2022, 10, 3319. [Google Scholar] [CrossRef]
- Guo, M.; Xue, X.; Li, R. The oscillation of delay differential inclusions and fuzzy biodynamics models. Math. Comput. Model. 2003. [Google Scholar] [CrossRef]
- Chang, S.S.L.; Zadeh, L.A. On Fuzzy Mapping and Control. IEEE Trans. Syst. Man Cybern. 1972. [CrossRef]
- Dubois, H.; Prade, D. Towards fuzzy differential calculus: Part 3, differentiation. Fuzzy Sets Syst. 1982, 8, 30–34. [Google Scholar] [CrossRef]
- Puri, M.L.; Ralescu, D.A. Differentials of fuzzy functions. J. Math. Anal. Appl. 1983, 91, 552–558. [Google Scholar] [CrossRef]
- Hukuhara, M. Integration des Applications Measurables dont la Valeur est un Compact Convexe. Funkc. Ekvacioj 1967, 10, 205–233. [Google Scholar]
- Kaleva, O. Fuzzy differential equations. Fuzzy Sets Syst. 1987, 24, 301–307. [Google Scholar] [CrossRef]
- Kaleva, O. The cauchy problem for fuzzy differential equations. Fuzzy Sets Syst. 1990, 24, 389–396. [Google Scholar] [CrossRef]
- Seikkala, S. On the fuzzy initial value problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Allahviranloo, T. Numerical solution of fuzzy differential equation. Math. Comput. Appl. 2002, 7, 41–52. [Google Scholar] [CrossRef]
- Bede, B.; Gal, S.G. Generalizations of the differentiability of fuzzy-number-valued functions with applications to fuzzy differential equations. Fuzzy Sets Syst. 2005, 151, 581–599. [Google Scholar] [CrossRef]
- Stefanini, L.; Bede, B. Generalized Hukuhara differentiability of interval-valued functions and interval differential equations. Nonlinear Anal. Theory Methods Appl. 2009, 71, 1311–1328. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Gouyandeh, Z.; Armand, A.; Hasanoglu, A. On fuzzy solutions for heat equation based on generalized Hukuhara differentiability. Fuzzy Sets Syst. 2015, 265, 1–23. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Papaevangelou, G.; Papadopoulos, K.; Evangelides, C. Fuzzy Analytical Solution to Vertical Infiltration. J. Softw. Eng. Appl. 2020, 13, 41–46. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. When upper probabilities are possibility Measures. Fuzzy Sets Syst. 1992, 49, 65–74. [Google Scholar] [CrossRef]
- Mylonas, N. Applications in Fuzzy Statistic and Approximate Reasoning. Ph.D. Thesis, Dimokritos University of Thrace, Komotini, Greece, 2022. (In Greek). [Google Scholar]
- Khastan, A.; Nieto, J.J. A boundary value problem for second order fuzzy differential equations. Nonlinear Anal. Theory Methods Appl. 2010, 72, 3583–3593. [Google Scholar] [CrossRef]
- Bede, B.; Stefanini, L. Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst. 2013, 230, 119–141. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzimopoulos, C.; Samarinas, N.; Papadopoulos, K.; Evangelides, C. Fuzzy Analytical Solution for the Case of a Semi-Infinite Unconfined Aquifer. Environ. Sci. Proc. 2023, 25, 70. https://doi.org/10.3390/ECWS-7-14303
Tzimopoulos C, Samarinas N, Papadopoulos K, Evangelides C. Fuzzy Analytical Solution for the Case of a Semi-Infinite Unconfined Aquifer. Environmental Sciences Proceedings. 2023; 25(1):70. https://doi.org/10.3390/ECWS-7-14303
Chicago/Turabian StyleTzimopoulos, Christos, Nikiforos Samarinas, Kyriakos Papadopoulos, and Christos Evangelides. 2023. "Fuzzy Analytical Solution for the Case of a Semi-Infinite Unconfined Aquifer" Environmental Sciences Proceedings 25, no. 1: 70. https://doi.org/10.3390/ECWS-7-14303
APA StyleTzimopoulos, C., Samarinas, N., Papadopoulos, K., & Evangelides, C. (2023). Fuzzy Analytical Solution for the Case of a Semi-Infinite Unconfined Aquifer. Environmental Sciences Proceedings, 25(1), 70. https://doi.org/10.3390/ECWS-7-14303







