Abstract
Many hydrological responses rely on the water content of the soil (WCS). Therefore, in this study, the surface WCS products of the Google Earth Engine Soil Moisture Active Passive (GEE SMAP) were modeled by a support vector machine (SVM), and extreme learning machine (ELM) models optimized by the teacher learning (TLBO) algorithm for Quebec, Canada. The results showed that the ELM model is only able to forecast 23 steps with Correlation Coefficient (R) = 0.8313, Root Mean Square Error (RMSE) = 6.1285, and Mean Absolute Error (MAE) = 5.0021. The SVM model could only estimate the future steps, one step ahead, with R = 0.8406, RMSE = 18.022, and MAE = 17.9941. Both models’ accuracy dropped significantly while forecasting longer periods.
1. Introduction
Numerous hydrological reactions depend on the amount of water in the soil. As soil moisture rises, more runoff is created, resulting in increased sediment movement. This environmental element affects the soil’s erosion resistance. Runoff, sediment, and erosion are crucial in hydraulic structure design and watershed studies. The variations in the WCS affect the agriculture section. The sustainable management of agricultural water and land resources depends on this factor. Many environmental parameters, such as soil and surface temperature, the amount of precipitation, and groundwater level, influence this parameter. Hydrological extremes and climate variations intensely impact these parameters, which increases the importance of studying WCS under changing climate conditions. The constraints of measuring and expenditure limitation cause this parameter not to be accessible at high spatio-temporal resolutions everywhere, particularly in vast areas like Quebec. Therefore, a strategy should be considered for collecting and modeling this useful parameter in data-scarce locations. This research will use SMAP products to model and forecast the WCS.
Accordingly, Google Earth Engine (GEE) cloud datasets will be used. Using this platform provides the possibility of obtaining curated datasets worldwide. This platform uses high-efficiency computing resources and cloud-based calculations to process planetary-scale data more efficiently. It also allows users to share their products and analysis in the form of an application (app) [1]. One of these valuable apps is SOILPARAM, developed by [2]. This app provides historical records of some soil parameters in the form of a time series.
Using machine learning (ML) methods in modeling and forecasting hydrological data analysis is common. The regression support vector machine (SVM) and extreme learning machine (ELM) models are two of many artificial intelligence (AI) methods that have proven their potential power in modeling natural phenomena. The inherent intense seasonality and stochastic patterns in the WCS make these modeling techniques suitable for forecasting and extracting patterns from the datasets. Both models are considerably fast and structurally simple when compared to other AI methods. They can be used for generating real-time results. ELM is a single-layer feed-forward network model known for its simple structure, fast computational process, and accuracy in forecasting non-linear, highly seasonal datasets [3]. The ELM’s accuracy in forecasting rainfall [3], flows in rivers [4], sediment transport [5], etc. has been proven. The authors of [6] used the ELM model and its integration with ensemble empirical mode decomposition to forecast the WCS in the upper layer of soil and compared it with a random forest. The model outcomes showed that ELM outperformed the random forest, and its hybridization increased the accuracy. Likewise, the SVM model has been used widely in modeling datasets because of its simplicity, and derivable equations. For instance, ref. [7] used SVM to forecast the WCS, five steps ahead by feeding the climatic factors as inputs to the model. They reported a good performance for the SVM model as a result of using six meteorological inputs and the first lag of WCS at 0.05 and 0.1 m.
The advantages of these two methods were addressed briefly. However, similar to other AI methods, they suffer from input selection, model parameters tuning, and kernel selection. Since the SVM model is a linear method, it may produce naïve results in intense non-linear data. Optimizing them, using the teacher-learning-based optimization (TLBO) algorithm [8] will reduce the tuning and input selection problems and helps find a better solution. The major advantage of the TLBO is that it has significantly fewer controlling parameters than its equivalents and is readily applied to different models. This study consists of sequence research on the GEE SMAP WCS product completed by [8]. In that study, they used a deep learning long short-term memory (LSTM) model and used the WCS as the sole input of the model with optimization and structural investigation approaches. The outputs of that study showed the potential power of LSTM in forecasting WCS in a dynamic and long-term manner. Therefore, this study investigates whether the introduced models can produce similar results. The TLBO optimization similarly will be used and different lags of WCS as inputs will be checked to obtain the models’ capacity. Lastly, the length of their accurate forecast horizon will be determined.
2. Model Descriptions
2.1. Support Vector Machine
This approach is praised for being generalizable, powerful, and precise. Support Vector Machine (SVM) uses statistical theories and risk minimization structural concepts. In this method, a decision function is created to boost model generalization and reduce modeling errors by employing a deep dimensional space called feature space (FS) and therefore optimizing margin border separation [9,10]. This strategy works with datasets containing few samples. The SVM framework is based on the non-linear mapping of input space into a high-dimensional domain for identifying a hyperplane. It minimizes generalization errors [11].
If the target values would be WCSi (i = 1:l) as {(L1,WCS1), …,( Li,WCSi)} and Li as the lag inputs, in a training set with i samples, the Fl(x) as a linear function for training the network can be defined as follows:
where the slack variables, is the weights matrix and B equals to bias. The maximum margin size is obtained by calculation of the Euclidean norm of weights. To estimate weights (β), compute the objective function as:
C denotes the penalty constant. The Fl function approximates the training points with an ε error and then generalizes it. L1.L is the input variables’ dot products. To avoid performing dot multiplication on transformed data samples, a kernel function is written to replace each occurrence of it.
2.2. Extreme Learning Machine
The extreme learning machine (ELM) is a development of feed-forward neural networks that tries to solve the problem of time-consuming training and local minima trapping. Trapping results in reducing the generalizability and customizability of model parameters [12]. Accordingly, input weights and neuron bias are set stochastically, and output weights are computed by solving a linear equation as follows:
where WI and WO are the input and output weights, and AF is the activation functions. Li is the input variable, and z is the number of samples in each input variable. The iterative technique outlined by [13] is used in the ELM model to regulate the random selection of input weights and bias neurons, and increase generalizability. A total of 1000 iterations are set to find the best weights. Extra iterations did not influence model errors.
3. Evaluation Criteria
This study uses the conventional Coefficient of Determination (R), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) to evaluate and compare the models.
4. Study Region and Dataset Description
The study point is in the south of Quebec City, Canada, with a latitude of 46.73 N and a longitude of 71.5 W. The region comprises the Jacques-Cartier South, Chaudière, and Sainte-Anne rivers. The WCS data was downloaded from the National Aeronautics and Space Administration (NASA) Enhanced SMAP Global Soil Moisture Dataset uploaded in the GEE environment by NASA [14]. The dataset time range is from 2015 to July 2022, with a 3-day measurement interval. This dataset was averaged weekly to obtain a total of 306 data points. To train and evaluate the model, considering the size of the dataset, it was partitioned by a 70:30 ratio. The first partition, which contains 70% of the time series data points, was used to train the networks and find the optimum weights, while the remaining 30% of the dataset was used to evaluate the model forecasts and estimated weights. The statistical features are presented in Table 1. The dataset’s download link is presented in the “Data Availability Statement” section.

Table 1.
The dataset’s characteristics.
5. Data Investigation and Model Tunning
The range for optimization and input definition is considered as [1 lag, 7 lags] based on the ACF results (Figure 1). The range for the ELM hidden neuron size parameter is [1, 34] with 1000 iterations. The ranges for the SVM model are also: C and σ ∈ [0.01, 2000], ε ∈ [0.001, 1]. The TLBO parameters are population = 20 and maximum iteration = 100.
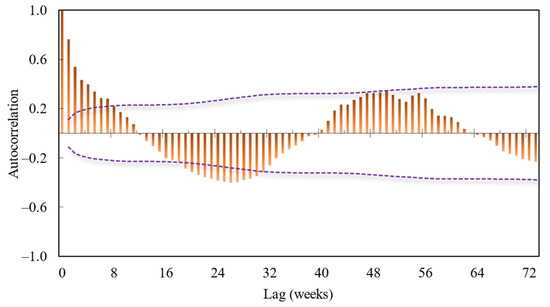
Figure 1.
The autocorrelation function of datapoints for ¼ of train data.
6. Model Results
A core i7 processor, with 16 Gigabytes of Random Access Memory (RAM), performed the modeling and the runtime for the ELM optimization was approximately 8 h. This time for the SVM model was 0.5 h, and, in both models, the optimum values were obtained in early iterations, specifically the SVM model (Figure 2a,b). After modeling, the optimum results were obtained by all seven inputs for both models and the maximum hidden neuron size for ELM. The optimum results of TLBO-ML integrations are presented in Table 2. The overall performance of both SVM and ELM models in the long-term forecast was very poor, and both methods generated very naïve results so that the most accurate outcome was obtained by ELM with R = 0.3654, RMSE = 17.9146, and MAE = 17.8131. The forecast process was performed based on the addition of each estimated step to the historical data, creating input lags and approximating the future step by the previous one. Therefore, both ELM and SVM forecasted the 77-point test period, and the long-term forecast was defined accordingly. This approach to forecasting failed, and it was found that both models’ forecasting accuracy is limited to less than 77 steps (Figure 3a,b).
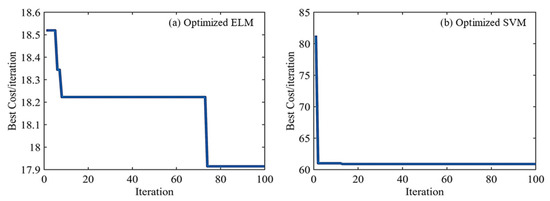
Figure 2.
The optimization process—the recordings of the best cost per iteration for ELM and SVM; the best costs per iteration of (a). optimized ELM model and (b). optimized SVM model.

Table 2.
The models’ evaluation results for the test period.
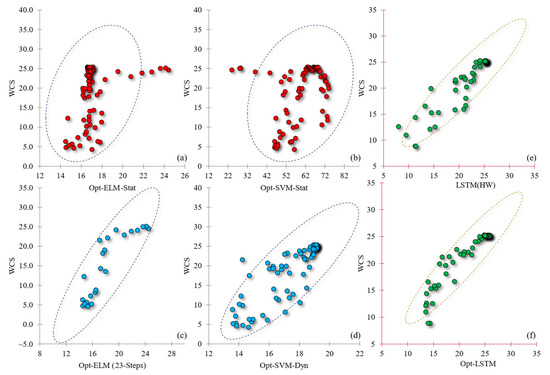
Figure 3.
The scatter plots of forecasted data points vs. observed WCS based on duration, stat: long-term-static, 77-step forecast, Dyn: 1-step forecast, Opt: Optimized. (a). static forecast of Opt.ELM, (b). static forecast of Opt.SVM, (c). short-term forecast of Opt.ELM, (d). dynamic forecast of Opt.SVM, (e). LSTM with HW preprocess, (f). forecast of Opt.LSTM, all vs. WCS [8].
By doing more research and defining the different forecasting steps in the modeling process, it was found that the ELM model can predict WCS values up to 23 steps into the future, with the correlation going up by 138%, the RMSE index going down by 65%, and the MAE index going down by 71% (Figure 3c,d). The SVM model’s forecasting accuracy is also limited to one step in the future, and considering the severe fluctuation in the dataset, this linear model is not able to forecast more than one step in the future. Nevertheless, the ELM (23-step) model was more successful in short-term forecasting than the SVM. In Figure 3c,d, it can be seen that the majority of the points are located in the 95% confidence intervals and estimations are closer to the linear form than the long-term forecasts.
Ref. [8] undertook a study on the same products of the GEE SMAP by an LSTM model. In that study, they used two approaches for the long-term forecasts of the WCS dataset. The results of both approaches are presented in Figure 3e,f. The LSTM model was more successful in estimating values and patterns than the long-term forecasts of the SVM and ELM. The best results of the LSTM in a 50-step, long-term forecast, were: R = 0.9220, RMSE = 1.9614, MAE = 1.2837 by the Holt–Winters (HW) preprocessing method, and by TLBO optimization it estimated the WCS values by R = 0.9337, RMSE = 1.7809, MAE = 1.1892, which is considerably more accurate than this study’s ML methods, even in the 23-step ELM and dynamic SVM forecasts. In conclusion, the ELM model is more capable of estimating the WCS values and fluctuation than the SVM, but it is limited to 23 steps, which is almost half of the dataset’s period. In other words, it can forecast up to half of the periodic patterns. However, using sole models without the methodology suggested in [8] cannot produce very accurate results. It is suggested that ELM or SVM integrate preprocessing techniques, such as advanced smoothing methods, or other seasonal methods in seasonal data, such as WCS, to reduce the fluctuations in the dataset’s structure, even if the periodic ACF pattern is not significant.
7. Conclusions
In this study, the surface soil moisture products of the GEE SMAP were modeled by SVM and ELM. The TLBO algorithm optimized these models to estimate future steps based on the forecast of each step. The results showed that the ELM model is only able to forecast 23 steps each time with R = 0.8313, RMSE = 6.1285, and MAE = 5.0021. The SVM model was only able to estimate the future steps one step ahead with R = 0.8406, RMSE = 18.022, and MAE = 17.9941. Both models’ accuracy dropped significantly while forecasting longer periods than the ones mentioned. Since this study is a sequence to a former study on the same product of SMAP by TLBO-LSTM, a comparison between the results was made. Accordingly, the proposed deep learning LSTM method in the former study is more successful in forecasting longer periods than ELM and SVM, with R = 0.9337, RMSE = 1.7809, and MAE = 1.1892. We suggest that advanced smoothing methods should be integrated, or other seasonal preprocessing techniques, to decrease both fluctuations and correlations in the time series structure.
Author Contributions
Conceptualization, H.B.; methodology, H.B. and M.Z.; software, M.Z.; validation, H.B. and M.Z.; formal analysis, M.Z.; investigation, M.Z.; resources, H.B.; data curation, M.Z.; writing—original draft preparation, M.Z.; writing—review and editing, H.B.; visualization, M.Z.; supervision, H.B.; project administration, H.B.; funding acquisition, H.B. and M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support provided by Fonds de recherche du Québec—Nature et technologies (FRQNT) (#316369) and Natural Sciences and Engineering Research Council of Canada (NCERT) Discovery Grant (#RGPIN-2020-04583) to perform the current research.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The readers can find the dataset by the following GEE app [SOILPARAM] developed by [2]: Link to app: https://zemoh.users.earthengine.app/view/soilparam (accessed on 24 December 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Zeynoddin, M.; Bonakdari, H.; Gumiere, S.J.; Caron, J.; Rousseau, A.N. SOILPARAM 1.0: A Global-Scaled Enhanced Remote Sensing Application for Soil Characteristics Data Retrieval—Google Engine Environment, An Open-Source Treasure. In Proceedings of the IAHR World Congress From Snow to Sea, Granada, Spain, 18–23 June 2022; Ortega-Sánchez, M., Ed.; International Association for Hydro-Environment Engineering and Research (IAHR): Granada, Spain, 2022; pp. 5309–5319, ISBN 978-90-832612-1-8. [Google Scholar]
- Zeynoddin, M.; Bonakdari, H.; Azari, A.; Ebtehaj, I.; Gharabaghi, B.; Madavar, H.R. Novel hybrid linear stochastic with non-linear extreme learning machine methods for forecasting monthly rainfall a tropical climate. J. Environ. Manag. 2018, 222, 190–206. [Google Scholar] [CrossRef] [PubMed]
- Deo, R.C.; Şahin, M. An extreme learning machine model for the simulation of monthly mean streamflow water level in eastern Queensland. Environ. Monit. Assess. 2016, 188, 90. [Google Scholar] [CrossRef] [PubMed]
- Bonakdari, H.; Ebtehaj, I. A comparative study of extreme learning machines and support vector machines in prediction of sediment transport in open channels. Int. J. Eng. 2016, 29, 1499–1506. [Google Scholar]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Soil moisture forecasting by a hybrid machine learning technique: ELM integrated with ensemble empirical mode decomposition. Geoderma 2018, 330, 136–161. [Google Scholar] [CrossRef]
- Khalil, A.; Gill, M.K.; McKee, M. New applications for information fusion and soil moisture forecasting. In Proceedings of the 2005 7th International Conference on Information Fusion, Philadelphia, PA, USA, 24–27 July 2005; IEEE: Piscataway, NJ, USA, 2005; p. 7, ISBN 0-7803-9286-8. [Google Scholar]
- Zeynoddin, M.; Bonakdari, H. Structural-optimized sequential deep learning methods for surface soil moisture forecasting, case study Quebec, Canada. Neural. Comput. Applic. 2022, 34, 19895–19921. [Google Scholar] [CrossRef]
- Sharafi, H.; Ebtehaj, I.; Bonakdari, H.; Zaji, A.H. Design of a support vector machine with different kernel functions to predict scour depth around bridge piers. Nat. Hazards 2016, 84, 2145–2162. [Google Scholar] [CrossRef]
- Azimi, H.; Bonakdari, H.; Ebtehaj, I. Design of radial basis function-based support vector regression in predicting the discharge coefficient of a side weir in a trapezoidal channel. Appl. Water Sci. 2019, 9, 78. [Google Scholar] [CrossRef]
- Yapıcı, E.; Akgün, H.; Özkan, K.; Günkaya, Z.; Özkan, A.; Banar, M. Prediction of gas product yield from packaging waste pyrolysis: Support vector and Gaussian process regression models. Int. J. Environ. Sci. Technol. 2022, 20, 461–476. [Google Scholar] [CrossRef]
- Bonakdari, H.; Qasem, S.N.; Ebtehaj, I.; Zaji, A.H.; Gharabaghi, B.; Moazamnia, M. An expert system for predicting the velocity field in narrow open channel flows using self-adaptive extreme learning machines. Measurement 2020, 151, 107202. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Soltani, K.; Amiri, A.; Faramarzi, M.; Madramootoo, C.A.; Bonakdari, H. Prognostication of Shortwave Radiation Using an Improved No-Tuned Fast Machine Learning. Sustainability 2021, 13, 8009. [Google Scholar] [CrossRef]
- Sazib, N.; Mladenova, I.; Bolten, J. Leveraging the Google Earth Engine for Drought Assessment Using Global Soil Moisture Data. Remote Sens. 2018, 10, 1265. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).