A Monthly Water Balance Model for Assessing Streamflow Uncertainty in Hydrologic Studies †
Abstract
:1. Introduction
2. Materials and Methods
2.1. The R-UTHBAL Model
2.2. Water Balance Modelling Procedure
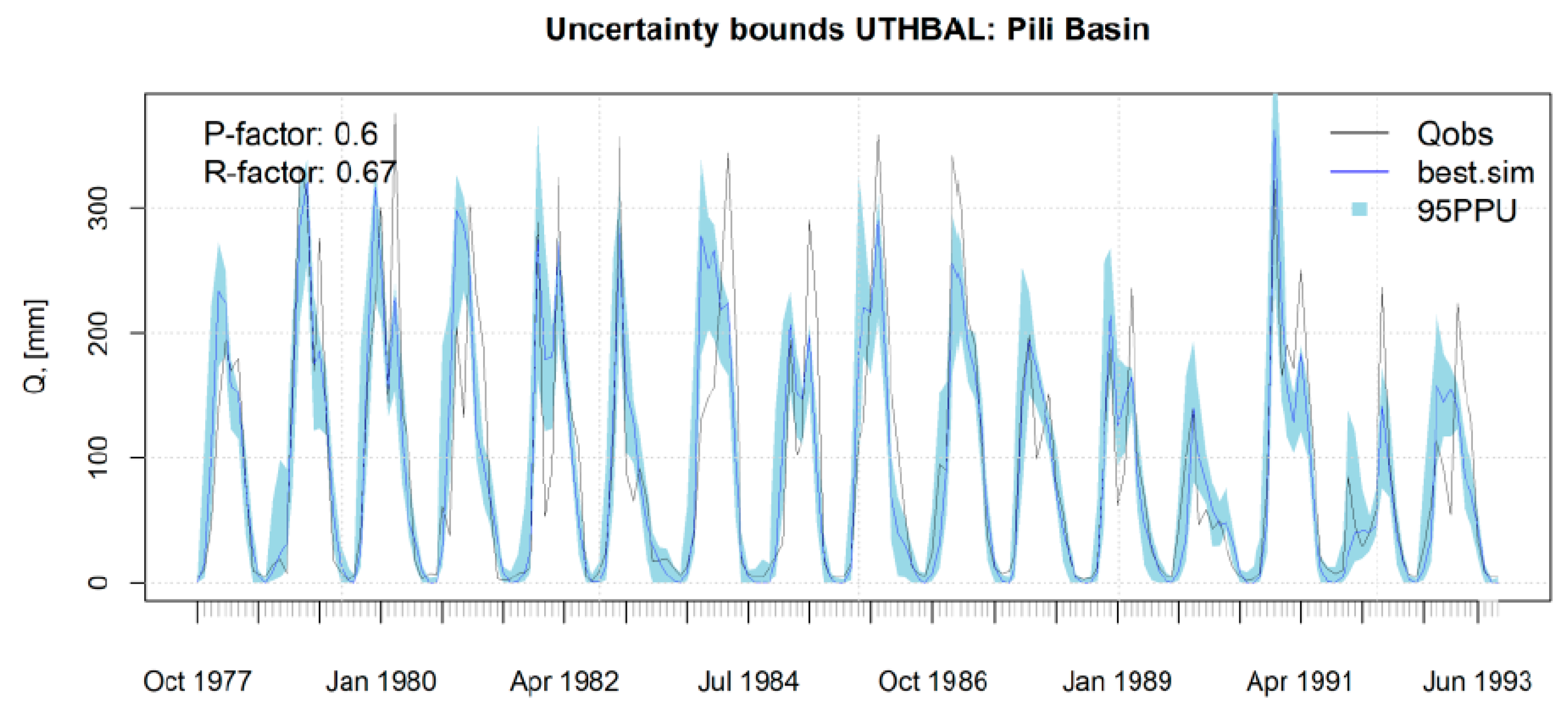
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Engeland, K.; Xu, C.-Y.; Gottschalk, L. Assessing Uncertainties in a Conceptual Water Balance Model Using Bayesian Methodology/Estimation Bayésienne Des Incertitudes Au Sein d’une Modélisation Conceptuelle de Bilan Hydrologique. Hydrol. Sci. J. 2005, 50, 9. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; van der Sluijs, J.P.; Højberg, A.L.; Vanrolleghem, P.A. Uncertainty in the Environmental Modelling Process—A Framework and Guidance. Environ. Model. Softw. 2007, 22, 1543–1556. [Google Scholar] [CrossRef]
- Loukas, A.; Mylopoulos, N.; Vasiliades, L. A Modeling System for the Evaluation of Water Resources Management Strategies in Thessaly, Greece. Water Resour. Manag. 2007, 21, 1673–1702. [Google Scholar] [CrossRef]
- Vasiliades, L.; Loukas, A. Hydrological Response to Meteorological Drought Using the Palmer Drought Indices in Thessaly, Greece. Desalination 2009, 237, 3–21. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Rojas, R. A Model-Independent Particle Swarm Optimisation Software for Model Calibration. Environ. Model. Softw. 2013, 43, 5–25. [Google Scholar] [CrossRef]
- Malamataris, D.; Kolokytha, E.; Loukas, A. Integrated Hydrological Modelling of Surface Water and Groundwater under Climate Change: The Case of the Mygdonia Basin in Greece. J. Water Clim. Change 2020, 11, 1429–1454. [Google Scholar] [CrossRef]
- Lyra, A.; Loukas, A.; Sidiropoulos, P.; Tziatzios, G.; Mylopoulos, N. An Integrated Modeling System for the Evaluation of Water Resources in Coastal Agricultural Watersheds: Application in Almyros Basin, Thessaly, Greece. Water 2021, 13, 268. [Google Scholar] [CrossRef]
- van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A Global Sensitivity Analysis Tool for the Parameters of Multi-Variable Catchment Models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff Conditions in the Upper Danube Basin under an Ensemble of Climate Change Scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]



| Parameter | Min Value | Max Value | Ranking Number | Normalised Relative Importance (%) | Optimised Value 1960–1977 | Optimised Value 1977–1993 |
|---|---|---|---|---|---|---|
| Cm | 0 | 12 | 6 | 09.96 | 6.660 | 2.149 |
| CN | 30 | 100 | 5 | 14.47 | 45.435 | 46.546 |
| K | 0 | 1 | 4 | 17.16 | 0.005 | 0.299 |
| α = aAET | 0 | 1 | 3 | 18.70 | 0.002 | 0.261 |
| β = CONMR | 0 | 1 | 2 | 19.66 | 0.120 | 0.091 |
| γ = CONGROUND | 0 | 1 | 1 | 20.02 | 0.943 | 0.988 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasiliades, L.; Mastraftsis, I. A Monthly Water Balance Model for Assessing Streamflow Uncertainty in Hydrologic Studies. Environ. Sci. Proc. 2023, 25, 39. https://doi.org/10.3390/ECWS-7-14192
Vasiliades L, Mastraftsis I. A Monthly Water Balance Model for Assessing Streamflow Uncertainty in Hydrologic Studies. Environmental Sciences Proceedings. 2023; 25(1):39. https://doi.org/10.3390/ECWS-7-14192
Chicago/Turabian StyleVasiliades, Lampros, and Ioannis Mastraftsis. 2023. "A Monthly Water Balance Model for Assessing Streamflow Uncertainty in Hydrologic Studies" Environmental Sciences Proceedings 25, no. 1: 39. https://doi.org/10.3390/ECWS-7-14192
APA StyleVasiliades, L., & Mastraftsis, I. (2023). A Monthly Water Balance Model for Assessing Streamflow Uncertainty in Hydrologic Studies. Environmental Sciences Proceedings, 25(1), 39. https://doi.org/10.3390/ECWS-7-14192







