Nonlinear Autoregressive Exogenous (NARX) Neural Network Models for Storm Tide Forecasting in the Venice Lagoon †
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Dataset
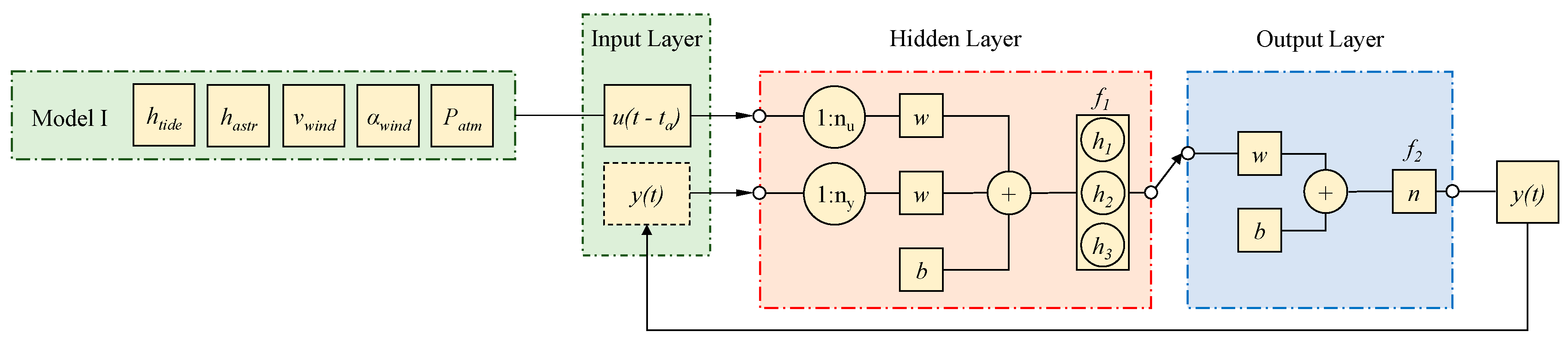
2.2. NARX Model Architectures
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Umgiesser, G. The impact of operating the mobile barriers in Venice (MOSE) under climate change. J. Nat. Conserv. 2020, 54, 125783. [Google Scholar] [CrossRef]
- Trincardi, F.; Barbanti, A.; Bastianini, M.; Benetazzo, A.; Cavaleri, L.; Chiggiato, J.; Papa, A.; Pomaro, A.; Sclavo, M.; Tosi, L.; et al. The 1966 Flooding of Venice: What Time Taught Us for the Future. Oceanography 2016, 29, 178–186. [Google Scholar] [CrossRef]
- Tosi, L.; Teatini, P.; Strozzi, T. Natural versus anthropogenic subsidence of Venice. Sci. Rep. 2013, 3, 2710. [Google Scholar] [CrossRef] [PubMed]
- Reimann, L.; Vafeidis, A.; Brown, S.; Hinkel, J.; Tol, R. Mediterranean UNESCO World Heritage at risk from coastal flooding and erosion due to sea-level rise. Nat. Commun. 2018, 9, 4161. [Google Scholar] [CrossRef] [PubMed]
- Canestrelli, E.; Canestrelli, P.; Corazza, M.; Filippone, M.; Giove, S.; Masulli, F. Local Learning of Tide Level Time Series using a Fuzzy Approach. In Proceedings of the IEEE International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007; pp. 1813–1818. [Google Scholar]
- Danandeh Mehr, A.; Nourani, V.; Karimi Khosrowshahi, V.; Ghorbani, M.A. A hybrid support vector regression—Firefly model for monthly rainfall forecasting. Int. J. Environ. Sci. Technol. 2019, 16, 335–346. [Google Scholar] [CrossRef]
- Di Nunno, F.; Alves, P.F.; de Marinis, G.; Di Felice, F.; Gargano, R.; Miozzi, M.; Granata, F. Deformation of Air Bubbles Near a Plunging Jet Using a Machine Learning Approach. Appl. Sci. 2020, 10, 3879. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Artificial Intelligence models for prediction of the tide level in Venice. Stoch. Environ. Res. Risk Assess. 2021, 35, 2537–2548. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Air Entrainment in Drop Shafts: A Novel Approach Based on Machine Learning Algorithms and Hybrid Models. Fluids 2022, 7, 20. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F.; Pham, Q.B.; de Marinis, G. Precipitation Forecasting in Northern Bangladesh Using a Hybrid Machine Learning Model. Sustainability 2022, 14, 2663. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A.E. Evaluation of seasonally classified inputs for the prediction of daily groundwater levels: NARX networks vs support vector machines. Environ. Model. Assess. 2019, 24, 223–234. [Google Scholar] [CrossRef]
- Riazi, A. Accurate tide level estimation: A deep learning approach. Ocean Eng. 2020, 198, 107013. [Google Scholar] [CrossRef]
- Ghamariadyan, M.; Imteaz, M.A. A Wavelet Artificial Neural Network method for medium-term rainfall prediction in Queensland (Australia) and the comparisons with conventional methods. Int. J. Climatol. 2021, 41, E1396–E1416. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F.; Gargano, R.; de Marinis, G. Prediction of spring flows using nonlinear autoregressive exogenous (NARX) neural network models. Environ. Monit. Assess. 2021, 193, 350. [Google Scholar] [CrossRef] [PubMed]
- Di Nunno, F.; de Marinis, G.; Gargano, R.; Granata, F. Tide Prediction in the Venice Lagoon Using Nonlinear Autoregressive Exogenous (NARX) Neural Network. Water 2021, 13, 1173. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F.; Gargano, R.; de Marinis, G. Forecasting of Extreme Storm Tide Events Using NARX Neural Network-Based Models. Atmosphere 2021, 12, 512. [Google Scholar] [CrossRef]
- Di Nunno, F.; Race, M.; Granata, F. A nonlinear autoregressive exogenous (NARX) model to predict nitrate concentration in rivers. Environ. Sci. Pollut. Res. 2022, 29, 40623–40642. [Google Scholar] [CrossRef] [PubMed]
- Comune di Venezia. Centro Previsioni e Segnalazioni Maree—La marea—La marea astronomica, 2020. Available online: https://www.comune.venezia.it/it/content/la-marea-astronomica (accessed on 13 May 2022).
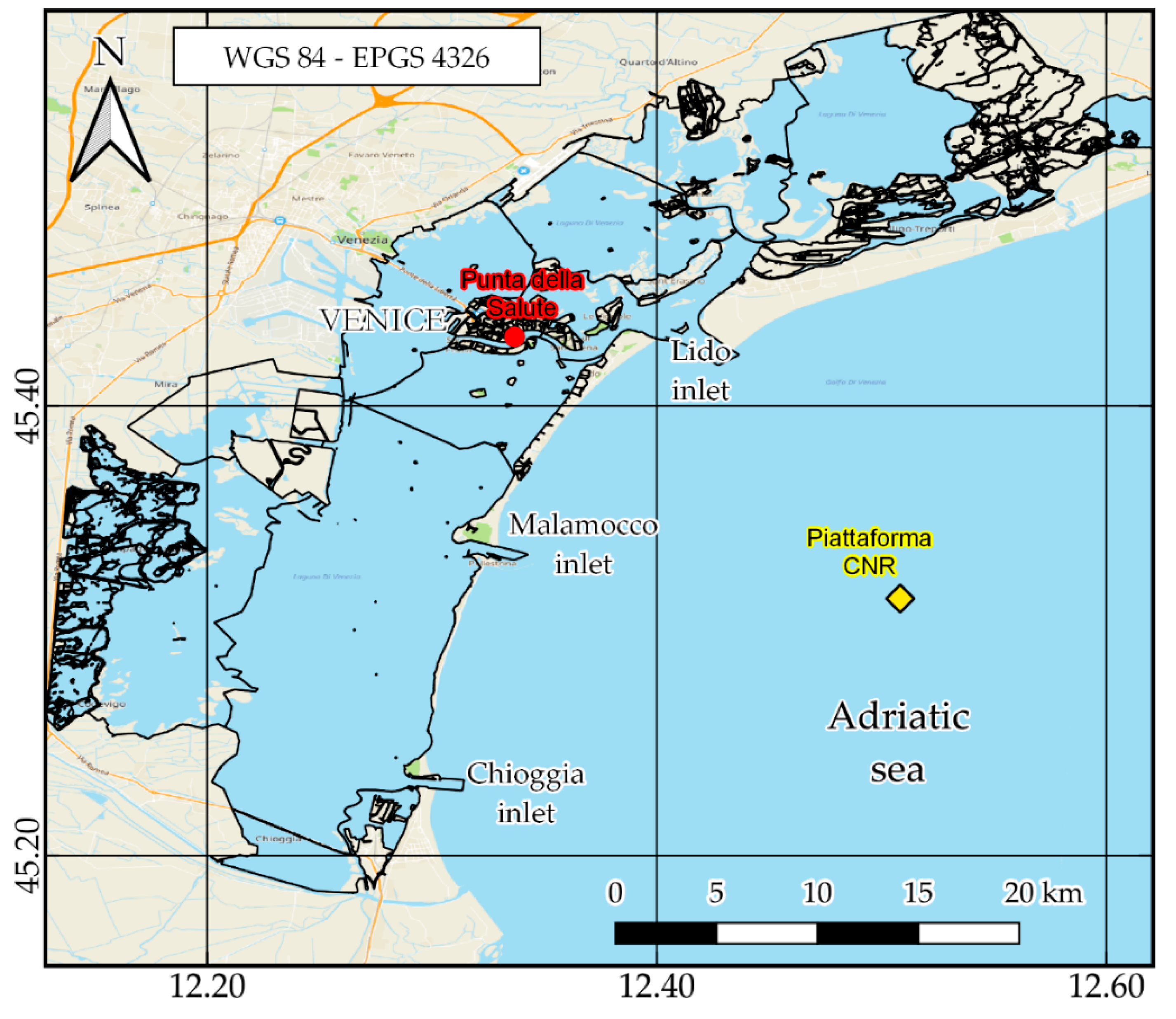
 ) and weather station (
) and weather station ( ).
).


| Evaluation Metrics | Description | Equation | |
|---|---|---|---|
| R2 | Measure of linear correlation between measured and predicted values | (3) | |
| MAE (cm) | Absolute error between predicted and measured values normalized by the number of samples | (4) | |
| RAE (%) | Ratio between absolute error between predicted and measured values and absolute value of the error of the simple measured values | (5) |
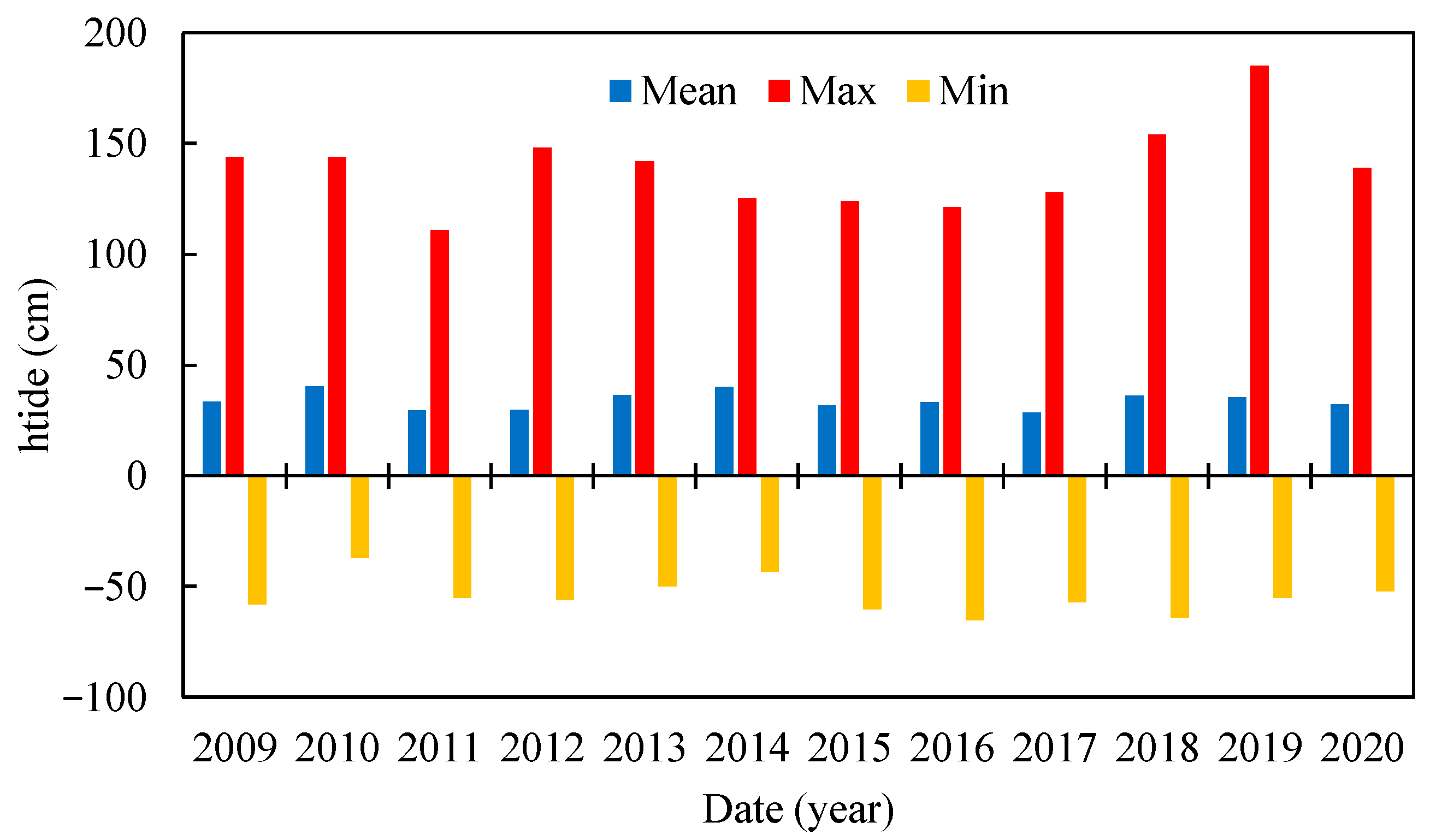
| Year | Mean (cm) | Max (cm) | Min (cm) | σ (cm) | Median (cm) | CV | SKEW |
|---|---|---|---|---|---|---|---|
| 2009 | 33.38 | 144.00 | −58.00 | 28.78 | 34.00 | 0.86 | −0.06 |
| 2010 | 40.52 | 144.00 | −37.00 | 28.17 | 41.00 | 0.70 | −0.05 |
| 2011 | 29.48 | 111.00 | −55.00 | 25.95 | 30.00 | 0.88 | −0.06 |
| 2012 | 29.56 | 148.00 | −56.00 | 28.65 | 30.00 | 0.97 | −0.05 |
| 2013 | 36.41 | 142.00 | −50.00 | 27.61 | 37.00 | 0.76 | −0.06 |
| 2014 | 40.02 | 125.00 | −43.00 | 26.81 | 40.00 | 0.67 | 0.00 |
| 2015 | 31.65 | 124.00 | −60.00 | 27.23 | 32.00 | 0.86 | −0.04 |
| 2016 | 33.18 | 121.00 | −65.00 | 26.63 | 34.00 | 0.80 | −0.09 |
| 2017 | 28.62 | 128.00 | −57.00 | 26.51 | 29.00 | 0.93 | −0.04 |
| 2018 | 36.17 | 154.00 | −64.00 | 27.00 | 36.00 | 0.75 | 0.02 |
| 2019 | 35.44 | 185.00 | −55.00 | 29.51 | 36.00 | 0.83 | −0.06 |
| 2020 | 32.12 | 139.00 | −52.00 | 27.57 | 33.00 | 0.86 | −0.10 |
| ta = 12 h | ta = 24 h | ta = 48 h | ta = 72 h | |
|---|---|---|---|---|
| R2 | 0.950 | 0.923 | 0.911 | 0.899 |
| MAE (cm) | 1.96 | 2.46 | 2.91 | 2.91 |
| RAE (%) | 23.03 | 28.95 | 34.21 | 34.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Nunno, F.; Granata, F.; Gargano, R.; De Marinis, G. Nonlinear Autoregressive Exogenous (NARX) Neural Network Models for Storm Tide Forecasting in the Venice Lagoon. Environ. Sci. Proc. 2022, 21, 93. https://doi.org/10.3390/environsciproc2022021093
Di Nunno F, Granata F, Gargano R, De Marinis G. Nonlinear Autoregressive Exogenous (NARX) Neural Network Models for Storm Tide Forecasting in the Venice Lagoon. Environmental Sciences Proceedings. 2022; 21(1):93. https://doi.org/10.3390/environsciproc2022021093
Chicago/Turabian StyleDi Nunno, Fabio, Francesco Granata, Rudy Gargano, and Giovanni De Marinis. 2022. "Nonlinear Autoregressive Exogenous (NARX) Neural Network Models for Storm Tide Forecasting in the Venice Lagoon" Environmental Sciences Proceedings 21, no. 1: 93. https://doi.org/10.3390/environsciproc2022021093
APA StyleDi Nunno, F., Granata, F., Gargano, R., & De Marinis, G. (2022). Nonlinear Autoregressive Exogenous (NARX) Neural Network Models for Storm Tide Forecasting in the Venice Lagoon. Environmental Sciences Proceedings, 21(1), 93. https://doi.org/10.3390/environsciproc2022021093









