Abstract
In this work, we investigate the spatial and temporal trend of short-duration (1 to 24 h) annual maximum rainfall depths, derived from the Improved Italian—Rainfall Extreme Dataset (I2-RED). The investigation is conducted using time series of at least 30 years of data both at the national and regional level using the record-breaking analysis, the Mann-Kendall test, the Regional Kendall test and the Sen’s slope estimator. The results confirm that rainfall extremes of different durations are not increasing uniformly over Italy and that separate tendencies emerge in different sectors, even at close distances.
1. Introduction
The impact of climate change on rainfall regimes is a debated topic: recent works do not seem to support the perception of an increase in rainfall frequency and severity over the entire globe. The different time scales used in such studies complicate the comparison. While most of them are performed at a daily scale, a limited number are focused on sub-daily durations. The lack of studies at sub-daily scales is exacerbated by less available, more fragmented and unevenly distributed short-duration (1 to 24 h) rainfall records.
Thanks to the recently released Improved Italian-Rainfall Extreme Dataset (I2-RED) [1], we performed both national- and regional-scale analyses of short duration (1, 3, 6, 12 and 24 h) rainfall depth trends, covering the period from early 1900 until now. The inclusion of more than 10 years of recent data in most of the Italian regions as compared to [2] allowed us to obtain an up-to-date picture of changes compared with [3]. This allows us to propose a comparison with analyses published in the past years.
Similarly to [3], we have analyzed the frequency of occurrences of the “extremes of the extremes” using a record-breaking (RB) test, while the possible trend in intensity has been investigated using Mann-Kendall test and Sen’s slope estimator. The comparison of results can provide new elements of assessment regarding the “speed” of change of some rainfall characteristics over Italy.
2. Data and Methods
2.1. Rainfall Data
The rainfall data used in this paper come from the Improved Italian-Rainfall Extreme Dataset (I2-RED). It represents an updated and quality-controlled version of the dataset [2] used in [3]. The increase in the number of stations is reported in Figure 1: the new database presents a significant improvement in terms of data availability, especially from 2005 onward.
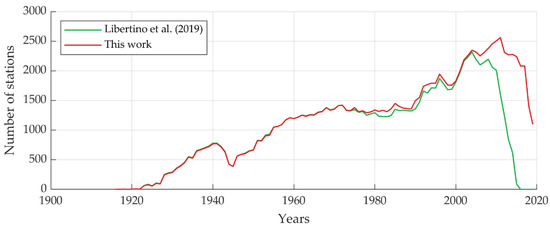
Figure 1.
Number of stations active in each year used in [3] and in this work.
Like [3], in this work we considered only time series with at least 30 years of data (either continuous or discontinuous).
The area under investigation corresponds to the whole of Italy, where the complex shape, marked mountainous characteristics (Figure 2a) and peculiarly varied climatic conditions determine significant variability of the spatial context analyzed. The methods described below are applied both at the national scale and over limited-area regions, selected as pilot cases (Figure 2b). These are: the upper Po basin (UP-PO), the Dolomites (DOL), the coastal areas between Liguria and Tuscany (LIG), the Calabria region (CAL) and the Sardinia region (SAR). These areas are hot-spots emerging from the previous analysis [3].
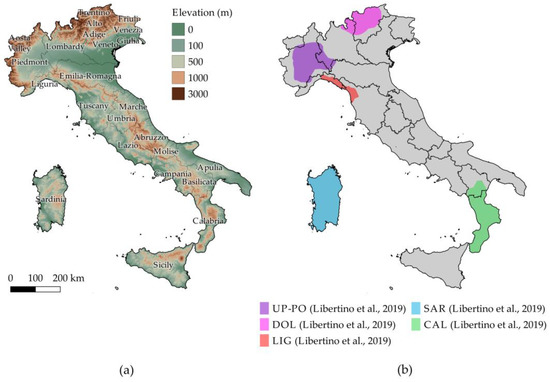
Figure 2.
Elevation data from NASA Shuttle Radar Topography Mission (SRTM) Digital Elevation Model (DEM) of Italy (m a.s.l.) with the boundaries of the 20 administrative Italian regions (a). Geographic extent of the 5 pilot cases used in [3] (b).
2.2. Record-Breaking (RB) Analysis
A rainfall measurement is considered as RB if it is higher than all the previous values in the time series [4]. The aim of the RB analysis [5] is thus the investigation of a possible increase or decrease in time of the frequency of occurrence of RB values.
Following what has been done in [3,4], we used annual maxima for each duration to create a matrix Mg with size ng × Y (where ng is the number of rain gauges and Y is the number of years). For each row of the Mg matrix, if the annual maximum is an RB value we set to 1 the corresponding value in the MRB matrix; otherwise, we set it to 0. We then obtained the vector of the observed annual RBs (Robs) by summing along the columns of MRB, and we compared it with the number of expected RBs in a stationary climate (Rexp). We obtained the vector Rexp by summing the values along the columns of Mexp, which is defined by assigning to each non-null value of each time series the expected RB probability under independent and identically distributed (iid) conditions. The annual RB anomaly [4] is then evaluated at each time step by computing the normalized difference between Robs and Rexp using
We tested the significance of the observed trends using a “field significance” bootstrap-based procedure [3]. We estimated the test statistics (in our case, the regional normalized annual RB anomaly) considering both the observed time series and 1000 replicates that we obtained by bootstrapping along the time axis. If the observed statistic falls inside the 95% confidence bound of the bootstrapped distribution, we can consider it compatible with the iid hypothesis.
2.3. Mann-Kendall Test and Sen’s Slope Estimator
The Mann-Kendall (MK) test [6] and Sen’s slope estimator were first applied to each individual station to investigate at-site statistically-significant trends. The MK is based on the ranking of observations, and not on their absolute values; being nonparametric it does not require assumptions on the distribution of observations. However, when the interest is on a region, the spatial correlation of the series of neighbor stations can be relevant. For this reason, the Regional Kendall test (RKT) is adopted to correct the site-specific MK results within a region by accounting for the cross-correlation between the series. The RKT provides one test statistic for each region (UP-PO, DOL, LIG, SAR, CAL and ITA) and for each time interval (1 to 24 h durations) that we considered. Then, we applied the van Bell and Hughes test [7] to assess the reliability of the RTK results by assessing the homogeneity among the different trends of the stations included in a specific region. If the stations of the same region have different trend directions, the RTK slope is not meaningful. In this case, while the single-station MK results can still be considered for a local trend analysis, their values are not representative of any large-scale spatial behavior.
3. National and Regional Trend Analyses
Most of the results that we obtained with the updated record-breaking analysis (Figure 3) and the RTK test (Table 1) are similar to the ones presented in [3], despite the inclusion of data in the most recent years (about +10% of new data for each duration).
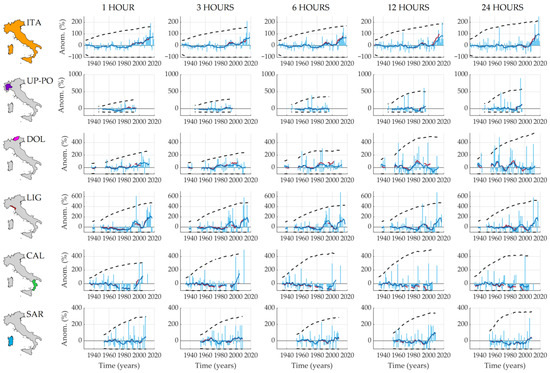
Figure 3.
Record-breaking analysis. Each row refers to a different region (ITA, UP-PO, DOL, LIG, CAL and SAR) while each column presents a different duration (1, 3, 6, 12 and 24 h). Light blue bars represent the annual RB anomalies and the blue line represents the long-term RB anomalies (obtained by smoothing using a 10-year moving average filter the annual RB anomalies). For comparison purposes, we inserted in red the long-term RB anomalies obtained in [3]. The 95% confidence interval for the iid model are also included (black dashed lines).

Table 1.
RKT analysis. The sign of the values indicates increasing/decreasing Kendall slopes. The values reported in bold represent a significant trend under a 5% significance level while the * indicates that the trend in the region is not homogeneous (van Belle and Hughes test [7]).
For the whole of Italy the results that we obtained are very similar to the ones reported in [3]: positive Kendall slopes were obtained for all the durations but the regional trend is neither homogeneous nor statistically significant.
Moving from a national to a limited-area analysis, we can mention also that in the Upper Po basin (UP-PO) the situation is quite similar to [3]: negative slopes characterize the 1 to 12 h duration, while the 24 h slope is positive. However, in our case, only the 1 h trend is statistically significant, even if the trend is homogeneous for all durations (except for the 12 h duration). Results comparable with [3] were obtained also for the LIG, CAL and SAR regions (not discussed here for the sake of brevity). It is worth mentioning that the inclusion of the most recent data in the LIG region allowed us to significantly expand the period that we covered with the RB analysis.
The massive inclusion of new data also in the DOL region (about +45% of new data) allowed us to cover a longer period. Like in [3], all the durations show a positive homogeneous statistically-significant trend, but the new analysis shows higher slope coefficients.
In Figure 4 we report the results obtained with the Mann-Kendall test while in Figure 5 we insert the Sen’s slope estimates.
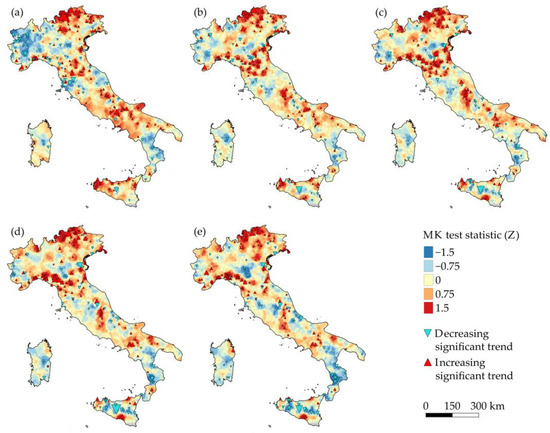
Figure 4.
Position of the rain gauges that present a significant trend at a 5% significance level in the case of (a) 1, (b) 3, (c) 6, (d) 12 and (e) 24 h duration. The size of the triangle is inversely proportional to the significance level. The background maps are obtained with a spatial interpolation of the Mann-Kendall test statistics performed using ordinary kriging.
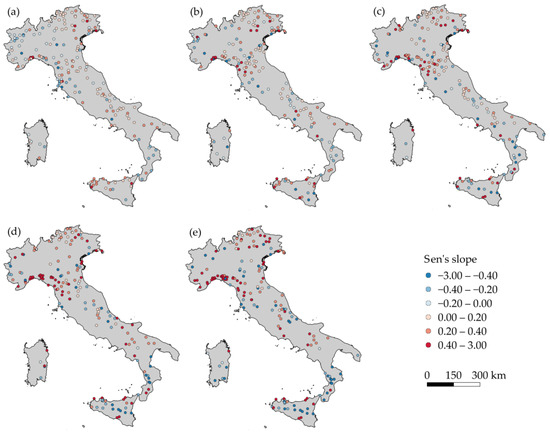
Figure 5.
Position of the rain gauges that present a significant trend at a 5% significance level in the case of (a) 1, (b) 3, (c) 6, (d) 12 and (e) 24 h duration. The color indicates the Sen’s slope.
The results obtained with the Mann-Kendall test confirm that rainfall extremes of different durations (that are related to different types of phenomena) are not increasing uniformly over Italy. Separate tendencies emerge in different sectors, such as the North East and the North West (Figure 4a). Some areas show a clear reduction in rainfall intensity over time, and in some others the decreasing trend loses spatial coherence. Compared to [3], increasing trends are reinforced in the North East, in Liguria and in some parts of Sicily.
A comparison with Sen’s slopes show the need to further investigate the spatial coherence of trends. It is interesting to notice that, despite the fact that the North-East of Italy presents a reinforced positive trend compared to [3], the Sen’s slope estimates are modest (Figure 5).
Over the North of Italy (Piedmont, Lombardy, Trentino Alto Adige, Veneto, Friuli Venezia Giulia and Emilia Romagna) an overall large presence of stations with increasing trends were detected by [8], especially in the North-East. Ref. [8] also highlighted that the difference between the number of increasing and decreasing statistically-significant trends grows with the duration. In this work we obtained similar results: for the 1 h duration, we obtained a cluster of decreasing trends in the North-West and a cluster of positive trends in the North-East. The number of positive trends in the North-West decreases with increasing durations. The inclusion of a considerable amount of data over [3] allowed us to detect a more pronounced positive rainfall trend in the North-East.
Over Lombardy, Ref. [9] found a general decrease of 1 h rainfall and an increase of longer duration events. The results are confirmed by our study. The only exception is the Alta Valtellina (North-East of Lombardy), where an increasing trend for all the durations is pointed out both in [3,9] and in this study.
In the Emilia Romagna region, most of the statistically-significant trends are located in the Apennines, along the borders with Liguria and Toscana, and in the North-Eastern area near Veneto. Quite similar results were obtained also by [10]. The inclusion of new data, compared with [3], allowed us to detect reinforced positive trends for 3 to 24 h durations.
Over Tuscany, the situation is more complex. In our analysis, we observed a general increase in the Northern part and a general decrease in the Southern part for all the durations. The only exception is for the 1 h data, where decreasing trends emerge in the North-West area near Liguria. Compared with [3] we obtained reinforced increasing trends in North Tuscany. Importantly, Ref. [11] observed a prevalence of decreasing trends in the analysis of all the data acquired in the 20th century and a large number of positive trends in the analysis of the 1970–1994 period.
Over the Umbria region, only four rain gauges show a statistically-significant trend (positive in the Northern part, negative in the Southern), even if only for some durations. The analysis carried out by [12] suggests that there is not a common trend in the area: the analysis of time series of a rain gauge in the North of the region suggests that variations are reduced, while the analysis of two rain gauges located in the Central part provided contrasting results: in one location the averages of annual maxima generally increase in the recent years, while in the other a significant reduction is observed.
The Sicily Island region [13,14,15] saw an increasing trend for short durations (the higher number of positive statistically-significant trends emerged when analyzing the 1 h duration) and [13,14] obtained a decreasing trend for longer durations. Ref. [14] also observed an increasing trend in stations near the coastline, but they were not able to detect a defined spatial pattern. Our results confirmed marked increasing trends for the 1 h duration, especially along the North and North-West coast. For durations longer than 6 h we detected a large number of locations with negative trends, especially in the central parts of the Island, far from the coastline. In contrast with [14], thanks to the massive inclusion of new data, the presence of spatial clusters emerges with evidence.
For all the other regions, a comparison is not possible due to the lack of similar studies.
4. Conclusions
In this work we conducted an improved spatio-temporal trend investigation of short-duration annual maximum rainfall depths, using the most complete collection of short-duration annual maximum rainfall depths available in Italy. The record-breaking analysis, the Mann-Kendall test (both at station-level and at a regional level) and the Sen’s slope estimator are used to investigate if statistically-significant trends are present over the Italian Territory.
The results confirmed that the presence of long-term trends cannot be evaluated by merging all the data collected over Italy, and that the segmentation of the territory is mandatory. Further studies can be conducted to evaluate new possible segmentation of the Italian territory for the evaluation of the Regional Kendall test.
Author Contributions
Conceptualization, P.C., D.G., P.M.; methodology, P.C., D.G., P.M.; software, P.M.; validation, P.M.; formal analysis, P.M.; investigation, P.M.; resources, P.C.; data curation, P.M.; writing—original draft preparation, P.M.; writing—review and editing, P.C., D.G., P.M.; visualization, P.M.; supervision, P.C.; project administration, P.C.; funding acquisition, P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The rainfall data was obtained from the I2-RED database. Although the Italian law requires an open-source policy for all public data, this right has not yet been implemented by all the Italian agencies involved in the management of the rain gauge network. The agreements we signed with some of these agencies, aimed at monitoring the correct use of the data, restricted their use to the aims of the authors’ project. As a result of these legal restrictions, a complete version of I2-RED can only be provided to two groups of people: members of the authors’ research group (which is already fully authorized to use the data), and people who can prove they have received clearance from the regional authorities. The entire quality-controlled database is available on Zenodo (https://doi.org/10.5281/zenodo.4065266) (accessed on 19 October 2022), albeit with restricted access. The data can be used by third parties, for an indefinite timeframe, upon having completed an agreement with the authors and with the regional agencies involved in the data collection. The raw data availability depends on the region: a complete description of how to access this data is reported in [1].
Acknowledgments
The authors acknowledge the 21 regional agencies involved in the management of the rain gauge networks that provided the rainfall measurements included in I2-RED. Full credits are reported in [1].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mazzoglio, P.; Butera, I.; Claps, P. I2-RED: A massive update and quality control of the Italian annual extreme rainfall dataset. Water 2020, 12, 3308. [Google Scholar] [CrossRef]
- Libertino, A.; Ganora, D.; Claps, P. Technical note: Space–time analysis of rainfall extremes in Italy: Clues from a reconciled dataset. Hydrol. Earth Syst. Sci. 2018, 22, 2705–2715. [Google Scholar] [CrossRef]
- Libertino, A.; Ganora, D.; Claps, P. Evidence for increasing rainfall extremes remains elusive at large spatial scales: The case of Italy. Geophys. Res. Lett. 2019, 46, 7437–7446. [Google Scholar] [CrossRef]
- Lehmann, J.; Coumou, D.; Frieler, K. Increased record-breaking precipitation events under global warming. Clim. Chang. 2015, 132, 501–515. [Google Scholar] [CrossRef]
- Glick, N. Breaking records and breaking boards. Am. Math. Mon. 1978, 85, 2–26. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- van Belle, G.; Hughes, J.P. Nonparametric tests for trend in water quality. Water Resour. Res. 1984, 20, 127–136. [Google Scholar] [CrossRef]
- Cesarini, L.; Martina, M. Are the short and intense precipitations in North of Italy affected by a significant trend? In Proceedings of the CLIMRISK2019, Trento, Italy, 23–25 October 2019. [Google Scholar]
- Uboldi, F.; Lussana, C. Evidence of non-stationarity in a local climatology of rainfall extremes in northern Italy. Int. J. Clim. 2018, 38, 506–516. [Google Scholar] [CrossRef]
- Persiano, S.; Ferri, E.; Antolini, G.; Domeneghetti, A.; Pavan, V.; Castellarin, A. Changes in seasonality and magnitude of sub-daily rainfall extremes in Emilia-Romagna (Italy) and potential influence on regional rainfall frequency estimation. J. Hydrol. Reg. Stud. 2020, 32, 100751. [Google Scholar] [CrossRef]
- Crisci, A.; Gozzini, B.; Meneguzzo, F.; Pagliara, S.; Maracchi, G. Extreme rainfall in a changing climate: Regional analysis and hydrological implications in Tuscany. Hydrol. Process. 2002, 16, 1261–1274. [Google Scholar] [CrossRef]
- Cifrodelli, M.; Corradini, C.; Morbidelli, R.; Saltalippi, C.; Flammini, A. The influence of climate change on heavy rainfalls in Central Italy. Procedia Earth Planet. Sci. 2015, 15, 694–701. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Cancelliere, A.; Rossi, G. Detecting trends of extreme rainfall series in Sicily. Adv. Geosci. 2005, 2, 7–11. [Google Scholar] [CrossRef]
- Arnone, E.; Pumo, D.; Viola, F.; Noto, L.V.; La Loggia, G. Rainfall statistics changes in Sicily. Hydrol. Earth Syst. Sci. 2013, 17, 2449–2458. [Google Scholar] [CrossRef]
- Treppiedi, D.; Cipolla, G.; Francipane, A.; Noto, L.V. Detecting precipitation trend using a multiscale approach based on quantile regression over a Mediterranean area. Int. J. Clim. 2021, 41, 5938–5955. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).