Abstract
In this study, lock-exchange experiments in a tank of rectangular upper cross section and a lower valley of trapezoidal shape are performed. This is a realistic model of the valleys, which occur in nature. The experiments are performed for equal depths of heavy and light fluid on both sides of the lock gate. Density difference between salt water and clear water is varied between 0.5% and 0.9%. This density difference exists in liquid waste whose spreading is an environmental problem. The release of pollutants into rivers, oil spills in the ocean and the outflow of desalinations plants are examples of man-made gravity currents that cause negative environmental impacts. The aim of this study is to contribute to a better understanding of the propagation and process of mixing of a gravity current with large density difference with water. The movement of the gravity current is monitored with a digital video of high definition, the front velocity is measured and the height of the front is captured. Twenty experiments were performed, ten inside the trapezoidal section (H = 5 or 10 cm) and ten over the trapezoidal section (H = 17.5 or 25 cm). Results are compared with those of gravity currents in lock-exchange experiments, which were performed by other researchers.
1. Introduction
Gravity currents, also known as density currents, are currents that occur in both natural and anthropogenic conditions. These currents are mainly manifested as horizontal flows and are usually caused by a density difference of even a small percentage (only a few percentage points) yet they can travel a great distance. Gravity currents are created either by the finite release of a liquid or by the continuous release.
Gravity currents can occur in both liquids and gases. Although their anatomy can be described in detail, it is not possible to define a general profile, as it is highly complex and dependent on various physical factors. Simpson (1997) [1] studied gravity currents with laboratory experiments and numerical models. The heavier liquid is propagated towards the tank with the lightest liquid along the bottom of the tank and the lighter liquid is spread along the free surface in the opposite direction.
Initially, Benjamin (1968) [2] studied gravity currents in lock-exchange experiments and concluded that the flow which has low dispersion and inertia prevails. Rottman and Simpson (1983) [3] proposed a shallow-water model considering the current as a two-dimensional two-layer flow bounded at the top and at the bottom by horizontal planes. They considered the partial-depth lock release, involving two inviscid, incompressible fluids with slightly different densities and assumed negligible mixing.
Shin et al., 2004 [4] described a new theory and experiments on gravity currents produced by lock-exchange flow, which suggested that the dissipation due to turbulence and mixing between the current and the surrounding ambient fluid is unimportant when the Reynolds number is sufficiently high. They provided an alternative theory that predicts the current speed and depth based on energy-conserving flow.
Marino et al., 2005 [5] on the basis of their experimental results showed that during the slumping phase (i.e., constant-speed phase) the Froude number can be defined in terms of lock depth, while during the second similar phase, which is no longer influenced by the initial conditions, the Froude number is better defined on the basis of the maximum height of the current’s head, which corresponds to the height at the rear of the head.
Tanino et al., 2005 [6] performed a lock-exchange experiment to investigate the propagation of gravity currents through a random array of rigid, emergent cylinders that represented a canopy of aquatic plants. As the canopy drag increased, the propagating front varied from the classic profile of an unobstructed gravity current to a triangular profile. The paper provided a template for understanding flow regimes that arise from the presence of vegetation and insight into ways in which the hydrodynamic effects of rigid vegetation may be incorporated into numerical models of convective circulation.
La Rocca et al., 2008 [7] studied the dynamics of three-dimensional gravity currents moving on smooth and rough beds by full-depth lock exchange experiments and numerical simulations, using a 2D shallow water model together with the single layer approximation. They investigated gravity current’s dynamics, keeping the width of the sliding gate and the initial density of the lighter fluid constant, while testing different values of initial density of the dense fluid, initial height of the two fluids and the bed’s roughness. They observed two different phases in three-dimensional gravity current’s evolution: the front’s velocity increases during the first phase and decreases during the second phase.
Few experimental studies have been performed for gravity currents in a valley. Monaghan et al., 2009a [8] investigated the motion of saline gravity currents propagating horizontally in a tank of rectangular upper cross section and lower V-shaped valley by lock-exchange experiments and a box model. The presence of valley results in three major differences in the gravity current compared to that flowing along a flat bottom. These are: (i) the front of the current is approximately “parabolic”, (ii) for sufficiently large time t the velocity of the current in the V-shaped valley varies in the flat bottom “case” and (iii) the width of the current in V-shaped valley decreases with time t. They have used the box model to predict the effect of changing the slope of the valley after obtaining good agreement between experiments and box model results. The result is that for equal volume currents, the steeper the valley the faster the flow. Also Monaghan et al., 2009b [9] in their paper extended previous studies of saline gravity currents at high Reynolds number flowing along a tank with a V-shaped valley. They used experiments and a box model to determine the primary features of the flow. The front of the current is approximately parabolic. The results can be described with remarkable accuracy by a box model using a generalization of the equation for sedimentation from a turbulent medium.
Keramaris and Prinos (2010) [10] investigated the motion of saline gravity currents in lock-exchange experiments which are carried out in a tank of rectangular upper cross section and a lower valley of trapezoidal shape. This is considered as more realistic model of the valleys, which occur in nature. The experiments are performed for equal depths of heavy and light fluid on both sides of the lock gate. Density difference between salt water and clear water is varied between 0.1% and 0.4% and hence the effect of density difference on the motion of the gravity currents is also investigated. The movement of the gravity current is monitored with a digital video of high definition, the front velocity is measured and the height of the front is captured. Twenty-four experiments were performed, twelve inside the trapezoidal section (H = 4, 6 or 8 cm) and twelve over the trapezoidal section (H = 12, 14 or 16 cm). The initial Reynolds number, based on the height of the valley and the reduced gravity, is greater than 10,000 for all cases indicating that the gravity currents are turbulent. The main conclusions of this research are: (a) the gravity current propagates with a parabolic head. The current with the greater density difference 0.4% travels faster than the others in both cases (H = 4 cm and H = 16 cm). This is due to the fact that the velocity of the gravity current increases with increasing density difference, (b) the effect of density difference is more pronounced in the case of composite section (upper rectangular and lower trapezoidal) than the trapezoidal section, (c) the dimensionless distance x* is plotted against the dimensionless time t* for both orthogonal and trapezoidal valleys. The effect of the valley section on the motion of the current is clear.
Longo and Di Federico (2014) [11] presented a novel formulation to analyze the axisymmetric propagation of single-phase gravity currents induced by the release of a time-variable volume of fluid in a porous domain. The analysis of the experimental data indicated that the diameter of the glass beads in an artificial porous medium is the source of most of the overall uncertainty in the current profile.
Keramaris and Prinos (2016) [12] performed laboratory experiments for rectangular and composite cross sections with the presence of vegetation in the bed to investigate the effect of cross-section on the motion of gravity currents. The results showed that the different cross section significantly influences the motion and velocity of the front of the gravitational currents.
Finally, Xiaoling et al., 2019 [13] conducted full-depth lock-exchange experiments of saltwater with a lock length of 40 m in a horizontal open channel in order to gain insight into the gravity currents of long lock releases. The current was analyzed using one-layer open-channel hydraulics. The theoretical results show that the front traveling length over time is a quadratic function and the front velocity decreases linearly based on the initial speed, which is related to the drag coefficient. The front height also decreases linearly from half of the total water depth.
In this study, experiments were carried out in a tank of complex cross section (trapezoidal cross-section at its lower part and rectangular in its upper part). The purpose of this research is to study the behavior of gravity currents with a high-density difference measured by a high-definition digital video while recording the velocity of the front with which it propagates in the fluid. Density difference between salt water and clear water is varied between 0.5% and 0.9%. This density difference exists in liquid waste whose spreading my cause an environmental problem. The release of pollutants into rivers, oil spills in the ocean and the outflow of desalination plants are examples of man-made gravity currents that cause negative environmental impacts. The results are compared with those of similar experiments (Shin et al., 2004, Monaghan et al., 2009, Keramaris and Prinos, 2010) with a lower ratio of densities. The comparisons revealed that gravity currents of a high density ration differ remarkably in propagation velocity and shape with common fronts with a density ratio close to the unit (Boussinesq currents).
2. Materials and Methods
Experimental Procedure
Experiments were performed in a tank of rectangular upper cross section and a lower valley of trapezoidal shape. The dimensions of the tank are: width W = 23 cm, height H = 25 cm and total length L = 2.2 m. The trapezoidal section of the valley has the following dimensions: bottom width = 5 cm, height = 10 cm and side slope 1:1. The slope of the channel was horizontal. The depth of the valley, measured vertically from the bed, is 10 cm. The distance from the lock gate to the front edge of the current head is denoted as x (Figure 1). The tank was separated into two reservoirs by a removable thick vertical partition, which was removed at the start of the experiments. These two sections containing liquids of different density, water (w) and salted water (sw). One reservoir was filled with H = 5, 10, 17.5 or 25 cm of well-mixed saltwater of density ρsw and the other with freshwater of density ρw (ρw < ρsw) until the free surface in both reservoirs was aligned. Twenty experiments were conducted, ten inside the trapezoidal section (H = 5 or 10 cm for five different densities) and ten over the trapezoidal section (H = 17.5 or 25 cm for five different densities). The density difference between salt water and clear water was varied between 0.5% and 0.9% (ρw = 1000 kg/m3, ρsw = 1050 or 1060 or 1070 or 1080 or 1090 kg/m3). These densities of 1050 kg/m3 up to 1090 kg/m3 simulate liquid waste whose spreading my cause an environmental problem. The release of pollutants into rivers, oil spills in the ocean and the outflow of desalinations plants are examples of man-made gravity currents that cause negative environmental impacts. In Table 1 the characteristics of the experiments are presented.
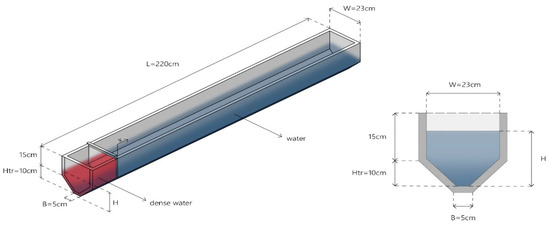
Figure 1.
Tank dimensions and symbols used.

Table 1.
Characteristics of experiments.
Experiments began with the removal of the vertical partition. The gravity current is generated, due to the horizontal density gradient, after the removal of the partition. The heavier fluid propagates towards the lighter fluid reservoir along the bottom of the tank and the lighter fluid propagates along the free surface in the opposite direction. For flow visualization, the saltwater was dyed with rhodamin (red color). Series of images were captured using a camera mounted on a stationary tripod in front of the tank after the initiation of the current. These recordings were subsequently analyzed to determine the front position and velocity as functions of time, by measuring the time required for the front to travel fixed-length intervals marked on the tank. A digital camera was used for the viewing of current and then measured the height and the position of the current front (Figure 2).

Figure 2.
Gravity current (H = 25 cm, Density Difference 0.5%) at three locations.
3. Analysis of Results
In Figure 3 and Figure 4, the effect of depth H on the motion of the gravity current is examined for the same density (ρsw = 1070 kg/m3) for both cases (trapezoidal and composite section). As it is observed, the gravity current with the greater depth H travels faster in all cases.
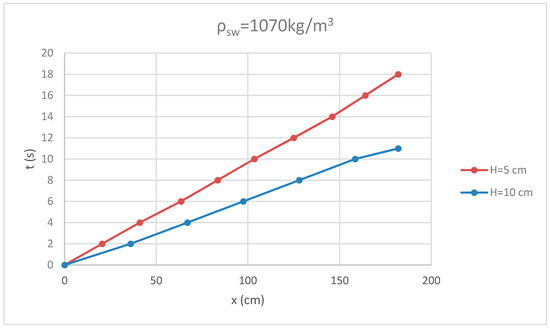
Figure 3.
Effect of depth H on the motion of gravity current in trapezoidal section.
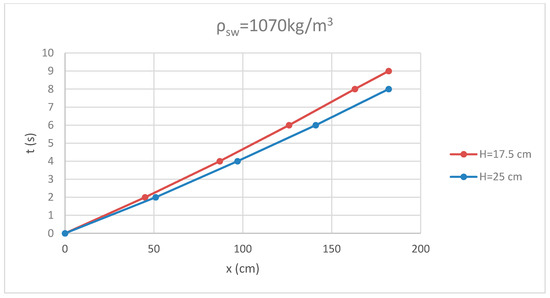
Figure 4.
Effect of depth H on the motion of gravity current in composite section.
In Figure 5 and Figure 6, the effect of density difference on the motion of the gravity current is examined. The current with the greater difference (ρ = 1080 kg/m3) travels faster than the other (ρ = 1060 kg/m3) in both cases (H = 5 and 10 cm within the valley and H = 17.5 and 25 cm in the composite section). This is due to the fact that the velocity of the gravity current increases with increasing density difference.
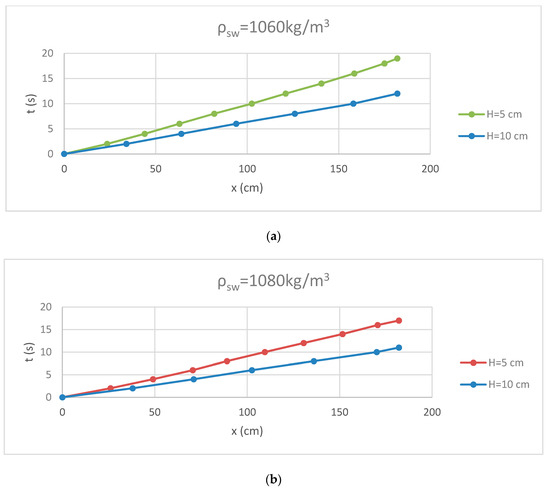
Figure 5.
Effect of density difference on the motion of gravity current in trapezoidal section: (a) ρsw = 1060 kg/m3 and (b) ρsw = 1080 kg/m3
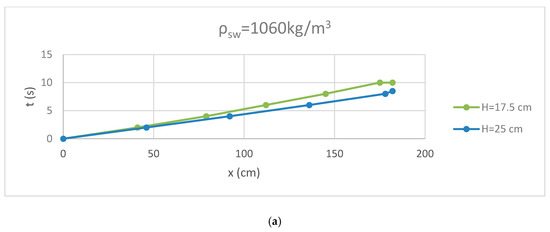
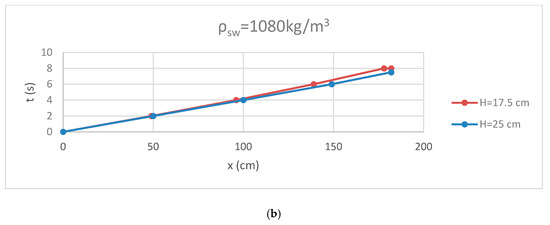
Figure 6.
Effect of density difference on the motion of gravity current in composite section: (a) ρsw = 1060 kg/m3 and (b) ρsw = 1080 kg/m3
In Figure 7 the dimensionless distance x* is plotted against the dimensionless time t* from the opening of the gate for gravity currents for all cases (all depths and all densities). The distance x is made dimensionless with the water depth H and the time t from the lock exchange with the parameter (). It is obvious from this figure that the currents with the greatest density and the greater depth H move faster.
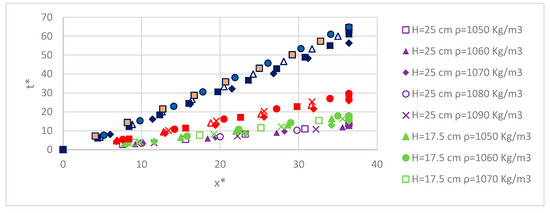
Figure 7.
Time development of gravity front for all cases (dimensionless).
Figure 8 includes box model results of Monaghan et al., (2009) for triangular valleys (slope of the valley is 12°, 23° and 41° to the horizontal with respective depths of the valley 0.03 m, 0.06 m and 0.12 m), results for orthogonal valley (Shin et al., 2004), results from Keramaris and Prinos (2010) together with experimental results of this study. The effect of the valley geometry and the steepness of the flanks on the motion is significant. It is shown that the motion of the current depends on the shape of the valley. The current moves faster within the trapezoidal section, which is in agreement with the analytical findings of Monaghan et al., (2009). In general, there is a good agreement between the results of the present study in comparison with the results of other researchers.
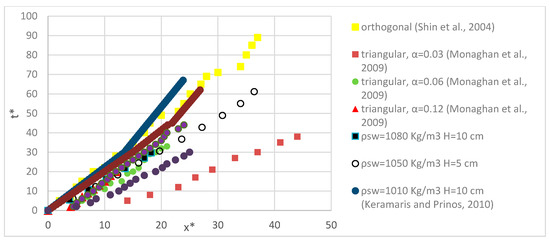
Figure 8.
Dimensionless comparison between triangular, orthogonal and trapezoidal shape.
4. Conclusions
In this study, the motion of saline gravity currents in a tank of rectangular upper cross section and a lower valley of trapezoidal shape is investigated. Lock-exchange experiments are performed for equal depths of heavy and light fluids on both sides of the lock gate. The gate separates the two fluids (water and saltwater) with density difference from 0.5%, up to 0.9%. The main conclusions of this study are: (a) the cross section of the tank plays an important role in the propagation of gravity currents. In particular, the presence of the trapezoidal shape at the bottom of the composite cross section results in a significant increase in the velocity of the gravity currents in comparison with the rectangular cross section, (b) the gravity current propagates with a parabolic head. The current with the greater density difference travels faster than the others in all cases. This is due to the fact that the velocity of the gravity current increases with increasing density difference, (c) the effect of density difference is more pronounced in the case of composite section than in the case of trapezoidal section and (d) the dimensionless distance x* is plotted against the dimensionless time t* for orthogonal, triangular and trapezoidal valleys. The effect of the valley section on the motion of the current is clear. Also results from the box model of Monaghan et al., (2009) for triangular valleys of different side wall steepness indicate the dependence of the current motion on the geometry of the valley.
Author Contributions
E.K. designed the experiments; S.V. and S.K. performed the experiments; S.V., S.K. and E.K. analyzed the data; E.K. wrote the paper. All authors have read and agree to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Simpson, J.E. Gravity Currents in the Environment and the Laboratory; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Benjamin, T.B. Gravity currents and related phenomena. J. Fluid Mech. 1968, 31, 209–248. [Google Scholar] [CrossRef]
- Rottman, J.W.; Simpson, J.E. Gravity currents produced by instantaneous release of a heavy fluid in a rectangular channel. J. Fluid Mech. 1983, 135, 95–110. [Google Scholar] [CrossRef]
- Shin, J.O.; Dalziel, S.B.; Linden, P.F. Gravity currents produced by lock-exchange. J. Fluid Mech. 2004, 521, 1–34. [Google Scholar] [CrossRef]
- Marino, B.M.; Thomas, L.P.; Linden, P.F. The front condition of gravity currents. J. Fluid Mech. 2005, 536, 49–78. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M.; Kulis, P.S. Gravity currents in aquatic canopies. Water Resour. Res. 2005, 41, 1–9. [Google Scholar] [CrossRef]
- La Rocca, M.; Adduce, C.; Sciortino, G.; Bateman Pinzon, A. Experimental and numerical simulation of three-dimensional gravity currents on smooth and rough bottom. Phys. Fluids 2008, 20, 106603. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Meriaux, C.A.; Huppert, H.E.; Mansour, J. Particulate gravity currents along V-shaped valleys. J. Fluid Mech. 2009, 631, 419–440. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Meriaux, C.A.; Huppert, H.E.; Monaghan, J.M. High Reynolds number gravity currents along V-shaped valleys. European. J. Fluid Mech. 2009, 28, 651–659. [Google Scholar]
- Keramaris, E.; Prinos, P. Gravity Currents in a Valley of Trapezoidal Shape. In Proceedings of the River Flow 2010: International Conference on Fluvial Hydraulics, Braunschweig, Germany, 8–10 September 2010; Volume 2, pp. 599–604. [Google Scholar]
- Longo, S.; Di Federico, V. Axisymmetric gravity currents within porous media: First order solution and experimental validation. J. Hydrol. 2014, 519, 238–247. [Google Scholar] [CrossRef]
- Keramaris, E.; Prinos, P. Gravity currents in a vegetated valley of trapezoidal shape. J. Appl. Fluid Mech. 2016, 9, 1051–1056. [Google Scholar] [CrossRef]
- Xiaoling, Y.; Yong, H.; Chen, L.; Shiyou, G.; Qingquan, L. Experimental Study on Front Spreading of Lock-Exchange Gravity Current with Long Lock Length. J. Eng. Mech. 2019, 146, 1696–1699. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).