Prediction of Soil Loss in a Reservoir Watershed Using an Erosion Model and Modern Technological Tools: A Case Study of Marathon Lake, Attica in Greece †
Abstract
1. Introduction
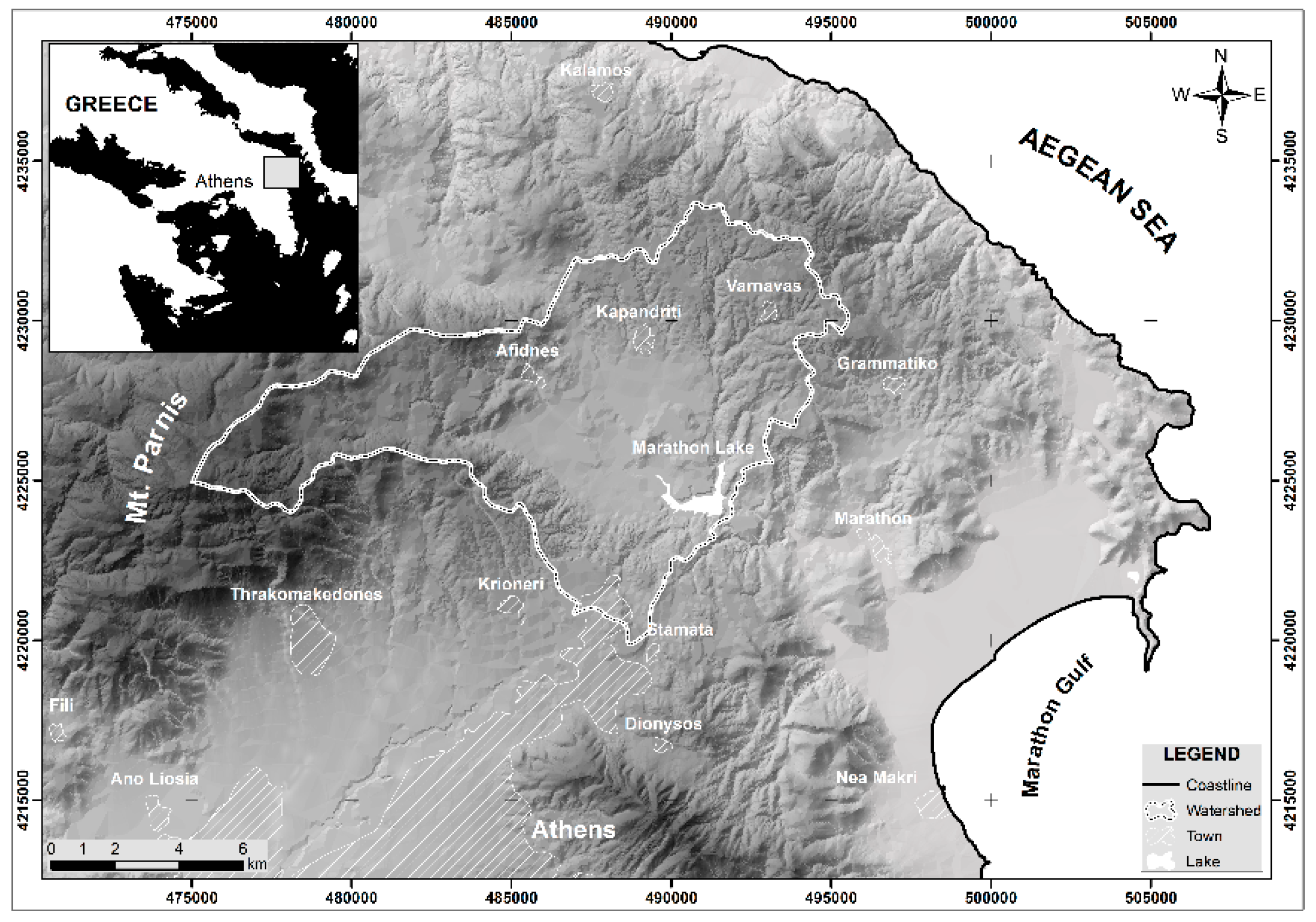
2. Study Area
3. Materials and Methods
3.1. Rainfall Erosivity Factor (R)
3.2. Soil Erodibility Factor (K)
3.3. Slope Length and Steepness Factors (LS)
3.4. Management Factor (C)
3.5. Conservation Practice Factor (P)
4. Results
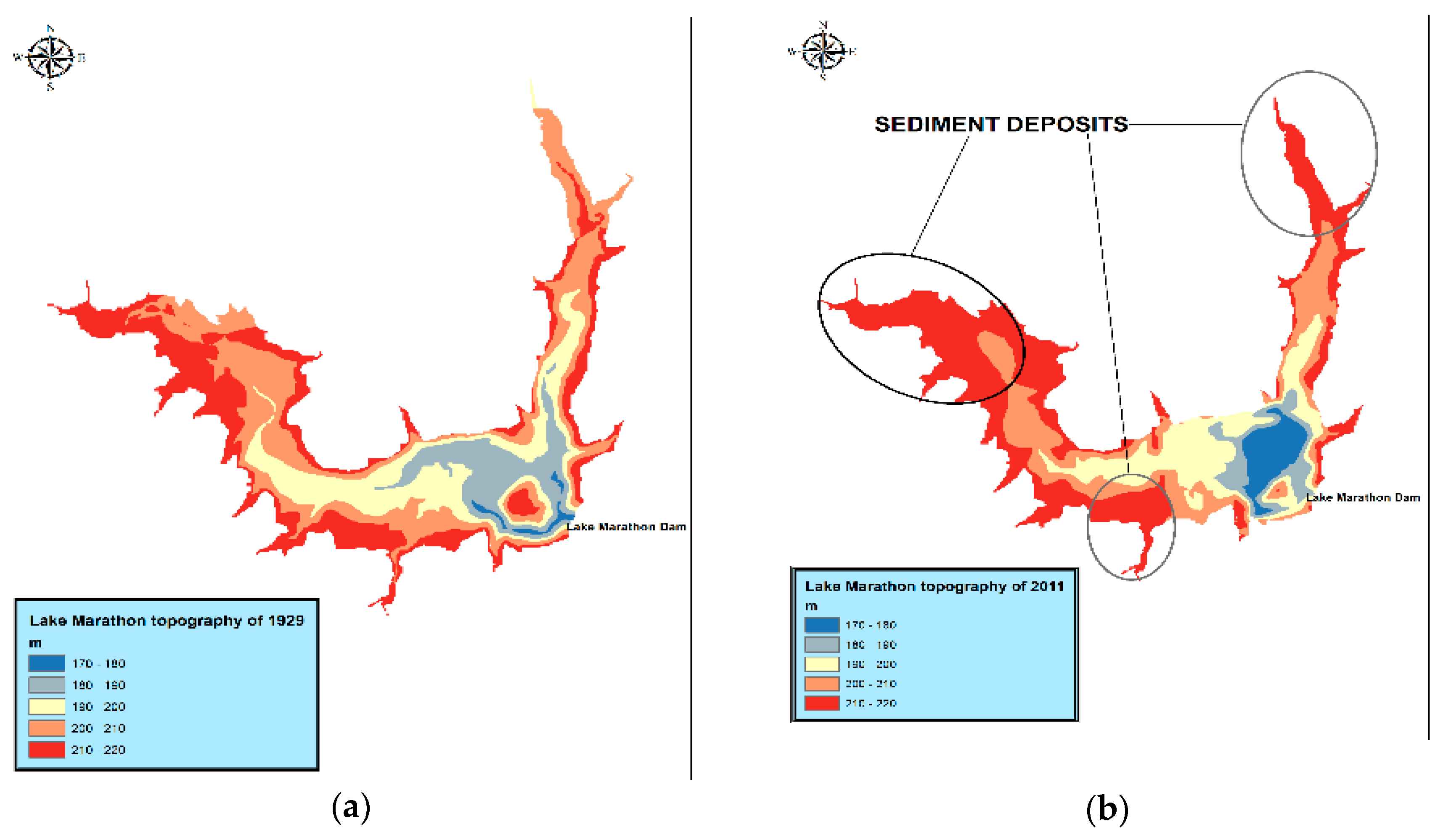
4.1. Results of the Bathymetric Study
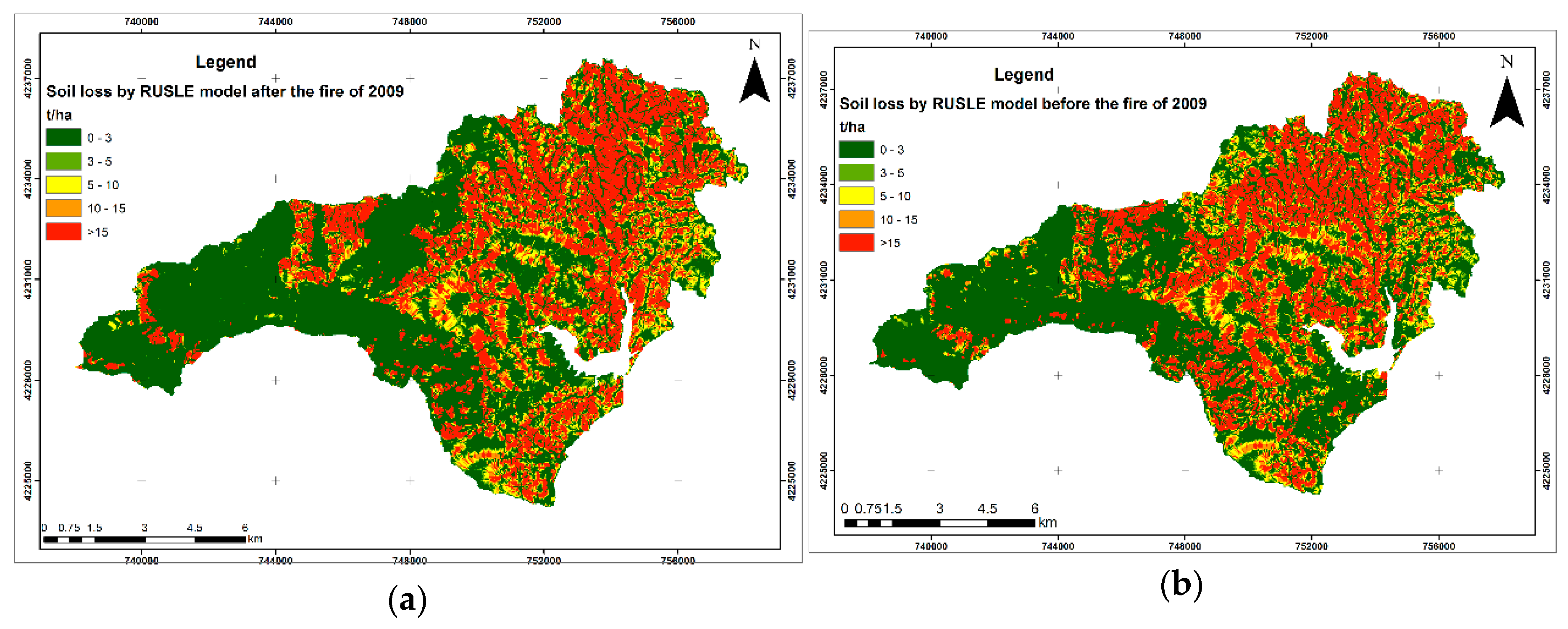
4.2. Estimated Soil Loss in the Marathon Lake Watershed According to the RUSLE Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lal, R. Soil Erosion and Land Degradation: The Global Risks. In Advances in Soil Science; Springer: New York, NY, USA, 1990; pp. 130–170. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting rainfall erosion losses: A guide to conservation planning. In USDA, Agriculture Handbook; U.S. Government Printing Office: Washington, DC, USA, 1978; p. 537. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE), Agriculture Handbook; USDA-ARS: Washington, DC, USA, 1997; p. 703.
- De Jong, S.M.; Riezebos, H. SEMMED: A Distributed Approach to Soil Erosion Modelling. Remote Sens. 1997, 96, 199–204. [Google Scholar]
- Aiello, A.; Adamo, M.; Canora, F. Remote sensing and GIS to assess soil erosion with RUSLE3D and USPED at river basin scale in southern Italy. Catena 2015, 131, 158–174. [Google Scholar] [CrossRef]
- Andreadaki, M.; Georgoulas, A.; Hrissanthou, V.; Kotsovinos, N. Assessment of reservoir sedimentation effect on coastal erosion in the case of Nestos River, Greece. Int. J. Sed. Res. 2014, 29, 34–48. [Google Scholar] [CrossRef]
- Xanthopoulos, G. Lessons learned from the dramatic fires of 2007 and 2009 in Greece. In Proceedings of the Technical Meeting of the Fire Service: Capacity for Managing Forest Fires, Girona, Catalonia, Spain, 18–19 November 2009; Available online: http://www.jornadesbombers.ctfc.cat/ang/documentacio.htm (accessed on 22 March 2020).
- Athens Water Supply and Sewerage Company (EYDAP), 2012. Fact Sheet Marathon Reservoir. Available online: http://www.eydap.gr/userfiles/c3c4382d-a658-4d79-b9e2-ecff7ddd9b76/fact-sheet-marathona.pdf (accessed on 21 February 2020).
- Pavlopoulos, K.; Maroukian, H. Geomorphic and morphotectonic observations in the drainage network of Kakotopia Stream, North East Attica, Greece. Geol. Balc. 1997, 27, 55–60. [Google Scholar]
- Zarris, D.; Lykoudi, E.; Koutsoyiannis, D. Sediment yield estimation of a hydrological basin using measurements of reservoir deposits: A case study for the Kremasta reservoir, Western Greece. In Proceedings of the 5th International Conference of European Water Resources Association: “Water Resources Management in the Era of Transition”; Tsakiris, G., Ed.; European Water Resources Association: Athens, Greece, 2002; pp. 338–345, ERDAS, Inc. ERDAS Imagine Field Guide, 5th ed.; Revised and Expanded; ERDAS, Inc.: Atlanta, GA, USA, 2011. [Google Scholar] [CrossRef]
- Schwertmann, U.; Vogl, W.; Kainz, M. Bodenerosion durch Wasser: Vorhersage des Abtrags und Bewertung von Gegenmassnahmen; Ulmer Verlag: Stuttgart, Germany, 1990. [Google Scholar]
- Hrissanthou, V.; Pyliotis, A. Estimation of sediment inflow into a reservoir under construction. In Proceedings of the 6th Conference of the Greek Hydrotechnical Union, Thessaloniki, Greece, 22–26 May 1995; pp. 355–362. (In Greek). [Google Scholar]
- Moore, I.D.; Wilson, J.P. Length slope factor for the Revised Universal Soil Loss Equation: Simplified method of solution. J. Soil Water Cons. 1992, 47, 423–428. [Google Scholar]
- ERDAS, Inc. ERDAS Imagine Field Guide, 5th ed.; Revised and Expanded; ERDAS, Inc.: Atlanta, GA, USA, 2011. [Google Scholar]
- Kotoulas, D. Mountain Hydronomics, Vol I: River Restoration Works; UTH Publication Department: Thessaloniki, Greece, 2001. (In Greek) [Google Scholar]
- Krysanova, V.; Hattermann, F.; Wechsung, F. Implications of complexity and uncertainty for integrated modeling and impact assessment in river basins. Environ. Model. Softw. 2007, 22, 701–709. [Google Scholar] [CrossRef][Green Version]
- Sapountzis, Μ.; Myronidis, D.; Stathis, D.; Stefanidis, P. Comparison of the results of application of soil erosion models USLE and Gavrilovič with actual measurements in river basin. In Proceedings of the 11th Panhellenic Conference of Greek Hydrotechnical Union, Volos, Greece; 1995; pp. 155–163. (In Greek). [Google Scholar]
- Lykoudi, E.; Zarris, D. Predicting of high-risk soil erosion areas in Cephalonia island, Greece using the Universal Soil Loss Equation. In Proceedings of the 6th Panhellenic Geographical Conference, Thessaloniki, Greece, 2–6 October 2002. (In Greek). [Google Scholar]
- Kirkby, M.J. Modelling water erosion processes. In Soil Erosion; Kirkby, M.J., Morgan, R.P.C., Eds.; John Wiley: New York, NY, USA, 1980; pp. 183–216. [Google Scholar]
| Geology | K |
|---|---|
| Hard limestone | 0.006 |
| Schist | 0.01 |
| Flysch | 0.015 |
| Tertiary deposits | 0.1 |
| Land Use Class | C |
|---|---|
| Fir forest (Abies cephalonica) | 0.001 |
| Pine forest (Pinus halepensis) | 0.001 |
| Shrubland (Macchia) | 0.03 |
| Phrygana (Garrigues) | 0.45 |
| Agricultural areas | 0.20 |
| Bare soil areas | 1.00 |
| Burned areas | 0.55 |
| Towns | 1.00 |
| Mean Soil Loss(t/ha) | Area(ha) | Sediment Delivery Ratio(SDR) | Years of Dam Function | Mean Soil Loss(103 kg) | Volume(m3) | Volume(hm3) | |
|---|---|---|---|---|---|---|---|
| Before fire of 2009 | 27.79 | 11 696 | 0.31 | 78 | 7,862,097.98 | 2,944,605.99 | 2.94 |
| After fire of 2009 | 28.95 | 11 696 | 0.31 | 2 | 210,004.02 | 78,653.19 | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xanthakis, M.; Pavlopoulos, K.; Kapsimalis, V.; Apostolopoulos, G.; Xanthopoulos, G.; Stefanidis, P.; Evelpidou, N. Prediction of Soil Loss in a Reservoir Watershed Using an Erosion Model and Modern Technological Tools: A Case Study of Marathon Lake, Attica in Greece. Environ. Sci. Proc. 2020, 2, 63. https://doi.org/10.3390/environsciproc2020002063
Xanthakis M, Pavlopoulos K, Kapsimalis V, Apostolopoulos G, Xanthopoulos G, Stefanidis P, Evelpidou N. Prediction of Soil Loss in a Reservoir Watershed Using an Erosion Model and Modern Technological Tools: A Case Study of Marathon Lake, Attica in Greece. Environmental Sciences Proceedings. 2020; 2(1):63. https://doi.org/10.3390/environsciproc2020002063
Chicago/Turabian StyleXanthakis, Michail, Kosmas Pavlopoulos, Vasilios Kapsimalis, Georgios Apostolopoulos, Gavriil Xanthopoulos, Panagiotis Stefanidis, and Niki Evelpidou. 2020. "Prediction of Soil Loss in a Reservoir Watershed Using an Erosion Model and Modern Technological Tools: A Case Study of Marathon Lake, Attica in Greece" Environmental Sciences Proceedings 2, no. 1: 63. https://doi.org/10.3390/environsciproc2020002063
APA StyleXanthakis, M., Pavlopoulos, K., Kapsimalis, V., Apostolopoulos, G., Xanthopoulos, G., Stefanidis, P., & Evelpidou, N. (2020). Prediction of Soil Loss in a Reservoir Watershed Using an Erosion Model and Modern Technological Tools: A Case Study of Marathon Lake, Attica in Greece. Environmental Sciences Proceedings, 2(1), 63. https://doi.org/10.3390/environsciproc2020002063








