A Gridded Database for the Spatiotemporal Analysis of Rainfall in Southern Italy (Calabria Region) †
Abstract
:1. Introduction
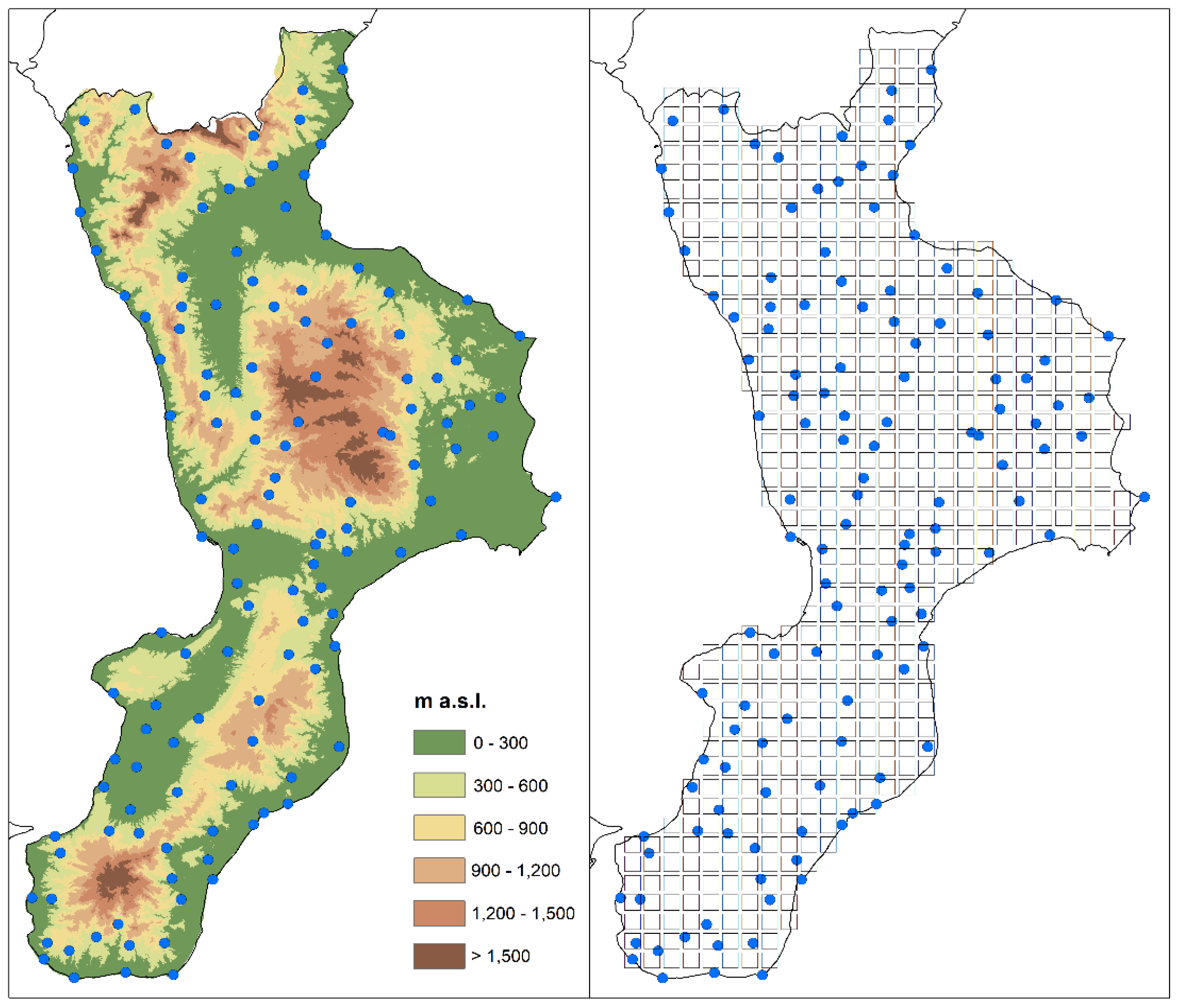
2. Study Area and Data
3. Methods
3.1. Inverse Distance Weighted
3.2. Trend Analysis
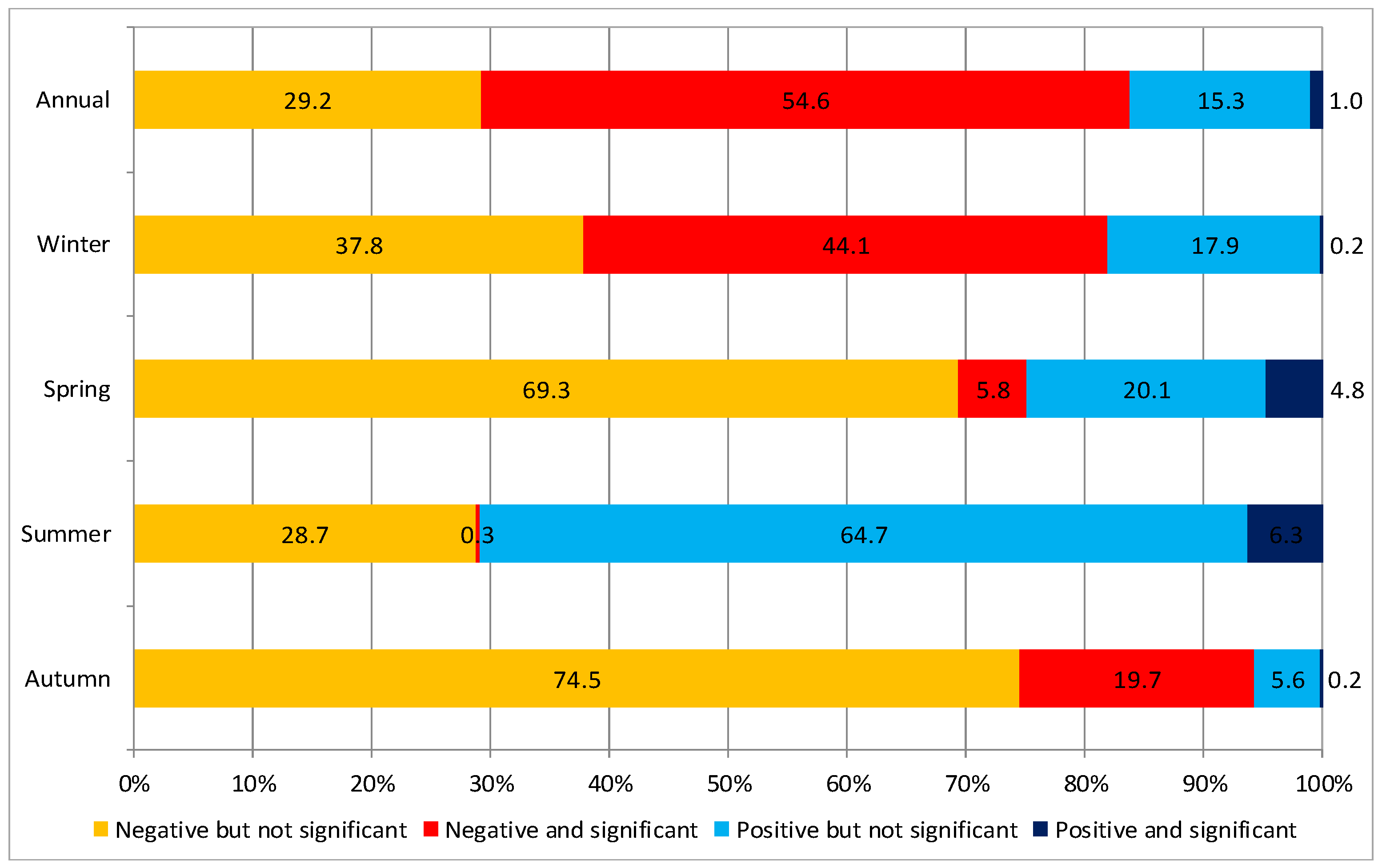
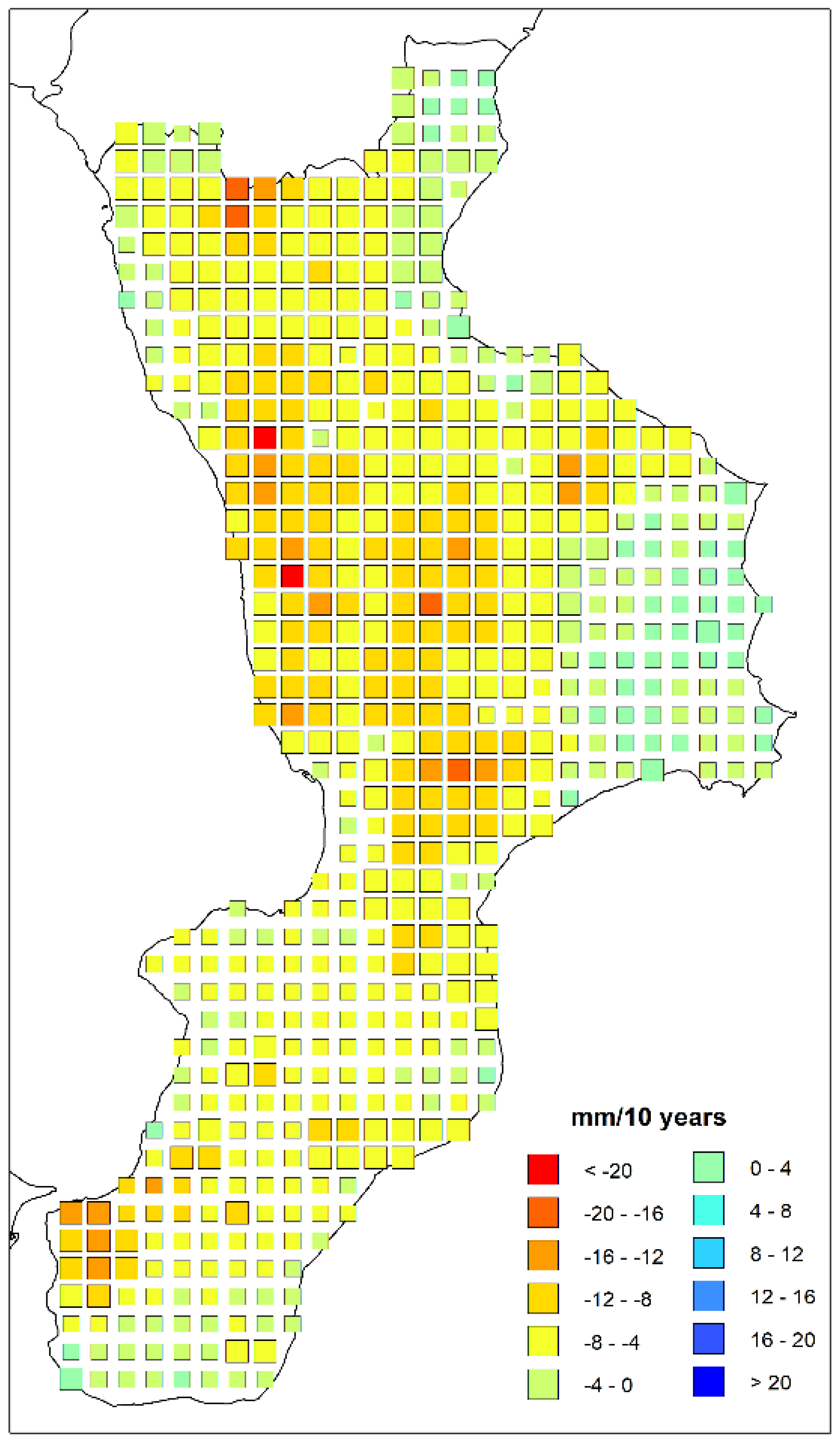
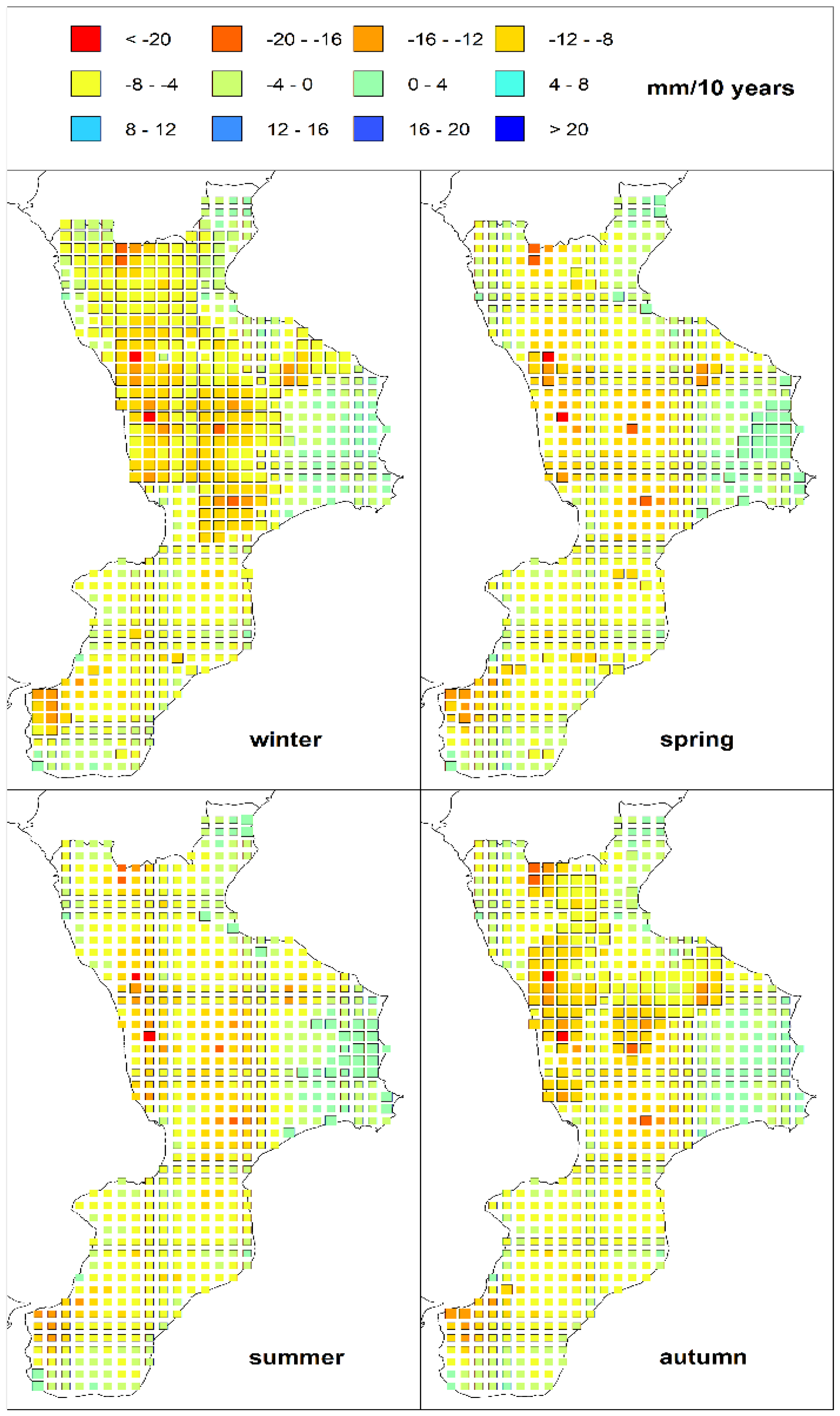
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IPCC. Summary for Policymakers. Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Elmeddahi, Y.; Mahmoudi, H.; Issaadi, A.; Goosen, M.F.A.; Ragab, R. Evaluating the ef-fects of climate change and variability on water resources: A case study of the Cheliff basin in Algeria. Am. J. Eng. Appl. Sci. 2016, 9, 835–845. [Google Scholar] [CrossRef]
- Caloiero, T.; Caloiero, P.; Frustaci, F. Long-term precipitation trend analysis in Europe and in the Mediterranean basin. Water Environ. J. 2018, 32, 433–445. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Maheras, P.; Tolika, K.; Anagnostopoulou, C.; Vafiadis, M.; Patrikas, I.; Flocas, H. On the relationships between circulation types and changes in rainfall variability in Greece. Int. J. Climatol. 2004, 24, 1695–1712. [Google Scholar] [CrossRef]
- Altin, T.B.; Barak, B. Changes and trends in total yearly precipitation of the Antalya District, Turkey. Proc. Soc. Behv. 2014, 120, 586–599. [Google Scholar] [CrossRef]
- Shohami, D.; Dayan, U.; Morin, E. Warming and drying of the eastern Mediterranean: Additional evidence from trend analysis. J. Geophys. Res. 2011, 116, D22101. [Google Scholar] [CrossRef]
- Ziv, B.; Saaroni, H.; Pargament, R.; Harpaz, T.; Alpert, P. Trends in rainfall regime over Israel, 1975-2010, and their relationship to large-scale variability. Reg. Environ. Chang. 2014, 14, 1751–1764. [Google Scholar] [CrossRef]
- Longobardi, A.; Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Spatial and temporal distribution of precipitation in a Mediterranean area (southern Italy). Environ. Earth Sci. 2016, 75, 189. [Google Scholar] [CrossRef]
- Diodato, N. Climatic fluctuations in southern Italy since 17th century: Reconstruction with precipitation records at Benevento. Clim. Chang. 2007, 80, 411–431. [Google Scholar] [CrossRef]
- Piccarreta, M.; Capolongo, D.; Boenzi, F. Trend analysis of precipitation and drought in Basilicata from 1923 to 2000 within a Southern Italy context. Int. J. Climatol. 2004, 24, 907–922. [Google Scholar] [CrossRef]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Analysis of spatial and temporal rainfall trends in Sicily during the 1921–2012 period. Theor. Appl. Climatol. 2016, 126, 113–129. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Mancini, M. Trend detection of annual and seasonal rainfall in Calabria (southern Italy). Int. J. Climatol. 2011, 31, 44–56. [Google Scholar] [CrossRef]
- Montaldo, N.; Sarigu, A. Potential links between the North Atlantic Oscillation and decreasing precipitation and runoff on a Mediterranean area. J. Hydrol. 2017, 553, 419–437. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Gaudio, R.; Leonardo, G.P. Precipitation trend and concentration in the Sardinia region. Theor. Appl. Climatol. 2019, 137, 297–307. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. An analysis of the occurrence probabilities of wet and dry periods through a stochastic monthly rainfall model. Water 2016, 8, 39. [Google Scholar] [CrossRef]
- Coscarelli, R.; Caloiero, T.; Minervino, I.; Sorriso-Valvo, M. Sensitivity to desertification of a high productivity area in Southern Italy. J. Maps 2016, 12, 573–581. [Google Scholar] [CrossRef]
- Caloiero, T.; Callegari, G.; Cantasano, N.; Coletta, V.; Pellicone, G.; Veltri, A. Bioclimatic analysis in a region of southern Italy (Calabria). Plant Biosyst. 2016, 150, 1282–1295. [Google Scholar] [CrossRef]
- Brunetti, M.; Caloiero, T.; Coscarelli, R.; Gullà, G.; Nanni, T.; Simolo, C. Precipitation variability and change in the Calabria region (Italy) from a high resolution daily dataset. Int. J. Climatol. 2012, 32, 57–73. [Google Scholar] [CrossRef]
- Shepard, D.S. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968. [Google Scholar]
- Shepard, D.S. Computer Mapping: The SYMAP Interpolation Algorithm. In Spatial Statistics and Models; Gaile, G.L., Willmott, C.J., Eds.; Springer: New York, NY, USA, 1984; pp. 133–145. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Hafner Publishing Company: New York, NY, USA, 1962. [Google Scholar]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Application of the Innovative Trend Analysis Method for the Trend Analysis of Rainfall Anomalies in Southern Italy. Water. Resour. Manag. 2018, 32, 4971–4983. [Google Scholar] [CrossRef]
- Ferrari, E.; Caloiero, T.; Coscarelli, R. Influence of the North Atlantic Oscillation on winter rainfall in Calabria (southern Italy). Theor. Appl. Climatol. 2013, 114, 479–494. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caloiero, T.; Coscarelli, R.; Pellicone, G. A Gridded Database for the Spatiotemporal Analysis of Rainfall in Southern Italy (Calabria Region). Environ. Sci. Proc. 2020, 2, 6. https://doi.org/10.3390/environsciproc2020002006
Caloiero T, Coscarelli R, Pellicone G. A Gridded Database for the Spatiotemporal Analysis of Rainfall in Southern Italy (Calabria Region). Environmental Sciences Proceedings. 2020; 2(1):6. https://doi.org/10.3390/environsciproc2020002006
Chicago/Turabian StyleCaloiero, Tommaso, Roberto Coscarelli, and Gaetano Pellicone. 2020. "A Gridded Database for the Spatiotemporal Analysis of Rainfall in Southern Italy (Calabria Region)" Environmental Sciences Proceedings 2, no. 1: 6. https://doi.org/10.3390/environsciproc2020002006
APA StyleCaloiero, T., Coscarelli, R., & Pellicone, G. (2020). A Gridded Database for the Spatiotemporal Analysis of Rainfall in Southern Italy (Calabria Region). Environmental Sciences Proceedings, 2(1), 6. https://doi.org/10.3390/environsciproc2020002006




