Abstract
Water network partitioning (WNP) represents an efficient strategy to improve management of water distribution networks, reduce water losses and monitor water quality. It consists in physically dividing of a water distribution network (WDN) into districted metered areas (DMAs) through the placement of flow meters and isolation valves on boundary pipes between DMAs. In this paper, a novel methodology for designing DMAs is proposed that provides districts with quite similar node elevations and minimizes the number of boundary pipes in order to simplify pressure management and reduce the number of devices to place into the network.
1. Introduction
District metered areas (DMAs) [] is one of the main methodologies for improving water system management and reducing water losses. The main benefits of the application of DMAs are: (a) improvement of the management of the supply system, through continuous monitoring of hydraulic magnitudes (pressure and flow), in order to prevent crisis situations and to plan maintenance and expansion works []; (b) simplifying the assessment of district water balance; (c) differential regulation of pressures []. Recent studies proposed DMAs techniques to protect water networks against both accidental and intentional contamination events [,], by using innovative sensors to measure water quality []. However, the partitioning of a water supply network inevitably produces a reduction in the hydraulic performance of the system.
Traditionally, the definition of DMAs was based on some empiric suggestions and criteria (number of users per DMA, pipe length and minimum or maximum DMA size) [], or on trial and error hydraulic simulation techniques. In recent years, various authors proposed automatic procedures for the water network partitioning. These procedures are usually organized in two phases []: the first one, the clustering phase, defines the shape and size of the DMAs and thus the boundary pipes; the second one, the dividing phase, provides the optimal placement of flow meters and isolation valves on boundary pipes, maximizing or minimizing one or more objective functions. Several algorithms were proposed for the clustering phase: spectral techniques [,], community detection [,,], graph partitioning [,], while the placement of flow meters and isolation valves can be solved by using heuristic optimization approaches based on economic criteria coupled with hydraulic performance indicators [,], or the reduction of background water leakages [].
Generally, pressure reducing valves (PRVs) can be installed on DMAs entry points to regulate pressure and reduce water losses, for this purpose DMAs were introduced as a management technique for water distribution network [].
As is well known, pressure varies in the network depending on the distance from the water supply tank to the given network point and the ground elevation of the point, e.g., two nodes located at equal distance from the tank (same head losses), but at different elevations, will have different pressure values. Therefore, defining a DMA with highly varying node elevations reduces the effectiveness of pressure regulation. In fact, low ground elevation nodes will be areas of high pressure while high ground elevation nodes will be areas of low pressure, as depicted in Figure 1. In this way, pressure regulation within a DMA with great difference of ground elevations will have a negligible effect on areas of high pressure, because it is necessary to ensure demand supply in areas of low pressure. For this reason, some authors modified the clustering phase to define the shape and size of DMAs that minimize the difference of ground elevations within the DMAs.
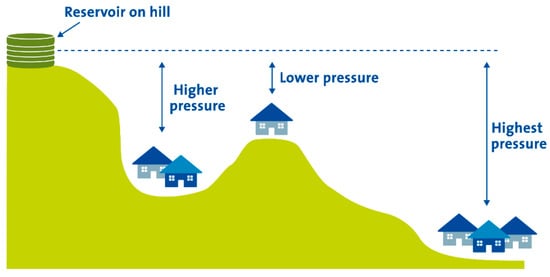
Figure 1.
Scheme of different value of pressure according the ground elevation.
Gomes et al. proposed the division of water supply networks into DMAs using the Floyd-Washall algorithm, with the flow direction, computed at peak hours consumption, and several design criteria, including minimizing differences in the ground elevations within DMAs []. Other authors [] defined DMAs using the Walktrap algorithm, a well-known community detection technique, coupled with different design criteria: total demand supplied in the DMA, total length of DMA pipes and the highest elevation of the DMA. Specifically, Brentan et al. [] observed that the criteria of total length and of maximum elevation are the most appropriate to facilitate the pressure management after dividing the network into DMAs.
Following these considerations, a new DMAs design approach is proposed, it considers ground elevation of network and can be applied to a wide range of clustering algorithms (spectral clustering, community detection, graph partitioning) that take into account a weighted graph as input. The proposed methodology, based on heuristic optimization, was applied to a case study in Mexico with promising results in term of pressure management and water loss reduction.
2. Methodology
The proposed DMAs design approach improves the clustering phase of water network partitioning by grouping nodes with similar ground elevation and minimizing the difference between minimum and maximum elevation within a DMA. As is well known, many clustering algorithms taking into account a weighted network as input. Therefore, it is possible to assign weights to nodes, links, or both elements of the network, and the choice of weight can significantly affect the result of the clustering phase. In other words, the choice of weights changes the shape and size of the DMAs. Taking advantage of this feature, the developed methodology provides a combination of weights, to assign to nodes or links (depending on the clustering algorithm), which forces the definition of clusters with similar elevation. Therefore, the algorithm produces a sequence of weights in order to generate DMAs with a minimum ground elevation. The developed weight search algorithm is described as follows:
- Step a.
- Selection of clustering algorithm, it is possible use several algorithms, such as graph partitioning, community detection, spectral clustering; in this work, for the sake of brevity, a multi-level recursive bisection (MLRB) algorithm [] was applied to test the proposed procedure.
- Step b.
- Define the number of DMAs NDMA.
- Step c.
- Set the initial number of weights, nw, to assign to nodes or links equal to the number of DMAs, specifically, nw represents the variable of the weight search algorithm.
- Step d.
- Divide the nodes of network into nc classes according their elevations, with nc equal to the number of weights, nw (step c).
- Step e.
- Assign the weights wj with j = 1, …, nw to the elements of the network (nodes or links) belonging to the same class; this step simplifies the allocation of weights and reduces the number of variables, because the weight is assigned to the class and not to a network element.
- Step f.
- Modify the weights wj and divide the network in clusters using the algorithm, selected in step a, minimizing the standard deviation of the DMAs ground elevations. To this aim, a genetic optimization algorithm was implemented; the optimization variables are the wj weights and the objective function (OF) to minimize is described as follows:
- Step g.
- Repeat from step c to step f, modifying the number of weights: +1.
- Step h.
- The algorithm ends when the condition is satisfied, in other words the value of objective function of i-th iteration is lower than the value of previous iteration.
It is worth noting that the proposed procedure does not involve hydraulic simulations, but is completely based on the topology of the network.
3. Case Study and Results
The weights search algorithm was applied to the water supply network of a part of Mexico City, that consists of 217 nodes, 289 pipes and one tank located at 348 m.a.s.l. The average daily supplied demand is about 120 l/s and the amount of water losses is about 45% of total inflow. The hydraulic simulations were carried out with the EPANET software [], while the leakages were modeled using the following relationship between pressure, h, and leak flow, :
where the coefficient c was considered constant for all nodes and computed iteratively; the exponent e is equal to 1.18 as reported in []. The minimum desired pressure h* to ensure to deliver the total demand to nodes h* = 10 m.
The minimum and maximum elevations are 264.00 m and 327.28 m, respectively. However, a large part of the network (about 150 nodes) is located at an elevation lower than 300 m, as shown in Figure 2, then a single PRV placed on the main pipe could not regulate pressures effectively, because the set point of valve is strongly limited by few higher elevation nodes.
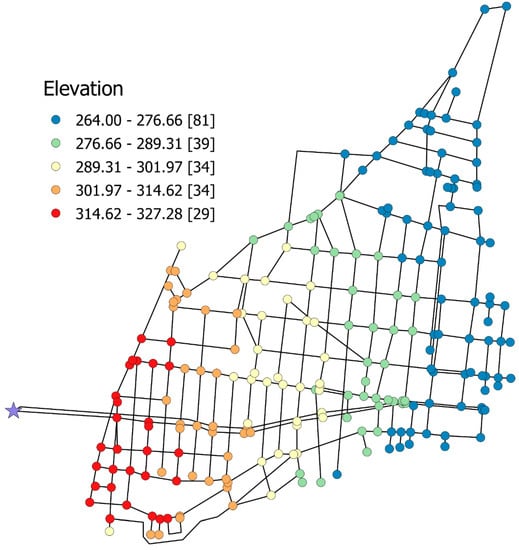
Figure 2.
Layout of water supply network, the nodes are grouped in five classes of elevations. The numbers in square bracket are the number of nodes belonging to the elevation class.
In order to improve pressure management and water loss reduction, the network was divided into two, three, four and five DMAs by using the MLRB technique and weights provided by the developed algorithm. To test the effectiveness of the proposed procedure, the results were compared with DMAs carried out by MLRB without weights.
Table 1, Table 2 and Table 3 show the results of the clustering phase: the number of nodes in each DMAs, the number of boundary pipes, Nec, the balance index IB, computed as the ratio between the largest size of cluster, in terms of nodes, multiplied by k (the number of DMAs), the average elevation zmean, the difference between the minimum and maximum elevation, ∆z and the standard deviation of elevation, σz, within a DMA.

Table 1.
Results of the clustering phase for the unweighted multi-level recursive bisection (MLRB) algorithm.

Table 2.
Results of the clustering phase for the weighted MLRB algorithm.

Table 3.
Results of the dividing phase and percentage of water losses after regulation of pressure.
The results obtained for the clustering phase show that the weights provided by the algorithm methodology affects significantly both the shape and size of the DMAs generated by the MLRB. In fact, the unweighted MLRB generates perfectly balanced DMAs (the balance index is about 1 for all studied configurations), while, by using the weights computed by weight search algorithm, the DMAs result unbalanced: the balancing index varies between 1.11 (3DMAs) and 1.59 (5DMAs). In addition, the weighted MLRB algorithm produces a larger set of boundary pipes than the unweighted MLRB for all DMAs layouts, this feature could represent a disadvantage from an economic, hydraulic and management point of view.
On the contrary, employing weights provided by the proposed methodology makes it possible to reduce the standard deviation of the ground elevations for each DMA and, in this way, the difference between the minimum and maximum altitude within the same DMA decreases significantly. In fact, comparing all the studied DMAs configurations, it is worth observing that the slightest difference for unweighted DMAs is equal to ∆z = 31.28 m (4DMAs and 5 DMAs), while, for weighted DMAs, it is ∆z = 12.03 m. Therefore, the use of weights improves the minimization of the elevation range within a DMA, compared to a DMA obtained without weights.
Therefore, the weighted MLRB improves the definition of DMAs with a minimum elevation difference, compared to the unweighted MLRB.
Then, to evaluate the influence of the computed weights on water losses reduction by placing PRVs on DMAs entry points, the dividing phase was carried out by minimizing the following multi-objective function, named MOF:
where nfm is the number of flow meters to install; Qi and Hi the delivered flow and head at the i-th node; n the number of nodes in the network; and hi is the pressure at the i-th node. The constraint of Equation (3) is necessary to ensure a minimum level of service for customers in terms of pressure.
The minimization of Equation (3) was carried out by the multi objective genetic algorithm NSGA-II []. At the end of the dividing phase, PRVs were placed at the DMAs entry points. The pressure regulation was applied during the hours of lowest consumption, from 00:00 to 7:00 and from 18:00 to 23:59. The PRV settings were defined by minimizing the total inlet water volume, ensuring the minimum design pressure h* in the network.
In Table 3, the minimum number of water meters to install, the number of PRVs, nprv, required to regulate pressures into network and the percentage of leakage are reported. Specifically, the number of PRVs is greater than the number of flow meters, because an additional valve is placed on the main pipe of the network.
The results in Table 3 show that, despite the greater number of boundary pipes, the DMAs configurations obtained by the weighted MLRB allow the placement of a greater number of isolation valves and, consequently, reduce the flow meters to install on boundary pipes. In fact, for all weighted conditions the number of meters is lower than for the unweighted configurations. It is worth observing that non partitioned network layout with a single PRV downstream of the tank has a low impact on water losses reduction (the leakage percentage is about 43%). In addition, the minimization of elevation differences within DMAs has a significant effect on water losses reduction, in fact, the percentage of losses is reduced from 45% to 33.49% for weighted DMAs, while the maximum loss reduction is 37.03% for unweighted DMAs layouts.
4. Conclusions
The weights search algorithm allows to minimize ground elevation differences within DMAs, and improves the performance of the unweighted clustering algorithm. A weighted network according to the proposed procedure has advantages both in the dividing phase and in the water losses reduction by installing PRVs on DMA entry points. The weights search algorithm computes weights without the need of any hydraulic simulation, and it can be coupled with several clustering algorithms that accept a weighted network as input. To test the effectiveness of the proposed methodologies, it is necessary study other networks and implement other clustering algorithms.
Author Contributions
All authors have read and agree to the published version of the manuscript. All authors contributed equally to the paper.
Funding
The authors have no funding to report.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morrison, J.; Tooms, S.; Rogers, D. Summary for Policymakers. In Climate Change 2013—The Physical Science Basis; Intergovernmental Panel on Climate Change, Ed.; Cambridge University Press: Cambridge, UK, 2007; pp. 1–30. [Google Scholar]
- Ainsworth, R. World Health Organization. In Safe Piped Water: Managing Microbial Water Quality in Piped Distribution Systems; Ainsworth, R., Ed.; IWA Publishing: London, UK, 2004; p. 147. ISBN 924156251X. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Venticinque, S. An Automated Tool for Smart Water Network Partitioning. Water Resour. Manag. 2013, 27, 4493–4508. [Google Scholar] [CrossRef]
- Grayman, W.M.; Murray, R.; Savic, D.A. Effects of Redesign of Water Systems for Security and Water Quality Factors. In Proceedings of the World Environmental and Water Resources Congress 2009, Kansas City, MO, USA, 17–21 May 2009; pp. 1–11. [Google Scholar]
- Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G. Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors. Water 2019, 11, 1315. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Optimal Early Warning Monitoring System Layout for Water Networks Security: Inclusion of Sensors Sensitivities and Response Delays. Civ. Eng. Environ. Syst. 2005, 22, 151–169. [Google Scholar] [CrossRef]
- UK Water Industry Research Limited. A Manual of DMA Practice; UK Water Industry Research Limited: London, UK, 1999. [Google Scholar]
- Sela Perelman, L.; Allen, M.; Preis, A.; Iqbal, M.; Whittle, A.J. Automated Sub-Zoning of Water Distribution Systems. Environ. Model. Softw. 2015, 65, 1–14. [Google Scholar] [CrossRef]
- Herrera, M.; Izquierdo, J.; Pérez-García, R.; Montalvo, I. Water Supply Clusters Based on a Boosting Semi-Supervised Learning Methodology. In Proceedings of the Seventh International Conference on Engineering Computational Technology, Valencia, Spain, 14–17 September 2010; Topping, B.H.V., Adam, J.M., Pallarés, F.J., Bru, R., Eds.; Civil-Comp Press: Stirlingshire, UK, 2010. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Weighted Spectral Clustering for Water Distribution Network Partitioning. Appl. Netw. Sci. 2017, 2, 19. [Google Scholar] [CrossRef] [PubMed]
- Ciaponi, C.; Murari, E.; Todeschini, S. Modularity-Based Procedure for Partitioning Water Distribution Systems into Independent Districts. Water Resour. Manag. 2016, 30, 2021–2036. [Google Scholar] [CrossRef]
- Laucelli, D.B.; Simone, A.; Berardi, L.; Giustolisi, O. Optimal Design of District Metering Areas for the Reduction of Leakages. J. Water Resour. Plan. Manag. 2017, 143, 04017017. [Google Scholar] [CrossRef]
- Diao, K.; Zhou, Y.; Rauch, W. Automated Creation of District Metered Area Boundaries in Water Distribution Systems. J. Water Resour. Plan. Manag. 2013, 139, 184–190. [Google Scholar] [CrossRef]
- Alvisi, S. A New Procedure for Optimal Design of District Metered Areas Based on the Multilevel Balancing and Refinement Algorithm. Water Resour. Manag. 2015, 29, 4397–4409. [Google Scholar] [CrossRef]
- Santonastaso, G.F.; Di Nardo, A.; Creaco, E. Dual Topology for Partitioning of Water Distribution Networks Considering Actual Valve Locations. Urban Water J. 2019, 16, 469–479. [Google Scholar] [CrossRef]
- Gomes, R.; Sousa, J.; Muranho, J.; Marques, A.S. Different Design Criteria for District Metered Areas in Water Distribution Networks. Procedia Eng. 2015, 119, 1221–1230. [Google Scholar] [CrossRef][Green Version]
- Awad, H.; Kapelan, Z.; Savić, D.A. Optimal Setting of Time-Modulated Pressure Reducing Valves in Water Distribution Networks Using Genetic Algorithms. In Proceedings of the Integrating Water Systems—10th International on Computing and Control for the Water Industry, CCWI 2009, Sheffield, UK, 1–3 September 2009. [Google Scholar]
- Brentan, B.M.; Campbell, E.; Meirelles, G.L.; Luvizotto, E.; Izquierdo, J. Social Network Community Detection for DMA Creation: Criteria Analysis through Multilevel Optimization. Math. Probl. Eng. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. Multilevelk-Way Partitioning Scheme for Irregular Graphs. J. Parallel Distrib. Comput. 1998, 48, 96–129. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2 User Manual; U.S. Environmental Protection Agency: Washington, DC, USA, 2000. [Google Scholar]
- Martinez, F.; Conejos, P.; Vercher, J. Developing an Integrated Model for Water Distribution Systems Considering Both Distributed Leakage and Pressure-Dependent Demands. In Proceedings of the 29th Annual Water Resources Planning and Management Conference, WRPMD 1999: Preparing for the 21st Century, Tempe, AZ, USA, 6–9 June 1999. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).