Optimal Valve Operation for Restoring Functionality of WDN during Critical Events ^†

Abstract

Water distribution networks are expected to fulfill the water demand by all consumers and at all times, even during critical scenarios, such as pipe failures. In this work, a methodology is proposed to maximize the quality of service during pipe failures by operating valves. The selection of the valves to operate is done by solving an optimization problem using Gondwana, a generic optimization tool for drinking water distribution networks. Different objective functions and different failure scenarios are investigated, considering a real-life water distribution network. The analysis is performed considering the peak demand condition. The proposed methodology is useful for water companies in managing the operation of their networks during critical scenarios.

1. Introduction

During abnormal events, it is very important to maintain a good level of service of water distribution networks (WDN), in terms of satisfying customer water demands. For this reason, the resilience of these systems is a key property [1]. In 2005, the World Conference on Disaster Reduction (WCDR) highlighted the importance of the term resilience, in the context of disaster scenarios, and many authors proposed new methods to quantify the resilience [2]. Ref. [3] proposed an evaluation of the disaster resilience, based on dimensionless analytical functions related to the variation of functionality, obtaining a tool for disaster assessment in structural engineering. Successively, [4] evaluated the performance of a WDN in the case of catastrophes using three indices: the number of users temporarily without water, the water level in the tank and the water quality.

In the framework of WDN, many definitions of resilience have been proposed over the years by different authors. Resilience has been used as a reliability indicator, together with other indexes. In the first developed approaches, the evaluation of the reliability of a WDN was made by the estimation of direct indicators, which required a high computational effort, due to the various scenarios and the complexity of real networks [5,6,7,8]. Successively, to reduce the computational time, reliability has been often expressed using indirect indexes. Many studies have been realized to understand which of the above-mentioned surrogate measures is the most appropriate, to better characterize the full reliability of the network depending on the considered problem.

The resilience index can be viewed either as a design parameter, aiming at maximizing resilience and minimizing investment costs, or as an operation parameter to consider how an existent network should be operated under crisis scenarios. The latter is considered as the main theme of this work, since the resilience assessment of an existing WDN is currently a main topic in the water research field. With this purpose, the resilience can be defined as the capability of a system to maintain and adapt its operational performance in the face of failures and other adverse conditions [9]. Recently, the Water Network Tool for Resilience (WNTR), an open source Python package designed to simulate and analyze resilience of WDN, has been developed [10]. It integrates hydraulic and water quality simulation, a wide range of damage and response options, and different metrics into a single software framework for evaluating water network resilience.

The problem at hand is understanding how a network performs during critical scenarios and then prioritizing the operational choices that can improve its performance. Methodologies based on simulation and optimization tools can help water utilities in individuating how to operate their networks in these cases.

In the study, a methodology to guarantee the highest possible resilience during critical scenarios is also developed. After the evaluation of the network resilience during critical scenarios, the next step is to select how to operate the network. In particular, considering a pipe failure, the network resilience is maximized by changing valve statuses. This is formulated as an optimization problem, in which the decision variables are the valves to operate (open or closed), and the objective function is to maximize the network resilience, expressed as demand satisfaction rate. Gondwana [11], a generic optimization tool for drinking water distribution networks, is used. Different objective functions are considered, in order to understand which is the most appropriate to improve network performance during critical scenarios. The methodology is tested on a real water distribution serving a city in The Netherlands. Different tests are realized, selecting 18 different critical scenarios and assessing resilience during the peak hour.

2. The Proposed Methodology

In the present paper, the resilience index is expressed through the demand satisfaction rate, DSR_s, defined as the ratio between the total available water that can be delivered to the consumers, $Q_s$, under the scenario $s$, and the total water that is required by the consumers, $D$ [12]:

$$DS{R}_s=\frac{Q_s}{D}=\frac{{\sum }_i^{ND}{q}_{i,s}}{{\sum }_i^{ND}{d}_i}$$

(1)

where, $d_i$ is the water demand at node i of the network, $q_{i,s}$ is the actual delivered water to node $i$ in the scenario $s$, $ND$ is the number of nodes in the network.The supplied water flow at each node is a function of the nodal pressure, evaluated as [13]:

$$q_{i,s}=\{\begin{array}{cc}0& if H_{i,s}<H_{i,0}\hfill \\ d_{i,s}{\left(\frac{H_{i,s}-H_{i,0}}{H_{i,min}-H_{i,0}}\right)}^{\gamma }& if H_{i,0}\le H_{i,s}<H_{i,min}\hfill \\ d_{i,s}& if H_{i,s}\ge H_{i,min}\hfill \end{array}$$

(2)

where, $H_{i,s}$ is the actual head at node $i$ and scenario $s$, $H_{i,0}$ is the minimum head to allow any flow to the node, and $H_{i,min}$ is the service head to fully satisfy nodal demand. The exponent $\gamma$ is usually set to 0.5 [11]. In order to compute pressure driven demands, the pressure driven demand extension for EPANET (EPANET.pdd) developed by [14] has been built in Gondwana. In this way, it is possible to compute, for each time step, the demand that is actually delivered to each node of the network during a critical event.

In order to investigate if it is possible to improve the network resilience under critical scenarios by changing its operational mode, the following methodology is performed:

Each critical scenario is created, considering one pipe failure.

The demand satisfaction rate is determined without changing valve statuses (current valve statuses), in order to get the initial resilience index of the WDN.

The valve statuses are changed using the numerical optimization technique implemented in Gondwana, in order to maximize the demand satisfaction rate, or in other words, to minimize the demand deficit. This is done considering the following objective functions:

• Total demand: Maximization of total demand satisfaction rate summed over all nodes n of the network and for the simulation period, t, which is obtained by maximizing the following function:

  $$max{\displaystyle \sum _t\sum _{i=1}^n}\frac{{\sum }_i^{ND}{q}_{i,s}}{{\sum }_i^{ND}{d}_i}$$

  (3)
• Maximum demand: Maximization of the demand satisfaction rate at the node with highest demand deficit ndef summed over all time steps of the simulation period, expressed as:

  $$max{\displaystyle \sum }_t\frac{q_{ndef,s}}{d_{ndef}}$$

  (4)
• Maximum nodal demand: Maximization of the demand satisfaction rate of the highest demand deficit for each node n evaluated over the entire simulation period, obtained through:

  $$max(mi{n}_t\frac{q_{i,s}}{d_i})$$

  (5)

In each scenario, the simulation is done with each of the three objective functions, in order to compare the results and assess which one is more appropriate in the context of the problem.

3. Results

3.1. The Case Study

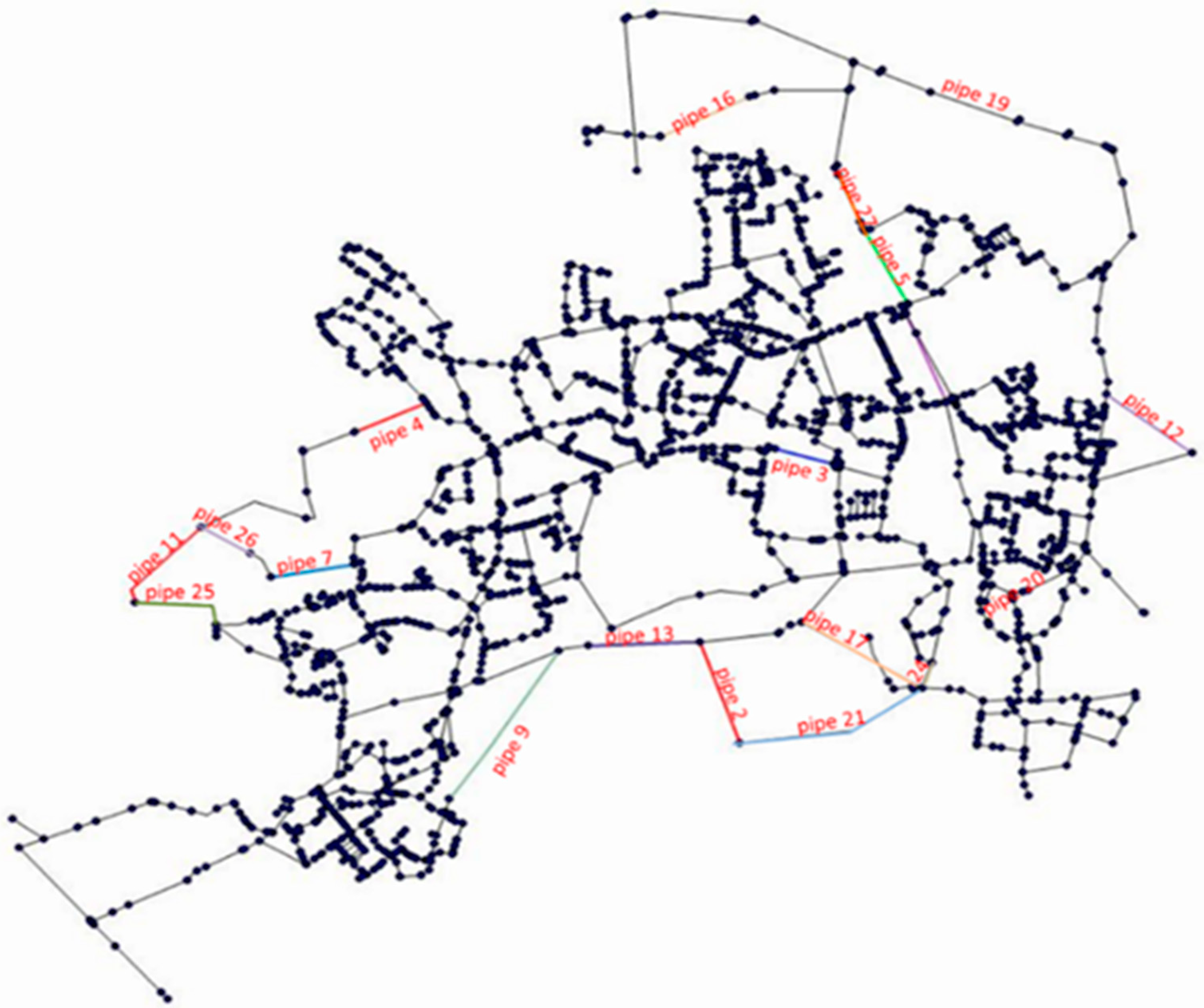
The proposed methodology is applied to a WDN serving a city in the Netherlands, with ca. 105 thousand inhabitants. The network supplies a total demand of 31,272 m³/day. The elevation varies between 15–23 m, and pipes are made of plastic materials (84%), steel (12%) and concrete (4%). The hydraulic simulations are performed with the software EPANET, adopting the Darcy–Weisbach resistance formula. The network scheme, reported in Figure 1, is composed of 4311 pipes, 5096 junctions, 5 reservoirs and 891 valves. In the model, three different demand patterns are assigned for considering different types of the consumptions.

3.2. The Considered Scenarios and the Performed Tests

Overall, 18 critical scenarios are considered, and each of them assumes one pipe out of service. To select the pipes for the failure scenarios, different criteria were considered, based on the diameter and length, highest flow, and proximity to the node with the highest base demand. The selected pipes are indicated in the network scheme of Figure 1. Two kinds of tests are performed. The former refers to a situation in which it is assumed that the valve statuses in the network model are an accurate representation of the real valve statuses, and in this case all valves are assumed open. Then, the optimization model selects the valves to close. This is often not the case: in fact, water utilities in the Netherlands believe that about 1% of valves are in a different status than described in the model, due to unregistered network operations. In order to assess the resilience taking into consideration some uncertainty about valve statuses, the same computations are performed on different network models assuming 1% of closed valves randomly placed in the network. Then, the optimization model selects the valves to close for optimizing the resilience.

It is assumed that the events take place during an entire simulation period (00:00–24:00). In real-life situations, it is important to consider the actual start time of an event and its duration, and compute the resilience in this time period. In all nodes, a service pressure, H_i,min, equal to 20 m is considered for the computation of the pressure delivered demand. This means that, for nodes with a pressure below 20 m, the volume of water that is actually delivered is less than the demand (Equation (2)). Gondwana uses a genetic algorithm (GA) for the optimization, and the GA parameters used are summarized in

Table 1. Optimization parameters used in Gondwana for the genetic algorithm.

Optimization Parameter
Population size (number of individuals)	200
Initialization	Current values
Selector	Tournament
Elitism rate	10%
Terminator	50 generations
Uniform matution rate	0.001
Crossover rate (one point crossover)	0.95

.

3.3. Results

In presenting the results, the 18 different scenarios are sorted, starting from the worse one, i.e., the one with a higher percentage of unsatisfied demand in the initial situation, DEF_p0, evaluated during the peak hour, defined as:

$$DE{F}_{p0}=1-DS{R}_{p0}$$

(6)

Referring to the case in which it is assumed that all valves are open (Test1),

Table 2. Percentage of unsatisfied demand in the initial condition and percentage improvement of the unsatisfied demand after the optimization for the three different objective functions (all valves open).

Pipe Out of Service	Critical Node	DEFp0 %	$\mathsf{\Delta }\mathit{D}\mathit{E}{\mathit{F}}_{\mathit{p}}\%$ (Total Dem.)	$\mathsf{\Delta }\mathit{D}\mathit{E}{\mathit{F}}_{\mathit{p}}\%$ (Max. Dem.)	$\mathsf{\Delta }\mathit{D}\mathit{E}{\mathit{F}}_{\mathit{p}}\%$ (Max. Nod. Dem.)
Pipe 2	lungend01	47.74%	24.05%	26.57%	24.23%
Pipe 13	X14321	37.43%	2.66%	1.11%	1.26%
Pipe 7	X00027a	31.37%	0.41%	0.41%	0.60%
Pipe 25	X08436	29.28%	0.68%	0.55%	0.10%

summarizes the results obtained for the four most critical scenarios. It reports the improvement of the unsatisfied demand after the optimization process $\Delta DE{F}_p=DE{F}_{p0}-DE{F}_p$.

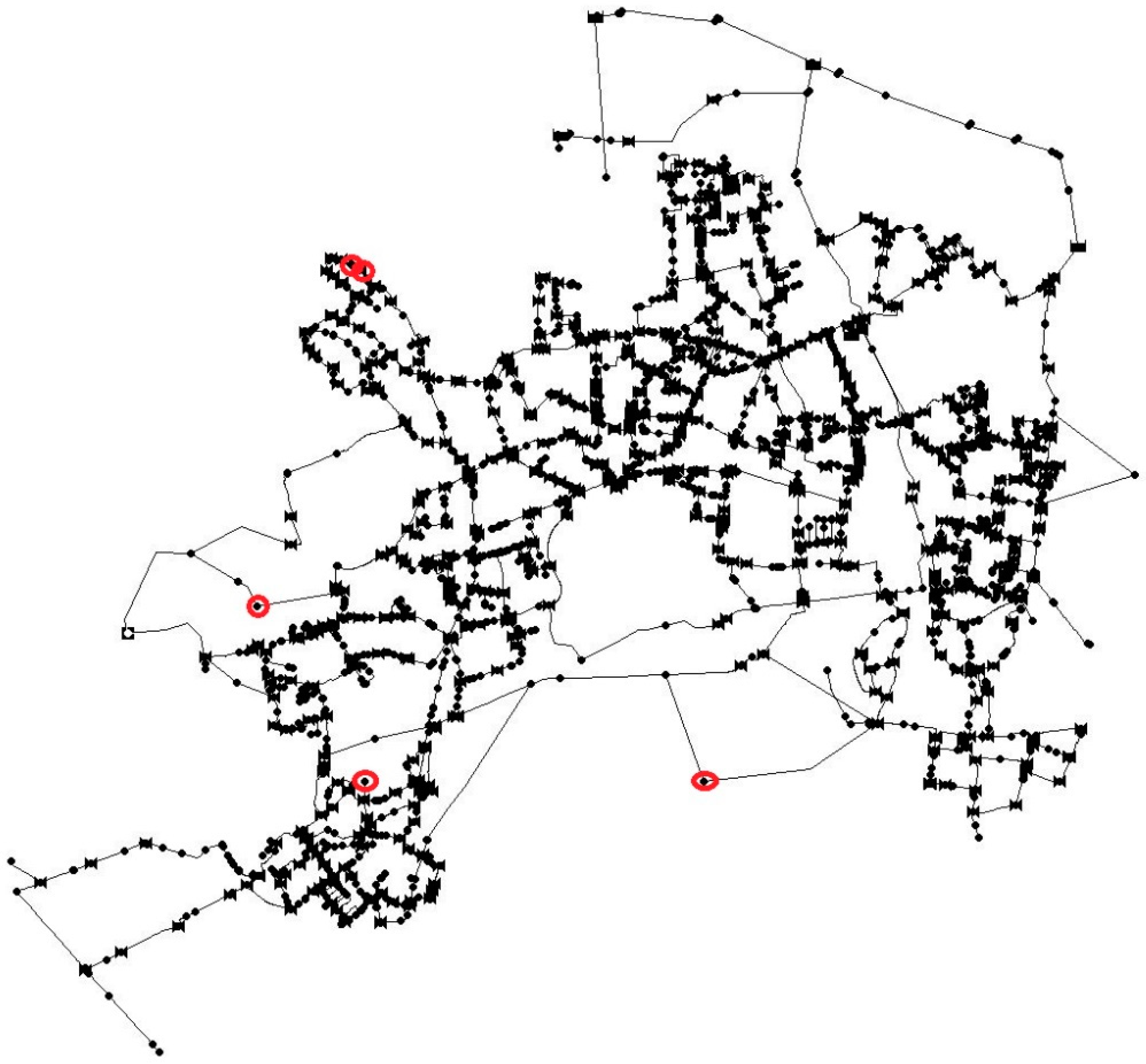
The second column reports the node which is most affected by the critical scenario (represented in Figure 2), while the third one indicates the percentage of unsatisfied demand in the current situation (i.e., before the optimization). The other three columns summarize the percentage decrease of the unsatisfied demand in the same node after the optimization, considering the three different objective functions. As shown in the table, the improvement after the optimization process is high only for the most critical scenario (failure of pipe number 2). The obtained improvement is similar for the three different analyzed objective functions.

Table 3. Percentage of unsatisfied demand in the initial condition and percentage improvement of the unsatisfied demand after the optimization for the Total Demand objective function (1% of closed valves).

Pipe Out of Service	Critical Node	DEFp0 %	$\mathsf{\Delta }\mathit{D}\mathit{E}{\mathit{F}}_{\mathit{p}}\%$ (Total Demand)
Pipe 7	X00027a	33.11%	3.77%
Pipe 25	X08436	31.00%	3.86%
Pipe 1	X12308	27.97%	3.83%
Pipe 11	X12308	27.47%	3.81%

. Percentage of unsatisfied demand in the initial condition and percentage improvement of the unsatisfied demand after the optimization for the Total Demand objective function (1% of closed valves)—shows the corresponding results relative to the case with 1% of valves initially closed (Test2). The four most critical scenarios are reported, and represented in Figure 2, along with the percentage of improvement after the optimization of valve statuses, obtained by considering only the objective function total demand.

Comparing the results of the two different tests, the two worst cases of Test 1 are not present in the first four of the second one, while the scenarios with the rupture in pipes 7 and 25 are present in both. For those ones, the percentage of unsatisfied demand is higher in the case with 1% of closed valves, and the obtained improvement, even if small, is higher with respect the other case. The results indicate that the analyzed network has, in general, a high resilience to the pipe failure.

In order to give a more customer-oriented view of the improvement, the user connections affected by the critical scenarios above a given demand deficit threshold, before and after the optimization process, are counted. In

Table 4. Number of connections affected by the pipe failures before and after the optimization process, considering demand deficits of 10, 15, 20, 25 and 30%.

All Open Valves Case
	Demand Deficit
Pipe out of service	30%		25%		20%		15%		10%
	Before	After	Before	After	Before	After	Before	After	Before	After
Pipe 2	1	0	1	0	742	739	2607	2551	4843	4808
Pipe 13	1484	1148	2522	2457	998	984	3346	3342	5077	5018
Pipe 7					815	767	2565	2548	4841	4829
Pipe 25			21	0	887	768	2568	2560	4871	4837
1% of closed valves case
Pipe out of service	30%		25%		20%		15%		10%
	Before	After	Before	After	Before	After	Before	After	Before	After
Pipe 7	9	9	594	12	6527	2664	12,242	9528	20,536	16,845
Pipe 25	3	0	929	68	6473	2984	12,302	9551	20,536	16,886
Pipe 1			1043	325	8174	4674	12,722	10193	21,497	18,482
Pipe 11			575	9	6861	2656	12,327	9554	20,568	16,914

, the results are summarized, considering an initial situation with all open valves, and an initial situation with 1% of closed valves. A reduction of the unsatisfied user connects is observed after the optimization, and in particular it is very consistent for the 25% of the demand deficit relative to the Test2. In this case, the performance of the network is significantly improved after the optimization.

Considering that in every scenario the optimization consists in changing the valve statuses in order to reach a higher resilience,

Table 5. Number of use for each valve valves in the WDN.

Sum
ValveID	81			253		839	1217	1857	2001	3101				6723			7361
N. used	5			5		9	2	7	3	5				7			2
Maximum Network
Valve ID	57		81			253–254	839	1857		2001		3101			6723
N. used	2		7			2	11	7		4		5			10
Maximum Element
Valve ID	81	83			253	835	839	2395	2769	4127	4611		4785			7275
N. used	5	5			3	4	11	5	8	8	3		3			3

reports the number of times that every single valve is used for each objective function. In this way, it is possible to check which are the critical valves of the network, and so the ones that the water utility has to pay extra attention to. It can be noted that there are two valves operated many times with all the objective functions. In particular, for all cases, the most operated one is the valve 839.

4. Conclusions

In the present paper, a methodology to maximize the quality of the service during a pipe failure event has been studied. The obtained results prove that it is possible to make a WDN more resilient, in terms of unsatisfied demands, by changing the valve statuses. It has been applied to an over-dimensioned and highly looped network that has resulted in being already very resilient to failures.

The methodology can be used either during critical scenarios, or during maintenance works. It indicated also the valves operated more frequently during critical scenarios, which is a useful information for network management to preserve their functioning. Moreover, this is a useful information also in performing valve location designing analysis.

In future studies, the methodology will be applied to more complex networks, in particular divided into district meter areas (DMAs), where the resilience is lower due to the closure of boundary valves. In particular, it is expected that, in this case, the optimization of valve manipulations can furnish a great improvement.