Flow Field Research of the Reciprocating Baffled Flocculation Tank †
Abstract
:1. Introduction
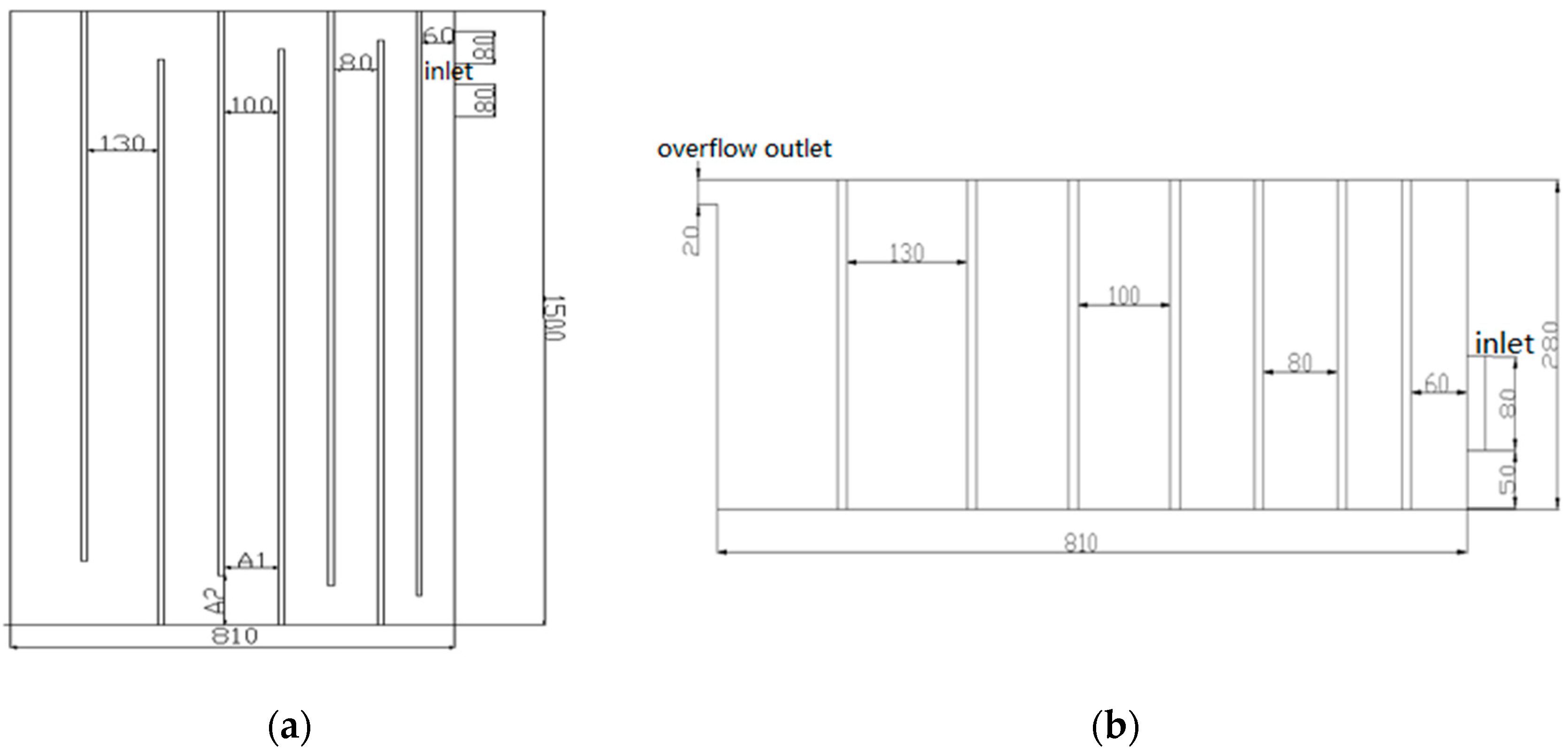
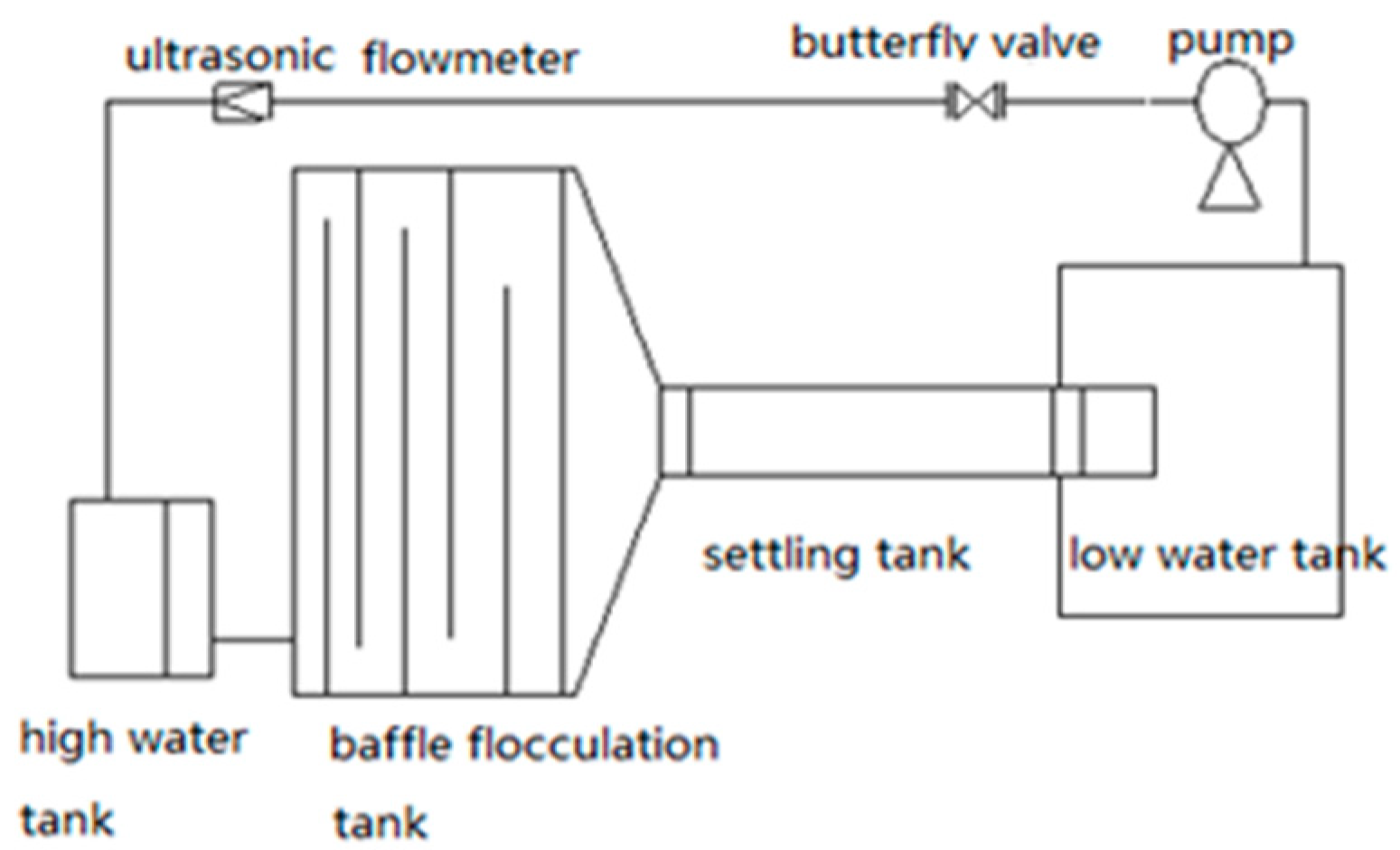
2. Experimental Apparatus
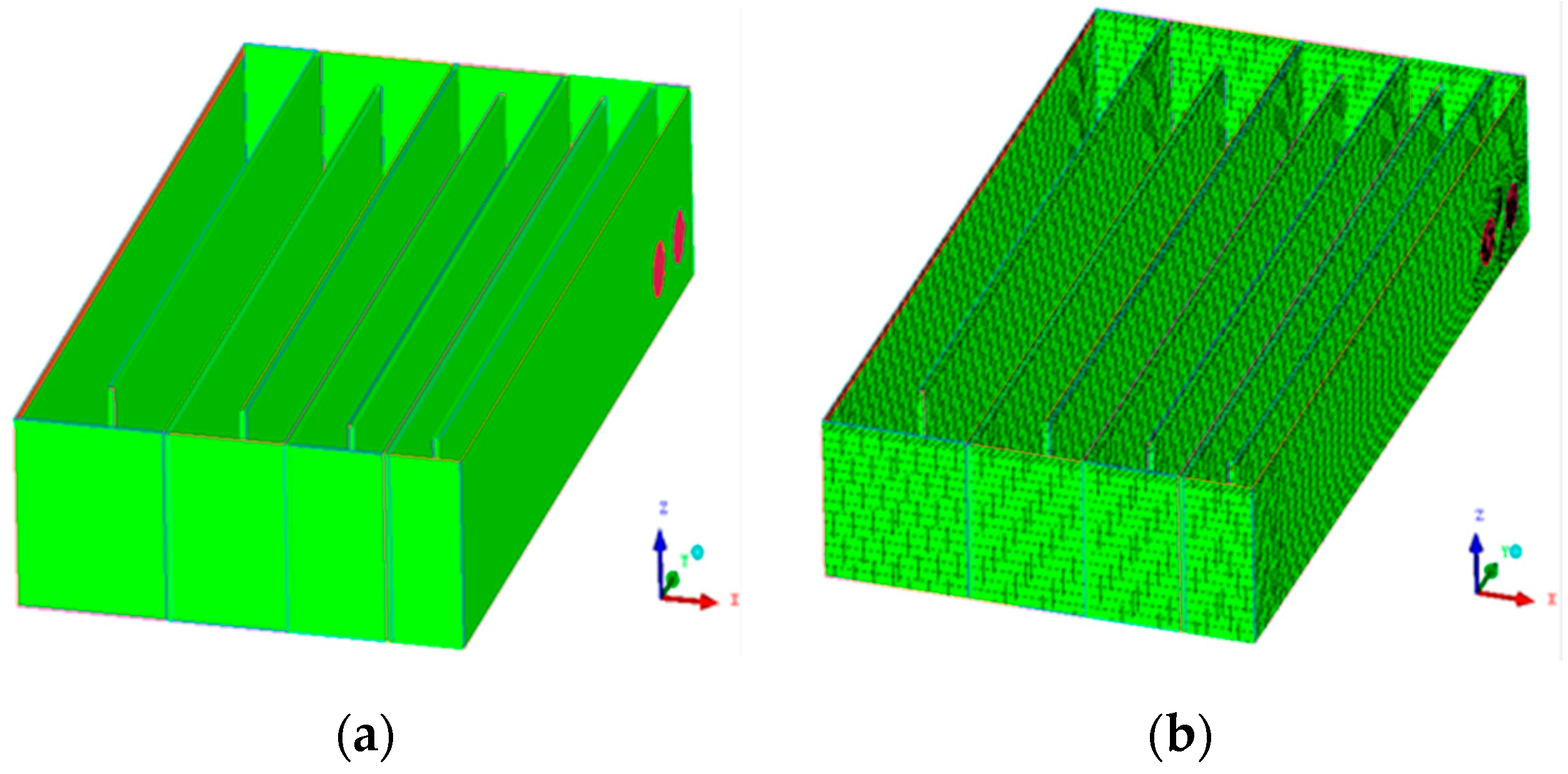
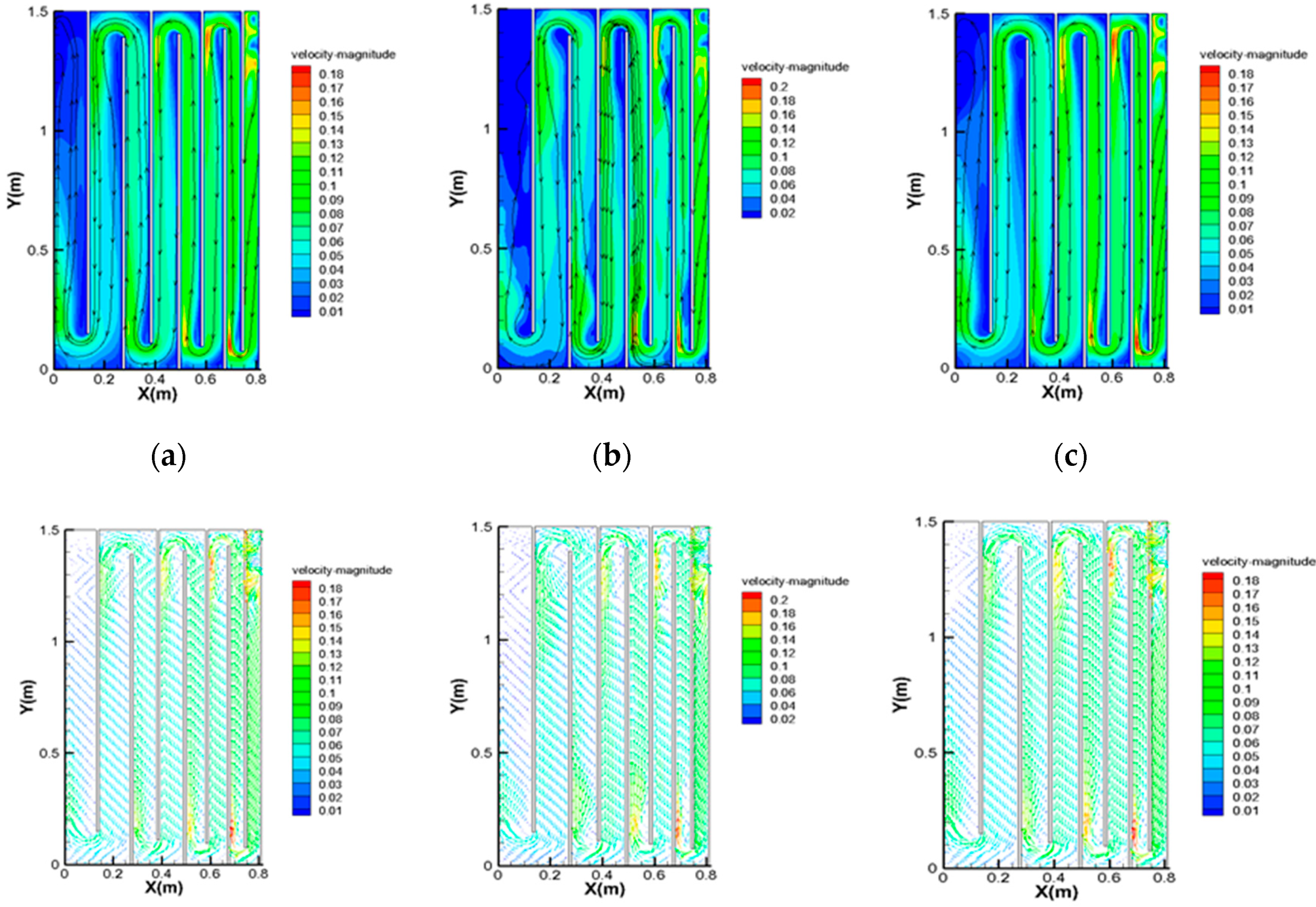
3. Numerical Simulations
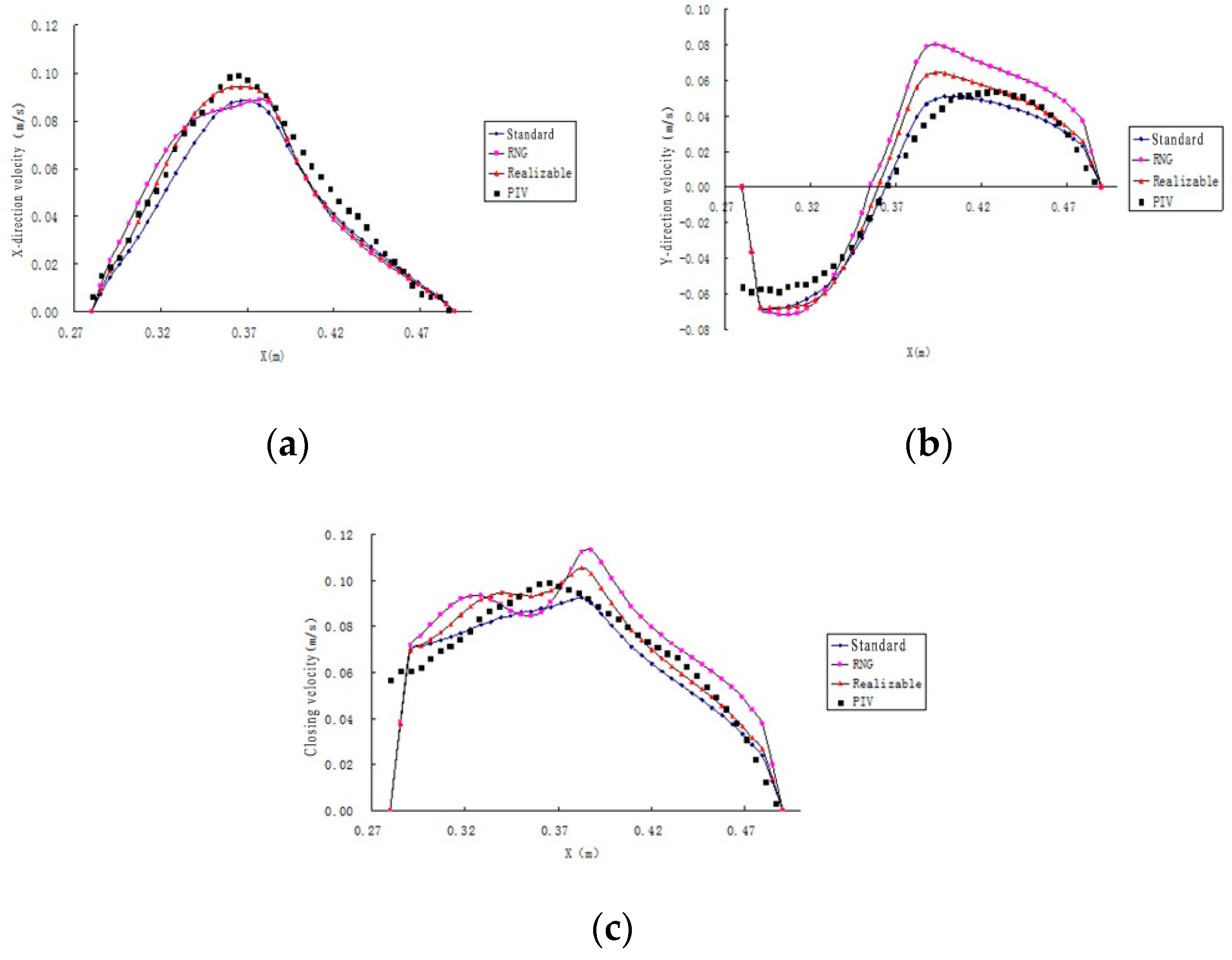
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, Y.G.; Jiang, X.C.; Ji, Q.J. Research progress of enhanced coagulation technology. Indust. Water Treat. 2005, 23, 9–14. [Google Scholar]
- Zhan, X.; Gao, B.Y.; Yue, Q.J.; Wang, Y.; Cao, B.C. Coagulation behavior of polyferric chloride for removing NOM from surface water with low concentration of organic matter and its effect on chlorine decay model. Sep. Purif. Technol. 2010, 75, 61–68. [Google Scholar] [CrossRef]
- Jarvis, P.; Jefferson, B.; Gretgory, J.; Palrsons, S. A review of floc strength and breakage. Water Res. 2005, 39, 3121–3137. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Nan, J.; Ji, X.; Yang, Y. Effect of the micro-flocculation stage on the flocculation/ sedimentation process: The role of shear rate. Sci. Total Environ. 2018, 633, 1183–1191. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.F.; Yu, J.S.; Wang, H.R.; Dou, J.; Wang, C. Fractal dimension of cohesive sediment flocs at steady state under seven shear flow conditions. Water 2015, 7, 4385–4408. [Google Scholar] [CrossRef]
- Chakrabortia, R.K.; Gardnerb, K.H.; Atkinsona, J.F.; Van Benschoten, J.E. Changes in fractal dimension during aggregation. Water Res. 2003, 37, 873–883. [Google Scholar] [CrossRef]
- Gregory, J.; Yukselen, M.A. The reversibility of floc breakage. Int. Miner. Process. 2004, 73, 251–259. [Google Scholar]
- Wang, Z.; Nan, J.; Yao, M.; Yang, Y. Effect of additional polyaluminum chloride and polyacrylamide on the evolution of floc characteristics during floc breakage and re-growth process. Sep. Purif. Technol. 2017, 173, 144–150. [Google Scholar] [CrossRef]
- Zhan, Y.; An, R.Y.; Wang, J.S. Application of Particle Image Velocimetry Technique in the Flow Field of Reciprocating Baffled Flocculation Tank. In Proceedings of the 2009 International Symposium on Environmental Science and Technology, Wuhan, China, 4–5 July 2009; pp. 1327–1330. [Google Scholar]
- Xu, J.; Li, X.Y. Investigation of the effect of nanoparticle exposure on the flocculability of activated sludge using particle image velocimetry in combination with the extended DLVO analysis. Colloids Surf. B Biointerfaces 2016, 143, 382–389. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Lam, X.Y.; Zhong, R.S.; Zhang, X.H. PIV characterization of flocculation dynamics and floc structure in water treatment. Colloids Surf. A Physicochem. Eng. Asp. 2011, 379, 27–35. [Google Scholar] [CrossRef]
- Bridgeman, J.; Jefferson, B.; Parson, S.A. The development and application of CFD models for water treatment flocculators. Adv. Eng. Softw. 2010, 41, 99–109. [Google Scholar] [CrossRef]
- Essemiani, K.; Traversay, C. Optimum design of coagulation/ flocculation vessels. In Proceedings of the WQTC 2002 Conference, Seattle, WA, USA, 2002. [Google Scholar]
- He, W.P.; Xie, Z.L.; Zhao, Z.Y.; Huang, M.; Pan, M. Effect of impeller clearance on floc growth behaviors in a baffled square stirred-tank reactor: Flocculation-test and CFD-aided studies. Sep. Purif. Technol. 2019, 212, 233–244. [Google Scholar] [CrossRef]
- Gao, H.W.; Stenstrom, M.K. Generalizing the effects of the baffling structures on the buoyancy-induced turbulence in secondary settling tanks with eleven different geometries using CFD models. Chem. Eng. Res. Des. 2019, 143, 215–225. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Wu, Y.; Liang, H.; Sun, Q. Flow Field Research of the Reciprocating Baffled Flocculation Tank. Environ. Sci. Proc. 2020, 2, 29. https://doi.org/10.3390/environsciproc2020002029
Xu Y, Wu Y, Liang H, Sun Q. Flow Field Research of the Reciprocating Baffled Flocculation Tank. Environmental Sciences Proceedings. 2020; 2(1):29. https://doi.org/10.3390/environsciproc2020002029
Chicago/Turabian StyleXu, Ying, Yuebin Wu, Huan Liang, and Qiang Sun. 2020. "Flow Field Research of the Reciprocating Baffled Flocculation Tank" Environmental Sciences Proceedings 2, no. 1: 29. https://doi.org/10.3390/environsciproc2020002029
APA StyleXu, Y., Wu, Y., Liang, H., & Sun, Q. (2020). Flow Field Research of the Reciprocating Baffled Flocculation Tank. Environmental Sciences Proceedings, 2(1), 29. https://doi.org/10.3390/environsciproc2020002029



