Machine Learning Approaches for Soil Moisture Prediction Using Ground Penetrating Radar: A Comparative Study of Tree-Based Algorithms
Abstract
1. Introduction
- Systematically compare single regression trees versus boosted tree ensembles for soil moisture prediction using GPR histogram features from 21 Eastern Thailand sites;
- Determine the performance trade-offs between model interpretability and predictive accuracy for operational deployment guidance;
- Assess model reliability through uncertainty analysis and cross-validation across diverse soil categories (coastal sandy, transitional mixed, inland clayey).
2. Literature Review
2.1. Soil Moisture Estimation Using GPR
2.2. Geophysical Data Analysis Using Machine Learning
2.3. Advanced GPR Signal Processing and Feature Extraction
2.4. Comparative Algorithm Studies and Research Gaps
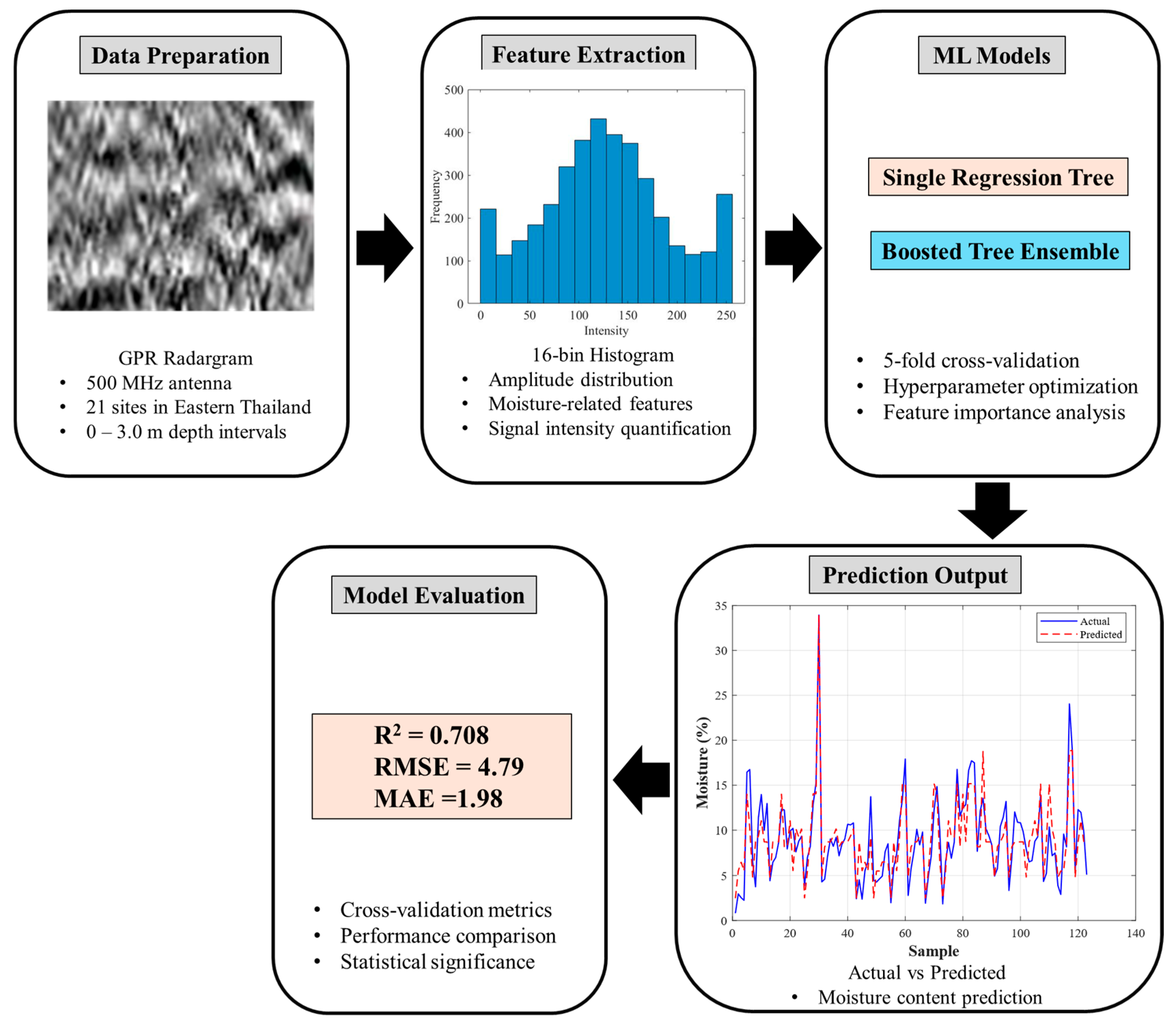
3. Methodology
3.1. Study Area and Site Selection
3.2. Field Data Collection
3.2.1. GPR Data Acquisition
3.2.2. Soil Sampling and Laboratory Analysis
3.3. Data Preprocessing
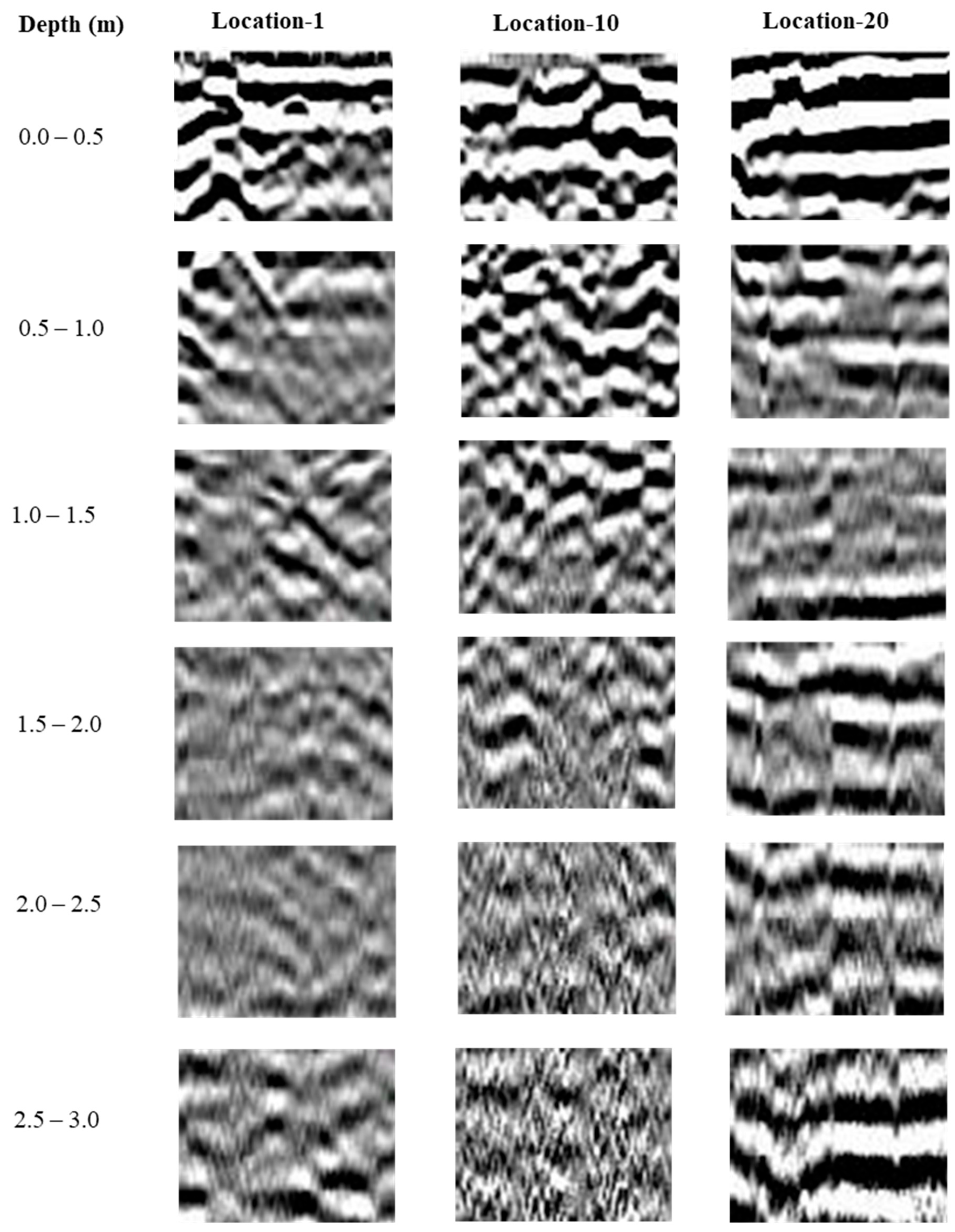
3.3.1. GPR Radargram Processing
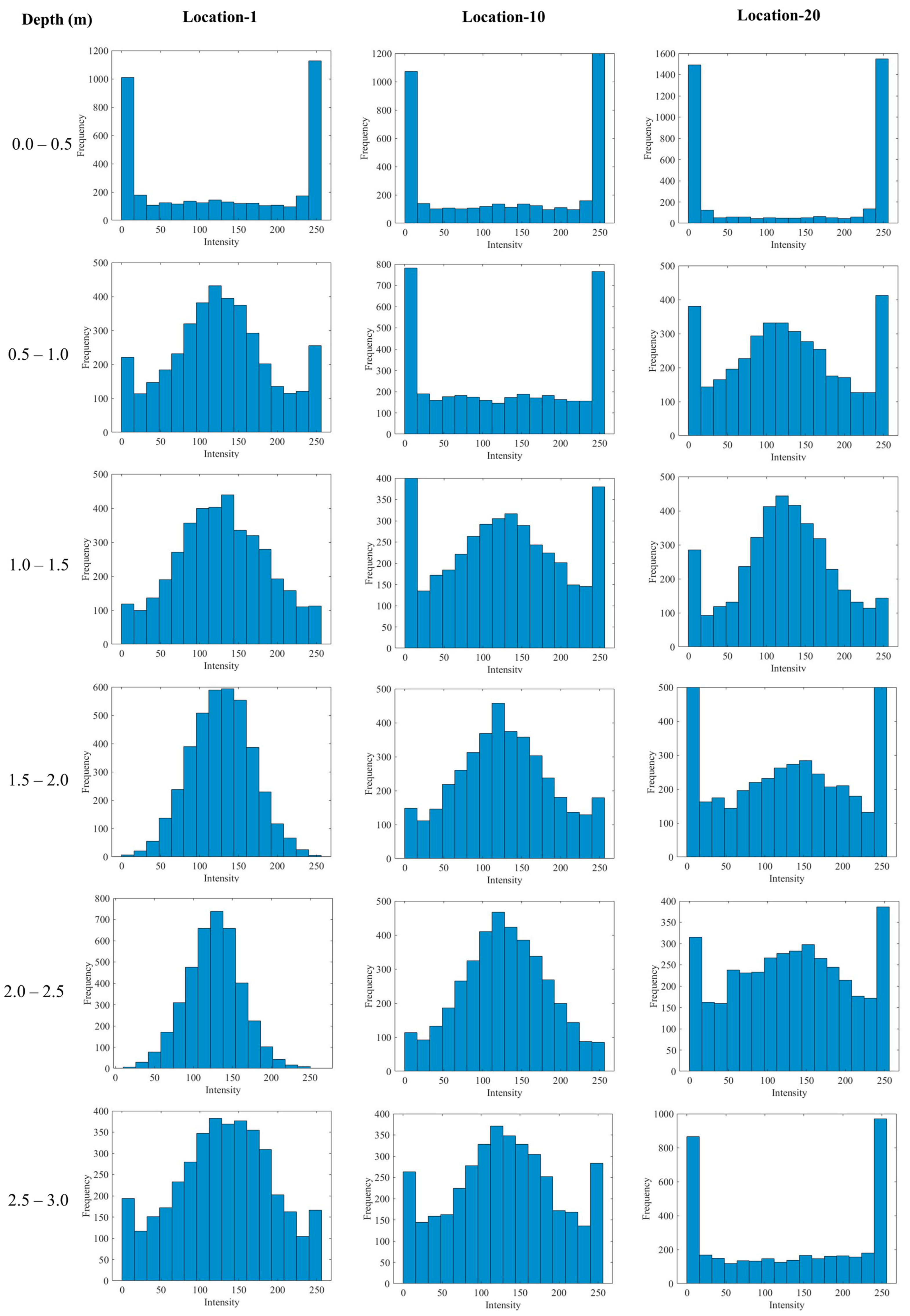
3.3.2. Histogram-Based Feature Extraction
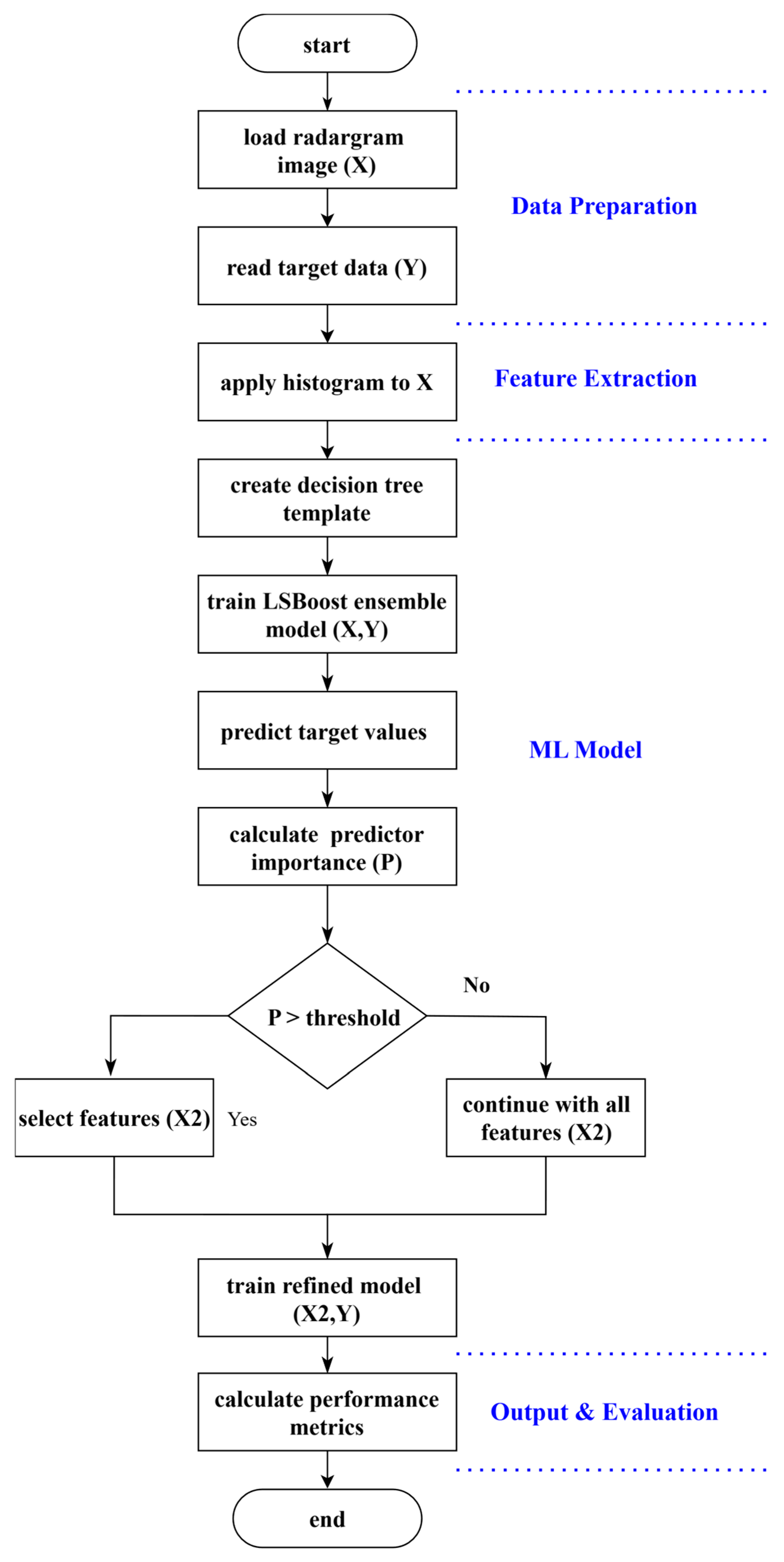
3.4. Machine Learning Implementation
3.4.1. Single Regression Tree Approach
3.4.2. Boosted Tree Ensemble Approach
3.5. Performance Evaluation
- Root Mean Square Error (RMSE) is used to evaluate the overall prediction accuracy by measuring the square root of the difference between the predicted and true values, as shown in Equation (8).
- R-squared (R2) represents the proportion of the variance in the observed data that is explained by the model, reflecting the explanatory power of the model, as shown in Equation (9).
- Mean Absolute Error (MAE) represents the average of the predicted errors, providing a measure of model accuracy that can be interpreted in terms of absolute deviation, as shown in Equation (10).
4. Results
4.1. Site Characteristics and Data Collection
4.2. Algorithm Optimization Results
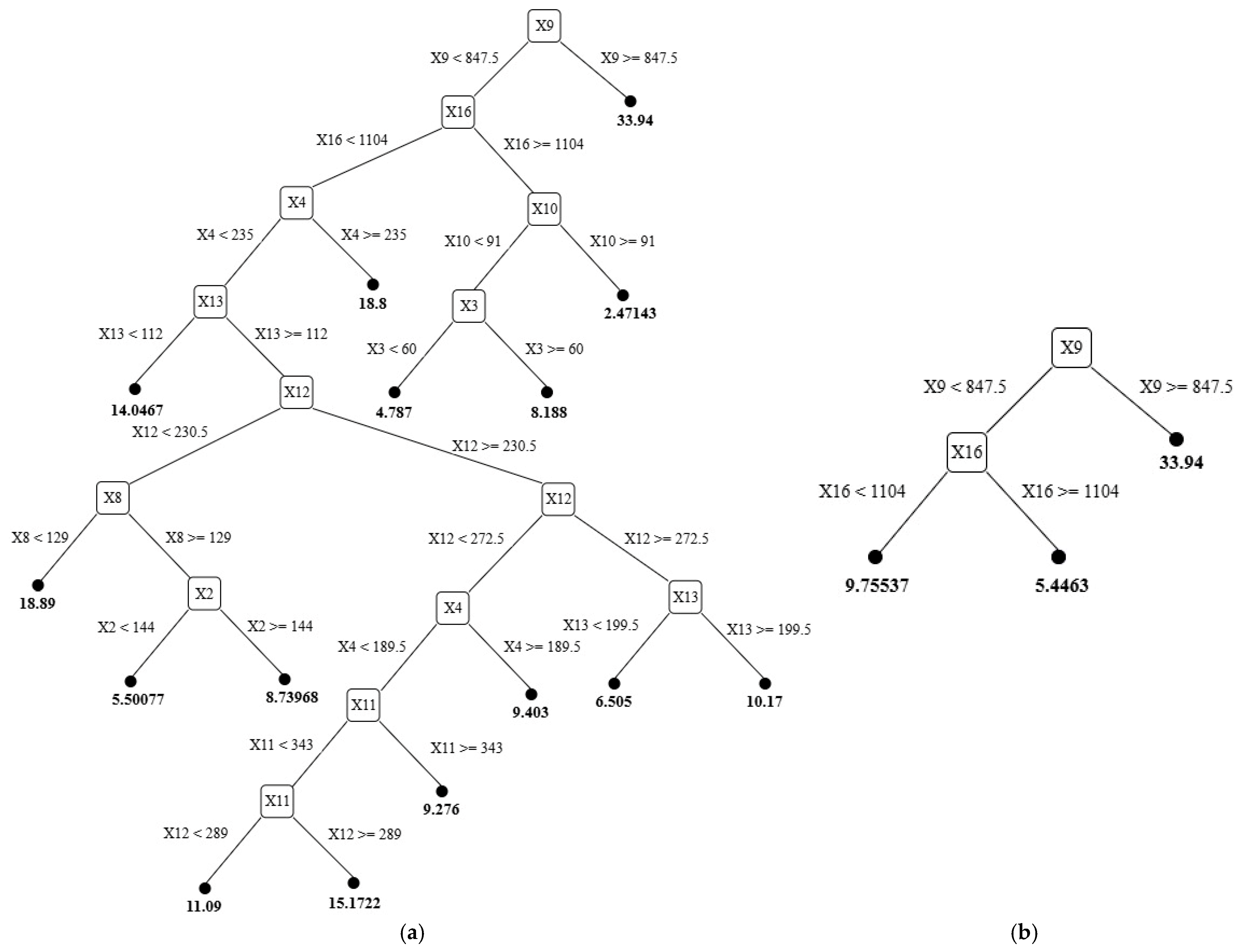
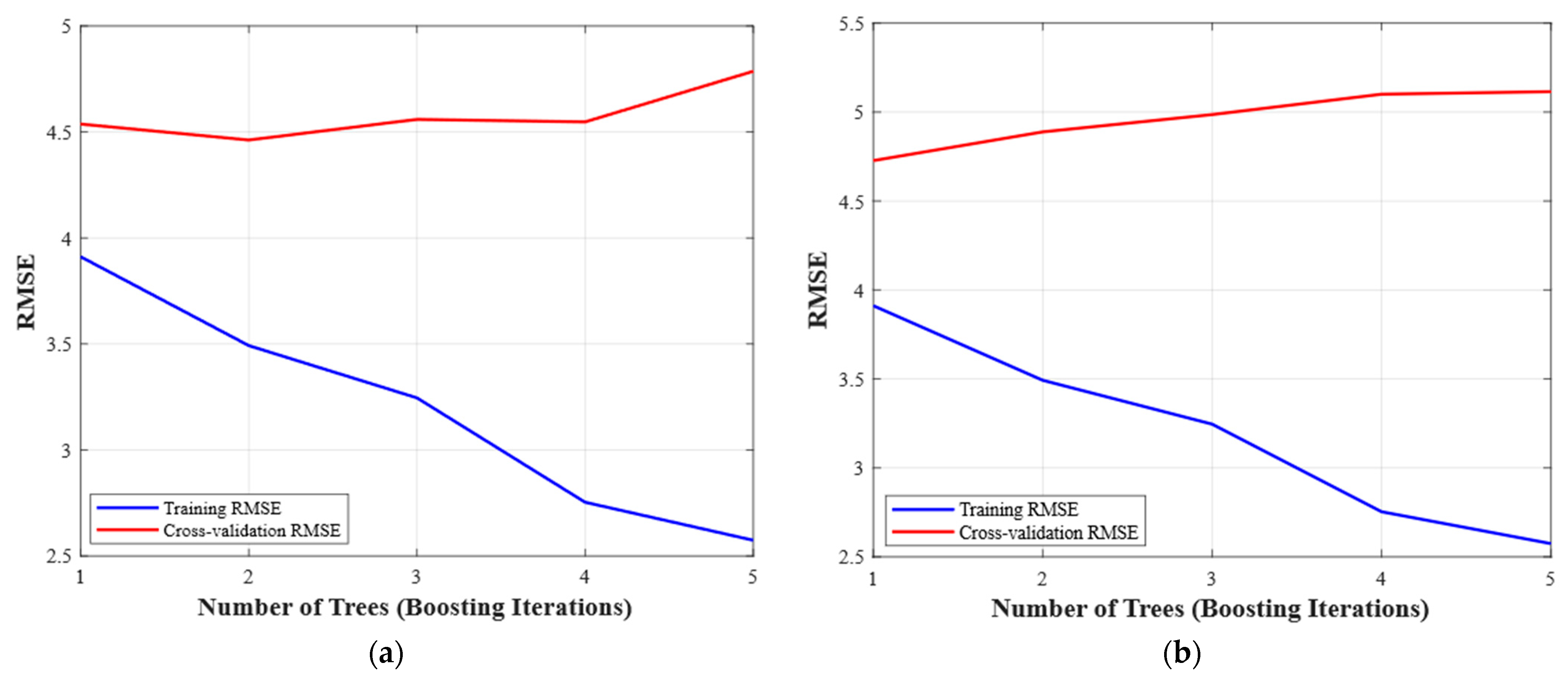
4.2.1. Single Regression Tree Optimization
- Decision Pathway 1
- Decision Pathway 2
- Decision Pathway 3
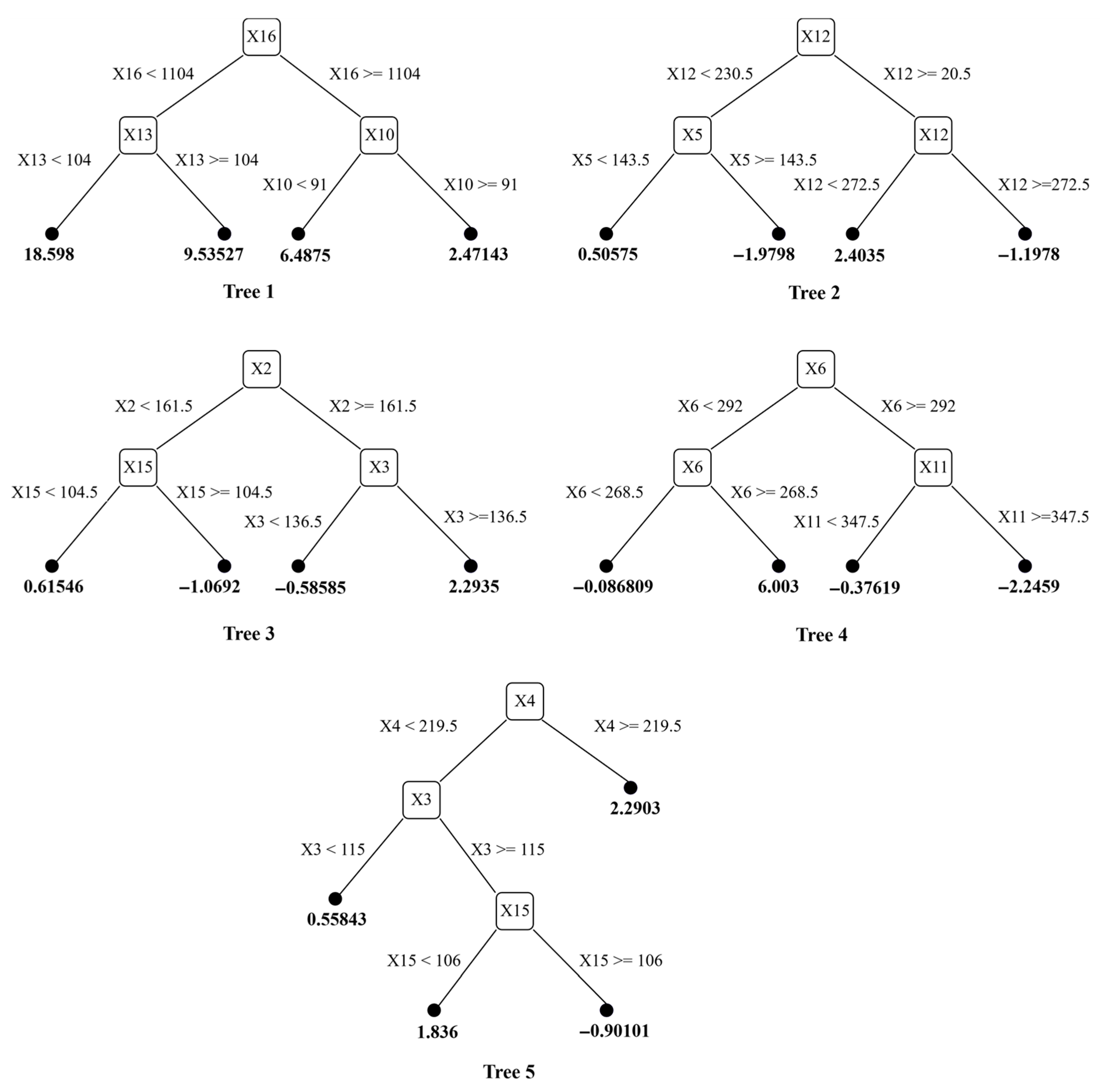
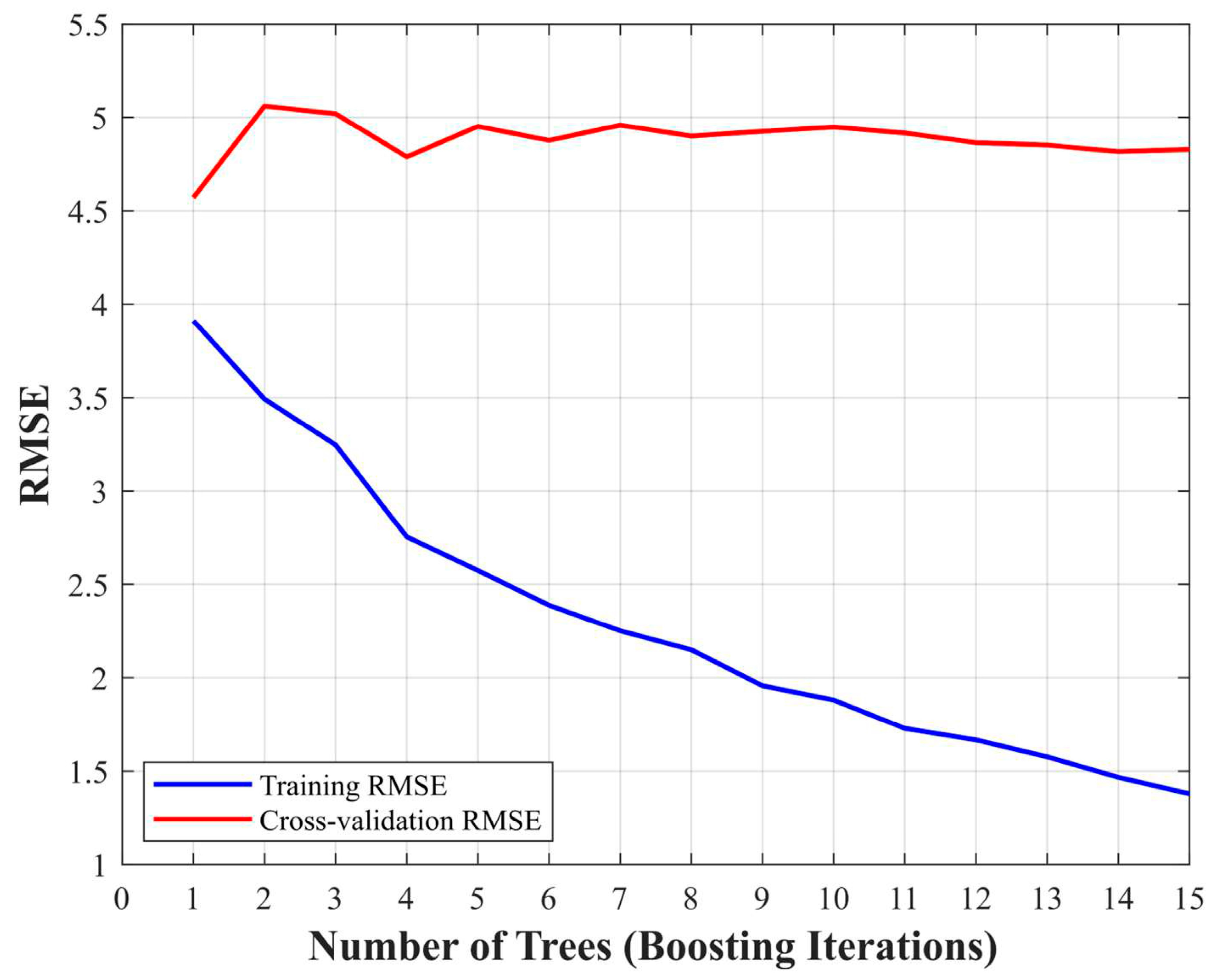
4.2.2. Boosted Tree Ensemble Optimization
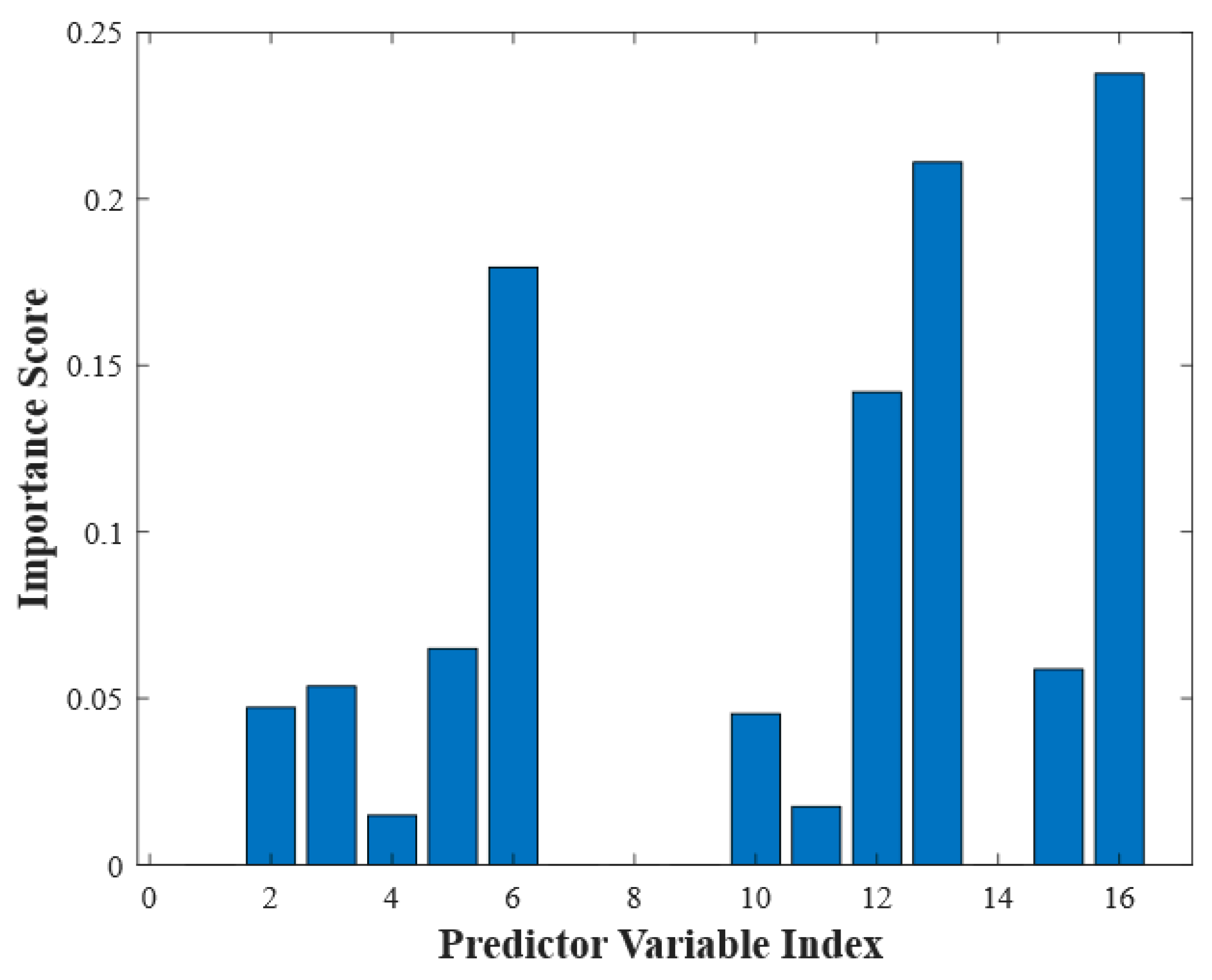
- Distributed Feature Utilization
- Sequential Error Correction
- Hierarchical Complexity Management
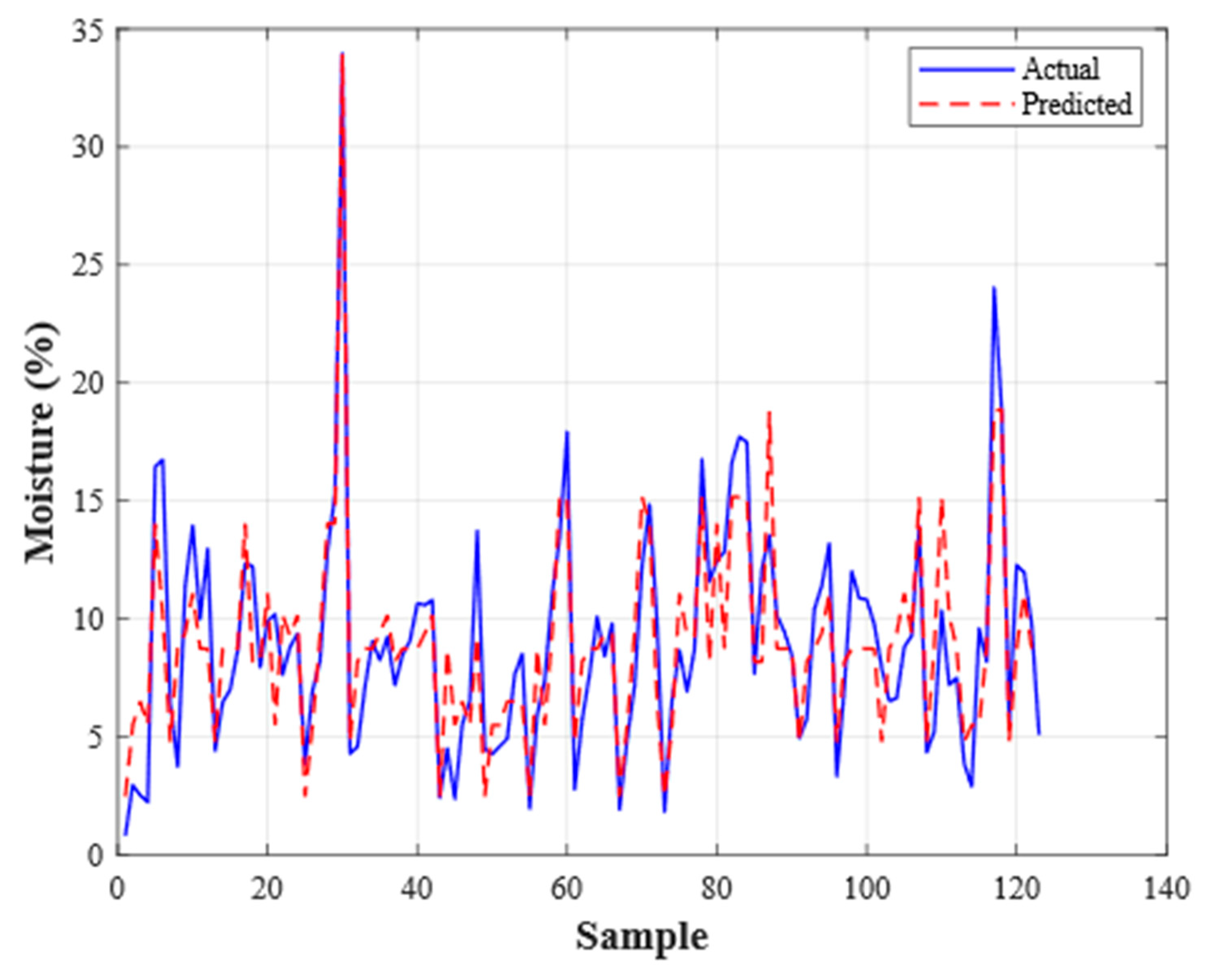
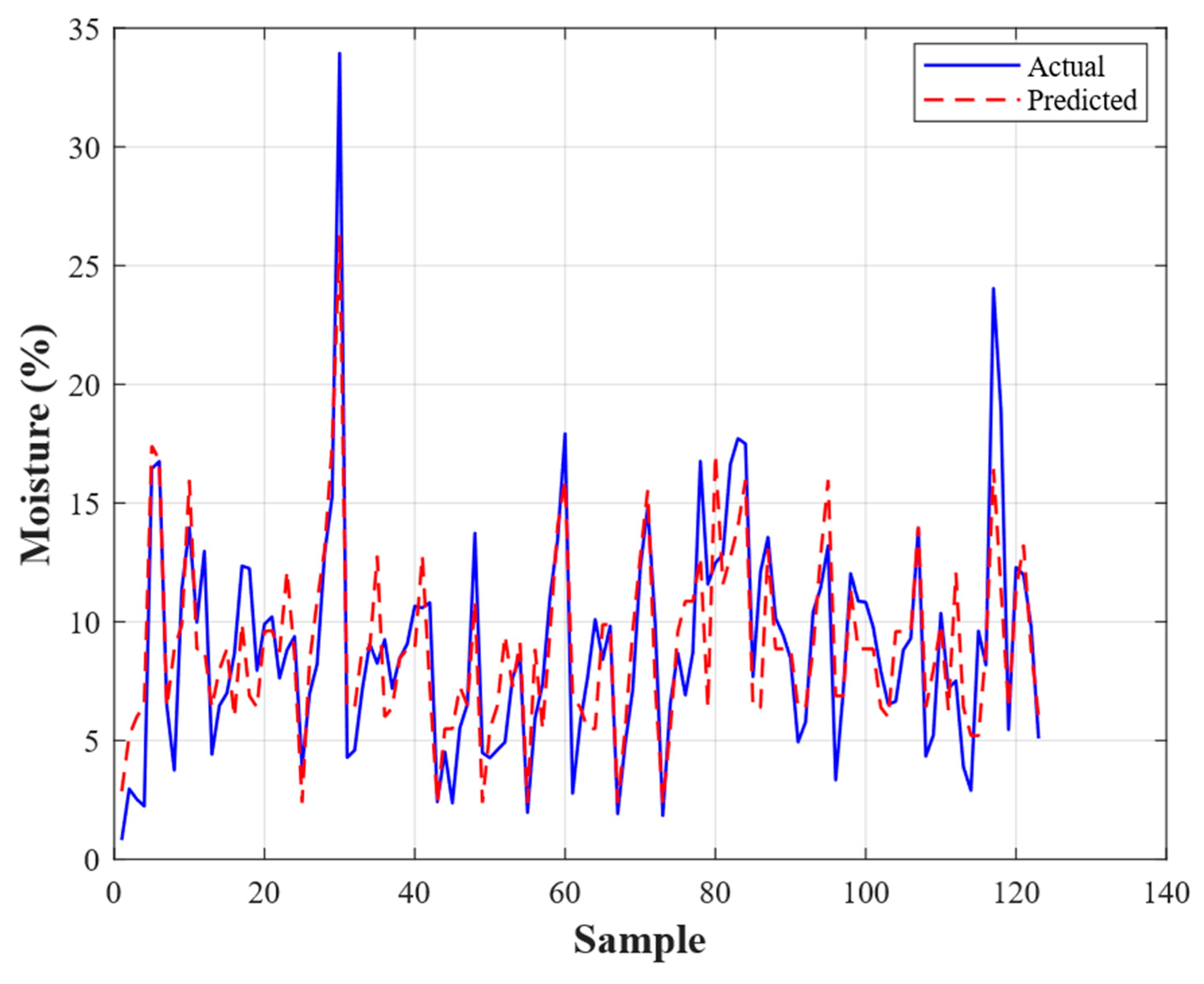
4.3. Comparative Performance Analysis
4.3.1. Overall Performance Comparison
4.3.2. Performance Analysis by Soil Category
4.3.3. Algorithm Trade-Off Analysis
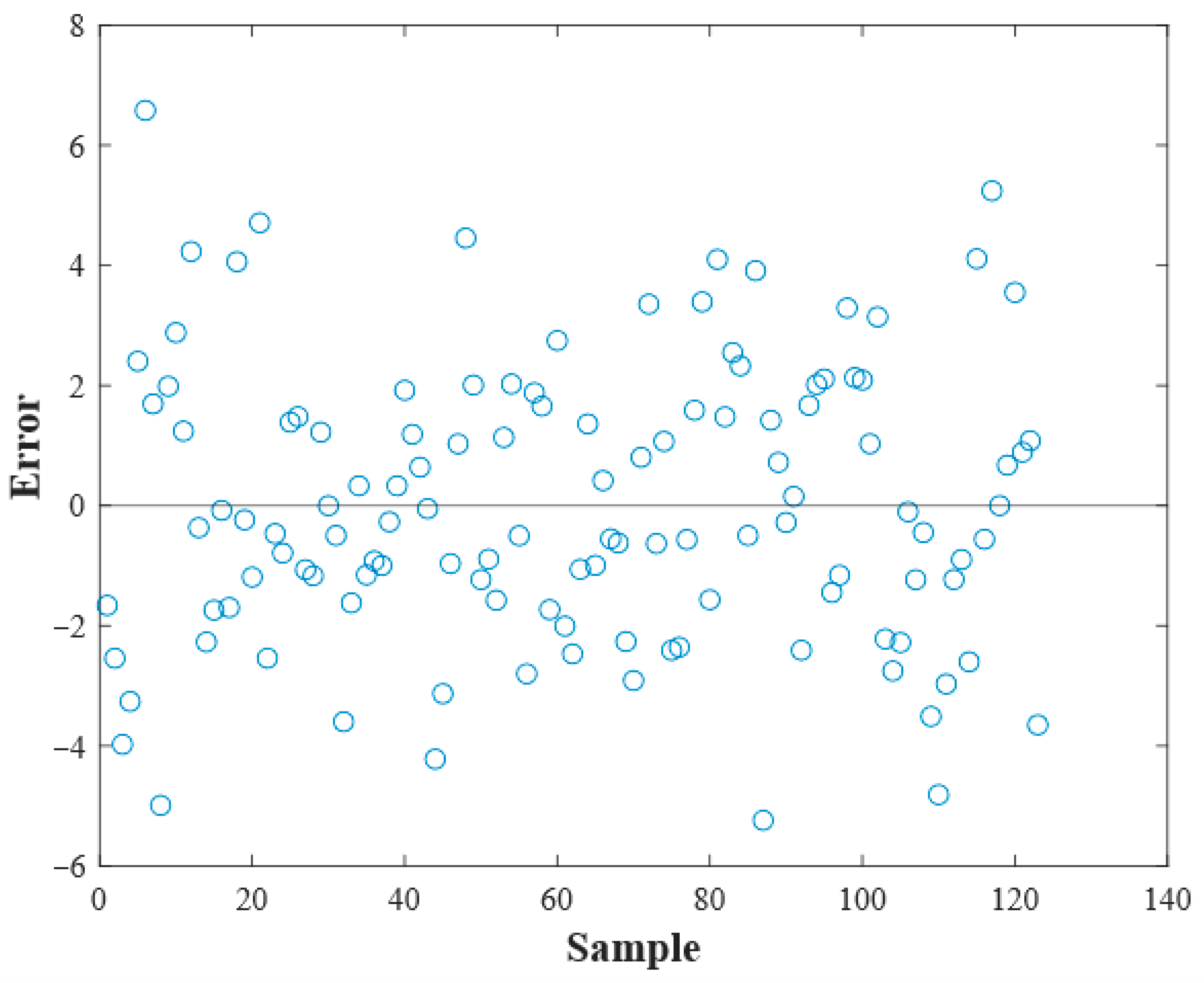
4.4. Statistical Uncertainty Assessment
5. Discussion
5.1. Key Research Findings
5.2. Comparison with Previous Research
5.3. Engineering Applications and Practical Implementation
5.4. Study Limitations
6. Conclusions
- Superior Ensemble Performance: Boosted tree ensembles achieved statistically significant generalization improvements with cross-validation RMSE of 4.7915 compared to 5.082 for single trees (5.7% improvement), confirmed through a 1000-iteration uncertainty analysis;
- Interpretability Trade-offs: Single regression trees provided transparent three-pathway decision structures utilizing only two histogram features, enabling direct validation against soil physics principles, while ensemble methods required understanding of five interrelated trees;
- Robust Cross-Condition Performance: Ensemble advantages were consistent across all soil categories, with the most significant improvements in transitional mixed soils (R2 = 0.868 vs. 0.618).
- Effective Feature Extraction: 16-bin histogram configuration optimally balanced training accuracy and generalization capability, with specific bins (6, 12, 14, and 16) contributing most significantly to prediction performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iwasaki, K.; Tamura, M.; Sato, H.; Masaka, K.; Oka, D.; Yamakawa, Y.; Kosugi, K. Application of Ground-Penetrating Radar and a Combined Penetrometer–Moisture Probe for Evaluating Spatial Distribution of Soil Moisture and Soil Hardness in Coastal and Inland Windbreaks. Geosciences 2020, 10, 238. [Google Scholar] [CrossRef]
- Davis, J.L.; Annan, A.P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Huisman, J.A.; Hubbard, S.S.; Redman, J.D.; Annan, A.P. Measuring soil water content with ground penetrating radar: A review. Vadose Zone J. 2003, 2, 476–491. [Google Scholar] [CrossRef][Green Version]
- Van Dam, R.L. Calibration functions for estimating soil moisture from GPR dielectric constant measurements. Commun. Soil Sci. Plant Anal. 2014, 45, 392–413. [Google Scholar] [CrossRef]
- Benedetto, A. Water content evaluation in unsaturated soil using GPR signal analysis in the frequency domain. J. Appl. Geophys. 2010, 71, 26–35. [Google Scholar] [CrossRef]
- Liu, K.; Lu, Q.; Zeng, Z.; Li, Z. Estimation of soil moisture content of farmlands based on AEA method of GPR. J. Phys. Conf. Ser. 2023, 2651, 12036. [Google Scholar] [CrossRef]
- Mesquita, M.J.L.; Luiz, J.G.; da Costa, J.P.R. Estimates of soil water content using ground penetrating radar in field conditions. Rev. Bras. Geofís. 2015, 33, 389–401. [Google Scholar] [CrossRef]
- Li, K.; Liao, Z.; Ji, G.; Zhang, D.; Liu, H.; Yang, X.; Zhang, S. Estimation of the Soil Moisture Content in a Desert Steppe on the Mongolian Plateau Based on Ground-Penetrating Radar. Sustainability 2024, 16, 8558. [Google Scholar] [CrossRef]
- Akinsunmade, A. Towards an Evaluation of Soil Structure Alteration from GPR Responses and Their Implications for Management Practices. Appl. Sci. 2025, 15, 6078. [Google Scholar] [CrossRef]
- Chen, L.; Xing, M.; He, B.; Wang, J.; Shang, J.; Huang, X.; Xu, M. Estimating soil moisture over winter wheat fields during growing season using machine-learning methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3706–3718. [Google Scholar] [CrossRef]
- Dabboor, M.; Atteia, G.; Alnashwan, R. Optimizing Soil Moisture Retrieval: Utilizing Compact Polarimetric Features with Advanced Machine Learning Techniques. Land 2023, 12, 1861. [Google Scholar] [CrossRef]
- Uthayakumar, A.; Mohan, M.P.; Khoo, E.H.; Jimeno, J.; Siyal, M.Y.; Karim, M.F. Machine learning models for enhanced estimation of soil moisture using wideband radar sensor. Sensors 2022, 22, 5810. [Google Scholar] [CrossRef] [PubMed]
- Qiao, X.; Yang, F.; Xu, X. The prediction method of soil moisture content based on multiple regression and RBF neural network. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 140–143. [Google Scholar]
- Liang, J.; Liu, X.; Liao, K. Soil moisture retrieval using UWB echoes via fuzzy logic and machine learning. IEEE Internet Things J. 2015, 2, 651–661. [Google Scholar] [CrossRef]
- Qiu, C.; Du, W.; Zhang, S.; Guo, W.; Liu, B.; Liu, Y. Shallow Subsurface Soil Moisture Estimation in Coal Mining Area Using GPR Signal Features and BP Neural Network. Water 2025, 17, 873. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Pathirana, S.; Lambot, S.; Krishnapillai, M.; Cheema, M.; Smeaton, C.; Galagedara, L. Integrated ground-penetrating radar and electromagnetic induction offer a non-destructive approach to predict soil bulk density in boreal podzolic soil. Geoderma 2024, 450, 117028. [Google Scholar] [CrossRef]
- Nduku, L.; Munghemezulu, C.; Mashaba-Munghemezulu, Z.; Malobola, N. Field-Scale Winter Wheat Growth Prediction Applying Machine Learning Methods with UAV Imagery and Soil Properties. Land 2024, 13, 299. [Google Scholar] [CrossRef]
- Atun, R.; Gürsoy, Ö.; Koşaroğlu, S. Field Scale Soil Moisture Estimation with Ground Penetrating Radar and Sentinel 1 Data. Sustainability 2024, 16, 10995. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Apostolopoulos, G.; Kofakis, P.; Gonos, I.F.; Tsokas, G.N.; Tsourlos, P.I.; Soupios, P.M. A Combined Hydrogeophysical System for Soil Column Experiments Using Time Domain Reflectometry and Ground-Penetrating Radar. Water 2025, 17, 2003. [Google Scholar] [CrossRef]
- Zhao, S.; Al-Qadi, I.L. Algorithm development for real-time thin asphalt concrete overlay compaction monitoring using ground-penetrating radar. NDT E Int. 2019, 104, 114–123. [Google Scholar] [CrossRef]
- Vahidi, M.; Shafian, S.; Frame, W.H. Multi-modal sensing for soil moisture mapping: Integrating drone-based ground penetrating radar and RGB-thermal imaging with deep learning. Comput. Electron. Agric. 2025, 236, 110423. [Google Scholar] [CrossRef]
- Haghniaz Jahromi, V.; Filardi, S.; Zekavat, Z.; Wang, J.; Thurber, D.; Hoffman, C.; Larson, R.; Petkie, D. Toward intelligent adaptive airborne GPR, implementation and data acquisition. In Proceedings of the 2024 IEEE International Conference on Wireless for Space and Extreme Environments (WiSEE), Seoul, Republic of Korea, 19–21 August 2024; pp. 253–258. [Google Scholar]
- He, Y.; Fang, L.; Peng, S.; Liu, W.; Cui, C. A ground-penetrating radar-based study of the structure and moisture content of complex reconfigured soils. Water 2024, 16, 2332. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Chlaib, H.K.; Fadhel, M.A.; Chen, Y.; Bai, J.; Albahri, A.S.; Gu, Y. Reliable deep learning framework for the ground penetrating radar data to locate the horizontal variation in levee soil compaction. Eng. Appl. Artif. Intell. 2024, 129, 107627. [Google Scholar] [CrossRef]
- Riese, F.M.; Keller, S. Fusion of hyperspectral and ground penetrating radar data to estimate soil moisture. In Proceedings of the 2018 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 23–26 September 2018; pp. 1–5. [Google Scholar]
- Wang, P.; Hu, Z.; Zhao, Y.; Li, X. Experimental study of soil compaction effects on GPR signals. J. Appl. Geophys. 2016, 126, 128–137. [Google Scholar] [CrossRef]
- Anbazhagan, P.; Chandran, D.; Burman, S. Investigation of soil compaction homogeneity in a finished building using ground penetrating radar. In Proceedings of the Forensic Engineering 2012, ASCE, San Francisco, CA, USA, 31 October–3 November 2012; pp. 773–782. [Google Scholar]
- Leng, Z.; Al-Qadi, I.L.; Lahouar, S. Development and validation for in situ asphalt mixture density prediction models. NDT E Int. 2011, 44, 369–375. [Google Scholar] [CrossRef]
- Plati, C.; Georgiou, P.; Loizos, A. A comprehensive approach for the assessment of HMA compactability using GPR technique. Near Surf. Geophys. 2016, 14, 117–126. [Google Scholar] [CrossRef]
- Liu, G.; Tian, S.; Xu, G.; Zhang, C.; Cai, M. Combination of effective color information and machine learning for rapid prediction of soil water content. J. Rock Mech. Geotech. Eng. 2023, 15, 2441–2457. [Google Scholar] [CrossRef]



| Bin Size | Single Regression Tree (Level 10) | Boosted Tree Ensemble (Refined Model) | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | CV-RMSE | R2 | RMSE | MAE | CV-RMSE | |
| 4-bin | 0.395 | 3.707 | 2.834 | 6.036 | 0.510 | 3.337 | 2.547 | 4.772 |
| 8-bin | 0.702 | 2.601 | 1.821 | 5.841 | 0.607 | 2.988 | 2.302 | 4.632 |
| 12-bin | 0.683 | 2.681 | 2.053 | 5.415 | 0.654 | 2.804 | 2.069 | 4.785 |
| 16-bin | 0.761 | 2.330 | 1.901 | 5.082 | 0.708 | 2.574 | 1.982 | 4.792 |
| 20-bin | 0.664 | 2.762 | 2.050 | 5.557 | 0.667 | 2.750 | 2.197 | 5.079 |
| 24-bin | 0.778 | 2.245 | 1.824 | 5.704 | 0.734 | 2.457 | 1.853 | 5.224 |
| Site Category | Number of Sites | Dominant Soil Types | Natural Water Content Range (%) | SPT N-Value Range (Blows/ft) | Geological Characteristics |
|---|---|---|---|---|---|
| Coastal Sandy | 8 | Poorly graded sands (SP), silty sands (SM) | 6.96–14.80 | 6–62 | Well-drained coastal deposits, low plasticity, variable density |
| Transitional Mixed | 8 | Silty sands (SM) | 5.74–13.52 | 6–53 | Mixed alluvial deposits, moderate moisture retention, dense |
| Inland Clayey | 5 | Low plasticity clays (CL), clayey sands (SP-CL) | 5.85–21.28 | 9–62 | Fine-grained soils, high moisture retention, plastic behavior |
| Performance Metric | Level | |||||
|---|---|---|---|---|---|---|
| 4 | 6 | 8 | 10 | 12 | 14 | |
| R2 | 0.835 | 0.822 | 0.785 | 0.761 | 0.726 | 0.657 |
| RMSE | 1.936 | 2.012 | 2.212 | 2.330 | 2.496 | 2.790 |
| MAE | 1.508 | 1.599 | 1.791 | 1.901 | 1.992 | 2.209 |
| RMSE cross-validation (K = 5) | 5.354 | 5.475 | 5.835 | 5.082 | 5.299 | 5.618 |
| Performance Metric | Maximum Number of Splits | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | |
| R2 | 0.399 | 0.708 | 0.829 | 0.856 | 0.907 | 0.930 | 0.957 | 0.963 |
| RMSE | 3.695 | 2.574 | 1.968 | 1.811 | 1.450 | 1.259 | 0.994 | 0.917 |
| MAE | 2.801 | 1.982 | 1.506 | 1.384 | 1.166 | 0.946 | 0.733 | 0.637 |
| RMSE cross-validation (K = 5) | 4.737 | 4.818 | 5.283 | 5.168 | 5.591 | 5.270 | 5.423 | 5.164 |
| Performance Matrices | Pruned Regression Tree | Boosted Tree Ensemble (Refined Model) |
|---|---|---|
| R2 | 0.761 | 0.708 |
| RMSE | 2.330 | 2.574 |
| MAE | 1.901 | 1.982 |
| RMSE cross-validation (K = 5) | 5.082 | 4.7915 |
| Soil Category | Algorithm | R2 | RMSE | MAE | CV-RMSE |
|---|---|---|---|---|---|
| Coastal Sandy | Sigle Tree (Pruned Level 3) | 0.832 | 2.177 | 1.686 | 5.923 |
| (8 sites) | Boosted Tree (Refined) | 0.906 | 1.632 | 1.265 | 6.081 |
| Transitional Mixed | Sigle Tree (Pruned Level 3) | 0.618 | 2.647 | 2.162 | 4.556 |
| (8 sites) | Boosted Tree (Refined) | 0.868 | 1.553 | 1.220 | 4.644 |
| Inland Clayey | Sigle Tree (Pruned Level 3) | 0.880 | 1.564 | 1.171 | 5.300 |
| (5 sites) | Boosted Tree (Refined) | 0.911 | 1.349 | 1.058 | 4.315 |
| Algorithm | Mean CV-RMSE | Standard Deviation | 95% Confidence Interval | Coefficient of Variation |
|---|---|---|---|---|
| Single Regression Tree (Level 10) | 5.4589 | 0.3374 | [5.4379, 5.4798] | 6.18% |
| Boosted Tree (Refined) | 4.9874 | 0.2596 | [4.9713, 5.0035] | 5.20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panyavaraporn, J.; Horkaew, P.; Arjwech, R.; Eua-apiwatch, S. Machine Learning Approaches for Soil Moisture Prediction Using Ground Penetrating Radar: A Comparative Study of Tree-Based Algorithms. Earth 2025, 6, 98. https://doi.org/10.3390/earth6030098
Panyavaraporn J, Horkaew P, Arjwech R, Eua-apiwatch S. Machine Learning Approaches for Soil Moisture Prediction Using Ground Penetrating Radar: A Comparative Study of Tree-Based Algorithms. Earth. 2025; 6(3):98. https://doi.org/10.3390/earth6030098
Chicago/Turabian StylePanyavaraporn, Jantana, Paramate Horkaew, Rungroj Arjwech, and Sitthiphat Eua-apiwatch. 2025. "Machine Learning Approaches for Soil Moisture Prediction Using Ground Penetrating Radar: A Comparative Study of Tree-Based Algorithms" Earth 6, no. 3: 98. https://doi.org/10.3390/earth6030098
APA StylePanyavaraporn, J., Horkaew, P., Arjwech, R., & Eua-apiwatch, S. (2025). Machine Learning Approaches for Soil Moisture Prediction Using Ground Penetrating Radar: A Comparative Study of Tree-Based Algorithms. Earth, 6(3), 98. https://doi.org/10.3390/earth6030098







