Abstract
Improving the quality of atmospheric precipitation measurements is crucial in the view of minimizing the uncertainty in weather forecasting, climate change impact assessment, water resource assessment and management, and drought and flood prediction. Remote sensing technology has considerably improved the spatio-temporal assessment of precipitation. Despite the advancement in the remote sensing technology, there is a need to investigate the robust approach towards integrating ground-based-measured and satellite-product precipitation to better understand the hydrologic process of any basin. Several data-merging methods have been proposed; however, the application of merged precipitation products for hydrological simulation has rarely been investigated. Thus, in this review, technical characteristics including basic assumptions, along with their procedures, are discussed. Moreover, the limitations of eight commonly used merging approaches, (1) Multiple Linear Regression, (2) Residual Inverse Distance Weighting, (3) Linearized Weighting, (4) Inverse Root-Mean-Square Error Weighting, (5) Optimal Interpolation, (6) Random-Forest-Based Merging Procedure, (7) Bayesian Model Averaging, and (8) the Kriging Method, and their advances with respect to hydrological simulation are discussed. Finally, future research directions towards improving data merging approaches are recommended.
1. Introduction
Atmospheric precipitation is the driving component of the hydrologic cycle. Its spatio-temporal distribution is very important for providing crucial information for weather forecasting [1,2], climate change impact studies [3], water resource management studies [4], drought and flood prediction [5,6], agricultural studies [7], hydrological simulation [8], and other areas of studies. However, in many cases, the availability of densely distributed rain-gauge observations (hereafter obs) is very rare [9]. Moreover, accurate measurements of precipitation cannot be easily acquired due to different sources of errors. For instance, the instrumental error associated with the improper design of rain-gauges and incorrect application of measuring principles might contribute to an inaccurate precipitation measurement [10,11]. Moreover, environmental factors including wind, splashing, evaporation, temperature gradient, blowing of snow, and wetting could induce errors on the precipitation measurement [12,13]. Previous studies pointed out that the wind effect on precipitation measurements is the major source of error among other environmental factors [12,14], resulting in the measured precipitation being lower than the actual precipitation amount [15]. Hence, the quality of precipitation measurements needs to be checked before its application.
To overcome the aforementioned problems, spatially distributed precipitation can be acquired (1) by applying spatial interpolation of the direct measurements (obs); (2) indirectly from satellite precipitation products (SPPs); (3) indirectly from satellite soil moisture (S-SM) observations; and (4) from reanalysis datasets which are produced by data assimilation and modeling approaches [16].
Several researchers applied various interpolation approaches to transform obs into areal precipitation [11,14]. Ma et al. [15] compared interpolated precipitation using Geographically and Temporally Weighted Regression (GTWR) and Multiple Linear Regression (MLR) in China. In this regard, the authors found better performance of GTWR compared to MLR. Similarly, ref. [17] also evaluated the performance of High-Accuracy Surface Modeling (HASM), inverse distance weight (IDW), ordinary kriging (OK), and Spline for interpolation of annual precipitation in the Dongjiang River Basin, and reported the better performance of the HASM method. Despite several studies highlighting the importance of spatial interpolation methods for precipitation estimation, using sparsely and irregularly distributed obs can be subject to large uncertainties [16,18].
The second approach, SPPs-based estimation, can provide areal precipitation, and can be taken as a possible alternative for the obs [19]. To retrieve precipitation from a satellite, images from different sensors can be used [7]. Based on the classification proposed by [20], precipitation estimation using remote sensing can be: (a) the cloud indexing method, which assigns a precipitation level to each cloud type identified in the satellite imagery; (b) the bi-spectral life history method, which is based on the relationship between cold and bright clouds, and (c) the life history method, which is based on a detailed analysis of the cloud’s life cycle. Despite precipitation estimation methods using remote sensing images having numerous advantages, they have also their own limitations [21]. For instance, some sensors do not penetrate clouds and may underestimate warm orographic precipitation [22].
The third approach, S-SM observations, can be used in poorly gauged areas as an alternative source of precipitation information. This is based on the fact that S-SM observations can provide information about the quantity of water stored in the soil after a precipitation event occurs. For this purpose, Brocca et al. [23] used an algorithm called soil moisture to estimate rainfall (SM2RAIN). The proposed algorithm works by the inversion of the soil water balance equation to drive precipitation. As highlighted in [24], S-SM observations are important for acquiring precipitation indirectly in near-real time for areas with low vegetation cover. However, the products of S-SM observations have low spatial resolution, a longer latency period, and poor performance in mountainous areas and densely vegetated areas [25]. To overcome these limitations, and to improve their quality, precipitation can be derived via SM2RAIN using different S-SM observations and then integrated with SPPs [26] for use as input for hydrological simulation. As an example, Brocca et al. [21] reported better performance of SM-integrated SPPs in West Africa for streamflow estimation.
In the fourth approach, the reanalysis datasets are precipitation products that are generated by data assimilation technology that combines numerical weather forecast results with obs, radar, and SPPs. For instance, ERA-Interim, developed by the European Centre for Medium-Range Weather Forecasts (ECMWF), is the most widely used reanalysis dataset [10,19,23]. Although reanalysis datasets provide continuous and long-term historical precipitation, their performance is mostly affected by model assumptions and by measurement errors that propagate from gauge, radar, and satellite data. Therefore, to enhance estimation of the spatial-temporal distribution of precipitation, researchers need to merge or combine precipitation products from multiple sources (obs, SPPs, S-SM observations, and reanalysis datasets), and then merged precipitation products can be used as input for hydrological simulation. In this regard, several researchers reported better performance of merged precipitation products for flood prediction [27], for water balance study [20,28], and for other hydrological modeling purposes.
Currently, numerous multi-source precipitation product merging algorithms have been proposed by several researchers. Among these, Bayesian model averaging (BMA) [29], Linearized Weight (LW) [30], Inverse-Root-Mean-Square Error weighting (IRMSE) [31], and geostatistical methods [32] are the common ones. Most recently, ref. [33] also proposed the random-forest-based merging (RF-MEP) procedure. A review of various interpolation and merging methods can be referred to in [23]. However, a detailed review of the technical aspects of various merging approaches including assumptions, equations, procedures, limitations, validation, and their application for improved hydrological simulation is not available yet. Hence, the aim of this paper is to conduct an in-depth review of precipitation merging approaches/algorithms for improved hydrological simulation. This paper is organized as follows: Section 2 presents basic information of SPPs (spatial and temporal resolution, coverage, data availability, and others); Section 3 presents technical aspects of selected merging approaches and their evaluation methods; Section 4 presents the application of merged precipitation products for improved hydrological simulation. Finally, under Section 5, conclusions and future research directions are presented.
2. Satellite-Based Precipitation Products
Precipitation can be derived from space-borne satellite sensors as an alternative for obs. This is because of the advantages of these sensors for detecting precipitation information at large spatial coverage and their capability to detect precipitation information at areas which are difficult to access such as oceans, seas, lakes, high mountains/hills, and deserts [26,34]. Precipitation can be retrieved from infrared (IR), passive microwave (PMW), active microwave (AMW), and multi-sensor precipitation (MPP) [23] sensors. Among these methods, currently available SPPs are generated from IR and PMW [33].
IR-based retrieval algorithms estimate precipitation by developing statistical relationships between precipitation intensity and cloud parameters such as cloud type, cloud areal coverage, and cloud top bright temperature detected by the optical sensors of geostationary satellites [35]. Among several methods of IR-based retrieval, the Cold Cloud Duration (CCD) method, which considers the duration of a cloud having a temperature below a threshold at a given pixel, is the most widely used method [7]. By using IR algorithms, continuous precipitation intensity information can be obtained. Since the CDD method is an indirect estimation method, it may result in poor performance in areas of complex meteorological and topographic conditions [19,36].
The second category of precipitation retrieval algorithms is based on PMW, which detects precipitation information from a microwave radiometer carried by a polar-orbiting satellite [37,38]. Compared to IR, PMW-based algorithms are more direct and effective due to the capability of microwaves to penetrate through clouds to detect the liquid water content of the atmosphere [35]; however, PMW cannot detect the vertical structure of precipitation. Additionally, PMW also underestimates heavy precipitation, probably due to not detecting small-scale convective precipitation [36]. Due to the advancement of remote sensing technology, nowadays, AMW overcomes the disadvantage of PMW by detecting the vertical structure of precipitation information. Tropical precipitation Measuring Mission (TRMM) with a single-frequency radar and Global Precipitation Mission (GPM) with dual-frequency radar are the two best examples of the AMW-based precipitation retrieval algorithms.
As mentioned formerly, IR- and PMW-based precipitation retrieval techniques have their own limitations. To overcome their limitations, the MPP-based algorithms that combine IR and PMW, have become the most widely applied methods in the present day. The algorithms of the Global Precipitation Climatology Project (GPCP), TRMM Multi-satellite Precipitation Analysis (TMPA), Climate Prediction Center (CPC) morphing technique (CMORPH), and Global Satellite Mapping of Precipitation (GSMaP) [39] are the best examples of MPP precipitation retrievals.
In the past, different SPPs were examined for different objectives. For instance, ref. [40] validated seven SPPs over Colombia at daily and decadal time scales to identify the best-performing one. From their study, CMORPH showed better performance relative to others. Lekula et al. [29] evaluated the capability of four SPP products, namely Early Warning Systems Network Rain Fall Estimation (FEWS-Net RFE), Precipitation Estimates from Remotely Sensed Information Using Artificial Neural Networks (PERSIANN), CMORPH, and TRMM, for spatio-temporal variability representation in the Central Kalahari Basin, and from the study they reported better performance of FEWS-Net RFE. Similarly, ref. [19] evaluated the performance of SPPs for a real-time spatio-temporal variability study over selected catchments which are found in Chile and concluded that site-specific assessment of individual SPPs is essential before utilizing them for hydrological studies. Furthermore, SPPs also show imprecisions due to systematic and random errors which need to be adjusted before being used in hydrologic models [41]. To summarize, the spatial and temporal resolution of the most widely used SPPs retrieved from satellites are presented below in Table 1.

Table 1.
Characteristics of the most widely used global and quasi-global satellite precipitation products.
From Table 1, the first seven listed SPPs are pure satellite products which are not blended with gauge obs, whereas the last three products are blended with gauge obs. For instance, the CHIRPS algorithm incorporates 0.05°-resolution satellite imagery with gauge obs to create gridded precipitation time series.
3. Precipitation Merging Approaches
In this review section, the technical features including basic assumptions, procedures, equations, and limitations of eight commonly used merging algorithms are outlined from Section 3.1, Section 3.2, Section 3.3, Section 3.4, Section 3.5, Section 3.6, Section 3.7 and Section 3.8.
3.1. Multiple Linear Regression (MLR)
The MLR approach has been implemented by a number of precipitation merging studies [50]. For applying the MLR approach, the following assumptions need to be considered, as indicated in [51]. These are:
- There must be a linear relationship between the dependent (SPPs) and independent (obs) variables, which is known as the linearity property.
- The errors between obs and merged precipitation should be normally distributed.
- Independent variables (obs) are not highly correlated with each other.
- The variance of error terms is alike throughout the values of the independent variables (obs).
Following the above assumptions, MLR can be expressed as follows:
where, in Equation (1), PMLR is the merged precipitation result based on the MLR method; Po…Pn are the precipitation values of different satellite products; αo … αn are regression coefficients of Po…Pn; and β is the intercept. In this approach, the regression coefficient values can be determined by the least squares method.
Despite the MLR method being important for merging SPPs and obs, it also has some limitations. From these, that the linearity assumption may not be always true and its sensitivity to outliers are some of the limitations which are described in [52].
3.2. Residual Inverse Distance Weighting (RIDW)
Dinku et al. [40] tested the RIDW approach by merging Tropical Applications in Meteorology using Satellite data (TAMSAT) and gauge obs precipitation at 10 km (spatial) and 10-day (temporal) scales in areas with complex terrain with a high density of obs. In their work, the authors found better performance of the merged precipitation compared to the individual product in reproducing historical precipitation. Manz et al. [36] also reported better performance of the RIDW merging approach when TRMM data were merged with obs at the monthly scale. In this approach, obs errors are neglected or assumed to be zero, which is one limitation of this merging approach.
To implement the RIDW merging approach, four main procedures can be followed which are summarized in [22]. These include (1) extraction of SSP values at gauge locations; (2) computation of the difference or the residual between the satellite precipitation value and obs values at each gauge location; (3) interpolation of the residual to each pixel using inverse distance weighting (IDW) as presented in Equation (2); and (4) addition of the interpolated residual back to the SSP values.
where Rp is precipitation at the unknown point “p”; Ri is precipitation at the known gauge station; N is number of gauge observations; Wi is the weighting of each obs; di is the distance from each gauge obs to the unknown point; and α is a parameter that affects the spatial distribution of P. According to Adhikary et al. [53], as the α value increases, the smoothness of RIDW output surfaces also increases.
Compared to other approaches, the limitation of this method is that it does not consider the error of the gauge obs, but simply estimates precipitation values as a function of distance [45].
3.3. Linearized Weighting (LW)
This approach was tested by Woldemeskel et al. [9] for merging monthly accumulated TRMM 3B42 precipitation values with gridded obs at about 5 km spatial resolution. To apply this approach, they proposed four main procedures. The first procedure involves comparison of SPPs and obs and other quality tests for gauge precipitation. Secondly, they proposed estimation of gridded obs. This step involves normalization, standardization, interpolation, and back-transformation. The third step is merging of the gridded obs values with SPPs using a linearized weighting equation which is expressed in Equation (4).
where is the merged precipitation; is the obs; is the satellite precipitation; is the weight for gauge obs; and is the weight for SPPs. The weights and from the merging Equation (4) can be determined using the error variances of each value using the following expressions.
where is the obs error variances and is the SPPs error variance.
Finally, cross-validation of errors is required to evaluate the performance of merged precipitation values using performance matrixes such as mean error (ME), mean absolute error (MAE) and root-mean-square error (RMSE).
In this approach, merged precipitation is assumed to be a linear weighted combination of SPPs and obs. However, error which propagates from spatial interpolation of obs may affect the merged product and this can be taken as one limitation.
3.4. Inverse Root-Mean-Square Error (IRMSE) Weighting
Similar to the above-mentioned approaches, the IRMS merging approach is important to produce high-quality precipitation. In Yang et al. [31], IRMSE approach was tested by merging PERSIANN-CCS SSP with obs at the daily scale over Chile. In their study, the researchers found high-precision precipitation data using this approach. They also proposed a framework for the approach which involves three main steps. These include: (1) bias correction of SSPs; (2) generation of gridded obs; and (3) merging, applying Equation (7).
where is the merged precipitation for the ith grid; is the bias-corrected satellite precipitation estimates for the ith grid; and and are weights for the bias-corrected SPPs and gridded obs, correspondingly. The weights can be determined using Equations (8) and (9).
where and are root-mean-square error for SPPs and gauge obs datasets, respectively, over the grid i. For computation of and refer to [31].
3.5. Optimal Interpolation (OI)
The OI merging approach was applied by several researchers for producing high-quality precipitation estimations. As an example [54], applied this approach to merge TMPA 3B42 satellite precipitation data over China and found an improved precipitation product. Most studies (for example, [43,44]) of this method assumed: (1) no bias in the obs and SPP data; (2) no correlation between error in the SPPs and error in the gauge obs; and (3) no correlation between errors of the obs at two different pixels. In this approach, the final merged value of (Mk) at a target grid box (k) can be determined using the following equation:
where Fk is the first guess at the grid box k; , , and are the gauge obs, first guess, and weighting, respectively, at grid box (j) where gauge obs are available; and n is the number of obs. The procedure for weight computation can be referred to in [55]. In this approach, the bias-corrected SPPs can be used as the first guess, while the gauge obs are used to modify the first guess.
Generally, the OI merging algorithm involves three main procedures: (1) bias correction of SPPs using the available bias correction methods (for example, using distribution mapping [56] or any other methods, (2) determination of optimal correction weights by minimizing error variance as recommended by [17], and (3) applying the optimal interpolation method described in Equation (10).
Similar to the other methods, no bias in the gauge obs assumption of the OI method is the main limitation.
3.6. Random-Forest-Based Merging Procedure (RF-MEP)
RF has vast applications in data science problems. Baez-Villanueva et al. [33] also proposed a novel RF method for merging SPPs and obs. The algorithm is named as the “RF-based Merging Procedure (RF-MEP)”. Most recently, ref. [48] applied the RF-MEP method to merge SPP data with obs for improved flood simulation. The researchers in the study report better performance of RF-MEP merged precipitation compared to the individual SPPs and obs. The approach works based on the following listed assumptions, which are summarized in [33]:
- Gauge obs bias is neglected; SPPs contain systematic error (bias).
- Merged precipitation products can represent spatio-temporal variability of precipitation.
Based on the above-listed assumptions, RF-MEP involves the following four main procedures as described in [35].
- Data acquisition: This step involves acquiring datasets such as SPPs, obs, and other spatial data such as a digital elevation model (DEM).
- Data processing: This step involves resampling of selected gridded precipitation and other spatial datasets to the same spatial resolution. In addition, partitioning of gauge obs for training and validating is done in this step.
- Merging: This step involves extraction of the covariate values, training of RF using the obs, and prediction using Equation (11).where PRf is final predicted precipitation; B is the total number of trees; and xb represents each individual decision tree. Here, the decision tree is a tree-like model for representing a series of decisions along with possible outcomes.
- Performance evaluation: This is the final step of RF-MEP for cross-validation of merged precipitation with independent gauge obs.
Compared to the above-mentioned approaches, RF-MEP is more efficient for merging precipitation products because it considers additional covariates or independent variables such as elevation, slope, aspect, and distance between gauges for merging. However, its error-free assumption for the gauge precipitation remains as a limitation.
3.7. Bayesian Model Averaging (BMA)
This approach to merging aims to produce a new dataset which is higher-quality than the original [29]. For merging, the BMA method accounts for a predicted mean of the precipitation mean of variable y, Here, let quantity y to be the merged precipitation product; be the obs training data with length of time series which can be described as ; and be the ensemble of the considered satellite precipitation product with the number. According to the total probability principle [29], the probabilistic prediction of y based on the multiple precipitation products for the given training data can be is described as:
where is the probabilistic prediction given by alone and is the likelihood that this prediction is the best for the given the training data. By identifying ) as a fractional statistical weight whose magnitude reflects how well matches the training data , it follows that .
According to Ma et al. [57], the BMA approach involves four main procedures. These are (1) input data preparation; (2) training the model using training data sets; (3) transformation of nonlinear obs and SPPs values to a Gaussian distribution; and (4) application of the expectation maximization EM algorithm to estimate BMA weights. More about this method can be found in [16].
3.8. Kriging Method (KM)
Kriging is a geostatistical approach for surface interpolation [55]. In the KM approach, the interpolation at the unsampled location is determined as a weighted linear blend of the known data that minimizes error [32]. Based on the difference in assumption and equation, the kriging method can be Ordinary Kriging, Universal Kriging, Kriging with External Trend, and Co-Kriging [23]. From these kriging methods, Ordinary Kriging (OK) is the only one that reflects the spatial autocorrelations of the estimated variable and assumes that the structural components are stationary [25,54], and it is also the most widely applied for merging precipitation products. For this review, the OK method proposed by Verdin et al. [25] for merging Climate Hazards Group Infrared Precipitation (CHIRP) and gauge obs is considered. Some of the assumptions of this approach are (1) no missing data in the obs; (2) the difference between the obs and the SPPs is considered as error; and (3) weak stationarity. In the OK method, the value of the dependent variable at any desired location x can be obtained by using the weighted combination of all the observations [58], which is expressed as follows:
where x is spatial locations xi, i = 1, …, Ns; Ns is the number of gauge locations with no missing data; and λi are the kriging weights, which can be obtained by solving the constrained optimization problem [32].
Generally, the OK approach involves four main steps [32]: (1) estimation of the empirical variogram at all obs location; (2) fitting a theoretical variogram to the binned empirical variogram; (3) determination of the kriging weights at any location using the minimization problem; and (4) application of the kriging method to estimate precipitation at the desired location.
3.9. Performance Evaluation of Merged Precipitation
In order to evaluate the performance of merged precipitation, several researchers (for example, [14,24,56] recommended cross-validation techniques using independent gauge stations (mostly 10% of the total number of gauges). For this purpose, continuous and categorical statistical measures can be applied [59,60]. Here, continuous statistical measures are important to quantify the overall performance of the merged precipitation, whereas categorical measures are other valuation methods which can be calculated using a contingency table [61]. For the purpose of simplicity, the most widely used performance measurement metrics are summarized in Table 2.

Table 2.
A summary of continuous and categorical performance measurement metrics.
4. Application of Merged Precipitation for Improved Hydrological Simulation
Numerous researchers evaluated the performance of different SPPs at the global scale [62], at the basin scale [63], and at the catchment or watershed scale [64]. For evaluation, most studies applied continuous and categorical statistical measures which are described in Table 2, while others mainly focused on evaluation using hydrological modeling by comparing observed and simulated flow rates derived from different SPPs (for example, [37,65,66]. Others also applied both statistical and hydrological model methods. For instance, most recently, ref. [61] evaluated the performance of CHIRPS, multi-source weighted-ensemble precipitation (MSWEP), and TRMM for Bilate basin, Ethiopia. In their work, the researchers applied point-to-pixel-wise comparison and a hydrological method by comparing observed and simulated flow rates derived by individual satellite precipitation products.
Despite the evaluation of the performances of different SPPs at different spatial and temporal scales using different performance measures, studies on the performance evaluation of merged precipitation for improved hydrological simulation are very limited. Hence, future studies are essential in this hot topic. In this review, the methodology of five studies that applied merged precipitation for improved hydrological simulation are presented in Table 3. In addition, the procedure followed by those studies is generalized as presented in Figure 1.

Table 3.
Methodology of different studies that have applied merged precipitation products for improved hydrological simulation.
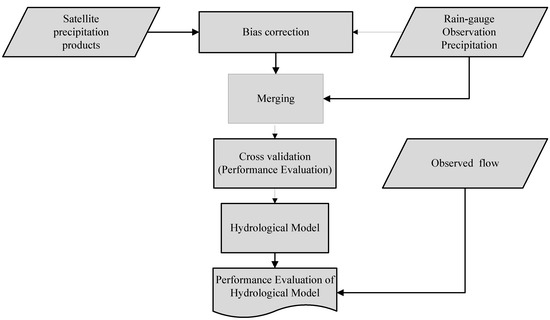
Figure 1.
General framework for the application of merged precipitation products for hydrological simulation.
5. Conclusions and Future Research Directions
In this review, a synthesis of eight commonly used satellite product and ground-based precipitation merging approaches were reviewed. In addition, the application of merged precipitation for improved hydrological simulation was also discussed. In general, the major findings of this review are summarized as follows:
- Worldwide, different SPPs have been utilized in data scarce regions, un-gauged basins, and areas with complex land features. Although there is no universally accepted logic and framework for choosing SPPs for the application of merging, several researchers [14,16,46] suggested different criteria, including performance of the SPP, spatio-temporal coverage, performance of the SPPs at complex topography, and condition of the study area. Hence, researchers need to consider all the stated criteria for selecting SPPs.
- In fact, different approaches to merging offer the opportunity to overcome the overestimation, underestimation, and false alarms of SPPs. However, researchers have to select merging approaches reasonably by considering their technical aspects. Researchers are also recommended to bias-correct satellite products before merging with gauge obs to avoid systematic error using the available methods. Most of the previous studies used linear scaling, delta change correction, power transformation, distribution mapping, quantile mapping, and so on [60,70] for bias-correcting satellite products. Quantile mapping is the most recommended one because of its capability in capturing weather events [58].
- Future studies need to focus on inter-comparisons of various precipitation merging approaches for better understanding of their merits and demerits.
- In addition, most of the previous studies applied traditional statistical measures such as NSE, r, PBIAS, RMSE, FAR, and POD, among others, for cross-validation of merged precipitation with gauge obs. However, to overcome the limitations of these traditional techniques, researchers need to apply other composite methods such as the Kling–Gupta efficiency method [71]. Moreover, it is also recommended to use multi-criteria decision analysis (MCDA) methods such as Fuzzy-Order of Preference by Similarity to Ideal Solution (TOPSIS), compromise programing, and others approaches for evaluating overall performance of the merged precipitation product.
- The study, in general, shows that the investigation of appropriate satellite product and ground-based-measured precipitation merging approaches can produce improved hydro-meteorological forecasting, water resources assessment and management, and flood and drought prediction.
It should be underlined that the quality of merged precipitation products is still influenced by systematic bias and random errors propagated from each individual component. More recently, several studies derived precipitation from S-SM observations by inverting the soil water balance equation. Hence, future studies need to focus on the merging of obs, SPPs, reanalysis, and S-SM-based products towards improving the quality of merged precipitation. Moreover, several studies also validated the performance of merged precipitation products using a dual comparison with a reference dataset, usually with ground-based obs. However, their validation method is not appropriate due to the lack of a sufficient number of rain-gauge obs in most parts of the world. Additionally, most of the previous studies neglected the random error associated with the reference dataset and its distribution during the validation processes. Thus, most of the limitations in the traditional validation approach can be improved by the application of the triple collocation (TC) method to describe uncertainties related to precipitation estimation [20,27,63]. Generally, this study strongly recommends the meteorological and hydrological community to apply the TC method for validation of merged precipitation products. In addition, it is of significant importance to assess the application of merged precipitation for hydrological simulation in the future studies.
Furthermore, the merging approaches often neglect the bias of rain-gauge obs, resulting in the incorrect estimation of merged precipitation due to the inherent instrumental and environmental sources of errors [12]. Therefore, it is recommended to bias-correct the gauge obs for different sources of errors, such as correction for wind, evaporation, and wetting.
Author Contributions
Conceptualization, H.B.; review methodology, H.B., G.T. and A.M.M.; writing—original draft preparation, H.B.; writing—review and editing, H.B., G.T. and A.M.M.; supervision, G.T. and A.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
For this work, the first author was financially supported by the Africa Center of Excellence for Water Management, Addis Ababa University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kumar, N.; Jha, G.K. Time Series ANN Approach for Weather Forecasting. Int. J. Control Theory Comput. Model. 2013, 3, 19–25. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Toride, K.; Cawthorne, D.L.; Ishida, K.; Kavvas, M.L.; Anderson, M.L. Long-term trend analysis on total and extreme precipitation over Shasta Dam watershed. Sci. Total Environ. 2018, 626, 244–254. [Google Scholar] [CrossRef] [PubMed]
- Haile, A.T.; Akawka, A.L.; Berhanu, B.; Rientjes, T. Changes in water availability in the Upper Blue Nile basin under the representative concentration pathways scenario. Hydrol. Sci. J. 2017, 62, 2139–2149. [Google Scholar] [CrossRef]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef]
- Iyengar, A.M.; Bharat, K.U.; Divya, M. Drought Prediction Using Machine Learning. Int. J. Adv. Comput. Sci. Cloud Comput. 2019, 7, 1–6. [Google Scholar]
- Domenikiotis, C.; Dalezios, N.R. Assessment of the Cold Cloud Duration (CCD) Methodology for Rainfall Estimation in Central Greece. In Proceedings of the International Symposium, Volos, Greece, 7–9 November 2003; pp. 185–194. [Google Scholar]
- Zhu, D.; Wang, G.; Ren, Q.; Ilyas, A.M. Hydrological evaluation of hourly merged satellite–station precipitation product in the mountainous basin of China using a distributed hydrological model. Meteorol. Appl. 2020, 27, e1909. [Google Scholar] [CrossRef]
- Woldemeskel, F.M.; Sivakumar, B.; Sharma, A. Merging gauge and satellite rainfall with specification of associated uncertainty across Australia. J. Hydrol. 2013, 499, 167–176. [Google Scholar] [CrossRef]
- La Barbera, P.; Lanza, L.; Stagi, L. Tipping bucket mechanical errors and their influence on rainfall statistics and extremes. Water Sci. Technol. 2002, 45, 1–9. [Google Scholar] [CrossRef]
- Molini, A.; Lanza, L.G.; La Barbera, P. The impact of tipping-bucket raingauge measurement errors on design rainfall for urban-scale applications. Hydrol. Process. 2005, 19, 1073–1088. [Google Scholar] [CrossRef]
- Cauteruccio, A.; Brambilla, E.; Stagnaro, M.; Lanza, L.G.; Rocchi, D. Experimental evidence of the wind-induced bias of precipitation gauges using particle image velocimetry and particle tracking in the wind tunnel. J. Hydrol. 2021, 600, 126690. [Google Scholar] [CrossRef]
- Jevons, W.S. LIV. On the deficiency of rain in an elevated rain-gauge, as caused by wind. London, Edinburgh, Dublin Philos. Mag. J. Sci. 1861, 22, 421–433. [Google Scholar] [CrossRef]
- Folland, C.K. Numerical models of the raingauge exposure problem, field experiments and an improved collector design. Q. J. R. Meteorol. Soc. 1988, 114, 1485–1516. [Google Scholar] [CrossRef]
- Cauteruccio, A.; Brambilla, E.; Stagnaro, M.; Lanza, L.G.; Rocchi, D. Wind Tunnel Validation of a Particle Tracking Model to Evaluate the Wind-Induced Bias of Precipitation Measurements. Water Resour. Res. 2021, 57, e2020WR028766. [Google Scholar] [CrossRef]
- Fu, Y.; Xia, J.; Yuan, W.; Xu, B.; Wu, X.; Chen, Y.; Zhang, H. Assessment of multiple precipitation products over major river basins of China. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2016, 123, 11–22. [Google Scholar] [CrossRef]
- Chen, F.-W.; Liu, C.-W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Yang, X.; Xie, X.; Liu, D.L.; Ji, F.; Wang, L. Spatial Interpolation of Daily Rainfall Data for Local Climate Impact Assessment over Greater Sydney Region. Adv. Meteorol. 2015, 2015, 563629. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Levizzani, V.; Amorati, R.; Meneguzzo, F. A Review of Satellite-Based Rainfall Estimation Methods. Music—Mult. Precip. Meas. Integr. Calibration Flood Forecast. 2002. Available online: https://www.researchgate.net/publication/252272255_A_Review_of_Satellite_Based_Rainfall_Estimation_Methods (accessed on 26 August 2022).
- Kidd, C.; Levizzani, V.; Laviola, S. Quantitative Precipitation Estimation from Earth Observation Satellites. Rainfall State Sci. 2013, 191, 127–158. [Google Scholar] [CrossRef]
- Dinku, T.; Hailemariam, K.; Maidment, R.; Tarnavsky, E.; Connor, S. Combined use of satellite estimates and rain gauge observations to generate high-quality historical rainfall time series over Ethiopia. Int. J. Clim. 2014, 34, 2489–2504. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall Spatial Estimations: A Review from Spatial Interpolation to Multi-Source Data Merging. Water 2019, 11, 579. [Google Scholar] [CrossRef]
- Crow, W.T.; Huffman, G.J.; Bindlish, R.; Jackson, T.J. Improving Satellite-Based Rainfall Accumulation Estimates Using Spaceborne Surface Soil Moisture Retrievals. J. Hydrometeorol. 2009, 10, 199–212. [Google Scholar] [CrossRef]
- Massari, C.; Crow, W.; Brocca, L. An assessment of the performance of global rainfall estimates without ground-based observations. Hydrol. Earth Syst. Sci. 2017, 21, 4347–4361. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Pellarin, T.; Abramowitz, G.; Filippucci, P.; Ciabatta, L.; Maggioni, V.; Kerr, Y.; Prieto, D.F. A daily 25 km short-latency rainfall product for data-scarce regions based on the integration of the Global Precipitation Measurement mission rainfall and multiple-satellite soil moisture products. Hydrol. Earth Syst. Sci. 2020, 24, 2687–2710. [Google Scholar] [CrossRef]
- Kidd, C. Satellite rainfall climatology: A review. Int. J. Clim. 2001, 21, 1041–1066. [Google Scholar] [CrossRef]
- Kidd, C.; Dawkins, E.; Huffman, G. Comparison of precipitation derived from the ecmwf operational forecast model and satellite precipitation datasets. J. Hydrometeorol. 2013, 14, 1463–1482. [Google Scholar] [CrossRef]
- Duan, Q.; Phillips, T.J. Bayesian estimation of local signal and noise in multimodel simulations of climate change. J. Geophys. Res. Atmos. 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Gebregiorgis, A.; Hossain, F. How Much Can A Priori Hydrologic Model Predictability Help in Optimal Merging of Satellite Precipitation Products? J. Hydrometeorol. 2011, 12, 1287–1298. [Google Scholar] [CrossRef]
- Yang, Z.; Hsu, K.; Sorooshian, S.; Xu, X.; Braithwaite, D.; Zhang, Y.; Verbist, K.M.J. Merging high-resolution satellite-based precipitation fields and point-scale rain gauge measurements-A case study in Chile. J. Geophys. Res. Atmos. 2017, 122, 5267–5284. [Google Scholar] [CrossRef]
- Verdin, A.; Funk, C.; Rajagopalan, B.; Kleiber, W. Kriging and Local Polynomial Methods for Blending Satellite-Derived and Gauge Precipitation Estimates to Support Hydrologic Early Warning Systems. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 2552–2562. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Thinh, N.X. RF-MEP: A novel Random Forest method for merging gridded precipitation products and ground-based measurements. Remote. Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Brocca, L.; Massari, C.; Pellarin, T.; Filippucci, P.; Ciabatta, L.; Camici, S.; Kerr, Y.H.; Fernández-Prieto, D. River flow prediction in data scarce regions: Soil moisture integrated satellite rainfall products outperform rain gauge observations in West Africa. Sci. Rep. 2020, 10, 12517. [Google Scholar] [CrossRef]
- Arkin, P.; Meisner, B.N. The Relationship between Large-Scale Convective Rainfall and Cold Cloud over the Western Hemisphere during 1982–1984. Mon. Weather. Rev. 1987, 115, 51–74. [Google Scholar] [CrossRef]
- Manz, B.; Buytaert, W.; Zulkafli, Z.; Lavado, W.; Willems, B.; Robles, L.A.; Rodríguez-Sánchez, J. High-resolution satellite-gauge merged precipitation climatologies of the Tropical Andes. J. Geophys. Res. Atmos. 2016, 121, 1190–1207. [Google Scholar] [CrossRef]
- Berg, W.; Olson, W.; Ferraro, R.; Goodman, S.J.; Lafontaine, F.J. An Assessment of the First- and Second-Generation Navy Operational Precipitation Retrieval Algorithms. J. Atmos. Sci. 1998, 55, 1558–1575. [Google Scholar] [CrossRef]
- Nativi, S.; Barrett, E.; Beaumont, M. Monitoring of rainfall integrating active and passive microwave sensors: Possibilities and problems. Phys. Chem. Earth 1997, 22, 229–233. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; et al. A Kalman Filter Approach to the Global Satellite Mapping of Precipitation (GSMaP) from Combined Passive Microwave and Infrared Radiometric Data. J. Meteorol. Soc. Jpn. 2009, 87, 137–151. [Google Scholar] [CrossRef]
- Dinku, T.; Ruiz, F.; Connor, S.J.; Ceccato, P. Validation and Intercomparison of Satellite Rainfall Estimates over Colombia. J. Appl. Meteorol. Clim. 2010, 49, 1004–1014. [Google Scholar] [CrossRef]
- Ringard, J.; Seyler, F.; Linguet, L. A Quantile Mapping Bias Correction Method Based on Hydroclimatic Classification of the Guiana Shield. Sensors 2017, 17, 1413. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite–Based Estimates of Tropical Rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Sorooshian, S.; Gao, X. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Knapp, K.; Ansari, S.A.; Bain, C.L.; Bourassa, M.A.; Dickinson, M.J.; Funk, C.; Helms, C.; Hennon, C.C.; Holmes, C.; Huffman, G.; et al. Globally Gridded Satellite Observations for Climate Studies. Bull. Am. Meteorol. Soc. 2011, 92, 893–907. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef]
- Ashouri, H.; Nguyen, P.; Thorstensen, A.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D. Assessing the Efficacy of High-Resolution Satellite-Based PERSIANN-CDR Precipitation Product in Simulating Streamflow. J. Hydrometeorol. 2016, 17, 2061–2076. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global Precipitation at One-Degree Daily Resolution from Multisatellite Observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Jiang, Q.; Sun, W.; Wen, J.; Gao, J. A Comparative Study of Four Merging Approaches for Regional Precipitation Estimation. IEEE Access 2021, 9, 33625–33637. [Google Scholar] [CrossRef]
- Uyanık, G.K.; Güler, N. A Study on Multiple Linear Regression Analysis. Procedia Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- Porter, A.; Connolly, T.; Heikes, R.G.; Park, C.Y. Misleading indicators: The limitations of multiple linear regression in formulation of policy recommendations. Policy Sci. 1981, 13, 397–418. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Sun, Z.; Lin, Q.; He, H. Improvement of a combination of TMPA (or IMERG) and ground-based precipitation and application to a typical region of the East China Plain. Sci. Total Environ. 2018, 640–641, 1165–1175. [Google Scholar] [CrossRef] [PubMed]
- Nie, S.; Wu, T.; Luo, Y.; Deng, X.; Shi, X.; Wang, Z.; Liu, X.; Huang, J. A strategy for merging objective estimates of global daily precipitation from gauge observations, satellite estimates, and numerical predictions. Adv. Atmos. Sci. 2016, 33, 889–904. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Chang. 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Ma, Y.; Hong, Y.; Chen, Y.; Yang, Y.; Tang, G.; Yao, Y.; Long, D.; Li, C.; Han, Z.; Liu, R. Performance of Optimally Merged Multisatellite Precipitation Products Using the Dynamic Bayesian Model Averaging Scheme Over the Tibetan Plateau. J. Geophys. Res. Atmos. 2018, 123, 814–834. [Google Scholar] [CrossRef]
- Li, M.; Shao, Q. An improved statistical approach to merge satellite rainfall estimates and raingauge data. J. Hydrol. 2010, 385, 51–64. [Google Scholar] [CrossRef]
- Mekonnen, K.; Melesse, A.M.; Woldesenbet, T.A. Merging satellite rainfall estimates and daily rain gauge observations for improved flood simulation in MelkaKuntire catchment, upper Awash Basin, Ethiopia. Remote Sens. Appl. Soc. Environ. 2022, 25, 100701. [Google Scholar] [CrossRef]
- Zhu, Q.; Gao, X.; Xu, Y.-P.; Tian, Y. Merging multi-source precipitation products or merging their simulated hydrological flows to improve streamflow simulation. Hydrol. Sci. J. 2019, 64, 910–920. [Google Scholar] [CrossRef]
- Ibrahim, A.H.; Molla, D.D.; Lohani, T.K. Performance evaluation of satellite-based rainfall estimates for hydrological modeling over Bilate river basin, Ethiopia. World J. Eng. 2022. ahead of print. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-Scale Evaluation of 22 Precipitation Datasets Using Gauge Observations and Hydrological Modeling. Adv. Glob. Chang. Res. 2020, 69, 625–653. [Google Scholar] [CrossRef]
- Yoshimoto, S.; Amarnath, G. Applications of Satellite-Based Rainfall Estimates in Flood Inundation Modeling—A Case Study in Mundeni Aru River Basin, Sri Lanka. Remote Sens. 2017, 9, 998. [Google Scholar] [CrossRef]
- Maggioni, V.; Massari, C. On the performance of satellite precipitation products in riverine flood modeling: A review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Rozante, J.R.; Moreira, D.S.; De Goncalves, L.G.; Vila, D.A. Combining TRMM and surface observations of precipitation: Technique and validation over South America. Am. Meteorol. Soc. 2010, 25, 885–894. [Google Scholar] [CrossRef]
- Shawky, M.; Moussa, A.; Hassan, Q.K.; El-Sheimy, N. Performance Assessment of Sub-Daily and Daily Precipitation Estimates Derived from GPM and GSMaP Products over an Arid Environment. Remote Sens. 2019, 11, 2840. [Google Scholar] [CrossRef]
- Liu, X.; Liu, F.M.; Wang, X.X.; Li, X.D.; Fan, Y.Y.; Cai, S.X.; Ao, T.Q. Combining rainfall data from rain gauges and TRMM in hydrological modelling of Laotian data-sparse basins. Appl. Water Sci. 2017, 7, 1487–1496. [Google Scholar] [CrossRef]
- Min, X.; Yang, C.; Dong, N. Merging Satellite and Gauge Rainfalls for Flood Forecasting of Two Catchments Under Different Climate Conditions. Water 2020, 12, 802. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Hsu, K.-L.; Chang, F.-J.; Hong, Y.; Sorooshian, S. Merging multiple precipitation sources for flash flood forecasting. J. Hydrol. 2007, 340, 183–196. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).