Grid-Forming Inverter Integration for Resilient Distribution Networks: From Transmission Grid Support to Islanded Operation

Abstract

The progressive replacement of synchronous machines by inverter-based resources (IBRs) reduces system inertia and short-circuit strength, making power systems more vulnerable to frequency and voltage instabilities. Grid-forming (GFM) inverters can mitigate these issues by establishing voltage and frequency references, emulating inertia and enabling autonomous operation during islanding, while grid-following (GFL) inverters mainly contribute to reactive power support. This paper evaluates the capability of GFM inverters to provide grid support under both grid-connected and islanded conditions at the distribution level. Electromagnetic transient (EMT) simulations in MATLAB/Simulink R2022b were performed on a 20 kV radial microgrid comprising GFM and GFL inverters and aggregated load. Small disturbances, including phase-angle jumps and voltage steps at the point of common coupling, were introduced while varying the GFM share and virtual inertia constants. Also, local variables were assessed during islanded operation and separation process. Results indicate that maintaining a GFM share above approximately 30–40% with inertia constants exceeding 2 s significantly enhances frequency stability, supports successful transitions to islanded operation, and improves overall resilience. The study highlights the complementary roles of GFM and GFL in enabling the stable and resilient operation of converter-dominated distribution systems.

1. Introduction

The transition toward decarbonization and phase-out of nuclear energy production, driven by large-scale integration of renewable energy (RE) technologies, requires a paradigm shift in power system design, planning and operation [1]. While RE integration provides environmental sustainability and energy independence, the increasing penetration of inverter-based resources (IBRs) introduces fundamental challenges. Unlike conventional synchronous generators, IBRs interfaced through grid-following (GFL) inverters lack rotational inertia, as they are designed to follow the reference of the connected grid. This reduction in system inertia and strength amplifies the severity of frequency events and increases the risk of instability. To address this, grid-forming (GFM) inverters can provide “virtual inertia” and establish voltage and frequency references in a manner similar to synchronous machines, through advanced control strategies, thereby autonomously stabilizing local grids.

Today’s power infrastructure, originally designed for centralized fossil-based generation, requires significant modernization to integrate decentralized RE sources. This modernization must address the growing complexity associated with bidirectional power flows, reactive power support, frequency containment reserves, short-circuit capabilities and system X/R ratios. In addition, external challenges such as intermittency (highlighting the need for large-scale storage), extreme weather events, cybersecurity threats, and the increasing need for coordination among multiple stakeholders further stress the system [2].

The April 2025 blackout in Spain, though still under investigation, underscored the urgent need for resilient power systems in a context where the technical transition is advancing faster than operators can adapt. Such events highlight the necessity of understanding the new dynamics of power systems to prevent shortages and to strengthen the ability to resist, stabilize, rebuild and reconfigure in order to restore service when disturbances occur [3]. One emergent strategy for improving resilience is the decentralization of ancillary services. By distributing functions such as frequency regulation, voltage control, islanding and black-start capability, distribution networks can enhance both local reliability and overall system stability. In extreme cases, local microgrids (MGs) can achieve self-sufficiency by islanding from the main grid and maintaining independent operation [4].

Modern power electronics and advanced control systems provide the flexibility required to address these challenges. GFMs act as voltage sources, setting frequency and voltage references, whereas GFLs function as current sources, injecting active and reactive power based on external signals. Their complementary use enables flexible and resilient grid operation: GFMs provide stability support, while GFLs contribute to reactive power balancing and efficiency [5]. Together with energy storage and demand-side flexibility, these technologies enable the development of MGs, Positive Energy Districts (PEDs), and smart energy communities [6]. Such systems not only provide ancillary services to the transmission grid, including virtual inertia, balancing and dynamic reactive power compensation, but also enhance local resilience by continuing operation during generalized blackouts.

The importance of GFMs has been acknowledged at both transmission and distribution levels. In May 2022, the four German transmission system operators (50 Hertz, Amprion, TenneT, and TransnetBW) issued requirements for GFM converters, emphasizing their role in maintaining stability as IBR penetration increases [7]. Similarly, the Stability Roadmap highlights GFMs as essential for islanded operation through robust local frequency and voltage control [8]. At the distribution level, MGs are increasingly viewed as aggregation systems that integrate distributed resources and storage for active power management and supply restoration.

The Stability Roadmap further promotes GFM deployment in distribution networks, where most RE capacity will be installed, supported by regulatory frameworks and pilot projects with manufacturers to validate capabilities and address integration challenges. Insights from these pilots are expected to inform replicable models and technical specifications [8].

Although no dedicated VDE standard for GFMs exists, the VDE FNN published Technical Requirements for Grid-Forming Properties Including the Provision of Momentary Reservein July 2024 [9]. These requirements cover imbalance management, rate-of-change-of-frequency (RoCoF), inertia response and fault behavior, along with testing guidelines. At present, GFMs must also comply with VDE-AR-N 4110, which defines connection and operation requirements for medium-voltage plants, including stability, voltage quality and fault ride-through.

This study aims to identify tendencies in frequency and voltage behavior during small disturbances with respect to changes in specific variables, such as the GFM/GFL ratio in the system, GFM inertia in Virtual Synchronous Machine (VSM) control mode, available power behind the inverters, and load reference power. By identifying these tendencies, the technical benefits of deploying the GFM inverter capacity at the distribution level under both grid-connected and islanded conditions, from the power systems point of view, can be addressed. The goal is not to define the optimal size, amount, or location of the GFM or GFL inverters but to identify operational ranges and trends where system performance remains within acceptable limits for long-term stability. The case studies were performed by means of electromagnetic transient (EMT) simulations in MATLAB/Simulink.

Current research has shown that GFM inverters operating under VSM control, when used in parallel with synchronous generators, can improve frequency stability and Rate of Change of Frequency (RoCoF) compared with systems based solely on synchronous generators, provided that the GFM inertia is adequate for the system dynamics [10]. However, in fully converter-based grids, modal stability analyses are necessary to determine the ratio of GFMs to GFLs required for stable operation under both grid-connected and islanded conditions due to the possible resonances and interactions between converters. Similarly, the optimal allocation [11,12] and sizing of GFMs, whether concentrated in a few large units or distributed across many smaller ones, require careful evaluation and will depend on the system characteristics.

Several analyses have indicated that deploying 25–35% of total capacity as GFMs ensures stable operation since smaller shares may provide insufficient inertia and larger shares may introducing oscillatory interactions [13]. Moreover, systems with fewer but larger GFMs tend to exhibit superior dynamic performance compared with those relying on many smaller units of equivalent aggregate capacity [14,15]. Since each system exhibits complex dynamics influenced by grid and converter parameters, dedicated studies are necessary for each case.

Field and modeling studies have progressively refined this range. Marchand et al. (2023) demonstrated through microgrid energization tests that a non-zero minimum GFM proportion is required to achieve successful voltage and frequency restoration in low-voltage networks with local renewables [13]. Wang (2022) analyzed the nonlinear stability of residential microgrids with grid-forming prosumers, revealing the influence of feeder impedance and power-sharing parameters on dynamic stability limits [15].

Complementary insights come from broader reviews and engineering guidance. Musca, Vasile, and Zizzo (2022) surveyed over twenty pilot and demonstrator projects implementing grid-forming controls, emphasizing the lack of standardized performance metrics and the scarcity of validated dynamic studies at distribution level [14]. Zhao, Thakurta, and Flynn (2022) identified through a national stability assessment for the Irish 100% converter-based grid that approximately 37–40% of GFM capacity (MVA) is required to maintain stable operation, with reduced requirements when GFM and GFL converters are co-located [16]. At the engineering-practice level, Winkens (2024) from RWTH Aachen proposed that converter-only islanded systems should allocate at least one quarter of total converter nominal power as grid-forming, scaled to the expected power imbalance, and that VSM-type controls offer the most tunable damping and inertia options [17].

Further methodological validation is found in international technical guidelines. The NREL report (2022) on grid-forming controls for future power systems and the ENTSO-E First Interim Report on Grid-Forming Capability of Power Park Modules (2024) both concluded that the optimal GFM fraction depends strongly on system topology, control type and disturbance scale, rather than a single universal percentage [18]. By taking this perspective, the paper contributes as a reference point to the ongoing discussion on how distribution networks can evolve into resilient systems that actively support transmission-level stability by providing distributed ancillary services. This approach highlights the role of IBRs not only as enablers of renewable integration but also as active participants in ensuring system reliability and flexibility.

It is well known that the interactions between control-based power electronics and electromechanical-based power system introduce dynamics which can influence different responses of the system. Therefore, the present work focuses on the power systems perspective by evaluating solely electrical variables for which long-term operational limits are well defined, while keeping the power electronics internal control and filter parameters constant, in order to avoid those from interfering with the analysis on the tendencies with respect to the parameters studied. Further work could take the results from this study as a starting point for control focused studies.

Similarly, large disturbance analysis would introduce variables which are not evaluated in this work, such as the presence of negative and zero sequence in the dq frame, fault-ride-through, and protection coordination studies, among others. Detailed renewable generation, load modeling and battery dynamics would either introduce statistical modeling and/or a quasi-dynamic point of view, with longer time frames for the simulations, such as days or months, but for the purpose of this study, assuming that there is a certain amount of power available from a source behind the inverter is enough to conduct the analysis and fulfill the goal of this work. Other topics, such as economic optimization and communication-based control schemes, are well beyond the scope of this study.

The paper is structured into four sections. Section 1, it provides a brief overview of grid support alternatives in distribution systems. Section 2, it describes the simulated test-bed for a medium-voltage (MV) grid. Section 4, it presents the simulation case studies along with the corresponding results. Section 5, the discussion and main conclusions are outlined.

2. Grid Support from Distribution Systems

The integration of RE introduces new challenges for grid operation, and ancillary services are no exception. Traditionally, the main task of system operation has been to maintain the active power balance between demand and generation. In modern grids, however, additional issues have emerged, including voltage fluctuations caused by the fast dynamics of power electronics, harmonic distortions and resonances. To address these challenges, grid facilities must offer advanced capabilities for controlling not only active power but also reactive power, voltage, angle, short-circuit current, and inertia. These non-frequency ancillary services are essential to support system stability.

IBRs call for a paradigm shift in stability analysis. On one hand, they alter the traditional understanding of grid dynamics; on the other, they can provide technical attributes that enhance stability through ancillary services. In Germany, regulatory frameworks such as the Renewable Energy Act (EEG) [19] and the Stability Roadmap [8] emphasize the need for distributed resources to contribute to ancillary services since centralized generation alone is insufficient to meet future stability requirements.

2.1. Frequency Services

The European interconnected grid operates at a nominal frequency of 50 Hz, established by the Union for the Coordination of the Transmission of Electricity (UCTE). This value must remain within a narrow range to ensure secure operation. In Germany, the permitted frequency range is 49.8–50.2 Hz, corresponding to only ±0.4% deviation from nominal. This makes frequency a critical and highly sensitive operational parameter. Figure 1 shows the frequency ranges and associated operational states (normal, alarm, or emergency), depending on the duration of the deviation [20].

To maintain stability, transmission and distribution system operators procure both frequency and non-frequency ancillary services. Frequency services are based on maintaining the balance between demand and generation. Traditionally, generators managed this balance by adjusting their output. However, distribution systems can also contribute by offering demand response (DR), in which controllable loads adjust their consumption in response to grid conditions or price signals [21].

Thermostatically controlled devices such as heat pumps, refrigerators, and cooling systems can serve as distributed thermal storage, enabling short-term flexibility without compromising end-user comfort. This flexibility allows DR to provide frequency regulation in a manner comparable to dispatchable generation [22]. Unlike emergency load shedding, DR is voluntary and contract-based. With the ongoing electrification of heating in Germany, which is expected to involve millions of heat pumps and expanded district heating networks by 2030 [23], DR is projected to play an increasingly important role in balancing demand and supply, provided that appropriate control and coordination mechanisms are implemented [22].

2.2. Non-Frequency Services

Non-frequency ancillary services address challenges beyond demand–supply balancing, including fast voltage fluctuations, harmonic distortions, and reduced inertia. While frequency services can be provided globally, non-frequency services such as voltage control, inertia provision, short-circuit current, black-start capability, and islanding must be delivered locally [24]. In modern grids, the rapid control capabilities of IBRs make distributed provision of these services feasible [25]. Unlike frequency services, non-frequency ancillary services currently lack standardized market mechanisms, primarily due to their local nature. At present, procurement relies on bilateral agreements [26]. However, regulatory initiatives foresee standardized procedures to enable more efficient coordination between transmission system operators (TSOs) and distribution system operators (DSOs) [24].

2.2.1. Inertia Provision for Damped Frequency Dynamics

With the massive integration of IBRs, faster dynamics are being introduced to the system in addition to a decrease in inertia. As mentioned, traditional power systems have been predominantly centralized, with large synchronous generators dominating the production of electricity and the dynamics of the system. These conventional generators are characterized by large rotating masses with stored kinetic energy. The swing Equation (1) describes the dynamic electro-mechanical coupling of the synchronous generator and the electrical system, where $\omega$ is the rotor speed, H is the inertia constant, and $P_m$ and $P_e$ are the mechanical and electrical active power, respectively. It shows that the rotor speed of the synchronous generators and their mechanical inertia are directly related to the frequency and active power balance. Typical inertia constant values for machines are in the range of 2–10 s [27]:

$${\displaystyle \frac{d\omega }{dt}}={\displaystyle \frac{\omega }{2H}}(P_m-P_e)$$

(1)

Essentially, two main statements can be concluded from this equation. First, if mechanical and electrical power are equal, meaning the generation matches exactly the demand, then there will not be an angular velocity change, which implies that there is no frequency deviation. Any unbalance between generation and demand will result in an angular acceleration of the rotor, which affects the frequency. Second, the angular acceleration is inversely proportional to the inertia of the machine, that is, to higher inertia constants, lesser frequency deviations will occur.

In other words, a higher inertia induces a damped and slower response to frequency deviations by increasing the response time of the system, which ultimately helps to maintain its stability. This can also be understood from the RoCoF point of view, which indicates how quickly the system frequency is changing at any given moment. The RoCoF is determined by Equation (2), where f is the electric frequency of the system. If the RoCoF is high, that means a rapid frequency deviation, usually associated with low inertia and weak grids [28].

$$RoCoF={\displaystyle \frac{df}{dt}}$$

(2)

GFM inverters can introduce virtual inertia by incorporating the swing Equation (1) by using the desired inertia constant as an input value in their control loops. This is known as the Virtual Synchronous Machine (VSM) control strategy, and it can help to compensate for the loss of mechanical inertia. VSM aims to emulate the rotor and governor dynamics of a synchronous generator. This creates the effect of a synthetic inertia during disturbances, avoiding rapid changes in the frequency, in other words, avoiding high RoCoF.

2.2.2. Voltage Support by Reactive Power

Voltage support refers to control actions that maintain voltage levels through reactive power compensation [29]. Traditionally, this has been provided by static devices such as capacitor banks or by dynamic equipment including synchronous condensers, on-load tap changers and FACTS devices [30]. Recent advances in power electronics, such as solid-state transformers, allow more flexible and continuous voltage regulation. With increasing penetration of IBRs, reactive power support can also be delivered at the distribution level through advanced inverter controls. However, their capability is limited by inverter sizing and active power output, often reducing reactive support when it is most needed [31]. Furthermore, high RE generation combined with low demand can lead to local over-voltage events, highlighting the need for adaptive voltage control. Addressing these challenges requires modern inverter technologies, updated grid codes, and improved coordination between distributed resources and system operators.

The grid code in Germany requires that the power factor at the connection point between TSO and DSO must not fall below 0.9. This must be achieved by reactive power control, which directly impacts voltage [32]. Different types of local reactive power control include constant power factor $cos\left(\varphi \right)$, power factor depending on active power $cos\left(\varphi \right(P\left)\right)$, and reactive power depending on the voltage $Q\left(V\right)$ droop control [26].

2.2.3. Islanding

Islanded operation refers to the ability of a MG to disconnect from the main grid and continue supplying local loads using distributed generation and storage. This can occur intentionally, for economic or operational reasons, or during grid disturbances such as blackouts, where local supply ensures continuity until reconnection is possible. Although proposed as an ancillary service, islanding has not yet been standardized in regulation. Technical guidance such as IEEE 1547.4 [33] highlights the requirements for reliable transitions, including sufficient local generation, inertia provision (from synchronous machines or grid-forming inverters), selective load shedding or demand response, and adaptive protection schemes. Once islanded, the MG must maintain voltage and frequency stability, with at least one unit acting as a reference bus. Effective voltage regulation, reactive power support, and harmonics control are also necessary to ensure power quality [30]. These challenges underscore the need for advanced inverter functionalities, coordinated control strategies, and adaptive protections to enable secure islanded operation as part of future distributed system services.

3. Medium Voltage (MV) Grid Model

The goal of this work is to evaluate the technical advantages of deploying GFM inverter capacity in a distribution grid, by testing the different case studies in both grid-connected and islanded operating conditions. The purpose is to identify tendencies with respect to the different variables involved, in order to develop general recommendations for distribution-level applications. This means the focus is on the operating points which present values that are considered acceptable for permanent operation.

The library deployed to model GFM, GFL inverters and external grid, was provided by the Lille Laboratory of Electrical Engineering and Power Electronics (in French, Laboratoire d’electrotechnique et d’electronique de Puissance de Lille) [34]. The main advantage of these models is that they allow a smooth integration of the blocks to grid models for power system application studies. First, they provide an ”Update Load Flow” block which allows to perform the Load Flow calculation including the converters, which is usually challenging for most available converter models for Matlab/Simulink. It is also not needed to tune the internal control parameters from the inverter models in order to obtain a stable output, with respect to all the different components of the system. This is the opposite case with most of the converter models available for Matlab/Simulink, which are usually designed for power electronics applications, and that makes them highly complex to adapt for power systems studies.

For the purpose of this study, a MV grid defined as the MG consisting of one GFM inverter, one GFL inverter, and one load was developed, together with an equivalent external grid. The model chosen for the simulations is a simplified representation of a European 20kV radial distribution system, with local generation connected through one GFM and one GFL inverter, and one load representing the total local demand. The details at the low-voltage level and high-voltage external grid were not modeled. The general model used for the simulations is shown in Figure 2.

The aim of the study is to analyze the connection of IBRs to the grid, and most of the simulation was performed in time frames of a few seconds; therefore, the sources behind the GFM and GFL inverters were not modeled. That means that the inverters are assumed to be connected to either RE sources, such as wind and PV systems, or storage systems without actually considering the quasi-dynamic behavior of these due to weather variations or resource availability in time frames of minutes, hours or longer. However, different operating points for the inverters depending on the availability of power generation from their corresponding source were evaluated, and throughout the document they are referred to as ”reference” or ”set-point”.

That being said, for the purpose of the study, it was generally assumed that the GFM inverter was connected to a battery in order to be able to provide the necessary grid support at any given moment and due to the ideal fast response from this technology. On the other hand, the GFL inverter was assumed to be connected to a weather-dependent source type, such as wind generators or PV panels. However, the details from the source type are not relevant for the analysis and therefore were not directly considered.

In the block parameters for the library external grid, GFM and GFL blocks, the type of bus (swing, PV, or PQ) can be selected, and the initial condition for the corresponding variables can be input. For example, if PV bus is selected, automatically the reference for active power and voltage magnitude are enabled to be set at the “Load flow” tab. Once the Power Flow script is executed, all the main variables affected by the Load Flow (Active power P, reactive power Q, voltage magnitude V and voltage angle $\delta$) are automatically calculated and updated at the point of common coupling (PCC) of the respective device with the system. That being said, further in this section, a description of the GFM and GFL inverter models is presented.

The model used for the load is the Three-Phase Parallel RLC Load block from the Matlab/Simulink Simscape/Electrical/Specialized Power Systems library, which allows to represent the load as an active power, inductive reactive power and capacitive reactive power. For the purpose of this study, which is not focused on the load modeling, a PQ load type model was selected with a nominal (peak) active power of 1 MW and inductive reactive power of 0.48 MVAR, keeping a power factor of 0.9.

Throughout the case studies, the reference value of the load will be varied between 0.25 pu (per-unit) and 1 pu. This refers to different points on the load profile, where it will be assumed that 0.25 pu is the minimum load or base load, and that 1 pu corresponds to the maximum or peak load.

The library used contains various GFM and GFL inverter models, depending on the type of analysis and application to be carried out. In both cases, the model includes internally the step-up transformer for connection to the grid. The “Nominal values” and “Passive component” tab is similar for both GFM and GFL models, containing the nominal values of frequency, power, voltages and transformer information. Both models also contain a “Control Parameter” tab where different control parameters such as PLL bandwidth, current loop bandwidth, virtual impedance, and others can be modified. However, as previously mentioned, this tuning is out of scope for this work. Finally, both blocks have the “Load flow” tab as previously mentioned.

The GFM block offers additionally a “Control Strategy” tab where the inertial response can be selected, along with the VSM or PI type. For this case, VSM was chosen in order to have the option of including a value of inertia for the dynamic response of the GFM inverter. At each study case, the specific parameters chosen will be addressed. The GFM block provides inputs for change in the voltage reference and in the active power reference, by the inputs $\Delta E$(pu) and $\Delta P$ (pu), respectively. The GFL block also provides inputs for change in the active and reactive power reference, by the inputs $\Delta P$ (pu) and $\Delta Q$ (pu), respectively. These inputs will later be used for simulating changes in the reference operating points of the GFM and GFL, respectively.

The power reference can be interpreted as the total power available of the source connected behind the inverter with respect to their nominal values. Since the modeling of the source connected behind the inverter is out of the scope of this work, it is assumed that either batteries, PV panels, or wind turbines are connected to the inverters, and they set the reference power depending on the availability of the resource.

Internally the GFL inverter control can be described by the simplified diagram shown in Figure 3. In blue, the inputs correspond to the reference values which can be given to the inputs $\Delta P$ (pu) and $\Delta Q$ (pu) of the block, while the output corresponds to the voltage signals, which are then sent to the bridge model in order to generate the three-phase inverter output. In yellow, the measured values from the grid correspond to three-phase voltages and currents (a, b and c). In green, the values are internally calculated based on the measured values or after being processed by the control blocks, such as active and reactive power from the grid, angle, measured and reference $dq$-currents and voltages. In purple, the main control blocks used, are active and reactive power control and current control.

The main control parameters of the GFL inverter used in the simulation model are summarized in

Table 1. Main GFL control parameters.

Category	Parameter	Value
PLL	Bandwidth [rad/s]	50
	Damping ratio	1
Outer Loop	Power control Bandwidth [rad/s]	10
	Kp	0.0333
	Ki	10
Current Loop	Bandwidth [rad/s]	1200
	Feedforward	Yes
	Kp	0.57296
	Ki	6

. It is worth noting that the fine tuning of the control parameters is out of the scope of this work, and therefore these are purely informative.

Similarly, the GFM inverter control can be described by the simplified diagram shown in Figure 4. In blue, the inputs correspond to the reference values which can be given to the inputs $\Delta P$ (pu) and $\Delta E$ (pu) of the block, while the output corresponds as well to the voltage signals, which are then sent to the bridge model in order to generate the three-phase inverter output. In yellow, again the measured values from the grid correspond to three-phase voltages and currents (a, b and c). In green, the values are internally calculated based on the measured values or after being processed by the control blocks, such as active and reactive power from the grid, angle, measured and reference $dq$-currents and voltages. In purple, the main control blocks used, are active power control (which handles the VSM strategy) and current and voltage control.

The main control parameters of the GFM inverter used in the simulation model are summarized in

Table 2. Main GFM control parameters.

Category	Parameter	Value
PLL	Bandwidth [rad/s]	50
	Damping ratio	1
VSM	Frequency Support Droop Gain [%]	4
	Damping ratio	1
	Kp	25
	Dp	289.44
	Dq	6.667
Current Loop	Bandwidth [rad/s]	1200
	Feedforward	Yes
	Kp	0.57296
	Ki	6

. It is worth noting that the fine tuning of the control parameters is out of the scope of this work, and therefore these are purely informative.

The strategy to evaluate the GFM inverter amount in the MG was to vary the amount of GFM with respect to GFL, keeping the total nominal load in the MG constant and the total amount of IBRs installed nominal capacity (GFM + GFL) as shown in Equation (3), where $S_{GFM}$ and $S_{GFL}$ are the nominal apparent powers of the GFM and GFL inverter, respectively, and $S_{total}$ is the total installed capacity in the MG:

$$S_{total}=S_{GFM}+S_{GFL}$$

(3)

The total amount of apparent power distributed between GFM and GFL throughout all the simulations is $1.1MVA$. This variation of the GFM and GFL ratio is introduced by a parameter “alpha” $\alpha$ which corresponds to the portion of the GFM inverter capacity with respect to the total generation capacity of the MG, as shown in Equation (4). This means that the GFL inverter nominal power is given by Equation (5):

$$\alpha ={\displaystyle \frac{S_{GFM}}{S_{total}}}$$

(4)

$$S_{GFL}=(1-\alpha )S_{total}$$

(5)

4. Simulation Results

Figure 5 shows an overview of the different case studies proposed for the analysis. This section is divided into two main parts: gird-connected operation and islanded operation.

The grid-connected operation includes addressing the operating point at the PCC: importing or exporting, depending on the MG elements reference points. Then, different grid support services were tested: frequency support by means of different inertias and amounts of GFM inverter, and voltage support under an event at the external grid, where the reactive power reaction from both GFM and GFL inverter was tested independently and compared.

For the islanded operation, two main case studies were tested: the ranges of acceptable operation of the island in steady states and the survivability at the moment of the disconnection with respect to the different operating points of the system. In both cases, different proportions of GFM, GFL, and load were tested.

4.1. Grid-Connected Operation

The first case studies correspond to grid-connected operation as shown in Figure 5. This implies that, at any given moment, the MG is either importing from the main grid when there is not enough total capacity from local sources to supply the load, or exporting to the main grid when there is not only enough total capacity from local sources to supply the load but also a surplus which can be injected to the main grid.

In all cases, the external grid was set as the slack or swing bus, the GFM inverter as PV, and the GFL inverter as PQ. Depending on the operating condition, a different event at the main grid was tested, and the MG proceeded to react accordingly to support the system. The events tested were small disturbances, such as phase jumps and voltage events.

4.1.1. Operating Point at the PCC

The first goal is to identify the different operating points (importing/exporting) with respect to the different ratios of generation and load in the MG. This is achieved by means of the power flow results. At every operating point the power flow calculation is performed, and the results for active power from the external grid are stored. If the value of active power for the external grid is positive, that means it is generating power and therefore acting as a source by feeding active power to the MG. On the other hand, if the value of active power for the external grid is negative, then the external grid acts as a “load” by consuming active power and therefore the MG is exporting and. The results are shown in Figure 6. Each subplot corresponds to a different combination of load and GFL inverter active power reference point. In each subplot, the x axis corresponds to alpha ($\alpha$), the amount of GFM in percentage with respect to the total generation power in the MG, and the y axis to the GFM reference active power with respect to the nominal. The white area corresponds to exporting operating points and the blue area to importing operating points.

In this case, sixteen different operating points were tested. First, varying the GFL inverter active power reference $P_{GFLref}$ to 0.25 pu, 0.5 pu, 0.75 pu, and 1 pu, assuming the inverter is connected to a weather-dependent source such as PV panels or wind turbines. Then, the load power $P_{Loadref}$ was changed by the same values, assuming different moments during the day, considering the load profile as 1 pu for the peak load and 0.25 pu for the base load. The GFM inverter was tested by having the availability of values from 0.1 pu to 1 pu in steps of 0.1 pu, assuming the GFM is connected to a battery. These three variables were iteratively changed with respect to the GFM amount ($\alpha$), and the operating point was defined statically by the active power load flow solution for the external grid as mentioned previously.

The tendency is clear and quite intuitive: at higher load references, a higher amount of GFL and GFM generation is required in order to have enough local generation to cover the demand and be able to export. However, it can be noted that the amount of GFM with respect to GFL plays an important role in defining the operating point. In every case, with higher amounts of GFM and at lower GFM reference points, the MG would be importing, and it can be seen that for the lower GFM reference point, it is more convenient to have lower amounts of GFM. Similarly, it is worth noting that for lower load values ($P_{Loadref}$ set to 0.25 pu), at any available amount of GFL active power, having a $P_{GFMref}$ of 0.2 pu or higher would result in generation surplus almost in every case (with the exception of higher amounts of GFM).

4.1.2. Frequency Support by Different GFM Inertias

For this case, the total local generation is enough to supply the load (and losses), and there is a surplus of power generation that can be exported to the main grid. In this case, a phase jump at the external grid was simulated, analyzing the dynamic tendency with respect to different inertias and different amounts of GFM inverter in the MG. A phase jump may result from a sudden change in power, for instance, loss of load or generation or a switching operation. When this happens, the system needs to compensate for the power unbalance by adjusting the generation units voltage angle. The recommended phase jump value for strong grids is $\pm \pi /36$ rad, which is equivalent to $\pm 5$ deg [18]. Since the grid tested in this work is assumed to be weak (inertia coefficient H of 2 s), the proposed value for phase jump test is $\pm \pi /40$ rad, which is equivalent to $\pm 4.5$ deg.

Taking an arbitrary exporting case from the results in Section 4.1.1, the values of active power reference of the GFM and GFL inverters and the load were kept constant, at 0.5 pu, 0.75 pu, and 0.5 pu, respectively. The simulation was executed for 5 s, and the corresponding phase jump was applied at the main grid block by inputting a $\Delta \theta =\pm \pi /40$rad to the external grid block at time $t_0=1$ s. The GFM amount was iterated by means of changing the value of $\alpha$ from 1% to 99% in steps of 1% and the inertia of the GFM inverter from 0.5 to 10 in steps of 0.5.

Table 3. Values applied for the frequency event simulation.

Variable	Values	Steps
Phase Jump $\Delta \theta$ [rad]	$\pm \pi /40$	-
Grid inerta $H_{grid}$ [s]	2	-
GFM inertia $H_{GFM}$ [s]	0.5–10	0.5
GFM amount $\alpha$ [%]	1–99	1
GFM Active Power Reference $P_{GFMref}$ [pu]	0.5	-
GFL Active Power Reference $P_{GFLref}$ [pu]	0.75	-
Load Active Power Reference $P_{Loadref}$ [pu]	0.5	-

summarized the information regarding the test. No topological changes, demand response, or power reference changes were applied.

The maximum and minimum frequency value for each simulation were stored and displayed in the form of heatmaps as depicted in Figure 7 and Figure 8, where Figure 7 corresponds to a positive phase jump (over-frequency) and Figure 8 to a negative phase jump (under-frequency). In Appendix A a randomly chosen specific point (GFM amount of 34% and GFM inertia of 5 s) of each heatmap is highlighted in order to make clear the meaning of the plots. Each point of the heatmaps corresponds to the maximum and minimum frequency reached after 5 s of dynamic simulation.

As it can be seen, the general tendency for both cases is that higher amounts of GFM in the system combined with higher inertias present a better response with respect to maximum and minimum frequencies reached, for the same phase jump applied. In both cases, a minimum of around 30% of GFM amount in the system is where the system reaches the acceptable frequency limits for permanent operation (49.8 Hz and 50.2 Hz). This means that for GFM amounts of 30% or higher, the GFM inverter is able provide a better frequency support to the grid.

However, there was an unexpected behavior; in both figures, the GFM amount obtained for the range of 1–3% can be attributed to simulation instabilities due to the control of the inverters, and therefore should not be considered in the tendency.

4.1.3. Voltage Support by Adjusting the Reactive Power Reference of GFM vs. GFL

In this case, an over-voltage event at the main grid was tested. As mentioned in Section 2.2.2, voltage instabilities must be compensated for with reactive power. In this case, the capabilities of both the GFM and GFL inverters to dynamically compensate for reactive power were tested and analyzed independently. Two tests were performed for the same grid conditions and event, taking an arbitrary exporting case from the results in Section 4.1.1, shown in

Table 4. Values applied for the voltage event simulation.

Variable	Value
Voltage Step $\Delta E$ [pu]	0.2
GFM inertia $H_{GFM}$ [s]	5
GFM amount $\alpha$ [%]	30
GFM Active Power Reference $P_{GFMref}$ [pu]	1
GFL Active Power Reference $P_{GFLref}$ [pu]	0.75
GFL Power Factor	0.9
Load Active Power Reference $P_{Loadref}$ [pu]	0.75
Load Power Factor	0.9

. A voltage event was induced at the main grid by inputting a step of 0.2 pu at $t_0=0.5$ s at the input $\Delta E$ of the external grid block, which caused the voltage at the grid to increase from 1.00 pu to almost 1.08 pu, which exceeds the permanent acceptable operation limits ($\pm 5\%$).

Two different cases were analyzed for compensation: first the voltage set point of the GFM inverter was changed, and in the second test the reactive power set point of the GFL inverter was changed.

In the first test, the voltage set point of the GFM inverter was adjusted by the input $\Delta E$ of the block. As seen in Figure 9a, by inputting a signal of −0.08 pu at $t_1=1$ s at $\Delta E$, the GFM inverter adjusts the reactive power within its capabilities, assuming that it can operate with power factors os 0.9 both lagging and leading. Therefore, it contributes to the voltage stability by making not only the grid voltage but also the voltages at every node return to normal operation conditions as seen in Figure 9b.

In the second test, the reactive power set point of the GFL inverter was adjusted by the input $\Delta Q$ of the block. As seen in Figure 10a, by inputting a signal of −0.4 pu at $t_1=1$ s at $\Delta Q$, the GFL inverter adjusted the reactive power within its capabilities, assuming that it can operate with power factors of 0.9 lagging and leading. Therefore, it contributes to the voltage stability by making not only the grid voltage but also the voltages at every node return to normal operation conditions as seen in Figure 10b.

In both cases, the grid voltage was able to return to normal operating conditions. The change in the GFM inverter reactive power set-point made the voltage return to the acceptable operating point faster than the GFL inverter. However, seen from the perspective of the reactive power, the GFL inverter could be a better option for reactive power control. The GFM inverter needed to completely change the operating point from positive reactive power (around 0.45 pu) to negative (around −0.36 pu), while the GFL inverter also needed to change from positive to negative but with a much lower magnitude (from 0.35 pu to around −0.05 pu).

4.2. Islanding Case Scenarios

The second group of the case studies corresponds to islanded operation as shown in Figure 5. This means that the MG is able to operate separated from the main grid. This implies that there is enough total capacity from local sources to supply the load and there is either a planned or unplanned disconnection from the main grid. Under these sections, different static and dynamic scenarios were tested: first, at the steady-state, where the best and worst case scenarios were addressed; after, the disconnection survivability was tested to determine the necessary initial conditions for the MG to be able to disconnect from the main grid and continue to operate.

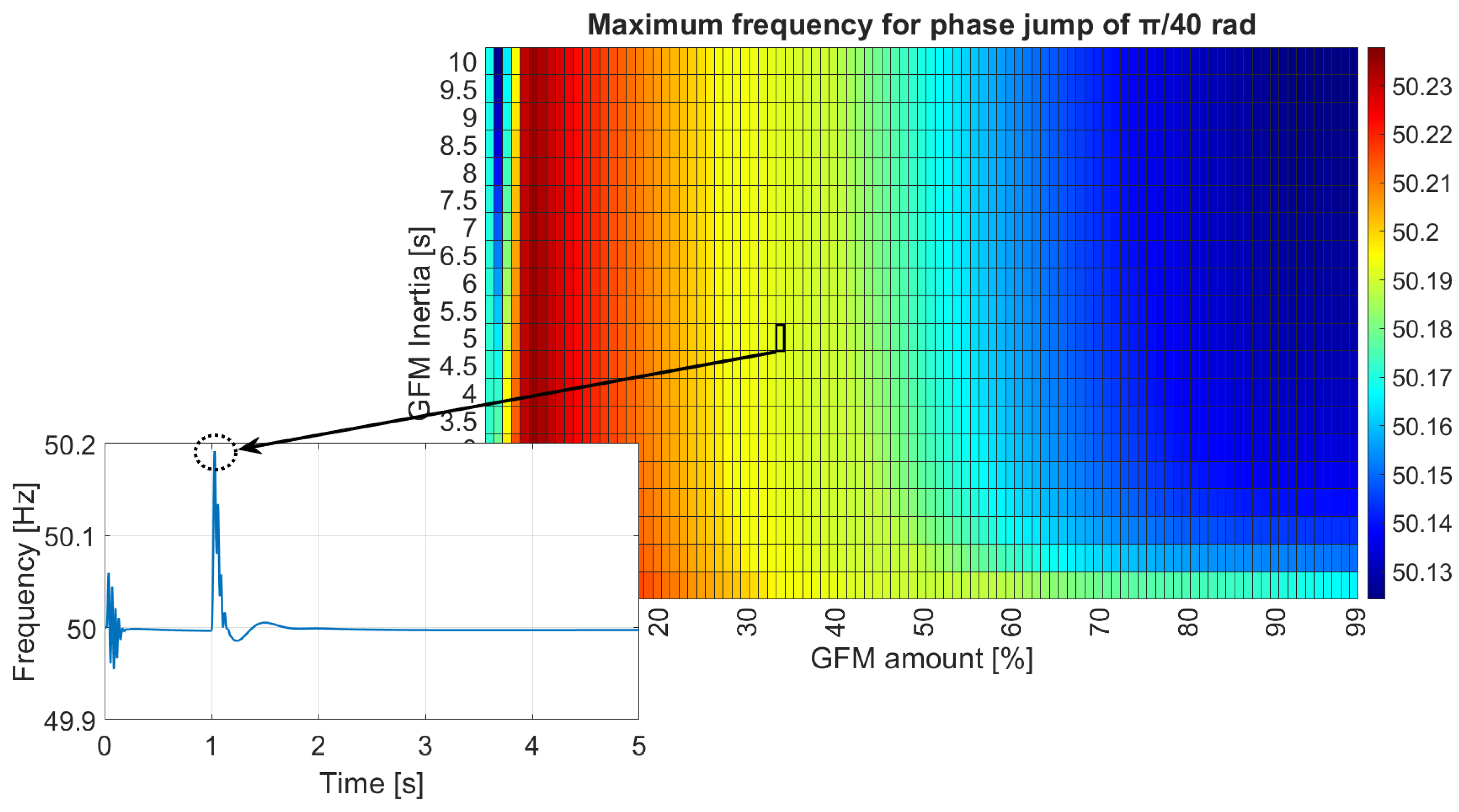
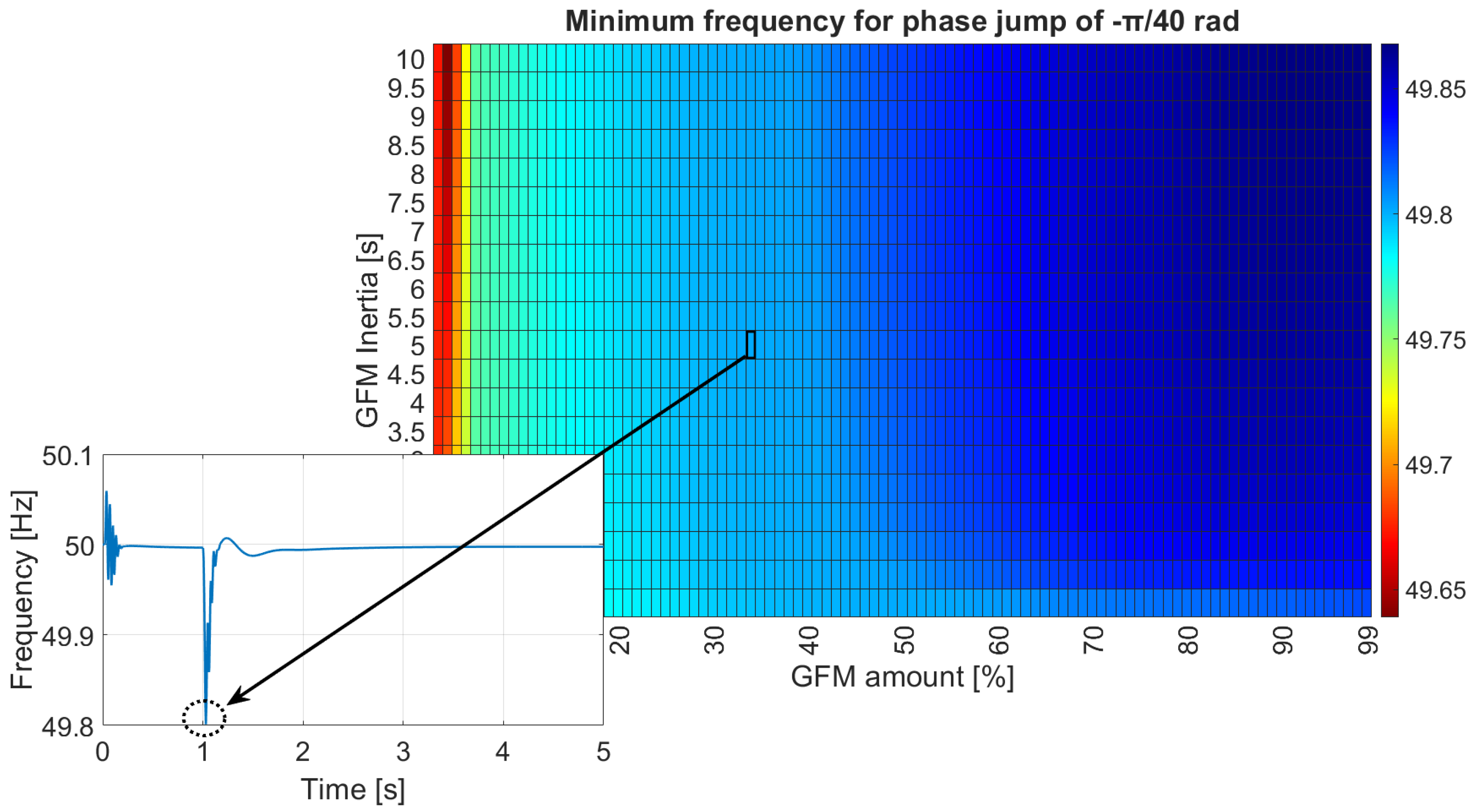
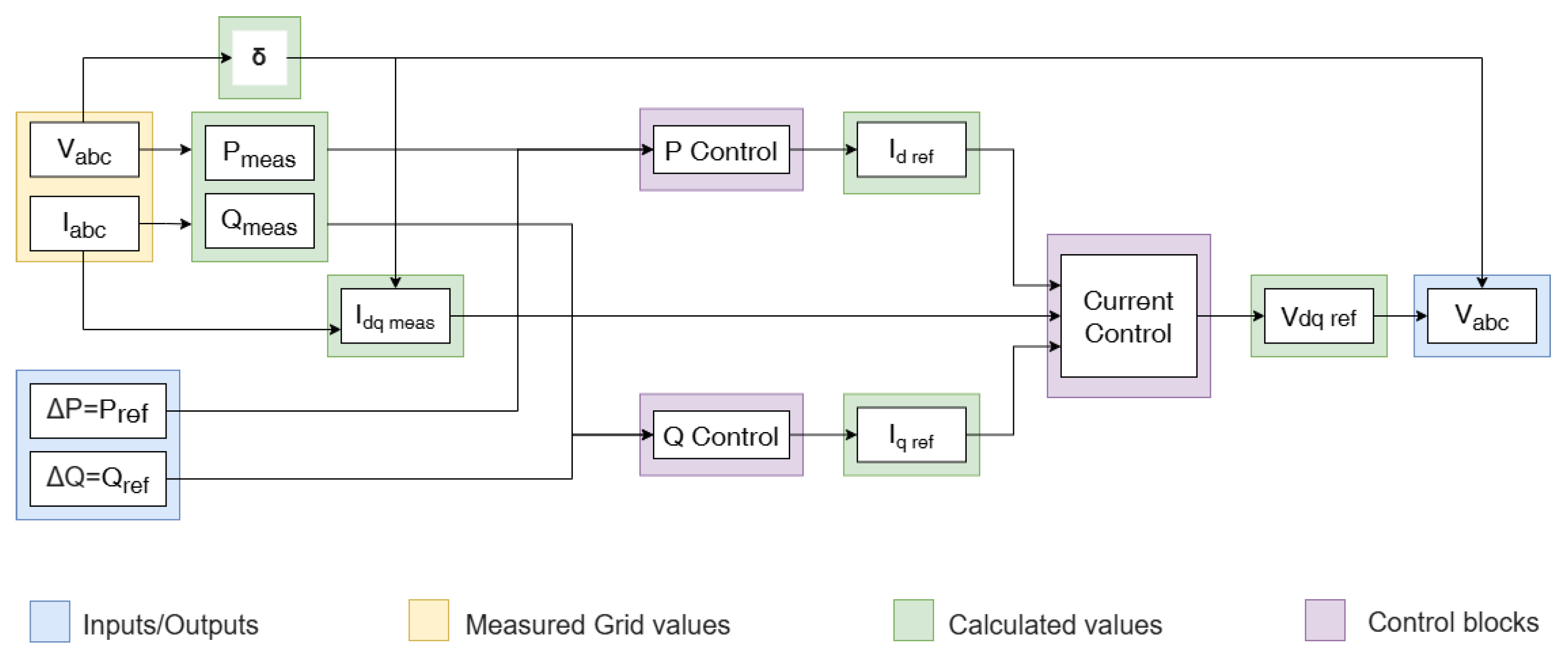
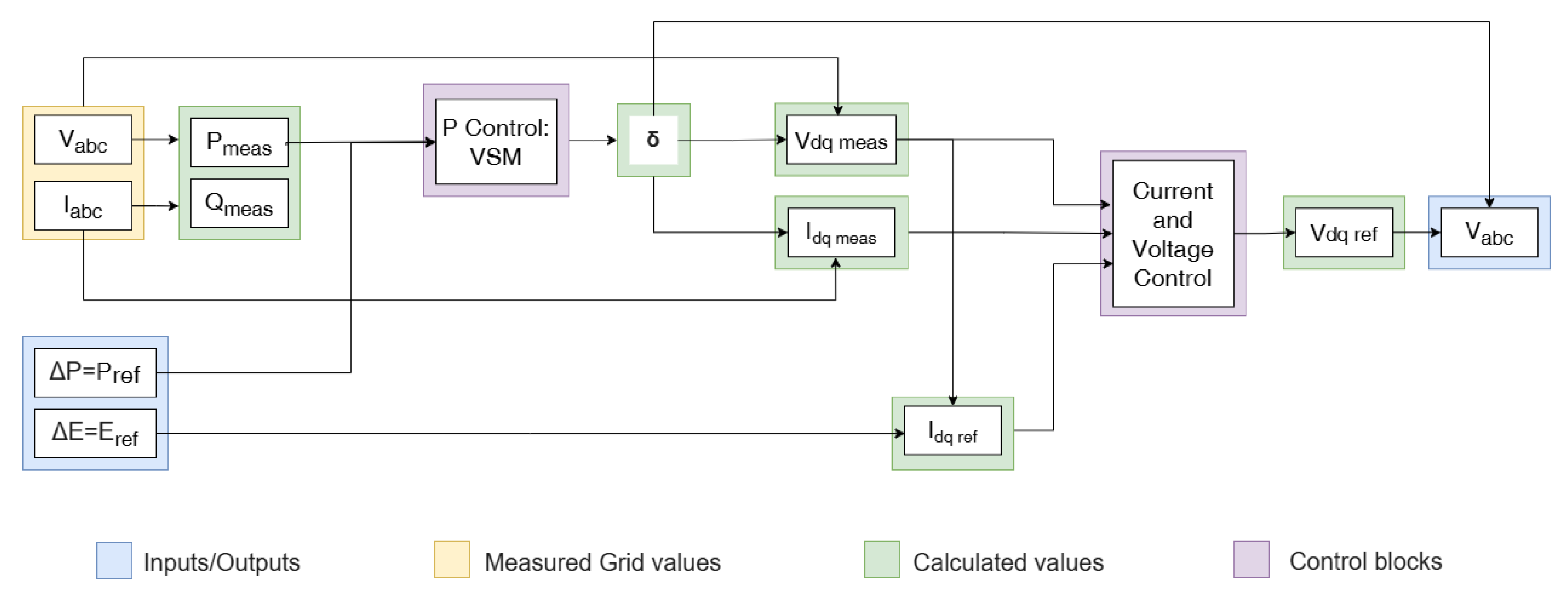
4.2.1. Islanded Operation

For the islanding operation, four different scenarios were tested in order to identify regions with acceptable operation conditions for the load voltage and the MG frequency. In this case, the external grid was completely deactivated and therefore the GFM inverter was set as the slack or swing bus, in order to be able to perform the load flow. This also implies that the GFM inverter is capable of adapting its active and reactive power output in order to meet the system conditions. The active power reference of the GFL inverter was tested with values of 0.25 pu, 0.5 pu, 0.75 pu, and 1 pu, implying different availability of the source connected.

The simulation on islanded operation was executed for 10 s with no event happening, in order to evaluate if the given conditions represented an acceptable operating point. For every given set point of the GFL inverter, simulations were executed changing the GFM amount $\alpha$ from 1% to 99% and the load active power set point from 0.1 pu to 1pu in steps of 0.1 pu.

Table 5. Values applied for the islanded operation simulation.

Variable	Values	Steps
GFM inertia $H_{GFM}$ [s]	5	-
GFM amount $\alpha$ [%]	1–99	1
GFM Active Power Reference $P_{GFMref}$ [pu]	According to Load Flow results	-
GFL Active Power Reference $P_{GFLref}$ [pu]	0.25–1.00	0.25
Load Active Power Reference $P_{Loadref}$ [pu]	0.10–1.00	0.10

summarizes the information used for the simulations.

The variables recorded were voltage and frequency. The last value of these two variables for each simulation was compared to the long term operational voltage limits of $\pm 10\%$ and the frequency limits of 49.8 Hz and 50.2 Hz. Even if the behavior of the variables did not show an oscillatory or unstable behavior (which is not displayed), for the evaluation of each case it was considered that if the voltage or frequency falls outside of this limits, the operating point is considered unacceptable.

Figure 11, Figure 12, Figure 13 and Figure 14 show the results illustrated as heatmaps. The white areas show the points where the corresponding variable was outside of the defined acceptable limits, while the color region shows the points were the variable presented a value within the limits. The color indicates the precise value as labeled by the side bar. A detailed analysis of the results for each case will be further provided.

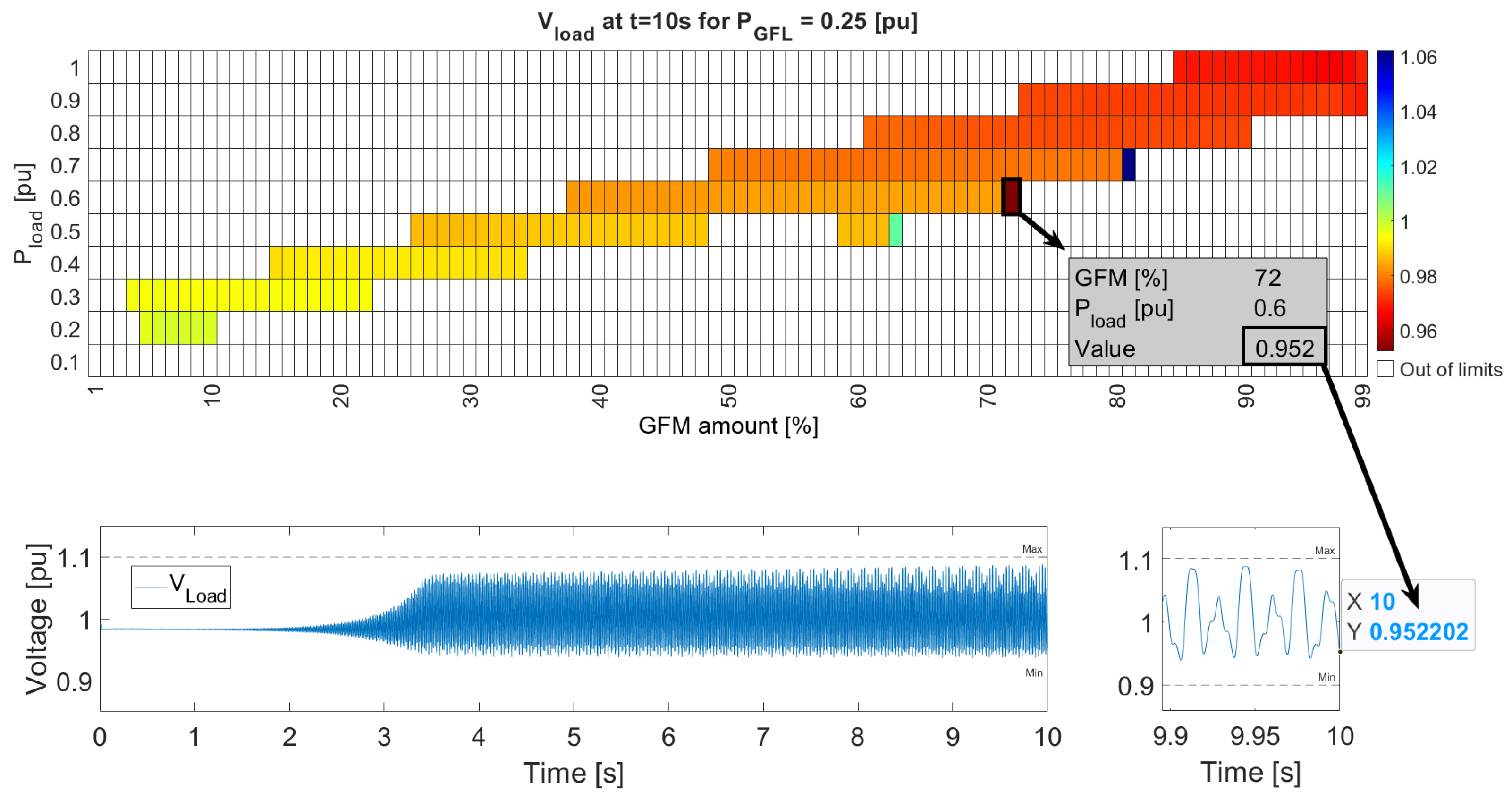
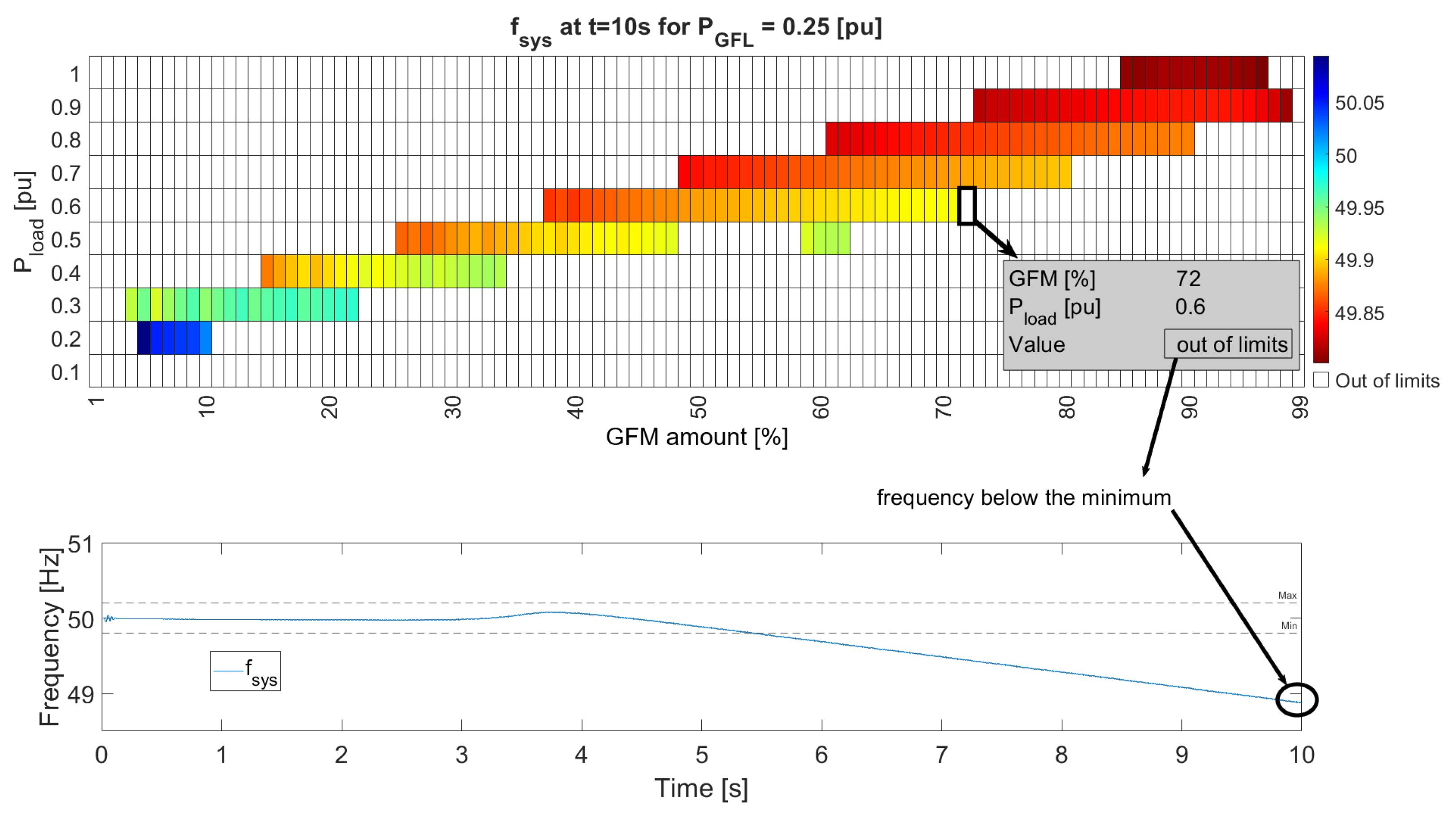
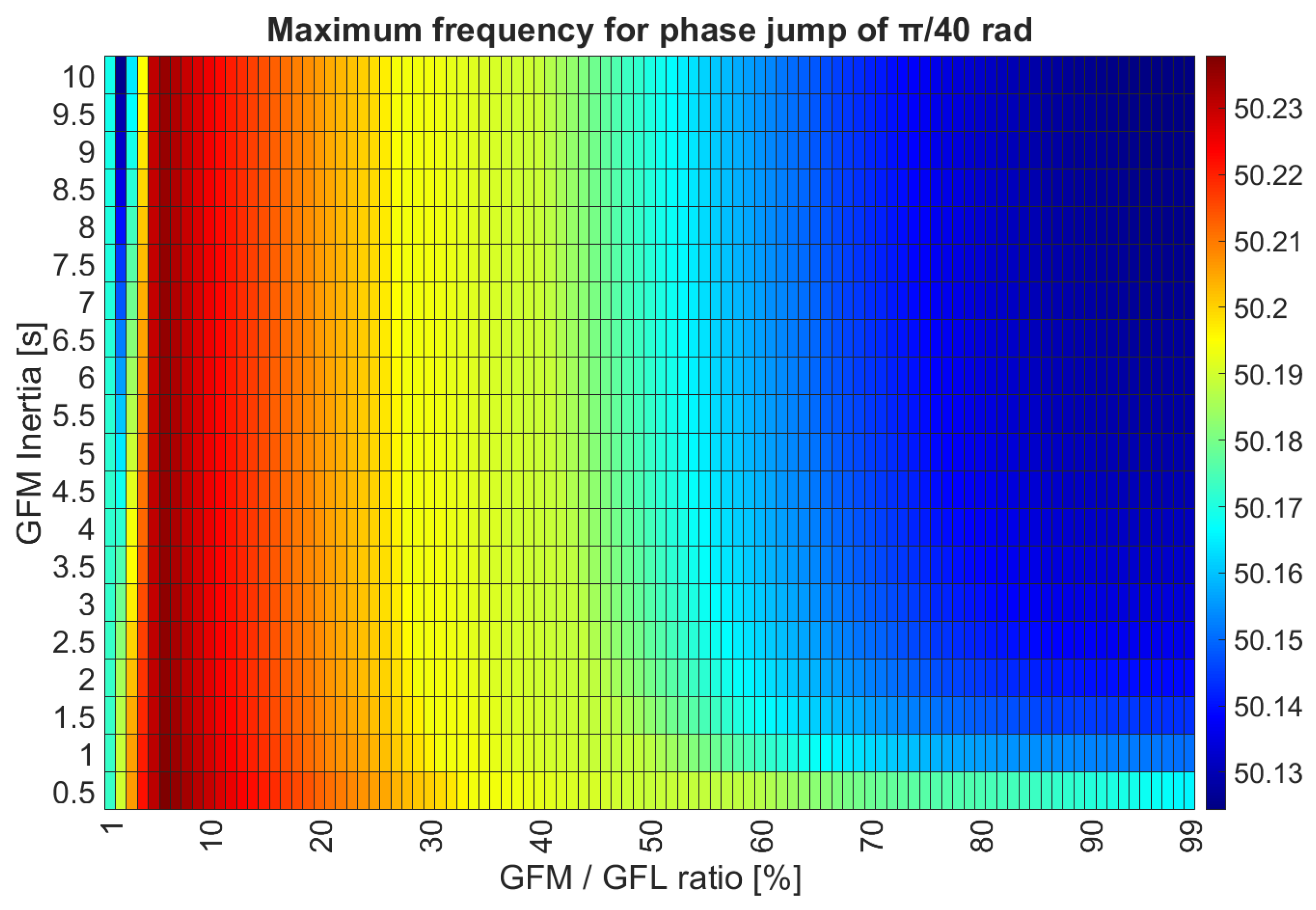
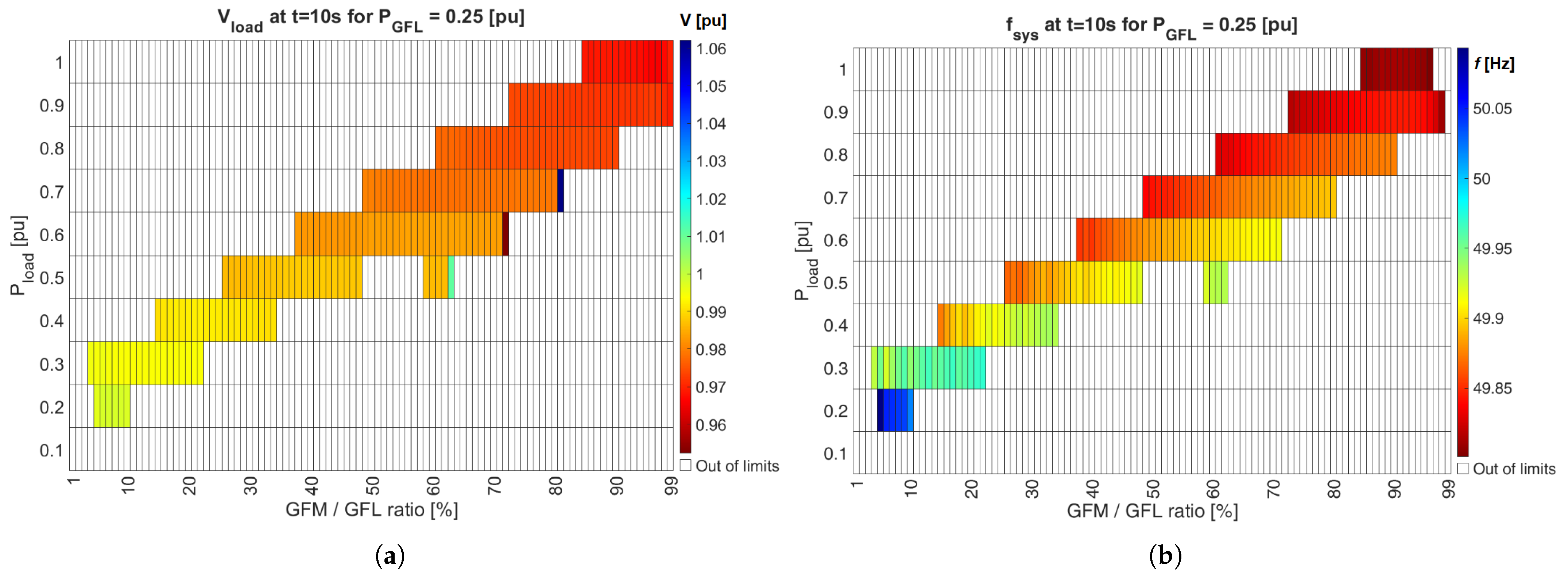
Case 1, $P_{GFL}=0.25$ pu: Figure 11 shows the voltages and frequencies obtained for the GFL inverter active power set point of 0.25 pu. It is clear the there is a linear tendency for the acceptable operating region. That means, the higher the load active power, the higher the requirement of GFM amount in the system in order to obtain a stale operating point, keeping the $P_{GFL}$ constant at 0.25 pu.

The acceptable points for the voltage were achieved for $P_{Load}$ reference points from 0.2 pu to 1 pu and for GFM amounts from 4% to 99%. The second tendency that can be observed is that the higher the load active power, the lower the final voltage value. In this sense, the best operating point (closest to the 1.00 pu) was located at $P_{Load}=0.2$ pu and $\alpha$ from 5% to 10%, which is a relatively small operating range.

With respect to the frequency, an overall similar region was observed, with the same linear tendency. The acceptable points for the frequency were achieved for $P_{Load}$ reference points from 0.2 pu to 1 pu as well but from 4% to 98% with respect to the GFM amount. The second tendency that can be observed is that the higher the load active power, the lower the final frequency value. However, the best operating point (blue region, closest to the 50 Hz) was located at the lowest $P_{Load}$ between 0.2 pu and 0.3 pu, with an $\alpha$ at around 10% to 20%.

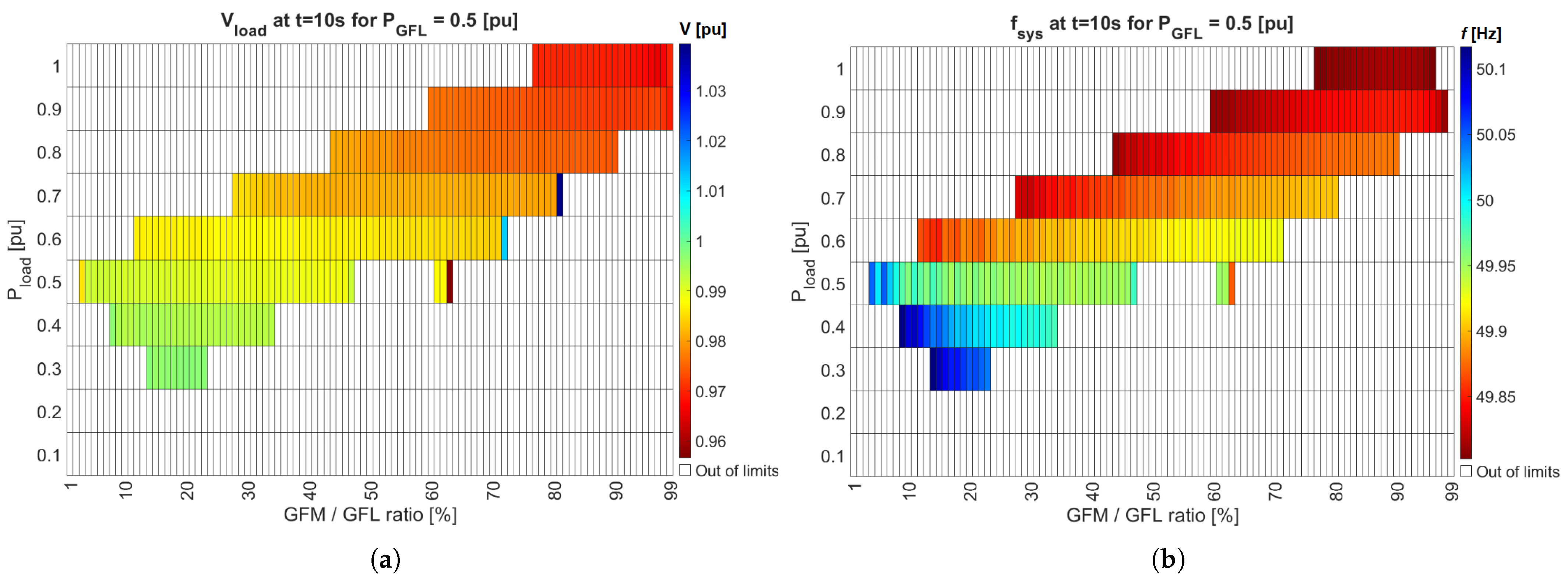
Case 2, $P_{GFL}=0.5$ pu: Figure 12 shows the voltages and frequencies obtained for the GFL inverter active power reference of 0.5 pu. In this case, the same linear tendency of the values for the acceptable operating region is observed. That means that, keeping the $P_{GFL}$ constant at 0.5 pu, the higher the load active power, the higher the requirement of the GFM amount in the system in order to obtain a stale operating point. However, in this case, the range of GFM amounts for which the operation is within the limits for each $P_{Load}$ operating point is wider. This means that stability can be reached with higher and lower GFM amounts at each load operating point.

It is worth noting, however, that the acceptable points for the voltage were achieved for $P_{Load}$ operating points from 0.3 pu to 1 pu, which is 10% more of the minimum load active power limit than the previous case. This implies that, for the given reference of GFL active power, the load must be at least 0.3 pu in order to be able to operate within the acceptable limits.

Also, for the lower load amounts in this case, higher amounts of GFM are needed, compared to the previous case. Acceptable values were reached for GFM amounts from 2% to 99% for the voltage. Similar to the previous case, the second tendency that can be observed is that the higher the load active power, the lower the final voltage value. In this sense, the best operating point (closest to the 1.00 pu) was located for $P_{Load}$ between 0.3 pu and 0.4 pu, with $\alpha$ from 14% to 23% and 8% to 34%, respectively, which is still a relatively small but larger operating range compared to the previous case.

With respect to the frequency, an overall similar region was observed. The acceptable points for the frequency were achieved for $P_{Load}$ operating points from 0.3 pu to 1 pu as well, and from 3% to 98% with respect to the GFM amount. Similar to the previous case, the second tendency that can be observed is that the higher the load active power, the lower the final frequency value. However, the best operating point (closest to the 50 Hz) was located for $P_{Load}$ at 0.4 pu and $\alpha$ from 17% to 34%, which is still a relatively small but larger operating range compared to the previous case.

Case 3, $P_{GFL}=0.75$ pu: Figure 13 shows the voltages and frequencies obtained for the GFL inverter active power reference of 0.75 pu. In this case, the linear tendency of the values for the acceptable operating region is still observed, but not as clear as in the previous two cases. In this case, the range of GFM amounts for which the operation is within the limits for each $P_{Load}$ operating point is wider and starts to take a “V” shape. This means that acceptable operating points can be reached with higher and lower GFM amounts at each load operating point, but for lower load operating points the acceptable ranges of $\alpha$ are smaller.

It is worth noting, however, that the acceptable points for the voltage were achieved for $P_{Load}$ operating points also from 0.3 pu to 1pu, which is similar to the previous case. Also, for the lower load amounts in this case, higher amounts of GFM are needed, compared to the previous case, and the acceptable range for 0.3 pu is much narrower. Acceptable values were reached for GFM amounts from 3% to 99% for the voltage. Similar to the previous case, the second tendency that can be observed is that the higher the load active power, the lower the final voltage value. In this sense, the best operating point (closest to the 1.00 pu) was located for $P_{Load}$ at 0.4 pu and $\alpha$ from 20% to 34%, which is still a relatively small and similar operating range compared to the previous case. It is important to mention that in general, the voltages resulted in a tendency to be lower than 1 pu.

With respect to the frequency, an overall similar region was observed. However, the acceptable points for the frequency were achieved for $P_{Load}$ operating points from 0.4 pu to 1pu and from 7% to 98% with respect to the GFM amount. Similar to the previous cases, the second tendency that can be observed is that the higher the load active power and the higher the GFM amount, the lower the final frequency value. However, the best operating point (green areas, closest to the 50 Hz) was located for $P_{Load}$ between 0.5 pu and 0.7 pu and for various ranges of $\alpha$ from around 12% to around 46%, depending on the $P_{Load}$ value. This is a relatively larger operating range compared to the previous cases.

Case 4, $P_{GFL}=1.00$ pu: Figure 14 shows the voltages and frequencies obtained for the GFL inverter active power set point of 0.75 pu. In this case, the linear tendency of the values for the acceptable operating region is even less clear than the previous cases, and instead the “V” shape is more predominant. In this case, the range of GFM amounts for which the operation is within the limits for each $P_{Load}$ operating point is larger. This means that stability can be reached with higher and lower GFM amounts at each load operating point.

It is worth noting that the acceptable points for the voltage were achieved for $P_{Load}$ operating points also from 0.4 pu to 1pu. Also, for the lower load amounts in this case, higher amounts of GFM are needed, compared to the previous cases, and the acceptable range for 0.4 pu is much narrower. Acceptable values were reached for GFM amounts from 6% to 99% for the voltage. Even though the tendency of the higher the load active power, the lower the final voltage value is still observed, the values in general remain much closer to the 1 pu, with a few exceptions at the limits, compared to the previous cases. In this sense, the best operating point (light blue region, closest to the 1.00 pu) was located for $P_{Load}$ between 0.4 pu and 0.6 pu and $\alpha$ from 20% to 45% depending on the $P_{Load}$ value, which is a relatively larger operating range compared to the previous cases. This exhibits the best voltage behavior so far from the four cases.

With respect to the frequency, an overall similar region was observed, presenting the same “V” shape. The acceptable points for the frequency were also achieved for $P_{Load}$ operating points from 0.4 pu to 1pu but from 10% to 98% with respect to the GFM amount. Similar to the previous cases, the second tendency that can be observed is that the higher the load active power and the higher the GFM amount, the lower the final frequency value. However, the best operating point (green areas, closest to the 50 Hz) was located for $P_{Load}$ between 0.5 pu and 0.9 and for a varied range of $\alpha$ from around 17% to around 50%, depending on the $P_{Load}$ value. This is a relatively larger operating range compared to the previous cases.

It is important to address the few cases at the edge of the color area in each plot which do not follow the tendency, but resulted in acceptable values. These were the result of an unstable case, for which by chance the last value falls into the acceptable range. However, they should not be considered part of the acceptable area. Two specific cases were simulated dynamically and are described in Appendix B.

4.2.2. Disconnection Process Survivability

As mentioned previously, the disconnection process was tested in order to determine if the MG would survive the disconnection or not, by analyzing the post-separation states achieved. Initially the MG is operating connected to the grid and at time $t_0=1$ s the circuit breaker at the PCC opens, and the simulation runs for a total of 10 s. The behavior after the disconnection was analyzed in order to determine if the conditions are permanently acceptable, temporarily acceptable subject to changes in the MG or unacceptable.

Four cases were simulated by using four different combinations of reference values for GFM amount $\alpha$, active power reference of the GFM, GFL inverters and the load, which are shown in

Table 6. Reference values for the four disconnection cases.

Variable	Case 1	Case 2	Case 3	Case 4
$\alpha$ [30%]	30	30	30	30
$P_{GFMref}$ [pu]	1	0.45	1	0.65
$P_{GFLref}$ [pu]	0.5	0.5	0.5	0.5
$P_{Loadref}$ [pu]	0.75	0.5	0.5	0.75

. At every simulation, the case without disconnection was first simulated, then the islanded case in order to establish the required conditions for acceptable operation before and after separating. Then, the disconnection was tested in order to identify if the system is able to reach acceptable operating conditions.

It is worth noting that, for the grid-connected case, the external grid was set as the slack bus, while for the islanded mode the GFM inverter was set as the slack bus. During the disconnection process, the slack cannot be dynamically changed, so initially the slack is the external grid and after, the MG loses its slack or swing bus. For this reason, the post-disconnection states may vary from the islanded ones since mathematically the simulation has a different reference.

The simulation results and a description for each case are provided next. At each plot, the blue line displays the behavior without disconnection (grid connected), the red line the behavior starting at islanded operation, and in yellow the behavior with the disconnection happening at $t_0=1$ s.

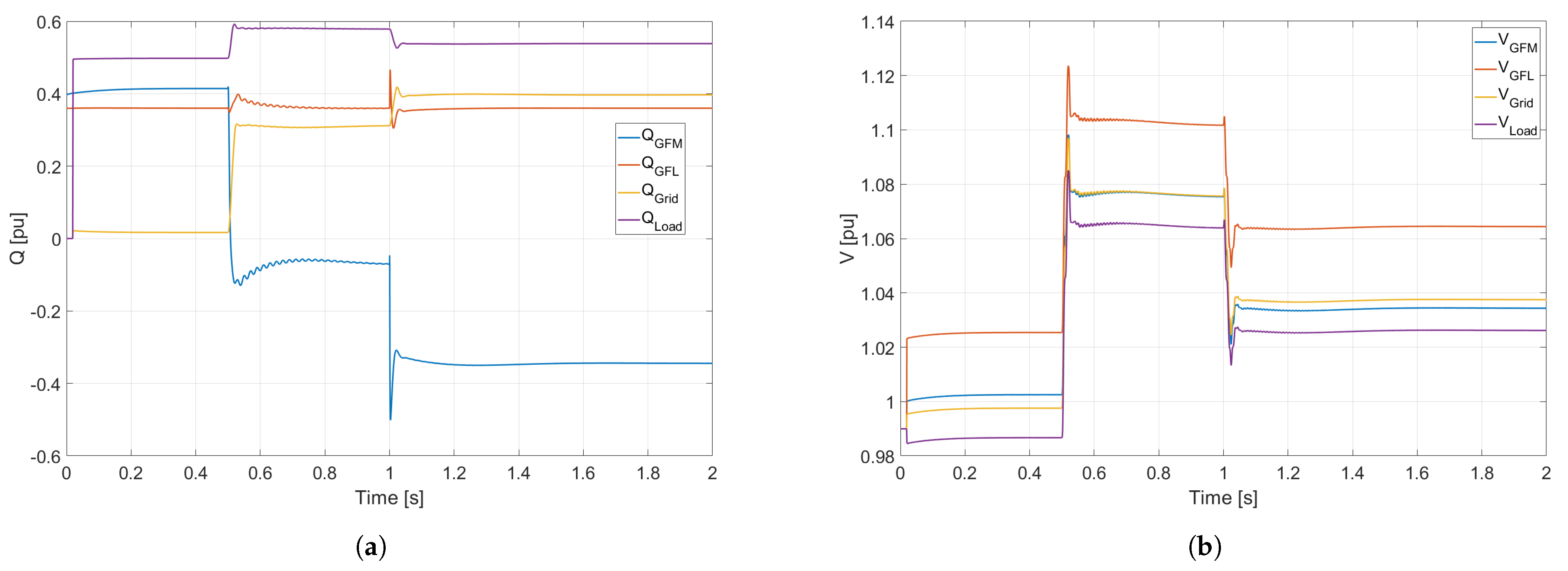
Case 1: Figure 15 shows the results for active and reactive power of both GFM and GFL inverters for Case 1. As it can be seen, this case is acceptable since all the variables were able to fully jump from the grid-connected condition to the islanded stable condition after the disconnection. In this case, only the GFM inverter reactive power presented a substantial change, reaching the new reference point after a transient period of about 1 s. The GFL inverter did not experience any change in the reference, meaning that the survivability depends completely on the ability of the GFM inverter to adapt its reference points.

Figure 16 displays the system frequency and load voltage for the Case 1. They confirm the survivability after the disconnection since both variables remain inside the acceptable operation limits.

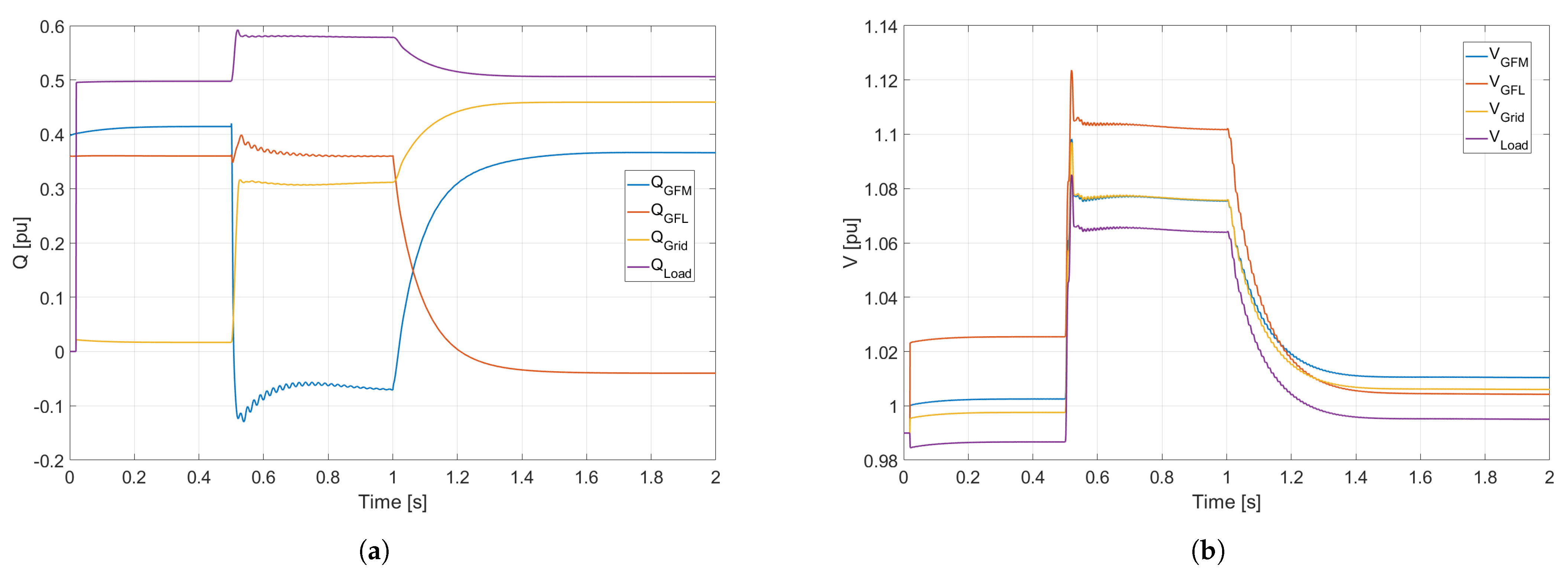
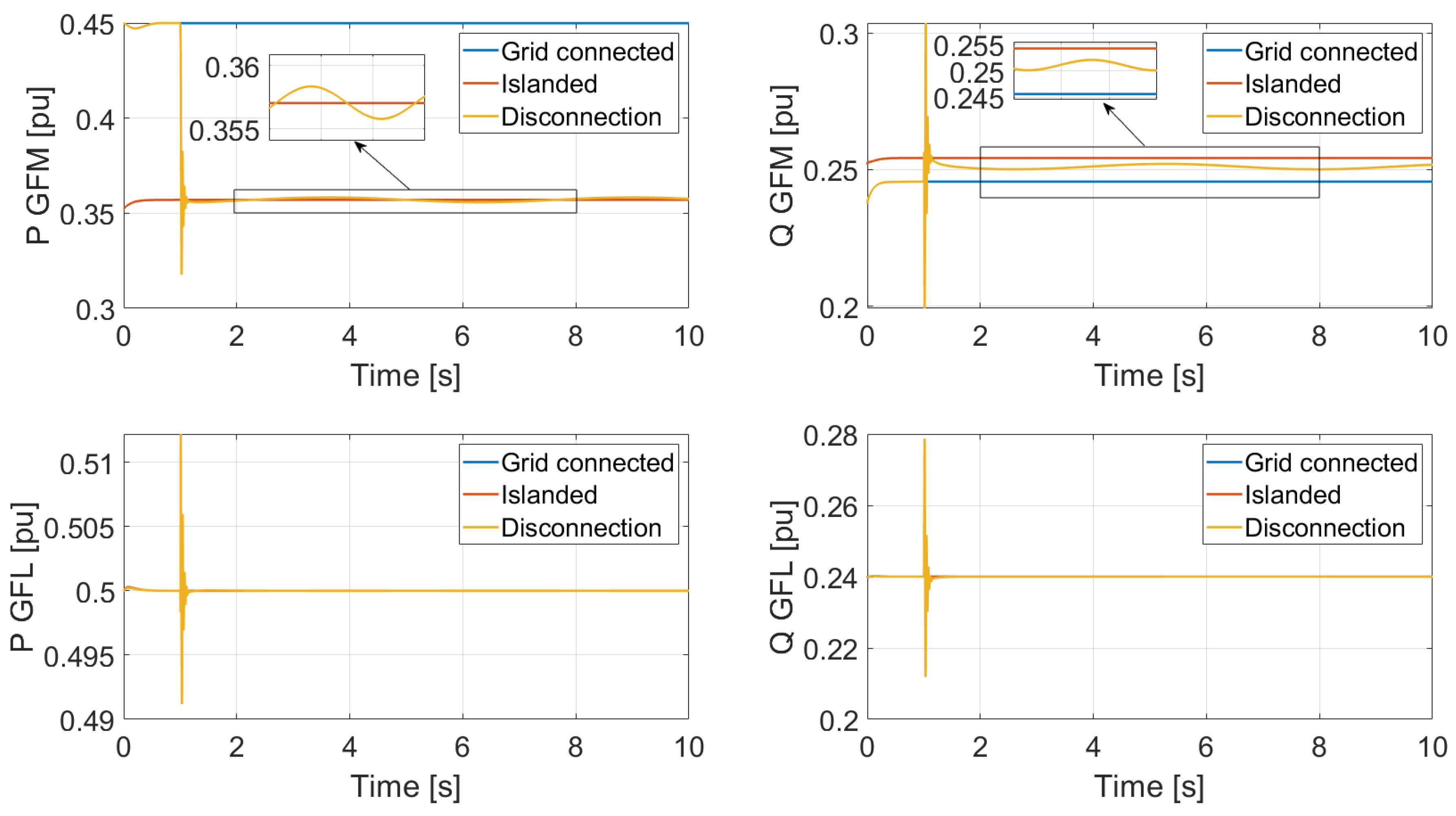
Case 2: Figure 17 shows the results for active and reactive power of GFM and GFL inverters for Case 2. As it can be seen, this case is also acceptable since the active power was able to fully jump from the grid-connected condition to the islanded stable condition after the disconnection. In this case, the GFM inverter both active and reactive power experienced a change. The active power jumped from 0.45 pu to 0.35 pu while the reactive power in this case experienced a much smaller jump from 0.245 to around 0.25 pu. In any case, the new reference point was reached after a very short transient period. However, both active and reactive power of the GFM present oscillations after the disconnection which need to be addressed in a short period of time to avoid resonances.

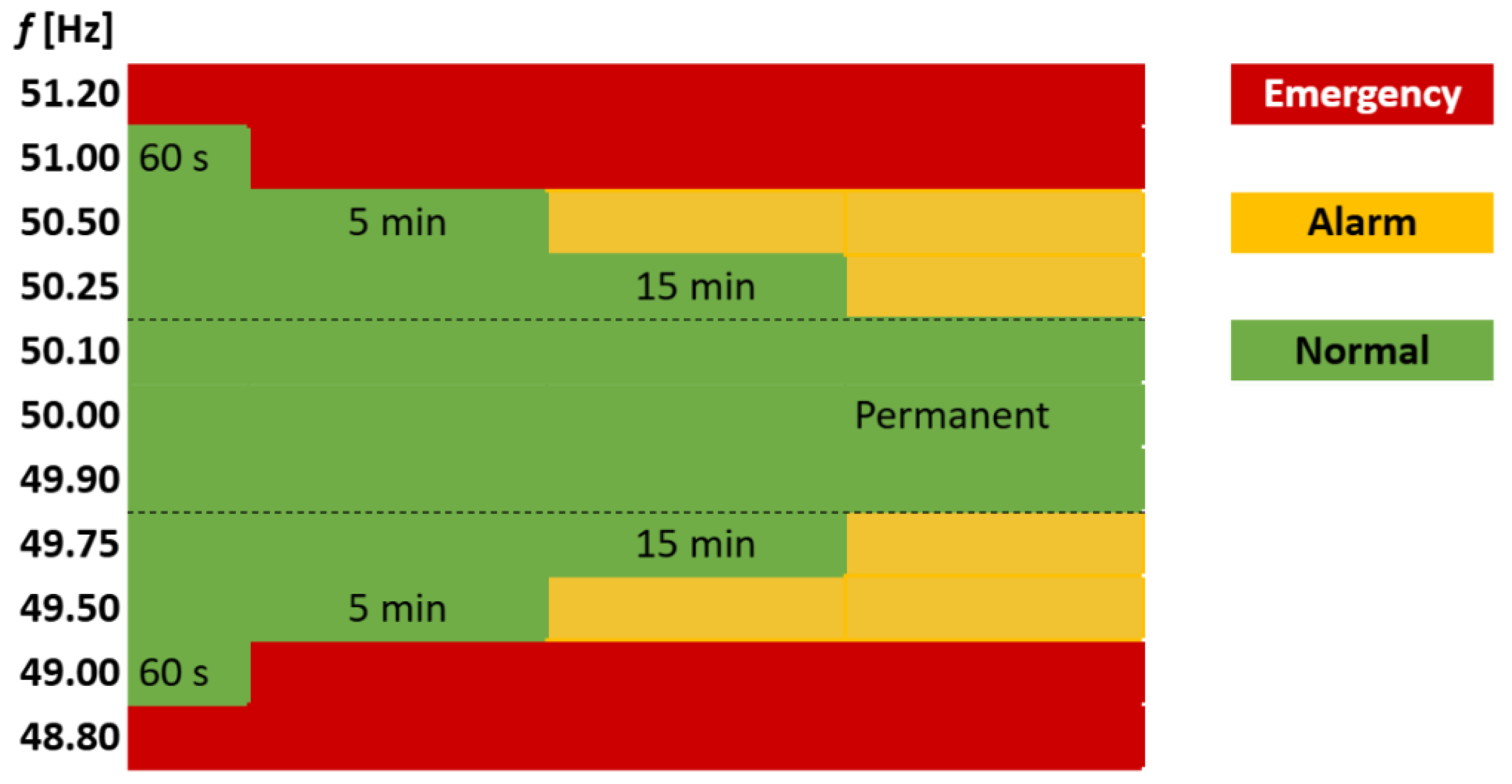
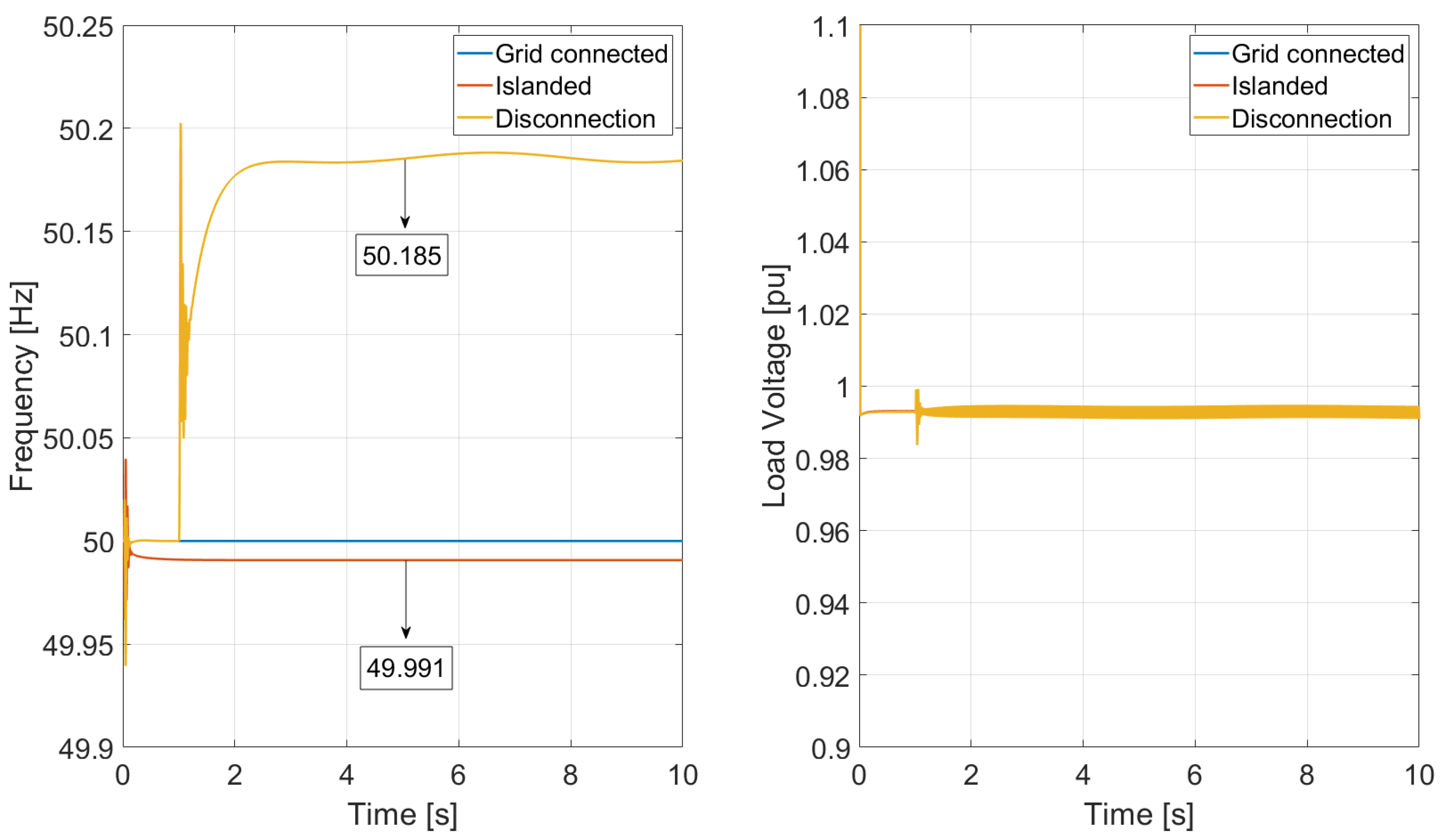
Figure 18 displays the system frequency and load voltage for the Case 2. They confirm the survivability after the disconnection, since both variables remain inside the acceptable operation limits. However, this value of frequency (50.185 Hz) is acceptable for a period of 15 min before reaching an alarm state as shown in Figure 1. This means that the MG has 15 min after the disconnection to take action in order to reach the permanently acceptable operating point. These actions could be generation curtailment or a change in the GFM inverter reference point in order to balance the over-frequency state. The voltage presents some oscillations caused by the GFM inverter reactive power observed in Figure 17, which also need to be addressed soon after the disconnection.

Case 3: Figure 19 shows the results for the active and reactive power of GFM and GFL inverters for Case 3. This case is not acceptable since the GFM inverter active power was not completely able to jump from the grid-connected condition to the islanded stable condition after the disconnection. The reference value for the GFM active power in islanded operation for this case is 0.357 pu, but the power was able to fall only to around 0.385 pu and with some oscillations. The reactive power was able to jump to the reference value, but it shows some oscillations as well.

The unbalance of around 3% in active power caused the frequency to reach an unacceptable value. Despite exhibiting stable behavior, in real-life applications the frequency shown in Figure 20 is not acceptable. According to Figure 1, the frequency reached after disconnection would make the system go into emergency state, leaving almost no time for action to be taken. Similarly, the voltage presents high-frequency oscillations with a magnitude of around 2% as shown also in Figure 20. Despite remaining inside the acceptable limits, these oscillations are not acceptable and may result in resonances.

Case 3 was made acceptable by adjusting the reference active power of the GFM inverter to 0.5 pu and the GFM amount $\alpha$ to 45%. The results are shown in Figure 21. It can be seen that a relatively small difference reached in the GFM inverter active and reactive power results in the frequency reaching a value which is inside the acceptable range (50.189 Hz) and the voltage to have a much less oscillatory behavior.

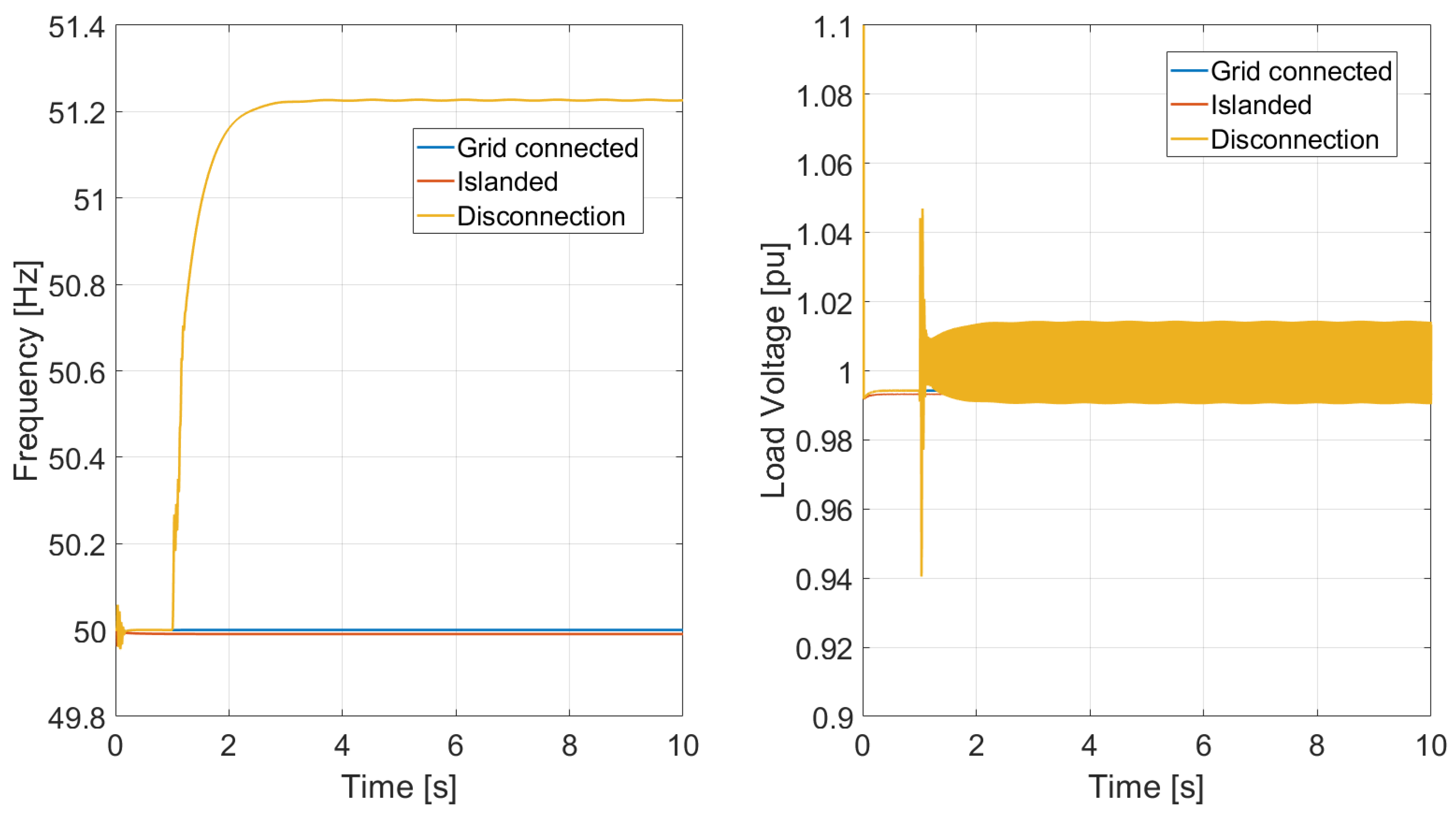
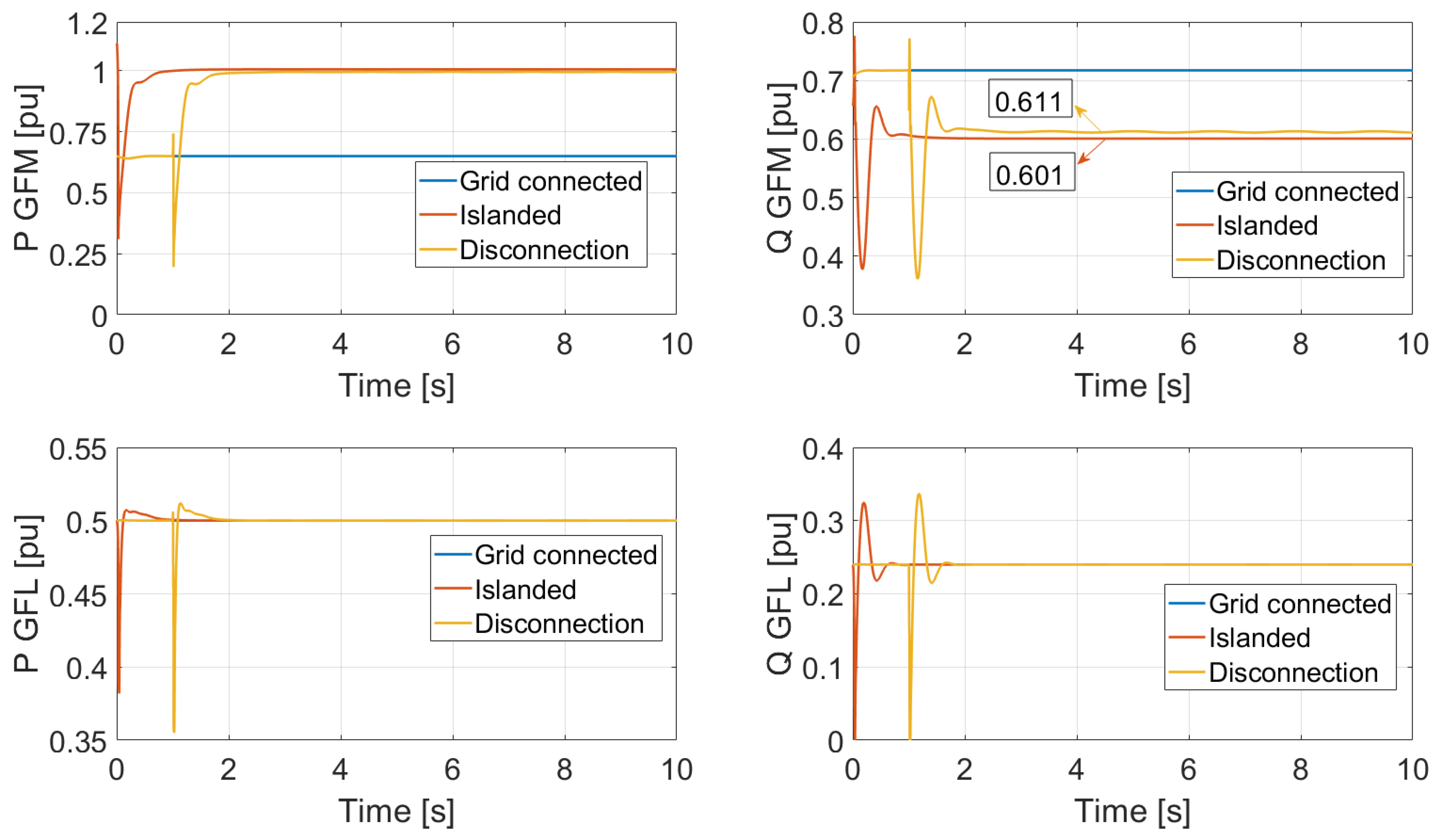
Case 4: Figure 22 shows the results for the active and reactive power of GFM and GFL inverters for Case 4. This case was also not acceptable since the GFM inverter reactive power was not completely able to fully jump from the grid-connected condition to the islanded stable condition after the disconnection. The reference value for the GFM reactive power in islanded operation for this case is 0.601 pu but the power was able to fall only to around 0.611 pu and with some oscillations.

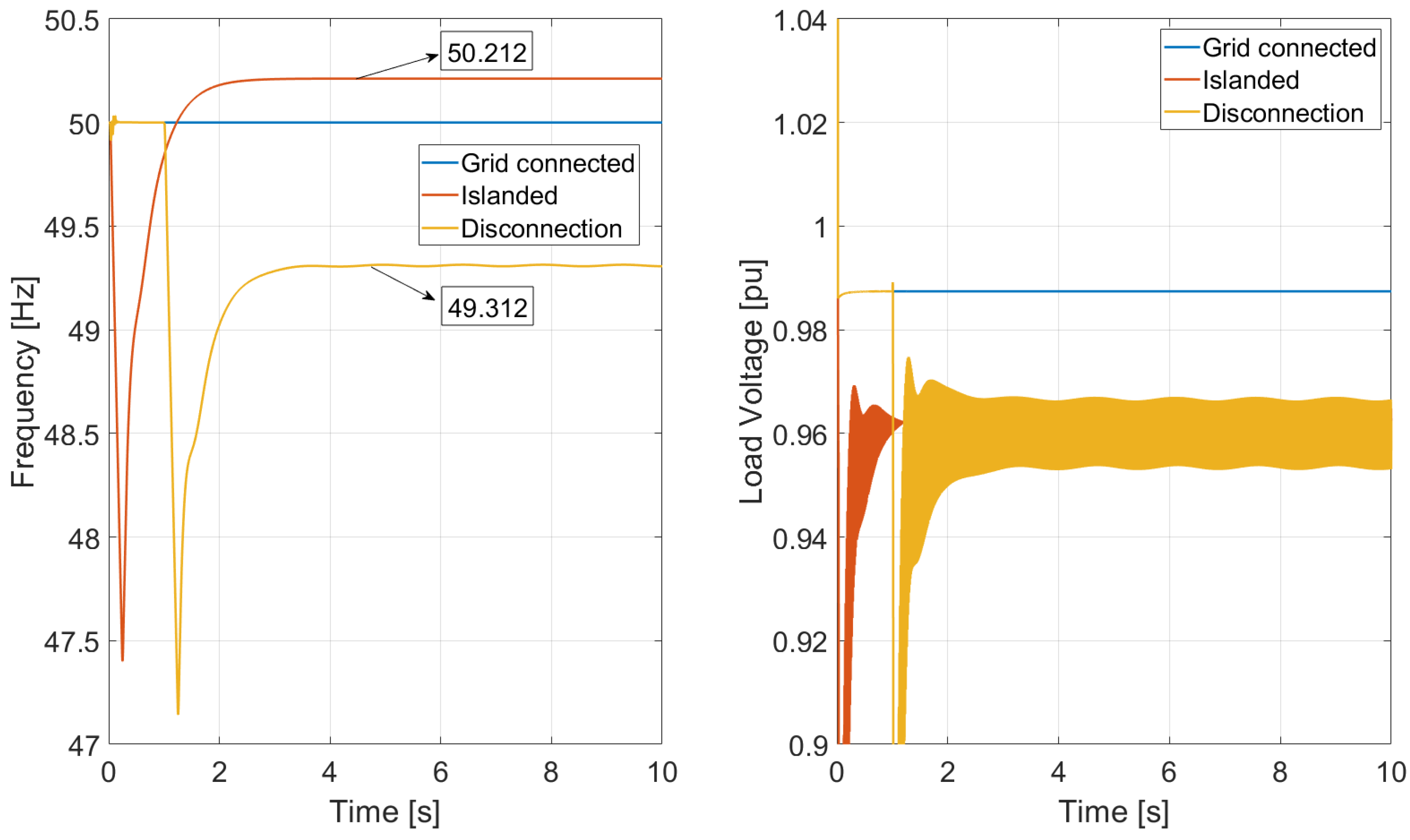
The unbalance of around 1% in reactive power caused the voltage to present high-frequency oscillations with a magnitude of around 2% as shown also in Figure 20. Despite remaining inside the acceptable limits, these oscillations are not acceptable and may result in resonances. The frequency also exhibits an unacceptable value. Despite having stable behavior, in real-life applications, the frequency shown in Figure 23 of 49.312 Hz is not acceptable for long-term operation. According to Figure 1, the frequency reached after disconnection would make the system go into emergency state after 60 s, leaving almost no time for action to be taken.

Case 4 was made acceptable by adjusting the GFM amount $\alpha$ to 75%. The results are shown in Figure 24. It can be seen that a significant difference reached in the GFM inverter active and reactive power results in the frequency and voltage reaching values inside the acceptable ranges (49.805 Hz and 1 pu, respectively) and damping the voltage oscillations, while still exhibiting a stable behavior.

5. Discussion and Conclusions

This work examined the integration of GFM inverters in MGs under both grid-connected and islanded conditions, with the aim of enhancing stability and resilience in systems with high penetration of IBRs. The analysis focused on the interaction between GFM and GFL inverters, considering their respective roles in frequency control, voltage support, and system survivability during disconnection.

Simulation results confirmed that long-term stability is generally guaranteed when GFMs provide around 30–40% of total capacity, combined with inertia constants above 2 s. Excessively low or high GFM shares were shown to degrade performance, while GFL inverters remain important for effective reactive power and voltage support.

Under islanded operation, maintaining acceptable voltage and frequency ranges requires sufficient and controllable local generation, with optimal operation found near nominal GFL reference values. Successful transitions to islanded mode depend largely on the ability of GFMs to adapt operating points, supported by adaptive protections and demand-side flexibility.

Overall, the findings align with recent regulatory and technical discussions in Europe, showing that GFMs are a key enabler of resilient, converter-dominated grids. Their deployment, combined with flexible loads, storage and coordinated standards, can support secure operation of decentralized power systems. Future work should focus on large-scale pilot projects, the refinement of GFM control tuning strategies, adaptive islanding control, and the development of interoperable communication frameworks to fully integrate MGs as active components of the energy transition.