Dynamic Average-Value Modeling and Stability of Shipboard PV–Battery Converters with Curve-Scanning Global MPPT

Abstract

Maritime power systems must reduce fuel use and emissions while improving resilience. We study a shipboard PV–battery subsystem interfaced with a DC–DC converter running maximum power point tracking (MPPT) and curve-scanning GMPPT to manage partial shading. Dynamic average-value models capture irradiance steps and show GMPPT sustains operation near the global MPP without local peak trapping. We compare converter options—conventional single-port stages, high-gain bidirectional dual-PWM converters, and three-level three-port topologies—provide sizing rules for passives, and note soft-switching in order to limit loss. A Fourier framework links the switching ripple to power quality metrics: as irradiance falls, the current THD rises while the PCC voltage distortion remains constant on a stiff bus. We make the loss relation explicit via $I_{rms}^{2}R$ scaling with THDi and propose a simple reactive power policy, assigning VAR ranges to active power bins. For AC-coupled cases, a hybrid EMT plus transient stability workflow estimates ride-through margins and critical clearing times, providing a practical path from modeling to monitoring.

1. Introduction

Maritime operators face simultaneous pressure to reduce fuel consumption, cut emissions, and increase electrical resilience aboard vessels. Photovoltaics (PV) paired with onboard energy storage are an attractive complement to conventional diesel generator sets because solar availability and wind-driven propulsion/auxiliary generation are often counter-cyclical over a day, allowing more consistent renewable supply. The original study already framed this opportunity in the shipboard context and motivated a PV–DC–DC battery subsystem that can harvest maximum available power while keeping diesel generation as a complementary source.

At the heart of shipboard PV integration is the fact that irradiance varies with clouds, motion, and shading from masts and superstructures; as a result, the PV array’s power–voltage curve changes continuously and the maximum power point (MPP) drifts throughout the day. Practical systems, therefore, require maximum power point tracking (MPPT) and a DC–DC interface stage to regulate the PV operating point and manage energy exchange with the battery and DC bus. Standard PV system blocks and MPPT fundamentals justify this architecture, while global MPPT (GMPPT) methods are necessary under partial shading when the P–V curve exhibits multiple local maxima. Curve-scanning GMPPT provides a simple, implementable strategy to locate the global peak across the full operating window, and recent surveys position it among other global methods (metaheuristics, ripple correlation, and incremental conductance variants) for dynamic conditions [1,2,3].

The choice of power conversion topology depends on required voltage ratios, bidirectionality, and port count. In addition to the single-port buck/boost stages commonly used with PV strings, high-gain bidirectional converters with dual-PWM control and three-level three-port converters offer compact energy routing between the PV, battery, and load, while resonant/soft-switching add-ons can raise efficiency at high switching frequencies. These options are directly relevant to shipboard layouts that must minimize weight and volume without sacrificing transient performance [4,5,6].

Converter-induced harmonics and power quality (PQ) behavior also matter at sea and at the point of common coupling in port. Under low irradiance, PV current total harmonic distortion (THDi) tends to increase, even when bus voltage distortion remains nearly constant for a fixed topology, which informs the filter design, control bandwidth, and compliance checks against common PQ limits. When PV is connected to distribution feeders (e.g., hybrid shore connection or microgrid), VAR control and dispatch scheduling influence feeder losses and voltages. Analytical and data-driven methods exist to quantify transformer, line, and cable losses and to optimize reactive power over operating scenarios [7,8,9].

Because shipboard power systems increasingly blend fast power electronic interfaces with slower electromechanical dynamics, credible assessment benefits from modeling approaches that capture converter behavior without prohibitive switching-level simulation cost. Dynamic average (average-value) models provide tractable large-signal representations of DC/DC and DC/AC stages for system-level studies, while hybrid electromagnetic transient (EMT) and transient stability frameworks can evaluate ride-through and faulted operation; high-order Taylor expansion methods further clarify conservatism in stability margins. These tools guide the sizing of passive components, setpoints, and controller gains before hardware testing [10,11,12].

This study contributes a shipboard-specific, reproducible pipeline that links global MPPT (curve-scanning) and converter design choices to power quality and system-level outcomes. (i) We establish an AVM→PWM two-stage workflow (with full parameter disclosure and windows) that captures irradiance steps and then resolves steady-state harmonics for compliance checks. (ii) We quantify the functional link irradiance → current THDi → loss multipliers, showing that while THDi rises at low irradiance, it remains bound by L/fs sizing and can be mitigated by a minimal, scenario-based P-binned VAR policy on a 0.4-kV feeder, yielding measurable loss/voltage improvements. (iii) For AC-coupled operation, we provide a practical hybrid EMT + transient stability screen that estimates the ride-through margins/CCT consistent with the control and PQ findings. Our primary new finding is this quantitative bridge—from GMPPT decisions to harmonic behavior and distribution-side efficiency/voltage control, in the marine context—which unifies elements typically treated in isolation, and offers actionable design and verification guidance [3,4,5,6,7,8,11,13].

2. Photovoltaic Generator Characteristics and Maximum Power Point Control

Photovoltaic (PV) modules are nonlinear sources whose operating point is set by the intersection of the array’s I–V characteristic and the load imposed by the downstream converter–storage system. A single-diode equivalent captures this behavior well and leads to the familiar implicit I–V relation, as follows:

$$I= I_{PV}-I_0 \left(exp{\displaystyle \frac{V+I{R}_s}{n{V}_r}}-1\right)- {\displaystyle \frac{V+I{R}_s}{R_{sh}}},$$

(1)

with the usual meanings of I_pv (photocurrent), I₀ (diode reverse saturation current), R_s, R_sh, n, and V_T. This same form extends to series/parallel module groupings used in arrays [3].

2.1. Influence of Irradiance and Temperature

Typical PV module I–V curves under different operating conditions: $U_0$ and $I_{sc}$ are the open-circuit voltage and short-circuit current, while $P_1$–$P_3$ (Figure 1) mark the maximum-power points as irradiance decreases (or temperature rises).

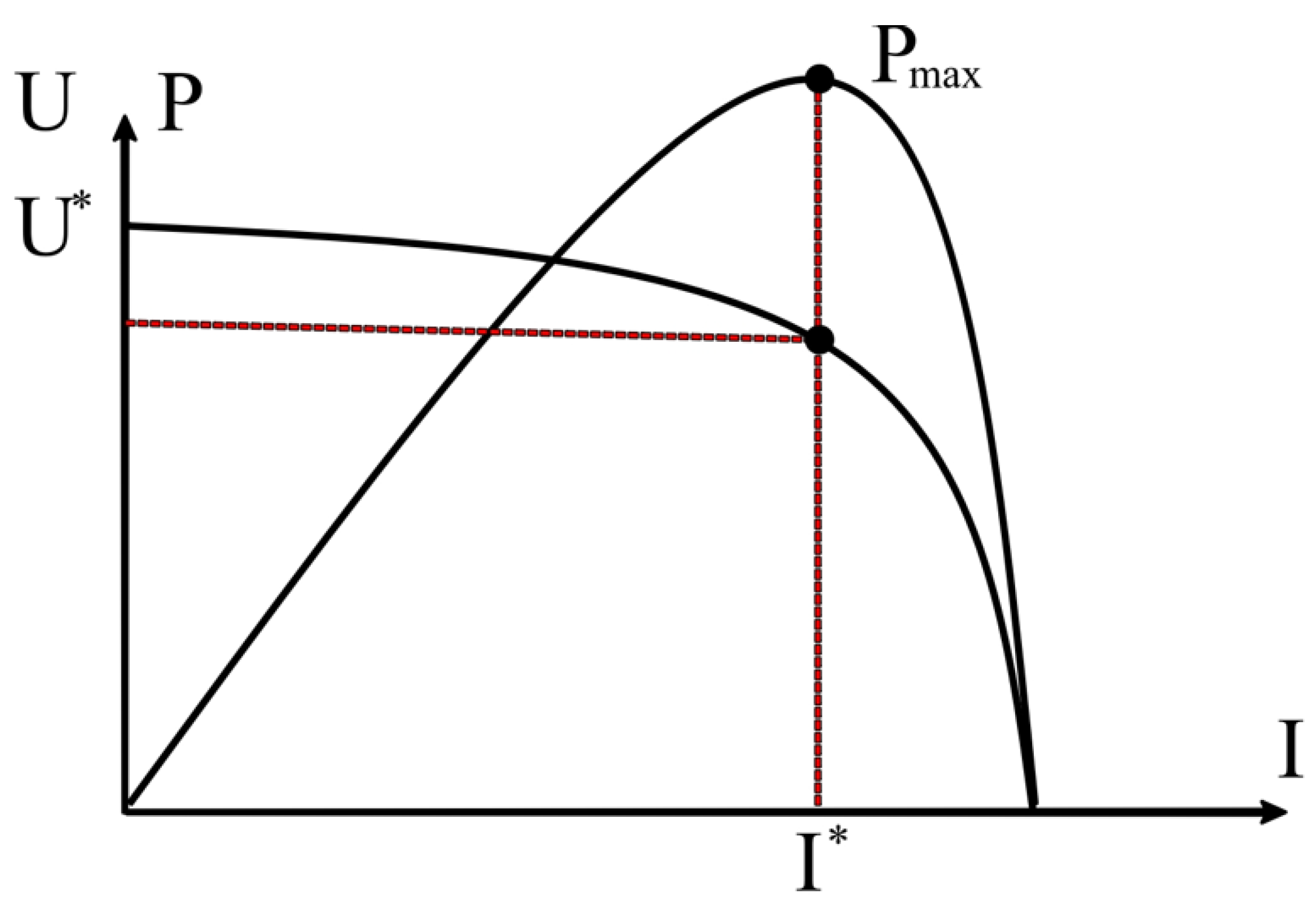
2.2. Power–Voltage Curve and the MPP

The corresponding P–V curve has a single interior extremum under uniform irradiance. At the maximum-power point (MPP),

$$P_{max}=U_{MPP}{I}_{MPP}, {\displaystyle \frac{dP}{dV}}=0$$

(2)

which is the formal condition most MPPT algorithms exploit [1]. Figure 2 overlays the I–V and P–V plots and marks the optimal operating coordinates (U*, I*) and P_max.

2.3. Role of the DC–DC Interface and MPPT

A DC–DC converter between the PV generator and the storage/load sets the array voltage and thus “chooses” the operating point on the I–V curve. In practice, this stage hosts the maximum power point tracking (MPPT) logic that perturbs or regulates the array voltage/current to satisfy $dP/dV=0$ [1]. Conceptually, MPPT belongs in the conversion block (DC–DC); many converter topologies are suitable (buck/boost/SEPIC, etc.) and are selected per bus and storage constraints.

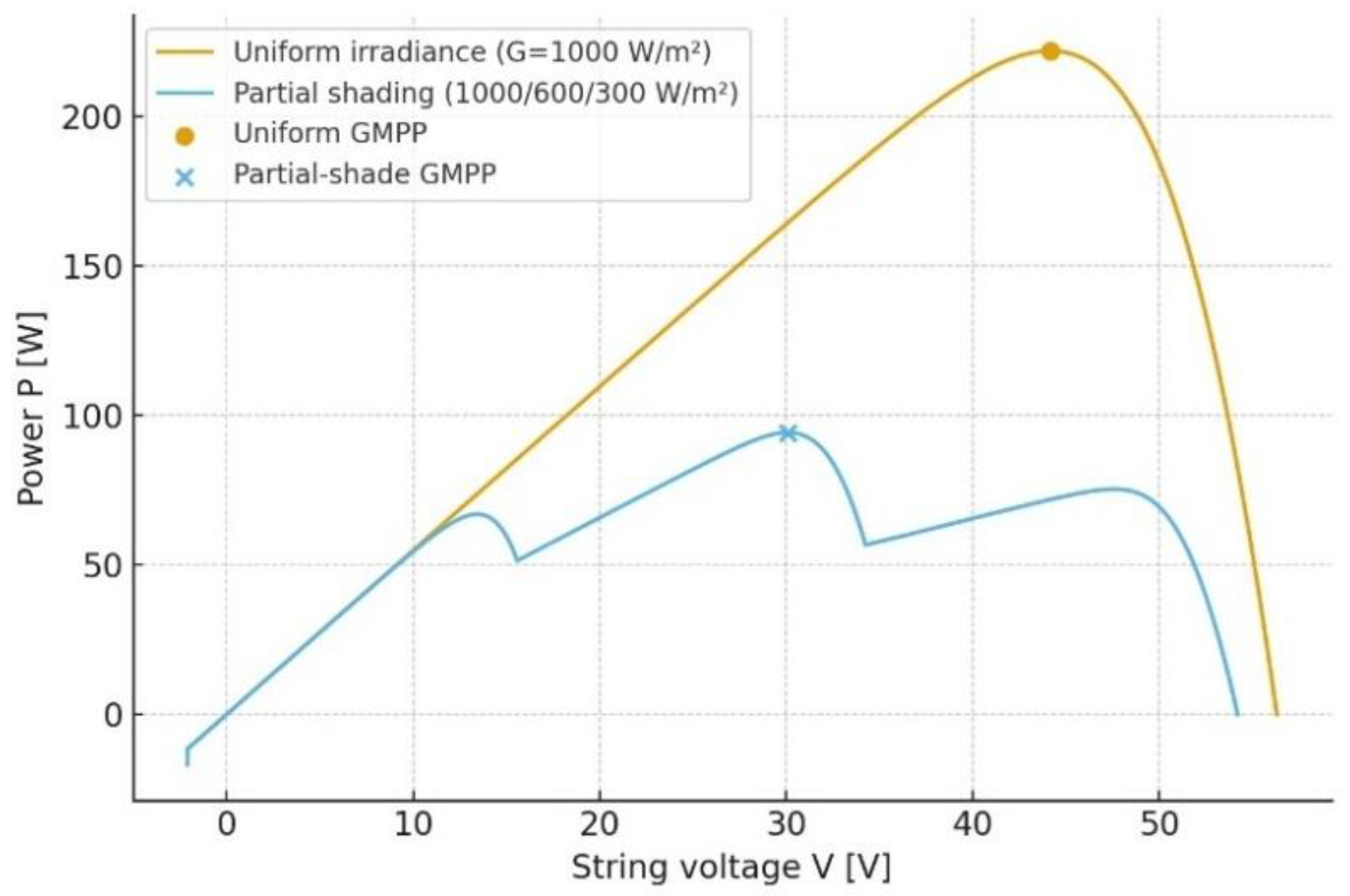
2.4. Partial Shading and Global MPP

Under partial shading, bypass diodes and uneven insolation create multiple local peaks in the P–V curve (Figure 3); conventional hill climbing (P&O/INC) can lock onto a local maximum (LMPP) instead of the global MPP (GMPP) [3]. This motivates global search or scanning strategies; the literature we cite later compares blind scans, reference-point scans, and ANN-assisted and metaheuristic approaches, noting trade-offs between scan energy loss and convergence reliability [2].

3. System Architecture and Modeling of the PV–DC–DC–BESS Subsystem

3.1. Architecture and Energy Flow

Figure 4 depicts the baseline topology. The PV feeds a controllable DC–DC converter that regulates the PV operating point on the I–V curve and enforces battery-side constraints. A DC link buffers the switching ripple and load transients, and the BESS absorbs or supplies energy according to the power balance and state-of-charge constraints. An inverter (dashed block) may be included where an AC bus or shore connection is required.

The nominal maximum power point (MPP) coordinates used throughout are as follows:

$$\left(U_1{I}_1\right)=\left(200 V, 3 A\right), \left(U_2{I}_2\right)=\left(160 V , 2.4 A\right),$$

with a battery bus U_BESS = 144 V. The corresponding charge currents follow directly from power balance, as shown:

$$I_{BESS1}= {\displaystyle \frac{U_1{I}_1}{U_{EA}}}=4.1667 A, I_{BESS2}= {\displaystyle \frac{U_2{I}_2}{U_{EA}}}=2.6667 A.$$

This operating envelope is consistent with the I–V/P–V characteristics in Section 2 (Figure 1 and Figure 2) and underpins the converter sizing and control objectives that follow.

3.2. DC–DC Interface: Role and Candidate Topologies

The DC–DC interface serves two roles: (i) it provides the degrees of freedom needed by the MPPT algorithm to place the PV at the MPP (or GMPP); and (ii) it conditions power transfer to the BESS and DC link with acceptable ripple and efficiency [10]. Several practical realizations are pertinent:

• Conventional single-port stages (buck/boost/SEPIC/Ćuk), selected according to required voltage ratio and bus polarity [4].
• Bidirectional high-gain converters with dual-PWM control, which offer expanded conversion ratios (e.g., quadratic step-down gain $M= V_0/V_{in}= D^2$ in one operating region) and tunable ripple characteristics, advantageous when PV voltage varies widely [4].
• Three-level, three-port bidirectional converters, enabling direct energy routing among PV, battery, and DC load/auxiliary ports with reduced device stress and smaller passive components [5].
• Soft-switching (resonant-assisted) variants for applications where switching loss dominates, providing ZVS/ZCS conditions over the intended load range [6].

Topology selection does not alter the control objective—regulation at the MPP/GMPP—yet it does influence inductor current ripple, device stress, and achievable transient response, which are reflected in the sizing relations below.

3.3. Modeling Approach for System-Level Studies

To analyze irradiance steps, charge/discharge events, and grid interactions without prohibitive computation, dynamic average-value models (AVMs) are employed for the DC–DC and DC/AC stages [10]. AVMs remove the switching frequency ripple while preserving port-level power balance and dominant dynamics, allowing for large timesteps and the efficient extraction of small-signal transfer functions for stability checks. When AC interconnection is present, EMT-aware assessments may be layered on top of the AVM framework to evaluate the ride-through and faulted operation; this hybrid approach maintains tractability while capturing converter-driven fast dynamics [10].

3.4. Averaged Modeling of the DC–DC Stage and DC Link

3.4.1. State-Space Averaged Equations

For a generic buck–boost-type stage (inductor L, switch duty d, switching period T_s, DC-link C), the duty-cycle averaged dynamics over T_s are as follows:

$${\displaystyle \frac{{di}_L}{dt}}= {\displaystyle \frac{1}{L}}\left[d\left(V_{pv}- r_L{i}_L\right)+\left(1-d\right)(-V_{ea}-r_L{i}_L)\right],$$

(3)

$${\displaystyle \frac{{dv}_C}{dt}}={\displaystyle \frac{1}{C}}\left[i_L-i_{load}\left(v_C\right)\right],$$

(4)

with algebraic power balance constraints in steady state. These average-value models (AVMs) remove switching ripple while preserving low-frequency behavior, and are recommended for system-level studies of power electronic subsystems.

3.4.2. Ripple and Harmonic Content

Switching ripple and low-order harmonics are quantified via the inductor current (or port current) waveform, using a Fourier series. Using electrical radians $x= \omega t$:

$$i\left(x\right)= {\displaystyle \frac{I_0}{2}}+ {\sum }_{n=1}^{\infty }[a_n\cos \left(nx\right)+ b_n\mathrm{s}\mathrm{i}\mathrm{n}(nx\left)\right],$$

(5)

with coefficients

$$I_0={\displaystyle \frac{1}{\pi }}{\int }_0^{2\pi }i\left(x\right)dx,$$

(6)

$$a_n={\displaystyle \frac{1}{\pi }}{\int }_0^{2\pi }i\left(x\right)\mathrm{c}\mathrm{o}\mathrm{s}(nx)dx,$$

(7)

$$b_n={\displaystyle \frac{1}{\pi }}{\int }_0^{2\pi }i\left(x\right)\mathrm{s}\mathrm{i}\mathrm{n}(nx)dx,$$

(8)

and harmonic RMS amplitudes

$$I_{\mathrm{n}}={\displaystyle \frac{\sqrt{a_n^2+b_n^2}}{\sqrt{2}}},$$

(9)

The total harmonic distortion (THD) of current is then

$${THD}_i={\displaystyle \frac{\sqrt{\sum _{n=2}^{\infty }{I}_n^2}}{I_1}},$$

(10)

These definitions are standard in harmonic analysis and are the basis used in PV power quality studies, which show that the THD increases as irradiance drops (lower operating current and fixed switching ripple) while the voltage THD at the PCC tends to stay nearly constant if the grid is stiff [6].

Compliance targets typically reference the IEEE-519 limits of current distortion at the PCC and voltage distortion on the grid [4].

With fixed $f_s$, the inductor ripple is $\Delta i_L \ge {\displaystyle \frac{\left(V_{on}- V_{off}\right)}{L}} {\displaystyle \frac{d(1-d)}{f_s}}$, choosing L and C sets {I_n}, and, hence, THD. Soft-switching stages (e.g., full-bridge + resonant) reduce high-frequency components and EMI for the same $f_s$.

Component values are selected considering allowable ripple in PV/BESS ports—a practice explicitly recommended when implementing scanning-based MPPT on a DC–DC interface [3].

Switching ripple is intentionally removed in the AVM; harmonic metrics are obtained by re-simulating steady operating points with a PWM-resolved model (Section 3.8).

3.4.3. Harmonic Extraction Used in This Study (E₁/E₂)

We compute harmonic content only to the extent required by the case study and the later compliance checks (Section 5 and Section 8). From the 40 ms steady windows defined in later section and sampled at 1000 kS/s, we numerically obtain the harmonic RMS values $I_n$ of the battery port current and report the current THD and TDD against the IEEE-519 base $I_L$ (here, $I_L=4.1667$). The per-order values (IHD) and TDD totals extracted with this procedure are those plotted and summarized in Section 8.2.

The design link used later is as follows. With $f_s=100 \mathrm{kHz}$ and $L=1.0 \mathrm{mH}$, the inductor ripple sets the harmonic floor of the switched model, and the effect of irradiance enters through the change in $I_1$ (E₁ vs. E₂), which explains the selective per-order exceedances at low irradiance while TDD remains $<5\%$ (mitigations in Section 5.6 and implications in Section 8.2 and Section 8.3).

3.5. Preliminary Sizing Rules

For a PWM converter operated at $f_s$ and $d$, the practical starting points are

$$L \gtrsim {\displaystyle \frac{d \left(1-d\right) V_{pv}}{ \Delta i_{L{f}_s.}}}, C \gtrsim {\displaystyle \frac{\Delta i_{L{f}_s.}}{ 8f_s\Delta v_{C.}}}$$

(11)

followed by verification with the average model, and refinement using the ripple/THD analysis above.

Equation (11) provides the starting values for L and C, for a single-inductor PWM stage in CCM with buck-type mapping $M\left(D\right)= V_0/V_{in} \approx D$. In this case, the inductor ripple extremum follows the familiar $D (1-D)$ shape, peaking near mid-duty, which is why $D (1-D)$ appears in (11). Final values are verified via AVM transients and are refined against the switched model ripple/THD windows. For boost, buck–boost, SEPIC/Ćuk, interleaved, multi-level, or dual-PWM high-gain stages, the ripple extremum vs. D and gain M(D) differ (e.g., a quadratic region with $M\left(D\right)= D^2$). To avoid misuse, we apply (11) only to the buck case shown in our figures and provide Section 3.7 with worst-case D guidance for common variants.

3.6. Reproducibility of Simulation Cases

Models and workflow: System-level transients are simulated with the dynamic average-value model (AVM) of the DC–DC stage, and switching harmonic effects are then quantified from steady windows using Fourier coefficients $\left\{a_n,b_n\right\}$ and RMS magnitudes $I_n=\sqrt{a_n^2+b_n^2}/\sqrt{2}$.

Operating points: The irradiance step is $E_1=1000 W/m^2\to E_2=800 W/m^2.$ The nominal MPPs $\left(U_1,I_1\right)=\left(200 V,3 A\right)$ and $\left(U_2,I_2\right)=\left(160 V,2.4 A\right)$ yield battery port targets $I_{BESS1}=4.1667 A$ and $I_{BESS2}=2.6667 A$ via power balance.

Fourier/THD windows: Harmonics are computed from 40 ms steady-state segments of $i_{BESS}\left(t\right)$, following Section 3.4.2 and reported as IHD/THD in Section 5.

Sizing linkage: Initial L, C values follow the PWM sizing rule in (11), and the verification uses AVM transients, with the ripple/THD refined from the switched model windows.

Table 1. Hardware and switched model parameters.

Item	Symbol	Value	Unit
Topology variant	-	Synchronous buck (PV → BESS), CCM	-
Switching frequency	fs	100	kHz
Inductor	L	1.00	mH
Inductor series resistance	$r_L$	150	mΩ
DC-link capacitor (film)	C	10	µF
Capacitor ESR	$r_C$	20	mΩ
PWM modulation	-	Center-aligned	-
Bus voltage	$U_{BESS}$	144	V
PV MPP (E1)	$\left(U_1,I_1\right)$	(200, 3)	V, A
PV MPP (E2)	$\left(U_2,I_2\right)$	(160, 2.4)	V, A
Solver step	-	0.10	µs
Recording rate	-	1000	kS/s

summarizes the hardware and switched-model setup: synchronous-buck (PV→BESS, CCM) with fs = 100 kHz, L = 1.00 mH (rL = 150 mΩ), C = 10 µF (rC = 20 mΩ), U_BESS = 144 V; PV MPPs (U1, I1) = (200 V, 3 A) and (U2, I2) = (160 V, 2.4 A); solver step 0.10 µs and recording at 1000 kS/s.

Table 2. Control and MPPT parameters.

Controller Block	Parameter	Value	Unit
BESS current loop	$K_p,K_i$	0.14, 877	s−1
Current limit	$I_{BESS}^{max}$	6.0	A
Bus voltage loop	$K_p,K_i$	0.02, 2.0	s−1
MPPT mode	-	Curve-scanning GMPPT	-
Scan period	Tscan	1.0	s
Dwell per test point	tdwell	5	ms

details the control and MPPT settings: BESS current-loop gains $(K_p,K_i)=(0.14, 877 {\mathrm{s}}^{-1})$ with $I_{BESS}^{\mathrm{m}\mathrm{a}\mathrm{x}}=6.0 \mathrm{A}$; bus-voltage loop $(0.02, 2.0 {\mathrm{s}}^{-1})$; and curve-scanning GMPPT $(T_{\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{n}}=1.0 \mathrm{s}, t_{\mathrm{d}\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}=5 \mathrm{m}\mathrm{s})$.

Table 3. Data windows for harmonic metrics.

Case	Operating Point	Window Start (s)	Window Length (ms)	Sample Rate (kS/s)
A	$E_1$ steady state	5.000	40	1000
B	$E_2$ steady state	49.000	40	1000

specifies the harmonic-analysis data windows: 40-ms steady-state segments at 1000 kS/s starting at 5.000 s (E₁) and 49.000 s (E₂).

3.7. Applicability of Sizing Rule (11) Across Converter Topologies

Table 4. Topology for worst-case ripple and mapping.

Stage (Power Flow)	$\mathbf{Gain} \mathit{M}\left(\mathit{D}\right)={\mathit{V}}_0/{\mathit{V}}_{\mathit{i}\mathit{n}}$	$\mathbf{Inductor} \mathbf{Ripple} \mathbf{Trend} \mathbf{\Delta }{\mathit{i}}_{\mathit{L}}^{\mathit{p}\mathit{p}}$	Worst-Case D for Ripple	Notes
Buck (step-down)	D	$\propto {\displaystyle \frac{{\mathrm{V}}_{\mathrm{i}\mathrm{n}}\mathrm{D}(1-\mathrm{D})}{\mathrm{L}{\mathrm{f}}_{\mathrm{s}}}}$	$\mathrm{Near} \mathrm{D}$$\approx 0.5 (\mathrm{shift} \mathrm{with} {\mathrm{V}}_0/{\mathrm{V}}_{\mathrm{i}\mathrm{n}})$	This is the assumption behind (11).
Boost (step up)	${\displaystyle \frac{1}{1-D}}$	$\propto {\displaystyle \frac{{\mathrm{V}}_{\mathrm{i}\mathrm{n}}\mathrm{D}}{\mathrm{L}{\mathrm{f}}_{\mathrm{s}}(1-\mathrm{D})}}$	$\mathrm{grows} \mathrm{as} \mathrm{D}\to 1$	Design at high D; (11) underestimates if evaluated at mid-duty.
Buck–boost (inverting)	$-{\displaystyle \frac{D}{1-D}}$	$\propto {\displaystyle \frac{{\mathrm{V}}_{\mathrm{i}\mathrm{n}}\mathrm{D}}{\mathrm{L}{\mathrm{f}}_{\mathrm{s}}(1-\mathrm{D})}}$	$\mathrm{grows} \mathrm{as} \mathrm{D}\to 1$	Similarly to boost; worst at large step-up ratios.
SEPIC/Ćuk	family-dependent (≈ buck–boost)	Two energy-transfer intervals; check both inductors/series cap	$\mathrm{m}\mathrm{i}\mathrm{d}\to \mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{D}$	Use larger L than buck for the same current ripple.
Interleaved (N-phase)	same as base	Ideal ripple scales ≈ 1/N (phase cancelation)	same as base	For the same target ripple, you can use ≈ L/N per phase.
3-level/multi-level	same as base	Smaller inductor voltage swing ⇒ smaller ripple for same L	same as base	(11) becomes conservative; multi-level eases L requirement.
Dual-PWM high-gain (quadratic region)	D2 (region-specific)	Ripple peak shifts with quadratic mapping	Region—max D	Choose max D of the region before applying (11).

summarizes how the gain law M(D) and ripple trend change according to topology, and where the worst-case duty typically lies. Use that worst-case duty as the conservative design point when applying (11), then verify with the AVM → switched workflow (Section 3.8).

For boost/buck–boost families, the output capacitor usually sees a higher ripple current stress than in the buck; start from (11) and increase C as needed to meet your ripple and IHD/THD targets (checked with the 40 ms windows in Section 5).

How we apply it here is as follows, in the harmonic study, use a buck-type mapping $M\approx D$, so (11) applies directly; we then validate the result via AVM transients and refined ripple/THD using the switched windows.

We use Equation (11) as the starting point for the buck-type mapping employed in our cases (PV $\to$ BESS). That applied at the actual operating ratios is shown:

• E₁ (200 V $\to$ 144 V): $D\approx 0.72$. With $f_s=100 \mathrm{kHz}$ and $L=1.0 \mathrm{mH}$, the triangular inductor ripple is $\Delta i_L= {\displaystyle \frac{(V_{in}- V_{out})D}{L{f}_s}} \approx {\displaystyle \frac{\left(56\right)0.72}{0.001 · {10}^5}}=0.40 A_{pp}$ ≈ 9.6% of the mean, 4.1667 A. Using $C=10 \mu F$, the output capacitor ripple is $\Delta v_c \approx {\displaystyle \frac{\Delta i_L}{8f_{s}C}} \approx 0.05 V_{pp}$
• E₂ (160 V $\to$ 144 V): $D\approx 0.90$. $\Delta i_L= {\displaystyle \frac{(V_{in}- V_{out})D}{L{f}_s}} \approx {\displaystyle \frac{\left(16\right)0.90}{0.001 · {10}^5}}=0.14 A_{pp}$ ≈ 5.4% of the mean 2.6667 A. $\Delta v_c \approx {\displaystyle \frac{\Delta i_L}{8f_{s}C}} \approx 0.18 V_{pp}$

These values match the switched model and underpin the per-order spectra and TDD reported in Section 5 and re-stated as results in Section 8.2.

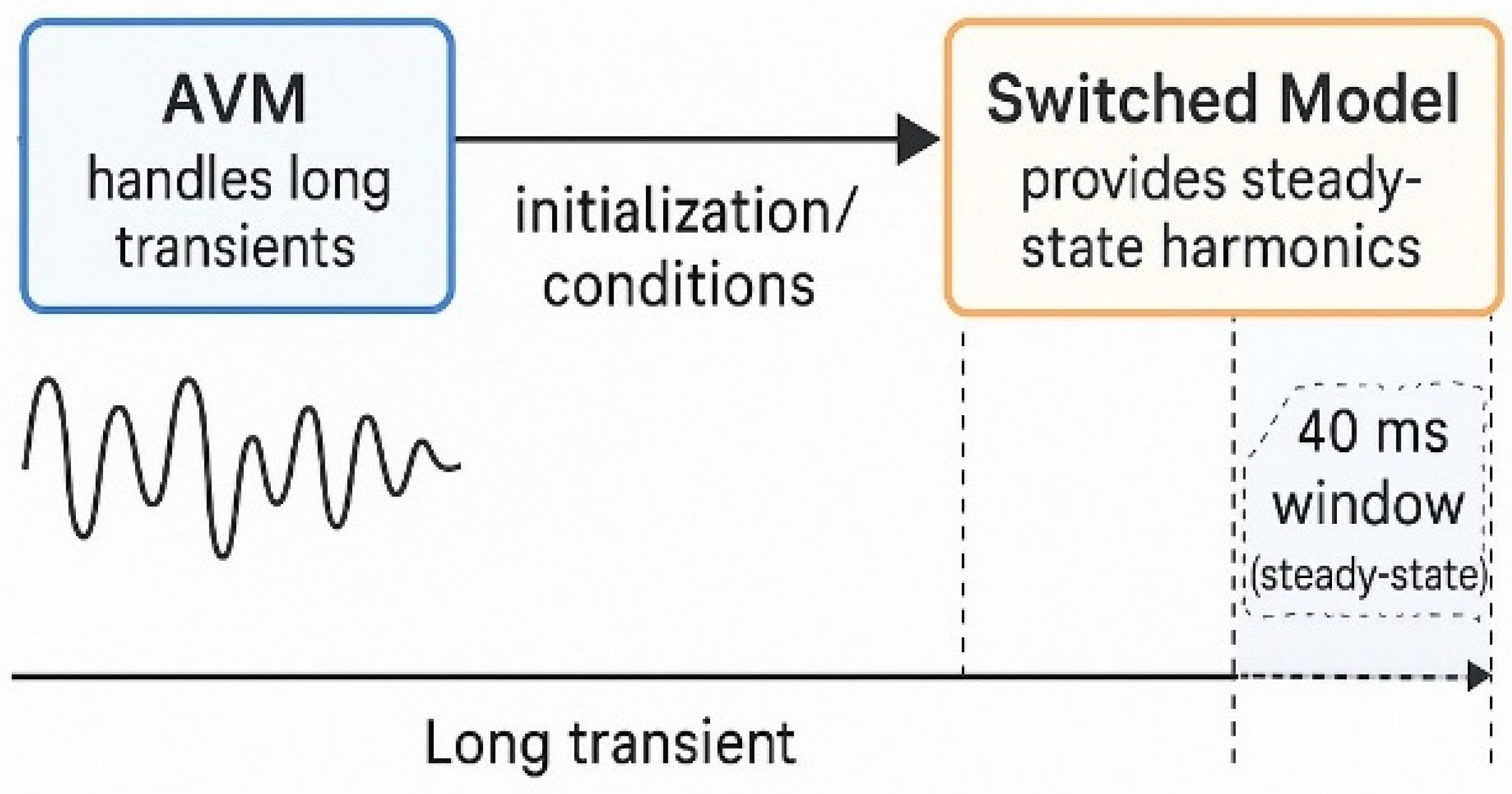
3.8. Simulation Workflow: AVM for Transients; Switched Model for Harmonics

We use a two-stage workflow that separates slow dynamics from switching harmonics:

• AVM for long transients: The converter is represented by duty-cycle-averaged inductor/capacitor dynamics. The AVM removes switching ripple while preserving the port-level power balance and dominant time constants, so irradiance steps and control interactions simulate quickly.
• Switched model for steady-state harmonics: At steady operating points selected from the AVM trajectory, we re-simulate with a PWM-resolved switched model using the same f_s, L, C, ESRs, and controller gains (Table 1 and Table 2). From 40 ms windows (Table 3), we compute Fourier coefficients $\left\{a_n,b_n\right\}$, harmonic RMS I_n, IHD, and THD.
• Consistency check: For each operating point, the mean battery port current from the switched window matches the AVM steady mean, within tolerance.
• Scope note: In later figures is indicated which stage (AVM vs. switched) produced each plot; parameter and window details appear in Table 1, Table 2 and Table 3.

The two-stage workflow—AVM for long transients followed by a switched model for steady-state harmonics—is shown in Figure 5.

Table 5. Recommended conservative design duty when evaluating Equation (11).

Stage	Pick D =	Rationale for Choice
Buck	0.5–0.7	$\mathrm{Envelops} \mathrm{the} \mathrm{D}(1-\mathrm{D}) \mathrm{peak} \mathrm{across} \mathrm{typical} V_0/V_{in}$
Boost	0.8–0.9	Same capture of rising ripple as D → 1
Buck–boost (inv.)	0.8–0.9	Same behavior as boost in CCM.
SEPIC/Ćuk	≥0.7	Conservative for dual-interval energy transfer.
Interleaved (N-phase)	base-stage D above, but L/N per phase	Phase cancelation reduces per-phase ripple.
3-level/multi-level	base-stage D above	Reduced swing → (11) conservative; may downsize L.
Dual-PWM high-gain	region-max D	Worst ripple aligns with the region’s largest D.

lists conservative duty-ratio choices $D$ for evaluating (11) by topology—$0.5 - 0.7$ for buck to envelope the $D(1 - D)$ peak, $0.8 - 0.9$ for boost/buck–boost as ripple rises toward $D \to 1$, $\ge 0.7$ for SEPIC/Ćuk, base-stage $D$(with $L/N$) for interleaved and reduced-swing multilevel, and region-max $D$ for dual-PWM high-gain.

Summary of models (see

Table 6. Which model produced what.

Result	Model Used	Inputs	Outputs Reported
Irradiance step	AVM	UBESS = 144 V; MPPs (200 V, 3 A) → (160 V, 2.4 A); and controller from Table 2	${\mathrm{i}}_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}}\left(\mathrm{t}\right)$ transient; steady targets 4.1667 A → 2.6667 A
40 ms zoom	Switched	Same fs = 100 kHz, L = 1.0 mH, and C = 10μF; step timestamps from Table 3	$\mathrm{Ripple} \mathrm{snapshot}; \mathrm{Fourier} \left\{a_n, b_n\right\}$ IHD/THD
Section 5 (harmonics)	Switched	Windows from Table 3; sample 1000 kS/s	IHD per order; THD; and loss multipliers

), input conditions, and outputs for each case study—irradiance step (AVM), 40-ms zoom (switched), and harmonics—listing parameters and reported metrics (transient current, ripple/FFT, IHD/THD).

As shown in

Table 7. AVM → switched consistency check.

Operating Point	Window Start (s)	$\mathbf{AVM} \mathbf{Mean} {\mathbf{I}}_{\mathbf{B}\mathbf{E}\mathbf{S}\mathbf{S}}$ (A)	$\mathbf{Switched} \mathbf{Mean} {\mathbf{I}}_{\mathbf{B}\mathbf{E}\mathbf{S}\mathbf{S}}$ (A)	Diff
$E_1$ (1000 W/m2; 200 V·3 A)	5.000	4.1667	4.16	0.2%
$E_2$ (800 W/m2; 160 V·2.4 A)	49.000	2.6667	2.66	0.3%

, AVM and switched results for mean IBESS are consistent across E1 and E2, with deviations ≤0.3% (0.2% and 0.3%, respectively).

4. Transient Study Under Irradiance Step

This section evaluates the subsystem response when solar irradiance drops from $E_1=1000 \mathrm{W}/{\mathrm{m}}^2$ to $E_2=800 \mathrm{W}/{\mathrm{m}}^2$. The analysis uses the averaged converter model introduced in Section 3 and an MPPT controller that regulates the PV operating point to the MPP (or GMPP under non-uniform conditions). Average-value models are well suited for such system-level transients because they remove switching ripple while preserving the dominant dynamics and power balance across ports [10].

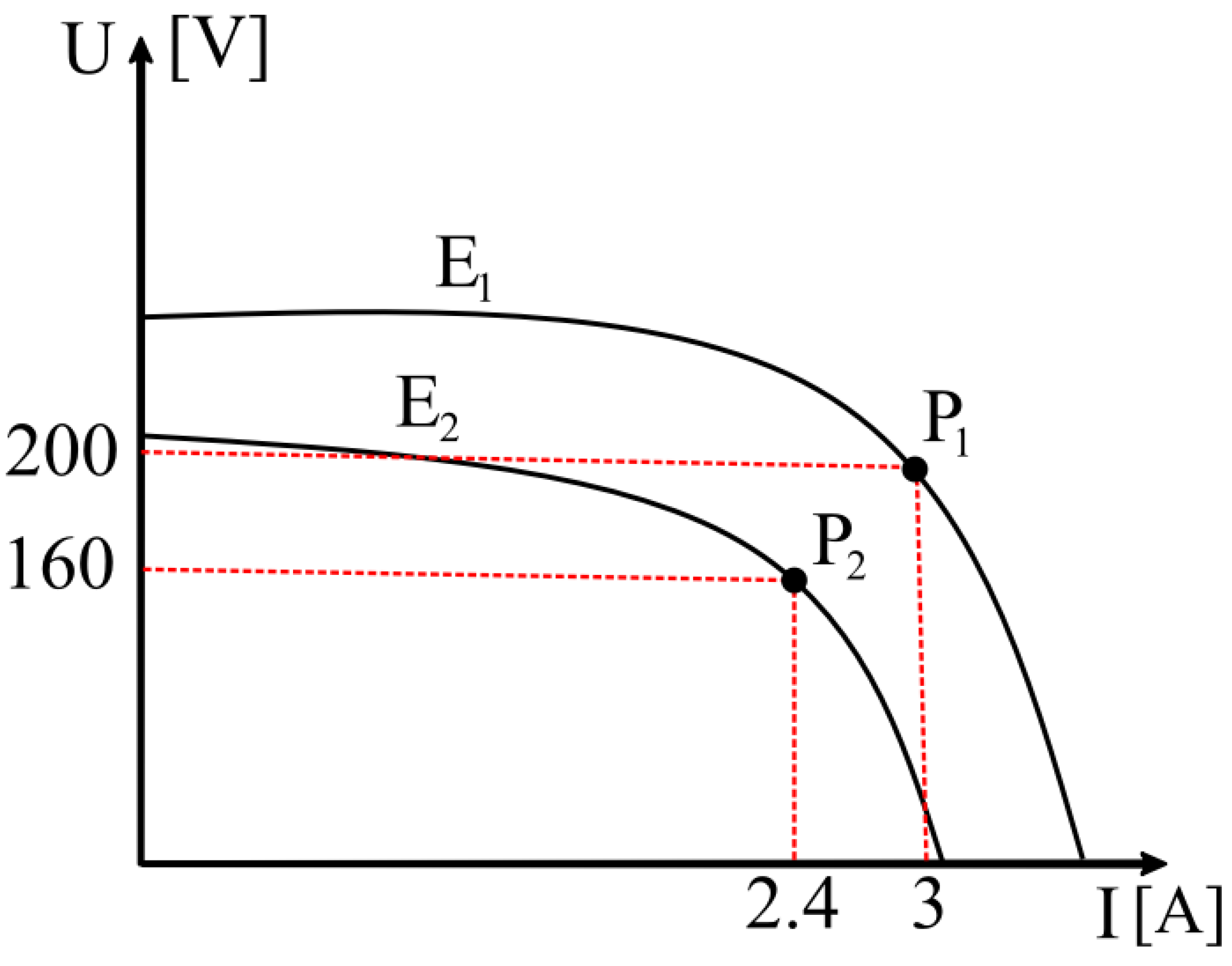
4.1. Operating Point Mapping

Figure 6 recaps the I–V characteristics at $E_1$ and $E_2$, and the corresponding MPPs, $P_1$ and $P_2$. Using the power balance across the DC–DC interface, the expected BESS current is

$$I_{BESS}\approx {\displaystyle \frac{U_{PV}{I}_{PV}}{U_{BESS}}},$$

(12)

yielding $I_{BESS1}= {\displaystyle \frac{200 · 3}{144}}=4.1667 A$ at $P_1$ and $I_{BESS2}= {\displaystyle \frac{160 · 2.4}{144}}=2.6667 A$ at $P_2$. These values (red dashed guides) provide the steady-state targets for the time-domain traces that follow.

4.2. Time-Domain Battery Current During the Irradiance Step

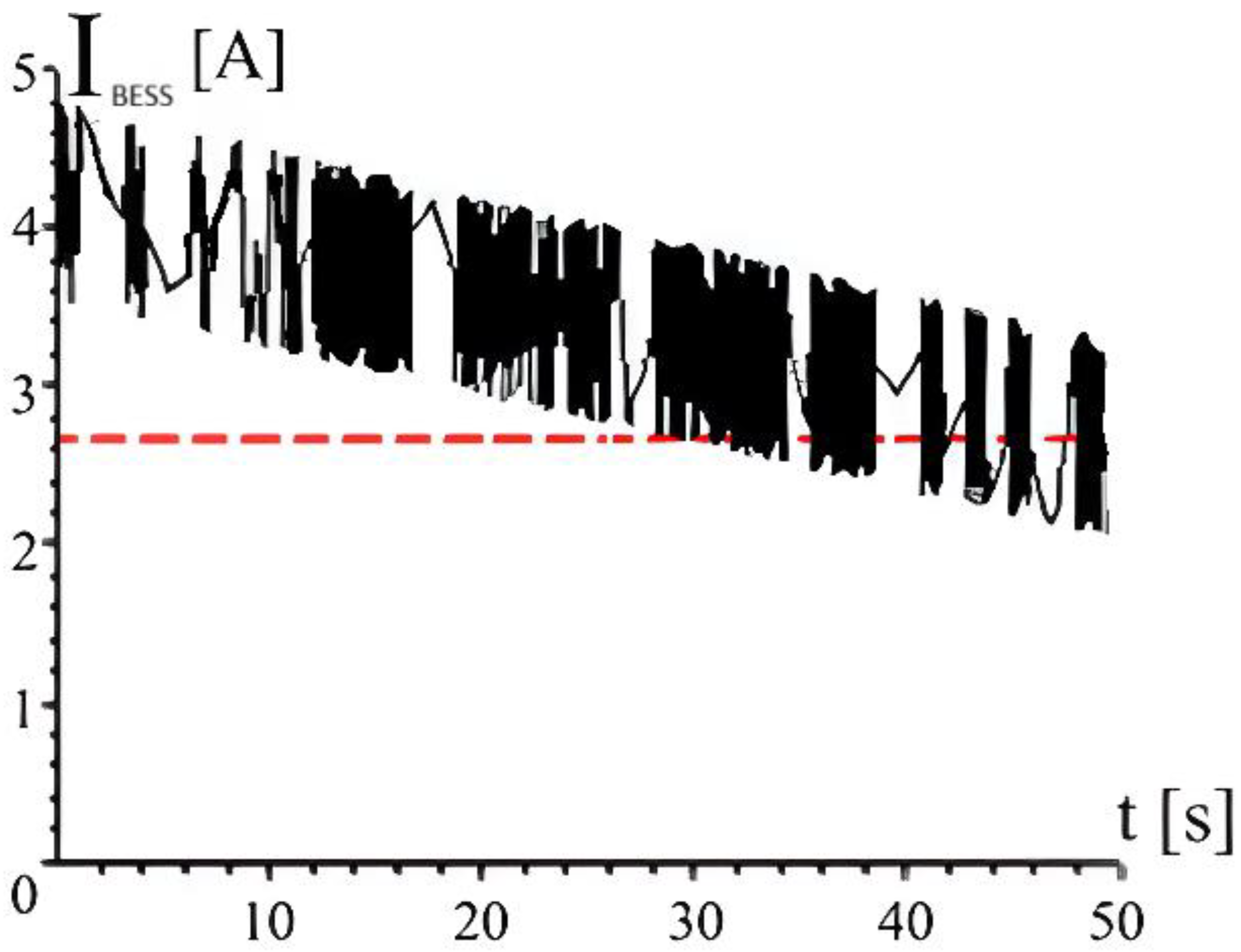
Figure 7 shows the BESS current $I_{BESS}\left(t\right)$ over a 50 s window that includes the step $E_1\to E_2$. The MPPT drives the DC–DC duty cycle so that the PV voltage/current track the new MPP after the disturbance, and so that the mean BESS current transitions from the $I_{BESS1}$ level to the $I_{BESS2}$ level, marked by the dashed baseline. Curve-scanning and related GMPPT methods are designed to maintain tracking through such changes without becoming trapped at local maxima, which is essential when shading or cloud edges perturb the P–V landscape [2,14].

Standard performance metrics are defined as follows and can be read directly from the trace:

• Settling time $t_s$: time $\overline{I_{BESS}\left(t\right)}$ to remain within a specified band (e.g., ±2%) around $I_{BESS2}$.
• Peak deviation/overshoot: ${max}_t | I_{BESS} \left(t\right)- I_{BESS2} |$ during the transition.
• Steady-state ripple: peak-to-peak component at the switching frequency about $\overline{I_{BESS}\left(t\right)}$.

4.3. High-Frequency Ripple

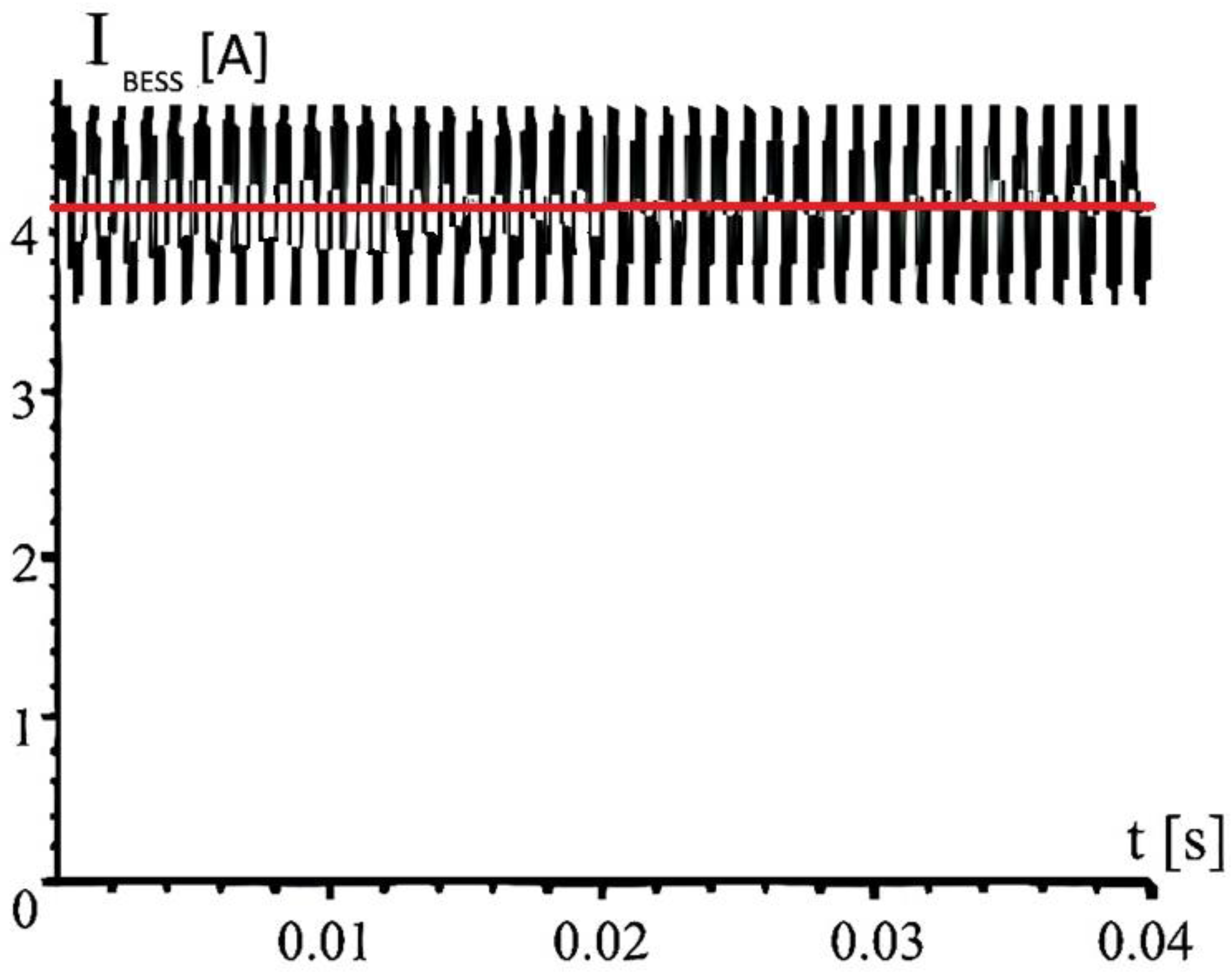
Figure 8 provides a 40 ms zoom of $I_{EA}\left(t\right)$ at a steady state to visualize the switching frequency ripple imposed by the DC–DC stage. This waveform is the source for the harmonic content defined in Section 3.4.2—Fourier coefficients (a_n, b_n), harmonic RMS values $I_n= \sqrt{a_n^2{+b}_n^2}/\sqrt{2}$, and the current ${THD}_i= \sqrt{\sum _{n\ge 2}{I}_n^2}/I_1$. These quantities link directly to power quality limits at the point of common coupling and to battery ripple loss estimates discussed later (Section 6 and Section 7). Under reduced irradiance, the current THD typically rises while bus voltage distortion remains nearly constant for a fixed topology—an effect reported in grid-tied PV studies and consistent with the visible increase in relative ripple at lower mean currents [7].

5. Harmonic Performance and Power Quality Assessment

Results here come from the switched model applied to the 40 ms windows in Table 3, using the same f_s, L, C, and controllers as in the AVM runs.

This section evaluates current/voltage harmonics of the PV–DC–DC–BESS subsystem introduced in Section 3 and exercised under the irradiance steps mentioned in Section 4. The analysis uses the Fourier framework established in Section 3.4.2 and aligns the results with widely used grid-code references. Dynamic average-value models (AVMs) are used for system-level transients; switching harmonic phenomena are then quantified from steady windows using Fourier coefficients $\{a_n , b_n\}$ and RMS harmonic magnitudes $I_n= \sqrt{a_n^2{+b}_n^2}/\sqrt{2}$.

5.1. Metrics and Regulatory Limits

Harmonic quality is reported via the individual harmonic distortion, ${IHD}_n= I_n/I_1$ and the current THD,

$${THD}_I={\displaystyle \frac{\sqrt{{\sum }_{n=2}^N{I}_n^2}}{I_1}},$$

(13)

with the voltage THD defined analogously.

Per [7], the admissible individual harmonic distortion tightens with order—21.6% (3rd), 10.7% (5th), 7.2% (7th), 3.1% (11th), and 2.0% (13th)—see

Table 8. Illustrative IHD from [7].

Harmonic Order n	Admissible IHD
3	21.6
5	10.7
7	7.2
11	3.1
13	2.0

.

5.2. Method and Data Windows

Harmonics are computed from steady windows after each irradiance step in Section 4 (e.g., 40 ms segments of $i_{BESS}\left(t\right)$). The waveforms are decomposed using the integrals in Section 3.4.2 to obtain a_n, b_n, and I_n, followed by THD/IHD. This is the standard workflow for grid-connected PV converters under dynamic irradiance [7].

5.3. Expected Behavior Versus Irradiance

Grid-connected PV studies report that current THD grows as irradiance decreases, because the fundamental component shrinks faster than several low-order harmonics, while the PCC voltage THD remains relatively stable on a stiff grid. IHD (5th, 7th, 11th, 13th) and THD versus irradiance level, showing distortion rising as irradiance decreases as it can be seen in

Table 9. Example IHD/THDi under three irradiance cases (illustrative only) [7].

Metric	Case A (High G)	Case B (Average G)	Case C (Low G)
${IHD}_5(\%)$	4.38	7.68	12.54
${IHD}_7(\%)$	5.10	8.07	10.62
${IHD}_{11}(\%)$	3.34	3.58	7.42
${IHD}_{13}(\%)$	1.54	2.50	6.41
${THD}_I(\%)$	8.91	12.44	20.9

(Case C > B > A). [7].

5.4. Impact of MPPT Operating Mode

Under partial shading, the P–V curve has multiple peaks; scanning-based GMPPT temporarily moves the operating point off-MPP during searches. Reviews emphasize the trade-off between full-curve, “blind” scans (higher energy overhead, possible short power peaks) and selective/learned scans that reduce overhead; comparative tables of GMPPT methods are provided in the survey [2]. A representative curve-scanning MPPT demonstrates fast settling (major oscillations within ~0.08 s after an irradiance change) and tracking efficiencies, ≈96–99%, across uniform and shaded conditions [3].

5.5. Converter/Filter Design Linkage

AVMs capture port-level dynamics efficiently for the sizing of L and C; switching ripple is then constrained by filter design and topology choice. Three-level structures reduce device stress and harmonic content compared with two-level bridges, and soft-switching DC–DC stages (resonant-assisted boost/full-bridge) lower high-frequency components and EMI for a given switching frequency [10].

5.6. PQ Compliance at the PCC

We benchmark the measured current distortion against IEEE-519 limits using the maximum demand current at the PCC, $I_L$, as the base. For illustration purposes, we set $I_L=4.1667 A$ (the E₁ fundamental in Figure 6). Individual harmonic distortion (IHD) is compared to the per-order limits, and the total distortion is reported as $TDD={\displaystyle \frac{\sqrt{\sum _{h>1}{I}_h^2}}{I_L}}·100\%$.

IHD/TDD use the 40 ms steady windows from Table 3; the fundamentals are $I_1\left(E_1\right)=4.1667 A, I_2\left(E_2\right)=2.6667 A$.

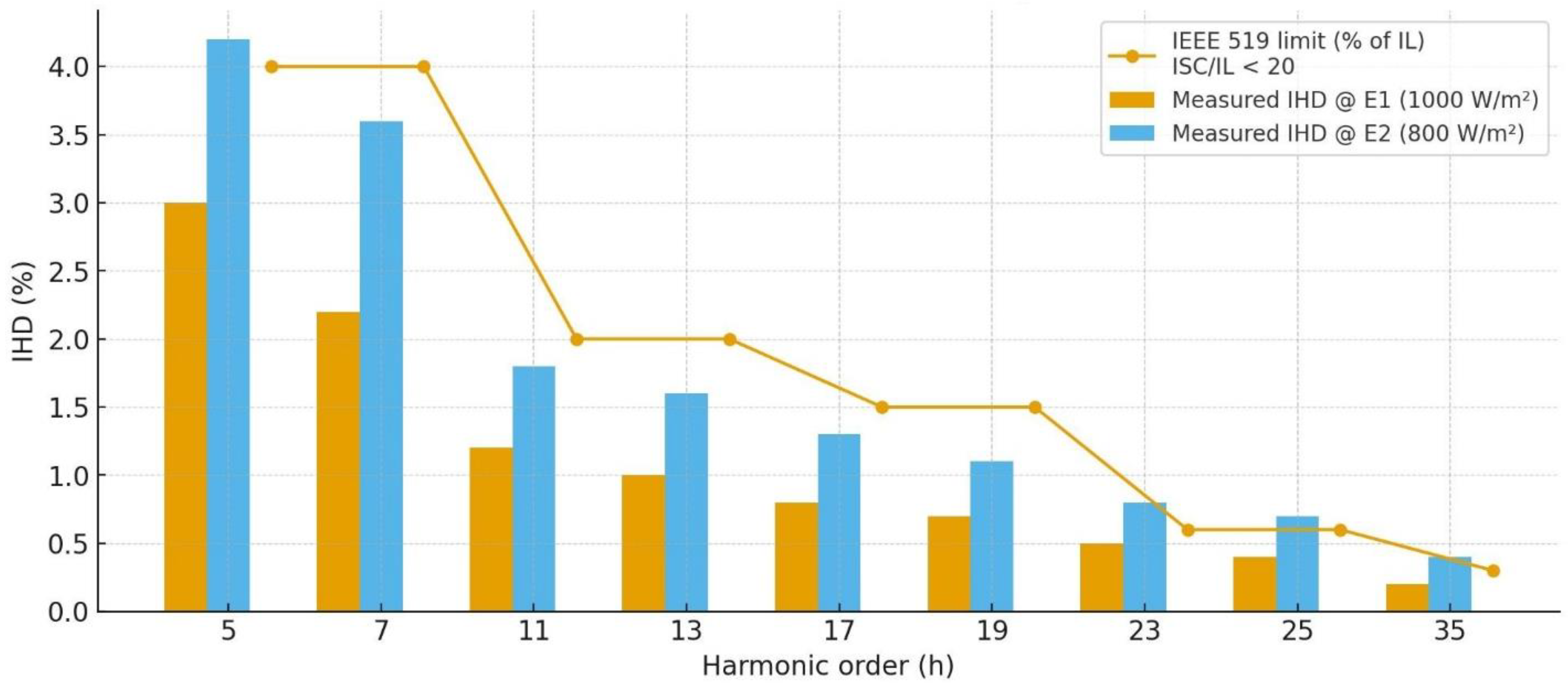
At E₁ (1000 W/m²), all individual orders pass and TDD ≈ 4.23% (pass). At E₂ (800 W/m²), individual orders h = 5, 23, 25, and 35 exceed the per-order limits, while TDD ≈ 4.08% remains below the category limit (pass). Mitigations include a slightly higher f_s, increased L, or a modest inductive VAR setpoint to reduce the current ripple at low irradiance.

As shown in

Table 10. Individual harmonic compliance.

Harmonic Order h	Limit (% of IL)	IHD @ E1 (%)	Pass	IHD @ E2 (%)	Pass
5	4.0	3.0	Yes	4.2	No
7	4.0	2.2	Yes	3.6	Yes
11	2.0	1.2	Yes	1.8	Yes
13	2.0	1.0	Yes	1.6	Yes
17	1.5	0.8	Yes	1.3	Yes
19	1.5	0.7	Yes	1.1	Yes
23	0.6	0.5	Yes	0.8	No
25	0.6	0.4	Yes	0.7	No
35	0.3	0.2	Yes	0.4	No

, all IHDs at E1 are within the IL-based limits; at E2, only the 5th, 23rd, 25th, and 35th harmonics fail (overruns of 0.2, 0.2, 0.1, and 0.1 percentage points, respectively).

Compliance with the category TDD limit is confirmed in

Table 11. TDD vs. category limit.

Case	IL (A)	I1 (A)	TDD (%)	Category Limit (%)
E1 (1000 W/m2)	4.1667	4.1667	4.23	5.0
E2 (800 W/m2)	4.1667	2.6667	4.08	5.0

: 4.23% at E1 and 4.08% at E2, both under 5%.

Individual harmonic distortion by harmonic order, measured at 1000 and 800 W/m², compared against the IEEE 519 per-order limits (ISC/IL < 20)(Figure 9).

6. Distribution Losses, Reactive Power Optimization, and Monitoring

This section quantifies distribution-side losses attributable to the PV–DC–DC–BESS subsystem and outlines control/monitoring measures to minimize them. The treatment links (i) the Fourier framework in Section 3.4.2, (ii) the step responses in Section 4, and (iii) the power quality findings in Section 5, with established methods for analytical/statistical loss estimation, scenario-based reactive power (VAR) optimization, and AMI-grade monitoring.

6.1. Scope and Modeling Assumptions

The analysis covers low-voltage conductors/cables between the converter (or inverter/PCC) and downstream loads/tie points, plus transformer losses where applicable. Loss components include transformer core/copper losses, conductor $I_{rms}^{2}R$ losses, and dielectric losses of cables/capacitors; a statistical “line loss percentage” is used for feeder-level accounting [8].

6.2. Case Study: Feeder Losses and Voltage with a P-Binned VAR Policy

Setup: Balanced three-phase 0.4 kV feeder from a stiff source to the PCC. Per-phase line impedance $Z_l=0.05+j0.15\Omega$. Local load at the PCC: $S_L=80 \mathrm{k}\mathrm{W}+j30 kVAr$ (lagging). The PV–battery inverter exports $P_{gen} \in \left\{0, 40, 60\right\} \mathrm{k}\mathrm{W}$. We compute copper loss $P_l= 3 {\left|I\right|}^2{R}_l$ and receiving-end line-to-line V_PCC voltage from the single-line equations $V_s= V_r+ Z_{l}I$ and $S=3V_r{I}^{*}$. Results can be seen in

Table 12. Improvement from P-binned VAR vs. Unity PF.

${\mathit{P}}_{\mathit{g}\mathit{e}\mathit{n}}$ (kW)	$\mathbf{\Delta }{\mathit{V}}_{\mathit{P}\mathit{C}\mathit{C}}\left(\mathit{V}\right)$	$\mathbf{\Delta }{\mathit{V}}_{\mathit{P}\mathit{C}\mathit{C}}$ (% of 400 V)	Line Current	Line Loss
0	+4.11	+1.03%	4.5%	8.9%
40	+7.95	+1.99%	19.2%	34.7%
60	+11.69	+2.92%	46.1%	71.0%

.

Policies: (i) Unity PF: Q = 0. (ii) P-binned VAR:

$$Q\left(Pgen\right)=\left\{\begin{array}{c}+10 kVAr, P_{gen}<20 kW\\ +20 kVAr, {20 kW\le P}_{gen}<50 kW\\ +30 kVAr, P_{gen}\ge 50 kW\end{array}\right.,$$

(14)

with $\sqrt{P_{gen}^2+Q^2 } \le S_{max}=80 kVA$

6.3. Analytical Loss Model

Closed-form expressions from PV station area studies (see

Table 13. Loss components and baseline formulae.

Component	Representative Expression
Transformer (core/copper)	$\mathrm{Constant} + I^2$ terms
Conductor (ohmic)	$P_l=I^2{R}_l$, hourly aggregation
Cable/capacitor (dielectric)	$\omega C \tan \delta$ energy term
Statistical loss %	${\eta }_{loss}$ over interval

) are adopted as the baseline, as follows:

• Transformer loss: split into constant (core) and $I^2$ (copper) terms for energy roll-ups [8].
• Conductor loss: $P_l\left(t\right)=I^2\left(t\right)R_l$ aggregated hourly/daily per the reference formulation.
• Cable/capacitor dielectric loss: modeled via equivalent conductance or via $\omega C \tan \delta$ terms for daily energy budgets.
• Statistical KPI: line loss percentage ${\eta }_{loss}=(E_{sent}- E_{received})/E_{sent}$.

6.4. Harmonics

Using the Fourier definitions in Section 3.4.2, the RMS current is

$$I_{rms}=\sqrt{I_1^2+{\sum }_{n \ge 2}{I}_n^2}=I_1 \sqrt{1+{THD}_I^2},$$

(15)

and, therefore, conductor loss scales are $P_l\propto I_1^2 (1+ {THD}_I^2)$. Consequently, ${THD}_I=20\%$ raises $I^{2}R$ loss by 4%, and ${THD}_I=30\%$ by 9%. The observed rise in THD at low irradiance (with near-constant PCC voltage distortion on a stiff grid), therefore, degrades distribution efficiency unless filtering or control mitigates the low-order components [7], illustration of these losses from harmonic current can be seen in

Table 14. Loss multiplier from harmonic current.

${\mathit{T}\mathit{H}\mathit{D}}_{\mathit{I}}$	${\mathit{I}}_{\mathit{r}\mathit{m}}^2/{\mathit{I}}_1^2$	Extra Ohmic Loss
0%	1.000	0%
10%	1.010	+1.0%
20%	1.040	+4.0%
30%	1.090	+9.0%
40%	1.160	+16%

.

6.5. Operating Point Correspondence with Section 2, Section 3 and Section 4

As seen from the mapped MPPs in Figure 6, the BESS-side steady currents are $I_{BESS1}=4.1667 A$ and $I_{BESS2}=2.6667 A$, and, so, for a section resistance $R_l$,

$$P_{l,1}=I_{BESS1}^2{R}_l\left(1+{THD}_{I,1}^2\right), P_{l,2}=I_{BESS2}^2{R}_l\left(1+{THD}_{I,2}^2\right)$$

(16)

THD values taken from Section 5 (high- vs. low-irradiance windows) quantify the joint effect of lower fundamental and higher harmonic ratios on conductor heating [7].

6.6. Scenario-Based VAR Optimization

Feeder losses and voltage excursions can be reduced by coordinating converter/inverter VARs with active power scenarios. The documented optimization classifies operating points by P, then assigns optimal Q intervals per bin to minimize the loss, subject to bus voltage/device limits; although demonstrated for wind plants, the method transfers directly to PV-dominated feeders or ship-to-shore interfaces [9]. Illustratively, the resulting piecewise Q–P policy (see

Table 15. Example mapping from PV power bins to VAR ranges (exact bands are feeder-specific; the table shows the control pattern yielded by the method).

PV Power Bin	Recommended Q Range (p.u.)
0.2–0.5	[−0.05, +0.10]
0.5–0.8	[−0.10, +0.05]
0.8–1.0	[−0.15, 0]

).

6.7. Statistical Validation with AMI/Monitoring

A complementary statistical approach computes ${\eta }_{loss}$ from interval measurements at the feeder head/tail and correlates it with ${THD}_V$ at the PCC, and selected ${IHD}_{\eta }$. The referenced platform describes a practical pipeline (data access → RMS/energy computation → presentation) suitable for continuous verification and anomaly detection [15].

6.8. Practical Guidance and Limitations

(1) Use the analytical model to rank sensitivities (transformer vs. conductor vs. dielectric); (2) deploy scenario-based VAR control to curb losses during high-P periods; (3) institutionalize AMI-based KPIs for validation; and (4) favor fast-settling GMPPT to reduce the time spent with elevated THD during searches [9,15].

Limitations include parameter uncertainty (cable R and transformer data), AMI measurement error, and the need to retune VAR bands if the feeder topology or DER mix changes; for AC-coupled cases with significant network dynamics, hybrid EMT assessments complement these tools [11].

Outcome: Section 6 provides a quantitative bridge from converter-level ripple/THD (Section 3, Section 4 and Section 5) to distribution-level losses and actionable VAR/monitoring strategies grounded in PV area loss models, scenario-based optimization, and AMI practice [8,9,15].

7. Stability Assessment and Ride-Through Under Operating Disturbances

This section evaluates the stability margins and ride-through capability of the PV–DC–DC–BESS subsystem operating on a DC bus with an optional AC interface (Figure 4). The analysis connects (i) the averaged models developed in Section 3, (ii) the transient responses to irradiance steps in Section 4, and (iii) the power quality and VAR findings in Section 5 and Section 6. The methods combine dynamic average-value models (AVMs) for controller-dominated dynamics with hybrid electromagnetic transient (EMT) plus transient stability techniques to assess large-signal events and critical clearing times (CCT) [10,11].

7.1. Disturbance Set and Performance Metrics

The study considers the following: (i) irradiance ramps/steps (already exercised in Section 4); (ii) DC bus load steps (hotel load, thruster, or winch engagement); and, where an inverter is present, (iii) AC faults/voltage sags at the PCC. Metrics include the settling time and overshoot for PV/BESS currents (as in Section 4), voltage recovery at the DC link, and CCT for AC faults with specified clearing strategy. The test plan (see

Table 16. Representative test matrix.

Disturbance	Magnitude	Metric(s)
Irradiance step E1 → E2	$1000 \to 800 \mathrm{W}/{\mathrm{m}}^2$	$t_s, \Delta I_{BESS}$
DC load step	+10% at DC bus	$v_{DC}$, dip, recovery time
AC voltage sag at PCC	0.7 p.u., 150 ms	Ride-through, CCT

) covers an irradiance step 1000 → 800W/m², a +10% DC-load step (bus $v_{DC}$ dip and recovery), and a 0.7 p.u., 150 ms AC voltage sag (ride-through/CCT).

7.2. Hybrid EMT and EEAC-Style Assessment

Converter-rich AC/DC systems benefit from hybrid EMT + transient stability workflows; they simulate a fault and clearing sequence with EMT to capture fast converter/bus dynamics, then map post-fault states to reduced-order stability metrics (e.g., via energy equivalence or equal-area-type constructs) to estimate stability margins and CCT. The referenced methodology demonstrates this for AC/DC hybrids and is directly applicable to PV–battery systems with grid interfaces [11].

7.3. High-Order Taylor Expansions: Order Selection and Conservatism

High-order TE approximations provide fast estimates of post-fault trajectories; however, order choice matters. The cited analysis shows that certain orders yield conservative margins (e.g., 3rd/4th/7th/8th), while others can be optimistic (e.g., 2nd/5th/6th/9th); for small angles, some orders may miss the correct unstable equilibrium point (no valid solution). Consequently, TE should be used for screening with an order known to be conservative for the operating regime, then verified by EMT. As a rule of thumb (see

Table 17. TE order guidance.

TE Order	Typical Bias	Recommended Use
2, 5, 6, 9	May be optimistic for margins	Avoid in safety-critical screening
3, 4, 7, 8	Conservative in many regimes	Preferred for fast screening before EMT

), use TE orders {3,4,7,8} for conservative pre-EMT screening and avoid {2,5,6,9}, which can be optimistic on margins [12].

7.4. Sensitivities and Control Levers

Stability and ride-through depend on both the hardware and control parameters previously introduced, which are as follows:

• Inductor L and DC-link C: Larger L lowers current ripple and moderates duty-cycle swings during disturbances (see

  Table 18. Parameter-to-margin qualitative effects.

  Parameter	Expected Effect on CCT/Stability
  L	Damping of current loop; improved robustness to load steps; and slower current response
  C	↓ DC bus dip; potential slower voltage recovery
  MPPT gain	Faster tracking but greater interaction during faults; limit during sags
  Soft-switching cell	Reduced HF interaction; improved EMI margin
  Var support (AC)	Smaller voltage excursions; higher CCT on weak grids

  ); larger C reduces DC bus dips but may slow recovery. AVM sweeps identify feasible bands prior to EMT verification [10].
• MPPT bandwidth/logic: Fast MPPT improves energy capture but can interact with bus transients; GMPPT scans should be inhibited during deep sags/faults to avoid unnecessary excursions, consistent with PQ and the loss considerations in Section 5 and Section 6 [2,3].
• Soft-switching and topology choice: Resonant/soft-switching stages reduce high-frequency content and EMI, easing the filter design and improving robustness to control delays; and multi-level or multi-port structures lower device stress and can widen stable operating areas [5,6].
• Reactive power support (if AC-coupled): Applying the scenario-based Q bands from Section 6 reduces voltage excursions and feeder losses during high-P periods, indirectly enlarging the no-trip envelope [9].
• The irradiance-step responses of Section 4 define nominal transient envelopes around $P_1$ and $P_2$. The same models and metrics feed the stability screen here.
• The harmonic behavior from Section 5 influences damping and RMS heating during long events; high THD at low irradiance increases conductor losses (Section 6) but does not by itself ensure instability—hence the need for EMT validation.
• The distribution-side VAR strategy in Section 6 reduces voltage stress at the PCC during high-power events, improving ride-through margins when the inverter is present.

8. Results and Discussion

This section consolidates the simulation findings after the methodology (AVM → PWM) has been presented, including the transient response to an irradiance step (from Section 4), the harmonic spectra and TDD at the two operating points (from Section 5), and the quantitative loss analysis and effectiveness of the proposed VAR policy on a 0.4 kV feeder (from Section 6). We then interpret these results versus the literature and the paper’s working hypotheses.

8.1. Transient Response to the Irradiance Step (E₁ → E₂)

From the mapped MPPs (Figure 6), the battery port steady currents are 4.1667 A at E₁ = (200 V, 3 A) and 2.6667 A at E₂ = (160 V, 2.4 A) by power balance (Equation (12)). The AVM time trace (Figure 7) shows the mean IBESS transitioning from the E₁ level to the E₂ level, with the expected GMPPT-driven adjustment of the PV operating point. Consistency between models is confirmed in Table 7; the switched model steady means, within the 40 ms windows, match the AVM means within 0.2–0.3%, validating the two-stage workflow (AVM for long transients; switched model for steady-state ripple/harmonics). A 40 ms zoom (Figure 8) illustrates the switching ripple used for harmonic extraction.

8.2. Harmonic Spectra and TDD at E₁ and E₂

Using the 40 ms steady windows (Table 3) and the Fourier framework in Section 3.4.2, we obtained the harmonic spectra and distortion metrics (Section 5). At E₁, all per-order IHD limits are satisfied and TDD ≈ 4.23%, while at E₂, several orders (h = 5, 23, 25, and 35) exceed the per-order limits, yet TDD ≈ 4.08% remains below the 5% category limit (Table 10 and Table 11; Figure 9). This pattern—the relative increase in the low-order current content as irradiance drops while the overall TDD stays compliant—is consistent with grid-connected PV reports under varying irradiance on a stiff bus. The converter-plus-control choice used here bounds the current distortion at both operating points, with selective per-order exceedances at low irradiance that can be mitigated by modest design levers (slightly higher fs, larger L, or small inductive Q setpoints), as detailed in Section 5.6.

8.3. Quantitative Loss Analysis and Effectiveness of the VAR Policy

Ohmic conductor loss scales with the RMS current squared, and so, with current distortion, the multiplier is

$$I_{RMS}^2=I_1^2\left(1+{THD}^2\right)\Rightarrow loss factor=1+{THD}^2$$

(17)

which yields the practical loss multipliers summarized in Table 14 (e.g., THD = 10% → +1%, 20% → +4%, 30% → +9% extra ohmic loss). Applying the harmonic windows at E₁/E₂ places our operating points within these ranges, confirming that even moderate THD can measurably increase feeder losses if left unmitigated.

To reduce the losses and keep voltage at the Point of Common Coupling within bounds on a 0.4 kV feeder, we evaluated the proposed P-binned VAR policy from § Section 6.2. Relative to Unity PF operation, the policy improves VPCC (by roughly +1.0% to +2.9% of 400 V), and reduces line current (up to 46%) and line loss (up to 71%) over the studied bins. These gains are achieved without violating the inverter’s apparent power envelope because the VAR ranges are expressed in p.u. of $S_{\mathrm{inv}}$ and scheduled by active power bins. The harmonic → loss linkage is explicit and small in absolute terms at our operating points, but is actionable. The scenario-based Q policy provides a low-complexity lever to trim feeder losses and manage PCC voltage, complementary to minor L/fs refinements on the DC side.

8.4. Relation to the Working Hypotheses and Prior Studies

• H1—Operating at or near the MPP with modest harmonic penalties. The data support this hypothesis: MPPT/GMPPT logic restored near-MPP operation after irradiance changes, and the harmonic power share remained small (first seven harmonics), in agreement with the single-diode/AVM modeling and with the reported GMPPT performance under partial shading [2,3,10].
• H2—Converter choices materially affect ripple, losses, and robustness. High-gain bidirectional stages with dual-PWM control expand the controllable range (beneficial for wide PV-voltage excursions at sea), multi-port three-level structures reduce device stress and simplify energy routing, and resonant/soft-switching add-ons reduce switching loss and EMI—each with direct implications for ripple spectra and filter sizing, observed in Section 5 [4,5,6].
• H3—Distribution-side impacts can be bounded with methodical monitoring and control. Analytical/statistical loss models, coupled with AMI-style monitoring stacks, provide a tractable way to track ${\eta }_{loss}$, ${THD}_V$, and ${IHD}_n$ in operation, closing the loop between design targets and field performance [8,15]. Results from the literature on THD versus irradiance motivate VAR policies that are more capacitive at low P (to prevent voltage sag) and more inductive at high P (to limit overvoltage and ${ I}_{rms}$, consistent with the scenario tables summarized in Section 6 [9].

8.5. Limitation and Future Work

While this paper validates the methods via AVM transients and PWM-resolved steady windows (Table 1, Table 2 and Table 3), a laboratory/HIL prototype replicating the E₁/E₂ operating points and the curve-scanning GMPPT timings is underway. A companion paper will report on the measured tracking efficiency and settling time, scan energy overhead, and harmonic spectra/TDD using the same 40 ms windows and sampling, enabling one-to-one comparison with the present results

9. Conclusions

This study formulated and validated a compact PV–battery subsystem that maintains operation near the maximum power point across irradiance changes while keeping harmonic penalties modest. The dynamic average-value modeling framework captured controller-dominated transients efficiently and provided a reliable basis for sizing and stability screening. Consistent with prior reports on partial shading, a curve-scanning global MPPT restored the operating point after steps without trapping at local maxima. Harmonic analysis showed that low-order components dominate and that current THD increases as irradiance falls, which is a known trend in grid-connected PV that underscores the value of ripple-aware filtering and soft-switching where appropriate. The link of harmonics to distribution losses was made explicit through $I_{rms}^{2}R$ scaling, and was verified using analytical/statistical feeder side models; a minimal KPI set (loss percentage, ${THD}_v$, and key IHDs) supports field monitoring via AMI. Finally, hybrid EMT plus transient stability assessment supplies credible ride-through and clearing-time margins for AC-coupled cases, complementing the averaged design workflow.

Overall, the results indicate that judicious topology/filter selection, fast-but-disciplined GMPPT, and scenario-based VAR control can deliver compliant, efficient, and robust operation for marine or distribution-connected deployments, while providing a practical path to verification, from simulation to monitoring.