Inertia in Converter-Dominated Microgrids: Control Strategies and Estimation Techniques
Abstract
1. Introduction
2. Literature Review Methodology
2.1. Databases and Search Strategy
- “virtual inertia control AND hybrid microgrid”
- “inertia estimation” AND “power system”
2.2. Inclusion and Exclusion Criteria
2.3. Selection Process
2.4. Data Extraction and Synthesis
- ▪
- Inertia estimation methods (analytical, adaptive, statistical, AI-driven, frequency-domain).
- ▪
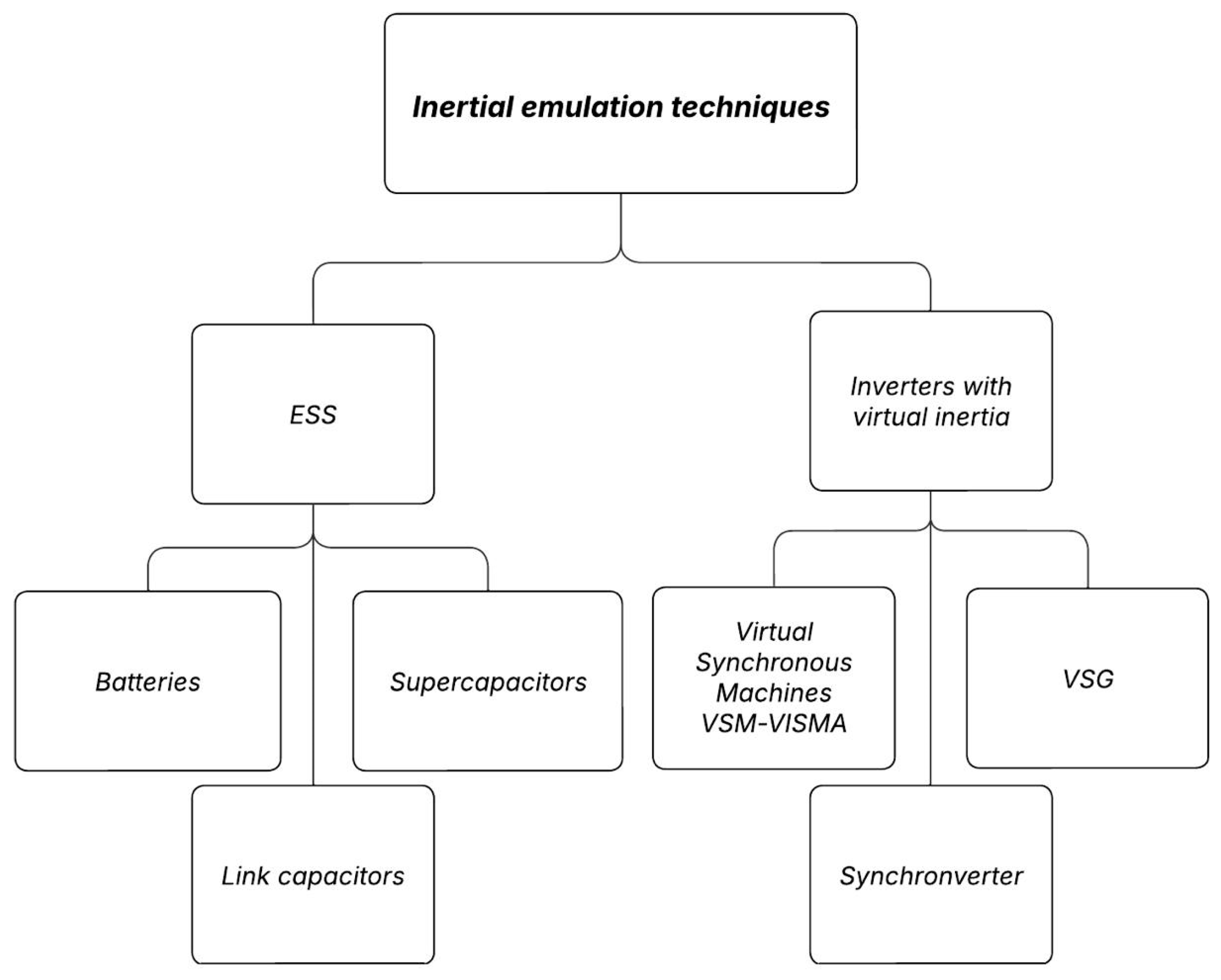
- Inertia emulation and control strategies (Virtual Synchronous Machines, Virtual Synchronous Generators, Synchronverters, and interlinking converter-based controls in hybrid AC/DC microgrids).
3. Results and Discussion
3.1. Inertia Modeling and Frequency Response in Modern Microgrids
3.1.1. Inertia
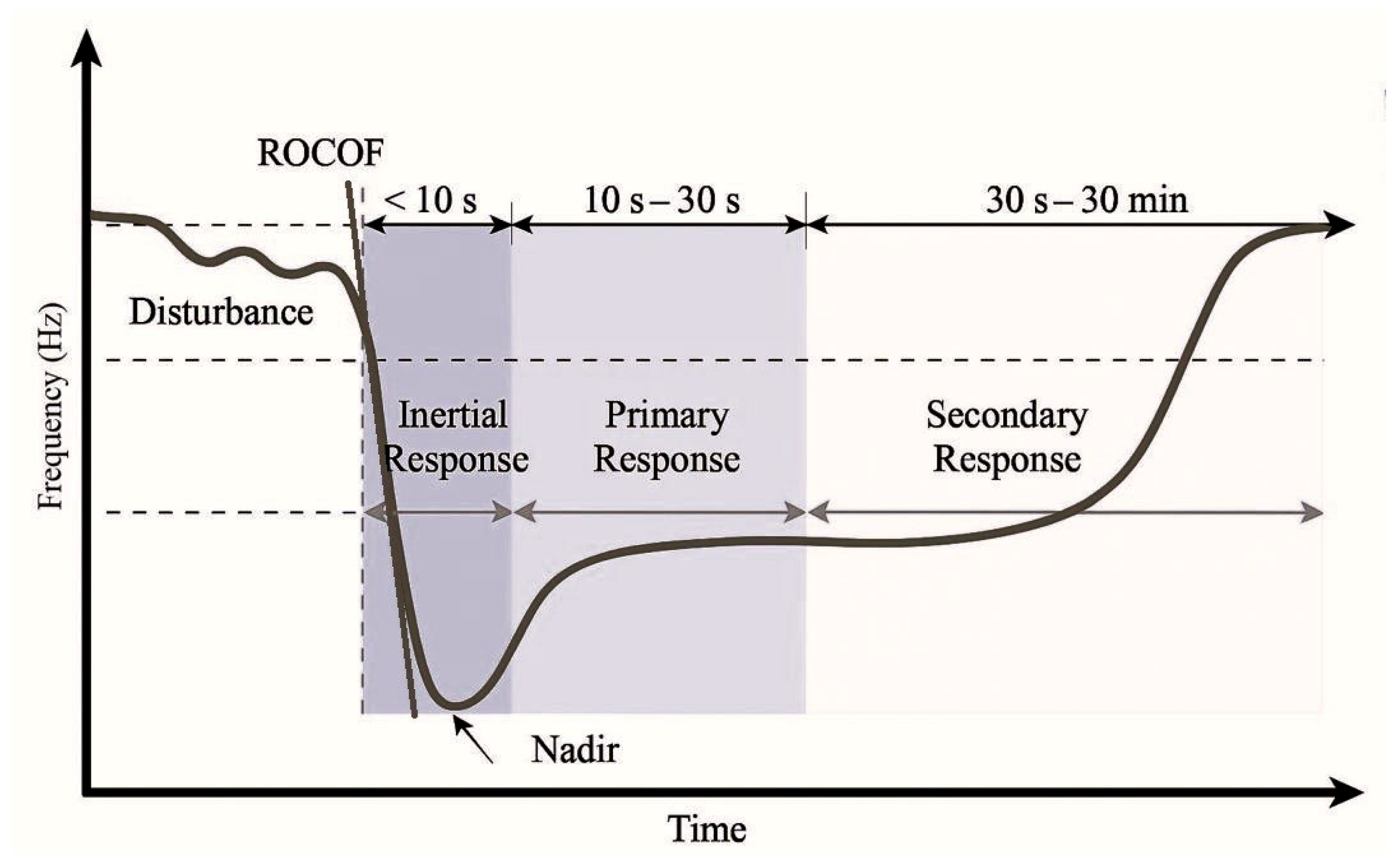
3.1.2. ROCOF
3.1.3. Microgrids
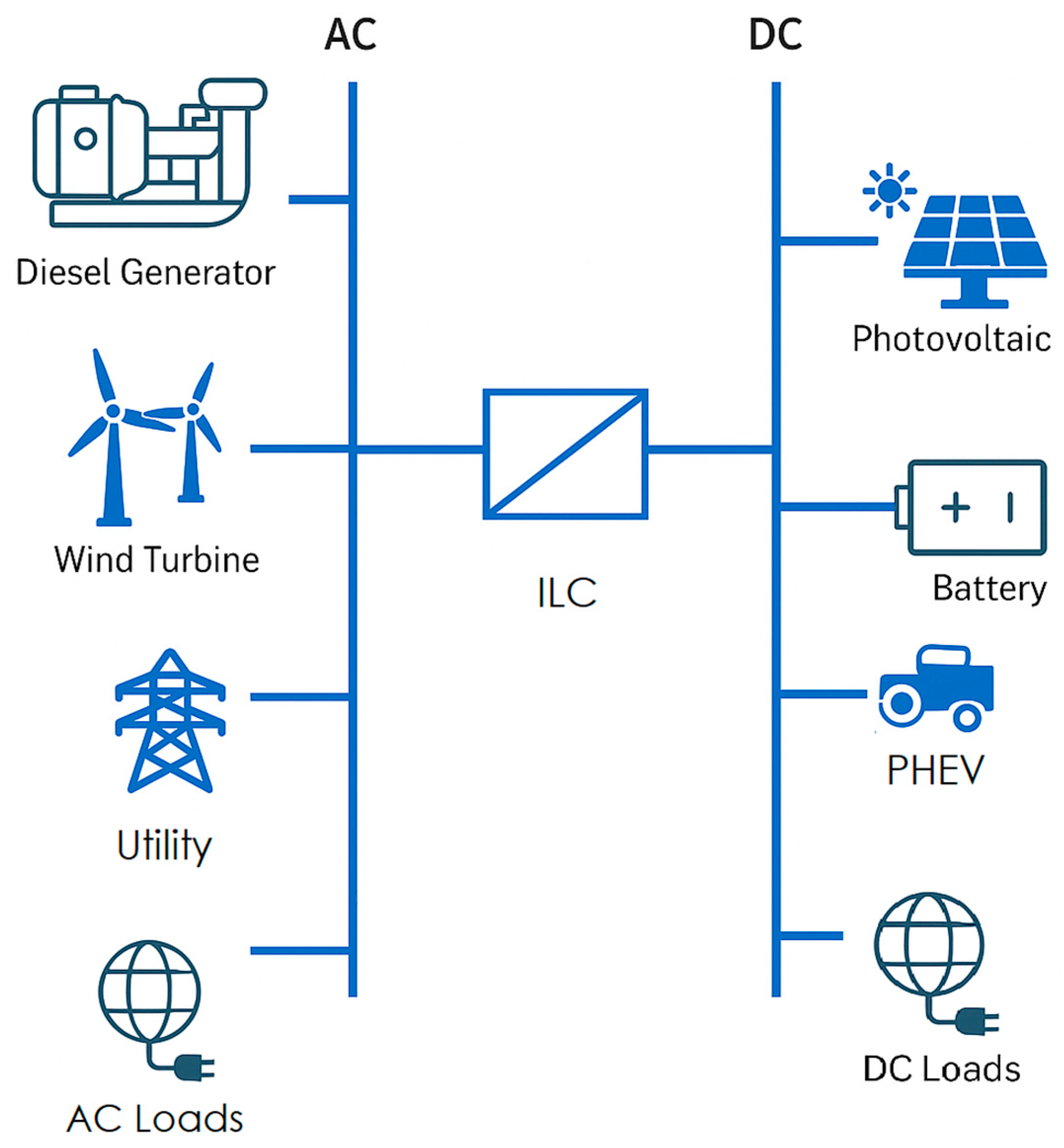
3.1.4. Hybrid Microgrids
3.1.5. Role of Inertia Estimation in Modern Power System Dynamics
3.2. Inertia Estimation Methods
3.2.1. Analytical Methods
3.2.2. Adaptive Methods
3.2.3. Statistics Methods
3.2.4. Model-Based Methods
3.2.5. Artificial Intelligence Based Methods
3.2.6. Frequency-Domain-Based Methods
3.2.7. Data-Driven Methods
3.3. Inertia Control
3.3.1. Inertia in AC Microgrids
3.3.2. Inertia in AC-DC Microgrids
3.4. Discussion and Future Work
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| AGC | Automatic Gain Control |
| ANN | Artificial Neural Network |
| ARIMA | Auto Regressive Integrated Moving Average |
| ARMAX | Auto Regressive Moving Average with eXogenous inputs |
| ARX | Auto Regressive with Extra Inputs |
| BP | Back Propagation |
| CIG | Converter Interfaced Generation |
| COI | Center of Inertia |
| DC | Direct Current |
| DER | Distributed Energy Resource |
| DFIG | Doubly fed induction generator |
| DFT | Discrete Fourier Transform |
| DMD | Dynamic Mode Decomposition |
| DREM | Dynamic Regressor Extension and Mixing |
| DTTFT | Discrete-Time Taylor–Fourier Transform |
| EKF | Extended Kalman Filter |
| ESS | Energy Storage System |
| EV | Electric Vehicles |
| GA | Genetic Algorithm |
| GA-BP | Back propagation neural network optimized by genetic algorithm |
| GF | Grid-Forming Converter |
| HIL | Hardware in Loop |
| HMG | Hybrid Microgrid |
| HSE | Harmonic State Estimation |
| ILC | Interlinking converter |
| ISHUKF | Improved Sage-Husa Unscented Kalman Filter |
| KF | Kalman Filter |
| LSM | Least Squares Method |
| MCMC | Markov Chain Monte Carlo |
| MPM | Micro Perturbation Method |
| MPPT | Maximum power point tracking |
| NPC | Normalized Power Coordination |
| PAO | Predict-and-Optimize |
| PHEV | Plug-in Hybrid Electric Vehicle |
| PI | Proportional Integral. |
| PMS | Power Management System |
| PMU | Phasor measurement unit |
| PRISMA | Preferred Reporting Items for Systematic reviews and Meta-Analyses |
| PSO–SVM | Particle Swarm Optimization—Support Vector Machine |
| PV | Photovoltaic |
| RES | Renewable Energy Sources |
| RES | Renewable energy source |
| ROCOF | Rate of change of frequency |
| ROCOV | Rate of change of voltage |
| SCADA | Supervisory Control And Data Acquisition |
| SG | Synchronous generator |
| SINDy | Sparse Identification of Nonlinear Dynamics |
| SoC | State of Charge |
| SWM | Sliding window method |
| TKEO | Teager-Kaiser energy operator |
| UKF | Unscented Kalman Filter |
| VI | Virtual Inertia |
| VIE | Virtual Inertia Emulator |
| VSC | Voltage Source Converter |
| VSG | Virtual Synchronous Generator |
| VSM | Virtual Synchronous Machines |
| WAMS | Wide Area Measurement System |
Appendix A. PRISMA Checklist
| Section and Topic | Item # | Checklist Item | Location Where Item Is Reported |
|---|---|---|---|
| TITLE | |||
| Title | 1 | Identify the report as a systematic review. | 1 |
| ABSTRACT | |||
| Abstract | 2 | The abstract provides a clear background and objective, briefly describes the methodology and time span of the evidence, summarizes the main findings, and highlights conclusions and future directions | 1 |
| INTRODUCTION | |||
| Rationale | 3 | Describe the rationale for the review in the context of existing knowledge. | 3 |
| Objectives | 4 | Provide an explicit statement of the objective(s) or question(s) the review addresses. | 3 |
| METHODS | |||
| Eligibility criteria | 5 | Specify the inclusion and exclusion criteria for the review and how studies were grouped for the syntheses. | 4 |
| Information sources | 6 | Specify all databases, registers, websites, organisations, reference lists and other sources searched or consulted to identify studies. Specify the date when each source was last searched or consulted. | 4 |
| Search strategy | 7 | Present the full search strategies for all databases, registers and websites, including any filters and limits used. | 4 |
| Selection process | 8 | Specify the methods used to decide whether a study met the inclusion criteria of the review, including how many reviewers screened each record and each report retrieved, whether they worked independently, and if applicable, details of automation tools used in the process. | 4 |
| Data collection process | 9 | Specify the methods used to collect data from reports, including how many reviewers collected data from each report, whether they worked independently, any processes for obtaining or confirming data from study investigators, and if applicable, details of automation tools used in the process. | 4 |
| Data items | 10a | List and define all outcomes for which data were sought. Specify whether all results that were compatible with each outcome domain in each study were sought (e.g., for all measures, time points, analyses), and if not, the methods used to decide which results to collect. | 5 |
| 10b | List and define all other variables for which data were sought (e.g., participant and intervention characteristics, funding sources). Describe any assumptions made about any missing or unclear information. | 5 | |
| Study risk of bias assessment | 11 | Specify the methods used to assess risk of bias in the included studies, including details of the tool(s) used, how many reviewers assessed each study and whether they worked independently, and if applicable, details of automation tools used in the process. | 4 |
| Effect measures | 12 | Specify for each outcome the effect measure(s) (e.g., risk ratio, mean difference) used in the synthesis or presentation of results. | N/A |
| Synthesis methods | 13a | Describe the processes used to decide which studies were eligible for each synthesis (e.g., tabulating the study intervention characteristics and comparing against the planned groups for each synthesis (item #5)). | N/A |
| 13b | Describe any methods required to prepare the data for presentation or synthesis, such as handling of missing summary statistics, or data conversions. | N/A | |
| 13c | Describe any methods used to tabulate or visually display results of individual studies and syntheses. | N/A | |
| 13d | Describe any methods used to synthesize results and provide a rationale for the choice(s). If meta-analysis was performed, describe the model(s), method(s) to identify the presence and extent of statistical heterogeneity, and software package(s) used. | N/A | |
| 13e | Describe any methods used to explore possible causes of heterogeneity among study results (e.g., subgroup analysis, meta-regression). | N/A | |
| 13f | Describe any sensitivity analyses conducted to assess robustness of the synthesized results. | N/A | |
| Reporting bias assessment | 14 | Describe any methods used to assess risk of bias due to missing results in a synthesis (arising from reporting biases). | N/A |
| Certainty assessment | 15 | Describe any methods used to assess certainty (or confidence) in the body of evidence for an outcome. | 4 |
| RESULTS | |||
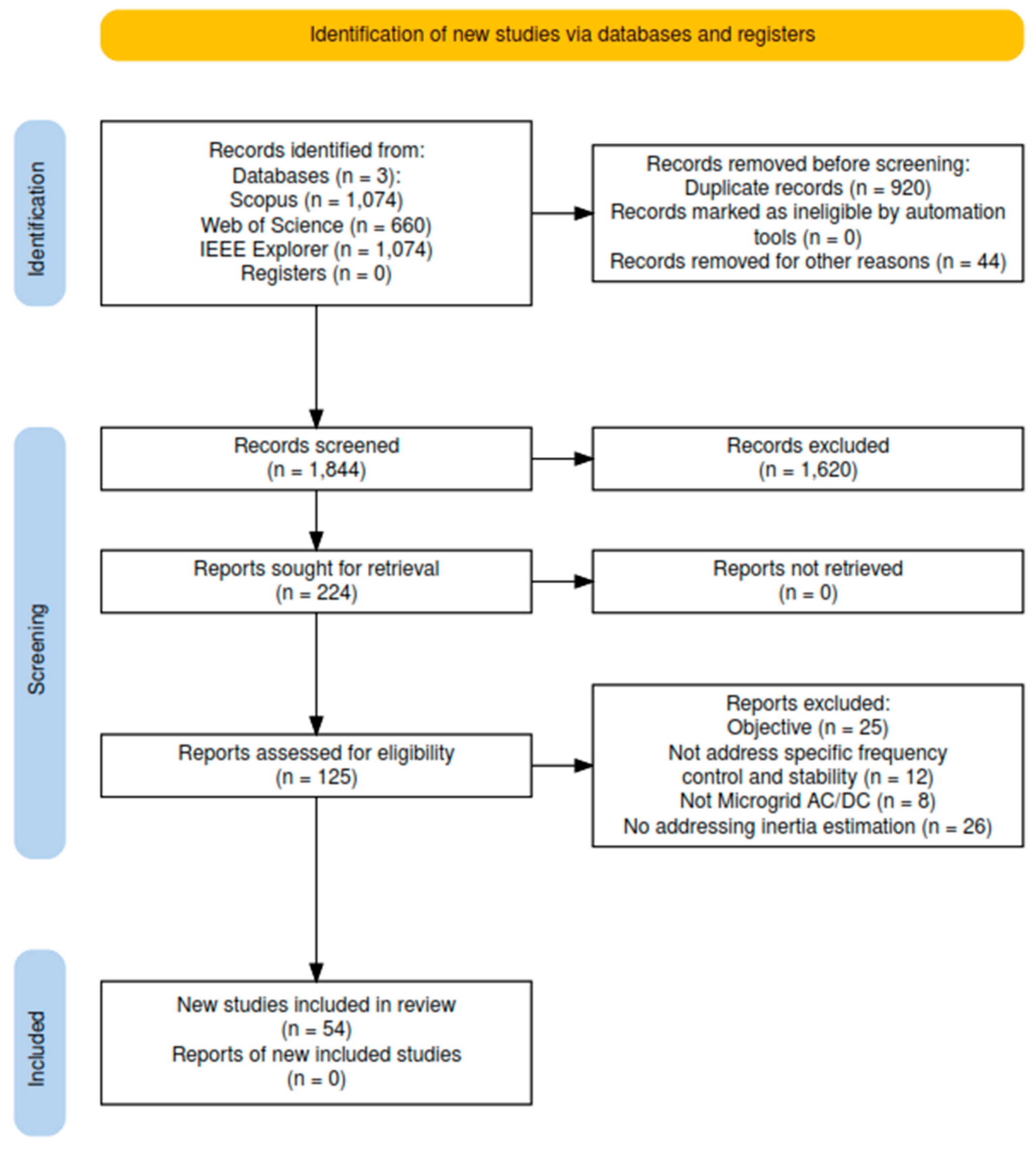
| Study selection | 16a | Describe the results of the search and selection process, from the number of records identified in the search to the number of studies included in the review, ideally using a flow diagram. | 4 |
| 16b | Cite studies that might appear to meet the inclusion criteria, but which were excluded, and explain why they were excluded. | N/A | |
| Study characteristics | 17 | Cite each included study and present its characteristics. | 4 |
| Risk of bias in studies | 18 | Present assessments of risk of bias for each included study. | N/A |
| Results of individual studies | 19 | For all outcomes, present, for each study: (a) summary statistics for each group (where appropriate) and (b) an effect estimate and its precision (e.g., confidence/credible interval), ideally using structured tables or plots. | N/A |
| Results of syntheses | 20a | For each synthesis, briefly summarise the characteristics and risk of bias among contributing studies. | 3 |
| 20b | Present results of all statistical syntheses conducted. If meta-analysis was done, present for each the summary estimate and its precision (e.g., confidence/credible interval) and measures of statistical heterogeneity. If comparing groups, describe the direction of the effect. | 8 | |
| 20c | Present results of all investigations of possible causes of heterogeneity among study results. | 8 | |
| 20d | Present results of all sensitivity analyses conducted to assess the robustness of the synthesized results. | N/A | |
| Reporting biases | 21 | Present assessments of risk of bias due to missing results (arising from reporting biases) for each synthesis assessed. | 11 |
| Certainty of evidence | 22 | Present assessments of certainty (or confidence) in the body of evidence for each outcome assessed. | N/A |
| DISCUSSION | |||
| Discussion | 23a | Provide a general interpretation of the results in the context of other evidence. | 21 |
| 23b | Discuss any limitations of the evidence included in the review. | 17 | |
| 23c | Discuss any limitations of the review processes used. | N/A | |
| 23d | Discuss implications of the results for practice, policy, and future research. | 20 | |
| OTHER INFORMATION | |||
| Registration and protocol | 24a | Provide registration information for the review, including register name and registration number, or state that the review was not registered. | N/A |
| 24b | Indicate where the review protocol can be accessed, or state that a protocol was not prepared. | N/A | |
| 24c | Describe and explain any amendments to information provided at registration or in the protocol. | 22 | |
| Support | 25 | Describe sources of financial or non-financial support for the review, and the role of the funders or sponsors in the review. | |
| Competing interests | 26 | Declare any competing interests of review authors. | 22 |
| Availability of data, code and other materials | 27 | Report which of the following are publicly available and where they can be found: template data collection forms; data extracted from included studies; data used for all analyses; analytic code; any other materials used in the review. | 22 |
References
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the Art in Research on Microgrids: A Review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for the Specification of Microgrid Controllers; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Alonso, A.M.S.; Marafão, F.P.; Tedeschi, E. Dispatchable Microgrids: An Extended Provision of Systemic Ancillary Services to Low-Voltage Distribution Grids. IEEE Access 2024, 12, 76692–76706. [Google Scholar] [CrossRef]
- Mallick, A.; Mishra, A.; Hota, A.R.; Bajpai, P. Distributed Coordination of Multi-Microgrids in Active Distribution Networks for Provisioning Ancillary Services. IEEE Syst. J. 2024, 18, 1492–1503. [Google Scholar] [CrossRef]
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future Low-Inertia Power Systems: Requirements, Issues, and Solutions—A Review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Frigo, G.; Negri, V.; Mingotti, A.; Tinarelli, R.; Peretto, L.; Rens, J.; Joubert, T. Validating Inertia Assessment Metrics in Distribution Systems with High RES Penetration. In Proceedings of the 2024 IEEE 14th International Workshop on Applied Measurements for Power Systems (AMPS), Caserta, Italy, 18–20 September 2024; pp. 1–5. [Google Scholar]
- Li, C.; Li, Y.; Du, Y.; Gao, X.; Yang, Y.; Cao, Y.; Blaabjerg, F. Self-Stability and Induced-Stability Analysis for Frequency and Voltage in Grid-Forming VSG System with Generic Magnitude–Phase Model. IEEE Trans. Ind. Inform. 2024, 20, 12328–12338. [Google Scholar] [CrossRef]
- Heylen, E.; Teng, F.; Strbac, G. Challenges and Opportunities of Inertia Estimation and Forecasting in Low-Inertia Power Systems. Renew. Sustain. Energy Rev. 2021, 147, 111176. [Google Scholar] [CrossRef]
- Cristaldi, L.; Faifer, M.; Laurano, C.; Ottoboni, R.; Petkovski, E.; Toscani, S. Power Generation Control Algorithm for the Participation of Photovoltaic Panels in Network Stability. IEEE Trans. Instrum. Meas. 2023, 72, 9000809. [Google Scholar] [CrossRef]
- Rajan, R.; Fernandez, F.M.; Yang, Y. Primary Frequency Control Techniques for Large-Scale PV-Integrated Power Systems: A Review. Renew. Sustain. Energy Rev. 2021, 144, 110998. [Google Scholar] [CrossRef]
- Wei, X.; Tang, F.; Li, Y.; Qin, F.; Zhang, T. Study on the Oscillation Center of DFIG-Based Wind Farm Power System. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar]
- Wu, F.; Li, Y.; Du, L. Inertia Estimation of Islanded Microgrids Integrated with Power-Electronics-Interfaced DERs. In Proceedings of the 2023 IEEE Transportation Electrification Conference & Expo (ITEC), Detroit, MI, USA, 21–23 June 2023; pp. 1–5. [Google Scholar]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Babu, T.S.; Pouryekta, A. Synchronverter: A Comprehensive Review of Modifications, Stability Assessment, Applications and Future Perspectives. IEEE Access 2020, 8, 131565–131589. [Google Scholar] [CrossRef]
- Mallemaci, V.; Mandrile, F.; Rubino, S.; Mazza, A.; Carpaneto, E.; Bojoi, R. A Comprehensive Comparison of Virtual Synchronous Generators with Focus on Virtual Inertia and Frequency Regulation. Electr. Power Syst. Res. 2021, 201, 107516. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.-Y. Virtual Inertia-Based Inverters for Mitigating Frequency Instability in Grid-Connected Renewable Energy System: A Review. Appl. Sci. 2019, 9, 5300. [Google Scholar] [CrossRef]
- Ren, M.; Sun, X.; Sun, Y.; Shi, K.; Xu, P. A Virtual Inertial Control Strategy for Bidirectional Interface Converters in Hybrid Microgrid. Int. J. Electr. Power Energy Syst. 2023, 153, 109388. [Google Scholar] [CrossRef]
- Du, Y.; Chong, P.; Wang, X.; Yang, X.; Yang, S. Adaptive RoCoX Droop Control Strategy for AC/DC Hybrid Microgrid. Int. J. Electr. Power Energy Syst. 2024, 157, 109860. [Google Scholar] [CrossRef]
- Bakeer, A.; Chub, A.; Abid, A.; Zaid, S.A.; Alghamdi, T.A.H.; Salama, H.S. Enhancing Grid-Forming Converters Control in Hybrid AC/DC Microgrids Using Bidirectional Virtual Inertia Support. Processes 2024, 12, 139. [Google Scholar] [CrossRef]
- Prabhakar, K.; Jain, S.K.; Padhy, P.K. Inertia Estimation in Modern Power System: A Comprehensive Review. Electr. Power Syst. Res. 2022, 211, 108222. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Orjuela-Canon, A.D.; Ganger, D.; Persson, M.; Gonzalez-Longatt, F.; Sood, V.K.; Martinez, W. Nadir Frequency Estimation in Low-Inertia Power Systems. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 918–922. [Google Scholar]
- Tan, B.; Zhao, J.; Netto, M.; Krishnan, V.; Terzija, V.; Zhang, Y. Power System Inertia Estimation: Review of Methods and the Impacts of Converter-Interfaced Generations. Int. J. Electr. Power Energy Syst. 2022, 134, 107362. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Static Synchronous Generators for Distributed Generation and Renewable Energy. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–6. [Google Scholar]
- Messasma, C.; Chouaba, S.E.; Sari, B.; Barakat, A.; Félix-Herrán, L.C. Improving Primary Frequency Response in Photovoltaic Systems Using Hybrid Inertia and Intelligent Control Techniques. J. Electr. Eng. 2024, 75, 351–362. [Google Scholar] [CrossRef]
- Kim, B.; Abed, E.H. Power System Fast Frequency Control in Low Inertia Environment Using MPC. In Proceedings of the 2024 IEEE Green Technologies Conference (GreenTech), Springdale, AR, USA, 3–5 April 2024. [Google Scholar]
- Zhang, Y.; Zhang, C.; Cai, X.; Liang, L.; Yu, Y. Frequency Support Analysis in Heterogeneous Multi-Machine System and Enhancement Frequency Control of The Grid-Forming Converter. In Proceedings of the 2023 IEEE 14th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Shanghai, China, 9–12 June 2023; pp. 792–799. [Google Scholar]
- Ghosh, R.; Tummuru, N.R.; Rajpurohit, B.S.; Monti, A. Virtual Inertia from Renewable Energy Sources: Mathematical Representation and Control Strategy. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar]
- Liu, D.; Jiang, K.; Ji, X.; Cao, K.; Xu, C.; Sang, S.; Yang, D. Improved VSG Strategy of Grid-Forming Inverters for Supporting Inertia and Damping. Front. Energy Res. 2024, 11, 1331024. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.; Wang, J.; Wang, M.; Chen, L.; Jiang, F.; Chen, M. Adaptive Inertia VSG Control Method Involving Power and Power Change Rate. In Proceedings of the 2023 6th International Conference on Electrical Engineering and Green Energy (CEEGE), Grimstad, Norway, 6–9 June 2023; pp. 80–84. [Google Scholar]
- Li, Q.; Ren, B.; Tang, W.; Wang, D.; Wang, C.; Lv, Z. Analyzing the Inertia of Power Grid Systems Comprising Diverse Conventional and Renewable Energy Sources. Energy Rep. 2022, 8, 15095–15105. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y.; Turschner, D.; Beck, H.-P. Enhanced Virtual Inertia Control Based on Derivative Technique to Emulate Simultaneous Inertia and Damping Properties for Microgrid Frequency Regulation. IEEE Access 2019, 7, 14422–14433. [Google Scholar] [CrossRef]
- Wang, B.; Sun, H.; Li, W.; Yang, C.; Wei, W.; Wu, J. Power System Inertia Estimation Method Based on Energy Conservation. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; pp. 705–711. [Google Scholar]
- Tan, B.; Zhao, J.; Terzija, V.; Zhang, Y. Decentralized Data-Driven Estimation of Generator Rotor Speed and Inertia Constant Based on Adaptive Unscented Kalman Filter. Int. J. Electr. Power Energy Syst. 2022, 137, 107853. [Google Scholar] [CrossRef]
- Zhong, W.; Tzounas, G.; Liu, M.; Milano, F. On-Line Inertia Estimation of Virtual Power Plants. Electr. Power Syst. Res. 2022, 212, 108336. [Google Scholar] [CrossRef]
- Zia, M.F.; Benbouzid, M.; Elbouchikhi, E.; Muyeen, S.M.; Techato, K.; Guerrero, J.M. Microgrid Transactive Energy: Review, Architectures, Distributed Ledger Technologies, and Market Analysis. IEEE Access 2020, 8, 19410–19432. [Google Scholar] [CrossRef]
- Khosravi, N.; Çelik, D.; Bevrani, H.; Echalih, S. Microgrid Stability: A Comprehensive Review of Challenges, Trends, and Emerging Solutions. Int. J. Electr. Power Energy Syst. 2025, 170, 110829. [Google Scholar] [CrossRef]
- Dinata, N.F.P.; Ramli, M.A.M.; Jambak, M.I.; Sidik, M.A.B.; Alqahtani, M.M. Designing an Optimal Microgrid Control System Using Deep Reinforcement Learning: A Systematic Review. Eng. Sci. Technol. Int. J. 2024, 51, 101651. [Google Scholar] [CrossRef]
- Chandak, S.; Rout, P.K. The Implementation Framework of a Microgrid: A Review. Int. J. Energy Res. 2021, 45, 3523–3547. [Google Scholar] [CrossRef]
- Jafarizadeh, H.; Yamini, E.; Zolfaghari, S.M.; Esmaeilion, F.; Assad, M.E.H.; Soltani, M. Navigating Challenges in Large-Scale Renewable Energy Storage: Barriers, Solutions, and Innovations. Energy Rep. 2024, 12, 2179–2192. [Google Scholar] [CrossRef]
- Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A Review of Microgrid Energy Management and Control Strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
- Rai, I.; Suchetha, C. Microgrid and Grid Synchronization: A Critical Analysis of Challenges and Opportunities. Electr. Power Syst. Res. 2025, 242, 111434. [Google Scholar] [CrossRef]
- Pourbehzadi, M.; Niknam, T.; Aghaei, J.; Mokryani, G.; Shafie-khah, M.; Catalão, J.P.S. Optimal Operation of Hybrid AC/DC Microgrids under Uncertainty of Renewable Energy Resources: A Comprehensive Review. Int. J. Electr. Power Energy Syst. 2019, 109, 139–159. [Google Scholar] [CrossRef]
- Agrawal, S.; Tyagi, B.; Kumar, V.; Sharma, P. Operation and Control of Parallel-Operated Interlinking Converter in Hybrid Microgrid. IEEE Trans. Ind. Appl. 2025, 61, 5660–5669. [Google Scholar] [CrossRef]
- Mohammadi, F.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B.; Ali, M.H.; Wei, W.; Erdinc, O.; Shirkhani, M. Robust Control Strategies for Microgrids: A Review. IEEE Syst. J. 2022, 16, 2401–2412. [Google Scholar] [CrossRef]
- Hu, P.; Li, Y.; Yu, Y.; Blaabjerg, F. Inertia Estimation of Renewable-Energy-Dominated Power System. Renew. Sustain. Energy Rev. 2023, 183, 113481. [Google Scholar] [CrossRef]
- Sanchez-Ocampo, A.; Paternina, M.R.A.; Ramos-Guerrero, J.M.; Mejia-Ruiz, G.E.; Ramirez-Arredondo, J.M.; Lugnani, L.; Munguia-Perez, F.; Zamora-Mendez, A.; Rodriguez-Rodriguez, J.R. Real-Time Inertia Estimation via ARMAX Model Representation and Synchrophasor Measurements. IEEE Lat. Am. Trans. 2025, 23, 405–414. [Google Scholar] [CrossRef]
- Kontis, E.O.; Pasiopoulou, I.D.; Kirykos, D.A.; Papadopoulos, T.A.; Papagiannis, G.K. Estimation of Power System Inertia: A Comparative Assessment of Measurement-Based Techniques. Electr. Power Syst. Res. 2021, 196, 107250. [Google Scholar] [CrossRef]
- Fernandes, L.L.; Paternina, M.R.A.; Dotta, D.; Chow, J.H. Data-Driven Assessment of Center of Inertia and Regional Inertia Content Considering Load Contribution. Int. J. Electr. Power Energy Syst. 2024, 156, 109733. [Google Scholar] [CrossRef]
- Dimoulias, S.C.; Kontis, E.O.; Papagiannis, G.K. On-Line Tracking of Inertia Constants Using Ambient Measurements. Electr. Power Syst. Res. 2023, 224, 109643. [Google Scholar] [CrossRef]
- Yang, D.; Wang, B.; Cai, G.; Chen, Z.; Ma, J.; Sun, Z.; Wang, L. Data-Driven Estimation of Inertia for Multiarea Interconnected Power Systems Using Dynamic Mode Decomposition. IEEE Trans. Ind. Inform. 2021, 17, 2686–2695. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.; Ooi, B.-T. Estimation of Inertia for Synchronous and Non-Synchronous Generators Based on Ambient Measurements. IEEE Trans. Power Syst. 2022, 37, 3747–3757. [Google Scholar] [CrossRef]
- Abouyehia, M.; Egea-Àlvarez, A.; Ahmed, K.H. Evaluating Inertia Estimation Methods in Low-Inertia Power Systems: A Comprehensive Review with Analytic Hierarchy Process-Based Ranking. Renew. Sustain. Energy Rev. 2025, 217, 115794. [Google Scholar] [CrossRef]
- Gutiérrez, F.; Riquelme, E.; Barbosa, K.A.; Chávez, H. State Estimation for Synthetic Inertia Control System Using Kalman Filter. In Proceedings of the 2021 IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Online, 22–26 March 2021; pp. 1–7. [Google Scholar]
- Wang, Y.; Yokoyama, A.; Baba, J. A Multifunctional Online Estimation Method for Synchronous Inertia of Power Systems Using Short-Time Phasor Transient Measurement Data With Linear Least Square Method After Disturbance. IEEE Access 2024, 12, 17010–17022. [Google Scholar] [CrossRef]
- Liu, M.; Chen, J.; Xie, Y.; Deng, X.; Milano, F. Least Square Method for the Identification of Equivalent Inertia Constant. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- Gotti, D.; Ledesma, P.; Amaris, H. A Recursive System Identification Inertia Estimator for Traditional and Converter-Interfaced Generators. Int. J. Electr. Power Energy Syst. 2023, 154, 109445. [Google Scholar] [CrossRef]
- Yin, H.; Wu, Y.; Qiu, W.; Zeng, C.; You, S.; Tan, J.; Hoke, A.; Kruse, C.J.; Rockwell, B.W.; Kawamura, K.A.; et al. Precise ROCOF Estimation Algorithm for Low Inertia Power Grids. Electr. Power Syst. Res. 2022, 209, 107968. [Google Scholar] [CrossRef]
- Phurailatpam, C.; Rather, Z.H.; Bahrani, B.; Doolla, S. Measurement-Based Estimation of Inertia in AC Microgrids. IEEE Trans. Sustain. Energy 2020, 11, 1975–1984. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Le, K.; Nguyen, T.-A.; Phan, O.-D. Estimation of Power System Inertia Using Traditional Swing Equation, Polynomial Approximation and RV Methods. In Proceedings of the 2020 International Symposium on Computer, Consumer and Control (IS3C), Taichung, Taiwan, 13–16 November 2020; pp. 347–350. [Google Scholar]
- Kummerow, A.; Monsalve, C.; Brosinsky, C.; Nicolai, S.; Westermann, D. A Novel Framework for Synchrophasor Based Online Recognition and Efficient Post-Mortem Analysis of Disturbances in Power Systems. Appl. Sci. 2020, 10, 5209. [Google Scholar] [CrossRef]
- Rodales, D.; Zamora-Mendez, A.; Serna, J.A.d.l.O.; Ramirez, J.M.; Paternina, M.R.A.; Lugnani, L.; Mejia-Ruiz, G.E.; Sanchez-Ocampo, A.; Dotta, D. Model-Free Inertia Estimation in Bulk Power Grids through O-Splines. Int. J. Electr. Power Energy Syst. 2023, 153, 109323. [Google Scholar] [CrossRef]
- Cao, X.; Stephen, B.; Abdulhadi, I.F.; Booth, C.D.; Burt, G.M. Switching Markov Gaussian Models for Dynamic Power System Inertia Estimation. IEEE Trans. Power Syst. 2016, 31, 3394–3403. [Google Scholar] [CrossRef]
- Lugnani, L.; Dotta, D.; Lackner, C.; Chow, J. ARMAX-Based Method for Inertial Constant Estimation of Generation Units Using Synchrophasors. Electr. Power Syst. Res. 2020, 180, 106097. [Google Scholar] [CrossRef]
- Shrestha, A.; Ghimire, B.; Gonzalez-Longatt, F. A Bayesian Model to Forecast the Time Series Kinetic Energy Data for a Power System. Energies 2021, 14, 3299. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, Z.; Zeng, J.; Liu, J. Estimation of Power System Inertia Using Discrete Dynamic Regressor Extension and Mixing. In Proceedings of the 2023 3rd International Conference on Energy Engineering and Power Systems (EEPS), Dali, China, 28–30 July 2023; pp. 691–696. [Google Scholar]
- Schiffer, J.; Aristidou, P.; Ortega, R. Online Estimation of Power System Inertia Using Dynamic Regressor Extension and Mixing. IEEE Trans. Power Syst. 2019, 34, 4993–5001. [Google Scholar] [CrossRef]
- Makolo, P.; Oladeii, I.; Zamora, R.; Lie, T.-T. Short-Range Inertia Prediction for Power Networks with Penetration of RES. In Proceedings of the TENCON 2021—2021 IEEE Region 10 Conference (TENCON), Auckland, New Zealand, 7–10 December 2021; pp. 765–770. [Google Scholar]
- Panda, R.K.; Mohapatra, A.; Srivastava, S.C. Online Estimation of System Inertia in a Power Network Utilizing Synchrophasor Measurements. IEEE Trans. Power Syst. 2020, 35, 3122–3132. [Google Scholar] [CrossRef]
- Zhao, J.; Tang, Y.; Terzija, V. Robust Online Estimation of Power System Center of Inertia Frequency. IEEE Trans. Power Syst. 2019, 34, 821–825. [Google Scholar] [CrossRef]
- Zhang, W.; Wen, Y.; Li, L.; Zhang, Q.; Cheng, C.; Li, J. Online Estimation of Inertia and Frequency Regulation Capability Based on Small Perturbation. Energy Rep. 2022, 8, 650–656. [Google Scholar] [CrossRef]
- Yu, P.; Sun, J. Improved Sage–Husa Unscented Kalman Filter for Harmonic State Estimation in Distribution Grid. Electronics 2025, 14, 376. [Google Scholar] [CrossRef]
- Ghosh, S. An Estimation of COI Frequency Using Minimal Measurements in Renewable Power Grid. IEEE Trans. Ind. Appl. 2025, 61, 2825–2834. [Google Scholar] [CrossRef]
- You, S.; Li, H.; Liu, S.; Sun, K.; Wang, W.; Qiu, W.; Liu, Y. Calculate Center-of-Inertia Frequency and System RoCoF Using PMU Data. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar]
- Ke, D.; Chung, C.Y.; Xu, J.; Shen, Y.; Sun, Y. Inertia Emulation Uncorrelated With Electromechanical Dynamics to Improve Frequency Transients Using Center of Inertia (COI) Frequency Signal. IEEE Trans. Power Syst. 2021, 36, 1736–1749. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Y.; Ding, P. Review of Equivalent Methods for Power System. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 143–150. [Google Scholar]
- Paidi, E.S.N.R.; Marzooghi, H.; Yu, J.; Terzija, V. Development and Validation of Artificial Neural Network-Based Tools for Forecasting of Power System Inertia With Wind Farms Penetration. IEEE Syst. J. 2020, 14, 4978–4989. [Google Scholar] [CrossRef]
- Wazirali, R.; Yaghoubi, E.; Abujazar, M.S.S.; Ahmad, R.; Vakili, A.H. State-of-the-Art Review on Energy and Load Forecasting in Microgrids Using Artificial Neural Networks, Machine Learning, and Deep Learning Techniques. Electr. Power Syst. Res. 2023, 225, 109792. [Google Scholar] [CrossRef]
- M, A.J.H.; Pinto, R.T. Artificial Neural Network-Based Inertia Estimation. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- Lakshminarayana, S.; Sthapit, S.; Maple, C. Application of Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation. Sustainability 2022, 14, 2051. [Google Scholar] [CrossRef]
- Amini, S.; Golpîra, H.; Bevrani, H.; Moshtagh, J. An Innovative Approach for Inertia Estimation in Power Grids: Integrating ANN and Equal Area Criterion. IET Gener. Transm. Distrib. 2025, 19, e70041. [Google Scholar] [CrossRef]
- Tuo, M.; Li, X. Long-Term Recurrent Convolutional Network-Based Inertia Estimation Using Ambient Measurements. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022; pp. 1–6. [Google Scholar]
- Yang, Q.; Duan, J.; Bian, H.; Zhang, B. Equivalent Inertia Prediction for Power Systems with Virtual Inertia Based on PSO-SVM. Electr. Eng. 2024, 107, 2997–3010. [Google Scholar] [CrossRef]
- Shen, F.; Cao, Y.; Shahidehpour, M.; Xu, X.; Wang, C.; Wang, J.; Zhai, S. Predict-and-Optimize Model for Day-Ahead Inertia Prediction Using Distributionally Robust Unit Commitment with Renewable Energy Sources. IEEE Trans. Power Syst. 2025, 40, 2688–2699. [Google Scholar] [CrossRef]
- Deng, X.; Mo, R.; Wang, P.; Chen, J.; Nan, D.; Liu, M. Review of RoCoF Estimation Techniques for Low-Inertia Power Systems. Energies 2023, 16, 3708. [Google Scholar] [CrossRef]
- Abouyehia, M.; Egea-Àlvarez, A.; Aphale, S.S.; Ahmed, K.H. Novel Frequency-Domain Inertia Mapping and Estimation in Power Systems Using Wavelet Analysis. IEEE Trans. Power Syst. 2025, 40, 2557–2567. [Google Scholar] [CrossRef]
- de Cavalcante Paiva, S.; de Araujo Ribeiro, R.L.; Alves, D.K.; Guerrero, J.M.; Rocha, T.D.O.A.; Costa, F.B. Wavelet-Based Frequency Tracking Monitor Applied for Low-Inertia AC Microgrids. IEEE Trans. Power Electron. 2021, 36, 6674–6684. [Google Scholar] [CrossRef]
- Brambilla, A.M.; del Giudice, D.; Linaro, D.; Bizzarri, F. Electric Power-System’s Global-Inertia Estimation. Int. J. Electr. Power Energy Syst. 2024, 160, 110135. [Google Scholar] [CrossRef]
- Frasetyo, M.B.; Wijaya, F.D.; Ali, H.R.; Wiranata, M.Z. Adaptive Synchronverter Algorithm Using Q-Learning for Microgrid Stability Control. IEEE Access 2025, 13, 53731–53747. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; El-Rifaie, A.M.; Bahr, B.A.; Keshta, H.E.; Ali, M.N.; Ahmed, M.M.R. Adaptive Control of a Hybrid Microgrid With Energy Storage System. IEEE Open J. Power Electron. 2025, 6, 196–211. [Google Scholar] [CrossRef]
- Yegon, P.; Singh, M. Optimization of Battery/Ultra-Capacitor Hybrid Energy Storage System for Frequency Response Support in Low-Inertia Microgrid. IET Power Electron. 2024, 17, 1713–1727. [Google Scholar] [CrossRef]
- Hardan, F.; Norman, R.; Tricoli, P. Virtual Inertia Methods for Supporting Frequency Stabilisation in Autonomous AC/DC Microgrids. Electronics 2024, 14, 91. [Google Scholar] [CrossRef]
- Safiullah; Hote, Y.V. Enhancement of Virtual Inertia via Delay Designed GADRC in Hybrid Microgrid with Communication Delay. Sustain. Energy Grids Netw. 2024, 39, 101411. [Google Scholar] [CrossRef]
- Chethan, M.; Ravi, K. Virtual Inertia Support for Renewable Energy Integration: A Review. IEEE Access 2025, 13, 11517–11531. [Google Scholar] [CrossRef]
- Skiparev, V.; Machlev, R.; Chowdhury, N.R.; Levron, Y.; Petlenkov, E.; Belikov, J. Virtual Inertia Control Methods in Islanded Microgrids. Energies 2021, 14, 1562. [Google Scholar] [CrossRef]
- Anttila, S.; Döhler, J.S.; Oliveira, J.G.; Boström, C. Grid Forming Inverters: A Review of the State of the Art of Key Elements for Microgrid Operation. Energies 2022, 15, 5517. [Google Scholar] [CrossRef]
- Criollo, A.; Minchala-Avila, L.I.; Benavides, D.; Arévalo, P.; Tostado-Véliz, M.; Sánchez-Lozano, D.; Jurado, F. Enhancing Virtual Inertia Control in Microgrids: A Novel Frequency Response Model Based on Storage Systems. Batteries 2024, 10, 18. [Google Scholar] [CrossRef]
- Kumar, K.A.; Kushwaha, P.; Prakash, V.; Bhakar, R.; Tiwari, H.; Sharma, K.G. Inertia Emulation Trends in Low Carbon Power System. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar]
- Mishra, A.K.; Mishra, P.; Mathur, H.D. An Improved Nonlinear Deloading Approach Based on the Fuzzy Controller for Wind Turbine Generators in an Islanded Microgrid. ISA Trans. 2023, 142, 20–39. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive Virtual Inertia Control Strategy of VSG for Micro-Grid Based on Improved Bang-Bang Control Strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Huang, A.Q. Integration of DC Microgrids as Virtual Synchronous Machines Into the AC Grid. IEEE Trans. Ind. Electron. 2017, 64, 7455–7466. [Google Scholar] [CrossRef]
- Phurailatpam, C.; Rather, Z.H.; Bahrani, B.; Doolla, S. Estimation of Non-Synchronous Inertia in AC Microgrids. IEEE Trans. Sustain. Energy 2021, 12, 1903–1914. [Google Scholar] [CrossRef]
- Dahane, A.S.; Sharma, R.B. Hybrid AC-DC Microgrid Coordinated Control Strategies: A Systematic Review and Future Prospect. Renew. Energy Focus 2024, 49, 100553. [Google Scholar] [CrossRef]
- Shami, H.O.; Basem, A.; Al-Rubaye, A.H.; Sabzevari, K. A Novel Strategy to Enhance Power Management in AC/DC Hybrid Microgrid Using Virtual Synchronous Generator Based Interlinking Converters Integrated with Energy Storage System. Energy Rep. 2024, 12, 75–94. [Google Scholar] [CrossRef]
- Tasnim, M.N.; Ahmed, T.; Ahmad, S.; Mekhilef, S. Implementation of Control Strategies for Energy Storage Systems and Interlinking Converters in an Interconnected Hybrid Microgrid System for Optimal Power Management Using OPAL-RT. IEEE Trans. Ind. Appl. 2024, 60, 8520–8531. [Google Scholar] [CrossRef]
- Zhang, K.; Su, M.; Liu, Z.; Han, H.; Zhang, X.; Wang, P. A Distributed Coordination Control for Islanded Hybrid AC/DC Microgrid. IEEE Syst. J. 2023, 17, 1819–1830. [Google Scholar] [CrossRef]
- Pham, X.H.T. Adaptive Power Controller for AC/DC Hybrid Microgrids. J. Power Electron. 2025, 25. [Google Scholar] [CrossRef]
- Jin, C.; Jia, C.; Fu, J.; Wang, S. Inertia Control and Dynamic Performance Optimization of Interlinking Converter Based on Parameter Adaptation. In Proceedings of the 2022 Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 21–23 October 2022; pp. 489–493. [Google Scholar]
- Jain, D.; Saxena, D. Comprehensive Review on Control Schemes and Stability Investigation of Hybrid AC-DC Microgrid. Electr. Power Syst. Res. 2023, 218, 109182. [Google Scholar] [CrossRef]
- Hamada, H.; Kusayanagi, Y.; Tatematsu, M.; Watanabe, M.; Kikusato, H. Challenges for a Reduced Inertia Power System Due to the Large-Scale Integration of Renewable Energy. Glob. Energy Interconnect. 2022, 5, 266–273. [Google Scholar] [CrossRef]
- Rezkalla, M.; Pertl, M.; Marinelli, M. Electric Power System Inertia: Requirements, Challenges and Solutions. Electr. Eng. 2018, 100, 2677–2693. [Google Scholar] [CrossRef]
- Pinheiro, B.; Viola, L.; Chow, J.H.; Dotta, D. An Analytical Formulation for Mapping the Spatial Distribution of Nodal Inertia in Power Systems. IEEE Access 2023, 11, 45364–45376. [Google Scholar] [CrossRef]

| Estimation Method | References | Advantages | Disadvantages |
|---|---|---|---|
| ARMAX-based estimation (statistical) | [46,47] | Robustness in systems with high penetration of renewables. | Computationally intensive, especially in large or highly variable systems. |
| SWM (adaptative) | [46,48] | Provides continuous inertia estimations. | High computational demand. |
| DMD (model-based) | [46,49] | Can estimate inertia using ambient data. | Accuracy may decrease in environments with a poor signal-to-noise ratio. |
| Models based on ROCOF and the swing equation (analytical) | [8,50,51] | Provides rapid inertia estimations. | Numerical instabilities may arise. |
| Post-mortem offline (measured data) | [8] | Low computational demand. | The accuracy of estimations can be affected by the magnitude of the disturbance. |
| Estimations via PMU measurements (analytical) | [49,50] | They provide synchronized and high-frequency data, which improves accuracy. | The continuous processing of large volumes of data requires advanced infrastructure and algorithms. |
| Continuous methods (statistical) | [8] | Provides a continuous stream of estimations. | It is difficult to accurately estimate power imbalances during normal operations. |
| Predictive methods (AI-based) | [46] | Significantly aids in operational planning. | Accuracy is heavily dependent on the quality of the input data. |
| Zonal or area-based estimation (analytical) | [8] | Allows for estimating inertia in large zones, key in networks where it is not feasible to track every machine. | Each area combines generators and inverters and unifying them into a single model introduces uncertainty and reduces precision. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, F.A.; Posada, J.; França, B.W.; Rosas-Caro, J.C. Inertia in Converter-Dominated Microgrids: Control Strategies and Estimation Techniques. Electricity 2025, 6, 58. https://doi.org/10.3390/electricity6040058
González FA, Posada J, França BW, Rosas-Caro JC. Inertia in Converter-Dominated Microgrids: Control Strategies and Estimation Techniques. Electricity. 2025; 6(4):58. https://doi.org/10.3390/electricity6040058
Chicago/Turabian StyleGonzález, Fabio A., Johnny Posada, Bruno W. França, and Julio C. Rosas-Caro. 2025. "Inertia in Converter-Dominated Microgrids: Control Strategies and Estimation Techniques" Electricity 6, no. 4: 58. https://doi.org/10.3390/electricity6040058
APA StyleGonzález, F. A., Posada, J., França, B. W., & Rosas-Caro, J. C. (2025). Inertia in Converter-Dominated Microgrids: Control Strategies and Estimation Techniques. Electricity, 6(4), 58. https://doi.org/10.3390/electricity6040058







