Exploring Evolutionary Algorithms for Optimal Power Flow: A Comprehensive Review and Analysis
Abstract
1. Introduction
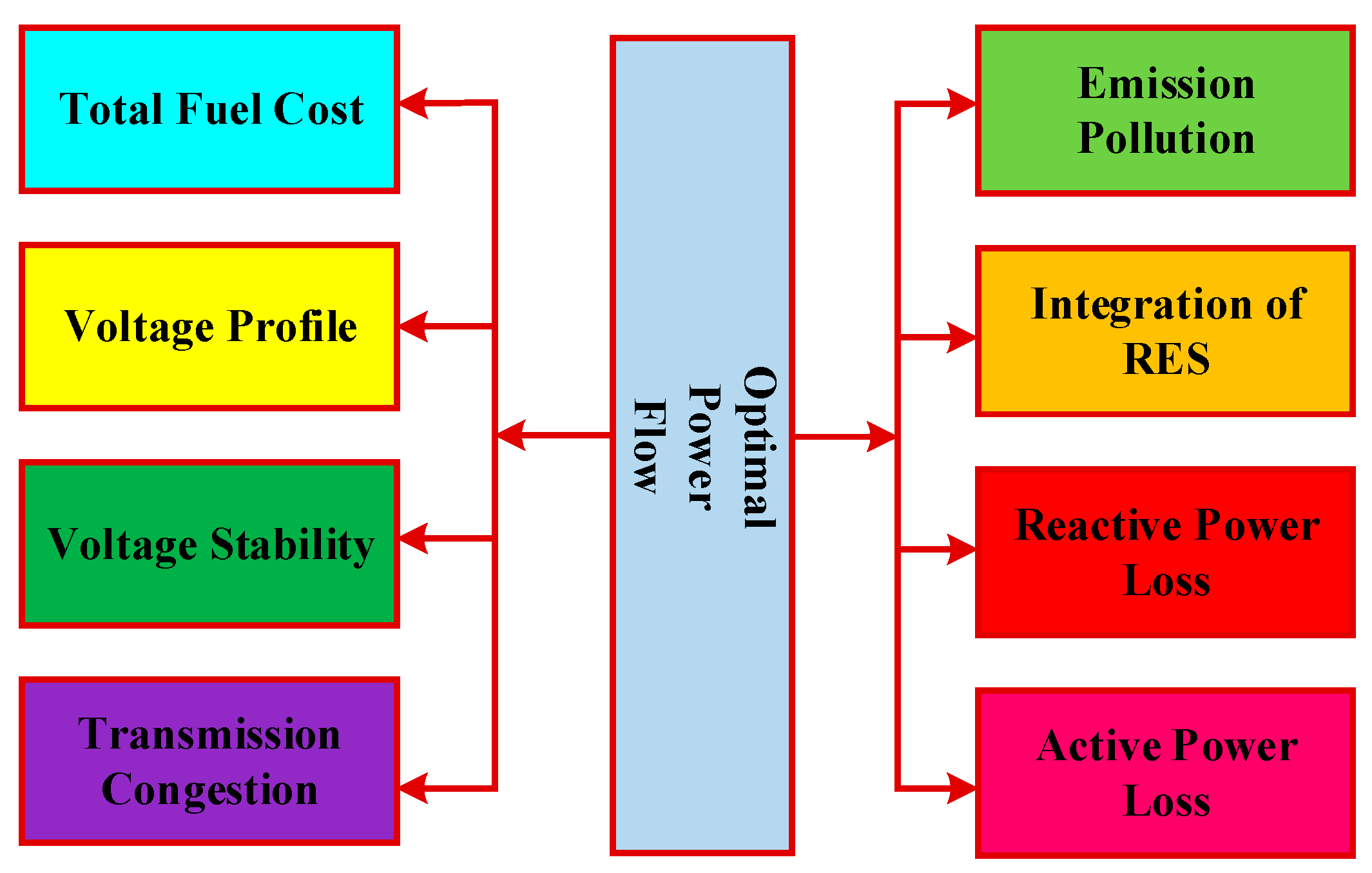
- Generator real power results;
- Generator bus voltages;
- Shunt reactors;
- Transformers taps;
- FACTS devices and phase shifters.
- Load bus voltages;
- MVA line flows;
- Generator reactive power limits;
- Slack bus active powers.
- This comprehensive review paper addresses several challenges associated with OPF issues. The discussion encompasses a range of methodologies, including convex, linear, and nonlinear approaches, and explores the integration of modern techniques such as Artificial Intelligence. The examination also extends to various constraints within AC optimal power flow (ACOPF), aiming to provide a deeper understanding of how these constraints impact and influence the optimal power flow.
- OPF challenge involves incorporating the anticipated active power production from renewable energy sources (RESs) and evaluating system’s performance across multiple indices. This analysis encompasses operating costs, voltage profile, and power losses, aiming to comprehend and optimize the intricate interplay between these factors.
2. Mathematical Formulation
2.1. Objective Functions
2.1.1. Minimization of Fuel Cost
2.1.2. Minimization of Cost with Valve Points
2.1.3. Minimization of the L-Index
2.1.4. Minimization of Transmission Loss
2.1.5. Minimization of Emission Pollution
2.2. Constraints
3. Numerous Algorithms Applied to Solve OPF Problems
3.1. Single-Objective Optimization
3.1.1. Genetic Algorithm
3.1.2. Particle Swarm Optimization
3.1.3. Differential Evolution
3.1.4. Gravitational Search Algorithm
3.1.5. Artificial Bee Colony
3.2. Multi-Objective Optimization Problem
3.2.1. Weighted Sum Technique
3.2.2. Non-Dominated Sorting Technique
3.3. Stochastic Optimal Flow Problem
- It is assumed that renewable energy sources, like solar and wind, have predictable patterns of availability that can be modeled for grid integration;
- The seamless integration of renewable energy into existing grids is assumed to not cause major disruptions, relying on current grid flexibility and capacity;
- The assumption is made that supportive government policies, such as subsidies and tax incentives for renewable energy projects, will remain stable, driving long-term adoption.
- A key limitation is underdeveloped energy storage technology, which restricts the potential to store and use renewable energy during non-generating periods S;
- The geographical dependency of renewable energy sources limits their effectiveness in regions lacking suitable solar or wind conditions F;
- The high initial cost of deploying large-scale renewable energy systems, including infrastructure upgrades and storage, presents a financial limitation;
- Existing grid infrastructure may not be fully capable of handling the intermittent and distributed nature of renewable energy sources, leading to a limitation in integration potential S.
- Climate change introduces uncertainty in the long-term availability and consistency of renewable resources like wind and solar energy;
- Fluctuations in energy market prices due to changing demand, supply conditions, and policy shifts introduce significant economic uncertainty for renewable energy investors;
- Economic uncertainties, such as fluctuating electricity prices and policy changes, affect the long-term feasibility of and investment in renewable energy systems.
3.3.1. Wind Generator Cost Modelling
3.3.2. Solar Energy Cost Modelling
- Need for real-time solutions to manage dynamic uncertainties in renewable generation;
- Limited exploration of integrating large-scale energy storage systems into OPF models;
- Challenges in the scalability of computational algorithms for large power systems with diverse energy sources;
- Insufficient integration of economic market dynamics into OPF solutions;
- Need for expanding environmental metrics in OPF models to include lifecycle analyses;
- Lack of development of multi-objective optimization models that balance technical, economic, and environmental factors.
4. Conclusions
Funding
Conflicts of Interest
References
- Dommel, H.W.; Tinney, W.F. Optimal power flow solutions. IEEE Trans. Power Aarat. Syst. 1968, PAS-87, 1866–1876. [Google Scholar] [CrossRef]
- Carpentier, J. Contribution e l’étude do Dispatching Economique. Bull. Soc. Fr. Electr. 1962, 3, 431–447. [Google Scholar]
- Squires, R.B. Economic dispatch of generation directly from power system voltages admittances. AIEE Trans. Power Aarat. Syst. 1961, PAS-79, 1235–1245. [Google Scholar]
- Sadat, S.A.; Sahraei, A. Linear Programming to solve AC Optima large networks. Int. J. Electri 2022, 137, 107807. [Google Scholar] [CrossRef]
- Huneault, M.; Galiana, F.D. A survey of the optimal power flow literature. IEEE Trans. Power Syst. 1991, 6, 762–770. [Google Scholar] [CrossRef]
- Duman, S.; Rivera, S.; Li, J.; Wu, L. Optimal power flow of power systems with controllable wind-photovoltaic energy systems via differential evolutionary particle swarm optimization. Int. Trans. Electr. Energy Syst. 2020, 30, e12270. [Google Scholar] [CrossRef]
- Momoh, J.A. Electric Power System Alications of Optimization; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
- Momoh, A.; Koessler, R.J.; Bond, M.S.; Stott, B.; Sun, D.; Papalexopoulos, A.; Ristanovic, P. Challenges to optimal power flow. IEEE Trans. Power Syst. 1997, 12, 444–455. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Abido, M.A.; Chaib, A.; Mehasni, R. Optimal power flow using the league championship algorithm: A case study of the Algerian power system. Energy Convers. Manag. 2014, 87, 58–70. [Google Scholar] [CrossRef]
- Kessel, P.; Glavitsch, H. Estimating the voltage stability of a power system. IEEE Trans. Power Deliv. 1986, 1, 346–354. [Google Scholar] [CrossRef]
- Momoh, J.A.; El-Hawary, M.E.; Adapa, R. A review of selected optimal power flow literature to 1993. IEEE Trans. Power Syst. 1999, 14, 96–111. [Google Scholar] [CrossRef]
- Momoh, J.A.; El-Harwary, M.E.; Adapa, R. A review of selected optimal power flow literature to 1993, part II: Newton, linear programming interior point methods. IEEE Trans. Power Syst. 1999, 14, 105–111. [Google Scholar] [CrossRef]
- AlRashidi, M.R.; El-Hawary, M.E. Applications of computational intelligence techniques for solving the revived optimal power flow problem. Electr. Power Syst. Res. 2009, 79, 694–702. [Google Scholar] [CrossRef]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal Power Flow: A Bibliographic Survey I. Energy Syst. 2012, 3, 221–258. [Google Scholar] [CrossRef]
- Capitanescu, F. Critical review of recent advances further developments needed in AC optimal power flow. Electr. Power Syst. Res. 2016, 136, 57–68. [Google Scholar] [CrossRef]
- Papi, N.; Balasubramanianc, G.; Venkateswararao, B. Optimal power flow control optimisation problem incorporating conventional renewable generation sources: A review. Int. J. Ambient Energy 2023, 44, 1119–1150. [Google Scholar] [CrossRef]
- Lee, K.Y.; Park, Y.M.; Ortiz, J.L. A united approach to optimal real reactive power dispatch. IEEE Trans. Power Aar. Syst. 1985, PAS-104, 1147–1153. [Google Scholar] [CrossRef]
- Wells, D.W. Method for economic secure loading of a power system. Proc. IEE 1968, 115, 1190–1194. [Google Scholar] [CrossRef]
- Sun, D.I.; Ashley, B.; Brewer, B.; Hughes, A.; Tinney, W.F. Optimal power flow by Newton approach. IEEE Trans. Power Aar. Syst 1984, 1039, 2864–2880. [Google Scholar] [CrossRef]
- Reid, G.F.; Hasdorff, L. Economic dispatch using quadratic programming. IEEE Trans. Power Aar. Syst. 1973, 92, 2015–2023. [Google Scholar] [CrossRef]
- Lai, L.L.; Ma, J.T.; Yokoyama, R.; Zhao, M. Improved genetic algorithms for optimal power flow under both normal contingent operation states. Elec. Power Energy Syst. 1997, 19, 287–292. [Google Scholar] [CrossRef]
- Bakirtzis, A.G.; Biskas, P.N.; Zoumas, C.E.; Petridis, V. Optimal power flow by enhanced genetic algorithm. IEEE Trans. Power Syst. 2002, 17, 229–236. [Google Scholar] [CrossRef]
- Younes, M.; Rahli, M.; Abdelhakem-Koridak, L. Optimal power flow based on hybrid genetic algorithm. J. Inf. Sci. Eng. 2007, 23, 1801–1816. [Google Scholar]
- Wankhade, C.M.; Vaidya, A.P. Optimal power flow using genetic algorithm: Parametric studies for selection of control state variables. Br. J. Appl. Sci. Technol. 2014, 4, 279–301. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal power flow using particle swam optimization, Elec. Power Energy Syst 2002, 24, 563–572. [Google Scholar] [CrossRef]
- Wang, C.R.; Yuan, H.J.; Huang, Z.Q.; Zhang, J.W.; Sun, C.J. A modified particle swarm optimization algorithm its application in optimal power flow problem. Proc. Int. Conf. Mach. Learn. Cybern. 2005, 5, 2885–2889. [Google Scholar]
- Ahmed, A.A.; Esmin, A.; Zambroni, C. A hybrid particle swarm optimization applied to loss power minimization. IEEE Trans. Power Syst 2005, 20, 0885–0895. [Google Scholar]
- Zhao, B.; Guo, C.X.; Cao, Y.J. Improved particle swam optimization algorithm for OPF problems. IEEE Conf. 2004, 4, 7803–8718. [Google Scholar]
- El Ela, A.A.A.; Abido, M.A.; Spea, S.R. Optimal power flow using differential evolution algorithm. Electr. Power Syst. Res. 2010, 80, 878–885. [Google Scholar] [CrossRef]
- Chang, C.; Wong, J.; Chiou, J.; Tzong, C. Robust searching hybrid differential evolution method for optimal reactive power planning in large-scale distribution systems. Electr. Power Syst. Res. 2007, 77, 430–437. [Google Scholar] [CrossRef]
- Nayak, M.R.; Krishnan, K.R.; Rout, P.K. Modified differential evolution optimization algorithm for multi-constraint optimal power flow. In Proceedings of the 2011 International Conference on Energy, Automation and Signal, Bhubaneswar, India, 28–30 December 2011; pp. 978–985. [Google Scholar]
- Pulluri, H.; Naresh, R.; Sharma, V. An enhanced self-adaptive differential evolution with mixed crossover for multi objective optimal power flow problems. Appl. Soft Comput. 2017, 54, 229–245. [Google Scholar] [CrossRef]
- Duman, S.; Sonmez, Y.; Guvenc, U. Application of gravitational search algorithm for optimal reactive power dispatch problem. In Proceedings of the 2011 International Symposium on Innovations in Intelligent Systems and Applications, Istanbul, Turkey, 15–18 June 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Yusuf, S.; Serhat, D.; Nuran, Y.; Ugur, G. Optimal power flow incorporating FACTS devices using gravitational search algorithm. In Proceedings of the 2012 International Symposium on Innovations in Intelligent Systems and Applications, Trabzon, Turkey, 2–4 July 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Duman, S.; Güvenç, U.; Sonmez, Y.; Yorukeren, N. Optimal power flow using gravitational search algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Kursat, A.; Ulas, K. Solution of transient stability-constrained optimal power flow using artificial bee colony algorithm. Turk. J. Electr. Engg. Comput. Sci. 2013, 21, 360–372. [Google Scholar]
- Ayan, K.; Kılıç, U. Artificial bee colony algorithm solution for optimal reactive power flow. Appl. Soft Comput. 2012, 12, 1477–1482. [Google Scholar] [CrossRef]
- Younes, M. Hybrid method for optimal power flow determination. Sci. Techn. Electrotechn. Energ. 2012, 3, 249–258. [Google Scholar]
- Li, Y.; Wang, Y.; Li, B. A hybrid artificial bee colony assisted differential evolution algorithm for optimal reactive power flow. Electr. Power Energy Syst. 2013, 52, 25–33. [Google Scholar] [CrossRef]
- Roa- Sepulveda, C.A.; Pavez-Lazo, B.J. A solution to the optimal power flow using simulated annealing. Electr. Power Energy Syst. 2003, 25, 47–57. [Google Scholar] [CrossRef]
- Chen, Y.L.; Ke, Y.L. Multi-objective VAr planning for large-scale power systems using projection-based two-layer simulated annealing algorithms. IEE Proc.-Gener. Transm. Distrib. 2004, 151, 555–560. [Google Scholar] [CrossRef]
- Pulluri, H.; Naresh, R.; Sharma, V. Preeti, Solving non-convex non-linear optimal power flow problems using colliding bodies optimization. In Proceedings of the International Conference on Recent Advances in Engineering & Computational Sciences -2015 (RAECS-2015), Chandigarh, India, 21–22 December 2015. [Google Scholar]
- Pulluri, H.; Naresh, R.; Sharma, V. Preeti, A new colliding bodies optimization for solving optimal power flow problem in power system. In Proceedings of the International Conference on Power Systems-2016, (ICPS-2016), New Delhi, India, 4–6 March 2016. [Google Scholar]
- Bouchekara, H.R.; Chaib, A.E.; Abido, M.A.; El-Sehiemy, R.A. Optimal power flow using an improved colliding bodies optimization algorithm. Appl. Soft Comput. 2016, 42, 119–131. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H. Optimal power flow using black-hole-based optimization aroach. Appl. Soft Comput. 2014, 24, 879–888. [Google Scholar] [CrossRef]
- Tan, Y.; Li, C.; Cao, Y.; Lee, K.Y.; Li, L.; Tang, S.; Zhou, L. Improved group search optimization method for optimal power flow problem considering valve-point loading effects. Neurocomputing 2015, 148, 229–239. [Google Scholar] [CrossRef]
- Roy, P.K.; Ghoshal, S.P.; Thakur, S.S. Biogeography based optimization for multi-constraint optimal power flow with emission non-smooth cost function. Expert Syst. Appl. 2010, 37, 8221–8228. [Google Scholar] [CrossRef]
- Kumar, A.R.; Premalatha, L. Optimal power flow for a deregulated power system using adaptive real coded biogeography-based optimization. Electr. Power Energy Syst. 2015, 73, 393–399. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Abido, M.A.; Boucherma, M. Optimal power flow using teaching-learning-based optimization technique. Electr. Power Energy Syst. 2014, 114, 49–59. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Gitizadeh, M.; Akbari, E. An improved teaching–learning-based optimization algorithm using Levy mutation strategy for non-smooth optimal power flow. Int. J. Electr. Power Energy Syst. 2015, 65, 375–384. [Google Scholar] [CrossRef]
- Pulluri, H.; Naresh, R.; Sharma, V. A solution network based on stud krill herd algorithm for optimal power flow problems. Soft. Comput. 2018, 22, 159–176. [Google Scholar] [CrossRef]
- Pulluri, H.; Naresh, R.; Sharma, V. Application of stud krill herd algorithm for solution of optimal power flow problems. Int. Trans. Electr. Energy Syst. 2017, 27, e2316. [Google Scholar] [CrossRef]
- Sivasubramani, S.; Swarup, K.S. Multi-objective harmony search algorithm for optimal power flow problem. Int. J. Electr. Power Energy Syst. 2011, 33, 745–752. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Abido, M.A.; Chaib, A.E. Optimal power flow using an improved electromagnetism-like mechanism method. Electr. Power Compon. Syst. 2016, 44, 434–449. [Google Scholar] [CrossRef]
- Attiaa, A.; Sehiemya, R.A.; Hasanien, H.M. Optimal power flow solution in power systems using a novel Sine-Cosine algorithm. Int. J. Electr. Power Energy Syst. 2018, 99, 331–343. [Google Scholar] [CrossRef]
- Chetan, M.; Shiv, P.S.; Jimit, R. Optimal power flow in the presence of wind power using modified cuckoo search. IET Gener. Transm. Distrib. 2015, 9, 615–626. [Google Scholar]
- Prasad, D.; Mukherjee, V. A novel symbiotic organisms search algorithm for optimal power flow of power system with FACTS devices. Eng. Sci. Technol. 2016, 19, 79–89. [Google Scholar] [CrossRef]
- Jadhav, H.T.; Bamane, P.D. Temperature dependent optimal power flow using g-best guided artificial bee colony algorithm. Electr. Power Energy Syst. 2016, 77, 77–90. [Google Scholar] [CrossRef]
- Warid, W. Optimal power flow using the AMTPG-Jaya algorithm. Appl. Soft Comput. 2020, 91, 106252. [Google Scholar] [CrossRef]
- Roy, P.K.; Paul, C. Optimal power flow using krill herd algorithm. Int. Trans. Electr. Energy Syst. 2014, 25, 1397–1419. [Google Scholar] [CrossRef]
- Abido, M.A.; Ali, N.A. Multi-objective optimal power flow using differential evolution. Arab. J. Sci. Eng. 2012, 37, 991–1005. [Google Scholar] [CrossRef]
- Medina, M.A.; Das, S.; Coello, C.A.C. Decomposition-based modern metaheuristic algorithms for multiobjective optimal power flow—A comparative study. Eng. Appl. Artif. Intell. 2014, 32, 10–20. [Google Scholar] [CrossRef]
- Ermis, S. Multi-objective optimal power flow using a modified weighted teaching-learning based optimization algorithm. Electr. Power Compo. Syst. 2023, 51, 2536–2556. [Google Scholar] [CrossRef]
- Bhowmik, A.R.; Chakraborty, A.K. Solution of optimal power flow using nondominated sorting multi objective gravitational search algorithm. Electr. Power Energy Syst. 2014, 62, 323–334. [Google Scholar] [CrossRef]
- Yi, W.; Lin, Z.; Lin, Y.; Xiong, S.; Yu, Z.; Chen, Y. Solving Optimal Power Flow Problem via Improved Constrained Adaptive Differential Evolution. Mathematics 2023, 11, 1250. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Akbel, M.; Duman, S. Optimization of Optimal Power Flow Problem Using Multi-Objective Manta Ray Foraging Optimizer. Appl. Soft Comput. 2022, 116, 108334. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, Y.; Jiang, R.; Su, Q. Surgical cases assignment problem using a multi-objective squirrel search algorithm. Expert Syst. Alications 2024, 235, 121217. [Google Scholar] [CrossRef]
- Masoud, A.; Zaipatimah, A.; Muhammad, M.O.; Rui, B.; Mohammad, S.J.; Hussein, M.R.; Moath, A.A. High-performance democratic political algorithm for solving multi-objective optimal power flow problem. Expert Syst. Alications 2024, 239, 122367. [Google Scholar]
- Radosavljevic, J.; Klimenta, D.; Jevtic, M.; Arsic, N. Optimal power flow using a hybrid optimization algorithm of particle swarm optimization gravitational search algorithm. Electr. Power Compon. Syst. 2015, 43, 1958–1970. [Google Scholar] [CrossRef]
- Guvenc, U.; Duman, S.; Kahraman, H.T.; Aras, S.; Kati, M. Fitness-Distance Balance based adaptive guided differential evolution algorithm for security-constrained optimal power flow problem incorporating renewable energy sources. Appl. Sof. Comput. 2021, 108, 1–35. [Google Scholar] [CrossRef]
- Owusu, P.A.; Sarkodie, A.; Dubey, S. A review of renewable energy sources, sustainability issues climate change mitigation. Cogent Eng. 2016, 3, 1167990. [Google Scholar] [CrossRef]
- Hafez, A.A.; Nassar, Y.F.; Hammdan, M.L. Technical economic feasibility of utility-scale solar energy conversion systems in saudi arabia. Iran J. Sci. Technol Trans. Electr. Eng. 2024, 44, 213–225. [Google Scholar]
- Mguel, A.; Vazquez, O.; Kirschen, D.S. Accessing the impacts of wind power generation on operating cost. IEEE Trans. Smart Grid 2010, 1, 295–301. [Google Scholar]
- Heras, I.S.; Escriva, G.S.; Ortega, M.A. Wind farm electrical power production model for load flow analysis. Renew. Energy 2011, 36, 1008–1013. [Google Scholar] [CrossRef]
- Gope, S. Dynamic Optimal Power Flow with the Presence of Wind Farm; Lambert Academic Publishing: Saarbrucken, Germany, 2012. [Google Scholar]
- Chen, G.; Chen, J.; Duan, X. Power flow dynamic optimal power flow including wind farms. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009. [Google Scholar]
- Shi, L.; Wang, C.; Yao, L.; Ni, Y.; Bazargan, M. Optimal power flow solution using incorporating wind power. IEEE Syst. J. 2012, 6, 233–241. [Google Scholar] [CrossRef]
- Jabr, R.A.; Pal, B.C. Intermittent wind generation in optimal power flow dispatching. IET Gener. Transm. Distr. 2009, 3, 66–74. [Google Scholar] [CrossRef]
- Xie, L.; Chiag, H.D.; Li, S.H. Optimal power flow calculation of power system with wind farms. In Proceedings of the IEEE Power Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011. [Google Scholar]
- Ambarish, P. Tripathy, Optimal power flow solution of wind integrated power system using modified bacteria foraging algorithm. Int. J. Electr. Power Energy Syst. 2014, 54, 306–314. [Google Scholar]
- Chen, H.; Chen, J.; Duan, X. Multi stage dynamic optimal power in wind power integrated system. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 18 August 2005. [Google Scholar]
- Teeparthi, C.; Vinod, D.M. Multi-objective hybrid PSO—APO algorithm based security constrained optimal power flow with wind thermal generators. Eng. Sci. Technol. Int. J. 2017, 20, 411–426. [Google Scholar] [CrossRef]
- Teeparthi, C.; Vinod, D.M. Security-constrained optimal power flow with wind thermal power generators using fuzzy adaptive artificial physics optimization algorithm. Neural Comput. Appl. 2018, 29, 855–871. [Google Scholar] [CrossRef]
- Chamanbaz, M.; Dabbeney, F.; Lagoaz, C. AC optimal power flow in the presence of renewable sources uncertain loads. IEEE Trans. Power Syst. 2017, 15, 1–22. [Google Scholar]
- Shilaja, C.; Ravi, K. Optimal power flow considering intermittent wind power using particle swarm optimization. Int. J. Renew. Energy Res. 2016, 6, 504–509. [Google Scholar]
- Biswas, P.P.; Suganthan, P.N.; Amaratunga, A.J. Optimal power flow solutions incorporating stochastic wind solar power. Energy Convers. Manag. 2017, 148, 1194–1207. [Google Scholar] [CrossRef]
- Elattar, E.E. ElSayed; Modified jaya algorithm for optimal power flow incorporating renewable energy sources considering the cost, emission, power loss voltage profile improvement. Energy 2019, 178, 598–609. [Google Scholar] [CrossRef]
- Ilyas, M.A.; Abbas, G.; Alquthami, T.; Awais, M. Multi-objective optimal power flow with integration of renewable energy sources using fuzzy membership function. Access IEEE 2020, 8, 14318–143200. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z. Optimal power flow incorporating stochastic wind solar generation by metaheuristic optimizers. Microsyst Technol. 2021, 27, 3263–3277. [Google Scholar] [CrossRef]
- Shilaja, C.; Arunprasath, T. Optimal power flow using moth swarm algorithm with gravitational search algorithm considering wind power. Future Gener. Comp. Syst. 2019, 98, 708–715. [Google Scholar]
- Syed, M.S.; Sureshz, V.; Chintalapudi, S.; Sirigiri, S. Optimal power flow solution in the presence of renewable energy sources. Iranian J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 61–79. [Google Scholar] [CrossRef]
- Alghamdi, A.S. optimal power flow of hybrid wind/solar/thermal energy integrated power systems considering costs emissions via a novel efficient search optimization algorithm. Appl. Sci. 2023, 13, 4760. [Google Scholar] [CrossRef]
- Mohamed, H.; Salah, K.; Abdelazim, G. Optimal power flow analysis considering renewable energy resources uncertainty based on an improved wild horse optimizer. IET Gener. Transm. Distr. 2023, 17, 3582–3606. [Google Scholar]
- Jomah, O.S.M.; Ahmed, A.A.; Alsharif, A.; Nassar, Y.F.; Mohamed, N.M.N. Assessing random power flow for vehicle-to-grid operation based on monte carlo simulation. In Proceedings of the 2024 IEEE 4th Int. Maghreb Meeting of the Conference on Sciences Techniques of Automatic Control Computer Engineering (MI-STA), Yokohama, Japan, 19–21 May 2024. [Google Scholar] [CrossRef]
- El-Khozondar, H.J.; Asfour, A.A.; Nassar, Y.F.; Shaheen, S.W.; El-Zaety, M.F.; El-Khozondar, R.J.; Khaleel, M.M.; Ahmed, A.A.; Alsharif, A.H. Photovoltaic Solar Energy for Street Lighting: A Case Study at Kuwaiti Roundabout, Gaza Strip, Palestine. Power Eng. Eng. Thermophys. 2024, 3, 77–91. [Google Scholar] [CrossRef]
- Trojovsky, P.; Trojovska, E.; Akbari, E. Economical-environmental-technical optimal power flow solutions using a novel self-adaptive wild geese algorithm with stochastic wind solar power. Sci. Rep. 2024, 14, 4135–4144. [Google Scholar] [CrossRef]
- Gurumoorthi, G.; Senthilkumar, S.; Karthikeyan, G.; Alsaif, F. A hybrid deep learning approach to solve optimal power flow problem in hybrid renewable energy systems. Sci Rep. 2024, 14, 19377. [Google Scholar] [CrossRef]
- Lei, X.; Yang, V.; Yu, J.; Zhao, J.; Gao, Q.; Yu, H. Data-driven optimal power flow: A physics-informed machine learning approach. IEEE Trans. Power Syst. 2021, 36, 346–354. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Noori, S.M.; Blackhall, L.; Scott, P. A comparison on power flow models for optimal power flow studies in integrated medium-low voltage unbalanced distribution systems. Sust. Energy Grids Net. 2024, 38, 2352–4677. [Google Scholar] [CrossRef]
- Vargas, L.S.; Quintana, V.H.; Vanneli, A. A tutorial description of an interior point method its applications to security-constrained economic dispatch. IEEE Trans. Power Syst. 1993, 8, 1315–1324. [Google Scholar] [CrossRef]
- Sivanam, S.N.; Deepa, S.N. Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lee, K.Y.; El-Sharkawi, M.A. Modern Heuristic Optimization Techniques: Theory Applications to Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 1–300. [Google Scholar]
- Coelho, L.S.; Mariani, V.C. Combining of chaotic differential evolution quadratic programming for economic dispatch optimization with valve-point effect. IEEE Trans. Power Syst. 2006, 21, 885–895. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization, Technical Report TR06; Computer Engineering Department, Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- Pulluri, H.; Kumar, N.G.; Rao, U.M.; Kumar, M.G. Krill Herd Algorithm for Solution of Economic Dispatch with Valve-Point Loading Effect, Applications of Computing. Autom. Wirel. Syst. Electr. Eng. 2019, 553, 383–392. [Google Scholar]
- Khatib, W.; Fleming, P. The stud GA: A mini revolution? In Proceedings of the 5th International Conference on Parallel Problem Solving from Nature, Amsterdam, The Netherlands, 27–30 September 1998; Eiben, A., Back, T., Schoenauer, M., Schwefel, H., Eds.; Springer-Verlag: New York, NY, USA, 1998; pp. 683–691. [Google Scholar]
- Piarajan, K.; Babulal, C.K. Fuzzy harmony search algorithm based optimal power flow for power system security enhancement. Int. J. Electr. Power Energy Syst. 2016, 78, 72–79. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, J.; Lu, Y.; Wang, Y.; Zhang, Y. Multi-objective differential evolution with adaptive Cauchy mutation for short-term multi-objective optimal hydrothermal scheduling. Energy Convers. Manag. 2010, 51, 788–794. [Google Scholar] [CrossRef]
- Wong, K.P.; Wong, Y.W. Genetic genetic/simulated-annealing aroaches to economic dispatch. IET Gener. Transm. Distrib. 1994, 141, 507–513. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Hybrid differential evolution with biogeography-based optimization for solution of economic. IEEE Trans. Power Syst. 2010, 25, 1955–1964. [Google Scholar] [CrossRef]
- Sivasubramani, K.S.; Swarup, S. Sequential quadratic programming based differential evolution algorithm for optimal power flow problem. IET Gener. Transm. Distrib. 2011, 5, 1149–1154. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghanbarian, M.M.; Ghavidel, S. Modified teaching learning algorithm double differential evolution algorithm for optimal reactive power dispatch problem: A comparative study. Inf. Sci. 2014, 278, 231–249. [Google Scholar] [CrossRef]
- Hetzer, J.; Yu, D.C.; Bhattarai, K. An economic dispatch model incorporating wind power. IEEE Trans. Energy Convers. 2008, 23, 603–611. [Google Scholar] [CrossRef]
- Xian, L.; Wilsym, X. Minimum emission dispatch constrained by stochastic wind power availability cost. IEEE Trans. Power Syst. 2010, 25, 1705–1713. [Google Scholar] [CrossRef]
- Feijoo, A.E.; Cidras, J. Modeling of wind farms in the load flow analysis. IEEE Trans. Power Syst. 2000, 15, 110–115. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Aziz, O.A.A.A.; Yasser, N. Power management strategy sizing optimization techniques for hybrid energy systems considering feature selection: Mini review. North Afr. J. Sci. Publ. 2023, 1, 1–6. [Google Scholar]

| Ref. | Year | Objective Functions | Test Systems Considered | Objectives | With RES | Method | Major Findings | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | |||||||
| [17] | 1985 | Y | Y | IEEE 6, 30 bus | S | GM | Constraints are used without penalties | ||||||
| [18] | 1968 | Y | IEEE 6-bus | S | GM | Constraints are used without penalties | |||||||
| [19] | 1984 | Y | IEEE 5-bus | S | Newton | Identifying binding inequalities is a challenging task | |||||||
| [20] | 1973 | Y | IEEE 57, 118 bus | S | QP | Both inequality and equality considered | |||||||
| [21] | 1977 | Y | Y | IEEE 30-bus | S | IGA | Line contingency is considered | ||||||
| [22] | 2002 | Y | IEEE RTS | S | EGA | Enhanced GA is introduced | |||||||
| [23] | 2007 | Y | IEEE 57 bus | S | HGA | MATPOWER is included with the GA | |||||||
| [24] | 2014 | Y | IEEE 30-bus | S | GA | Necessity of control parameters is explained | |||||||
| [25] | 2002 | Y | Y | Y | Y | IEEE 30-bus | S | PSO | New algorithm is introduced | ||||
| [26] | 2005 | Y | IEEE 5-bus | S | HPSO | Enhanced PSO is introduced | |||||||
| [27] | 2005 | Y | IEEE 118-bus | S | MPSO | Multi-objective PSO is introduced | |||||||
| [28] | 2004 | Y | IEEE 9, 30 118 bus | S | IPSO | Improved PSO is introduced | |||||||
| [29] | 2010 | Y | Y | Y | Y | IEEE 30-bus | S&M | DE | Numerical based DE is introduced | ||||
| [30] | 2007 | Y | IEEE 9, 33, 66, 132 | S | HDE | Hybrid DE is introduced | |||||||
| [31] | 2011 | Y | Y | IEEE 30-bus | S&M | MDE | Weighted matrix for MO | ||||||
| [32] | 2017 | Y | Y | Y | Y | IEEE 30, 57, Algerian 59 bus | S&M | ESDE-MC | Non-dominated sorting MO | ||||
| [33] | 2011 | Y | Y | IEEE 30 bus | S | GSA | Reactive power dispatch is considered | ||||||
| [34] | 2012 | Y | IEEE 30 bus | S | GSA | Included FACTS devices | |||||||
| [35] | 2012 | Y | Y | Y | Y | Y | IEEE 30, 57 bus | S&M | GSA | Weighted matrix for MO | |||
| [36] | 2012 | Y | IEEE 9, 30 bus | S | ABC | Transient stability constraints are considered | |||||||
| [37] | 2012 | Y | Y | IEEE 30, 118 bus | S | ABC | Reactive power dispatch is considered | ||||||
| [38] | 2013 | Y | IEEE 25, 30 bus | S | ABC-mGA | Security constraints are considered | |||||||
| [39] | 2013 | Y | IEEE 14, 57 bus | S | ABC | Reactive power dispatch is considered | |||||||
| [40] | 2003 | Y | IEEE 30-bus | S | SA | Quadratic constraint considered | |||||||
| [41] | 2004 | Y | Y | Y | IEEE 30-bus | S&M | SA | Weighted matrix for MO is considered | |||||
| [42] | 2015 | Y | Y | Y | IEEE 9, 26 bus | S&M | CBO | Weighted matrix for MO is considered | |||||
| [43] | 2016 | Y | Y | Y | Y | IEEE 3bus | S | CBO | New EA is introduced | ||||
| [44] | 2016 | Y | Y | Y | Y | Y | Y | IEEE 30, 57, 118 | S&M | ICBO | Weighted matrix for MO is considered | ||
| [45] | 2014 | Y | Y | Y | Y | IEEE 30, Algerian 59 | S&M | BHBO | Weighted matrix for MO is considered | ||||
| [46] | 2015 | Y | 26 bus, IEEE 30, 57 | S | IGSO | Improved version of GSO is introduced | |||||||
| [47] | 2015 | Y | Y | Y | Y | IEEE 9, 30 bus | S | BBO | New EA is introduced | ||||
| [48] | 2015 | Y | Y | Y | Y | Y | IEEE 30, 57 bus | S&M | ARBBO | Weighted matrix for MO is considered | |||
| [49] | 2014 | Y | Y | Y | Y | IEEE 30, 118 bus | S&M | TLBO | Weighted matrix for MO is considered | ||||
| [50] | 2015 | Y | Y | Y | Y | IEEE 30, 57 bus | S&M | ITLBO | Enhanced version of TLBO is introduced | ||||
| [51] | 2016 | Y | Y | Y | Y | Y | IEEE 14, 30 & 57 bus | S | SKH | Stud GA is added to KH algorithm | |||
| [52] | 2017 | Y | Y | Y | Y | Y | IEEE 30, Algerian 59, 118 | S | SKH | Stud GA is added to KH algorithm | |||
| [53] | 2011 | Y | Y | Y | IEEE 30-bus | M | HSA | Non-dominated technique is used | |||||
| [54] | 2016 | Y | Y | IEEE 30, 118-bus | S | FHSA | Fuzzy technique is introduced with HSA | ||||||
| [55] | 2018 | Y | Y | Y | IEEE 30, 118-bus | S | MSCA | Modified version of SCA is used | |||||
| [56] | 2015 | Y | IEEE 30, 57 | S | Y | MCS | WRIG generator is considered | ||||||
| [57] | 2016 | Y | Y | Y | Y | IEEE 30, 57 bus | S&M | SOS | Weighted matrix for MO | ||||
| [58] | 2016 | Y | IEEE 30, 57 bus | S | G-ABC | Temperature of the TL is considered | |||||||
| [59] | 2020 | Y | Y | Y | IEEE 30, 118 bus | S | Jaya | Weighted matrix for MO is considered | |||||
| [60] | 2014 | Y | Y | Y | Y | Y | IEEE 30, 57, 118 bus | S | KH | Weighted matrix for MO is considered | |||
| [61] | 2012 | Y | Y | Y | IEEE 30, 118 bus | S&M | DE | Weighted matrix for MO is considered | |||||
| [62] | 2014 | Y | Y | Y | IEEE 30 bus | S&M | ABC | Non-dominated technique is used | |||||
| [63] | 2014 | Y | Y | Y | IEEE 14, 30, 118 bus | S&M | TLBO | Non-dominated technique is used | |||||
| [64] | 2015 | Y | Y | Y | Y | IEEE 30 bus | S&M | GSA | Non-dominated technique is used | ||||
| [65] | 2017 | Y | Y | Y | Y | IEEE 30, 118 Algerian 59, | S&M | ESDE | Non-dominated technique is used | ||||
| [66] | 2022 | Y | Y | IEEE 30 bus | S&M | MRF | Non-dominated technique is used | ||||||
| [67] | 2024 | Y | Y | Y | IEEE 30 bus | S&M | SCA | Non-dominated technique is used | |||||
| [68] | 2024 | Y | Y | IEEE 30 bus | S&M | DPA | Non-dominated technique is used | ||||||
| [69] | 2015 | Y | Y | Y | Y | Y | Y | IEEE 30, 118 bus | S&M | PSO GSA | Weighted matrix for MO is considered | ||
| [70] | 2021 | Y | PEGASE 13, bus | S | Y | PPOPF | Intermittent nature of RES is considered | ||||||
| [71] | 2023 | Y | IEEE 33, 69, 118 bus | S | Y | PSO | Intermittent nature of RES is considered | ||||||
| [72] | 2022 | Y | Y | Y | IEEE 30 bus | S | Y | FFA | Penalty and reserve costs are considered | ||||
| [73] | 2010 | Y | IEEE 30 bus | S | Y | W&S | Wind forecast is considered | ||||||
| [74] | 2011 | Y | IEEE 5-bus | S | Y | Wind model is generated | |||||||
| [75] | 2012 | Y | IEEE 30- bus | S | Y | ABC | Fixed speed WT is considered | ||||||
| [76] | 2009 | Y | IEEE 30-bus | S | Y | PSO | Dynamic OPF is considered | ||||||
| [77] | 2012 | Y | IEEE 39-bus | S | Y | EP | The Monte Carlo simulation is used | ||||||
| [78] | 2009 | Y | IEEE 30-bus | S | Y | QP | Stochastic model of wind power | ||||||
| [79] | 2011 | Y | IEEE 118-bus | S | Y | IP | Up and down spinning reserves are considered | ||||||
| [80] | 2014 | Y | Y | IEEE 30-bus | S | Y | BFA | WECS is considered | |||||
| [81] | 2005 | Y | IEEE 5-bus | S | Y | GM | New Q-V model of IG is considered | ||||||
| [82] | 2017 | Y | Y | IEEE 30, 75 bus | S | Y | PSO-APO | Security constrained OPF is considered | |||||
| [83] | 2016 | Y | Y | IEEE 30 & 75 bus | S | Y | FAAPO | Security constrained OPF is considered | |||||
| [84] | 2017 | Y | England 39-bus | S | Y | SC | Stochastic model of wind power | ||||||
| [85] | 2016 | Y | IEEE 30-bus | S | Y | PSO | PDF used for wind power generation | ||||||
| [86] | 2017 | Y | Y | IEEE 5-bus | S | Y | DE | Wind PDF is considered | |||||
| [87] | 2019 | Y | Y | Y | Y | IEEE 30, 118-bus | S | Y | MJaya | Solar, wind, and hydro generation are considered | |||
| [88] | 2020 | Y | Y | Y | IEEE 30-bus | S | Y | PSO | Wind PDF is considered | ||||
| [89] | 2021 | Y | Y | Y | IEEE 30-bus | S&M | Y | GOA | Stochastic model of wind power | ||||
| [90] | 2019 | Y | Y | IEEE 30, 57 & 118 bus | S | Y | MSA_GSA | Analysis with and without wind power | |||||
| [91] | 2020 | Y | Y | 14 & 124-bus | S | Y | P-ELM | Penalty and reserve costs of wind and solar | |||||
| [92] | 2023 | Y | Y | Y | IEEE 30-bus | S | Y | SCO | Modelling of solar and wind is considered | ||||
| [93] | 2023 | Y | Y | Y | Y | IEEE 30-bus | S | Y | WHO | Stochastic model of wind and solar is considered | |||
| [94] | 2024 | Y | - | S | Y | Manto Carlo | Micro grid with EVs is considered | ||||||
| [95] | 2024 | Y | - | S | Y | - | Case Study at Kuwaiti Roundabout | ||||||
| [96] | 2024 | Y | IEEE 30 bus | S | Y | WGA | Wind uncertainties are considered | ||||||
| [97] | 2024 | Y | IEEE 30 bus | S | Y | DRL | Deep learning techniques are considered | ||||||
| [98] | 2021 | ||||||||||||
| [99] | 2024 | ||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pulluri, H.; Basetti, V.; Srikanth Goud, B.; Kalyan, C.N.S. Exploring Evolutionary Algorithms for Optimal Power Flow: A Comprehensive Review and Analysis. Electricity 2024, 5, 712-733. https://doi.org/10.3390/electricity5040035
Pulluri H, Basetti V, Srikanth Goud B, Kalyan CNS. Exploring Evolutionary Algorithms for Optimal Power Flow: A Comprehensive Review and Analysis. Electricity. 2024; 5(4):712-733. https://doi.org/10.3390/electricity5040035
Chicago/Turabian StylePulluri, Harish, Vedik Basetti, B. Srikanth Goud, and CH. Naga Sai Kalyan. 2024. "Exploring Evolutionary Algorithms for Optimal Power Flow: A Comprehensive Review and Analysis" Electricity 5, no. 4: 712-733. https://doi.org/10.3390/electricity5040035
APA StylePulluri, H., Basetti, V., Srikanth Goud, B., & Kalyan, C. N. S. (2024). Exploring Evolutionary Algorithms for Optimal Power Flow: A Comprehensive Review and Analysis. Electricity, 5(4), 712-733. https://doi.org/10.3390/electricity5040035








