Abstract
This paper compares concentrated and distributed reactive power compensation to improve the power factor at the point of common connection (PCC) of an industrial electrical system (IES) with harmonics. The electrical system under study has a low power factor, voltage variation, and harmonics caused by motors operating at low loads and powered by variable-speed drives. The designed compensation system mitigates harmonics and reduces electrical losses with the shortest payback period. Four solutions were compared, considering concentrated and distributed compensation with capacitor banks and harmonic filters. Although the cost of investment in concentrated compensation is lower than that of distributed compensation, a higher reduction in electrical losses and a lower payback period are obtained with distributed compensation. Although the lowest payback period was obtained with distributed compensation with capacitor banks (0.4 years), it is not recommended in the presence of harmonics because the effects of current harmonics significantly reduce the useful life of these elements. For this reason, distributed compensation with harmonic filters obtained a payback period of 0.6 years, and it was proposed as the best solution. These results should be considered in projects aimed at power factor compensation in IESs with harmonics. The concentrated compensation of the capacitor bank at the PCC is proposed because of the lower investment cost and ease of installation. However, the advantages of distributed compensation with harmonic filters have not been evaluated. An energy efficiency approach is used to analyze the impact of the location methods of the power factor compensation equipment on the electrical losses of the IES.
1. Introduction
Most industrial electrical systems (IESs) have inductive loads such as electric motors, ventilation, refrigeration, air conditioning, and fluorescent lighting that reduce the power factor (PF) [1]. Inductive loads of the IES produce a consumption of active and reactive power. Active power is converted into useful energy (heat, light, and mechanical energy); however, reactive power cannot be converted [2].
Low PF in IESs requires a large reactive power transfer from the utility network to mitigate the problem [3]. It increases the electrical losses in the network and energy cost, reduces the voltage magnitudes, and impacts reliability and safety [4]. From the system operator’s perspective, a low PF requires greater capacity in both generation and transmission to supply the same amount of active power component due to the increase in total apparent power caused by inductive loads [5]. From consumers’ perspective, a low PF creates component oversizing, increases IES losses, and generates additional costs because of penalties [6]. The lower the PF of the system, the more inefficient it is, which incurs more costs during operation [7]. Therefore, from a conservation energy perspective, there is always a need to improve PF in industries.
On the other hand, the propagation of loads that generate harmonics in the IES continues to increase [8]. Power electronic circuits for energy conversion are a fundamental technology for numerous classical and modern applications, and they represent one of the critical elements in the electrification of the energy sector [9]. Power electronics is a technical field focused on the transmission, conversion, control, and delivery of electrical energy and the provision of power to electronic devices [10]. Currently, more than 70% of electrical energy is processed by power electronics, and this percentage continues to increase rapidly [11]. It is estimated that 80% of all generated electrical energy will pass through power electronics-based converters [12].
AC–AC converters are widely used in industrial applications where an AC load output voltage with different amplitudes, phases, and frequencies is required [12]. Power electronics-based converters can be classified according to the type of input and output power: alternating current to direct current (AC–DC) rectifiers, DC–AC inverters, DC–DC converters, and AC–AC cycloconverters [13]. The most basic DC–DC converter plays an essential role in power electronics [14]. Although these devices allow for improved control and energy efficiency in processes, they constitute nonlinear loads that generate harmonic distortion [15]. Harmonics produce premature failures and equipment degradation in a power system, low PF, and unwanted disconnections [16]. Among the equipment that can be affected by harmonics in an IES are transformers, motors, cables, and load switches [17]. In addition, they can cause overheating of electrical equipment and wiring, malfunction of sensitive equipment, and reduced efficiency of consumer equipment and generation sources [18].
To avoid costly installation and additional expansion of capacity, utilities generally apply a penalty for low PF by charging a demand component (based on kVA) over a period of time to customers [6]. On the other hand, a low PF means a higher electricity bill for the same amount of active energy consumption (kW) for an end consumer. Consequently, savings in power demand and billing can be achieved by improving the PF of a site [19]. To solve these problems, a circuit topology that can improve the PF is essential, especially with the significant presence of nonlinear loads in the IES [20].
The specialized literature reports several studies that propose the most effective and economical methods to improve PF. Corrective measures such as on-site synchronous machines and installing capacitor banks to reduce reactive power locally are analyzed in [21]. In [22], the correction of PF with large current line switched converters using variable series capacitors is studied.
Other studies have optimized the capacity and location of capacitors at the lowest investment cost. They have focused on solving voltage problems and PF. Some of these studies have implemented heuristic techniques based on artificial intelligence. In [23], genetic algorithms are used; in [24], a crow search algorithm is utilized; in [25], an ant colony search algorithm is employed; and in [26], a particle swarm optimization algorithm is implemented.
Several authors have addressed the impact of reliability on the optimal placement of PF correction capacitors. In [26,27,28], researchers focus on improving capacitors in electrical systems to minimize the power line failure rate after capacitor installation. In [29,30], the phenomena of transient switching events and their impact on the system are discussed.
These studies focus only on installing the capacitor bank and do not consider the effect of harmonics. However, when a capacitor bank is installed in the presence of harmonics, resonance may occur due to the cancellation of the reactive component of the system impedance [31]. Furthermore, capacitor banks are an easy path to high-frequency current under these conditions. Resonance phenomena and low impedance to high-frequency currents considerably increase current circulation in the capacitor. This causes overheating and bulging of the coating near the terminals, reducing the useful life of the equipment [32].
Some technologies based on active filters have been developed for harmonic mitigation, PF enhancement, and voltage regulation [33]. PF correction and harmonic control lead the way for complete power quality control [34]. Harmonic cancellation is performed by reverse injection of harmonic currents with appropriate self-canceling load combinations. The smart impedance concept can be used to overcome the physical limitations of tuned notch filters. Smart hybrid active filters can improve the PF [35].
In [36], a technical solution is reported for reactive power compensation and harmonic attenuation in an industrial application. The industry under study has a large nonlinear load with a nominal power of 2.9 MW and 765 V, generating high levels of harmonics and low PF. As a solution for this case, four specially designed active harmonic filters connected in parallel are proposed, each with a nominal current of 300 A. Complementary line reactors and an auto-transformer are also intended to power the active filters at their nominal voltage.
In [37], the P-Q theory proposed by Akagi is used considering a shunt active power filter compensation that helps to reduce reactive power generation, harmonics, and load imbalance. In [38], a series of active power filters based on fixed five- and seven-level neutral points is studied using a modified instantaneous reactive power control strategy to compensate for harmonics and all voltage disturbances. In [39], an active power shunt filter based on PQ theory is studied, considering low-pass filters such as Butterworth, Chebyshev II, and Elliptic.
Although active filters are proposed as an effective solution to the growing problems of low PF and harmonics in IESs, they are still expensive and designed to be installed at the point of common connection (PCC). The filters installed on the PCC improve the PF, harmonics, and voltage drop at this point, eliminating the penalty of low PF for service companies. However, this solution is insufficient to optimize energy losses throughout the IES, as compensation in the PCC has practically no effects on downstream circuits.
In summary, given the problem of low PF in the IES, optimization studies have been developed at the location of the capacitor bank. However, this solution is insufficient if the IES presents harmonics. On the other hand, new active filter technologies have been proposed to improve PF, voltage variation, and harmonic mitigation. However, as they are solutions designed to be installed in the PCC, they do not guarantee optimization to improve voltage variation and reduce losses of the entire IES.
Based on these aspects, this research proposes a new study in which four alternative solutions are evaluated to improve the PF in the PCC of an IES in the presence of harmonics. The alternatives evaluated are compensation concentrated in the PCC with capacitor banks, distributed compensation with capacitor banks, compensation concentrated in the PCC with harmonic filters, and distributed compensation with harmonic filters. The ability to improve the PF in the PCC according to Colombian regulations, the reduction of losses, and the mitigation of harmonics with the shortest payback period (PP) are considered as comparison criteria. The analysis of the studies examined focuses on evaluating proposals for power factor compensation methods using various technologies. However, these studies do not address the influence of the locations of these compensators, nor do they include an energy analysis, nor do they evaluate the presence of harmonics. Based on these shortcomings, this study proposes the following contributions:
- This study compares technical and economic aspects of concentrated and distributed power factor compensation in IESs.
- This study considers the mitigation of harmonics in IESs affected by power quality problems.
- This evaluation incorporates an energy efficiency approach to analyze the impact on electrical losses with the location of power factor compensators in an IES.
2. Materials and Methods
The main technical criterion for this study was that the PF at the PCC should reach values between 0.9 and 1, according to regulation [6]. In addition, the THDV was less than 8% at the PCC, according to the standard [40]. The centralized installation of the capacitor banks and harmonic filters was analyzed at the PCC. However, it also analyzed the distributed installation of this equipment at load nodes with PF less than 0.9 and THDV greater than 8%.
The research was carried out in three stages. In the first stage, the main existing methods for designing reactive power compensation systems in IES were examined. This stage established the characteristics of the main reactive power and harmonic compensation methods.
Next, in the second stage, a case study was selected as an IES with low PF, high incidence of induction motors, and nonlinear loads. The single-line diagram and the IES load data were obtained. The electrical parameters were measured at different points of the IES. System measurement data and IES loads were implemented in the NEPLAN® software version 5.5.3. Subsequently, the main electrical parameters of the IES, such as PF, voltage variation, and resonance, were examined. Finally, four solutions based on concentrated and distributed compensation were studied. The IES circuit was configured with each case in the NEPLAN software, and the load flow, harmonics, and short circuit results were obtained.
Finally, the best solution to enhance the PF in the PCC of the IES was established in the third stage. The effect of harmonics and the feasibility of the investment were considered. In addition, energy losses, cost of the investment (CI), PP, and impact of harmonics were calculated for each solution. Subsequently, the results of each solution were compared, and the solution with the shortest PP that considered the effects of harmonics was selected as the best solution.
The best solution was selected based on compliance with the main technical criterion (i.e., PF at the PCC between 0.9 and 1). This solution must also ensure harmonic mitigation and loss reduction, with the lowest PP, without affecting the life of the compensation equipment due to the resonance effect.
Figure 1 shows the methodology applied in the research and its steps. The methodology comprises five sequential steps ranging from the IES characterization to the definition of the best solution scenario. Each step is described below with its components.
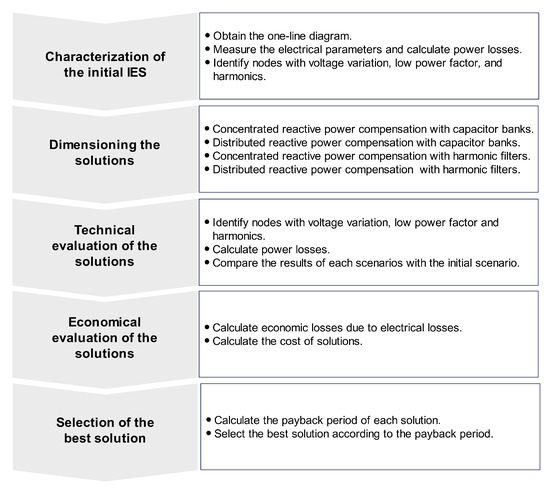
Figure 1.
Methodology for reactive power compensation in an IES.
2.1. Characterization of the IES
The reactive power compensation system was designed to avoid resonance problems and voltage variations in an IES with a predominant use of electric motors and variable speed drives. This IES has also installed new production lines to increase electrical loads. Figure 2 shows the single-line diagram of the IES implemented in NEPLAN software.The diagram highlights the nodes analyzed for concentrated compensation and filtering, marked with a yellow block representing the respective devices. Likewise, the nodes evaluated for distributed compensation and filtering are identified, indicated by a blue block symbolizing the corresponding compensators and filters.
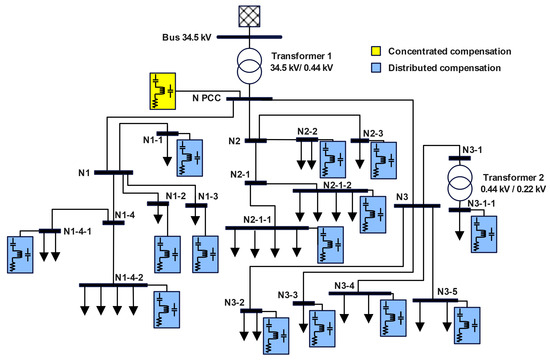
Figure 2.
Single-line diagram of the IES implemented in the NEPLAN software.
The IES has 21 nodes that connect the transformers and loads or act as links to other nodes in the network. An 8000-kVA transformer of 34.5/0.44 kV in the PCC supplies the entire IES at 440 V. The system has a 500-kVA transformer of 0.44/0.22 kV to supply administrative loads at 220 V.
Active power, reactive power, and current harmonics were measured at each node with a network analyzer for a week according to the NTC 5001 standard [41]. Considering that the daily behavior of the industry is almost constant and with slight variation in loading conditions, the average value was used.
Load flow, short circuit, and harmonic analyses were performed to characterize the system in the NEPLAN software. The variables of the system were calculated according to the following considerations:
- The voltage variation is calculated with the NEPLAN software.
- The load factor is calculated as the ratio between the measured power and the nominal power of the transformer in the PCC.
- The PF is calculated with the NEPLAN software.
- The total harmonic distortion of voltage (THDV) is calculated with the NEPLAN software.
- The electrical losses due to harmonics are calculated as the difference between the total and the fundamental power.
- The resonance frequency is calculated as in Equation (1) [42]. The term is the harmonic of the resonance frequency, is the apparent short-circuit power obtained, and is the reactive power of the capacitor bank.
- The electrical losses are calculated as the difference between the power in the PCC and the power of the loads. The difference corresponds to the power dissipated in the lines [43,44].
- The total losses are calculated as the sum of harmonic losses and electrical losses.
In the IES analysis, voltage variation, low PF, harmonics, and solution evaluation were carried out with the NEPLAN software. For this, the single-line diagram presented in Figure 2 was implemented with the nominal data of the transformers and lines and the measured powers and harmonics of the loads. Table 1 shows the characteristics of the nodes and the loads in the IES.

Table 1.
Characteristics of the nodes and loads in the IES.
The voltage variation indicator was used to identify undervoltage or overvoltage problems. In NEPLAN software, this indicator is determined as the percentage ratio of the voltage at the node over the nominal voltage of the IES [45]. The nodes with voltage variation problems present values lower than 92% and higher than 105%. These values are considered according to the limits established by the NTC 1340 standard [46] for low-voltage urban customers. Nodes with low PF have values less than 0.9. These values are considered according to CREG Resolution 015 of 2018 [6]. The nodes with harmonic problems are those with THDV values greater than 8%, according to the IEEE 519 standard [40].
Table 2 shows the PF, voltage variation, and THDV of each node under the initial condition (IC). This table shows that the IES under study has low PF, with values lower than 0.9 in all nodes, including the PCC. There are voltage variation values lower than 0.92 in seven nodes, and all nodes present harmonic problems with THDV values greater than 8%. Low PF is due to electric motors operating at low load, low voltage is due to line overloading, and variable speed drives cause harmonics.Based on these results, distributed PF compensation and harmonic mitigation at all nodes were evaluated.

Table 2.
PF, voltage variation, and THDV in the IC.
Table 3 shows the line losses, harmonic losses, and total electrical losses. The results in Table 2 and the losses in Table 3 are used to evaluate the impact of the proposed improvement solutions.

Table 3.
Line losses, harmonic losses, and total losses.
2.2. Dimension of the Solutions
Based on the problems of low PF, voltage variation, and harmonics identified in the IES, the following solutions were evaluated:
- Solution 1 (S1): concentrated reactive power compensation with capacitor banks.
- Solution 2 (S2): distributed reactive power compensation with capacitor banks.
- Solution 3 (S3): concentrated reactive power compensation with harmonic filters.
- Solution 4 (S4): distributed reactive power compensation with harmonic filters.
The main objective of these solutions is to ensure that the PF in the PCC complies with the provisions of CREG Resolution 015 of 2018 [6], with the PF between 0.9 and 1.
The capacitor banks proposed as an improvement solution were conventional and installed in parallel in the PCC and the load nodes. The dimension of the capacitor banks was calculated from Equation (2) [47]. In this equation, the term is the capacity of the capacitor bank (kVARc), P is the power demanded at the point of analysis (kW), is the actual PF (p.u), and is the desired PF specified as 0.9 (p.u).
The harmonics present in the IES were mainly of the 5th order. Therefore, tuned passive filters or pass band filters were sized. These filters were installed in parallel in the PCC and at the distribution nodes. This type of harmonic filter comprises series circuits of a capacitor, an inductance, and a low-value resistance calculated with Equation (3) [48]. The term is the capacitive reactance (), is the nominal voltage (V), n is the order of the harmonics to eliminate, and is the reactive power to compensate (kVAr).
The capacitance can be calculated from as expressed in Equation (4) [49]. In this equation, C is the capacitance (F), and f is the main frequency (Hz).
Now, the term is the inductive reactance represented in ohms (), calculated as defined in Equation (5).
Considering the previous term , the inductance can be calculated as in Equation (6) [49]. The term L is the inductance in Henries (H).
The resistance is calculated as expressed in Equation (7). The term R is the resistance in , and Q is the filter quality factor that can be selected between 20 and 50 [48].
It is important to note that the harmonic filters’ capacitors allowed not only harmonics filtering but also the correcting of the PF [50]. Subsequently, based on these calculations, the capacitor banks and harmonic filters were selected from a manufacturer catalog. The closest or higher values were chosen because manufacturers do not always have devices with the same values as those calculated.
2.3. Evaluation of Solutions
A technical evaluation was carried out for each solution based on the following aspects:
- Verify that in the PCC, the PF complies with the provisions of CREG resolution 015 of 2018 [6].
- Quantify the number of nodes (PCC and distribution) with PF outside the range established in CREG resolution 015 of 2018 [6].
- Quantify the number of nodes (PCC and distribution) with voltage outside the range established by the NTC 1340 standard [46].
- Quantify the number of nodes (PCC and distribution) with harmonics outside the range established by the IEEE 519 standard [40].
- Calculation of harmonic losses in the lines and total electrical losses in the IES.
- Economic evaluation of solutions.
For the economic evaluation of the solutions, the PP was calculated with Equation (8). The term PP refers to the number of years required to recover the original investment (years), CI is the cost of the investment (USD), and AES is the annual energy savings due to electricity (USD/year).
The CIs in S1 and S2 correspond to the costs of the capacitor banks, while the CIs in S3 and S4 were obtained from the costs of the harmonic filters.
The AES due to electricity savings were calculated as in Equation (9). The term CE is the cost of electricity considered at 0.2 USD/kWh, are the energy losses in the IC of the IES in (kWh/year), and are the energy losses of each solution in (kWh/year).
2.4. Comparison and Best Solution
After the technical and economic evaluation of each solution, the best option was selected. The best solution was the one that had the shortest recovery period and guaranteed that the PF in the PCC complied with CREG resolution 015 of 2018 [6].
3. Results and Analysis
The results of the technical and economic evaluations of the four power factor compensation solutions are presented in this section.
3.1. Solution 1
Solution 1 (S1) refers to the concentrated reactive power compensation with capacitor banks. Table 4 shows the data of the capacitor bank, costs, the apparent short-circuit power (), and the harmonic corresponding to the resonance frequency (). The dimension of the bank was obtained using Equation (2), the manufacturer’s availability, and the verification that the PF in the PCC was between 0.9 and 1 [6]. With the selected capacitor bank, a second-order resonance harmonic was obtained. Although this is an even harmonic that is uncommon in the IES, attention must be paid, as it is of low order (less than 10).

Table 4.
S1 in PCC.
Table 5 shows the active power, reactive power, PF, voltage variation, and THDV for each node of the IES when applying S1. This table shows that only the PF in the PCC improved considering the solution based on concentrated compensation with the capacitor bank. At the same time, the voltage variation problems were eliminated in four nodes and the problem was maintained in three nodes. However, a reduction of harmonics can be observed in all nodes as a result of the filtering carried out by the PCC capacitor bank. In this last aspect, it must be considered that although a capacitor bank can filter harmonics because of its low impedance at high frequency, it is not sized for this purpose. Therefore, it can overheat due to an increased harmonic current, causing the coating to bulge near the terminals and reducing its useful life [51].

Table 5.
Active power, reactive power, PF, voltage variation, and THDV for each node of the IES when applying S1.
Table 6 presents the line losses, harmonic losses, and total losses for this solution.

Table 6.
Line losses, harmonic losses, and total losses for S1.
Table 6 shows a reduction in electrical losses of 21.4 kW (electrical losses in the input data minus electrical losses with this solution) relative to the IC. With this solution, the concentrated capacitor bank solved three problems:
- Improve the PF in the PCC.
- Reduction of harmonics.
- Reduction of electrical losses.
The drawback of the solution is that current harmonics cause a reduction in the useful life of the installation.
3.2. Solution 2
Solution 2 (S2) refers to distributed reactive power compensation with capacitor banks (S2). Table 7 shows the data on the capacitive reactive power of the capacitor bank distributed in the nodes with low PF. In addition, it shows the cost, the apparent short-circuit power, and the harmonics corresponding to the resonance frequency. The availability of the manufacturer and the requirement that the PCC be between 0.9 and 1 were also considered [6].

Table 7.
S2: Distributed capacitor bank.
Table 7 shows that in nodes N1-4-2, N2-1-1, N2-2, N2-3, N3-4, and N3-5, the harmonics that generate resonance were of low order. Therefore, the occurrence of resonance was likely associated with damage to the capacitor banks and the electrical system [52].
Table 8 shows the active power, reactive power, PF, voltage variation, and THDV for each node of the IES when applying S2.

Table 8.
Active power, reactive power, PF, voltage variation, and THDV for each node of the IES when applying S2.
Table 8 shows that distributed compensation with a capacitor bank improved PF in the PCC, while voltage variation problems were eliminated at all nodes. On the other hand, the reduction of harmonics can also be observed in all nodes due to the filtering carried out by the PCC capacitor bank. In this solution, as in the previous one, it must be considered that, although a capacitor bank can also filter harmonics, it can overheat and reduce its useful life since it is not sized for this purpose [51].
Table 9 presents the line losses, harmonic losses, and total losses for this solution.

Table 9.
Line losses, harmonic losses and total losses for S2.
Table 9 shows a loss reduction of 82.1 kW (losses in input data minus losses with this solution) relative to the IC. With this solution, the capacitor banks solved four problems:
- Improvement of the PF in the PCC.
- Elimination of voltage variation problems throughout the circuit.
- Reduction of harmonics.
- Reduction in electrical losses.
The drawback of the solution is that current harmonics reduce the useful life of the capacitor bank [51].
3.3. Solution 3
Solution 3 (S3) refers to the concentrated reactive power compensation with harmonic filters. Table 10 shows the capacitive reactive power, cost, capacitance, inductance, and resistance of the harmonic filter bank concentrated in the PCC. The quality factor of the selected filter was 50. The dimension of the bank was obtained from the calculations of Equations (2)–(7), the availability of the manufacturer, verifying that the PF in the PCC was between 0.9 and 1 [6] and the THDV in the PCC was less than 8% [40].

Table 10.
S2: Harmonic filter concentrated in the PCC.
Table 10 shows that for the same capacitance, the price of the harmonic filter was higher than the capacitor bank because the filters had, in addition to the capacitors, inductances, resistors, and other components with higher thermal capacity [48].
Table 11 shows the active power, reactive power, PF, voltage variation, and THDV for each node of the IES when applying S3.

Table 11.
Active power, reactive power, PF, voltage variation, and THDV for each node of the IES when applying S3.
Table 11 shows that considering the solution of concentrated compensation with the harmonic filter, only the PF in the PCC was improved. In addition, the low voltage was maintained in three nodes. On the other hand, a greater reduction in harmonics can be observed in all nodes due to the harmonic filter function.
Table 12 presents the results of line losses, harmonic losses, and total losses for S3.

Table 12.
Line losses, harmonic losses, and total losses when applying S3.
Table 12 shows a reduction in losses of 21.2 kW (losses in input data minus losses with this solution) relative to the IC. With this solution, the concentrated capacitor bank corrected three problems:
- Improvement of the PF in the PCC.
- Reduction of harmonics.
- Reduction in electrical losses.
In this case, there is no risk of overheating, unlike with the capacitor bank [51].
3.4. Solution 4
Solution 4 (S4) refers to the distributed reactive power compensation with harmonic filters. Table 13 shows the capacitive reactive power, cost, capacitance, inductance, and resistance of the distributed harmonic filter bank in nodes. The quality factor of the selected filter was 50. The dimension of the bank was obtained from the calculations of Equations (2)–(7), the availability of the manufacturer, checking that the PF in the PCC was between 0.9 and 1 [6], and the THDV in the PCC was less than 8% [40].

Table 13.
S4: Distributed harmonic filter.
Table 13 shows that harmonic filters cost more than capacitor banks of the same capacity because they have more components and greater thermal capacity. Table 14 shows the active power, reactive power, PF, voltage variation, and THDV for each node of the IES when applying S4.

Table 14.
Active power, reactive power, PF, voltage variation, and THDV for each node of the IES when applying S4.
Table 14 shows that distributed compensation with harmonic filter improved the PF in the PCC and eliminated voltage variation and harmonic problems in all nodes with the most significant reduction in THDV due to the harmonic filtering. In contrast, Table 15 presents the line losses, harmonic losses, and total losses for S4.

Table 15.
Line losses, harmonic losses, and total losses for S4.
Table 15 shows a loss reduction of 81.6 kW (losses in input data minus losses with this solution) relative to the IC. With this solution, the harmonic filters solved four problems:
- Improvement of the PF in the PCC.
- Elimination of voltage variation problems throughout the circuit.
- Reduction of harmonics.
- Reduction in electrical losses.
In this case, the device is not affected by harmonic overheating, as in S2 [51].
3.5. Comparison
Next, the technical–economic comparison of the solutions is performed. Figure 3 shows the PF, voltage variation, and harmonics for each node of the IES in the IC. In addition, the figure shows each solution with their respective limits according to CREG 015 of 2018 [6], NTC 1340 [46], and IEEE 519 [40].
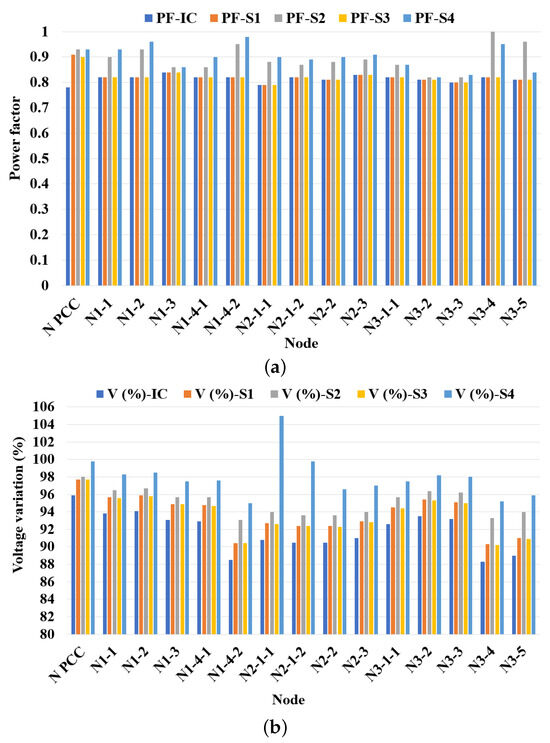
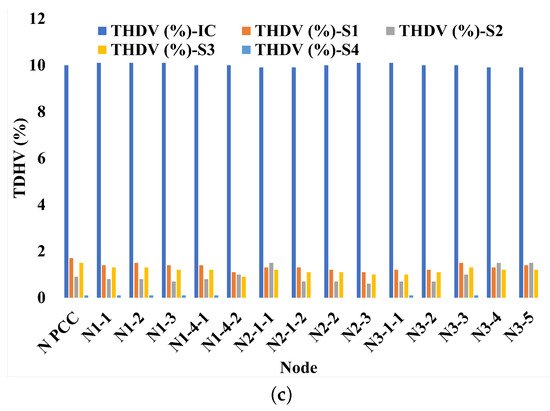
Figure 3.
Values of (a) PF, (b) voltage variation, and (c) THDV for all conditions.
Figure 3 shows that in the IC, all nodes presented low power factors, seven nodes low voltages, and five nodes high harmonics. With S1 and S3 (concentrated), only the PF in the PCC improved, and in three nodes (N1-4-2, N3-4, and N3-5), the low voltage was maintained. With S2 and S4 (distributed), the PF was improved in six and nine nodes, respectively, while voltage variation problems were eliminated in all nodes. Harmonics, for their part, were mitigated when considering the four solutions (S1, S2, S3, and S4), with S4 as the solution with the greatest reduction.
Another aspect that could be observed is that with S2, in node N3-4, the PF reached the value of 1, which is the upper limit established by CREG 015 of 2018 [6]. This is presented for the following reasons [52,53]:
- Permanently connected fixed capacitor banks.
- Automatic capacitor banks with measurement in a single phase, the phase with the highest consumption.
With S4, an overvoltage of 105% was reached at node N2-1-1, which is the upper limit value established by NTC 1340 [46]. As in the previous case, this can be explained by the use of fixed capacitor banks.
Concerning the parameters of PF, voltage variation, and harmonics, it can be concluded that the best solutions were offered by distributed compensation with a bank of capacitors and filters. It is observed that improving all the parameters of the nodes is a difficult task to perform. In addition, some nodes presented an increase in PF and overvoltages as a result of possible overcompensation.
Figure 4 graphically summarizes the number of nodes outside the limits established by CREG 015 of 2018 [6], NTC 1340 [46], and IEEE 519 [40] under the IC and for each solution (S1–S4).
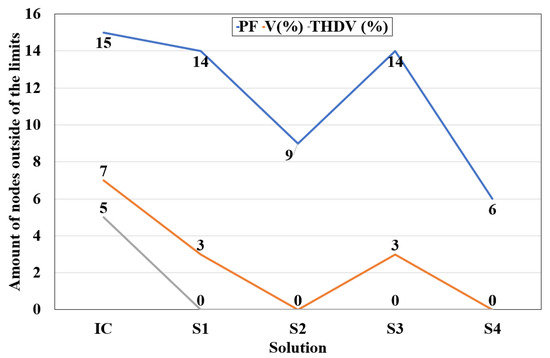
Figure 4.
Number of nodes with out-of-bounds parameters in each solution.
Figure 5 shows the line losses, harmonic losses, total losses, and loss reduction corresponding to the IC and each solution (S1–S4).
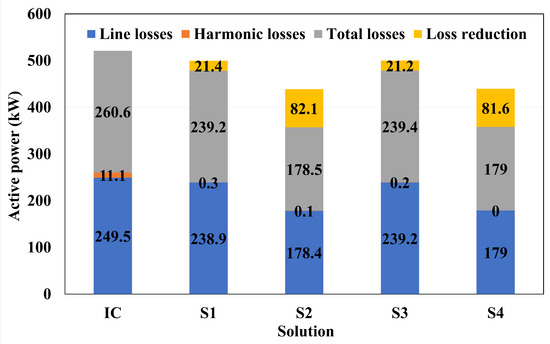
Figure 5.
Losses and loss reduction in each solution.
Figure 5 shows that distributed compensation (S2 and S4) results in the most significant reduction in loss relative to the IC. For S2, the losses are reduced by 32%, while for S4, they are reduced by 31%. The loss reduction with distributed compensation is also 3.8 times greater than with concentrated compensation (S1 and S3).
In the solutions with distributed compensation (S2 and S4), a more significant number of nodes was also obtained where the PF and voltage variation improved regarding concentrated compensation (S1 and S3). This shows a direct correspondence among loss reduction, PF improvement, and voltage variation at the nodes.
Figure 6 shows the CI, PP, and AES.
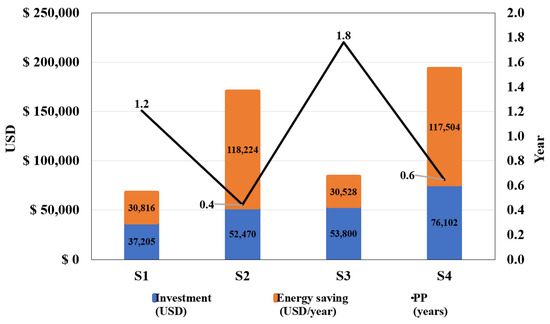
Figure 6.
PP and AES for each solution.
When comparing the CIs of S1 and S2 and the CIs of S3 and S4, it can be observed that the cost of distributed compensation is greater than the concentrated compensation for the capacitor bank and the harmonic filters, respectively. However, comparing these same solutions with distributed compensation, greater savings are obtained in billing for energy consumption than with concentrated compensation. Taking the same comparisons as references, the PP of the investment in solutions with distributed compensation is observed to be shorter than with concentrated compensation. This is because, in solutions with distributed compensation, AES predominates over the CI.
When comparing the distributed compensation solutions of capacitor banks (S2) about harmonic filters (S4), it can be seen that with S2, the CI is lower and the AES are greater. Therefore, the PP is shorter than that of S4. From these results, it could be assumed that S2 is the best solution of the four options. However, considering the technical criterion that in an electrical system with harmonics, the useful life of the capacitor banks is significantly reduced due to the overheating produced by current harmonics, it is suggested not to select the solution with a distributed capacitor bank (S2) but with distributed harmonic filters (S4). S4 has the advantage of a short PP of less than eight months.
Table 16 summarizes the technical–economic criteria that allowed us to select S4 as the best solution to improve PF in the PCC of the IES under study. It shows that S4 meets all technical requirements and also presents a short PP that is favorable to company decision-making.

Table 16.
Summary of the economic and technical criteria in each solution.
4. Conclusions
In this study, solutions were evaluated to improve PF in IES. Some problems were faced, such as low PF, low voltage, and harmonics. Two compensation approaches were compared: concentrated and distributed, using capacitor banks and harmonic filters.
The following conclusions are obtained from the results and analysis:
- The results show that distributed compensation is more effective in improving PF, reducing voltage variation, and mitigating harmonics in the PCC and IES nodes. Although the initial investment in concentrated compensation was lower, the savings from energy losses in distributed compensation resulted in a better PP.
- These results demonstrate that, for the analysis of a technical solution to an engineering problem, consultants’ expertise is required because sometimes technical and economic evaluations alone are not always sufficient, but comprehensive analyses must be carried out, such as the case presented.
- Implementing capacitor banks or harmonic filters reduced harmonics throughout the IES. However, the capacitor banks showed a reduction in their useful life due to overheating caused by current harmonics. Selecting the optimal solution considered both technical and financial aspects, resulting in the preference for distributed harmonic filters due to their effectiveness and lower impact on the useful life of the devices.
- Despite the common practice of concentrated compensation of capacitor banks in the PCC due to its low initial cost and easy installation, it was concluded that this is not the most viable solution, especially in environments with increasing nonlinear loads that affect the useful life of the capacitor banks and provide negligible improvements in the PF and the voltage variation in the IES nodes.
- Exploring technologies based on active filters that can be installed at different points in the IES circuit, not only at the PCC, is recommended. In addition, the need to continue research on electrical power quality problems in IESs is emphasized, as studies focus on distribution and power systems.
Author Contributions
Conceptualization, investigation, methodology, and software, S.A.G.Y. Formal analysis, writing—review and editing, J.E.C.-B., K.B.S., J.d.l.C. and V.S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors thank the Universidad de la Costa, Servicio Nacional de Aprendizaje, Universidad Nacional de Colombia, Sede Medellín, and Aalborg University for the support provided to perform this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lin, L.; Wang, J.; Gao, W. Effect of load power factor on voltage stability of distribution substation. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–4. [Google Scholar]
- Sagiroglu, S.; Colak, I.; Bayindir, R. Power factor correction technique based on artificial neural networks. Energy Convers. Manag. 2006, 47, 3204–3215. [Google Scholar] [CrossRef]
- Hofmann, W.; Schlabbach, J.; Just, W. Reactive Power Compensation: A Practical Guide; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Jain, R.; Sharma, S.; Sreejeth, M.; Singh, M. PLC based power factor correction of 3-phase Induction Motor. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–5. [Google Scholar]
- Mendis, S.R.; Bishop, M.T.; Blooming, T.M.; Moore, R.T. Improving system operations with the installation of capacitor filter banks in a paper facility with multiple generating units. In Proceedings of the Conference Record of 1995 Annual Pulp and Paper Industry Technical Conference, Vancouver, BC, Canada, 12–16 June 1995. [Google Scholar]
- CREG. Metodología para la Remuneración de la Actividad de Distribución de Energía Electrica en el Sistema Interconectado Nacional; Resolución CREG 015-2018, Technical Report; Comisión de Regulación de Energía y Gas—CREG: Bogotá, Colombia, 2018. [Google Scholar]
- Grainger, J.J.; Stevenson, W.U.D., Jr. Power System Analysis; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Riaz, M.T.; Afzal, M.M.; Aaqib, S.M.; Ali, H. Analysis and Evaluating the Effect of Harmonic Distortion Levels in Industry. In Proceedings of the 2021 4th International Conference on Energy Conservation and Efficiency (ICECE), Lahore, Pakistan, 16–17 March 2021; pp. 1–7. [Google Scholar]
- Singh, R.; Paniyil, P.; Zhang, Z. Transformative Role of Power Electronics: In solving climate emergency. IEEE Power Electron. Mag. 2022, 9, 39–47. [Google Scholar] [CrossRef]
- Williamson, S.S. The success of electric mobility will depend on power electronics. Nat. Electron. 2022, 5, 14–15. [Google Scholar] [CrossRef]
- Tang, Y.; Cao, D.; Xiao, J.; Jiang, C.; Huang, Q.; Li, Y.; Chen, Z.; Blaabjerg, F.; Hu, W. AI-aided power electronic converters automatic online real-time efficiency optimization method. Fundam. Res. 2023; in press. [Google Scholar]
- Hannan, M.A.; Lipu, M.S.H.; Ker, P.J.; Begum, R.A.; Agelidis, V.G.; Blaabjerg, F. Power electronics contribution to renewable energy conversion addressing emission reduction: Applications, issues, and recommendations. Appl. Energy 2019, 251, 113404. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Zhao, B.; Assawaworrarit, S.; Santhanam, P.; Orenstein, M.; Fan, S. High-performance photonic transformers for DC voltage conversion. Nat. Commun. 2021, 12, 4684. [Google Scholar] [CrossRef]
- Angarita, E.N.; Santos, V.S.; Donolo, P.D.; Quispe, E.C. Assessing power quality in individual circuits of industrial electrical system. Int. J. Elect. Computer Syst. Eng. 2024, 14, 4888–4896. [Google Scholar] [CrossRef]
- Waleed, A.; Javed, M.R.; Riaz, M.T.; Virk, U.S.; Khan, S.; Mujtaba, A.; Ahmad, S.; Arshad, G. Study on Hybrid Wind-Solar System for Energy Saving Analysis in Energy Sector. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; pp. 1–6. [Google Scholar]
- Waleed, A.; Virk, U.S.; Riaz, M.T.; Mehmood, S.B.; Ahmad, S.; Javed, M.R.; Raza, A. Effectiveness and comparison of digital substations over conventional substations. Adv. Sci. Technol. Eng. Syst. J. 2019, 4, 431–439. [Google Scholar] [CrossRef]
- Ma, H.; Zheng, C.; Yu, W.; Lai, J.S.j. A single-stage integrated bridgeless AC/DC converter for electrolytic capacitor-less LED lighting applications. Int. J. Circuit Theory Appl. 2015, 43, 742–755. [Google Scholar] [CrossRef]
- Zheng, F.; Zhang, W. Long term effect of power factor correction on the industrial load: A case study. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, VIC, Australia, 19–22 November 2017; pp. 1–5. [Google Scholar]
- Babu, V.; Manikandan, M. Total harmonic distortion reduction for power quality improvement: A review. Int. J. Sci. Res. 2017, 6, 1681–1684. [Google Scholar]
- El-Mahayni, R.; Van De Vijver, R.; Rashidi, R.; Al-Nujaimi, A. Corporate wide power factor correction application: Economic and technical assessment. In Proceedings of the 2017 Petroleum and Chemical Industry Conference Europe (PCIC Europe), Vienna, Austria, 16–18 May 2017; pp. 1–13. [Google Scholar]
- Matsumoto, I.; Nomura, S. Power factor correction of large current line commutated converters using variable series capacitors. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–9. [Google Scholar]
- Farag, H.E.Z.; El-Saadany, E.F. Optimum Shunt Capacitor Placement in Multimicrogrid Systems With Consideration of Islanded Mode of Operation. IEEE Trans. Sustain. Energy 2015, 6, 1435–1446. [Google Scholar] [CrossRef]
- Askarzadeh, A. Capacitor placement in distribution systems for power loss reduction and voltage improvement: A new methodology. IET Gener. Transm. Distrib. 2016, 10, 3631–3638. [Google Scholar] [CrossRef]
- Tahir, M.J.; Bakar, B.A.; Alam, M.; Mazlihum, M.S. Optimal capacitor placement in a distribution system using ETAP software. Indones. J. Electr. Eng. Comput. Sci. 2019, 15, 650. [Google Scholar] [CrossRef]
- Etemadi, A.H.; Fotuhi-Firuzabad, M. Distribution system reliability enhancement using optimal capacitor placement. IET Gener. Transm. Distrib. 2008, 2, 621. [Google Scholar] [CrossRef]
- Rahmani-andebili, M. Reliability and economic-driven switchable capacitor placement in distribution network. IET Gener. Transm. Distrib. 2015, 9, 1572–1579. [Google Scholar] [CrossRef]
- Kavousi Fard, A.; Niknam, T. Optimal stochastic capacitor placement problem from the reliability and cost views using firefly algorithm. IET Sci. Meas. Technol. 2014, 8, 260–269. [Google Scholar] [CrossRef]
- Blooming, T.M. Capacitor failure analysis. IEEE Ind. Appl. Mag. 2006, 12, 38–48. [Google Scholar] [CrossRef]
- Blooming, T.M.; Carnovale, D.J. Capacitor Application Issues. IEEE Trans. Ind. Appl. 2008, 44, 1013–1026. [Google Scholar] [CrossRef]
- Shakeri, S.; Rezaeian Koochi, M.H.; Ansari, H.; Esmaeili, S. Optimal power quality monitor placement to ensure reliable monitoring of sensitive loads in the presence of voltage sags and harmonic resonances conditions. Electr. Power Syst. Res. 2022, 212, 108623. [Google Scholar] [CrossRef]
- Boonseng, C.; Gitnumlapcharoen, P. Effect of Low Harmonic Current Under Large Transformers on Harmonic Resonance Assessment in Industrial Systems. In Proceedings of the 2022 IEEE International Conference on Power and Energy (PECon), Langkawi, Kedah, Malaysia, 5–6 December 2022; pp. 181–185. [Google Scholar]
- Kalair, A.; Abas, N.; Kalair, A.R.; Saleem, Z.; Khan, N. Review of harmonic analysis, modeling and mitigation techniques. Renew. Sustain. Energy Rev. 2017, 78, 1152–1187. [Google Scholar] [CrossRef]
- Karuppanan, P.; Mahapatra, K.K. Active harmonic current compensation to enhance power quality. Int. J. Electr. Power Energy Syst. 2014, 62, 144–151. [Google Scholar] [CrossRef]
- Gonzatti, R.B.; Ferreira, S.C.; da Silva, C.H.; Pereira, R.R.; da Silva, L.E.B.; Lambert-Torres, G. Smart Impedance: A New Way to Look at Hybrid Filters. IEEE Trans. Smart Grid 2016, 7, 837–846. [Google Scholar] [CrossRef]
- Ioana, G.; Cazacu, E.; Stănculescu, M.; Pușcașu, S. Power Factor Correction and Harmonic Mitigation for a Heavy Industrial Nonlinear Load. In Proceedings of the 2023 13th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 March 2023; pp. 1–6. [Google Scholar]
- Satish, G.; Rameshkumar, K.; Dhanasakkaravarthi, B.; Jeyalakshmi, K.; Chaudhary, S.; Singh, N. Non-Linear Controller Based 3–Phase Shunt Active Filter for Improvement of Power Quality in Non-Linear Load. In Proceedings of the 2023 IEEE International Conference on Integrated Circuits and Communication Systems (ICICACS), Raichur, India, 24–25 February 2023; pp. 1–4. [Google Scholar]
- Chennai, S.; Electrical Engineering Department CRNB, B.P.O. 180 Ain-Ousserra, Algeria. Series APF based on Five and Seven-Level NPC Inverters using modified PQ Method. Electroteh. Electron. Autom. 2023, 71, 22–29. [Google Scholar] [CrossRef]
- Kamat, P.R.; Naik, A.J. Performance Evaluation of Butterworth, Chebyshev, and Elliptic filter for Harmonic Mitigation using P-Q based SAPF. In Proceedings of the 2022 International Conference on Smart Generation Computing, Communication and Networking (SMART GENCON), Bangalore, India, 23–25 December 2022; pp. 1–5. [Google Scholar]
- IEEE Std 519-2022; IEEE Standard for Harmonic Control in Electric Power Systems. Technical Report; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2022.
- Icontec. Norma téCnica NTC 5001. Calidad de la Potencia Eléctrica; Technical Report; Instituto Colombiano de Normas Técnicas y Certificación—ICONTEC: Bogotá, Colombia, 2008. [Google Scholar]
- Attachie, J.C.; Amuzuvi, C.K. Investigating harmonic resonance and capacitor bank switching at a power distribution substation using a fixed capacitor bank. Res. J. Eng. Appl. Sci. 2013, 2, 343–348. [Google Scholar]
- Candelo, J.E.; Hernández Riaño, H. Location and size of distributed generation to reduce power losses using a bat-inspired algorithm. In Proceedings of the VII Simposio Internacional sobre la Calidad de la Energía Eléctrica—SICEL 2013, Medellín, Colombia, 27–29 November 2013; pp. 1–9. [Google Scholar]
- Arias, J.; Calle, M.; Turizo, D.; Guerrero, J.; Candelo-Becerra, J.E. Historical Load Balance in Distribution Systems Using the Branch and Bound Algorithm. Energies 2019, 12, 1219. [Google Scholar] [CrossRef]
- IEEE Std 1159-2019; IEEE Recommended Practice for Monitoring Electric Power Quality. Technical Report; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2019.
- Icontec. Norma Técnica NTC 1340. Tensiones y Frecuencias Nominales en Sistemas de Energía Eléctrica en Redes de Servicio Publico; Technical Report; Icontec: Bogota, Colombia, 2013. [Google Scholar]
- Legrand. Compensación de Energía Reactiva y Monitoreo de la Calidad de la Potencia; Technical Report; Legrand: Limoges, France, 2018. [Google Scholar]
- Pérez Abril, I. Cálculo de parámetros de filtros pasivos de armónicos. Ing. Energética 2012, XXXIII, 134–143. [Google Scholar]
- Boylestad, R.L. Introducción al Análisis de Circuitos, 12th ed.; Pearson Educación: Naucalpan de Juárez, Mexico, 2019. [Google Scholar]
- Frutos Cabrera, C.L.; Cayetano Lotero, R. Compensación reactiva en sistemas eléctricos industriales con presencia de armónicos. FPUNE Sci. 2019, 12, 53–69. [Google Scholar]
- Reyes Calderón, G. Armónicas en Sistemas de Distribución de Energía Eléctrica. Master Thesis, Universidad Autónoma de Nuevo León, San Nicolás de los Garza, Mexico, 1996. [Google Scholar]
- Aguado Giraldo, E.J.; Bravo Jordán, R.D. Efectos Causados por Los Armónicos en Bancos de Condensadores; Corporación Universitaria Autónoma de Occidente: Santiago de Cali, Colombia, 1995. [Google Scholar]
- Arcos Lopez, E.R.; Chicaiza Díaz, D.M. Diseño y Construcción de un Tablero de Control Automático Para la Corrección del Factor de Potencia, Empleando un Módulo DCRA. Escuela Politécnica Nacional—Escuela de Formación de Tecnólogos. 2015. Available online: https://bibdigital.epn.edu.ec/handle/15000/10583 (accessed on 3 September 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).