Harnessing Field-Programmable Gate Array-Based Simulation for Enhanced Predictive Control for Voltage Regulation in a DC-DC Boost Converter

Abstract

This paper presents the design of a predictive controller for a boost converter and validation through real-time simulation. First, the boost converter was mathematically modeled, and then the electronic components were designed to meet the operation requirements. Subsequently, a model-based predictive controller (MBPC) and a digital PI (Proportional–Integral) controller were designed, and their performance was compared using MATLAB/SIMULINK^®. The controls were further verified by implementing test benches based on an FPGA (Field-Programmable Gate Array) with an OPAL-RT real-time simulator, which included the RT-LAB and RT-eFPGAsim simulation packages. These tests were successfully carried out, and the methodology used for this design was validated. The results showed a better response obtained with MBPC, both in terms of stabilization time and lower overvoltage.

1. Introduction

The sustained increase in global temperature is a significant concern globally. NASA (the National Aeronautics and Space Administration) reports that from 1880 to 2020, the global temperature increased by 1.02 °C [1]. Humans cause global warming by creating the greenhouse effect by burning fossil fuels, highlighting the importance of renewable energy in mitigating excessive temperatures and severe climatic variations [2,3].

According to IRENA (the International Renewable Energy Agency), from 2000 to 2015, photovoltaic (PV) energy experienced a growth of up to 18,461% in installed capacity [4]. With a growth rate of around 40%, PV panels and other derivatives have become cheaper, making them accessible for residential, commercial, and industrial applications. The electrical network uses the surplus of PV energy to distribute it to various places of consumption. In addition, PV panels have a life cycle of 25 to 30 years, making them profitable and efficient overall [5]. Irradiance, temperature, and the appropriate choice of semiconductors are some variables that can affect power quality in PV systems.

The power generated by the PV panels is injected into a DC bus using a DC-DC power converter for its consumption by DC loads or stored using a battery bank. Among the available DC-DC converters, the boost converter is one of the most common topologies for this task. A comparative study is required to select the best control method for a boost converter.

Regarding related works, various classical and advanced control methods have been employed for a boost converter. In [6], a PD (Proportional–Derivative) controller was designed based on fuzzy logic and tested in two different DC-DC converters. In [7], a feedback controller was developed, and its parameters were obtained with optimization techniques such as the Genetic Algorithm (GA) and Bacterial Foraging Optimization Algorithm (BFOA). Similarly, in [8], another optimization technique, Particle Swarm Optimization (PSO), was used. Additionally, in [9], a non-linear control technique, Sliding Mode Control (SMC), was employed. In [10], an SMC combined with a fuzzy logic controller was developed. Finally, in [11], two types of robust controllers were designed. The first was a PID (Proportional–Integral–Derivative) controller with hysteresis, while the second was combined with SMC.

Table 1. Some control strategies applied to boost converters.

Controller Type	Input Voltage (V)	Output Voltage (V)	Efficiency	Load (Ω)	Stabilization Time (ms)
PD-Fuzzy logic [6]	8	25	93.6%	100	15
PD-Fuzzy logic [6]	20	25	96.44%	100	50
GA [7]	12	24	95.71%	120	27.6
BFOA [7]	12	24	95.71%	120	20.4
PSO [8]	16.97	30	96.52%	110	43
SMC [9]	48	60	95.18%	25	30
Fuzzy logic + SMC [10]	110	220	99.35%	490	35
PID + Hysteresis [11]	24	48	96.99%	100	450
PID + SMC [11]	24	48	96.99%	100	450

summarizes the types of controllers mentioned and their respective parameters of interest, including efficiency, which is an important factor in DC-DC converters [12]. Thus, the PD-like Fuzzy Logic controller with an 8 V input voltage is the fastest.

A comprehensive review of the state of the art of MBPC was carried out in [13], and the use of some MBPC variants in PV-based DC microgrids was analyzed using, among other things, a boost converter. It was found that that the oscillations around the MPPT (Maximum Power Point Tracking) were significantly reduced depending on the predictive control method.

With some predictive methods with a discrete observer, a better response under rapidly changing weather conditions is obtained, and with others, MBPC generates optimal energy management and power-sharing applied to hybrid networks [14].

Based on a review of the state of the art of DC microgrids, a boost converter and an MBPC are proposed to study and reduce the stabilization features.

In addition, comparisons of our proposal with classic and mixed controllers will be developed. The proposal will also be tested in a real-time simulator with an FPGA-based library. Among its other characteristics, we intend to take advantage of its high operating frequencies to regulate the DC output voltage.

2. Proposed Topology and System Modeling

2.1. PV Modules and Arrays

Typically, PV panels comprise numerous interconnected PV cells, which are mechanically protected and suitable for sites with high solar radiation. Their principle of operation is based on the photoelectric effect, which explains that electrons are released when photons hit the PV panel.

Installing a single PV panel, such as for swimming pool heating, is sufficient in applications requiring only small amounts of energy. However, implementing PV arrays is necessary for more significant PV generation scenarios. In this case, PV panels are connected in series to achieve a greater voltage, in parallel to achieve a higher current, and in a mixed configuration to achieve higher power.

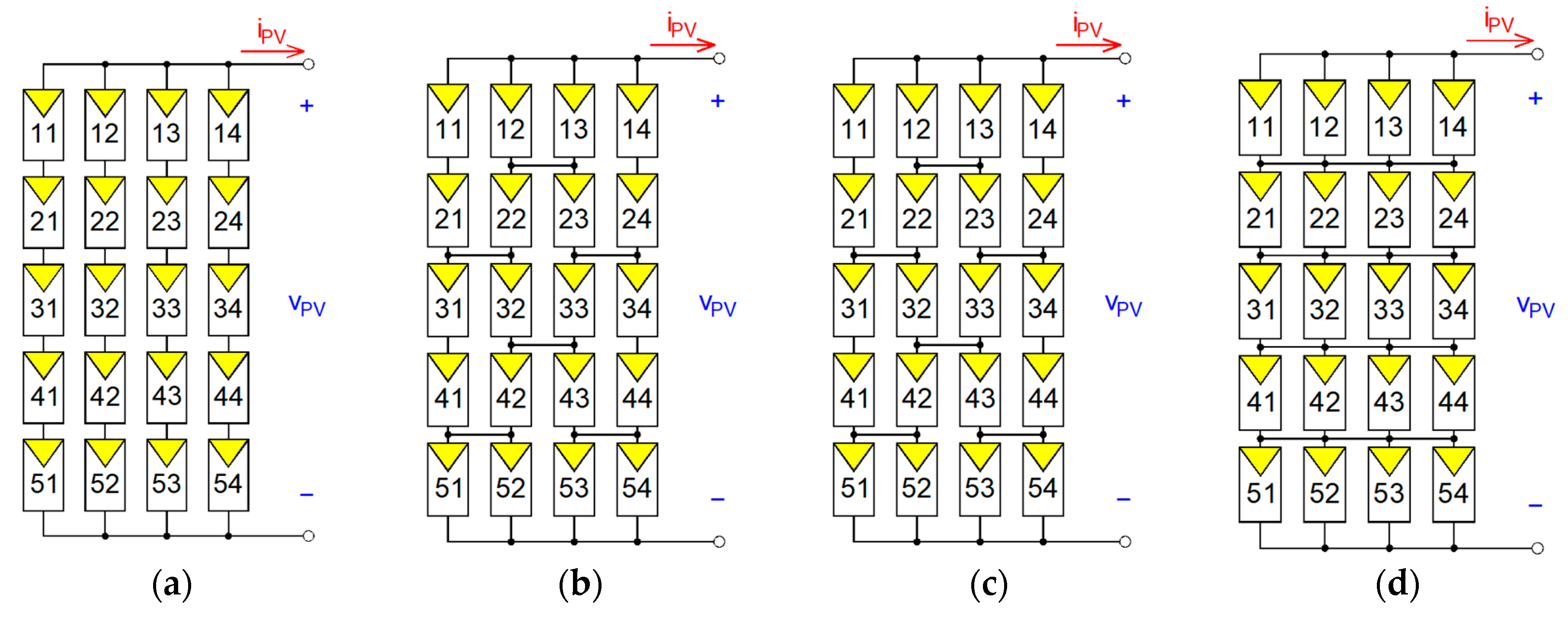
Figure 1 presents some connection topologies for a PV array, these being the Series–Parallel (SP), Bridge-linked (BL), Honeycomb (HC), and Total-Cross-Tied (TCT) [15]. This paper considers the SP array. Its size depends on the maximum operating conditions of each connected PV panel and the manufacturer’s data.

Conventionally, these are operated at the maximum power point (MPP) to extract the maximum available PV power. The MPP depends on several conditions, such as the PV panels’ properties, climatic changes like light intensity decreasing due to the appearance of clouds, or unforeseen weather changes [16]. MPP tracking can be implemented in the control circuit of the DC-DC converter to match the impedance of the PV array. This way, its operation can be stabilized at the maximum power point (MPP) or as close as possible to it. This power peak can be seen in Figure 2 in the current/power characteristic curves of PV panels as a function of the voltage at their terminals. These characteristic curves indicate the MPP values for the PV arrays’ sizing. Their parameters are the I_MPP current and P_MPP power at a V_MPP voltage or remarkably close values [17]. Additionally, the ranges of these curves are limited by the short-circuit current I_SC and the open-circuit voltage V_OC.

2.2. Boost Converter Design and Modeling

Power electronics-based energy conversion systems are used to optimize and efficiently use energy from PV systems. Since their output voltage is DC, a DC-DC converter such as the boost converter can be employed. When larger DC voltages are needed with lower input voltages and high efficiency, these converters are used in battery power applications, automotive applications, industrial drives, and adaptive control applications [18].

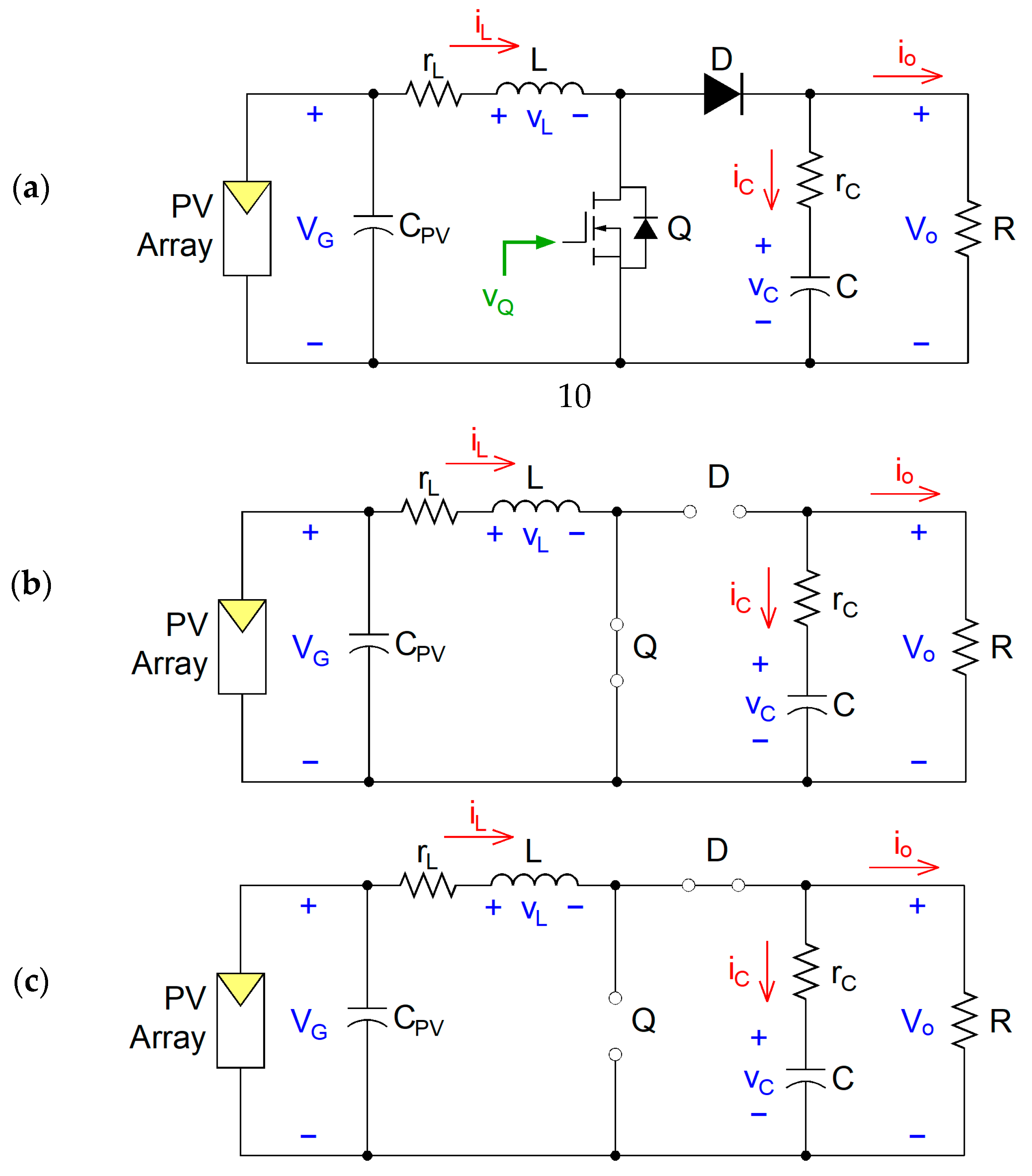
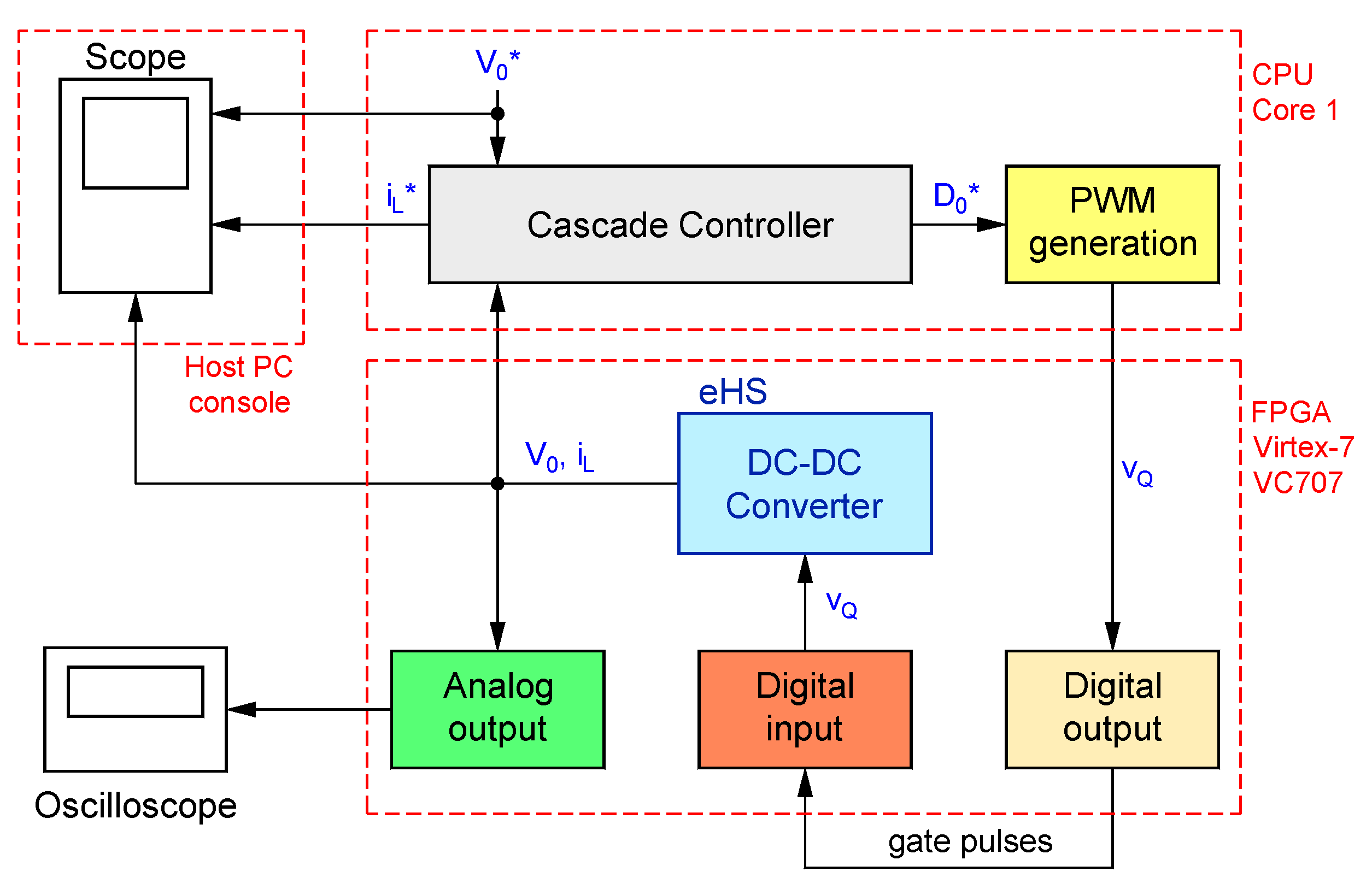
Figure 3a shows the power circuit of a boost converter, which is characterized by two operating states: In the “On-state”, shown in Figure 3b, the Q semiconductor acts as a switch, and when it is closed, an increase in the level of the inductor current L is experienced. In contrast, the switch opens during the “Off-state” shown in Figure 3c. The only possibility for inductor current to flow is through diode D and the parallel configuration of output capacitor C and load resistor R. This leads to the capacitor transferring energy, which is acquired by it during the “On-state”. Additionally, the PV-generated power will oscillate due to a PV voltage ripple, resulting in a reduced average power output, and this is because of the installation of a C_PV capacitor for smoothing voltage ripples [19].

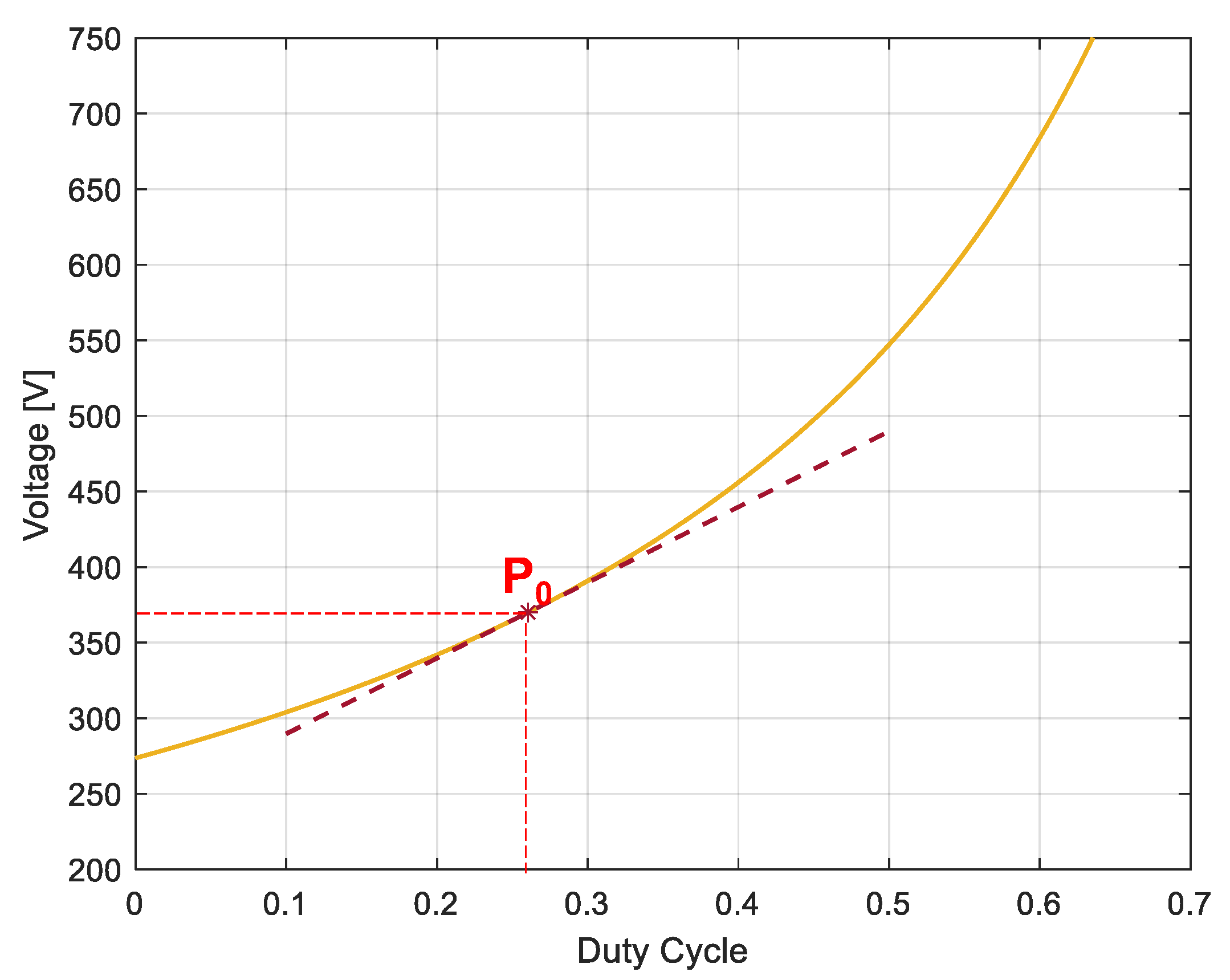
Due to the operation of the semiconductor Q, the output load voltage is chopped according to an operating duty cycle D₀ at a high switching frequency f_SW and is calculated according to (1), where V_G is the PV voltage, and V₀ is the output voltage.

$$D_0=1-{\displaystyle \frac{V_G}{V_0}}$$

(1)

Continuous conduction mode (CCM) operation is desired in DC-DC switching converters. This means that the primary current, which is the inductor current in the converter, is not canceled out. The minimum values of its passive components R, L, and C together must be determined, along with its associated series resistances, considering primarily the power P_n of the converter. In (2), the minimum inductance for the CCM current is determined according to [20]. On the other hand, the minimum output capacitance can be determined by (3), according to [20], where the output voltage ripple specification is usually between 1% and 5%.

$$L_{min}={\displaystyle \frac{D_0{\left(1-D_0\right)}^2{V_0}^2}{{2f}_{SW}{P}_n}}$$

(2)

$$C_{min}={\displaystyle \frac{D_0{P}_n}{{{\left(\frac{{∆V}_0}{V_0}\right)}^2{V_0}^{2}f}_{SW}}}$$

(3)

Using a Schottky diode as a natural switching device and an IGBT as a forced switching device was considered to reduce power losses due to its higher current rating compared to a MOSFET.

The principle of DC-DC converter control is PWM (Pulse Width Modulation), which is generated through the comparison of a constant modulating signal and a sawtooth carrier signal v_st at a switching frequency of f_SW [21], or at a switching period of T_SW. Figure 4 shows these waveforms together with their comparative results. Depending on whether the nominal duty cycle D₀ is increased or decreased, the resulting square signal pulse v_Q will either be broader or narrower at a constant frequency comparable to f_SW. It is important to note that the control signal D₀ will come from the implemented digital or predictive controller, and in some cases, it may come directly from an MPPT controller.

This technique has variations, such as the control signal being compared against an unbiased triangle wave instead of a sawtooth wave. Another novel method is establishing boundary voltages for the control signal, thus achieving an improved dynamic response [22].

Once the parameters of the boost converter have been determined, the mathematical model of the system may be derived, with the averaged model state space matrixes A_p, B_p, C_p, and D_p, the state vector x = [i_L v_C]^T, V_G as an input, and V₀ as an output. V_G is considered only as an input because we aim to find the system dynamics only in the power stage. In this type of system, the input does not have a direct influence on the outputs, and for this reason, the D_p matrix is considered null.

Figure 3b shows the power circuit in the On-state [13], where Kirchhoff’s current/voltage laws are applied in the first instance together with the laws of each energy storage component, thus obtaining (4) and (5):

$$L{\displaystyle \frac{d{i}_L}{dt}}=V_G-r_L{i}_L$$

(4)

$$R{i}_o=r_c{i}_c+v_C$$

(5)

Considering the output mesh:

$$C{\displaystyle \frac{d{v}_C}{dt}}=i_c=-i_o$$

(6)

With these expressions, the system behavior is obtained:

$$\left(\begin{array}{c}{\displaystyle \frac{d{i}_L}{dt}}\\ {\displaystyle \frac{d{v}_C}{dt}}\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{{-r}_L}{L}}& 0\\ 0& {\displaystyle \frac{-1}{C(R+r_c)}}\end{array}\right)\left(\begin{array}{c}{i}_L\\ v_C\end{array}\right)+\left(\begin{array}{c}{\displaystyle \frac{1}{L}}\\ 0\end{array}\right)V_G$$

(7)

By applying a voltage divider on the output mesh, the output voltage in the On-state will be:

$$v_o=\left(\begin{array}{cc}0& {\displaystyle \frac{R}{R+r_c}}\end{array}\right)\left(\begin{array}{c}{i}_L\\ v_C\end{array}\right)$$

(8)

Similarly, the following expression in the first mesh for the boost converter in the Off-state [13] will be:

$$L{\displaystyle \frac{d{i}_L}{dt}}=V_G-r_L{i}_L-v_o$$

(9)

The second mesh is analyzed as follows:

$$v_o=v_c+r_{C}C{\displaystyle \frac{d{v}_C}{dt}}$$

(10)

$$i_o=i_L-C{\displaystyle \frac{d{v}_C}{dt}}={\displaystyle \frac{v_o}{R}}$$

(11)

In this case, first, the output expression will be determined by replacing (11) in (10):

$$v_o={\displaystyle \frac{v_C+r_C{i}_L}{\left(1+\frac{r_C}{R}\right)}}$$

(12)

Considering (12) in the previous expressions, the following system behavior in a steady state is obtained:

$$\left(\begin{array}{c}{\displaystyle \frac{d{i}_L}{dt}}\\ {\displaystyle \frac{d{v}_C}{dt}}\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{{-r}_{L}R-r_L{r}_c-r_{c}R}{L\left(R+r_c\right)}}& {\displaystyle \frac{-R}{L(R+r_c)}}\\ {\displaystyle \frac{R}{C(R+r_c)}}& {\displaystyle \frac{-1}{C(R+r_c)}}\end{array}\right)\left(\begin{array}{c}{i}_L\\ v_C\end{array}\right)+\left(\begin{array}{c}{\displaystyle \frac{1}{L}}\\ 0\end{array}\right)V_G$$

(13)

$$v_o=\left(\begin{array}{cc}{\displaystyle \frac{R{r}_c}{R+r_c}}& {\displaystyle \frac{R}{R+r_c}}\end{array}\right)\left(\begin{array}{c}{i}_L\\ v_C\end{array}\right)$$

(14)

Representation of the average model in steady space is performed for both switching periods. For t_ON during a duty cycle d and t_OFF during a complementary duty cycle 1 − d, the following average A_p, B_p, and C_p matrixes are obtained:

$$\begin{array}{c}{A}_p=A_{ON}d+A_{OFF}\left(1-d\right)\\ B_p=B_{ON}d+B_{OFF}\left(1-d\right)\\ C_p=C_{ON}d+C_{OFF}\left(1-d\right)\end{array}$$

(15)

With these matrixes, a system with two inputs, u = [d V_G]^T, two states, x = [i_L v_C]^T, and one output, V₀, for the voltage regulation of the converter, as a function of slight duty cycle changes, is obtained.

$$\begin{array}{c}{A}_p=\left[\begin{array}{cc}-{\displaystyle \frac{r_{L}R+r_L{r}_c+r_{c}R\left(1-d\right)}{L(R+r_c)}}& -{\displaystyle \frac{R\left(1-d\right)}{L\left(R+r_c\right)}}\\ {\displaystyle \frac{R\left(1-d\right)}{C\left(R+r_c\right)}}& -{\displaystyle \frac{1}{C\left(R+r_c\right)}}\end{array}\right]\\ B_p={\left[{\displaystyle \frac{1}{L}}0\right]}^T\\ C_p=\left[\begin{array}{cc}{\displaystyle \frac{R{r}_c\left(1-d\right)}{R+r_c}}& {\displaystyle \frac{R}{R+r_c}}\end{array}\right]\end{array}$$

(16)

3. Digital and Predictive Control

The state matrixes referring to the system that describes the boost converter’s dynamics have non-linear components. For this reason, these matrixes must be linearized around an operating point whose parameters can be determined by solving x₀’ = [i_L0 v_C0]^T from the nominal data V₀ and D₀. With the linearized state matrixes A_p0, B_p0, and C_p0, two transfer functions, V₀(s)/d(s) and V₀(s)/V_G(s) [23] can be determined, thus achieving direct voltage control (DVC) from d and V_G variations.

However, the transfer function V₀(s)/d(s) is in the non-minimum phase; therefore, even if a controller with good regulation performance is implemented, the voltage V₀ will have a wide ripple voltage. Figure 5a shows a DVC scheme using a digital PI (Proportional–Integral) controller. These control diagrams show components whose functions will be explained below.

The cascade feedback control structure is reliable for controlling DC-DC and DC-AC power converters and electric drives. The inner control loop regulates the converter current. In contrast, in the external control loop, the primary desired variable is controlled—for example, voltage or active power in microgrids, such as the boost converter output voltage.

The key to the success of cascade control lies in the difference between the time constants of both loops so that the current response time will be much faster. Some cascade control topologies have been developed in this paper, such as the digital control loops shown in Figure 5b, and the combined control loops shown in Figure 5c, where the internal one is predictive, while the external one is digital, with both predictive control loops shown in Figure 5d.

To implement this control scheme, in the first instance, it is necessary to determine the transfer functions I_L(s)/d(s) and I_L(s)/V_G(s) [23] for the internal loop control with the matrixes of linearized states A_p0 and B_p0 at the operating point, and since i_L is intended to be the output variable, we consider C_p0 = [10].

After this, the transfer function V₀(s)/I_L(s) must be determined for the control of the outer loop [23]. This can be achieved by finding this transfer function averaged over the boost converter output loop for t_ON during a duty cycle d and for t_OFF during the complementary duty cycle 1 − d. Around operating point p₀, the averaged function described by (17) is obtained:

$${\displaystyle \frac{V_0\left(s\right)}{I_L\left(s\right)}}={\displaystyle \frac{R\left(1-D_0\right)\left(r_{C}Cs+1\right)}{\left({R+r}_C\right)Cs+1}}$$

(17)

Within the theory of predictive control, some variations have been developed, among which we have Dynamic Matrix Control (DMC), Generalized Predictive Control (GPC), Non-Linear Model Predictive Control (NMPC), Extended Prediction Self Adaptive Control (EPSAC), and Model Predictive Control with Autoregressive Disturbance (MPC-AR), among others [13]. There are differences between several types of controllers, which lie in how the model is approached, the kind of optimization applied, whether restrictions are considered when optimizing, and even whether disturbances are included or not [24].

3.1. Digital Control

Digital signal processors are widely used in power conversion systems since semiconductor pulse signals are transmitted at high speeds, either to IGBTs or MOSFETs. As previously mentioned, in addition to these external components, DC-DC converters have a PWM stage whose pulse generation can be implemented with digital electronic schemes such as a free-running counter, an up/down counter, and a hardware accumulator [25]. In microprocessor applications, the operating voltage drops from 5 V to 3.3 V or even lower, and the load current switches from sleep mode to high-speed computation mode faster.

For these reasons, solutions based on digital control are appropriate for DC-DC converters, with the implementation of analog and digital signal converters and vice versa for the execution of control actions. Signal scaling or conditioning blocks are often implemented for processing.

The conversion of signals referring to boost converter current/voltage measurements is usually carried out using zero-order hold circuits (ZOH) at a sampling time of T_s and, in some cases, digital low pass filters (DLPF) to mitigate stochastic noise. In addition to correctly sizing the inductor L, it must be ensured that the boost converter conduction mode has a direct current; it is for this reason that a digital controller is used to regulate the current i_L, and an external control is used in cascade for the regulation of output voltage V₀, this being the variable of interest, as shown in Figure 5b.

It is necessary to apply a Zeta transform to the transfer functions I_L(s)/d(s) and I_L(s)/V_G(s) for the tuning of the digital controllers, where it is also considered that the variations in the voltage V_PV due to climatic changes would be control system disturbances.

An essential point for tuning the voltage controller in the system’s external loop, whether using digital or predictive control, is that the transfer function of the current internal loop is considered to be approximately unitary; this is because the current of the inductor i_L reaches its reference value i_L* very quickly.

3.2. Predictive Control

The MBPC comprises a set of control methods with common characteristics, such as using the system model to calculate the output at future times and using an optimal control action calculated from a cost function [26]. This control technique slides the horizon toward the future at each instant, and a new optimized prediction is calculated in each iteration. Various constraints on the process variables of interest can also be implemented. Among its benefits, SISO (Single Input, Single Output) and MIMO (Multiple Input, Multiple Output) systems can be handled.

The steps in the hierarchical predictive structure are as follows: measurements are needed initially; then, model outputs are computed; and lastly, a control method resolves a quadratic programming or classical optimization issue. Figure 6a presents this prediction process, and Figure 6b displays a microgrid’s control sequence.

In this paper, the representation of the system is carried out through state spaces, with the state x(k) = [i_L(k) v_C(k)] and the input vector and u(k) = [d(k) V_i(k)]. Additionally, the operational outputs V₀ e I_L0 are considered. Based on the sliding horizon principle, it is assumed that u(k) does not affect y(k) simultaneously. Therefore, the discrete system with average matrixes will be represented by:

$$\left\{\begin{array}{c}x\left(k+1\right)=A_{p}x\left(k\right)+B_{p}u\left(k\right)\\ {y\left(k\right)=C}_{p}x\left(k\right)\end{array}\right.$$

(18)

As can be seen, the output predictions are made from the present state variables and the present and future control signal increments. For this, the vectors ∆U and Y are defined, where the dimensions of the vectors are N and P, respectively:

$$\left\{\begin{array}{c}∆U={\left[\begin{array}{ccc}∆u\left(k\right)& ∆u(k+1)& \dots ∆u(k+N-1)\end{array}\right]}^T\\ Y={\left[\begin{array}{ccc}y(k+1)& y(k+2)& \dots y(k+P)\end{array}\right]}^T\end{array}\right.$$

(19)

The general equation represented in matrix format will be Y = Fx(k) + G∆U, where the respective matrixes are:

$$\left\{\begin{array}{c}F={\left[\begin{array}{ccc}{C}_p{A}_p& C_p{A_p}^2& \dots \end{array}{C}_p{A_p}^P\right]}^T\\ G=\left[\begin{array}{ccc}\begin{array}{c}{C}_p{B}_p\\ C_p{A}_p{B}_p\\ \begin{array}{c}{C}_p{A_p}^2{B}_p\\ ⋮\\ C_p{A_p}^{P-1}{B}_p\end{array}\end{array}& \begin{array}{c}0\\ C_p{B}_p\\ \begin{array}{c}{C}_p{A}_p{B}_p\\ ⋮\\ C_p{A_p}^{P-2}{B}_p\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}0\\ 0\\ \begin{array}{c}{C}_p{B}_p\\ ⋮\\ C_p{A_p}^{P-3}{B}_p\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ \ddots \\ \dots \end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ ⋮\\ C_p{B}_p\end{array}\end{array}\end{array}\end{array}\right]\end{array}\right.$$

(20)

The cost function or objective function that weights the system error and the control actions of the MBPC [27] is given by (21), where N₁ is when a sample occurs after the delay if the system has one. In addition, δ and λ are the weighting weights of the error and the control action, respectively.

$$J=\sum _{j=N_1}^P\delta \left(j\right)\left[\widehat{y}\right(k+j/k)-w\left(k+j\right){]}^2+\sum _{j=1}^N\lambda \left(j\right){\left[\mathsf{\Delta }u(k+j-1)\right]}^2$$

(21)

As can be seen, the control action acts at a lower instant and is used to calculate the new output, and is represented in matrix format as follows:

$$J={\left(\widehat{y}-w\right)}^T\delta (\widehat{y}-w)+\mathsf{\lambda }\text{∆}{U}^T∆U$$

(22)

Finally, to find the cost function in vector format, we calculate:

$$J={\left(G∆U+Fx\left(k\right)-w\right)}^T\delta (G∆U+Fx(k)-w)+\mathsf{\lambda }{∆U}^T∆U$$

(23)

In the case without restrictions, the minimum of J is analytically expressed in (24). It can be noticed that everything with W − Fx(k) is a matrix, called K for simplicity, whose values will be calculated only once and from which the first row will be used.

$$∆U={{(G}^T\delta G+\mathsf{\lambda }I)}^{-1}{G}^T{\delta }^T(W-Fx(k\left)\right)$$

(24)

The law control obtained without restrictions will be:

$$∆U=K(W-Fx\left(k\right))$$

(25)

The prediction stage can be summarized in the prediction process of the electrical variable of interest, where the objective is to reduce the errors of this variable between its reference value and the values measured in the converter, as later, a cost function from these measurements’ errors is minimized. In the case of i_L and V₀, the cost functions J_i and J_v, respectively, would be defined by (26):

$$\begin{gathered} J_i=\left|∆I_L\left(k+1\right)\right|=\left|{I_L}^{*}\left(k\right)-I_L\left(k+1\right)\right| \\ {J}_v=\left|∆V_o\left(k+1\right)\right|=\left|{V_o}^{*}\left(k\right)-V_o\left(k+1\right)\right| \end{gathered}$$

(26)

4. System Loop Control Design

As a first step, a power value was chosen that would be supplied by the PV array for its sizing. The manufacturer of the selected PV panels was AE SOLAR, from Königsbrunn, Germany, with part number AE340SMM6-72. These PV panels have electrical characteristics that were obtained with tests under standard conditions, with 1 kW/m² at 25 °C, shown in

Table 2. PV panel and array standard condition specifications.

Parameter	Description	PV Panel	PV Array
PMPP	MPP power	340 W	16.66 kW
VMPP	MPP voltage	39.09 V	273.63 V
IMPP	MPP current	8.7 A	60.9 A
VOC	Open-circuit voltage	46.94 V	328.58 V
ISC	Short-circuit current	9.48 A	66.36 A

. Additionally, it should be noted that each PV panel comprises 72 cells, with V_OC and I_SC temperature coefficients of −0.29%/°C and 0.05%/°C, respectively. Choosing a PV array power of 15 kW, the same as the power in the MPP (Maximum Power Point), and a voltage in the MPP close to the reference value V₀* = 370 V, a quantity of seven panels connected in series were obtained, and seven of these arrays were connected in parallel. With these values, the specifications of the PV array were found, which are also shown in Table 2.

Table 3. Parameters found in the boost converter.

Parameter	Description	Value
VG	Input voltage	273.63 V
V0	Output voltage	370 V
D0	Nominal duty cycle	0.2605
Lmin	Minimum inductance	0.13 mH
L	Inductance	1.3 mH
rL	Inductor series resistance	0.1 μΩ
Cmin	Minimum output capacitance	570.77 μF
C	Output capacitance	1000 μF
rC	Output capacitance series resistance	0.1 μΩ
CPV	Input capacitance	1000 μF
rCPV	Input capacitance series resistance	0.1 μΩ
R	Load resistance	9.13 Ω

shows the components of the chosen boost converter. Initially, the converter load resistance was sized based on the required power/voltage parameters. Subsequently, the operating duty cycle was calculated according to (1) considering the input/output voltage requirements. In addition, f_SW = 5 kHz was chosen for the minimum component sizing of the boost converter, the same ones found following (2) and (3). Commercial values above the minimum estimated values were considered when determining capacitances, and a value ten times higher than the minimal calculated inductance was considered when choosing an inductance. On the other hand, standard values were considered for the converter components’ series resistances.

With the considered values of the converter parameters, the obtained state matrixes are indicated in (27).

$$\left\{\begin{array}{c}{A}_{p0}=\left[\begin{array}{cc}-0.001& -568.8342\\ 739.5405& -109.569\end{array}\right]\\ B_{p0}={\left[\begin{array}{cc}\mathrm{284,590}& -\mathrm{54,820}\end{array}\right]}^T\end{array}\right.$$

(27)

From these matrixes, transfer functions i_L(s)/d(s) and V₀(s)/i_L(s) were obtained. Then, these transfer functions were discretized for tuning the digital controllers. When testing and adjusting several controllers using MATLAB/SIMULINK control tools during the manual tuning process, the best parameters for current/voltage regulation were those indicated in

Table 4. Digital controllers’ parameters.

Parameter	Description	For iL	For V0
KP	Proportional gain	0.000551	0.204
KI	Integral gain	0.312	15.6

considering a control sampling time equivalent to T_s = 100 µs.

On the other hand, these transfer functions will also be helpful for the design of MBPC controllers, both for current and voltage regulation. This could be achieved by considering both the prediction horizons P = 10 and control horizons N = 3, together with a control sampling time of T_s = 200 µs. In these controllers’ designs, the operating values of the boost converter were also considered.

Regardless of the applied type of control, be it digital PI or MBPC, it is worth mentioning that, in the design of the current controller, the restriction of a control action between 0 and 1 was considered, this being the value of the duty cycle sent to the PWM pulse generator. It should be noted that for the design of the voltage controller, the transfer function V₀(s)/i_L(s) was considered, and that the closed-loop transfer function i_L(s)/i_L*(s) was unitary since the reference current was quickly reached.

5. Real-Time Simulation for Boost Converter

Real-time (RT) simulation is necessary when a CPU requires a similar operation to a physical system. An RT simulator achieves deterministic responses by connecting real hardware or implementing a hardware-in-the-loop (HIL) scheme. It is crucial to indicate that the RT concept can be applied strictly according to the requirements of each system’s restrictions. This implies that the sampling would not be the same for an electronic system as for a thermal or mechanical system. This type of simulation is carried out according to a sampling time T_{s_CPU} that can be adjusted according to the implemented system.

ESPOL possesses the tools to conduct R&D projects in innovative academic and commercial solutions for power electronics and power systems industries. The RT-LAB development package includes a 32-core OPAL-RT RT simulator, a processor based on the Xilinx VC707 Virtex-7 FPGA (San José, CA, USA) architecture capable of exchanging voltage/current I/Os, and an OMICRON CMS 356 power amplifier to exchange voltage/current signals with protection relays. It is also completely integrated with MATLAB/Simulink^®. Figure 7 shows part of the equipment in the RT simulation laboratory in ESPOL, with an AMETEK 90 kVA power amplifier for high AC and DC power systems applications.

In power electronics-based applications, RT simulation presents some challenges in HIL implementations, such as the ability to capture I/O as PWM pulse signals at high frequencies and the mathematical resolution of coupled semiconductors and switches [28].

OPAL-RT offers the eFPGAsim library, ensuring all FPGA-based models exhibit extremely low loop latency. This library uses an FPGA solver called the Electric Hardware Solver (eHS) to customize power electronics stages. The sampling time T_{s_FPGA}, which is a parameter dependent on the complexity of the circuit to be implemented [28], from ns to ms, is typically much smaller than T_{s_CPU}.

In offline simulations or simulations executed purely in software, the switches are typically calculated using conductance matrixes. Therefore, an optimal value of the switching conductance G_S should be obtained since the switches are represented by the Pejovic method in the FPGA simulation [29]. This method replaces the switch with an inductor L_s when it conducts and a capacitor C_s when it does not conduct in the nodal matrix, resulting in G_S not changing. This parameter is defined in (28).

$$G_s={\displaystyle \frac{T_{S\_FPGA}}{L_s}}={\displaystyle \frac{C_s}{T_{S\_FPGA}}}$$

(28)

Another challenge in RT simulations is the control of the conduction and cut-out of the switches. Pulse generation using typical Simulink blocks causes the comparison result to be related to the T_{s_CPU} sampling time; the switching state will change only when a rising edge of T_{s_CPU} occurs, with the possible loss of states [29]. For this reason, it is recommended that PWM pulses be generated by configuring a digital output of the FPGA, specifying the switching frequency and operating duty cycle, and consequently connected to a digital input. This technique, called loopback, is a solution to generate high-frequency triggers between T_{s_CPU} transitions.

This RT simulation project consists of two subsystems. The first subsystem, called the master subsystem, has an eHS stage where the power circuit of the converter is implemented and a stage in the CPU where the cascade control is implemented along with blocks for the triggering of the PWM pulses. A second subsystem, called the console subsystem, displays the current/voltage measurements in the converter. An overall simulation scheme is shown in Figure 8, where all the CPU/FPGA boundaries are indicated. Additionally, an oscilloscope is used to more accurately monitor voltage/current signals.

6. Simulation and Results

6.1. Boost Converter Non-Linear Behavior

Power stage modeling aims to represent the system’s DC behavior around an operating point P₀ (D₀, V₀). Figure 9 shows the non-linear behavior of the boost converter output voltage V₀ as a function of its duty cycle d. A tangent line has been drawn around the calculated operating duty cycle D₀, representing the linearization of the system. These graphs demonstrate that the duty cycle and voltage setpoint V₀* variations should be kept small around the operating point. If the operation conditions were significantly displaced from P₀, the variations in the non-linear model would seriously affect the converter’s response. On the other hand, for high-duty cycles greater than 0.9, the converter’s voltage gain and output voltage would be so high that the converter would not have the capacity to supply them. It should be noted that the linearized output voltage $\widehat{v_o}$ as a function of the linearized duty cycle $\widehat{d}$ is described by (29), which also depends on the input voltage V_G.

$$\widehat{v_o}\cong {V_o}^{*}+\left[{\displaystyle \frac{V_G}{{\left(1-D_o\right)}^2}}\right]\left(\widehat{d}-D_o\right)$$

(29)

6.2. Boost Converter Offline Simulations

This section shows the results of offline simulations, in which the DVC experiment has yet to be considered since it is outside the context of this paper. This type of control is slow compared to schemes based on cascade control. Figure 10 shows the boost converter output voltage V₀ and inductor current i_L behavior when the cascade control-based schemes control the converter. The simulation lasts six seconds.

Initially, a load variation of ±10 V was considered, but this displaced the operation conditions from the operating point P₀. With this, steady-state errors appeared, and to fix this anomaly, the load variation was decreased, acting as a disturbance variation.

During the 2nd and 4th seconds, the forced load voltage varies by 1 V; subsequently, the load voltage varies by −1 V. The overshoot levels (OS) and stabilization times (T_SS) were evaluated in each simulation section. These load variations were like disturbances in the DC-DC converter, and with this, the results detailed in

Table 5. Output voltage response specification data in offline simulations.

Parameter	0 < t < 2 s	2 s < t < 4 s	4 s < t < 6 s
Digital PI + PI
OS	5.61%	1%	0.98%
TSS	62 ms	51 ms	74 ms
Combined scheme
OS	6%	0.97%	0.85%
TSS	23 ms	20 ms	28 ms
MBPC + MBPC
OS	7.15%	3.71%	0.96%
TSS	36 ms	22.1 ms	25.8 ms

were obtained.

Table 6. Output voltage and inductor current ripple and average data in offline simulations.

Parameter	Digital PI + PI	Combined Scheme	MBPC + MBPC
∆V0	2.744 V	3.509 V	2.819 V
V0(avg.)	369.759 V	369.7185 V	370.0255 V
∆iL	12.9717 A	13.1608 A	12.6679 A
iL(avg.)	54.6185 A	55.36 A	55.38125 A

shows all the ripple and average data in V₀ and i_L for each cascade control scenario. In the voltage case, the average data are close to V₀^*; in the current case, the average values are approximate in all cases. These data were kept constant during the simulations.

6.3. Boost Converter RT Simulations

Electrical SCADA (Supervisory Control and Data Acquisition) systems use the console output from RT simulation equipment to display the voltage/current RMS readings for many applications. As previously discussed, an oscilloscope is necessary to better visualize signals in converter circuits, even though they are also commonly employed in power electronics applications. The I/O channels of the simulator, which are scaled by a factor of 0.1, were used to connect this equipment. This is because extra scaling is possible when the base circuit is built in the eHS block; these channels offer acceptable security. Scaling for V₀ was set at 0.01 units/V, whereas scaling for i_t was set at 0.01 units/A.

This section presents the RT simulation results. Figure 11 shows the behavior of the boost converter output voltage V₀ and inductor current i_L with an oscilloscope, which was implemented within the OPAL-RT FPGA.

Similarly to the previous section, this simulation lasted six seconds, and the load voltage was changed by ±1 V after the 2nd and 4th seconds, producing the results shown in

Table 7. Output voltage response specification data in RT simulations.

Parameter	0 < t < 2 s	2 s < t < 4 s	4 s < t < 6 s
Digital PI + PI
OS	5.44%	0.98%	0.95%
TSS	62.5 ms	52 ms	76 ms
Combined scheme
OS	5.8%	1.01%	0.87%
TSS	72 ms	15 ms	27.6 ms
MBPC + MBPC
OS	6.84%	3.65%	0.72%
TSS	26 ms	20.8 ms	25.2 ms

. It can be noticed that with the forced variation of ±1 V, V₀ was not affected no matter the cascade control scenario.

In the same way as offline simulations,

Table 8. Output voltage and inductor current ripple and average data in RT simulations.

Parameter	Digital PI + PI	Combined Scheme	MBPC + MBPC
∆V0	5.662 V	4.204 V	4.001 V
V0(avg.)	370.455 V	369.786 V	370.0945 V
∆iL	14.7024 A	18.416 A	17.7422 A
iL(avg.)	55.8731 A	55.5625 A	55.8936 A

shows all the ripple and average data for the voltage/current measurements. These data were kept constant during the RT simulations, and the results are similar to those obtained in offline simulations.

7. Discussion

Table 9. Comparison between current work and related works.

Reference	PV Feed	DC-DC Converter Design	Offline Validation	Exp. Validation	η	TSS (ms)	Min. OS
PD-Fuzzy logic#1 [6]			√		93.6%	15	7%
PD-Fuzzy logic#2 [6]			√		96.44%	50	7%
GA [7]			√	√	95.71%	27.6	20.92%
BFOA [7]			√	√	95.71%	20.4	23.38%
PSO [8]		√	√	√	96.52%	43	-
SMC [9]		√	√		95.18%	30	-
Fuzzy logic + SMC [10]	√		√		99.35%	35	4.5%
PID + Hysteresis [11]		√	√		96.99%	450	4%
PID + SMC [11]		√	√		96.99%	450	-
Current work	√	√	√	√	95.69%	15	1.01%

shows the collection of data, including renewable the energy integration, design of the DC-DC converter parameters, validation, efficiency (η), and output voltage response parameters, between the current work and the control techniques adopted for boost converters in related works. Based on the data obtained, some related works did not carry out an experimental validation, unlike the current work developed in an RT simulator.

The output voltage response was the fastest, with a minimum overshoot. Based on the reported works, whose parameters are presented in Table 9, the efficiency values exceed 90%, while our designed converter, with 15 kW power, has 95% efficiency.

On the other hand,

Table 10. Relative error data between offline and RT simulations for output voltage response parameters.

Parameter	0 < t < 2 s	2 s < t < 4 s	4 s < t < 6 s
Digital PI + PI
OS	3.13%	2.04%	3.16%
TSS	0.80%	1.92%	2.63%
Combined scheme
OS	3.45%	3.96%	2.30%
TSS	68.06%	33.33%	1.45%
MBPC + MBPC
OS	4.53%	1.64%	33.33%
TSS	38.46%	6.25%	2.38%

and

Table 11. Relative error data between offline and RT simulations for ripples and average data.

Parameter	Digital PI + PI	Combined Scheme	MBPC + MBPC
∆V0	51.54%	16.53%	29.54%
V0(avg.)	0.19%	0.02%	0.02%
∆iL	11.77%	28.54%	28.60%
iL(avg.)	2.25%	0.36%	0.92%

detail the relative errors between offline and RT simulation data. Time limitations, external interferences, and model simplifications are some of the reasons why offline and RT simulations differ in accuracy. RT simulations must work under tight time constraints, which might result in approximations and decreased accuracy, whereas offline simulations frequently rely on idealized conditions and higher-precision computations.

In addition, a SWOT (Strengths, Weaknesses, Opportunities, and Threats) matrix was developed to better comprehend the current work’s features and strategic planning. Based on the SWOT analysis shown in Figure 12, the most notable characteristic is the low-cost RT implementation, even with a hardware-in-the-loop test, which uses the high-frequency channels available on the equipment.

8. Conclusions

After analyzing how the boost converter operates, it is notable that the sizing of its components is crucial since they must be accurately predicted to meet the load requirements. Additionally, the mathematical model of the boost converter depends on its components. Even the PWM generation stage’s settings must be carefully chosen and kept constant.

PI controllers should be utilized in digital control systems rather than PID controllers due to their more straightforward design and high reliability. In some circumstances, cost savings could be achieved when the hardware benefits the controlled system.

MBPC is advantageous for forced-commutation-based power converters in power electronics applications because its model is crucial. It can forecast future events and adapt the current control strategy optimally. MBPC can manage SISO and MIMO systems, making it a more straightforward and suitable control solution. Another of its advantages is its digital implementation, so it is feasible to develop controllers in digital signal processors. For this reason, DLPF and ZOH are used in all cascade control schemes.

The MBPC’s computational load is high, but when operating in a real-time simulator, with its high frequency, this weakness is compensated and does not affect the voltage response. Depending on the complexity of the optimization algorithm used, the cost function could provide an adequate response, but obtaining it would take longer.

In the MBPC stage, choosing an initial prediction horizon of less than 50 is good practice, except when the sampling time is minimal. A small control horizon demands more controller computations due to quadratic programming.

This paper illustrates that with some cascade control techniques (digital PI + digital PI, digital PI + MBPC, and MBPC + MBPC), the output voltage reaches better stabilization compared to the other control techniques mentioned in the Introduction. It can even be seen that the inductor current settles faster than the output voltage in all cases. After comparing the outcomes and assessing each technique’s efficacy, the MBPC + MBPC scheme is found to be the most successful option in offline and RT simulations.

Real-time simulation offers low implementation costs compared to the actual costs of implementing a microgrid. In addition, using a real-time simulator allows many tests to validate solutions that present minimal defects when implemented.

An FPGA can implement any MPPT algorithm and the PWM control stage that produces the commutation pulses. The RT equipment can execute an FPGA-in-the-loop simulation. In this case, boost converter testing with an embedded controller is feasible due to the deployment of the MATLAB/Simulink^® platform for any existing code based on the Hardware Description Language.