Model Predictive Operation Control of Islanded Microgrids under Nonlinear Conversion Losses of Storage Units
Abstract
:1. Introduction
1.1. Literature Review
1.2. Statement of Contributions
- (i)
- We derive the model of an islanded MG with uncertain renewable generation and loads with a very high share of RES. This model, motivated by [22], considers a possible limitation of renewable infeed, while limitations on transmission lines are approximately accounted for using DC power flow approximations.
- (ii)
- We model storage devices as grid-forming units, and, to make the MG model more realistic, we consider the conversion losses of the storage units, the losses of the power electronic devices when converting Alternating Current (AC) to Direct Current (DC) (and vice versa), as well as ohmic losses in the batteries as the quadratic functions in the dynamics of storage units.
- (iii)
- We take into account power-sharing with the active conventional units. Therefore, the load fluctuations and renewable units influence all units’ power and the storage units’ state of charge. In this way, the model can also work where only RES and storage units are active, and no conventional unit is required.
- (iv)
- We propose a novel MPC approach for the optimal operation of an islanded MG with a very high share of renewable energy sources. To solve the optimization problem and mitigate the effect of errors in the storage units’ state of charge prediction, we reformulate the conversion loss functions as the mixed-integer linear inequality functions and include them in the proposed scheme.
- (v)
- We confirm the properties of the proposed operation control scheme via realistic simulations with a high renewable share.
1.3. Paper Organization
1.4. Mathematical Notation
2. Microgrid Model
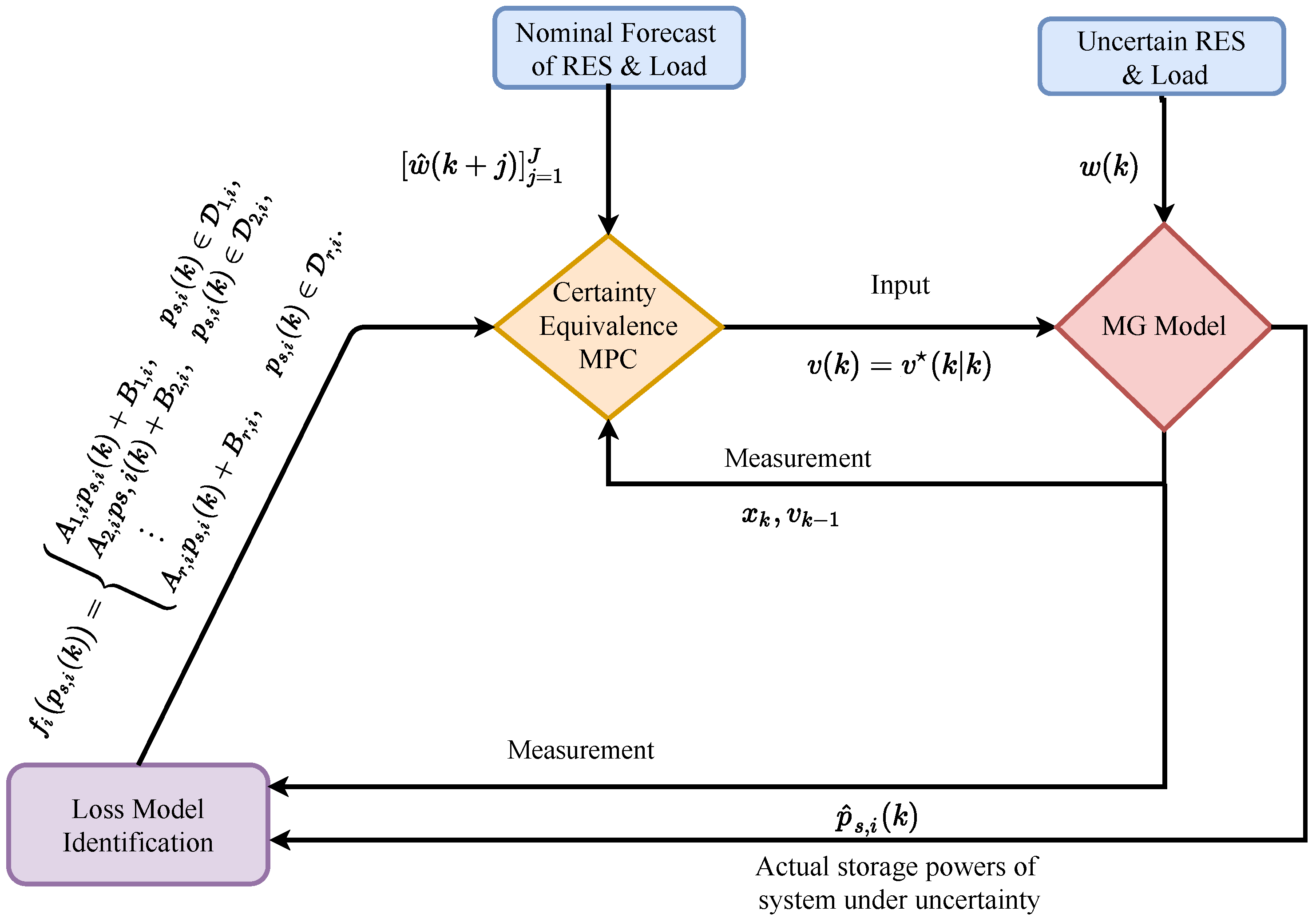
3. Certainty Equivalence Model Predictive Control
3.1. Plant Model Interface
3.2. Power of Units
3.2.1. Active Power at RES Units
3.2.2. Active Power at Conventional Units
3.2.3. Active Power at Storage Units
3.3. Power Sharing of Grid-Forming Units
3.4. Dynamics of Storage Units
3.5. Transmission Network
3.6. Overall Model
4. Operating Costs
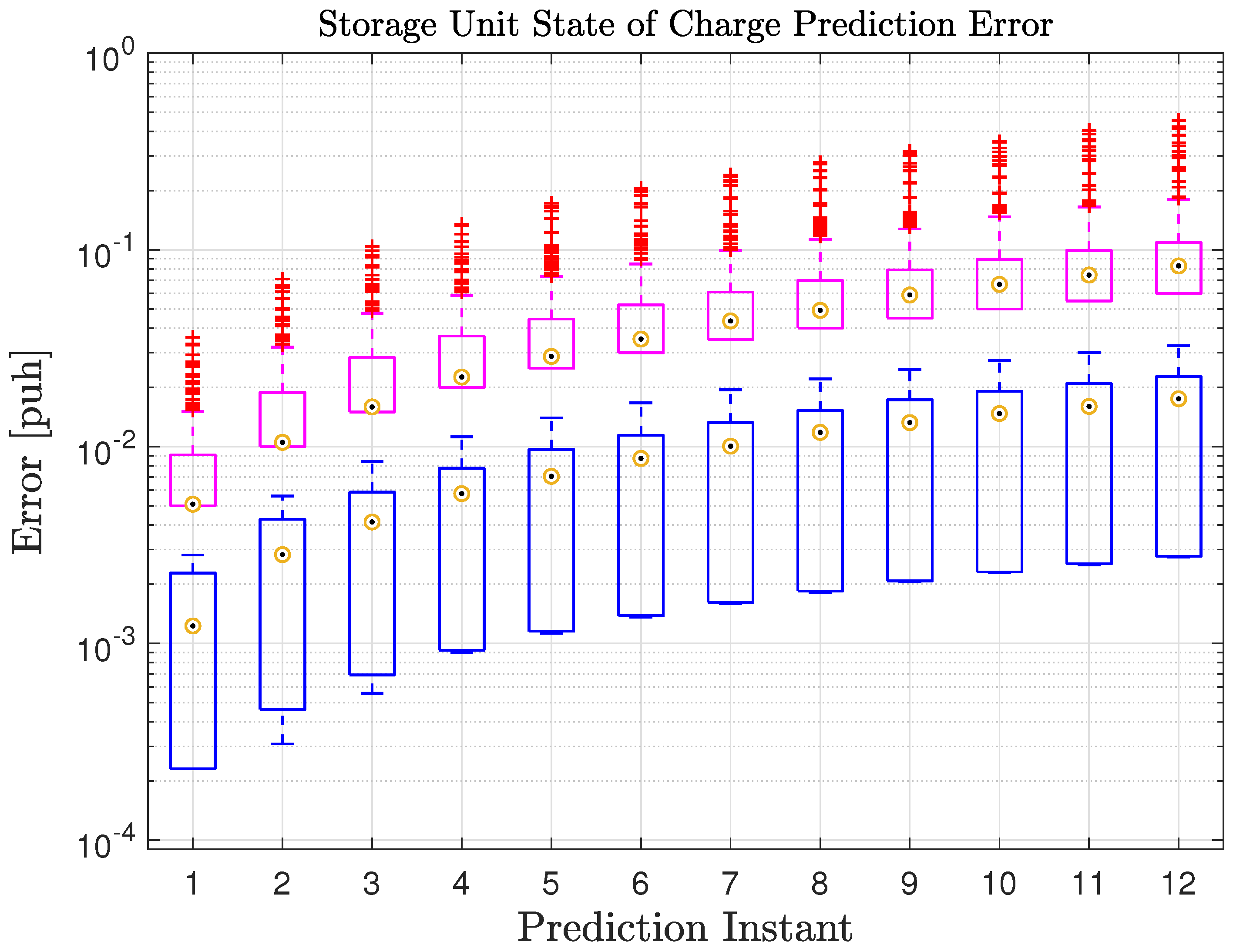
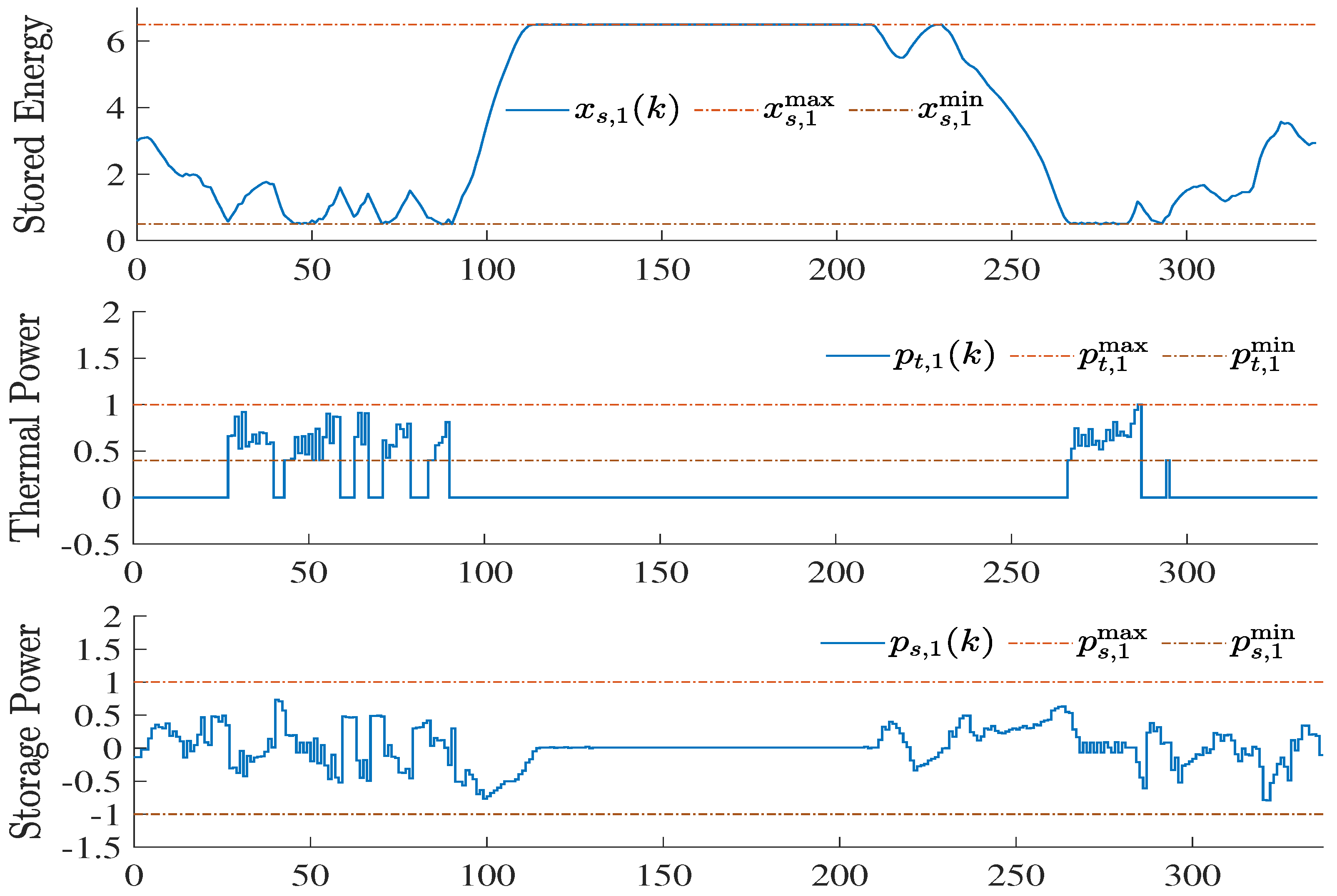
5. Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, P.A.; Fouad, A.A. Power System Control and Stability; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Pehnt, M. Dynamic life cycle assessment (LCA) of renewable energy technologies. Renew. Energy 2006, 31, 55–71. [Google Scholar] [CrossRef]
- Peças, J.A.; Moreira, C.L.; Madureira, A.G. Defining control strategies for microgrids islanded operation. IEEE Trans. Power Syst. 2006, 21, 916–924. [Google Scholar]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Gholami, M.; Pilloni, A.; Pisano, A.; Usai, E. Robust Distributed Secondary Voltage Restoration Control of AC Microgrids under Multiple Communication Delays. Energies 2021, 14, 1165. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.L.; Chiang Loh, P. Advanced control architectures for intelligent microgrids—Part I: Decentralized and hierarchical control. IEEE Trans. Ind. Electron. 2012, 4, 1254–1262. [Google Scholar]
- Kanagawa, M.; Nakata, T. Assessment of access to electricity and the socio-economic impacts in rural areas of developing countries. Energy Policy 2008, 36, 2016–2029. [Google Scholar] [CrossRef]
- Barklund, E.; Pogaku, N.; Prodanovic, M.; Hernandez-Aramburo, C.; Green, T.C. Energy management in autonomous microgrid using stability-constrained droop control of inverters. IEEE Trans. Power Electron. 2008, 23, 2346–2352. [Google Scholar] [CrossRef] [Green Version]
- Logenthiran, T.; Srinivasan, D. Short term generation scheduling of a microgrid. In Proceedings of the TENCON 2009—2009 IEEE Region 10 Conference, Singapore, 23–26 January 2009; pp. 1–6. [Google Scholar]
- Chen, C.; Duan, S.; Cai, T.; Liu, B.; Hu, G. Smart energy management system for optimal microgrid economic operation. IET Renew. Power Gener. 2011, 5, 258–267. [Google Scholar] [CrossRef]
- Palma-Behnke, R.; Benavides, C.; Lanas, F.; Sev, B.; Reyes, L.; Llanos, J.; Sáez, D. A microgrid energy management system based on the rolling horizon strategy. IEEE Trans. Smart Grid 2013, 4, 996–1006. [Google Scholar] [CrossRef] [Green Version]
- Heymann, B.; Bonnans, J.F.; Martinon, P.; Silva, F.J.; Lanas, F.; Guillermo, J.E. Continuous optimal control approaches to microgrid energy management. Energy Syst. 2018, 9, 59–77. [Google Scholar] [CrossRef] [Green Version]
- Mayhorn, E.; Kalsi, K.; Elizondo, M.; Zhang, W.; Lu, S.; Samaan, N.; Butler-Purry, K. Optimal control of distributed energy resources using model predictive control. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Olivares, D.E.; Cañizares, C.A.; Kazerani, M. A centralized energy management system for isolated microgrids. IEEE Trans. Smart Grid 2014, 5, 1864–1875. [Google Scholar] [CrossRef]
- Hans, C.A.; Nenchev, V.; Raisch, J.; ReinckeCollon, C. Minimax model predictive operation control of microgrids. IFACProceedings 2014, 47, 10287–10292. [Google Scholar] [CrossRef] [Green Version]
- Sui, Q.; Wei, F.; Wu, C.; Lin, X.; Li, Z. Day-Ahead Energy Management for Pelagic Island Microgrid Groups Considering Non-Integer-Hour Energy Transmission. IEEE Trans. Smart Grid 2020, 11, 5249–5259. [Google Scholar] [CrossRef]
- Tran, Q.T.T.; Riva Sanseverino, E.; Zizzo, G.; Di Silvestre, M.L.; Nguyen, T.L.; Tran, Q.-T. Real-Time Minimization Power Losses by Driven Primary Regulation in Islanded Microgrids. Energies 2020, 13, 451. [Google Scholar] [CrossRef] [Green Version]
- Nair, U.R.; Costa-Castelló, R. A Model Predictive Control-Based Energy Management Scheme for Hybrid Storage System in Islanded Microgrids. IEEE Access 2020, 8, 97809–97822. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M.; Guerrero, J.M. Energy Management System for an Islanded Microgrid with Convex Relaxation. IEEE Trans. Ind. Appl. 2019, 55, 7175–7185. [Google Scholar] [CrossRef]
- Hans, C.A.; Sopasakis, P.; Raisch, J.; Reincke-Collon, C.; Patrinos, P. Risk-averse model predictive operation control of islanded microgrids. IEEE Trans. Control Syst. Technol. 2020, 28, 2136–2151. [Google Scholar] [CrossRef] [Green Version]
- Lei, J.; Hans, C.A.; Sopasakis, P. Optimal operation of microgrids with risk-constrained state of charge. arXiv 2021, arXiv:2104.08357. [Google Scholar]
- Hans, C.A.; Braun, P.; Raisch, J.; Grüne, L.; Reincke-Collon, C.R. Hierarchical distributed model predictive control of interconnected microgrids. IEEE Trans. Sustain. Energy 2019, 10, 407–416. [Google Scholar] [CrossRef] [Green Version]
- Sampathirao, A.K.; Hofmann, S.; Raisch, J.; Hans, C.A. Distributed Conditional Cooperation Model Predictive Control of Interconnected Microgrids. arXiv 2021, arXiv:1810.03361v2[cs.SY]. [Google Scholar]
- Gholami, M.; Pisano, A.; Usai, E. Robust Distributed Optimal Secondary Voltage Control in Islanded Microgrids with Time-Varying Multiple Delays. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020; pp. 1–8. [Google Scholar]
- Pilloni, A.; Gholami, M.; Pisano, A.; Usai, E. On the robust distributed secondary control of islanded inverter-based microgrids. In Variable-Structure Systems and Sliding-Mode Control; Springer: Cham, Switzerland, 2020; pp. 309–357. [Google Scholar]
- Purchala, K.; Meeus, L.; Van Dommelen, D.; Belmans, R. Usefulness of DC power flow for active power flow analysis. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; pp. 454–459. [Google Scholar]
- Krishna, A.; Hans, C.A.; Schiffer, J.; Raisch, J.; Kral, T. Steady state evaluation of distributed secondary frequency control strategies for microgrids in the presence of clock drifts. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; pp. 508–515. [Google Scholar]
- Bemporad, A.; Morari, M. Control of systems integrating logic, dynamics, and constraints. Automatica 1999, 35, 407–427. [Google Scholar] [CrossRef]
- Petrollese, M.; Valverde, L.; Cocco, D.; Cau, G.; Guerr, J. Real-time integration of optimal generation scheduling with MPC for the energy management of a renewable hydrogen-based microgrid. Appl. Energy 2016, 166, 96–106. [Google Scholar] [CrossRef]
- Zivic Djurovic, M.; Milacic, A.; Krsulja, M. A simplified model of quadratic cost function for thermal generators. In Proceedings of the 23rd International DAAAM Symposium, Zadar, Croatia, 24–27 October 2012; Volume 23, pp. 25–28. [Google Scholar]
- Vetter, J.; Novak, P.; Wagner, M.R.; Veit, C.; Moller, K.-C.; Besenhard, J.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]



| Symbol | Explanation | Unit | Size |
|---|---|---|---|
| x | Energy of storage units (state) | S | |
| Setpoint inputs of conventional units | T | ||
| Setpoint inputs of storage units | S | ||
| Setpoint inputs of renewable units | R | ||
| u | Setpoint inputs of all units | U | |
| Boolean inputs of conventional units | - | T | |
| v | Vector of all control inputs | - | Q |
| Uncertain available renewable power | R | ||
| Uncertain load | D | ||
| w | Vector of all uncertain inputs | W | |
| Active power of conventional units | T | ||
| Active power of storage units | S | ||
| Active power of renewable units | R | ||
| p | Active power of all units | U | |
| Power over transmission lines | E | ||
| Boolean auxiliary variables | - | R | |
| Real-valued auxiliary variable | - | 1 | |
| Vector of all auxiliary variables | - | Q |
| Parameter | Value | Weight | Value |
|---|---|---|---|
| 0.1178 | |||
| 0.0001 | |||
| 3 | 1 | ||
| 0.09 | |||
| 0.1 | 0.01 | ||
| −0.17 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami, M.; Pisano, A. Model Predictive Operation Control of Islanded Microgrids under Nonlinear Conversion Losses of Storage Units. Electricity 2022, 3, 33-50. https://doi.org/10.3390/electricity3010003
Gholami M, Pisano A. Model Predictive Operation Control of Islanded Microgrids under Nonlinear Conversion Losses of Storage Units. Electricity. 2022; 3(1):33-50. https://doi.org/10.3390/electricity3010003
Chicago/Turabian StyleGholami, Milad, and Alessandro Pisano. 2022. "Model Predictive Operation Control of Islanded Microgrids under Nonlinear Conversion Losses of Storage Units" Electricity 3, no. 1: 33-50. https://doi.org/10.3390/electricity3010003







