Optimization of 1D/3D Electro-Thermal Model for Liquid-Cooled Lithium-Ion Capacitor Module in High Power Applications

Abstract

Lithium-ion capacitor technology (LiC) is well known for its higher power density compared to electric double-layer capacitors (EDLCs) and higher energy density compared to lithium-ion batteries (LiBs). However, the LiC technology is affected by a high heat generation problem in high-power applications when it is continuously being charged/discharged with high current rates. Such a problem is associated with safety and reliability issues that affect the lifetime of the cell. Therefore, for high-power applications, a robust thermal management system (TMS) is essential to control the temperature evolution of LiCs to ensure safe operation. In this regard, developing accurate electrical and thermal models is vital to design a proper TMS. This work presents a detailed 1D/3D electro-thermal model at module level employing MATLAB/SIMULINK^® coupled to the COMSOL Multiphysics^® software package. The effect of the inlet coolant flow rate, inlet coolant temperature, inlet and outlet positions, and the number of arcs are examined under the cycling profile of a continuous 150 A current rate without a rest period for 1400 s. The results prove that the optimal scenario for the LCTMS would be the inlet coolant flow rate of 500 mL/min, the inlet temperature of 30 °C, three inlets, three outlets, and three arcs in the coolant path. This scenario decreases the module’s maximum temperature (T_max) and temperature difference by 11.5% and 79.1%, respectively. Moreover, the electro-thermal model shows ±5% and ±4% errors for the electrical and thermal models, respectively.

1. Introduction

Electric vehicles (EVs) are becoming popular due to their zero emissions by employing electrical energy storage systems (ESSs) for traction [1]. The most-used ESSs are electric double-layer capacitors (EDLC) and lithium-ion batteries (LiBs) [2]. EDLCs show longer lifetime and higher power ratios, while they suffer from low energy density [3]. Although LiBs are exceptional solutions for high energy densities, low power density is their major drawback [4]. In this respect, lithium-ion capacitors (LiCs) have emerged that are hybrid ESSs [5]. The main benefits of LiCs are higher power compared to LiBs and higher energy compared to EDLCs, which make LiCs very reliable in high-power applications [6]. Nevertheless, excessive heat generation in high-power applications can reduce their performance and lifetime [7]. Thus, a robust cooling system should be designed to control the LiC’s temperature [8].

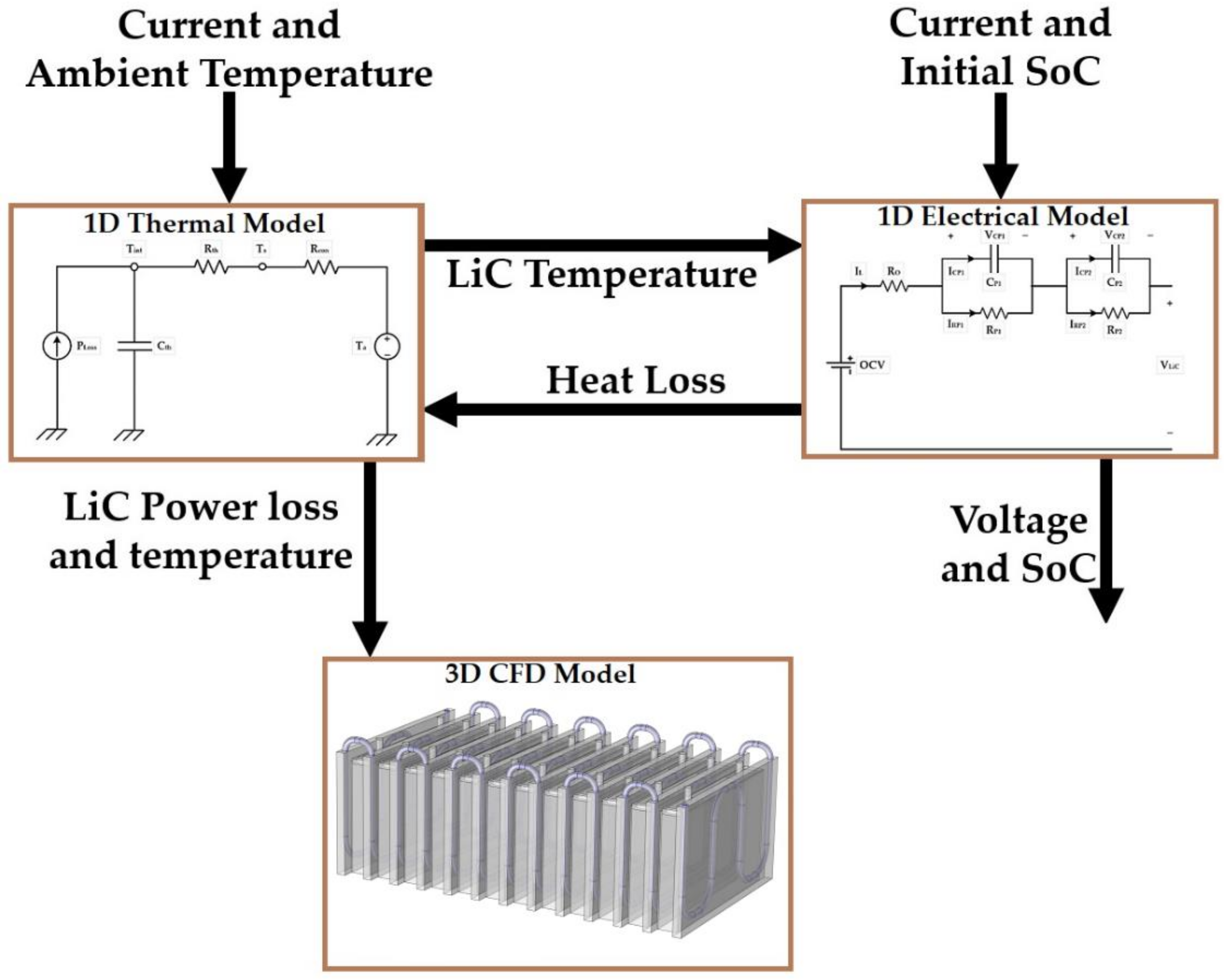
Before designing a thermal management system (TMS), the development of accurate electrical and thermal models is vital for further optimization of the developed system to guarantee the robustness of the proposed system [9]. In this context, following the development of a 1D electro-thermal model, a 3D thermal model should be developed [10]. A 3D thermal model is a computational fluid dynamics (CFD) model aiming for system optimization [11]. A 1D electrical model is responsible for extracting the electrical parameters, such as internal resistance, capacitance, and open-circuit voltage (OCV) [12], which will be used to extract the heat loss of the cell through the 1D thermal model [13]. The 3D thermal model will then employ the extracted power loss to predict the LiC’s thermal behavior [14]. The 1D model in this work was developed in the MATLAB/SIMULINK^® environment, and the 3D model was built in the COMSOL Multiphysics^® software package.

Generally, active and passive cooling systems are the main methods to control the ESSs [15,16]. Passive systems include heat sinks [17], heat pipes [18], and phase change materials (PCM) [19]. Heat sinks are metal plates to enhance the heat flow away from a heat source [20]. Heat pipes are highly thermally conductive substances that remove the generated heat from heat sources; they have some drawbacks, such as complex design [21], low performance in high-power applications [22], and gravity dependency [23]. PCMs are materials that absorb and reject heat generation (thermal energy) when they are melted and frozen [24]. During the thermal cycling process, PCMs change their phase from solid to liquid. The major problem of PCMs is their very low thermal conductivity, which limits their applications [25]. Therefore, other highly conductive materials, such as heat pipes [26], graphite [27], nanomaterials [28], nanofluids [29], copper foams [30], or aluminum foams [31], should be added to PCMs to cope with this drawback.

On the other hand, active cooling systems comprise air and liquid cooling methods [32,33]. Air-cooled TMSs are reasonable solutions at low ambient temperatures when the inlet and outlet positions are well-structured and the inlet flow velocity is set accordingly [34]. The heat transfer rate of liquid-cooled TMSs is higher than air, making them a perfect candidate in high-power applications. Karimi et al. [34] developed an air cooling system for a LiC 2300 F cell and decreased the maximum temperature of the cell by 14%. Akbarzadeh et al. [35] compared an air cooling system with a liquid cooling system for a module of LiB, in which they proved that the temperature uniformity of the liquid-cooled system was better than that of the air cooling system. Gungor et al. [36] proposed a liquid cooling design for EVs. They proved that a canopy-to-canopy architecture has high thermal performance to maintain the battery cell in the desired range. Tang et al. [37] designed and optimized a lightweight cooling system for four prismatic batteries. Their proposed design had 1.88% and 2.36% weight ratios. Tang et al. [38] designed an automatic calibrated model for TMS based on the SVR model with RBF kernel. Cao et al. [39] upgraded a liquid cooling TMS using composite PCMs. They showed that the battery’s maximum temperature and temperature uniformity were below 46 °C and 4 °C, respectively. Rui et al. [40] established a 3D thermal runaway propagation (TRP) model with liquid-cooled structures and showed that the criticality boundary could guide the safety design aspects for the TMS.

To the best of the authors’ knowledge, no work in the literature has proposed a liquid-cooled system for a module of 12 LiC cells cycled under a 150 A harsh current rate. This paper continues the work published in [41], in which two cold plates cooled a LiC cell. Moreover, in this article, a detailed 1D/3D electro-thermal model is developed at module level employing MATLAB/SIMULINK^® coupled to the COMSOL Multiphysics^® software package, used to optimize the proposed cooling system. The design optimization parameters are the effect of the inlet coolant flow rate, inlet coolant temperature, inlet and outlet positions, and the number of arcs. Finally, a conclusion is made at the end of this work that combines all the optimized design parameters to yield the most optimized liquid-cooled TMS (LCTMS) regarding the proposed cooling system’s architecture and geometry.

2. Numerical Solution

The present work introduces a 1D electro-thermal model coupled to a 3D thermal model to validate and optimize a forced liquid-cooled TMS (LCTMS). The proposed LCTMS is responsible for cooling down the LiC 2300 F in high-power applications. In this regard, a high current rate of 150 A is applied to the module continuously without a rest period for 1400 s. The characteristics of the target cell used in the module are listed in

Table 1. LiC 2300 F specifications.

Parameters	Value	Unit
Nominal capacity	1	Ah
Voltage	2.2–3.8	V
DC-IR @25 °C	0.7	mΩ
Energy density	14	Wh/L
Power density	14.7	kW/L
Heat generation	76,477	W/m3

.

In this experimental and numerical study, the 1D/3D numerical simulation analysis has been carried out using MATLAB SIMULINK^® and COMSOL Multiphysics^®. In the coupled 1D/3D model, the 1D electrical model identifies the electrical parameters used while the 1D thermal model extracts the thermal parameters. The heat dissipation of the cell is extracted using the 1D model. Then, the system’s heat loss is imported into the 3D thermal model to develop the LCTMS CFD simulation and optimization. The 1D electrical and thermal models are developed in the MATLAB SIMULINK^® environments, while the 3D thermal model is developed in COMSOL Multiphysics^®. This coupled 1D/3D model development reduces the simulation time. Figure 1 exhibits how the 1D electrical and thermal models are linked to the 3D CFD model.

2.1. LiC 2300 F Electrical Model

The 1D electrical model is developed to identify the internal electrical parameters (open-circuit voltage (OCV [V]), ohmic resistance ($R_0$ [Ω]), polarization resistance ($R_P$ [Ω]), and polarization capacitance ($C_P$ [F])) of 2300 F LiC under high current rates ($I$ [A]) within a wide range of temperatures (T [°C]). The electrical model is a second-order equivalent circuit model (ECM) that includes two RC circuits. RC denotes the resistance and capacitance of the LiC cell. Based on the governing equations and the chosen second-order ECM, the electrical parameters of the LiC are identified. The terminal voltage ($V_t$ [V]) of the 2300 F LiC is expressed as [12]:

$$V_t=OCV\left(SoC,T\right)-I_L{R}_0\left(SoC,T,I_L\right)-V_{CP1}\left(SoC,T,I_L\right)-V_{CP2}\left(SoC,T,I_L\right)$$

(1)

$$\frac{d{V}_{CPi}}{dt}=-\frac{1}{R_{Pi}{C}_{Pi}}{V}_{CPi}+\frac{1}{C_{Pi}}{I}_L$$

(2)

$${\tau }_i=R_{Pi}{C}_{Pi}$$

(3)

The extracted parameters for the second-order ECM at 25 °C under a high current rate of 150 A for 100% SoC values are listed in

Table 2. Extracted parameters of the electrical model at 25 °C, 150 A current rate, and 100% SoC.

Extracted Parameters	Value	Symbols
Open-circuit voltage	3.8	OCV [V]
Ohmic resistance	0.0011	$R_0$ [Ω]
Polarization resistance	0.00013	$R_P$ [Ω]
Time constant	0.1336	$\tau$ [s]

. As is evident, all these parameters depend highly on temperature. Figure 2 shows the current and voltage applied to the cell. It is revealed that the heat loss of the cell increases sharply at the beginning of the cycling, following a slight decrease that comes from the temperature change of the cell during the charge and discharge processes.

2.2. LiC 2300 F Thermal Model

The thermal model of the LiC is divided into one-dimensional and three-dimensional models. The first one is responsible for extracting the heat loss of the cell. In contrast, the second one uses the extracted loss to simulate the LiC under various operating conditions for validation purposes and optimization analysis.

2.2.1. 1D Thermal Model

In this work, the surface temperature of the LiC is modeled to estimate the thermal parameters precisely. The essential parameters of the model are the heat loss of the LiC, the initial temperature of the cell, and ambient temperature. The heat loss of the cell is divided into reversible and irreversible heat that stems from the entropy changes and internal resistance of the cell, respectively. The entropy change (reversible heat) can be positive or negative, but the internal resistance (irreversible heat) is always positive. In this regard, the power loss of the cell is expressed as [13]:

$$P_{loss}=I_L^2{R}_0\left(SoC,T,I_L\right)+I_{RP1}^2{R}_{P1}\left(SoC,T,I_L\right)+I_{RP2}^2{R}_{P2}\left(SoC,T,I_L\right)-I_L{T}_{cell}\frac{\partial OCV\left(T_{cell},SoC\right)}{\partial T_{cell}}$$

(4)

where $P_{loss}$ [W] denotes the heat loss of the LiC cell and $T_{cell}$ [°C] is the temperature of the LiC. Figure 3 demonstrates the heat loss under fast charge/discharge with a continuous 150 A current rate during the 1400 s experimental test.

The generated heat of the LiC regarding its dimensions for a 150 A fast charging and fast discharging profile is listed in

Table 3. The generated heat of the LiC regarding its dimensions for a 150 A current profile.

LiC Dimensions (mm)	Heat Generation (W/m3)
150 × 91.5 × 15.5	76,477

, which demonstrates that the generated heat of the LiC is 3.5 times larger than the normal heat generation condition of LiBs [42].

2.2.2. 3D Thermal Model

Heat generation of the LiC during its operation occurs mainly because of the ion migration process, which incorporates the electrochemical reaction, the side reaction, and the Joule losses [43]. The losses related to side reactions can be neglected due to the LiC’s operation at safe temperatures [44]. As mentioned in the 1D thermal modeling subsection, the reversible (${\dot{q}}_{rev}$) and irreversible (${\dot{q}}_{irr}$) heat sources are the main contributors to the heat generation of the LiC (${\dot{q}}_{gen}$), which come from entropy change and internal resistance, respectively [45]. In addition, cell and tab domains are considered in the heat generation modeling of the LiC due to the non-uniform temperature distribution. The heat generation of the cell domain can be expressed as:

$${\dot{q}}_{gen}={\dot{q}}_{irr}+{\dot{q}}_{rev}=I\left(U-V\right)-IT\frac{\partial U}{\partial T}$$

(5)

For the tab domain, the heat generation is expressed as:

$${\dot{q}}_{gen}=\frac{R{I}^2}{V_{tab}}$$

(6)

Based on the density ($\rho$) and specific heat ($C_p$) in the 3D thermal model, the energy conservation is expressed as:

$$\rho C_p\Delta V\frac{\partial T}{\partial t}=\Delta {\left(UA\right)}_x\frac{\partial T}{\partial x}+\Delta {\left(UA\right)}_y\frac{\partial T}{\partial y}+\Delta {\left(UA\right)}_z\frac{\partial T}{\partial z}+\Delta {\dot{q}}_{gen}$$

(7)

For the liquid cooling system model, the Reynolds number determines the turbulent or laminar flow, which directly depends on the hydraulic diameter ($d_c$), coolant density (${\rho }_c$), and velocity ($v_c$):

$$Re=\frac{{\rho }_c{v}_c{d}_c}{u_c}$$

(8)

$$d_c=\frac{4A_c}{P_c}\frac{4\pi r_c^2}{2\pi r_c}$$

(9)

where $A_c$, $P_c$, and $r_c$ represent the channel cross-sectional area, perimeter, and radius. In the present work, the length of the channel is much larger than its cross-sectional area. Therefore, the flow should be considered as a fully developed flow. The Gnielinski correlation is employed to obtain the convective heat transfer coefficient [46]:

$$N{u}_{cool}=\frac{(\frac{f_{cool}}{8})(R{e}_{cool}-1000)P{r}_{cool}}{1+12.7{(\frac{f_{cool}}{8})}^{1/2}(P{r}_{cool}^{0.66}-1)},2300<R{e}_{cool}<5\times {10}^6$$

(10)

The Darcy friction factor ($f_{cool}$) for the coolant is achieved by having the channel’s aspect ratio ($\gamma$) [47]:

$$f_{cool}=\left(1.0875-0.1125\gamma \right)·f_{cool,0}$$

(11)

Considering the channel length ($L$) and diameter ($D$), the pressure drop of the LCTMS is expressed as:

$$\Delta P={\displaystyle \sum _{i=1}^n}{f}_{cool}{\rho }_{cool}{(\frac{L}{D})}_{eqv}\frac{v_{cool}^2}{2}$$

(12)

The system’s parameters, initial conditions, and boundaries are set in the 3D CFD model to verify the numerical simulations against the experiments.

Table 4. Initial conditions and boundaries of the 3D thermal system.

Domain	Condition	Value	Unit
Module domain	Tinit	23	°C
Cold plates	Tinit	23	°C
Type of coolant	water	-	-
Coolant pressure	Reference level	1	atm
Coolant domain	Tinlet	23	°C
Coolant flow rate	Qinlet	100	mL/min
Coolant flow rate	Turbulent	Incompressible	-
Coolant tube	wall	No-slip	-
Coolant outlet	POutlet	To ambient	-
Coolant outlet	Qoutlet	Suppressed outflow	-

shows the initial conditions and boundaries of the LCTMS.

The next step would be mesh generation and setting the step time and solver directly related to the system’s complexity and computational time. After analyzing different grid densities, the mesh element number of 6,426,351 was utilized with a 1 s time step.

3. Experimental Test Bench

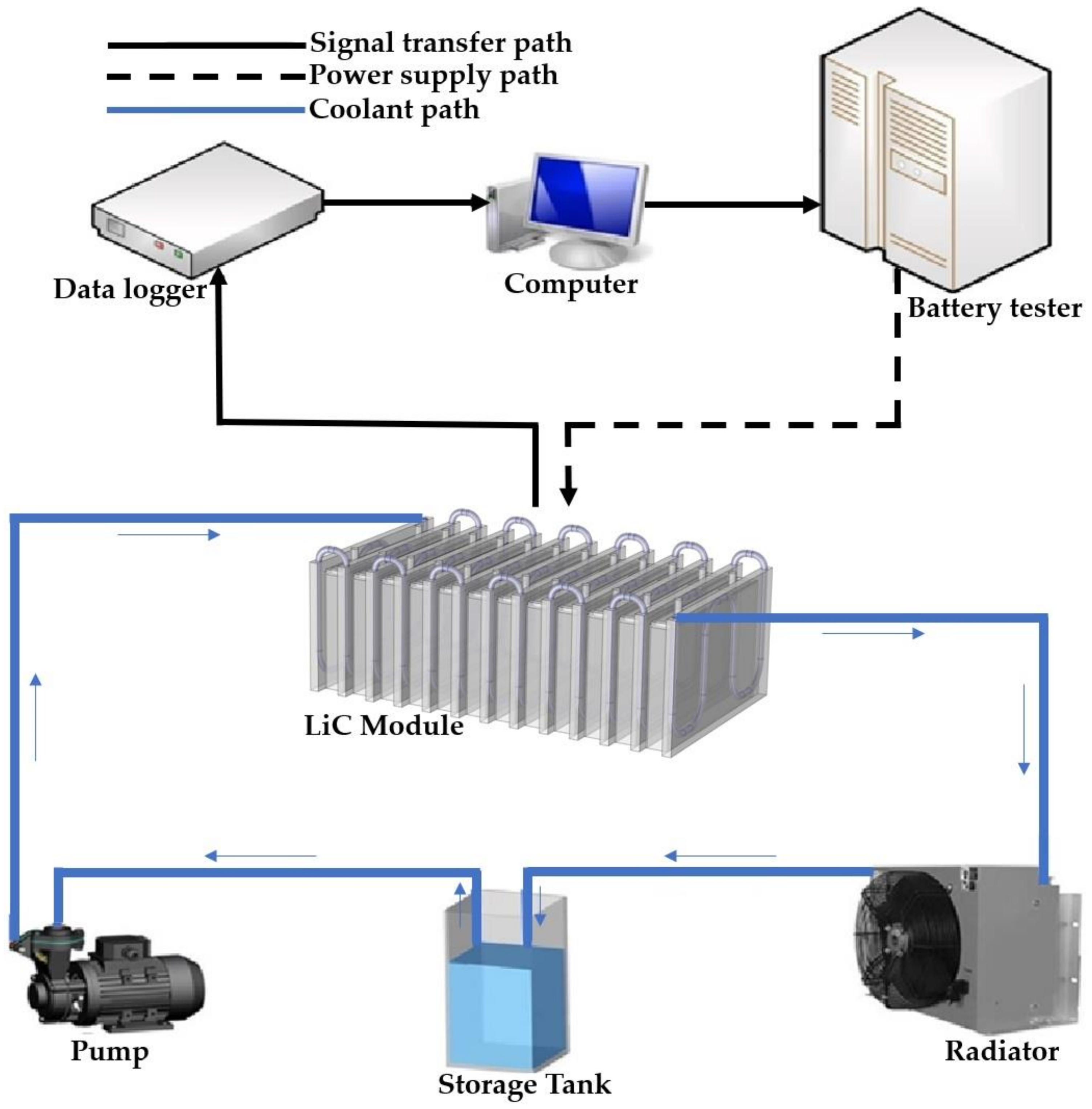
The facilities used in the experimental investigation are a module of 12 LiC cells, 13 cold plates, a battery management system (BMS), a data logger, eight k-type thermocouples, a radiator, a pump, a power supply, a battery tester, and a computer.

3.1. Battery Management System (BMS)

The most vital element of the module used to monitor and control the voltage of all the cells, balance the state of charge (SoC), and monitor the temperature of each cell is the battery management system (BMS). The BMS is necessary to protect the cells against over-charging/discharging, and they are connected in series. The importance of the BMS lies in overcoming the voltage and SoC imbalance among the cells. In this work, a passive BMS is used to balance the LiC cells with low costs. The main functions of the utilized BMS are:

• Parameter measurement (voltage, current, resistance, and temperature);
• Safety and protection against over-charging/discharging, over-temperature, current limit;
• Communication through CAN-bus or RS-485 port.

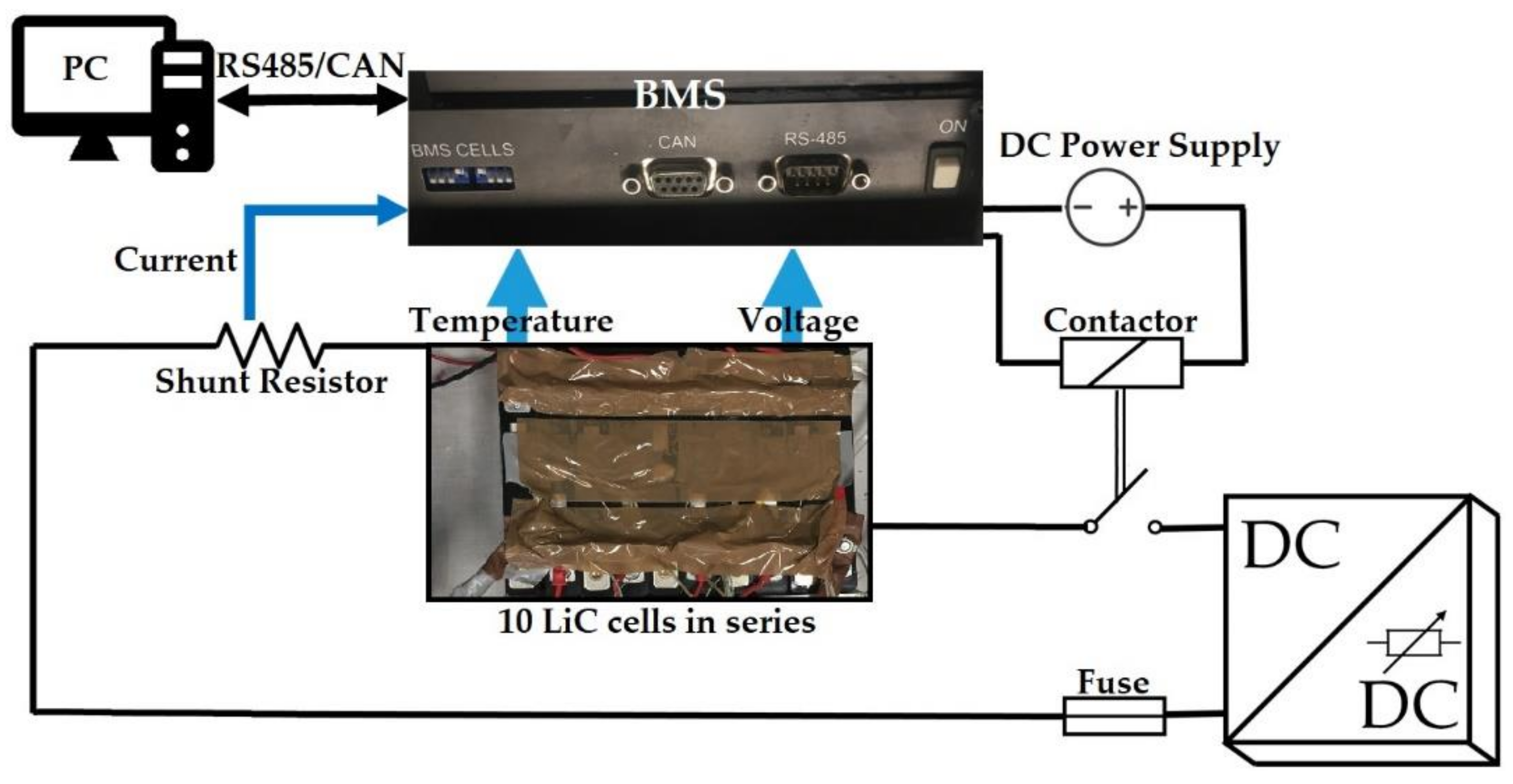
In this work, the BMS is used to equalize the LiC voltages by using 10 ohmic resistors called the switched shunt resistor. Figure 4 exhibits the block diagram of the experimental test bench for the LiC module while employing a BMS for balancing the cells and protecting the module. This can be done by monitoring the module’s temperature, voltage, and current at each time step. The current of the module is measured by a low-side precision shunt ohmic resistor with 0.25% accuracy. Additionally, the voltage drop of the module is measured by the shunt ohmic resistor thanks to its four-wire Kelvin connection. The BMS is connected to the shunt ohmic resistor via a short shielded cable. The ADC (analog to digital converter) with high accuracy filters out the noise or the current spikes. The temperature profile of the module is monitored by the K-type thermocouples and a data logger. Two small fans and a heat sink are added to protect the BMS from over-heating. The prototype of the used BMS and the wiring/connections is depicted in Figure 5.

3.2. Test Bench Setup

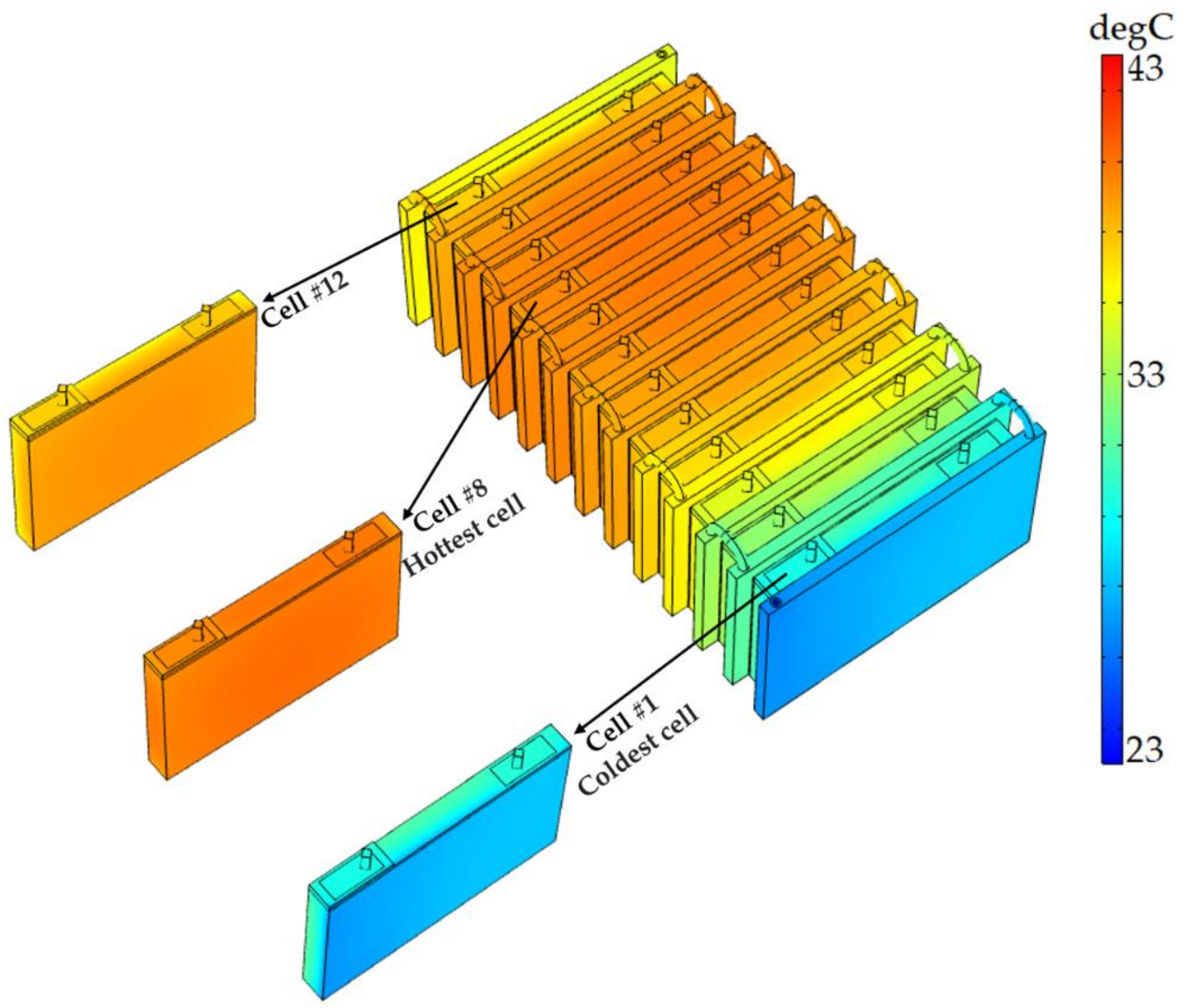
A forced LCTMS is used for cooling purposes in this work to cool down the temperature rise of the LiC 2300 F module in harsh operating conditions. The module is composed of 12 prismatic LiC cells connected in series. The LCTMS is composed of 13 cold plates, meaning that every two cold plates are attached to the left and right sides of the larger surface of the LiC cell. In the main case study, the inlet flow rate is set at 100 mL/min with an initial temperature of 23 °C. The pump is responsible for drawing the coolant from the tank storage to the cold plates. The coolant flow path is from the first cold plate to the last cold plate. Therefore, it is expected that the first cells experience a lower temperature, while the middle cells to the last should be hotter. The last cell (cell #12) is expected to be colder than the adjacent cells due to the heat flux, since one side of this cell is exposed to the ambient temperature. Figure 6 demonstrates the facilities used in this work.

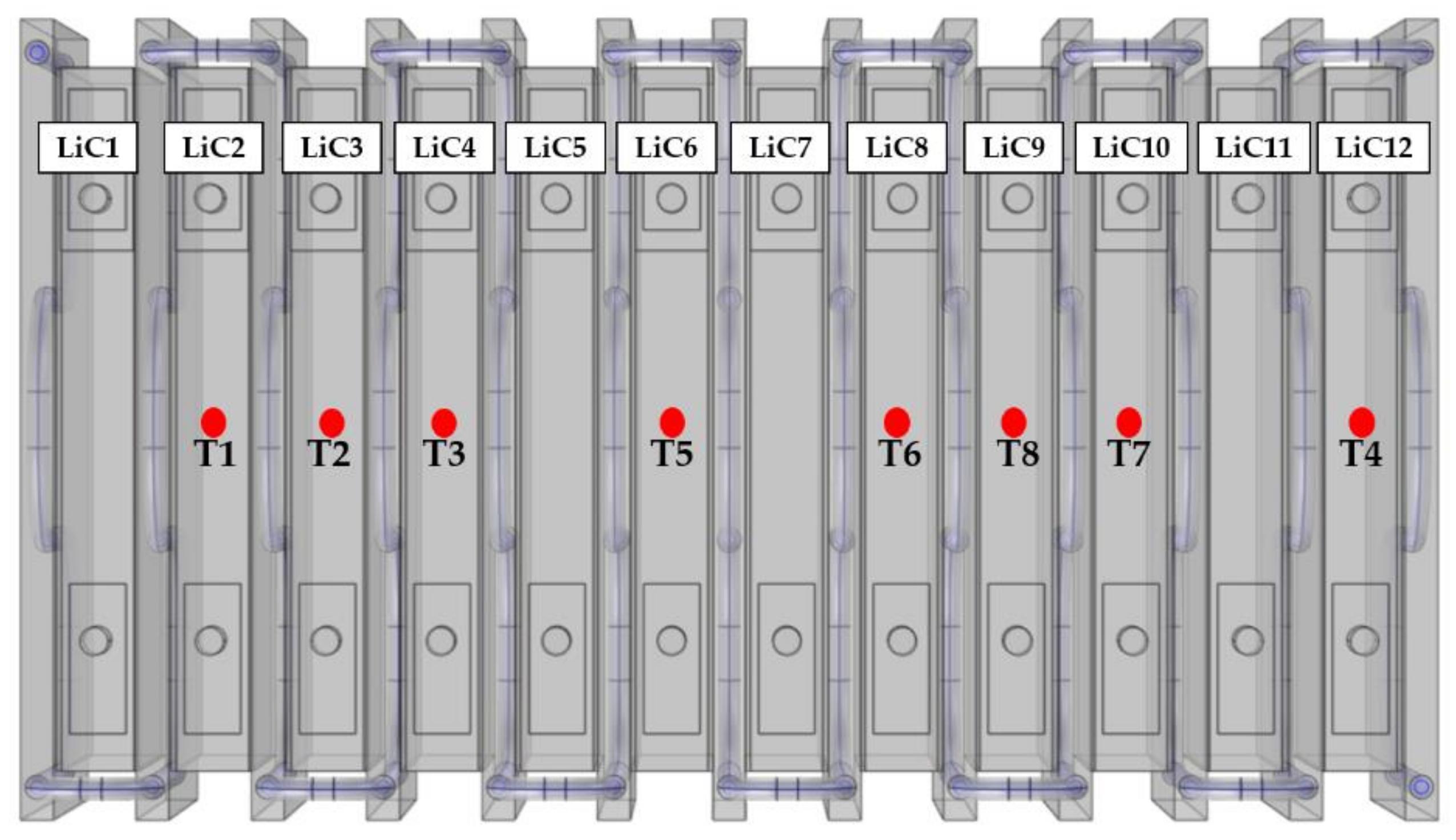
As is depicted in Figure 7, the computer is connected to the BMS through a CAN-bus or RS-485 port. On the other side, the computer is connected to the data logger to monitor the module’s temperature evolution during the experiments. The battery tester is responsible for applying the current and voltage to the module for cycling the cells. Two fans and a heat sink are embedded in the BMS part to cool it down in order to avoid failure of the BMS. The radiator cools down the coolant coming from the outlet of the cold plates. The coolant outlet temperature is directly proportional to the heat generation rate, but the inlet temperature of the coolant is almost 23 °C, thanks to the highly efficient radiator. The pump flows the coolant from the storage tank to the inlet of the LCTMS. In addition, 8 K-type thermocouples monitor the temperature at each time step, for which, in this work, the time step of the data logger and thermocouples is set to 1 s. This means that the thermocouples and the data logger save the temperature data every 1 s. 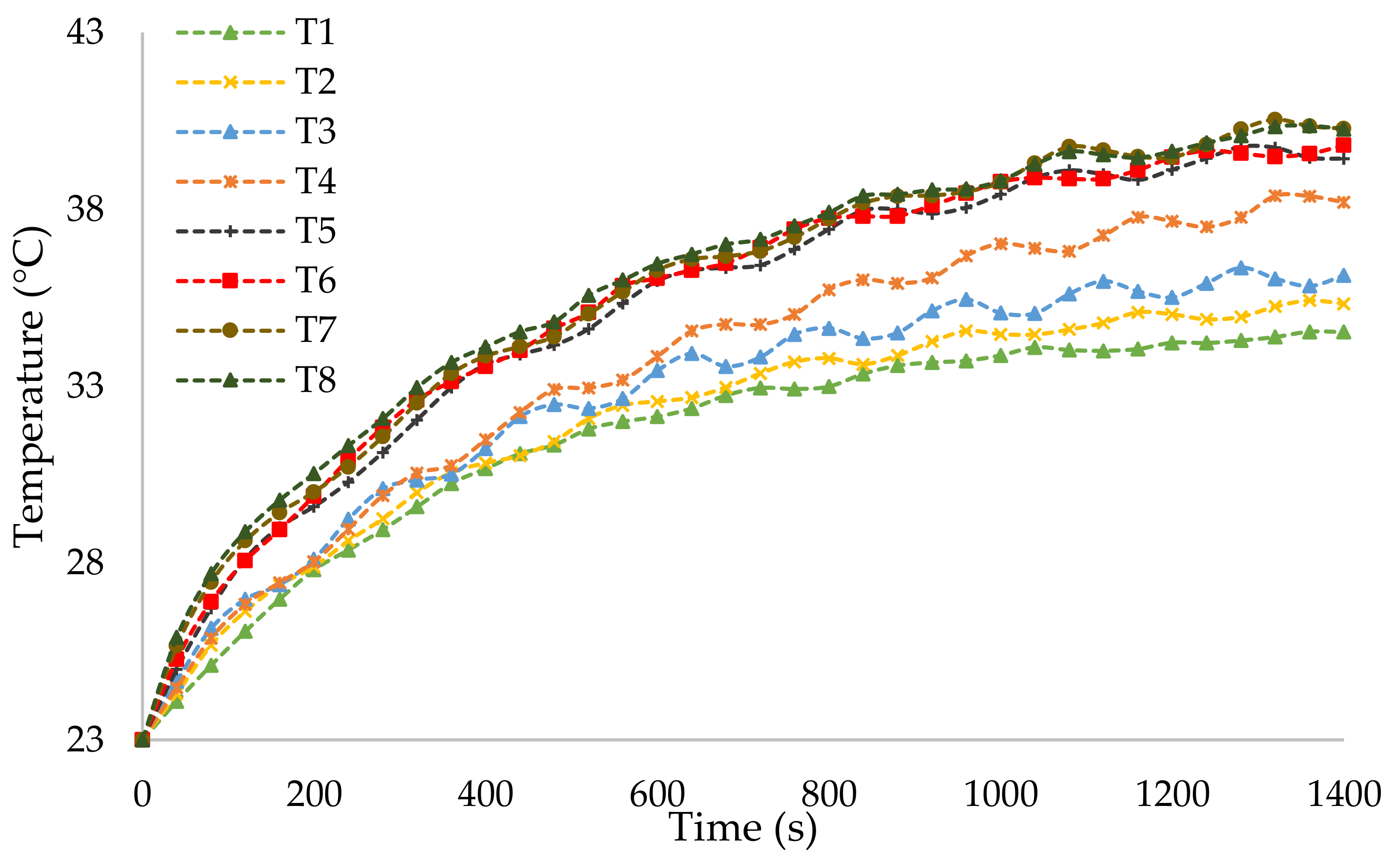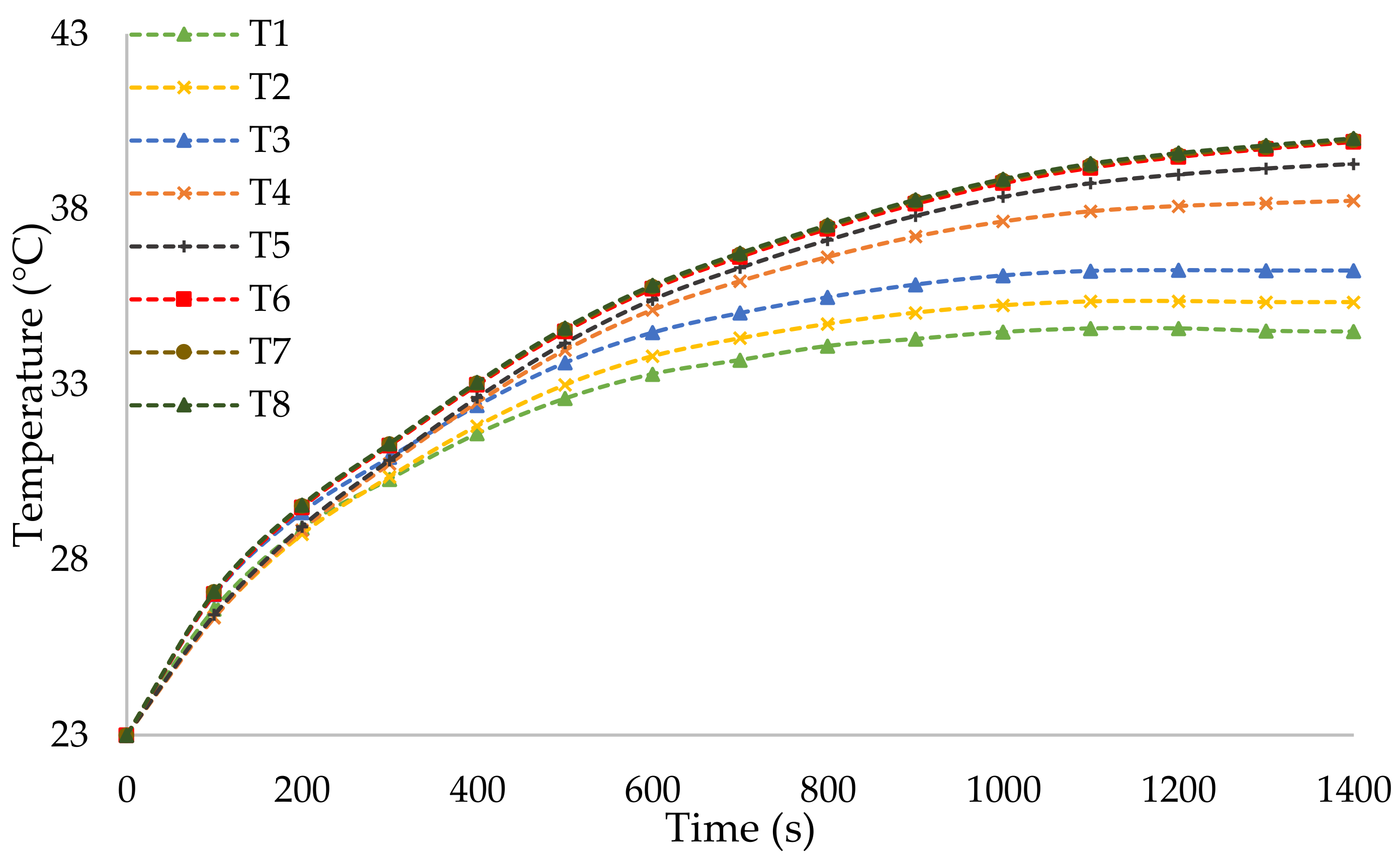The position of the thermocouples is shown in Figure 8. Based on the temperature of the cells, from colder to hotter cells, the number of the thermocouples was set to be more apparent from colder to hotter points in the graphical temperature evolution curves. The expected results would be colder temperatures for the T1 to T4 thermocouples and hotter temperatures for the T5 to T8 thermocouples. The experimental results are explained in the next section.

3.3. Experimental Results

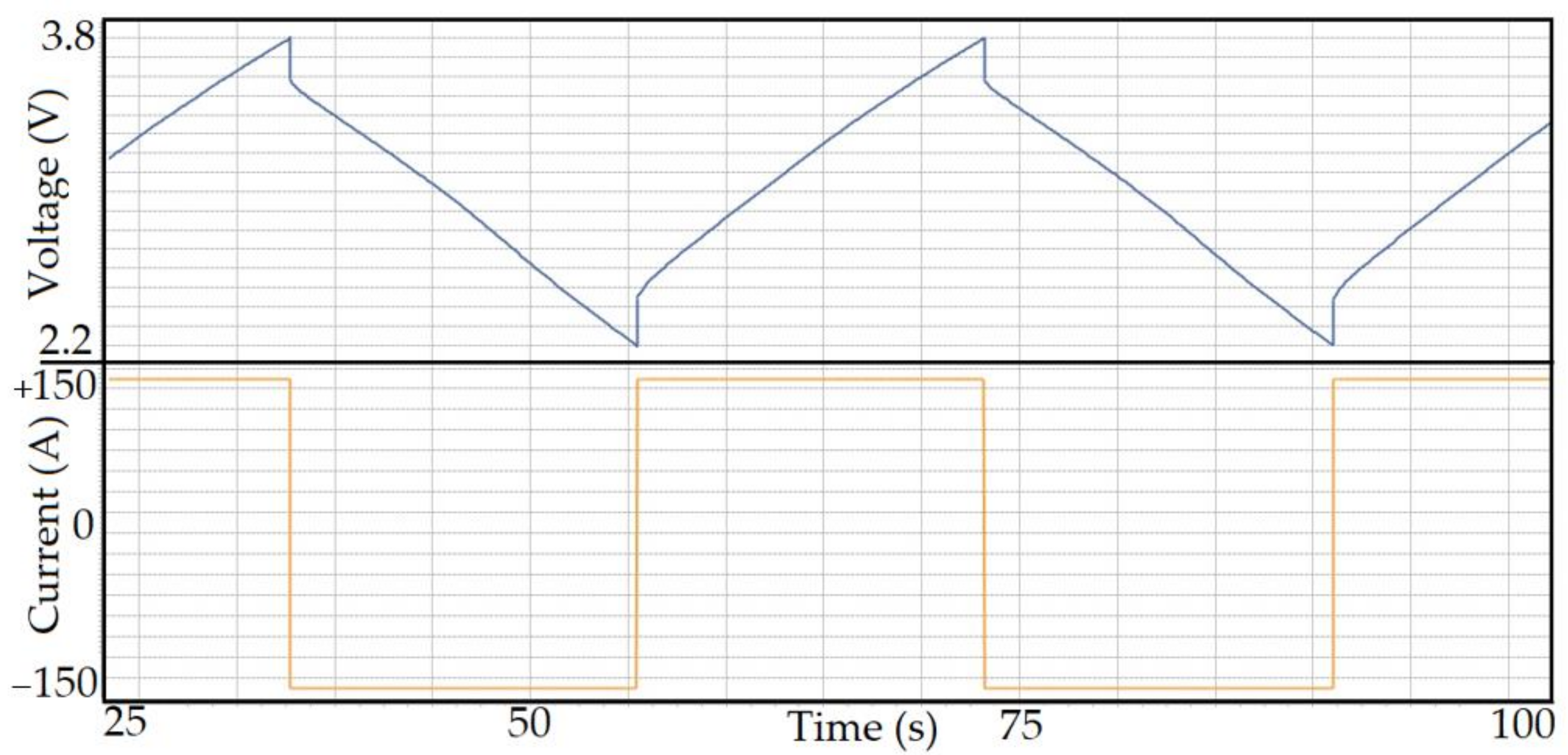
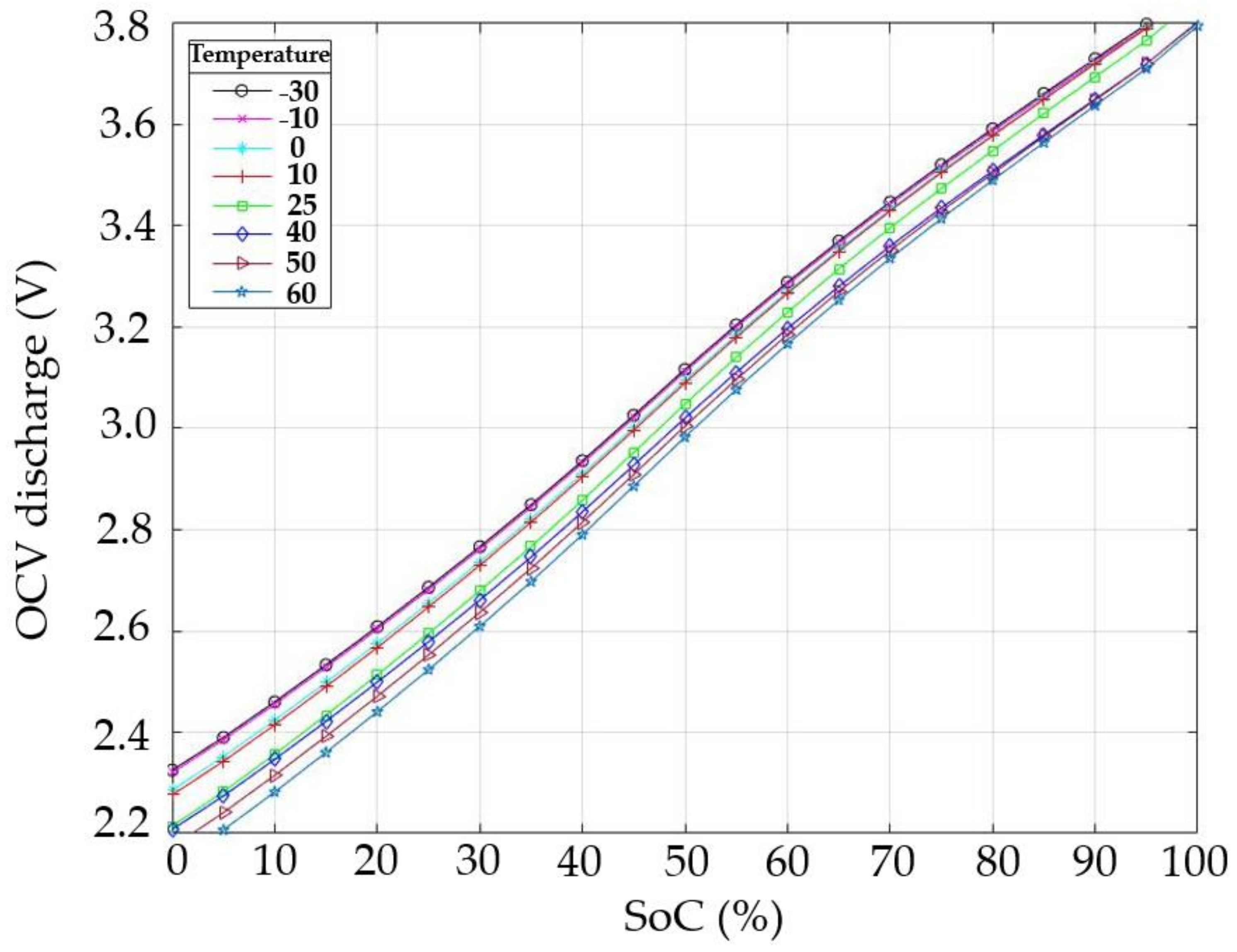
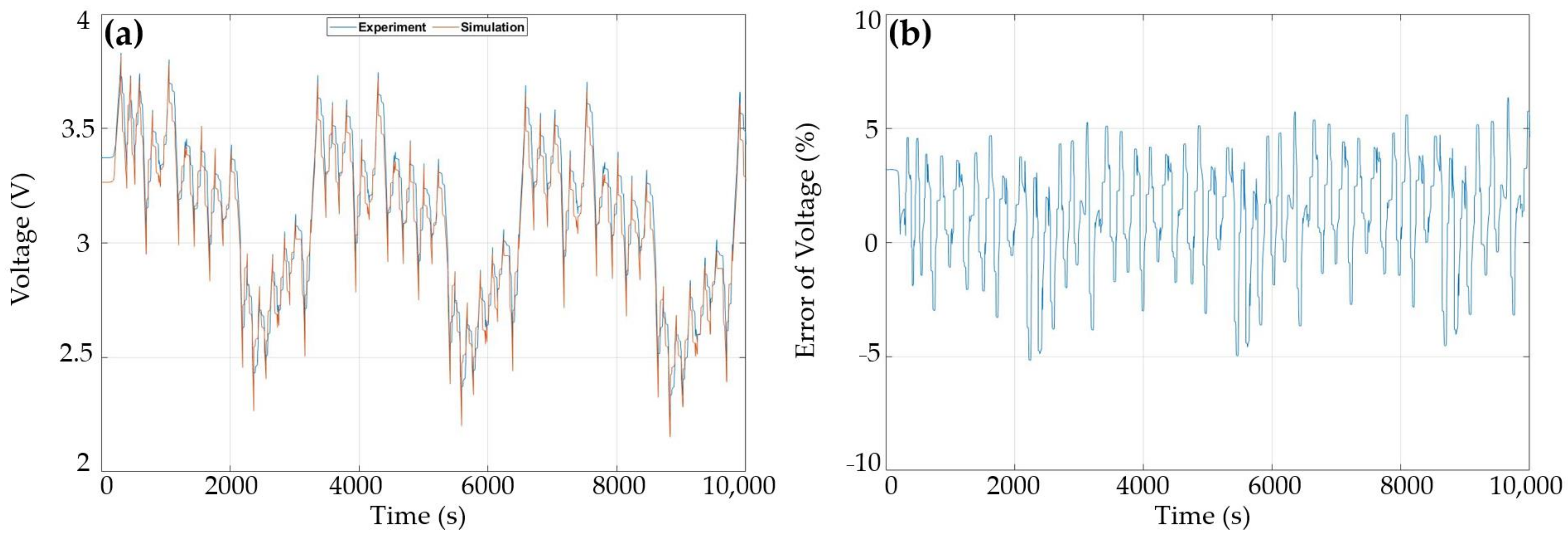
The experimental results have two parts: electrical results and thermal results. The electrical part explains the results of the extracted parameters for the electrical model. Figure 9 shows the open circuit voltage of the LiC versus SoC for the discharging of the cell at a 10 A current rate. Figure 10 demonstrates the validation of the electrical model regarding the extracted parameters within a heavy-duty driving profile with high current rates. The voltage simulation results are compared with the experiments in Figure 10a, which shows ±5% and ±3% for current rates higher than 100 A and lower than 100 A, respectively, as is seen in Figure 10b.

The experiments for thermal studies were conducted under the 150 A current profile for the LiC module when using LCTMS as the proposed cooling system. Before using the LCTMS, the thermal performance of the module without any cooling system under natural convection (NC) was evaluated. In this case, the maximum temperature of the module under NC is around 70 °C, which is much higher than the safe operating temperature of 40 °C announced by the manufacturer (JSR company). Therefore, an adequate cooling regime should be applied to the system to control its temperature. The temperature evolution of the module for all the thermocouples is depicted in Figure 11, in which the expected explained temperature rise for the cells within the module is proven. As is observed, the T1, T2, and T3 thermocouples are mounted on the top surface of the cell at the beginning of the module, where the coolant air is still cold. Therefore, their temperature rise is lower than that of the other cells. The T4 thermocouple relates to cell number 12, which is the last cell, and there are no cells after this cell. Therefore, T4 is exposed to the environment from one side, causing this cell to be colder than the other cells in the middle of the module. The T5, T6, T7, and T8 thermocouples relate to the cells in the middle, so from one side, their heat sources are generating heat, and from another side, the conduction effect is the dominant phenomenon between two adjacent cells. Thus, the middle cells to the last cell are much higher than the rest of the module (the first five cells).

4. Numerical Investigation and Optimization

The experimental analysis is validated with numerical simulations in this section to prove the accuracy of the 1D/3D models. Later, the developed 3D model is optimized to obtain the best design for the proposed solution.

4.1. Forced Liquid-Cooled Simulation Results

The results of the 3D thermal model are presented in this section, thanks to the COMSOL Multiphysics software package. In the software, the heat transfer in solids module is employed to model the heat source and the general physics of the system, while the fluid flow module (k-ε turbulent flow) is used to model the cooling system and the coolant. The initial conditions, boundary conditions, materials, parameters, and geometry of the system are set in the software, and the mesh is generated in the last step. The simulation results are shown in Figure 12 for the main case study regarding Table 4. Comparing the simulation and experimental results exhibits less than 3% error, which shows the precision of the developed 1D electro-thermal model’s extracted parameters and the accuracy of the designed 3D thermal model. The graphical thermal results of the LCTMS for the LiC module are depicted in Figure 13. This provides a better insight into the temperature distribution over each module cell, resulting in better optimization of the system. As can be seen, the coldest cell is the first cell, and the hottest one is cell number 8 in the middle-end of the module.

Two performance indicators are evaluated in the numerical simulations:

• T_max: the maximum temperature on the LiC module’s surface that is monitored by eight thermocouples.
• ΔT_max: the temperature difference between the maximum and minimum temperatures that are sensed by the thermocouples.

4.2. Impact of the Inlet Flow Rate

The inlet flow rate of the coolant medium is a critical controlling factor for the LCTMS that directly affects the thermal performance and power consumption of the system. In order to study the impact of the inlet flow rate on the thermal performance of the LiC module, under the initial conditions and boundaries in Table 4, the inlet flow rate was set as 200 mL/min, 300 mL/min, 400 mL/min, 500 mL/min, and 1000 mL/min, where the inlet and outlet positions and the tube diameter were kept constant. The thermal performance of the LiC module is depicted in Figure 14 for all six case studies, where the inlet flow rate of the main case study is 100 mL/min. The main reason for ΔT_max along the module is the inconsistency of the heat transfer rate of each LiC cell in the module, which is due to the tube structure, cell location, and other factors. Therefore, when the liquid enters the copper tube, the cells’ temperature changes rapidly, widening the temperature gap between the coldest and hottest points monitored by the thermocouples.

Table 5. The thermal performance of the system with various inlet flow rates.

Inlet Flow Rate	Tmax (°C)	ΔTmax (°C)
100 mL/min (Main case)	40.3	9.1
200 mL/min	39.7	7.6
300 mL/min	38.7	7.9
400 mL/min	37.5	7.4
500 mL/min	36.4	6.8
1000 mL/min	33.2	5.1

shows T_max and ΔT_max for the proposed inlet flow rates. Based on the table, increasing the coolant’s inlet flow rate reduces the maximum module’s temperature and ΔT_max along with the cells. This reduction trend diminishes more when the inlet flow rate exceeds 500 mL/min. Nevertheless, increasing the inlet flow rate would increase the parasitic power consumption exponentially, which will lead to gradually weakening the advantages of increasing the inlet flow rate and increasing the corresponding costs [48].

4.3. Impact of the Inlet Temperature

The inlet temperature of the coolant is one of the crucial structural parameters to uniformize the temperature alongside the cells in the module, which is evaluated in this section, as shown in Figure 15. The coolant inlet temperature affects the cooling performance parameters such as ΔT_max between the coldest and hottest points of the module monitored by the thermocouples. As can be seen, when increasing the inlet temperature of the coolant, the heat transfer of the cells is faster and closer to the coolant’s temperature, leading to gradually decreasing ΔT_max. However, T_max remains almost constant—both inlet temperatures of 30 °C and 40 °C exhibit good thermal performance under high current rates.

T_max and ΔT_max are evaluated in detail in

Table 6. The thermal performance of the system with various inlet temperatures.

Inlet Temperature (°C)	Tmax (°C)	ΔTmax (°C)
23 (°C) (Main case)	40.3	9.1
30 (°C)	40.4	3.9
40 (°C)	40.4	1.4

. According to the data in Table 6, T_max and ΔT_max with an inlet temperature of 30 °C are 40.4 °C and 3.9 °C, respectively, in which ΔT_max is reduced by 57% compared with the main case study, where the inlet temperature of the coolant is 23 °C. In addition, for the inlet temperature of 40 °C, ΔT_max is diminished by 84% compared to the main case study, showing the importance of this factor in the design of the LCTMS.

4.4. Optimization of the Inlet and Outlet Positions

In the LiC module with the LCTMS as a cooling solution, the heat from the LiCs is transferred to the liquid medium through the copper pipes to the aluminum cold plates. The inlet and outlet positions have a significant impact on the performance of the proposed TMS. Therefore, the thermal performance of the LiC module with LCTMS is evaluated in detail at different inlet and outlet positions when the inlet flow rate, inlet temperature, and the other initial and boundary conditions are kept constant. In this regard, four different topologies are proposed based on Figure 16. P1 has two inlets in the first and the last cold plates, where its two outlets are placed in the middle of the module. P2 has two inlets in the first cold plate, and the middle of the module, where one of the outlets is in the middle and the other one is placed in the last cold plate. P3 has three inlets and three outlets, and P4 has four inlets and four outlets.

As the temperature distribution of the module for four various inlet and outlet positions is exhibited in Figure 17 and is listed in

Table 7. The thermal performance of the system with different inlet and outlet positions.

Inlet Temperature (°C)	Tmax (°C)	ΔTmax (°C)
Main case study	40.3	9.1
P1	40.3	10.1
P2	39.6	6.8
P3	38.9	3.3
P4	38.8	3.1

, P1 does not show good performance regarding T_max and ΔT_max. Compared to the main case study, the P2 case study shows better performance than P1 while decreasing T_max by 1.7% and ΔT_max by 25.2%. The P3 and P4 case studies behave almost the same, showing that increasing the number of inlets and outlets may result in a better outcome, but a greater increase will not guarantee a greater reduction in terms of ΔT_max or T_max. P3 can be the best choice in this section due to better results and optimum inlet and outlet points. This case study decreases T_max by 3.5% and ΔT_max by 63.7%, respectively.

4.5. The Impact of the Number of Arcs in the Coolant Path

The number of arcs in the tube is of high importance for thermal performance analysis. In this context, the number of arcs is increased from two arcs (the main case study) to three arcs in the LCTMS (Figure 18). As is shown in Figure 19 and

Table 8. The thermal performance of the system with different arc numbers.

Inlet Temperature (°C)	Tmax (°C)	ΔTmax (°C)
Two arcs (main case)	40.3	9.1
Three arcs	37.3	2.9

, by increasing the number of arcs in the coolant path design, T_max is decreased by 7.5%. In comparison, ΔT_max is decreased by 63.7%, compared to the main case study.

4.6. The Selected Optimal Solutions

In this section, two optimal solutions are proposed to evaluate the performance of the developed 1D/3D thermal model with the optimized boundaries. The best scenarios of the numerical simulations have been selected to set in the LCTMS cooling system to conclude with the most optimal solution regarding the proposed geometry and structure. In this context, the inlet flow rate of 500 mL/min, with an inlet temperature of 30 °C, was set in the model. In addition, the P3 inlet and outlet position where three inlets and three outlets have been designed in the system was selected as the inlet and outlet topology. With the defined conditions mentioned above, two arcs per tube were selected for the first optimized solution, while the second optimized solution uses three arcs per tube.

By mixing such optimal cases for two arcs in the first optimized solution, T_max and ΔT_max are 37.1 °C and 1.4 °C, respectively. This trend shows 8% and 85% improvement compared with the main case study in T_max and ΔT_max, respectively. The temperature distribution of this optimal solution is depicted in Figure 20.

The second optimized case using three arcs per channel in the cooling path can control T_max at 35.7 °C, showing an 11.5% improvement compared to the main case study. In addition, this case study reduced the temperature uniformity by 79.1%. Overall, the optimal solution #2 would be better due to the lower T_max and temperature uniformity below 2 °C. The comparative study based on the explained results is shown in

Table 9. The thermal performance of the system for the optimal solutions.

Inlet Temperature (°C)	Tmax (°C)	ΔTmax (°C)
Two arcs (Main case)	40.3	9.1
Optimal case #1	37.1	1.4
Optimal case #2	35.7	1.9

.

5. Conclusions

In the present article, a module of 12 LiCs was used to evaluate a liquid-cooled thermal management system (LCTMS). Prior to testing the module, predicting the electrical parameters is of high importance since the extracted electrical and thermal parameters can lead to predicting the heat loss with high precision. Therefore, a 1D electro-thermal model was developed from −30 °C to +60 °C. Moreover, high current rates were applied, including 0.1 A to 500 A as a loading profile. The open-circuit voltage, the resistances and capacitance of the cell, and thermal parameters were extracted in this regard. The voltage error was ±5% and ±3% for current rates higher than 100 A and lower than 100 A, respectively. Then, the 3D thermal model evaluation was performed experimentally and optimized numerically, thanks to the extracted parameters from the electro-thermal model. The effects of the inlet coolant flow rate, inlet coolant temperature, inlet and outlet positions, and the number of arcs were examined. The cycling profile consisted of a 1400 s continuous 150 A current rate without a rest period. The conclusions can be drawn as follows:

• In the case of cycling the module under the 150 A current profile, the maximum temperature (T_max) of the module exceeds 70 °C, which may lead to thermal runaway.
• The LCTMS with a 100 mL/min inlet flow rate, 23 °C inlet temperature, and two arcs in the coolant channel (main case study) can control T_max at 40.3 °C, which shows 42.4% improvement compared to the natural convection. ΔT_max was 9.1 °C, which can be improved.
• The 1D electro-thermal model extracted the electrical and thermal parameters with high precision, used in the 3D thermal model. The 3D thermal model was validated against the experiments with an error lower than 2%, employed for optimization purposes. The optimization parameters were the inlet coolant flow rate, inlet coolant temperature, inlet and outlet positions, and the number of arcs per coolant channel.
• Increasing the inlet flow rate of the coolant from 100 mL/min to 500 mL/min decreased T_max and ΔT_max by 9.7% and 25.2%, respectively. By increasing the inlet flow rate to 1000 mL/min, these values were 17.6% and 43.9%, showing the importance of the inlet flow rate to minimize T_max and ΔT_max.
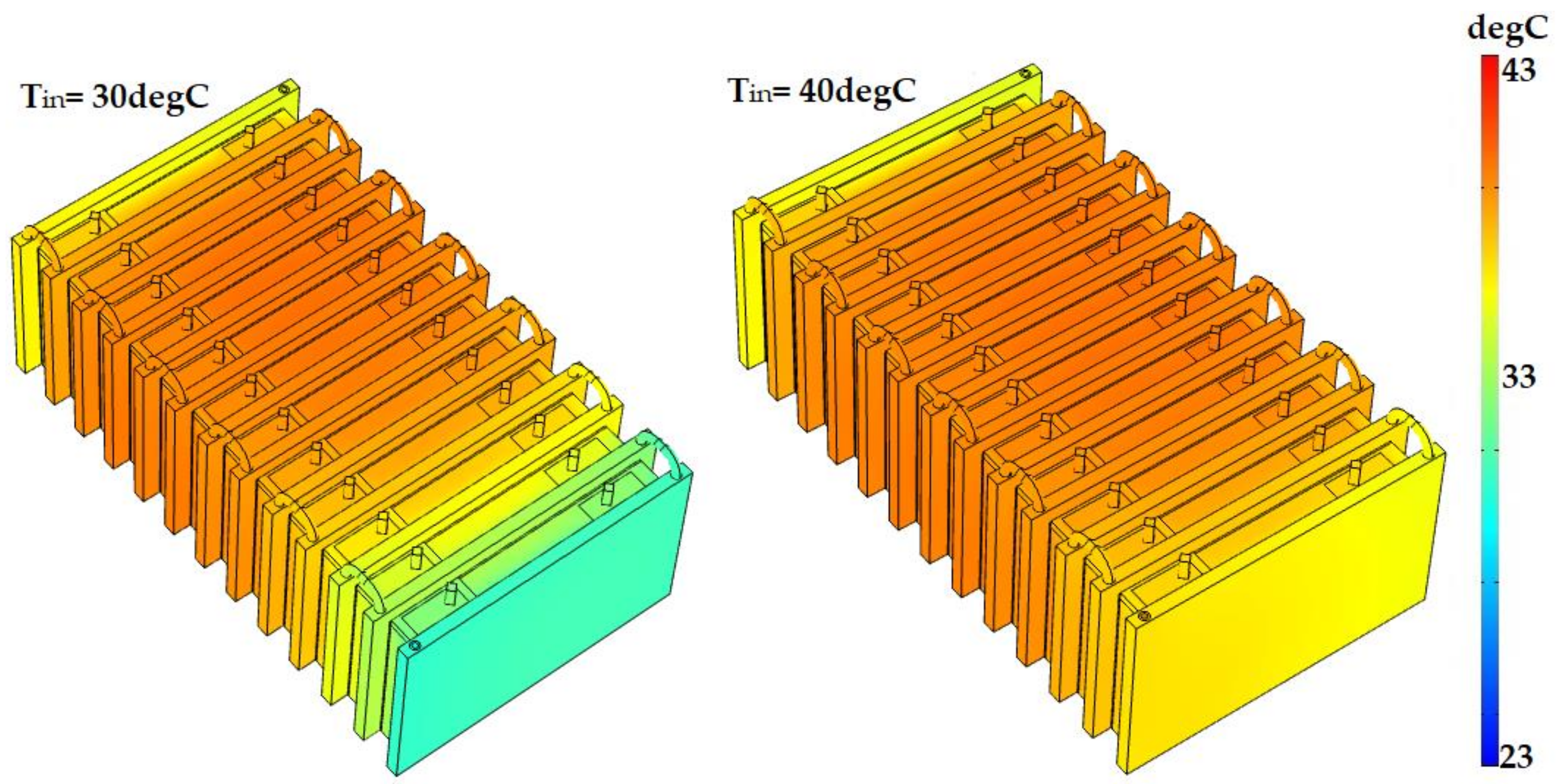
• Increasing the inlet temperature did not significantly impact T_max but was enhanced ΔT_max. By increasing the inlet temperature from 23 °C to 30 °C and 40 °C, ΔT_max was reduced by 57% and 84%, respectively.
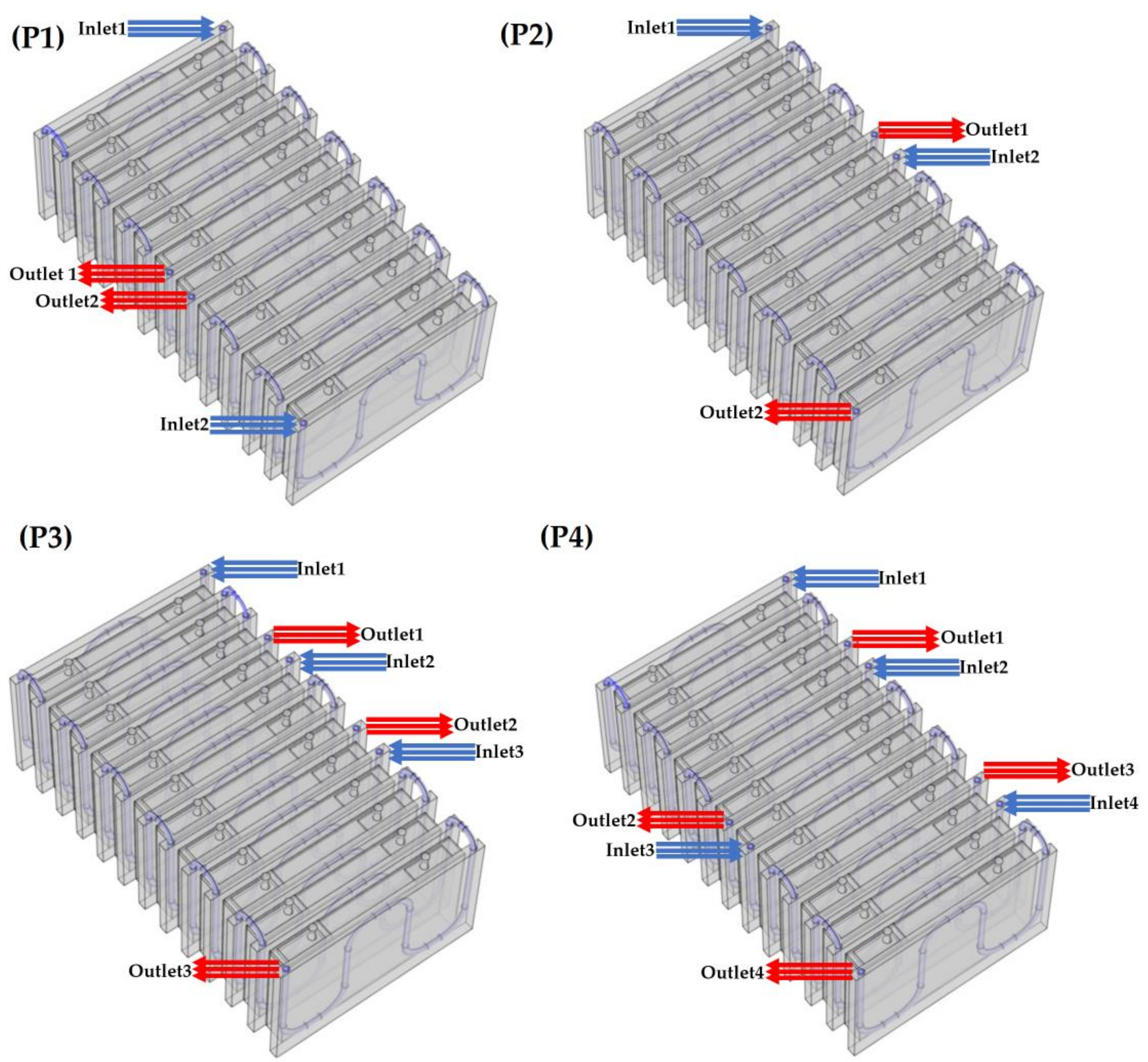
• Inlet and outlet configuration had a significant effect on T_max and ΔT_max. The best scenario for the LCTMS would be three inlets and three outlets, where T_max and ΔT_max were decreased by 3.5% and 63.7%, respectively.
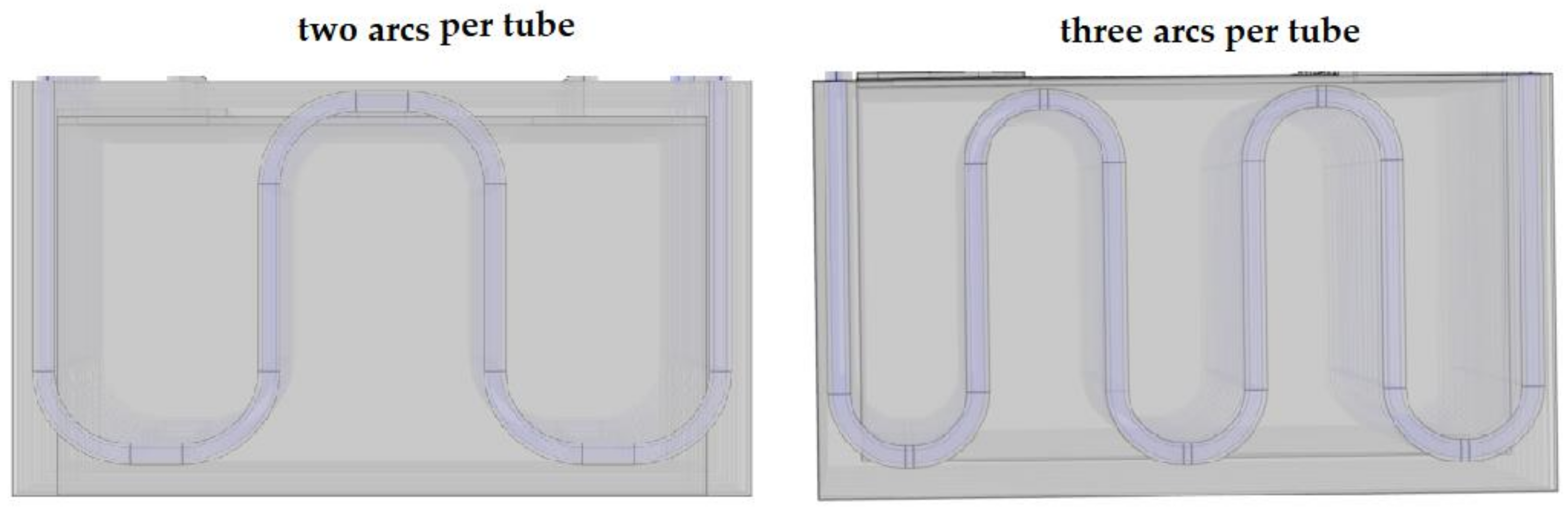
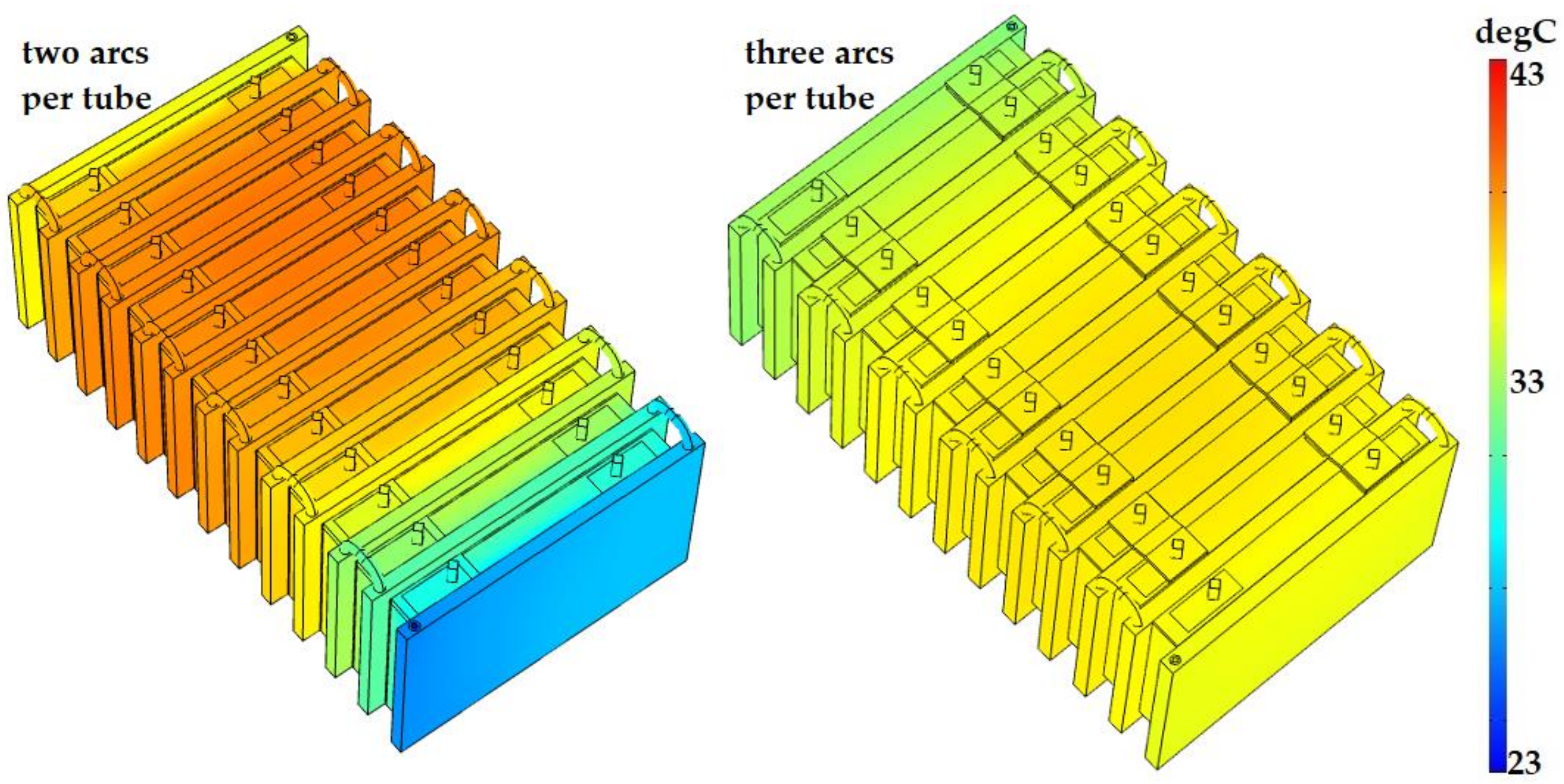
• Compared to the main case study, increasing the number of arcs in the coolant path design reduced T_max by 7.5% and ΔT_max by 63.7%.
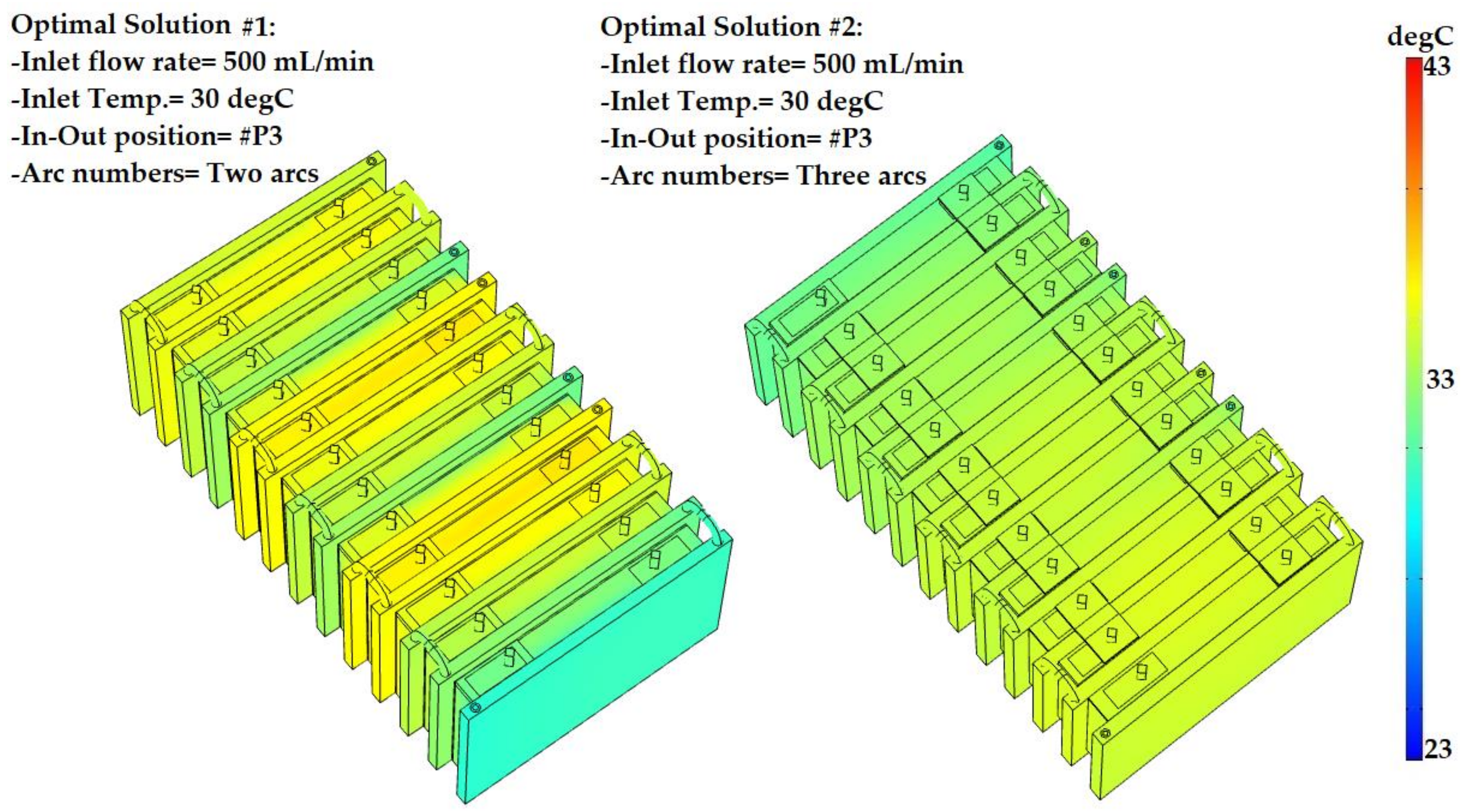
• The most optimal scenario for the LCTMS would be the inlet coolant flow rate of 500 mL/min, the inlet temperature of 30 °C, three inlets and three outlets, and three arcs in the coolant path. This scenario decreased T_max and ΔT_max by 11.5% and 79.1%, respectively.