Elastic and Plastic Properties of Gyroid Sheet Foams †
Abstract
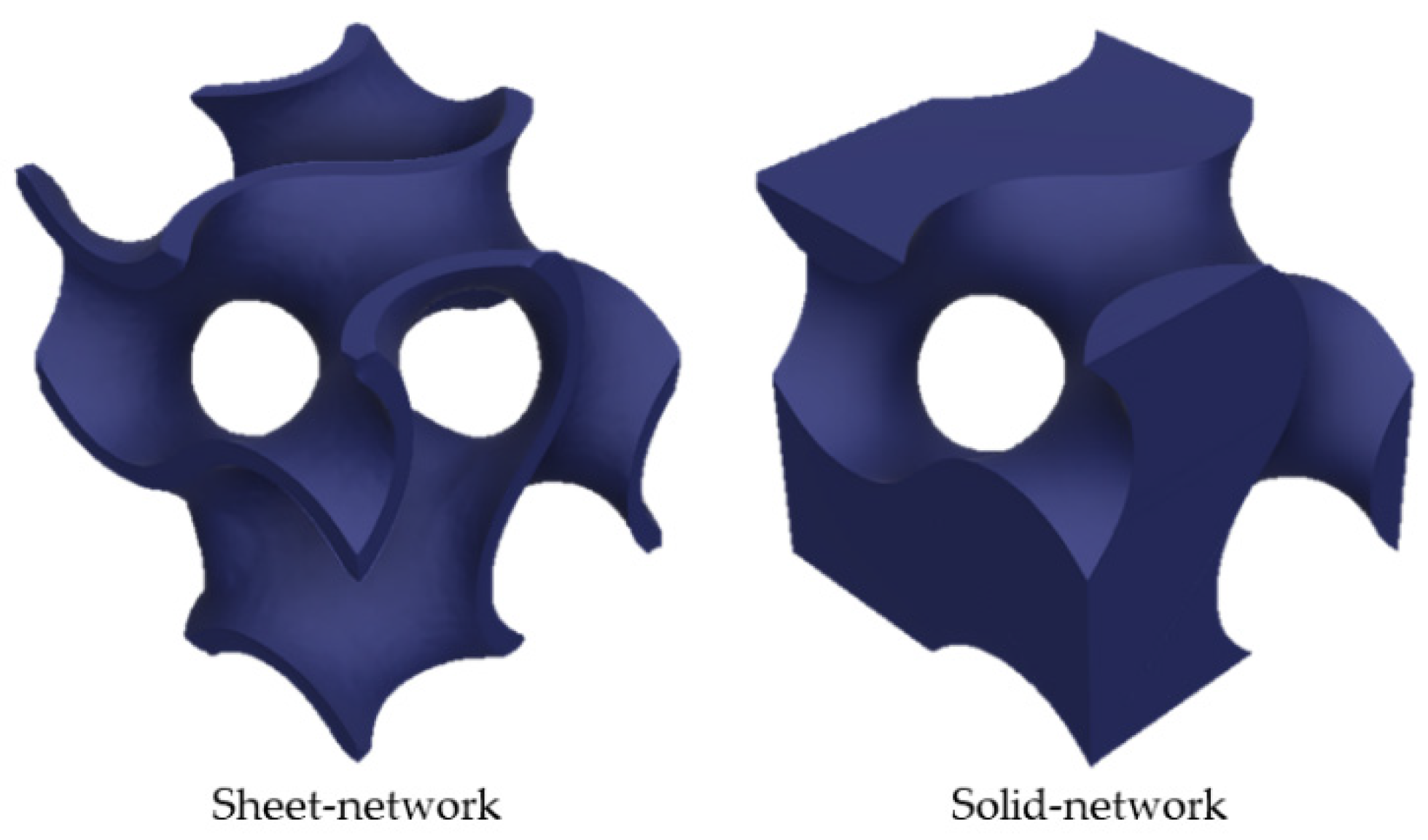
:1. Introduction
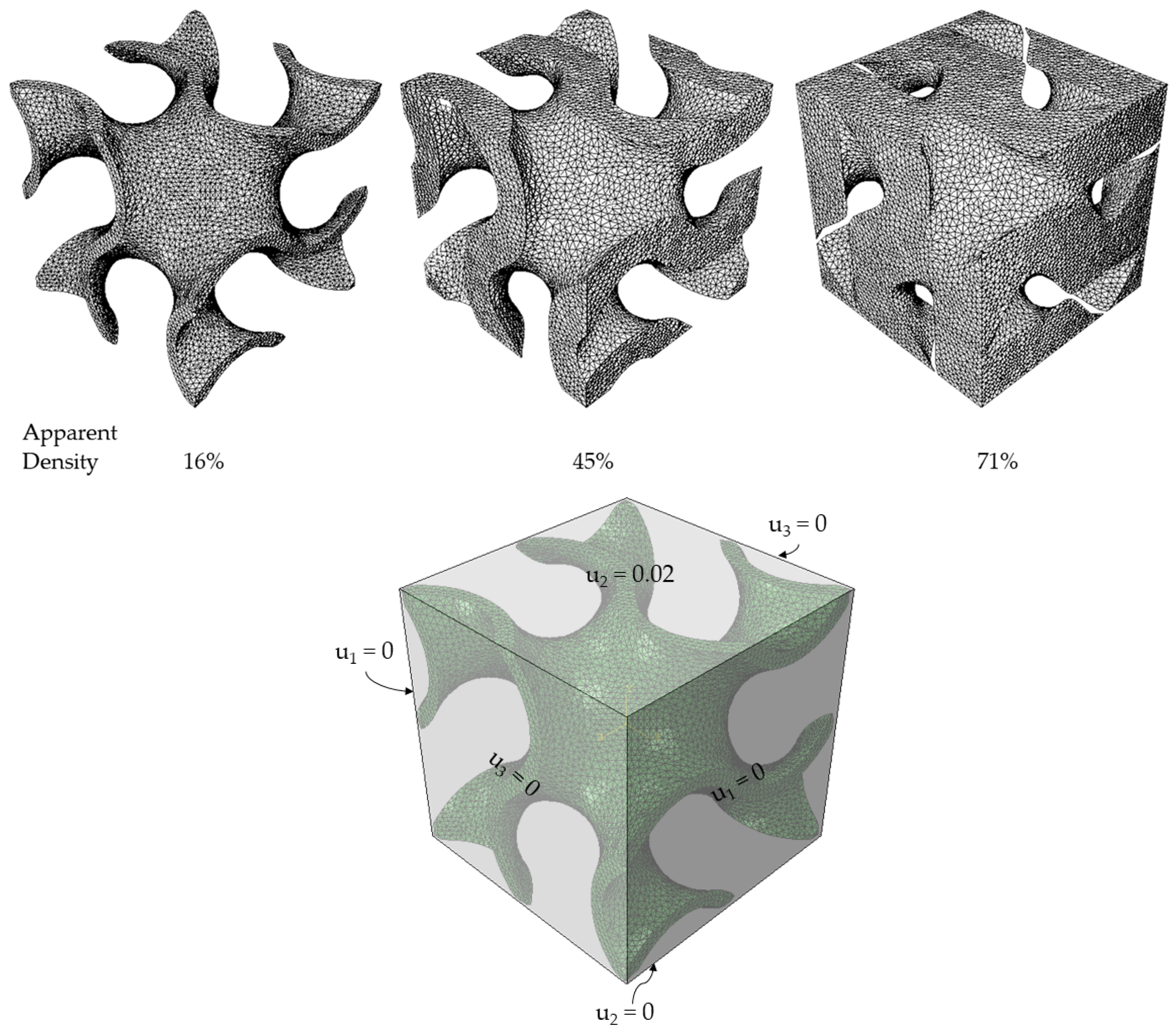
2. Materials and Methods
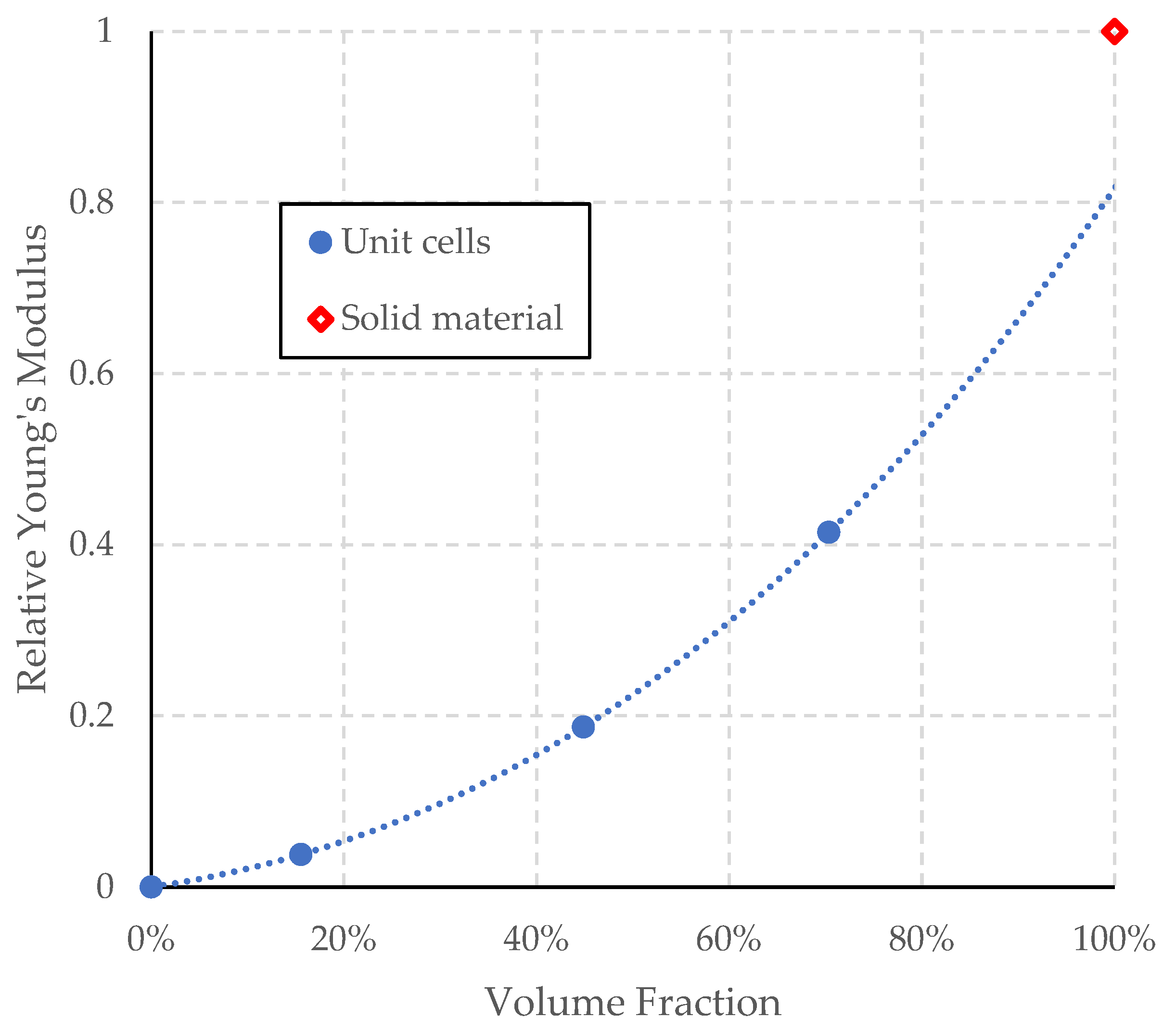
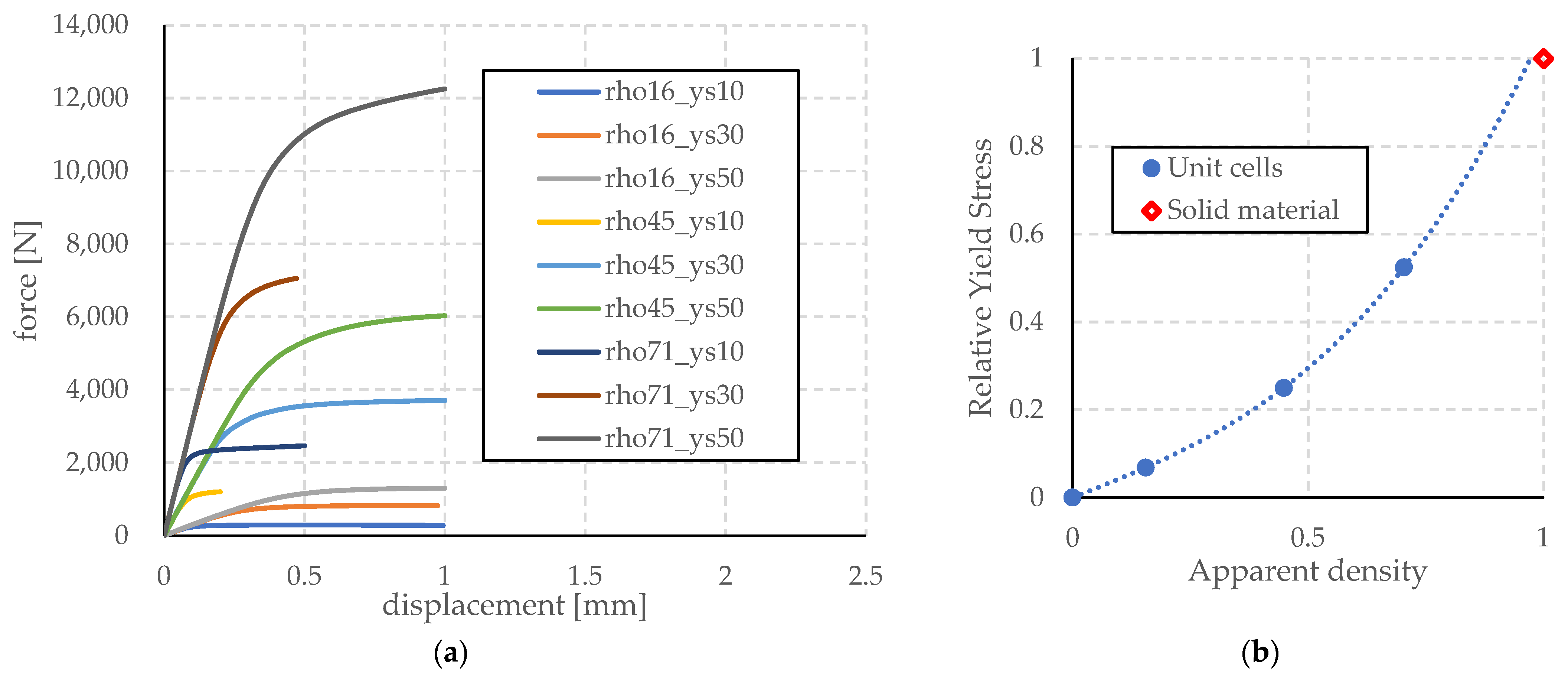
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bobbert, F.S.L.; Lietaert, K.; Eftekhari, A.A.; Pouran, B.; Ahmadi, S.M.; Weinans, H.; Zadpoor, A.A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, S.; Tang, Q.; Feng, Q.; Song, J.; Han, X.; Guo, F. Mechanical behaviours and mass transport properties of bone-mimicking scaffolds consisted of gyroid structures manufactured using selective laser melting. J. Mech. Behav. Biomed. Mater. 2019, 93, 158–169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, D.; Liao, W.; Dai, N.; Dong, G.; Tang, Y.; Xie, Y.M. Optimal design and modeling of gyroid-based functionally graded cellular structures for additive manufacturing. CAD Comput. Aided Des. 2018, 104, 87–99. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Günther, F.; Wagner, M.; Pilz, S.; Gebert, A.; Zimmermann, M. Design procedure for triply periodic minimal surface based biomimetic scaffolds. J. Mech. Behav. Biomed. Mater. 2022, 126, 104871. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pais, A.; Alves, J.L.; Belinha, J. Elastic and Plastic Properties of Gyroid Sheet Foams. Mater. Proc. 2022, 8, 90. https://doi.org/10.3390/materproc2022008090
Pais A, Alves JL, Belinha J. Elastic and Plastic Properties of Gyroid Sheet Foams. Materials Proceedings. 2022; 8(1):90. https://doi.org/10.3390/materproc2022008090
Chicago/Turabian StylePais, Ana, Jorge Lino Alves, and Jorge Belinha. 2022. "Elastic and Plastic Properties of Gyroid Sheet Foams" Materials Proceedings 8, no. 1: 90. https://doi.org/10.3390/materproc2022008090
APA StylePais, A., Alves, J. L., & Belinha, J. (2022). Elastic and Plastic Properties of Gyroid Sheet Foams. Materials Proceedings, 8(1), 90. https://doi.org/10.3390/materproc2022008090





