Correlations between the Physical Mechanical Properties of Greek Dimension Stones ^†

Abstract

This study focuses on the investigation of possible relations betweenthe physical mechanical properties of natural stones from various places in Greece, i.e., limestones, marbles, sandstones and schists. Specimens were prepared to perform laboratory tests according to the applicable EN. Overall and “by stone type” correlation equations were established between flexural strength under concentrated load valueswithout and either after freeze–thaw cycling or thermal shock, indicating a linear and a powerrelationship, respectively. A power function was establishedbetween flexural strength under a concentrated load and under a constant moment. Results have also shown that water absorption increases linearly with open porosity.

1. Introduction

Greek dimension stones are among the most famous ones, used widely either as structural materials or in decorative art, and Greece is a major producer and exporter of these materials at a global level. Since 2007, when CEmarking has become obligatory in Greece, these materials must be tested to determine their physical mechanical properties and assess their quality characteristics; evaluating the stone’s durability is important for the selection process.

Given the experience gained in the LITHOS laboratory from a considerable amount of tests conductedover the years, there is strong evidence of a connection between some of the most important mechanical and physical properties of stones. Thus, it was found prudent to study the results derived from the corresponding tests in order to unveil any potential correlation between them. Few researchers have studied the relationship between mechanical or/and physical properties of dimension stones [1,2,3,4,5]. Ozcelik and Ozguven [6] presented the results of detailed evaluations based on the relationships of physical properties of different types of natural stones with their water absorption. Figarska-Warchoł and Stańczak [7] investigated the effects of petrographic characteristics on the physical and mechanical properties of specific types of limestones, and proposed methods for the prediction of strength properties based on non-destructive tests. Other researchers have given more attention to the effect of temperature or thermal damage on stones’ properties [8,9] or freeze–thaw weathering [10,11,12,13,14,15]. The present study investigates the types of possible relations between various physical mechanical properties of Greek natural stones. The study focuses particularly on flexural strength, durability in environmental conditions and water absorption of stones quarried from various places in Greece and differing in composition, structure and textural properties, i.e., limestones, marbles, sandstones and schists.

2. Materials and Methods

A large number of limestones, calcitic and dolomitic marbles, sandstones and schists/slates, which are frequently used in various construction projects, were chosen for performing the laboratory studies in this research. Specimens were appropriately prepared in order to perform the relevant tests at LITHOS, the ornamental stones quality control laboratory of the Hellenic Survey of Geology and Mineral Exploration (HSGME), according to the applicable EN. Namely, they underwent tests for determining flexural strength (EN 12372 and EN 13161), frost resistance (EN 12371), resistance to ageing by thermal shock (EN14066), open porosity (EN 1936) and water absorption at atmospheric pressure (EN 13755). For each type of stone, the average value of each test was calculated and used in evaluations.

2.1. Flexural Strength

Flexural strength tests were conducted on various types of the most frequently used Greek ornamental stones (10 specimens per stone). These tests concern the determination of the strength either under a concentrated load (FS₃) or under a constant moment (FS₄), known also as 3-point or 4-point bending tests, which are very important, especially for applications in places exposed to different kinds of load.The testing machine used for the determination of flexural strength under a concentrated load (Figure 1a) and the experimental procedure are described in EN 12372:2006 [16]. A 10-specimen set from 48 marbles, 43 limestones, 9 sandstones and 33 schists/slates was appropriately prepared to undergo the test and the relevant flexural strength was determined as the average value of each set. The flexural strength under a constant moment, as described in EN 13161:2008 [17], was also determined (Figure 1b) for 28 marbles (10-specimen set from each marble).

2.2. Freeze–Thaw Cycling

Freeze–thaw action is one of the most powerful physical weathering agents, which may cause a rapid change in the mechanical properties of stones and limit their durability. In the freezing process, as well as in almost all other processes concerning the deterioration of stone, water plays a very important role.

For this reason, all 10-specimen sets from 48 marbles, 43 limestones, 9 sandstones and 33 schists/slates start their freeze–thaw cycling tests in a saturated condition according to EN 12371:2010 [18]. Each cycle consisted of a 6 h freezing period in air from +17 °C to −12 °C, followed by a 6 h thawing period in water from −12 °C to +17 °C. This is shown in Figure 2, together with the upper and lower limits allowed for temperature. Specimens were subjected to 48 cycles. After completion, their flexural strength was determined in compliance with EN 12372.

2.3. Thermal Shock

Thermal shock testing is important for measuring the decay of a rock and its resistance to failure from sudden extreme temperature changes over a short period of time. The test procedure was conducted according to EN 14066:2013 [19]. Sets of 10 specimens from 21 marbles were subjected to 20 successive cycles formed by drying and immediate immersion in water, as per the above standard, and finally their flexural strength under a concentrated load was determined according to EN 12372.

2.4. Water Absorption at Atmospheric Pressure and Open Porosity

Water absorption is one of the most important parameters of natural stones, which obviously has a negative impact on various mechanical properties. The test procedure was conducted on six specimens from 66 marbles, 39 limestones and 29 schists/slates, according to EN 13755:2008 [20]. Open porosity is also a very important parameter, which characterizes the natural stone and seems to be highly related to water absorption. As open porosity increases, the water absorption increases too. Thus, the same stone types tested for water absorption were also tested for open porosity, in order to determine the relationship between these two physical properties of marbles, limestones and schists/slates. The test procedure concerning open porosity was performed according to EN 1936:2006 [21].

3. Analysis of the Test Results

The present investigation focuses on the relationship between the strength parameters of dimension stones, being very important as these materials are used in a wide range of applications. The corresponding property values of the tested stones were correlated using the least squares regression method by linear, power or exponential fitting analyses, and the equation with the highest correlation coefficient was selected, either for the overall results or for the “individual” stone types, provided that this selection is physically valid. All calculations were executed by means of Microsoft Office Excel.

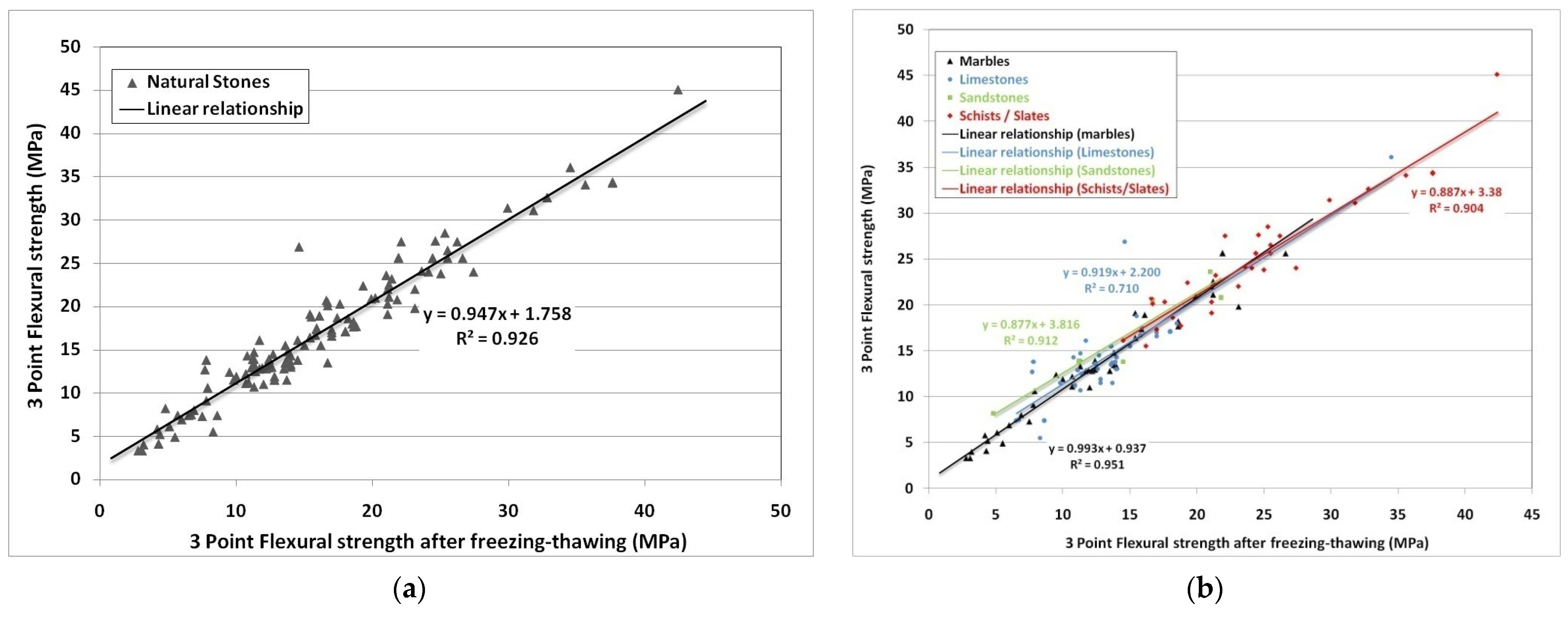
3.1. Relationship between Flexural Strength without and after Freeze–Thaw Cycling

Average values of FS₃ without freeze–thaw action and after 48 freezing–thawing cycles (FTFS₃) were calculated for 48 marbles (33 calcitic and 15 dolomitic), 43 limestones, 9 sandstones and 33 schists/slates. Since there is a direct connection between the two methods, as strength values are derived from both tests, it is possible to associate the corresponding test results. Figure 3a shows that a linear relationship, as expressed by Equation (1), can be fitted to the experimental data with very good correlation (R² = 0.926):

$$F{S}_3=0.947\times FTF{S}_3+1.758,$$

(1)

There is little effect of freeze–thaw action on the flexural strength of the tested stones, resulting in a slight decrease after 48 cycles.

Taking into consideration each “individual” stone type, linear correlation equations were established between the corresponding values of flexural strength determined for limestones, although it indicated a moderate relationship (R² = 0.710) due to their structural diversity, while marbles, sandstones and schists/slates indicated sufficient correlation coefficients, i.e., higher than R² = 0.9, as shown in Figure 3b. According to these results, a negative effect of the 48 freeze–thaw cycles was indicated on the flexural strength of sandstones and schists/slates in particular, despite the fact that surface weathering of the specimens was not observed; the effect on the other stone types seemed to be low.

3.2. Relationship between Flexural Strength without and after Thermal Shock

Tests were conducted on 15 dolomitic and 6 calcitic marbles. The best fit for all the experimental data (R² = 0.917) was achieved through a power Equation (2), as given below and shown in Figure 4a.

It is noted that in this Figure the part of the power curves appears approximately as straight lines within the range of the values involved. Power relationships hold also between the corresponding values FS₃ (flexural strength) and TSFS₃ (flexural strength after thermal shock) when calcitic and dolomitic marbles were separately examined, as shown in Figure 4b.

$$F{S}_3=1.104\times TSF{S}_3^{0.976},$$

(2)

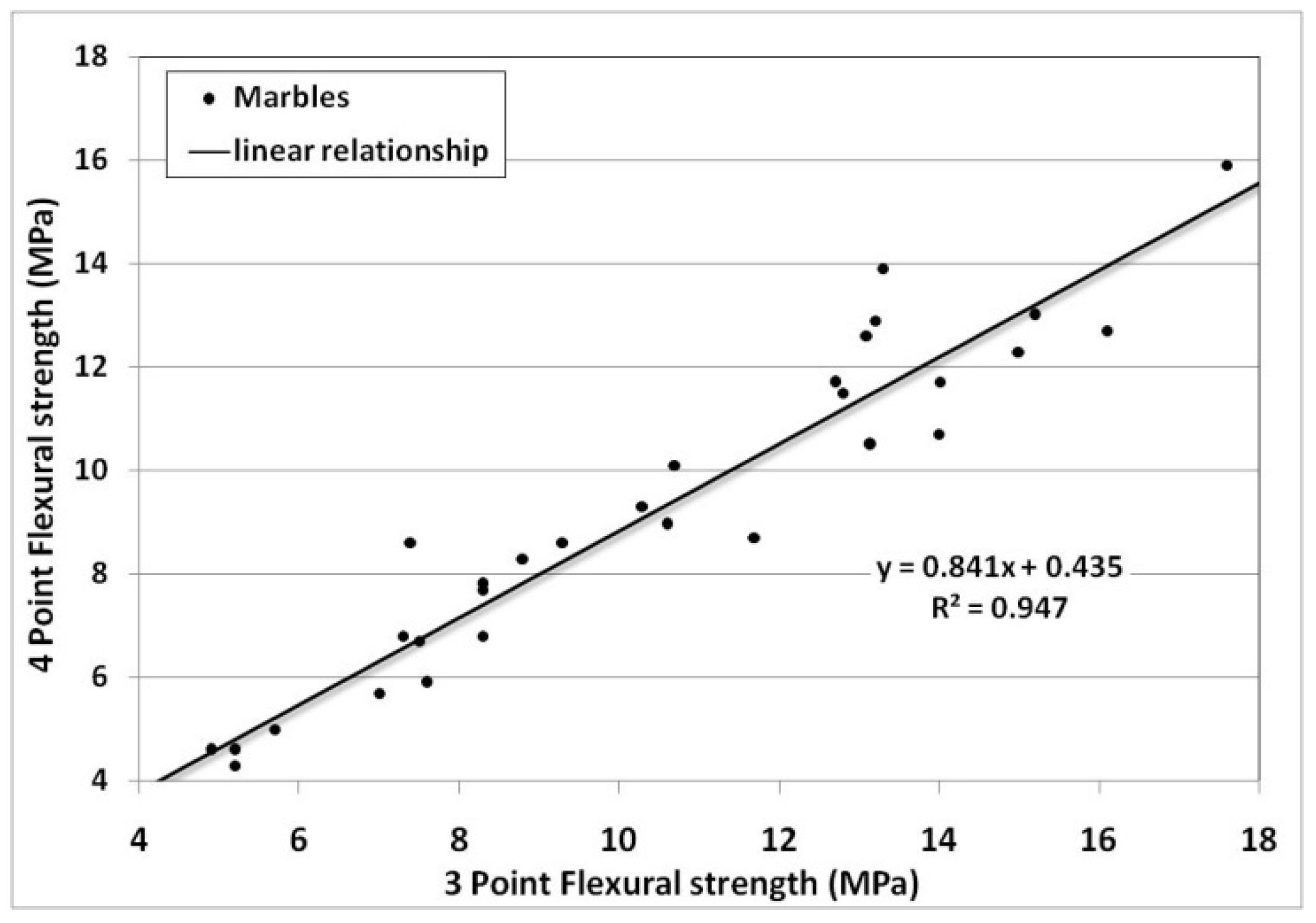
3.3. Relationship between Flexural Strength under a Concentrated Load and under a Constant Moment

Three- and four-point flexural strength tests were carried out for 28 marbles (16 dolomitic and 12 calcitic). Due to its sufficient R² = 0.95, the linear Equation (3), describing the relationship between the corresponding results, may be used as a practical tool for a first estimation of the four-point flexural strength after performing only the simpler three-point test. Four-point flexural strength values calculated were approximately 11% to 13% lower than those derived by the three-point flexural strength test, especially in the case of high strength, shown in Figure 5.

$$F{S}_4=0.84\times F{S}_3+0.435$$

(3)

Çobanoğlu and Çelik [2] collected six Denizli travertine samples in order to correlate three- and four-point flexural strength, resulting in a linear relationship (4) (R² = 0.87), which also indicated a slightly higher flexural strength under a concentrated load:

$$F{S}_4=0.987\times F{S}_3+0.094$$

(4)

3.4. Relationship between Water Absorption and Open Porosity

Average values of open porosity and water absorption at atmospheric pressure were calculated for 66 marbles (53 calcitic and 13 dolomitic), 39 limestones and 29 schists/slates.

A high level of correlation between water absorption (WA) and open porosity (OP) was observed, indicating a linear relationship given in Equation (5) and shown in Figure 6a:

$$WA=0.320\times OP+0.014,$$

(5)

As open porosity increases so does the water absorption. However, the relationship between open porosity and water absorption studied separately on dolomitic marbles, calcitic marbles, limestone and schists/slates indicated low or moderate correlation concerning marbles (R² = 0.52 to 0.55), relatively good for schists/slates (R² = 0.865) and strong for limestones (R² = 0.927). This is explained by the fact that marble values are low and fall in a narrow range; as values become higher and more spread out (from schists/slates to limestones), the correlation is gradually stronger. All derived equations have a linear trend and are presented in Figure 6b.

4. Conclusions

Correlation analyses may be a useful tool for the formulation of models and to highlight the relationship and interdependency ofphysical mechanical properties of ornamental stones.Taking into account the wide range of the stones examined in the presentstudy, as well as the nature of the corresponding data for determining the relationship between certain physical mechanical properties (flexural strength, frost resistance, thermal shock, open porosity and water absorption), the calculated correlation coefficientswere considered sufficient for serving the objective of this work. Freeze–thaw action seemed to have little effect on the flexural strength of natural stones, especially of sandstones and schists/slates, whose strength without being exposed to 48 cycles was quite high. A linear relationship between those strengths was established. Marbles subjected to 20 cycles of thermal shock were found to be negatively affected, and a power relationship between the determined flexural strength values without and after thermal shock was established. The different type of correlation equations established for the above two cases (freeze–thaw vs. thermal shock) is justified by the fact that, in general, a power function describes better more random phenomena (e.g., thermal shock) than the linear one. The nature of thermal shock cycling affects the intragranular and intergranular behavior of specimens, thus causing more randomly expressed fatigue. On the other hand, in freeze–thaw cycling, what is mainly affected is the intragranular behavior of specimens, leading to the decreasing randomness of the relevant fatigue.

The results of this study also revealed a linear relation between flexural strength under a concentrated load and under a constant moment, which led to approximately 11% to 13% higher values derived by the three-point test. Furthermore, it is obvious that there is a direct connection between open porosity and water absorption at atmospheric pressure, hence a high level of an overall correlation was observed between the corresponding values for marbles, limestones and schists/slates.